
A Particle Swarm Optimizer for Solving the Set Partitioning Problem
in the Presence of Partitioning Constraints
Gerrit Anders, Florian Siefert and Wolfgang Reif
Institute for Software & Systems Engineering, Augsburg University, Augsburg, Germany
Keywords:
Set Partitioning Problem, Clustering, Particle Swarm Optimization, Evolutionary Computing.
Abstract:
Solving the set partitioning problem (SPP) is at the heart of the formation of several organizational structures
in multi-agent systems (MAS). In large-scale MAS, these structures can improve scalability and enable coop-
eration between agents with (different) limited resources and capabilities. In this paper, we present a discrete
Particle Swarm Optimizer, i.e., a metaheuristic, that solves the NP-hard SPP in the context of partitioning con-
straints – which restrict the structure of valid partitionings in terms of acceptable ranges for the number and
the size of partitions – in a general manner. It is applicable to a broad range of applications in which regional
or global knowledge is available. For example, our algorithm can be used for coalition structure generation,
strict partitioning clustering (with outliers), anticlustering, and, in combination with an additional control loop,
even for the creation of hierarchical system structures. Our algorithm relies on basic set operations to come to
a solution and, as our evaluation shows, finds high-quality solutions in different scenarios.
1 INTRODUCTION AND
RELATED WORK
In numerous multi-agent systems (MAS), a crucial
step is to establish an organizational structure that
supports the agents’ and system’s objectives (Horling
and Lesser, 2004). Among other things, these struc-
tures allow agents to benefit from the capabilities of
others, thereby increasing their own value of partic-
ipating in the system. In large-scale systems, orga-
nizations are also a way to deal with complexity and
scalability issues, which is often accomplished by the
formation of hierarchies (Steghöfer et al., 2013).
In many cases, these organizations are based on
structures that can be described as a partitioning.
In the set partitioning problem (SPP) (cf. (Chu and
Beasley, 1998)), a set A =
{
a
1
, . . . , a
n
}
of n > 1 agents
a
i
is partitioned into non-empty and pairwise disjoint
subsets, called partitions, that together constitute a
partitioning at minimal cost. Feasible, i.e., valid, par-
titions B =
{
b
1
, . . . , b
m
}
are predefined and finding
the optimal partitioning is NP-hard. In this paper, we
assume that feasible partitions are only constrained
in terms of a minimum s
min
and maximum s
max
size.
This will often result in a very large number of fea-
sible partitions. In the unbounded case, i.e., the com-
plete SPP, there are 2
|A|
−1 partitions and the size of
the search space is given by the nth Bell number B
n
(e.g., B
50
≈ 1.86 · 10
47
), which satisfies Dobi´nski’s
formula (Bender et al., 1999). Thus, the search space
does not only grow exponentially with the number m
of feasible partitions but also with the number n of
agents. Even in a system in which the set of agents A
is not subject to change over time, it would not be
suitable to pre-calculate all feasible partitions in ad-
vance (for |A| = 50, this needs more than one week
on our Xeon machine). To differentiate this specific
problem from the original SPP more clearly, we will
refer to it as the partitioning problem (PP). In contrast
to the SPP’s original definition – in which the costs of
having a partition b
j
included are additive and prede-
fined –, we allow a more flexible objective function in
the PP: We only presume an application-specific met-
ric that evaluates if a partitioning, i.e., a combination
of partitions, is fit for purpose. If the metric specifies
to group similar or dissimilar agents, the PP is equiv-
alent to strict partitioning clustering (with outliers
1
)
or anticlustering
2
(Valev, 1998), respectively. If the
metric defines how well agents can work together on
a common task, the PP is equivalent to coalition struc-
ture generation (cf. (Shehory and Kraus, 1998)).
If an algorithm solves the PP by representing each
a
i
∈ A by a vector g
i
of those attributes of a
i
that are
relevant to solve the PP, it actually has to solve a mul-
1
Supported by a separate partition that holds all outliers.
2
In anticlustering, the resulting partitions are similar.
151
Anders G., Siefert F. and Reif W..
A Particle Swarm Optimizer for Solving the Set Partitioning Problem in the Presence of Partitioning Constraints.
DOI: 10.5220/0005220501510163
In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART-2015), pages 151-163
ISBN: 978-989-758-074-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

tiset partitioning problem (MPP) for the multiset G =
*g
1
, . . . , g
n
+. That is because we might have g
i
= g
j
for two agents a
i
6= a
j
. In the MPP, the multiset sum
U
K∈P
K of all partitions K (here, non-empty multi-
sets) in the partitioning P must equal G. In this paper,
we assume heterogeneous agents so that all vectors g
i
are different (i.e., ∀a
i
, a
j
∈ A : a
i
6= a
j
→ g
i
6= g
j
).
Hence, G is a set and the problem is reduced to a PP.
Algorithms for the solution of the PP in MAS have
a broad area of application, e.g., in sensor networks,
energy management systems, manufacturing systems,
communication systems, or e-commerce: In (You-
nis and Fahmy, 2004), a highly decentralized algo-
rithm is used to assign each sensor node a cluster head
within its communication radius and to allow all clus-
ter heads to communicate with each other. (Anders
et al., 2012) present a decentralized graph-based algo-
rithm, called SPADA, that allows power plants to self-
organize into virtual power plants in order to lower the
time needed to create power plant schedules. In (An-
ders et al., 2011), existing organizational structures
are exploited in form of input/output relations be-
tween agents to guide a decentralized coalition forma-
tion that reconfigures a production cell. (Al Faruque
et al., 2008) show an agent-based clustering approach
for networks on chip that is used to map tasks to pro-
cessing elements. In (Buccafurri et al., 2002), the cos-
tumers of e-commerce websites are categorized into
different profiles on the basis of global knowledge.
Some algorithms that solve instances of the PP,
e.g., those formulated and solved as a linear program-
ming problem, require global system knowledge but
yield optimal solutions (e.g., (Rahwan et al., 2009)).
Because of the PP’s complexity they are often de-
signed as anytime algorithms or distribute this global
knowledge, i.e., the search space, among the agents,
which allows to calculate the utility of all possible
partitions and pick the best one after a global an-
nouncement (e.g., (Shehory and Kraus, 1998)). Other
approaches, such as (Anders et al., 2012) or (Ogston
et al., 2003), rely on local knowledge and solve the
PP in a completely decentralized fashion. While such
strong self-organization approaches can deal with
very large systems (Di Marzo Serugendo et al., 2005),
the lack of regional or global knowledge is some-
times reflected in the solutions’ quality. Especially in
self-organizing hierarchical systems (Steghöfer et al.,
2013), we can often assume that regional knowledge
is available: In such systems, the overall system is
decomposed in a system of systems in which each
subsystem is represented by an intermediary. Since
intermediaries encapsulate the essence of the agents
they control, we can often suppose they have regional
knowledge (i.e., global knowledge with regard to their
subsystem) about their subordinates (Abdallah and
Lesser, 2004). Intermediaries can use this information
to create a suitable partitioning of their subordinates.
Usually, algorithms that solve the PP are either
1) specialized to a specific problem in a specific do-
main or 2) very restrictive with regard to the possibil-
ity to specify mandatory characteristics of the result-
ing partitioning’s structure in the form of the num-
ber and the size of partitions. These properties limit
the algorithms’ applicability. With respect to point
2), most algorithms either do not allow to characterize
valid partitionings at all (e.g., (Ogston et al., 2003)) or
the user or the agents have to be very specific. Using
the well-known k-means clustering algorithm (Mac-
Queen, 1967), for instance, the user has to specify the
number of partitions k exactly. Because a suitable ex-
act number of partitions is often not known (further
drawbacks of k-means, e.g., the formation of parti-
tions of similar size, are discussed in (Äyrämö and
Kärkkäinen, 2006)), there are different approaches
that extend the k-means algorithm by the possibility to
automatically find a suitable number of partitions for
a given data set, such as the x-means algorithm (Ish-
ioka, 2005). In contrast to these approaches, we want
to allow the user or the system itself to specify suit-
able ranges for the number and the size of partitions,
i.e., the minimum n
min
and the maximum n
max
number
of partitions as well as their minimum s
min
and max-
imum s
max
size. These partitioning constraints allow,
e.g., to specify appropriate sizes of subsystems in the
context of compartmentalization in MAS. As men-
tioned at the beginning of this section, compartmen-
talization is a possibility to decompose the complexity
of a system’s task. In (Steghöfer et al., 2013), e.g., the
clustering of power plants into virtual power plants
decreases the time needed to calculate schedules for
them, a task whose complexity depends on the num-
ber of power plants involved. In this example, it is re-
quired that the size of each virtual power plant is not
less than two and below a certain threshold restricting
the maximum time needed for schedule creation.
In this paper, we present PSOPP, a Particle
Swarm Optimizer for the Partitioning Problem.
PSOPP is based on Particle Swarm Optimiza-
tion (PSO) (Kennedy and Eberhart, 1995), a
biologically-inspired computational method and
metaheuristic for optimization in large search spaces.
The application of a metaheuristic is suitable because
of the PP’s complexity. For this reason, a plethora of
metaheuristics solving related problems can be found
in the body of literature: In (Chu and Beasley, 1998),
a genetic algorithm (GA) is used to solve the original
SPP, meaning that the GA needs a pre-calculated
set of feasible partitions. As discussed before, we
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
152

want to avoid this in our approach. In theory, their
GA could also be extended to respect prescribed
ranges for the number of partitions by so-called base
constraints. However, since their GA allows the
generation of invalid solutions, it would not benefit
from a reduced search space and require additional
heuristics for the correction of solution candidates.
Using PSO for data clustering has been proposed
in (Van der Merwe and Engelbrecht, 2003), where
each particle represents a complete solution of the
clustering. In (Alam et al., 2008), the authors present
an evolutionary PSO algorithm in which a new
generation of particles can replace those contributing
to a bad solution to be able to leave local optima.
Importantly, their particles represent partial solutions,
i.e., a single centroid, instead of a complete solution.
In contrast to these and the other afore-mentioned
approaches, PSOPP 1) solves the PP in a general man-
ner and 2) allows to specify and efficiently deal with
suitable ranges for the number as well as the size of
partitions. Our central idea – which could also be
applied to other metaheuristics – is to use basic set
operations to come to a solution. Because we de-
fine these operations in a way that their application
always maintains solution correctness, PSOPP combs
through a search space that only contains correct solu-
tions, which is advantageous with regard to its perfor-
mance. Because PSOPP is initialized with a correct
solution candidate, it is an anytime algorithm. More-
over, PSOPP can be customized to a specific applica-
tion by devising an appropriate fitness function that
assesses the quality of solutions and thus steers the
search for them. Due to these characteristics, PSOPP
can be applied to many different applications in which
solving the PP is relevant and global knowledge is
available. In conjunction with the control loop pre-
sented in (Steghöfer et al., 2013), PSOPP can be used
to establish self-organizing hierarchical system struc-
tures that overcome the drawbacks of strictly weak
self-organization (Di Marzo Serugendo et al., 2005).
The remainder of this paper is structured as fol-
lows: In Sect. 2, we give an introduction to the princi-
ple of PSO and some of its variants for combinatorial
optimization. Afterwards, we present our algorithm,
PSOPP, in Sect. 3. Sect. 4 outlines evaluation results
showing that PSOPP efficiently solves the PP in var-
ious scenarios. Finally, we conclude the paper and
give an outlook on future work in Sect. 5.
2 PARTICLE SWARM
OPTIMIZATION
PSO is a search heuristic for optimization problems.
Its principle is based on the flocking behavior of birds
or schools of fish. Before we present a special form of
PSO that is applicable to discrete optimization prob-
lems, such as the PP, in Sect. 2.2, we explain the basic
idea of PSO in Sect. 2.1.
2.1 General Definition
In the original definition of PSO (Kennedy and Eber-
hart, 1995), a swarm of particles moves around in
an n-dimensional continuous search space in order to
find nearly optimal solutions by iteratively improv-
ing candidate solutions of the optimization problem.
Such a candidate solution is represented by a parti-
cle’s position in the search space. Its quality is rated
by a fitness function: the better the fitness, the better
the solution. To be able to improve the quality of its
solution over time in a target-oriented manner, each
particle Π
i
is aware of its best found solution B
i
and
the best found solution B
N
i
in its neighborhood N
i
. If
a particle’s neighborhood consists of all particles, B
N
i
corresponds to the global best found solution B.
Initially, particles usually start at random posi-
tions. In each iteration, the particles update their po-
sitions and best found solutions. The algorithm termi-
nates, e.g., after a certain amount of iterations or if the
particles converge to a (local) optimum. Its outcome
is the global best found solution B. In detail, a par-
ticle Π
i
determines its position x
i
(t + 1) for the next
iteration t +1 on the basis of its current position x
i
(t)
and its updated velocity v
i
(t +1):
x
i
(t +1) = x
i
(t) + v
i
(t +1) (1)
v
i
(t +1) = ω ·v
i
(t) + c
1
·r
1
·(B
i
−x
i
(t)) (2)
+ c
2
·r
2
·(B
N
i
−x
i
(t))
with ω, c
1
, c
2
∈ R
+
0
, r
1
, r
2
∈ [0, 1],
and ∀t : x
i
(t), v
i
(t), B
i
, B
N
i
∈ R
n
Because v
i
(t + 1) depends on the current velocity
v
i
(t), it embodies a certain inertia. To establish the
right balance between exploitation and exploration, a
particle’s motion in the search space is further influ-
enced by its best found solution B
i
and the best found
solution B
N
i
in its neighborhood N
i
. The particle’s
inertia and its attraction towards B
i
and B
N
i
, i.e., the
trade-off between exploration and exploitation, can be
adjusted by the constants ω, c
1
, and c
2
. The random
numbers r
1
and r
2
are regenerated in every iteration.
2.2 Discrete Particle Swarm
Optimization
PSO as defined in Sect. 2.1 is not applicable to
discrete, e.g., combinatorial, optimization problems,
AParticleSwarmOptimizerforSolvingtheSetPartitioningProbleminthePresenceofPartitioningConstraints
153

such as the PP. (Kennedy and Eberhart, 1997) solve
this dilemma for n-dimensional binary search spaces
by introducing Discrete PSO (DPSO) in which the
positions x
i
(t), B
i
, and B
N
i
are values of the do-
main {0, 1}
n
. While the domain and the defini-
tion of the velocity v
i
(t +1) ∈R
n
are not modified
(see Eq. 2), the semantics of the velocity changes.
In contrast to the original definition, each compo-
nent (v
i
(t +1))
j
∈ R of the vector v
i
(t + 1) represents
a probability that the jth component of the particle’s
position x
i
(t + 1) is either 0 or 1. Eq. 1 therefore be-
comes invalid.
Another DPSO approach, which is called Jump-
ing PSO (JPSO) (Garcia and Perez, 2008), omits the
concept of the velocity as defined in (Kennedy and
Eberhart, 1995). In simplified terms, JPSO redefines
the motion of particles by replacing the linear combi-
nations in Eq. 1 and Eq. 2 by an “either-or” operation
that makes them “jump” through the search space:
x
i
(t +1) =
rdm(x
i
(t)) if r
i
≤ c
rdm
appr(x
i
(t), B
i
) if c
rdm
< r
i
≤ c
∗
B
i
appr(x
i
(t), B
N
i
) if c
∗
B
i
< r
i
≤ c
∗
B
N
i
appr(x
i
(t), B) otherwise
(3)
c
rdm
, c
B
i
, c
B
N
i
, c
B
∈ [0, 1], c
rdm
+ c
B
i
+ c
B
N
i
+ c
B
= 1,
r
i
∈ [0, 1], c
∗
B
i
= c
rdm
+ c
B
i
, c
∗
B
N
i
= c
rdm
+ c
B
i
+ c
B
N
i
Eq. 3 states that a particle Π
i
either makes a ran-
dom move rdm(x
i
(t)) with a probability of c
rdm
or
approaches appr(x
i
(t), β) a specific solution candi-
date β ∈ {B
i
, B
N
i
, B} with a probability of c
B
i
, c
B
N
i
,
or c
B
, respectively. In each iteration, this direction
is determined by a random number r
i
that is gener-
ated individually for each particle. Similarly to Eq. 2,
the constants c
rdm
, c
B
i
, c
B
N
i
, and c
B
stipulate the par-
ticles’ attitude towards exploration and exploitation.
The idea of JPSO has been successfully applied to a
number of high dimensional combinatorial problems
(see, e.g., (Consoli et al., 2010; Seren, 2011)).
3 THE PARTICLE SWARM
OPTIMIZER FOR SOLVING
SET PARTITIONING
PROBLEMS
With regard to our algorithm, PSOPP, each particle
embodies a solution of the PP, i.e., a partitioning of
the set of elements G. PSOPP is inspired by DPSO’s
derivative JPSO (see Sect. 2.2). The motion of parti-
cles is thus not subject to inertia, i.e., x
i
(t + 1) does
not depend on the modifications made to move from
x
i
(t −1) to x
i
(t). In PSOPP, a particle’s motion is
influenced by its best found solution B
i
and the best
found solution B
N
i
in its neighborhood N
i
. This com-
plies with the general definition of PSO outlined in
Sect. 2.1. While we could easily extend PSOPP such
that its particles’ motion is additionally influenced by
the global best solution B – as is the case with the
definition of JPSO (see Sect. 2.2) –, we deliberately
omit this feature for the sake of simplicity. With re-
spect to the definition of JPSO’s behavior in Eq. 3,
this corresponds to a probability of c
B
= 0.
3.1 Constraining Valid Solutions
As stated in Sect. 1, PSOPP allows to specify manda-
tory characteristics of a solution, i.e., partitioning, in
terms of the minimum n
min
and the maximum n
max
number of partitions (1 ≤ n
min
< n
max
≤ |G|) as well
as their minimum s
min
and maximum s
max
size (1 ≤
s
min
< s
max
≤ |G|). These boundaries represent hard
constraints. Obviously, as the possible number and
size of partitions are interconnected, one has to make
sure that the problem is not overconstrained. In case
of G = {g
1
, g
2
, g
3
}, e.g., there is no valid solution if
we set n
min
and s
min
to 2. Either n
min
or s
min
would
have to be relaxed, i.e., set to 1. Because we define
PSOPP’s operations for the particles’ motion in a way
that always preserves the correctness of solution can-
didates with respect to the constraints, partitionings
that do not meet them are not represented in the search
space. As we show in our evaluation in Sect. 4, suit-
able boundaries can thus lower the time needed to find
high-quality solutions. In the following, we call these
boundaries partitioning constraints.
3.2 The Algorithm’s Basic Procedure
Having defined valid partitionings by means of
n
min
, n
max
, s
min
, s
max
as well as the particles’ attitude
towards exploration and exploitation by fixing the
constants c
rdm
, c
B
i
, c
B
N
i
, PSOPP creates a predefined
number of particles at random or predetermined posi-
tions (the set of particles does not change at runtime).
The latter is especially suitable when a reorganization
of an existing system structure has to take place: If the
current structure does not contradict the partitioning
constraints, it can be used as a starting point for the
self-organization process. Mixing predefined and ran-
domly generated initial partitionings allows to hold up
diversity. When searching for an initial system struc-
ture, particles are created at random positions.
The position x
i
(t) of each particle Π
i
represents
a partitioning P (in the following, we use P syn-
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
154

Update Best
Found Solution in
Neighborhood
Evaluate
Termination
Criterion
Update
Personal Best
Found Solution
Evaluate
Fitness
Apply Move
Operation
Determine
Move Operation
[else]
[fitness > f(personalBest)]
[else]
[isTermination
CriterionMet]
Figure 1: Actions performed by particles in each iteration.
onymous for x
i
(t)) that consists of |P | partitions
(n
min
≤|P |≤n
max
). Every partition K ∈P consists of
s
min
≤|K| ≤ s
max
elements. All particles concurrently
explore the search space in search of better solutions
by modifying their current positions (at random or by
approaching other solutions) as long as a specific ter-
mination criterion is not met. For this purpose, in each
iteration, a particle Π
i
performs the following actions
that are also depicted in Fig. 1:
1. Evaluate the fitness f (P ) of the represented parti-
tioning P. The fitness function corresponds to the
“metric” used in the PP’s definition in Sect. 1.
2. If the particle’s fitness f (P ) is higher than the fit-
ness f (B
i
) of its best found solution B
i
, set B
i
to P
and inform other particles Π
j
with Π
i
∈ N
j
about
the improvement so that they can update their best
found solution B
N
j
in their neighborhood N
j
.
3. Update the best found solution B
N
i
in the parti-
cle’s neighborhood N
i
.
4. Stop if the termination criterion is met.
5. Otherwise, opt for the direction in which to move
by randomly generating r
i
∈[0, 1] (see Eq. 3), i.e.,
choose whether a random move or an approach
operation should be applied. In case of an ap-
proach operation, r
i
also determines the position
that should be approached (see Eq. 3).
6. Determine the new position P
0
by applying the se-
lected move operation to P .
Once all particles terminated, PSOPP returns the
best found solution B. Possible termination criteria
are, e.g., a predefined amount of time, a predefined
number of iterations (i.e., moves through the search
space), a predefined threshold for the minimum fit-
ness value, or a combination of these criteria.
3.3 Similarity of Partitionings
The purpose of an approach operation is to increase
the similarity of two partitionings P and Q by assim-
ilating characteristics from Q into P . With regard to
the search space, the intention is that the particle rep-
resenting P might find better solutions in the neigh-
borhood of Q . In this section, we define the similar-
ity of partitionings based on a definition by (Kudo and
Murai, 2009). Note that the similarity does not give
an indication of how many operations/moves are nec-
essary to transfer one partitioning into another (i.e., to
move from one position to another). Instead, it com-
pares partitionings with regard to their composition.
According to (Kudo and Murai, 2009), we base the
definition of the similarity of two partitionings P , Q
on the definition of a refinement and the intersection
of two partitionings.
Definition (Refinement). Partitioning P is a refine-
ment ref (P , Q ) of partitioning Q if and only if all
partitions K ∈ P are subsets of partitions L ∈Q :
ref (P , Q ) :⇔∀K ∈ P : ∃L ∈Q : K ⊆ L (4)
Hence, if P is a refinement of Q , P does not con-
tain less partitions than Q (i.e., |P | ≥ |Q |). For in-
stance, P = {{g
1
, g
2
}, {g
3
}, {g
4
}} is a refinement of
Q = {{g
1
, g
2
, g
3
}, {g
4
}}.
Definition (Intersection of Partitionings). The inter-
section P ∩Q of two partitionings P , Q is the set of
all non-empty intersections of partitions in P and Q :
P ∩Q :⇔ {K ∩L |K ∈ P ∧L ∈ Q ∧K ∩L 6=
/
0}
Note that the intersection P ∩Q is always a re-
finement of P and Q . For example, the intersec-
tion R ∩Q = {{g
1
, g
2
}, {g
3
}, {g
4
}}, which equals
P in the example above, is a refinement of R =
{{g
1
, g
2
}, {g
3
, g
4
}} and Q = {{g
1
, g
2
, g
3
}, {g
4
}}.
Definition (Similarity of Partitionings). The similar-
ity sim(P , Q ) ∈ ]0, 1] of two partitionings P , Q is
based on the ratio of the sum of their cardinalities to
the cardinality of their intersection:
sim(P , Q ) :=
|P |+ |Q |
2 ·|P ∩Q |
The intention of this definition of similarity is the
following: If the elements of a partition K ∈ P are
distributed over multiple partitions in Q , the similar-
ity decreases with the cardinality of the intersection
P ∩Q . So the more elements are in the same par-
titions in P and Q (i.e., the more elements consti-
tute the partitions’ intersection), the smaller |P ∩Q |
and thus the more similar the partitionings. In other
words, the intersection P ∩Q (i.e., the refinement)
should be as similar as possible to the two given parti-
tionings. Resulting from this definition, sim(P , Q ) =
1 if and only if P = Q , because then P ∩Q = P =
Q . While not required, note that this definition of
similarity does not allow to compare two similarity
values sim(P , Q ) and sim(R , S ) if they stem from
four different partitionings. Regarding the two ex-
amples above, sim(R , Q ) =
2+2
2·3
=
4
6
is smaller than
sim(P , Q ) =
3+2
2·3
=
5
6
since P is a refinement of Q .
AParticleSwarmOptimizerforSolvingtheSetPartitioningProbleminthePresenceofPartitioningConstraints
155

Based on these definitions, we show that the op-
erations enabling particles to approach each other al-
ways increase the similarity of the represented parti-
tionings (see Sect. 3.5). Before we explain these oper-
ations in detail, we introduce the basic operations by
means of random moves in the search space.
3.4 Random Moves in the Search Space
The motion of particles is a key factor in PSO be-
cause it is the only measure to find better solution
candidates. As a solution of the PP is a partitioning
(that is a set of sets), the motion of particles in the
search space can be realized by the two set operations
split and join (Apt and Witzel, 2007). In each itera-
tion, each PSOPP particle makes exactly one move,
either in a random direction or by approaching a spe-
cific position in the search space in a target-oriented
manner (see Sect. 3.5). The corresponding operator
is randomly selected. In this section, we concentrate
on random moves, i.e., operators that modify the par-
titioning at random. In case the selected operator can-
not be applied without violating a constraint, another
operator is chosen. Because of the partitioning con-
straints, there are situations in which neither the split
nor the join operator can be applied. For such situa-
tions, we introduce an additional exchange operation.
Unless otherwise stated, we use P
∗
=
{{g
1
, g
2
, g
4
, g
5
}, {g
3
, g
6
}, {g
7
, g
8
}} with s
min
= 2,
s
max
= 4, n
min
= 2, and n
max
= 3 to illustrate the
operators’ application in our examples.
Random Split. The split operation divides a ran-
domly splitable partition K ∈ P into two new non-
empty disjoint partitions L and M such that K =
L ∪ M. For the resulting partitioning P
0
, we have
P
0
= (P \{K}) ∪{L, M}. Note that a split operation
can only be applied if the original partitioning K is
big enough, i.e., if |K| ≥ 2 ·s
min
. That is because the
resulting partitions L and M both have to fulfill the
minimum size constraint, i.e., |L|, |M|≥s
min
. Further-
more, because the split operation increases the num-
ber of partitions |P
0
| of the resulting partitioning P
0
compared to the original partitioning P by one (i.e.,
|P
0
| = |P |+ 1), it can only be applied if the number
of partitions |P | in P is below the maximum num-
ber of partitions n
max
. That way, it is ensured that P
0
also complies with n
max
. Summarizing, the set of ran-
domly splitable partitions σ
rdm
(P ) is defined as:
σ
rdm
(P ) :⇔{K | K ∈ P ∧|K| ≥ 2 ·s
min
∧|P | < n
max
}
In our example P
∗
, only K
∗
= {g
1
, g
2
, g
4
, g
5
} is
randomly splitable, resulting, e.g., in a partitioning
P
∗
0
= {{g
1
, g
2
}, {g
4
, g
5
}, {g
3
, g
6
}, {g
7
, g
8
}}.
Random Join. The join operation merges a ran-
domly joinable partition K ∈ P and a randomly join-
able counterpart L ∈P into a single new partition M
such that K ∪L = M. For the resulting partitioning
P
0
, we have P
0
= (P \{K, L}) ∪{K ∪L}. Because
the resulting partition M has to meet the maximum
size constraint, L must be a partition that can be in-
tegrated into K without exceeding the maximum al-
lowed size, i.e., |K|+ |L| ≤ s
max
. Since the join op-
erator decreases the number of partitions in the re-
sulting partitioning P
0
by one, the operator can fur-
ther only be applied if P features a sufficient num-
ber of partitions, i.e., if |P | > n
min
. Otherwise, P
0
would violate the minimum number of partitions con-
straint. Summarizing, the sets of randomly joinable
partitions ι
rdm
(P ) and randomly joinable counter-
parts ι
rdm
(K, P ) are defined as follows:
ι
rdm
(P ) :⇔ {K | K ∈ P ∧ι
rdm
(K, P ) 6=
/
0
∧|P | > n
min
}
ι
rdm
(K, P ) :⇔ {L |L ∈P ∧|K|+ |L| ≤ s
max
∧K 6= L}
With regard to our example P
∗
, randomly join-
able partitions are L
∗
= {g
3
, g
6
} and M
∗
= {g
7
, g
8
}
with randomly joinable counterparts {M
∗
} and
{L
∗
}, respectively. Merging L
∗
and M
∗
yields
P
∗
0
= {{g
1
, g
2
, g
4
, g
5
}, {g
3
, g
6
, g
7
, g
8
}}.
Random Exchange. Obviously, there are situations
in which neither the split nor the join operator can be
applied (particles must not violate the constraints tem-
porarily since the search space only contains valid so-
lutions). For example, if s
min
and s
max
or n
min
and n
max
are equal, not a single particle is able to make a move
using the split or the join operation: For instance, con-
sider a set of elements G = {g
1
, . . . , g
6
}, boundaries
s
min
= 2, s
max
= 4, n
min
= 2, and n
max
= 2, and a par-
titioning P = {{g
1
, g
2
, g
3
}, {g
4
, g
5
, g
6
}}. But even if
s
min
6= s
max
and n
min
6= n
max
, specific combinations of
s
min
, s
max
, n
min
, and n
max
can cause individual particles
to freeze, e.g., if we replace n
max
= 2 by n
max
= 3 in
our example. To prevent the particles from becoming
jammed, we additionally introduce an exchange op-
erator that atomically swaps some of the elements of
two partitions.
The exchange operation interchanges the proper
subset
ˆ
K ⊂ K (with
ˆ
K 6=
/
0) and the subset
ˆ
L ⊆ L (
ˆ
L is
allowed to be the empty set
/
0) between a randomly
exchangeable partition K ∈ P and a randomly ex-
changeable counterpart L ∈ P . Using the non-empty
proper subset
ˆ
K of K avoids that the operation has no
effect at all (as would be the case if all or no elements
of K were integrated into L and vice versa). We delib-
erately allow
ˆ
L to be empty in order to handle situa-
tions as given in the example above: Regarding parti-
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
156

tioning P = {{g
1
, g
2
, g
3
}, {g
4
, g
5
, g
6
}}, we can sim-
ply move
ˆ
K = {g
3
} from K = {g
1
, g
2
, g
3
} into L =
{g
4
, g
5
, g
6
}. If we did not allow
ˆ
L =
/
0, we would have
to perform multiple consecutive exchange operations
to achieve the same result. With respect to the exam-
ple, we would need two operations, e.g., by exchang-
ing {g
2
, g
3
} and {g
4
}, and finally {g
4
} and {g
2
}.
Basically, the exchange operation corresponds to a
join that is followed by a split. Since
ˆ
K is a non-empty
proper subset of K, as the split operation, it yields two
non-empty partitions. Because an exchange between
two partitions of size one would contradict this char-
acteristic or not have any effect, we define the sets of
randomly exchangeable partitions ε
rdm
(P ) and ran-
domly exchangeable counterparts ε
rdm
(K, P ) as:
ε
rdm
(P ) :⇔ {K | K ∈ P ∧|K|> 1}
ε
rdm
(K, P ) :⇔ P \{K}
When integrating an arbitrary non-empty subset
ˆ
K ⊂
K into L,
ˆ
K as well as the subset
ˆ
L ⊆ L that is in-
tegrated into K must be specified in a way that the
condition |K
0
|, |L
0
| ∈ [s
min
, s
max
] holds for the result-
ing partitions K
0
, L
0
. More precisely, while the size
of
ˆ
K is randomly chosen between 1 and |K| − 1
to ensure that
ˆ
K is a non-empty proper subset of
K, valid cardinalities of
ˆ
L are subject to |
ˆ
K|. In
detail, |
ˆ
L| ≤ min{|L|, min{(|L| + |
ˆ
K|) − s
min
, s
max
−
(|K| − |
ˆ
K|)}} and |
ˆ
L| ≥ max{max{0, s
min
− (|K| −
|
ˆ
K|)}, (|L| + |
ˆ
K|) − s
max
} must hold for the ran-
domly determined set
ˆ
L to guarantee that the re-
sulting partitioning P
0
= (P \ {K, L}) ∪ {(K \
ˆ
K) ∪
ˆ
L, (L \
ˆ
L) ∪
ˆ
K} respects s
min
and s
max
. In our exam-
ple P
∗
, we can, e.g., exchange
ˆ
K
∗
= {g
1
, g
2
, g
5
} and
ˆ
M
∗
= {g
7
} between K
∗
and L
∗
, resulting in P
∗
0
=
{{g
4
, g
7
}, {g
3
, g
6
}, {g
1
, g
2
, g
5
, g
8
}}. If all partitions
are singletons (i.e., if |P | = |G|), it is not possible to
apply the random exchange operator since ε
rdm
(P ) =
/
0. In such a case, PSOPP tries to apply either the ran-
dom split or the random join operator.
These three operations allow to create new or dis-
solve existing partitions or exchange elements be-
tween them while maintaining the properties of a par-
titioning and complying with the partitioning con-
straints (see Sect. 3.1). In this section, we focused
on random moves, where we cannot make any state-
ment with regard to the change in similarity to another
partitioning. In the next section, we explain how par-
ticles use the basic split, join, and exchange operators
to approach a specific position in the search space.
3.5 Approach of Other Particles
When a particle Π
i
approaches B
i
or B
N
i
, we en-
sure that the similarity of the modified partitioning P
and the approached partitioning Q ∈ {B
i
, B
N
i
} is in-
creased. Recalling the definition of the similarity
(see Sect. 3.3), this can, among other possibilities, be
achieved by increasing |P |, i.e., the number of parti-
tions in P without changing |P ∩Q | at all, or decreas-
ing |P ∩Q | (note that a decrease of |P ∩Q | might
come along with a decrease of |P |). The former can
be obtained by splitting a partition that contains ele-
ments that are members of two or more partitions in
Q , whereas the latter can be obtained by merging two
partitions that both contain elements that are mem-
bers of a single partition in Q . In contrast to random
moves, the applicability of the approach operations
does not only depend on P ’s cardinality and the size
of its partitions but also on P ’s and Q ’s composition.
Obviously, an approach is not possible if P = Q .
Unless otherwise stated, we use a partition-
ing P
∗
= {{g
1
, g
2
, g
4
, g
5
}, {g
3
, g
6
}, {g
7
, g
8
}} that ap-
proaches Q
∗
= {{g
1
, g
2
}, {g
4
, g
6
, g
7
}, {g
3
, g
5
, g
8
}}
with s
min
= 2, s
max
= 4, n
min
= 2, and n
max
= 4 to
illustrate the operators’ application in our examples.
Approach Split. Analogously to the definition of
σ
rdm
(P ), this operator can only be applied if |P | <
n
max
. Furthermore, a partition K must fulfill |K| ≥
2 ·s
min
to be contained in the set of splitable parti-
tions σ(P , Q ). Here, this property results from the
definition of extractable subsets σ
↑
(K, P , Q ):
σ(P , Q ) :⇔ {K | K ∈ P ∧σ
↑
(K, P , Q ) 6=
/
0
∧|P | < n
max
}
σ
↑
(K, P , Q ) :⇔ {L |L ∈(P ∩Q ) ∧L ⊂ K
∧|K \L| ≥ s
min
∧|L| ≥ s
min
}
An extractable subset L ∈ σ
↑
(K, P , Q ) is thus a
proper subset of K ∈ P , i.e., with respect to Q , K
contains further elements that are not contained in
the same partition as the elements in L. Hence,
the split operator cannot be applied to approach an-
other particle if all partitions in P are subsets of par-
titions in Q , i.e., if P is a refinement of Q (see
Eq. 4). For the resulting partitioning, we have P
0
=
(P \{K}) ∪ {K \ L, L}. Extracting the set L from
K increases the similarity between P and Q be-
cause |P
0
| = |P | + 1, Q is not changed, and P
0
∩
Q = P ∩Q , i.e., the intersection of the partition-
ings does not change either. With regard to P
∗
and
Q
∗
, K
∗
= {g
1
, g
2
, g
4
, g
5
} is the only splitable parti-
tion with extractable subset L
∗
= {g
1
, g
2
} (L
∗
is the
only element of σ
↑
(K
∗
, P
∗
, Q
∗
)). A split results in
P
∗
0
= {{g
1
, g
2
}, {g
4
, g
5
}, {g
3
, g
6
}, {g
7
, g
8
}}.
Approach Join. As before, a join can only be
applied if |P | > n
min
. Similarly to the defini-
tion of randomly joinable partitions, joinable parti-
AParticleSwarmOptimizerforSolvingtheSetPartitioningProbleminthePresenceofPartitioningConstraints
157

tions ι(P , Q ) are those partitions for which joinable
counterparts ι
(K, P , Q ) exist:
ι(P , Q ) :⇔ {K | K ∈ P ∧ι
(K, P , Q ) 6=
/
0
∧|P | > n
min
}
ι
(K, P , Q ) :⇔ {L |L ∈ P ∧|K|+ |L| ≤ s
max
∧K 6= L ∧∃M ∈ Q : (M ∩K 6=
/
0 ∧M ∩L 6=
/
0)
| {z }
C
}
Please note that the definition of joinable counter-
parts ι
(K, P , Q ) is very similar to the definition of
randomly joinable counterparts ι
rdm
(K, P ). To ensure
that P approaches Q , we introduce an additional con-
dition C that implies M * K because M does not only
contain elements of K but also of L (with M ∈ Q and
K, L ∈P ). That way, we bring together elements that
are in a single partition in Q but spread over two or
more partitions K, L in P . Note that Q cannot be ap-
proached by a join if all partitions in P are super-
sets of partitions in Q , i.e., if Q is a refinement of
P (see Eq. 4). For the resulting partitioning, we have
P
0
= (P \{K, L}) ∪{K ∪L}. The similarity between
P and Q is increased because |P
0
| = |P|−1, Q is
not changed, and |P
0
∩Q | ≤ |P ∩Q |−1. Note that
we have to write “≤” since K and L might both con-
tain elements that are contained in a further partition
M
0
∈ Q with M
0
6= M. With regard to P
∗
and Q
∗
,
K
∗
= {g
3
, g
6
} and L
∗
= {g
7
, g
8
} are joinable parti-
tions with counterparts L
∗
and K
∗
, respectively. A join
results in P
∗
0
= {{g
1
, g
2
, g
4
, g
5
}, {g
3
, g
6
, g
7
, g
8
}}.
Approach Exchange. If neither a split nor a join can
be used to approach a partitioning Q 6= P , PSOPP
falls back on the exchange operator that swaps one or
more elements between a partition K contained in the
set of exchangeable partitions ε(P , Q ) and one of K’s
exchangeable counterparts ε
(K, P , Q ):
ε(P , Q ) :⇔ {K | K ∈ P ∧ε
(K, P , Q ) 6=
/
0}
ε
(K, P , Q ) :⇔ {L |L ∈ P ∧K 6= L ∧∃M ∈ Q :
∃
ˆ
K ⊂ K :
ˆ
K ∩M 6=
/
0 ∧L ∩M 6=
/
0 ∧
ˆ
K ∈ 2
P ∩Q
∧
∃
ˆ
L ⊆L :
ˆ
L ∩M =
/
0 ∧
ˆ
L ∈2
P ∩Q
∧s
min
≤ |(K \
ˆ
K) ∪
ˆ
L| ≤ s
max
∧s
min
≤ |(L \
ˆ
L) ∪
ˆ
K| ≤ s
max
Note that
ˆ
K ∩M 6=
/
0∧L∩M 6=
/
0 implies that K as well
as L contain elements that are contained in the same
partition M ∈Q and should be brought together by the
exchange operation. Also note that
ˆ
L ⊆L might be an
empty set
/
0, whereas
ˆ
K ⊂ K is always non-empty.
On the one hand,
ˆ
K ⊂ K and
ˆ
K ∈ 2
P ∩Q
(2
P ∩Q
denotes the power set of P ∩Q ) ensure that we in-
crease the similarity of P and Q when integrating
ˆ
K into L. That is because we leave |P | and |Q | un-
changed and reduce |P ∩Q | by ≥ 1. On the other
hand, since
ˆ
L represents the elements that should be
integrated back into K,
ˆ
L ∩M =
/
0 ensures that we
merge elements of M. Further,
ˆ
L ∈ 2
P ∩Q
ensures that
we do not spread a set of elements V ∈ (P ∩Q ) (V
is thus contained in a single partition in P and Q )
over K and L by merging
ˆ
L into K. This has to be
avoided because it would decrease the similarity of P
and Q . The conditions s
min
≤ |(K \
ˆ
K) ∪
ˆ
L| ≤ s
max
and s
min
≤ |(L \
ˆ
L) ∪
ˆ
K| ≤ s
max
restrict the size of the
resulting partitions to the allowed range.
For the resulting partition, we have P
0
= (P \
{K, L}) ∪{(K \
ˆ
K) ∪
ˆ
L, (L \
ˆ
L) ∪
ˆ
K}. The similarity
between P and Q is increased because |P
0
| = |P |, Q
is not changed, and |P
0
∩Q | ≤ |P ∩Q | −1. With
regard to P
∗
and Q
∗
, e.g., K
∗
= {g
1
, g
2
, g
4
, g
5
} is
an exchangeable partition with exchangeable coun-
terparts L
∗
= {g
3
, g
6
} and M
∗
= {g
7
, g
8
}. For in-
stance, we can exchange
ˆ
K
∗
= {g
4
} and
ˆ
L
∗
=
/
0
between K
∗
and L
∗
by which we obtain P
∗
0
=
{{g
1
, g
2
, g
5
}, {g
3
, g
4
, g
6
}, {g
7
, g
8
}}.
However, there are situations in which the ex-
change operator cannot be applied: For example, con-
sider a partitioning Q = {N, O, P}, where each parti-
tion has a cardinality of 100 and s
min
= s
max
= 100. A
partitioning P = {K, L, M} cannot approach Q , e.g.,
if K contains 39, 27, and 34, L contains 25, 40, and 35,
and M contains 36, 33, and 31 elements of N, O, and
P, respectively. In such situations, one might relax the
constraint
ˆ
L ∈ 2
P ∩Q
to
ˆ
L = U ∪V , where U ∈ 2
P ∩Q
and V ⊂W ∈(P ∩Q ). While this relaxation allows to
apply the operator in each situation, it only guarantees
to not decrease the similarity of P and Q because we
spread the elements of W over two partitions.
4 EVALUATION
In our evaluation, we analyze PSOPP’s performance
in various scenarios: We 1) identify suitable values
for c
rdm
, c
B
i
, c
B
N
i
, 2) investigate the influence of the
numbers of elements |G| and particles on PSOPP’s
performance with regard to the quality of the result
and the number of moves particles perform, 3) ex-
amine PSOPP’s convergence, 4) compare its behav-
ior with less and more constrained partitionings on
the basis of the partitioning constraints introduced in
Sect. 3.1, 5) make these investigations for clustering
as well as anticlustering, and 6) compare our results
to those achieved with IBM ILOG CPLEX
3
and an
x-means implementation
4
as, to the best of our knowl-
3
IBM ILOG CPLEX Optimizer, Version 12.4, 2011:
http://www-01.ibm.com/software/commerce/optimization/
cplex-optimizer/
4
Weka, Version 3.6: http://weka.sourceforge.net
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
158

edge, there is no other renowned algorithm supporting
more of our partitioning constraints out of the box.
Where not otherwise stated, we performed 500
simulation runs for each evaluation scenario. All pre-
sented results are average values. For evaluation, we
used a Java implementation of PSOPP in which each
particle runs in its own thread, thereby allowing for
the parallel examination of the search space. Because
we expected PSOPP to achieve good results with a
relatively small number of particles, we used particle
neighborhoods N
i
that contain all particles in the sys-
tem. As mentioned in Sect. 2.1, B
N
i
thus corresponds
to B. In each setting, the examined algorithms solved
the PP for a set of elements G = {0, 1, 2, . . . , n}, where
n = |G| is the number of elements to partition.
All evaluation scenarios were performed for both
clustering as well as anticlustering (see Sect. 1). In
both cases, the goal is to maximize the fitness. In case
of clustering, we therefore use the negative Euclidean
distance (this corresponds to the “classic” k-means
distance measure) as fitness value. To assess the fit-
ness of a partitioning in case of anticlustering, for
each partition, we calculate the mean of the contained
elements. As the goal is to have homogeneous clus-
ters of heterogeneous elements, i.e., to equalize these
mean values, the standard deviation σ
part
of the mean
values should be minimized. Because we can normal-
ize the elements’ values to the interval [0, 1], σ
part
is
between 0 and
√
0.5. We thus define a partitioning’s
fitness F
anti
(σ
part
) in case of anticlustering as follows:
F
anti
(σ
part
) =
1
σ
part
+1
−
1
1
√
2
+1
·
1 −
1
1
√
2
+1
−1
F
anti
(σ
part
) monotonically decreases on the interval
[0,
√
0.5]. We have F
anti
(0) = 1 for optimal partition-
ings where each partition has the same mean value,
and F
anti
(
√
0.5) = 0 for the maximum σ
part
. Because
we expect PSOPP to perform well, F
anti
(σ
part
) is par-
ticularly sensitive to changes when σ
part
is small.
Where not otherwise stated, we used a time limit
of 10s as termination criterion. Further, apart from
s
min
= 2 (i.e., each partition has to consist of more
than one element) and n
min
= 2, which prevents the
“grand coalition”, we did not restrict valid partition-
ings (i.e., s
max
= n, n
max
=
n
2
). As discussed in Sect. 1,
such restrictions enable hierarchical decomposition.
The influence of restrictions on PSOPP’s behavior is
examined in a separate scenario.
Identification of Suitable Parameters. First, we
identified suitable parameter sets for different num-
bers of elements n ∈ {100, 500, 1000} and particles
#P ∈ {4, 16} for clustering as well as anticluster-
ing. Values for c
rdm
, c
B
i
, and c
B
were taken from
0.0
0.2
0.4
0.6
0.8
1.0
-40
-35
-30
-25
-20
-15
-10
-5
0
0.0
0.2
0.4
0.6
0.8
1.0
Fitness x 10
6
c
Bi
c
rdm
Figure 2: Parameter search: fitness achieved with PSOPP
when partitioning 1000 elements using the k-means fit-
ness function and 4 particles with different combinations
of c
rdm
, c
B
i
, c
B
. Results are averaged over 100 runs.
the set {0.0, 0.1, 0.2, . . . , 1.0}. For each combination,
we performed 100 simulation runs. The results for
clustering with #P = 4 and n = 1000 are depicted in
Fig. 2. The plateau of moderate to good fitness values
for 0.0 < c
rdm
< 0.5 indicates the trade-off between
exploration and exploitation. In case of clustering,
c
rdm
= 0.3, c
B
i
= 0.0, and c
B
= 0.7 turned out to be
useful parameters for all combinations of n and #P.
For anticlustering, c
rdm
= 0.2, c
B
i
= 0.7, and c
B
= 0.1
are suitable parameters. Consequently, approaching
B
i
is far more important for anticlustering than clus-
tering. We assume that the fitness landscape of an-
ticlustering contains more spikes that are worth to
be explored in more detail, while clustering requires
all particles to work together in order to improve a
specific solution candidate (less but more prominent
spikes in the fitness landscape). In both cases, the
greater n, i.e., the problem to solve, the more im-
portant the parametrization. Furthermore, we exam-
ined the effect of allowing particles to apply a random
move operator if an approach is not possible. In case
of clustering, this feature yields to a very high robust-
ness with regard to different values for c
rdm
, c
B
i
, c
B
:
For #P = 4 and n = 1000, for instance, the fitness im-
proves by an average of 51.65% (standard deviation
σ = 50.76%) for 0.0 < c
rdm
< 0.5, and by 21.67% for
the best parametrization. With regard to anticluster-
ing, we could not observe such an increase in robust-
ness. In contrast, the fitness values slightly decrease
by an average of 0.39% (σ = 1.33%). We used the
identified parameters in our following investigations.
Influence of the Number of Elements to Partition.
We evaluated the influence of n for the set of problem
sizes N = {100, 250, 500, 1000, 2000, 3000, 4000}.
As shown in Table 1, an increase of n comes along
with a decrease in the no. of moves particles make in
AParticleSwarmOptimizerforSolvingtheSetPartitioningProbleminthePresenceofPartitioningConstraints
159

Table 1: Selected clustering and anticlustering results obtained with PSOPP using a time limit of 10s for different values of
the number of elements and particles. All values are averages over 500 runs. Values in parentheses denote standard deviations.
clustering anticlustering
#Elements 250 500 1000 1000 3000
#Particles 4 32 4 32 4 32 4 32 4 32
Optimal Fitness -62.50 -125.00 -250.00 1.00 1.00
Fitness −78.16
(6.14)
−106.88
(12.23)
−3694.88
(440.71)
−95462.66
(15732.15)
−1.10·10
6
(1.12 ·10
5
)
−2.25·10
7
(2.26 ·10
6
)
1.00
(0.00)
1.00
(0.00)
0.96
(0.08)
0.99
(0.03)
#Partitions 121.43
(1.33)
121.81
(1.37)
242.82
(2.43)
243.44
(2.98)
478.67
(7.59)
468.55
(7.78)
2.03
(0.67)
2.01
(0.12)
147.21
(259.87)
24.56
(48.55)
Partition Size 2.06
(0.25)
2.05
(0.22)
2.06
(0.24)
2.05
(0.23)
2.09
(0.29)
2.06
(0.23)
492.61
(322.56)
496.52
(320.91)
20.38
(166.51)
122.17
(402.50)
#Total Moves
[in 1000]
690.16
(12.14)
509.69
(8.84)
292.85
(3.69)
176.73
(8.93)
90.22
(2.31)
102.74
(13.60)
212.10
(34.47)
224.29
(20.99)
54.36
(22.67)
63.33
(8.49)
#Rdm. Moves
[in 1000]
321.34
(6.28)
219.13
(4.73)
134.09
(1.72)
59.97
(2.47)
38.58
(0.93)
31.37
(3.97)
89.42
(21.20)
113.32
(16.31)
24.94
(10.31)
35.88
(5.12)
#Appr Moves
[in 1000]
368.81
(5.90)
290.57
(4.62)
158.76
(2.07)
116.76
(6.56)
51.65
(1.49)
71.37
(9.63)
122.68
(20.21)
110.97
(12.70)
29.43
(13.82)
27.45
(4.41)
#Moves/Particle
[in 1000]
172.54
(3.06)
15.93
(0.94)
73.21
(0.99)
5.52
(0.49)
22.56
(0.78)
3.21
(0.65)
53.03
(10.99)
7.01
(6.82)
13.59
(10.58)
1.98
(2.22)
the search space in clustering as well as anticluster-
ing. Evidently, that is because the application of move
operators (especially the approach operators) needs
more time. Since the size of the search space grows
exponentially with n (see Sect. 1), it is therefore not
surprising that the achieved fitness drops with greater
n (please note that, in case of clustering, the fitness
values cannot be compared between two runs with
different n): While PSOPP obtains good results for
n = 100 and moderate fitness values for n = 250 (only
16.60% and 25.06% worse than the optimal fitness,
respectively) in case of clustering, we need a higher
time limit (i.e, more than 10s) for n ≥500 (see conver-
gence evaluation). Nevertheless, PSOPP notices that
it is a good idea to establish small clusters (of size two
in the best case) for all n. In anticlustering, PSOPP
scales much better with n. For #P = 4 and n = 4000,
PSOPP’s fitness is still 93.15% (σ = 9.42%) of the
optimal fitness value. For n ≤ 1000, PSOPP realizes
that a partitioning with two partitions is appropriate
and achieves optimal results in all runs (σ = 0.00%).
Influence of the Number of Particles. For all
n ∈ N, we also varied the no. of particles #P ∈
{2, 4, 8, 16, 32}(see Table 1). We observed that the to-
tal no. of moves only shows slight increases (if not de-
creases) for #P > 4 in case of clustering as well as an-
ticlustering (the threshold of 4 can be attributed to our
4-core Xeon machines). In most cases, the coefficient
of variation of the no. of moves per particle increases
significantly with #P > 4, meaning that some particles
made many and others only few moves. This charac-
teristic together with a remarkable drop of the aver-
age no. of moves per particle seems to be rather prob-
lematic for clustering since the search space has to
be explored more systematically, which is reflected in
lower fitness values, whereas a greater no. of particles
yield better fitness values for n > 1000 in case of anti-
clustering. Summarizing, there is certainly a trade-off
between the no. of moves per particle and the pro-
vision of diversity through a greater no. of particles
that represent and improve different solution candi-
dates. In the following, we use #P = 4 as it yields
good results in both cases. Because of our 4-core ma-
chines, compared to #P = 2, #P = 4 allows to make
86.15% (σ = 27.06%) or 58.18% (σ = 34.67%) more
moves in total and improves the fitness by 19.99%
(σ = 21.46%) or 2.47% (σ = 3.21%) in case of clus-
tering or anticlustering, respectively.
Influence of Partitioning Constraints. To exam-
ine the influence of constrained partitionings on
PSOPP’s behavior, we additionally used n
max
=
n
2
,
n
min
= 0.98 ·n
max
, s
min
= 2, and s
max
= n −(n
min
−
1) ·s
min
for clustering, and n
min
= 2, n
max
= n ·0.02,
s
min
=
n
n
max
, and s
max
=
n
n
min
for anticlustering. These
parametrizations are compatible to the average num-
ber and size of partitions PSOPP found in the other
evaluation scenarios (see Table 1): In clustering, it
is preferred to create partitions that contain two very
similar elements (e.g., a partition containing i and
i + 1), whereas it is preferred to create two big par-
titions with similar mean values in anticlustering. We
observed that the greater restrictions allow PSOPP to
improve the fitness by an average of 16.84% (σ =
4.43%) in case of clustering, and 4.10% (σ = 2.84%)
for n > 1000 in case of anticlustering. In anticlus-
tering, the greater restrictions thus allowed PSOPP
to find optimal solutions even for n > 1000 in all
runs. This improvement is accompanied by an av-
erage increase of the total no. of moves by 8.77%
(σ = 15.24%) in clustering, and even 73.90% (σ =
31.26%) in anticlustering. This shows that PSOPP
cannot only deal with constrained partitionings but
also benefits from them. While the former is not to be
taken for granted (as outlined in Sect. 1, to the best of
our knowledge, there is no partitioning algorithm that
supports all of these constraints out of the box), the
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
160
Fitness x 10
6
Time in s
0 10
20
40 50 6030
0
-10
-20
-30
-40
-50
-1.2
-0.8
-0.4
0
10 20 4030 50 60
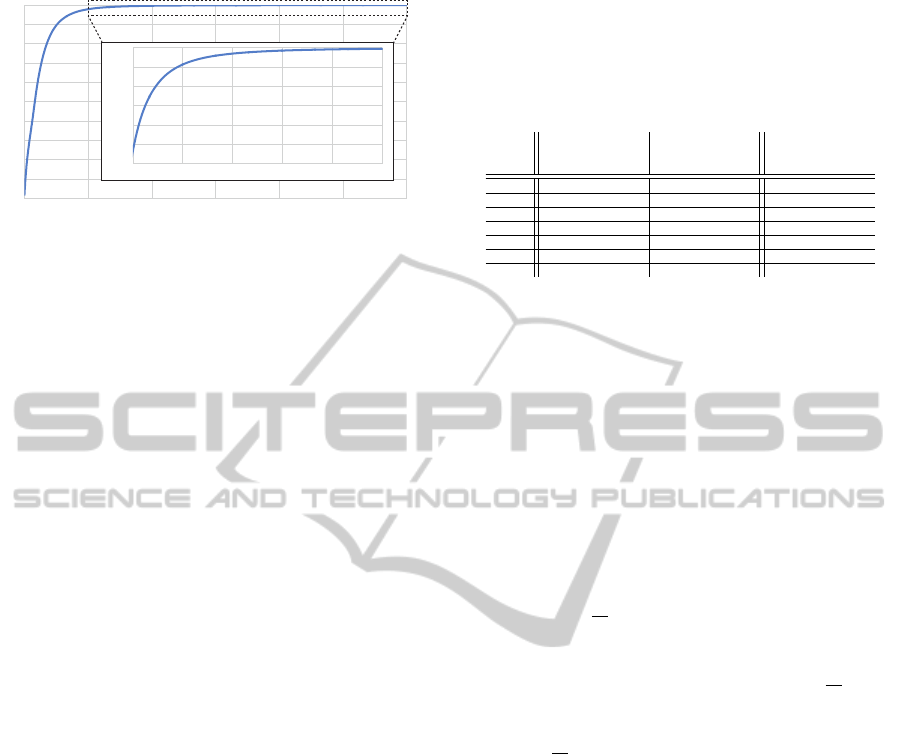
Figure 3: PSOPP’s convergence for n = 1000, #P = 4, and a
time limit of 60s in case of clustering (average of 500 runs).
latter is mainly because the partitioning constraints
reduce the size of the search space.
Convergence. For the evaluation of PSOPP’s con-
vergence, we ran experiments for additional time lim-
its of 30s and 60s for all n ∈N. Especially clustering
benefits from higher time limits in case of n > 250:
On average, the fitness is 67.97% (σ = 25.99%) and
84.92% (16.67%) higher after 30s and 60s, respec-
tively, compared to a limited runtime of 10s. The to-
tal no. of moves increases by an average of 191.41%
(σ = 88.75%) and 512.77% (σ = 261.02%), respec-
tively. In anticlustering and n > 1000, PSOPP already
yields very high-quality results after 10s. The fitness
therefore only improves by 3.08% (σ = 1.91%) and
3.89% (σ = 2.65%) after 30s and 60s, respectively,
while the total no. of moves grows by 261.68% (σ =
22.98%) and 700.54% (σ = 92.06%). Fig. 3 illus-
trates PSOPP’s convergence, i.e., the mean develop-
ment of f (B), for clustering over a time frame of 60s.
Comparison with CPLEX and x-means. As
stated before, we used CPLEX and an x-means im-
plementation for comparison. We evaluated 100 runs
for the following scenarios. Regarding CPLEX, we
formulated the clustering and anticlustering problems
as 0-1 programming problems. For n = 100, CPLEX
obtains a solution after 30s with an average fitness of
−38382.75 and 0.55 that is improved to −23014.93
and 0.63 after 60s in case of clustering and anticlus-
tering, respectively (in all cases, σ = 0.00). PSOPP
already yields far better results after 10s (−29.15 with
σ = 1.93 and 1.00 with σ = 0.00, respectively). While
CPLEX even needs about 720s to calculate a solution
for n = 250, results for n = 500 cannot be obtained
since it exceeds our 32GB of available memory. This
demonstrates the problem’s complexity and the need
for metaheuristics. In contrast to PSOPP which solves
the PP in a general manner, x-means is specialized
to a specific problem, i.e., clustering, and is not able
to solve, e.g., the anticlustering problem. Moreover,
Table 2: The avg. time needed by PSOPP to find 99% /
100% optimal solutions for anticlustering / clustering (op-
timal fitness: 1.00 / 0.00) in 99% of the 500 runs, and the
avg. fitness obtained by x-means after the avg. time PSOPP
needed to find the optimum for clustering (s
min
= n
min
= 1,
s
max
= n
max
= n). Parentheses contain standard deviations.
PSOPP PSOPP x-means
anticlustering clustering clustering
Runtime in s Runtime in s Fitness
#Elements
100 0.032 (0.029) 0.027 (0.019) -176.44 (516.95)
250 0.14 (0.12) 0.12 (0.078) -349.78 (477.80)
500 0.57 (0.49) 0.43 (0.29) -738.00 (491.30)
1000 2.30 (2.25) 1.71 (1.19) -5040.00 (0.00)
2000 11.88 (13.21) 8.53 (6.15) -10080.00 (0.00)
3000 34.29 (41.96) 20.31 (15.76) -34232.00 (0.00)
4000 81.38 (97.29) 45.88 (34.58) -20160.00 (0.00)
PSOPP allows to restrict valid partition sizes, which
is not possible in x-means. Because it is not obvious
how to extend x-means by this feature, we used s
min
=
1 to compare PSOPP to x-means. In this situation, we
have to admit that the highly specialized x-means per-
forms much better than PSOPP for n ≥ 250 (with n ∈
N). After 10s, PSOPP’s fitness is 19.03% higher for
n = 100. In case of n = 250, x-means obtains a fitness
of −68.00 (σ = 0.00), whereas PSOPP yields a fitness
of −195.44 (σ = 25.51). PSOPP achieves a compa-
rable value of −81.38 (σ = 2.70) after 60s. However,
we observed that PSOPP outperforms x-means when
we do not constrain valid partitionings at all (here,
s
min
= n
min
= 1 and s
max
= n
max
= n). Table 2 depicts
the average time r
n
PSOPP needed to find optimal so-
lutions in case of clustering and solutions with a fit-
ness of 99% of the optimum in case of anticlustering
for all n ∈N (please note the cubic growth of r
n
with
n). In contrast to PSOPP, x-means was not able to find
optimal solutions for clustering; the fitness values ob-
tained after r
n
seconds are also depicted in Table 2.
5 CONCLUSION AND FUTURE
WORK
In this paper, we introduced PSOPP, a PSO that solves
the partitioning problem (PP) outlined in Sect. 1. In
contrast to the majority of other approaches, PSOPP
solves the PP in a general manner and is thus appli-
cable to diverse problems – comprising strict parti-
tioning clustering (with outliers), anticlustering, and
coalition structure generation, among others – in var-
ious domains (see Sect. 1 for examples). It can be
customized to a specific application by defining an
appropriate fitness function that evaluates the qual-
ity of solution candidates. Valid partitionings can be
specified in terms of a minimum and maximum num-
ber and size of partitions. This clearly distinguishes
PSOPP from other partitioning methods. To explore
the search space, PSOPP uses basic set operations like
AParticleSwarmOptimizerforSolvingtheSetPartitioningProbleminthePresenceofPartitioningConstraints
161

split, join, and exchange. Our evaluation shows that
PSOPP finds high-quality solutions respecting spec-
ified partitioning constraints in different evaluation
scenarios with a low number of particles.
In this paper, we assumed that PSOPP partitions a
set of elements (see Sect. 1). In future work, we will
revise the definition of the similarity of partitionings
and adjust PSOPP’s approach operations so that it can
solve multiset partitioning problems. In this context,
we want to examine which influence these changes
have on PSOPP’s performance. Furthermore, we will
extend PSOPP with regard to multi-objective opti-
mization to gather solutions lying on a pareto frontier.
ACKNOWLEDGEMENT
This work is partly sponsored by the research unit
FOR 1085 of the German Research Foundation.
REFERENCES
Abdallah, S. and Lesser, V. (2004). Organization-Based Co-
operative Coalition Formation. Int. Conference on In-
telligent Agent Technology, pages 162–168.
Al Faruque, M. A., Krist, R., and Henkel, J. (2008). ADAM:
run-time agent-based distributed application mapping
for on-chip communication. In Proc. of the 45th an-
nual Design Automation Conf., pages 760–765. ACM.
Alam, S., Dobbie, G., and Riddle, P. (2008). An Evolution-
ary Particle Swarm Optimization Algorithm for Data
Clustering. In IEEE Swarm Intelligence Symposium,
2008, pages 1–6.
Anders, G., Seebach, H., Nafz, F., Steghöfer, J.-P., and Reif,
W. (2011). Decentralized Reconfiguration for Self-
Organizing Resource-Flow Systems Based on Local
Knowledge. In 8th IEEE Int. Conference and Work-
shops on Engineering of Autonomic and Autonomous
Systems (EASe), pages 20–31.
Anders, G., Siefert, F., Steghöfer, J.-P., and Reif, W. (2012).
A decentralized multi-agent algorithm for the set par-
titioning problem. In PRIMA 2012: Principles and
Practice of Multi-Agent Systems, volume 7455 of
Lecture Notes in Computer Science, pages 107–121.
Springer Berlin / Heidelberg.
Apt, K. R. and Witzel, A. (2007). A Generic Approach to
Coalition Formation. Proc. of the Int. Workshop on
Computational Social Choice COMSOC, 11(3).
Äyrämö, S. and Kärkkäinen, T. (2006). Introduction to
partitioning-based clustering methods with a robust
example. Technical report, Reports of the Department
of Mathematical Information Technology, Series C.
Software and Computational Engineering of the Uni-
versity of Jyväskylä.
Bender, C., Brody, D., and Meister, B. (1999). Quantum
field theory of partitions. Journal of Mathematical
Physics, 40:3239.
Buccafurri, F., Rosaci, D., Sarnè, G., and Ursino, D. (2002).
An Agent-Based Hierarchical Clustering Approach
for E-commerce Environments. In E-Commerce and
Web Technologies, volume 2455 of LNCS, pages 109–
118. Springer.
Chu, P. and Beasley, J. (1998). Constraint handling in ge-
netic algorithms: The set partitioning problem. Jour-
nal of Heuristics, 4(4):323–357.
Consoli, S., Moreno-Pérez, J., Darby-Dowman, K., and
Mladenovi
´
c, N. (2010). Discrete Particle Swarm Opti-
mization for the minimum labelling Steiner tree prob-
lem. Natural Computing, 9(1):29–46.
Di Marzo Serugendo, G., Gleizes, M.-P., and Karageorgos,
A. (2005). Self-organization in multi-agent systems.
The Knowledge Engineering Review, 20:165–189.
Garcia, F. and Perez, J. (2008). Jumping frogs optimization:
a new swarm method for discrete optimization. Tech-
nical Report 3, Documentos de Trabajo del DEIOC,
Department of Statistics, O.R. and Computing, Uni-
versity of La Laguna, Tenerife, Spain.
Horling, B. and Lesser, V. (2004). A survey of multi-agent
organizational paradigms. The Knowledge Engineer-
ing Review, 19(04):281–316.
Ishioka, T. (2005). An expansion of x-means for automat-
ically determining the optimal number of clusters. In
Proceedings of International Conference on Compu-
tational Intelligence, pages 91–96.
Kennedy, J. and Eberhart, R. (1995). Particle Swarm Op-
timization. In Proc. of the IEEE Int. Conf. on Neural
Networks, 1995, volume 4, pages 1942 –1948.
Kennedy, J. and Eberhart, R. (1997). A Discrete Binary
Version of the Particle Swarm Algorithm. In IEEE
International Conference on Systems, Man, and Cy-
bernetics, 1997. Computational Cybernetics and Sim-
ulation., volume 5, pages 4104–4108.
Kudo, Y. and Murai, T. (2009). On a criterion of similar-
ity between partitions based on rough set theory. In
Rough Sets, Fuzzy Sets, Data Mining and Granular
Computing, volume 5908 of LNCS, pages 101–108.
Springer Berlin / Heidelberg.
MacQueen, J. (1967). Some methods for classification and
analysis of multivariate observations.
Ogston, E., Overeinder, B., Steen, M. V., and Brazier, F.
(2003). A Method for Decentralized Clustering in
Large Multi-Agent Systems. In Proc. of the 2nd Int.
Joint Conference on Autonomous Agents and Multia-
gent Systems, pages 789–796.
Rahwan, T., Ramchurn, S. D., Jennings, N. R., and Giovan-
nucci, A. (2009). An Anytime Algorithm for Optimal
Coalition Structure Generation. Journal of Artificial
Intelligence Research, 34:521–567.
Seren, C. (2011). A Hybrid Jumping Particle Swarm
Optimization Method for High Dimensional Uncon-
strained Discrete Problems. In 2011 IEEE Congress
on Evolutionary Computation, pages 1649–1656.
Shehory, O. and Kraus, S. (1998). Methods for Task Allo-
cation via Agent Coalition Formation. Artificial Intel-
ligence, 101(1-2):165–200.
Steghöfer, J.-P., Behrmann, P., Anders, G., Siefert, F., and
Reif, W. (2013). HiSPADA: Self-Organising Hierar-
chies for Large-Scale Multi-Agent Systems. In Pro-
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
162

ceedings of the Ninth International Conference on Au-
tonomic and Autonomous Systems (ICAS). IARIA.
Valev, V. (1998). Set partition principles revisited. In Ad-
vances in Pattern Recognition, volume 1451 of LNCS,
pages 875–881. Springer.
Van der Merwe, D. and Engelbrecht, A. P. (2003). Data
clustering using particle swarm optimization. In The
2003 Congress on Evolutionary Computation, vol-
ume 1, pages 215–220. IEEE.
Younis, O. and Fahmy, S. (2004). HEED: A Hybrid,
Energy-Efficient, Distributed Clustering Approach for
Ad Hoc Sensor Networks. IEEE Transactions on Mo-
bile Computing, 3:366–379.
AParticleSwarmOptimizerforSolvingtheSetPartitioningProbleminthePresenceofPartitioningConstraints
163
