Estimating Positive Definite Matrices using Frechet Mean
Mehdi Jahromi, Kon Max Wong and Aleksandar Jeremic
∗
Department of Electrical and Computer Engineering, McMaster University, Hamilton, Ontario, Canada
Keywords:
Covariance Estimation, Constrained Optimization, Fr´echet Mean.
Abstract:
Estimation of covariance matrices is a common problem in signal processing applications. Commonly applied
techniques based on the cost optimization (e.g. maximum likelihood estimation) result in an unconstrained
estimation in which the positive definite nature of covariance matrices is ignored. Consequently this may result
in accurate estimation of the covariance matrix which may affect overall performance of the system. In this
paper we propose to estimate the covariance matrix using Fr´echet mean which ensures that the estimate also
has positive definite structure. We demonstrate the applicability of the proposed technique on both estimation
and classification accuracy using numerical simulations. In addition we discuss some of the preliminary results
we obtained by applying our techniques to high content cell imaging data set.
1 INTRODUCTION
The covariance matrix, or equivalently, the power
spectral density (PSD) matrix, of the signals from a
multi-sensor system is a feature useful for many pur-
poses in statistical signal processing including detec-
tion, estimation, classification, and signal design. In
a recent paper (Li and Wong, 2013) the importance of
power spectral density matrix in classification of EEG
signals was demonstrated.
In many applications of signal processing, the co-
variance matrix of the observed signal is utilized as
a feature from which information is extracted. Of-
ten, for extraction of information, averaging and in-
terpretation of these matrices are needed. To develop
algorithms for such evaluations, one important fact
has to be born in mind that the structural constraints,
i.e., Hermitian symmetry and positive definiteness,
on such matrices must be maintained (Li and Wong,
2013), (Jeuris et al., 2012). More specifically in high
content cell images many of the features that are com-
monly used in analysis exhibit large degree of ran-
dom variations from class to class (i.e well to well).
In these cases it is expected that covariance structure
may play significant role in correct classification as
their distinguishing properties may be determined by
type of randomness rather than the center of the mass
of the cluster corresponding to particular well of cells
used for screening.
In this paper, the focus of our attention is on the
estimation of the Frechet mean of the covariance ma-
∗
This work was supported by Natural Sciences and En-
gineering Research Council of Canada.
trices on the manifold M using the different measures
of Riemannian distances. The necessary frame work
and algorithms to obtain the mean of covariance ma-
trices from group of sample covariance matrices us-
ing Riemannian distances on manifold of positivedef-
inite matrices M will be developed and studied in this
chapter. In Section 2 we introduce the Fr´echet mean
based on several Riemannian distances. In Section 3
we discuss computational algorithms for calculating
the proposed distance means. In Section 4 we present
numerical results that demonstrate applicability of our
results.
2 FR
´
ECHET MEAN
The history of defining mean goes back 2500 years
when the ancient Greeks introduced ten types of dif-
ferent means. Among them only three of them survive
and are still being used. These are the arithmetic, the
geometric and the harmonic means.
We use the notion of Fr´echet mean to unify the
method of finding the mean of positive definite matri-
ces. The Fr´echet mean is given as the point which
minimizes the sum of the squared distances (Bar-
baresco, 2008):
ˆ
S = argmin
S ∈M
n
∑
i=1
d
2
(S
i
,S ) (1)
where {S
i
}
n
i=1
represents the symmetric positive defi-
nite matrices and d(.,.) denotes the metric being used
respectively.
In fact if we have a closer look at the definition
295
Jahromi M., Wong K. and Jeremic A..
Estimating Positive Definite Matrices using Frechet Mean.
DOI: 10.5220/0005277902950299
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2015), pages 295-299
ISBN: 978-989-758-069-7
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

of arithmetic mean of positive measurement {x
i
}
n
i=1
,
which is denoted as ¯x =
1
n
∑
n
i=1
x
i
, and using the usual
distance, we can see that it has the variational prop-
erty. This means that it minimizes the sum of the
squared distances to the points x
k
:
¯x = argmin
x≥0
n
∑
i=1
|x−x
i
|
2
(2)
with respect to metric
d(x,y) = |x −y| (3)
In fact if we form the quadratic cost function
f(x) =
n
∑
i=1
(x−x
i
)
2
(4)
By taking the derivative of Eq.(4) with respect to the
variable x and set it equal to zero one can obtain the
¯x which is the arithmetic mean of positive scalars
{x
i
}
n
i=1
.
2.1 Riemannian Metrics
So far we only considered the Euclidean distance
which is valid on the space with zero sectional cur-
vature.
To measure the distance between two M ×M co-
variance matrices A and B on manifold of positive
definite matrices M , we consider the metrics which
have been developed to measure distance between
two points on the manifold itself. The following
metrics will be considered throughout the remaining
chapters.
The first metric is obtained when we lift the points
A,B to the horizontal subspace U ⊂H using the fiber
and measure the distance between them(Li and Wong,
2013):
d
R
1
(A,B) = argmin
˜
U
1
,
˜
U
2
∈U(M)



A
1
2
˜
U
1
−B
1
2
˜
U
2



2
(5)
where U(M) denotes the space of unitary matrices of
size M ×M. Alternatively Eq.(5) can be rewritten as:
q
Tr(A) + Tr(B)−2Tr(A
1
2
BA
1
2
)
1
2
(6)
In general for any positive definite matrix A its square
root is defined as A
1
2
= S
√
LD
H
; where A = SLD
H
is
the eigenvalue value decomposition of matrix A with
diagonal matrix L consisting of eigenvalues of A.
In Eq(5), U
1
and U
2
are the left and right mul-
tiplicative of singular value decomposition of B
1
2
A
1
2
(Mardia et al., 1979). Let the points A,B ∈ M and
let X be a the point on the manifold at which we
construct a tangent plane ( it is usually denoted as
T
M
X). According to the inner-product hA, Bi
X
=
Tr(X
−1
AX
−1
B) the log- Riemannian metric is given
as (Moakher, 2005):
d
R
3
(A,B) =



log(A
−
1
2
BA
−
1
2
)



2
=
s
M
∑
i=1
log
2
(L
i
) (7)
where the L
i
’s are the eigenvalues of the matrix A
−1
B
(Absil et al., 2009). (Metric d
R3
has been developed
in various ways and has, for a long time, been used in
theoretical physics).
Obtaining the Fr´echet mean of set of positive defi-
nite Hermitian matrices {S
i
}
n
i=1
with respect to metric
d
R1
results in:
argmin
S ∈M
n
∑
i=1




S
1
2
i
U
i
−S
1
2
U




2
2
(8)
In the next section we discuss numeri-
cal/analytical methods for calculating corresponding
means.
3 COMPUTATIONAL
ALGORITHMS
Following the approach of (Crosilla and Beinat, 2002)
we first define function g as
g(A
1
,A
2
,A
3
,..., A
n
) =
1
n
n
∑
i=1
∑
j≥i


A
i
U
i
−A
j
U
j


2
2
.
(9)
where in Eq.(9) U
i
’s are unitary operators.
The next algorithm simultaneously find the set of
unitary matrices{U
i
}
n
i=1
in order to minimize function
g(A
1
,A
2
,..., A
n
) in (9) and as a consequent finding
the Fr´echet mean with respect to metric d
R1
.
Algorithm for computing the Fr
´
echet mean of
metric d
R
1
:
Algorithm 1: Fr´echet mean for metric d
R
1
.
1. Initialize the positive threshold value ε. For the set {S
i
}
n
i=1
of
positive definite matrices on manifold M find the square root
of each element: A
i
= S
1
2
i
; i = 1,2, ...,n.
2. For each i = 1,2,...,n consider
ˆ
A
i
:=
1
n−1
∑
n
j6=i
A
j
and find
ˆ
U
i
which minimizes


ˆ
A
i
−A
i
U
i


2
; then consider
ˆ
A
inew
:= A
i
ˆ
U
i
3. At iteration (k + 1) set A
i
=
ˆ
A
inew
;i = 1,2,...,n and Evaluate
g
k+1
using Eq.(9)
4. Repeat step 2 until:
|g
k
(A
1
,A
2
,...,A
n
) −g
k+1
(A
1
,A
2
,...,A
n
)|≤ ε .
5. Calculate
ˆ
C =
1
n
∑
n
i=1
ˆ
A
i
U
i
.
6. The resulting Fr´echet mean on manifold M is then obtained as
ˆ
S =
ˆ
C
ˆ
C
H
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
296

The optimization problem in Eq.(1) with respect
to the metric d
R2
and given positive definite hermitian
matrices {S
i
}
n
i=1
, is expressed as:
ˆ
S = argmin
S ∈M
n
∑
i=1



S
i
1
2
−S
1
2



2
2
(10)
The optimization problem (10) has closed form solu-
tion on manifold of positive definite matrices. It can
be obtained through the following lemma:
For the set of positive definite Hermitian matrices
{S
i
}
n
i=1
on manifold M we consider L
i
= (S
i
)
1
2
; i =
1,2,...,n . Then we have:
ˆ
L = argmin
L
n
∑
i=1



L
i
−L
1
2



2
2
=
1
n
n
∑
i=1
L
i
(11)
The Fr´echet mean with respect to metric d
R3
for
the set of positive definite matrices {S
i
}
n
i=1
in mani-
fold M using Eq.(1) can be formulated as:
ˆ
S = argmin
S ∈M
n
∑
i=1
d
2
R3
(S
i
,S ) (12)
Before going through the algorithm for finding
the optimum solution of Eq.(12) we show that this
optimization problem has a unique solution. It has
been demonstrated that the directional derivative of
the function f(X) =
∑
n
i=1




log(A
−
1
2
i
XA
−
1
2
i
)




2
2
,where
{A
i
}
n
i=1
∈ M , is given by:
D
Y
f(X) = 2
n
∑
i=1

X
−1
log(XA
−1
i
),Y

(13)
At this point we can use gradient descent algo-
rithm to find the minimizer of f(X).
4 EVALUATION OF FR
´
ECHET
MEAN OF SYMMETRIC
POSITIVE DEFINITE
MATRICES
We have introduced different estimators correspond-
ing to the different distance measures to find the
Fr´echet mean of set of symmetric positive definite
matrices {S
i
}
n
i=1
on manifold M . In order to com-
pare the performance of each estimator we consider a
population of M×M covariance matrices and find the
mean of them using each estimator. We will consider
different models having the same true means so that a
comparison of the closeness of the different estimates
to this true mean is possible.
4.1 Model Description
To come up with the first model we consider the
known symmetric positive definite matrix S as the
nominal value. Then we apply the Cholesky decom-
position to it. By definition the Cholesky factor of a
symmetric positive definite matrix S is a lower trian-
gular matrix W with positive diagonal elements such
that S = W W
H
.
We denote the Cholesky factor of S in the model with
W and set W =Chol(S ); where Chol represents the
Cholesky factor of S . We also consider set of ma-
trices {X
i
}
n
i=1
with the entries
n
x
i
jk
o
j,k
drawn from
a normal distribution with zero mean and prescribed
variance S
2
. Now to form the new population of co-
variance matrices {S
i
}
n
i=1
with respect to the nominal
covariancematrix S we consider the followingmodel:
S
i
= (W + X
i
)(W + X
i
)
H
(14)
In order to take to account the signature of ran-
domness in producing samples using model (14) we
use Eq.(15) to measure the discrepancy in several
simulation runs; This approach is known as Monte
Carlo simulation (MacKay, 1998). In this method
for the fixed covariance matrix S one can generate
the population set {S
i
}
n
i=1
for N times. Each time
the Fr´echet mean of the population will be evaluated,
˜n = 1, 2,...,N. Finally, the criterion which is known
as Root Mean Square Error or (RMSE) is formed as
follows :
RMSE
d
F
=
s
1
N
N
∑
˜n=1
d
F
2

S ,
ˆ
S
˜n

(15)
Where metric d
F
is defined as :
d
F

S ,
ˆ
S

=


S −
ˆ
S


2
(16)
in which for matrix A, kAk
2
=
√
TrAA
H
.
First we consider the model (14) to demonstrate
the performance of the Fr´echet mean of Riemannian
distances. For this reason we consider a Covariance
matrix S
3×3
. The eigenvalues of the covariance ma-
trix is L = diag[1, 0.3573,0.065]. As far as the model
(14) is concerned the Cholesky factor of the covari-
ance matrix is considered. The additive random noise
matrix {X
i
}
n
i=1
has independent and identically dis-
tributed (i.i.d) entries come from Gaussian distribu-
tion with zero mean:
E

x
i
j,k

= 0 j,k = 1,2,3 ,i = 1, 2,.., n (17)
where E denotes the expected value of the random
variable. The standard deviation of the entries of ran-
dom noise is 0.09 in this experiment.
EstimatingPositiveDefiniteMatricesusingFrechetMean
297

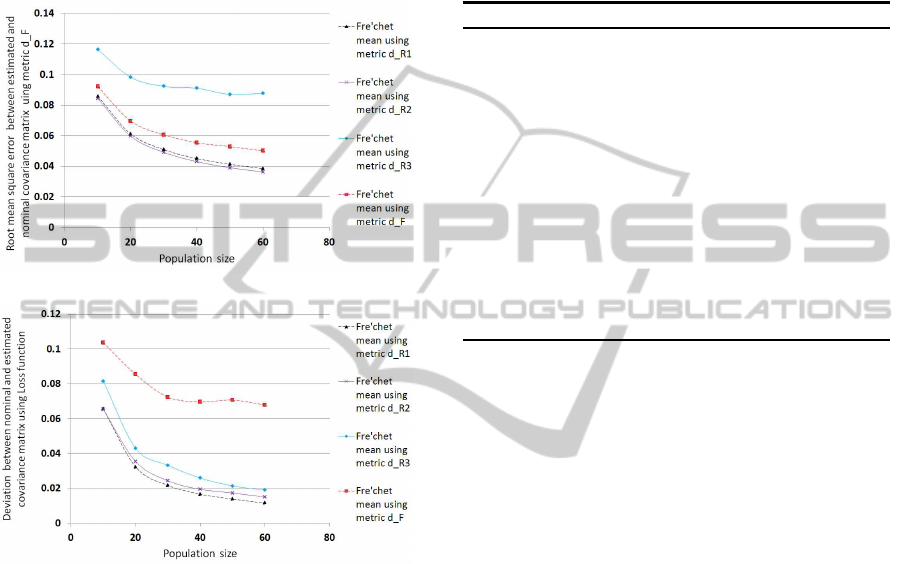
The population size of the covariance matrices,
{S
i
}
n
i=1
, varies between 10 to 60 in step size 10. In or-
der to take to account the signature of randomness of
the additive Gaussian noise matrix X
i
’s in model (14),
for each population we perform the Monte-Carlo sim-
ulation 2000 times and obtain the resulting error be-
tween
ˆ
S and the nominal covariance matrix using loss
function, RMSE
d
F
. The results are shown in Figure 1.
(a)
(b)
Figure 1: (a): Error is measured using metric d
F
.(b): Error
is measured using Loss function.
4.2 Classification Based on the Distance
to the Center of Mass
So far we have mathematically developed the concept
of mean for group of positive definite Hermitian ma-
trices on manifold M from the distance point of view.
Moreover, we have seen that depending on model
and the criterion of measuring the closeness of each
estimator to the nominal covariance matrix, Fr´echet
means of Riemannian distances are better estimators.
The concept of Fr´echet mean can be utilized in
distance based detection and classification on mani-
fold M (Pigoli et al., 2014),(Barachant et al., 2010).
For this purpose suppose that we have a set of covari-
ance matrices {S
ik
}
n
k
i=1
where k represents the label
of each class and n
k
denotes the number of covari-
ance matrices within k
th
class. For each class k the
Fr´echet mean of the class, depending on type of met-
ric, can be obtained as representative of each class.
For the unknown observation its covariance matrix is
formed and considered as the unknown feature. The
observation is assigned to the class which has mini-
mum distance to the Fr´echet mean of the class. This
method can be recapitulated in form of the following
algorithm.
Algorithm 2: Distance to the center of mass algorithm.
1. Input: the given known classes 1,2,3, ,..., k and set
of covariance matrices {S
ik
}
n
k
i=1
within each class.
2. For each class k compute
ˆ
S
ik
as the Fr´echet mean
of {S
ik
}
n
k
i=1
.
3. For the covariance matrix S of unknown observa-
tion compute
ˆ
k = argmin
k
d (S,S
k
). (18)
4. The covariance matrix S corresponding to the un-
known observation in step 3 will be assigned to
class
ˆ
k.
In order to inspect and evaluate the Algorithm 1
we perform it on the simulated data set. For this
purpose we consider three classes C
1
, C
2
and C
3
consisting of samples {x
1
(i)}
10000
i=1
, {x
2
(i)}
10000
i=1
and
{x
3
(i)}
10000
i=1
drawn from the normal distribution with
zero mean and covariance matrices S
1
, S
2
and S
3
re-
spectively. At the same time Gaussian random noise
with mean zero and standard deviation S is added to
the samples of both classes. Then we split each class
to the half for train and test purpose and perform two
fold cross validation .
At training step we consider training sets C
1train
, C
2train
and C
3train
. From each training set
C
j
train
, j = 1,2,3; we form a sequence of

X
k, j

of observations k = 1,2,.., 20. Each observation

X
k, j

has 40 samples which can be shown as

x
jk
(1),x
jk
(2),..., x
jk
(40)

T
.
The Frech´et mean of the covariance matrices

S
k, j

of the observation

X
k, j

are obtained using
metrics d
R
1
,d
R
2
, d
R
3
and d
F
respectively. The method
of distance to the center of mass is performed to clas-
sify the new observation X
test
according to its ob-
served covariance matrix S
test
.
From (Johnson and Wichern, 2002) it has been
known that when we have sample of observations
from a p-variate normal distribution with zero mean
and covariance matrix S then N
¯
xS
−1
¯
x
T
has chi-
square distribution with p degrees of freedom where
¯
x
is the sample mean vector of size 1× p for the obser-
vation X of size N × p; which is taken over columns
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
298

of X and N is the sample size. When the sample size
is fairly large we can replace S with
ˆ
S (Anderson,
1954). As a result, a new observation X
test
is classi-
fied to class j whenever:
χ
2
p
(1−α/2) ≤ N
¯
x
test
ˆ
S
−1
j
¯
x
T
test
≤ χ
2
p
(α/2) (19)
where χ
2
p
(α) is given by:
P

χ
2
p
> χ
2
p
(α)

= α
In Eq.(19) the significant level is set to be α = 0.05.
At the same time we also compare the result of dis-
tance to the center of mass in classification with the
result of Eq.(19).
Table 1: Probability of correct classification within three
classes C
1
,C
2
and C
3
in comparison to the resulting classi-
fier using Eq.(19).
Accuracy
Class 1 (%)
Accuracy of
Class 2 (%)
Accuracy
for Class 3 (%)
d
R3
0.92 0.86 0.95
d
F
0.83 0.39 0.62
d
R1
0.91 0.51 0.78
d
R2
0.92 0.51 0.82
Eq.(19) 0.80 0.60 0.72
In addition we applied our technique to the clas-
sification of human breast cancer cells undergoing
treatment of different drugs. As explained before our
technique is based on classification in clusters based
on the covariance estimate distances rather than cen-
ter of the class (corresponding to the mean of the data
point cloud). The original data set consisted of 11
different labels corresponding to 11 different treat-
ments. Each label consisted of 382 wells which were
imaged using Perkin Elmar high content imaging sys-
tem. Our preliminary results indicate that our aver-
age classification error is approximately 13% when
the half of the cells are used for training. The pre-
liminary comparison with commonly used clustering
techniques based on the sample average (mean) indi-
cate that our performance is significantly better (5%)
however it may be due to the large training set.
5 CONCLUSIONS
In this paper we proposed a new technique to for es-
timating positive definite matrices in the presence of
uncertainty. Unlike commonly used techniques our
method uses Frechet mean which implicitly accounts
for the positive definite structure of the covariance
matrix which is ignored in commonly used estima-
tors which do not exploit geometric constraint given
by positive definite property. We demonstrate the cal-
culation of the proposed mean using three different
distance measures which may be better choice in dif-
ferent applications. We demonstrated the applicabil-
ity and performance of our techniques on a simulated
data set and established that in the preliminary anal-
ysis the results look promising for high content cell
imaging classification problem.
REFERENCES
Absil, P.-A., Mahony, R., and Sepulchre, R. (2009). Opti-
mization algorithms on matrix manifolds. Princeton
University Press.
Anderson, T. W. (1954). An Introduction To Multivariate
Statistical Analysis. Wiley Eastern Private Limited;
New Delhi.
Barachant, A., Bonnet, S., Congedo, M., and Jutten, C.
(2010). Riemannian geometry applied to BCI classi-
fication. In Latent Variable Analysis and Signal Sepa-
ration, pages 629–636. Springer.
Barbaresco, F. (2008). Innovative tools for radar signal pro-
cessing based on Cartans geometry of SPD matrices
& information geometry. Radar Conference, 2008.
RADAR’08. IEEE, pages 1–6.
Crosilla, F. and Beinat, A. (2002). Use of generalised pro-
crustes analysis for the photogrammetric block adjust-
ment by independent models. ISPRS Journal of Pho-
togrammetry and Remote Sensing, 56(3):195–209.
Jeuris, B., Vandebril, R., and Vandereycken, B. (2012). A
survey and comparison of contemporary algorithms
for computing the matrix geometric mean. Electronic
Transactions on Numerical Analysis, 39:379–402.
Johnson, R. A. and Wichern, D. W. (2002). Applied mul-
tivariate statistical analysis, volume 5. Prentice Hall
Upper Saddle River, NJ.
Li, Y. and Wong, K. M. (2013). Riemannian distances for
EEG signal classification by power spectral density.
IEEE journal of selected selected topics in signal pro-
cessing.
MacKay, D. J. (1998). Introduction to Monte Carlo meth-
ods. In Learning in graphical models, pages 175–204.
Springer.
Mardia, K. V., Kent, J. T., and Bibby, J. M. (1979). Multi-
variate analysis. Academic Press.
Moakher, M. (2005). A differential geometric approach
to the geometric mean of symmetric positive-definite
matrices. SIAM Journal on Matrix Analysis and Ap-
plications, 26(3):735–747.
Pigoli, D., Aston, J. A., Dryden, I. L., and Secchi, P.
(2014). Distances and inference for covariance op-
erators. Biometrika.
EstimatingPositiveDefiniteMatricesusingFrechetMean
299