Split-and-Merge Method for Accelerating Convergence

of Stochastic Linear Programs

Akhil Langer

and Udatta Palekar

Department of Computer Science, University of Illinois at Urbana-Champaign, Illinois, U.S.A.

Department of Business Administration, University of Illinois at Urbana-Champaign, Illinois, U.S.A.

Keywords:

Stochastic Optimization, Decomposition, Scenario-based Decomposition, Multicut L-shaped Method,

Resource Allocation, US Military Aircraft Allocation.

Abstract:

Stochastic program optimizations are computationally very expensive, especially when the number of scenar-

ios are large. Complexity of the focal application, and the slow convergence rate add to its computational

complexity. We propose a split-and-merge (SAM) method for accelerating the convergence of stochastic lin-

ear programs. SAM splits the original problem into subproblems, and utilizes the dual constraints from the

subproblems to accelerate the convergence of the original problem. Our initial results are very encouraging,

giving up to 58% reduction in the optimization time. In this paper we discuss the initial results, the ongoing

and the future work.

1 INTRODUCTION

Stochastic programs are used for decision making un-

der uncertainty. For example, product production de-

cisions under resource constraints are to be taken at

a time when future demand for the products is not

known with certainty. Stochastic programs assume

that a probabilistic distribution of these uncertain fu-

ture outcomes is known. An instantiation of the un-

certain parameters is called as a scenario. Equation 1

gives a standard representation of a stochastic pro-

gram.

min cx +

∑

)

s.t. Ax ≤ b

∀s, W

+ T

x ≤ h

(1)

where, x corresponds to the strategic decisions corre-

sponding to the known parameters that are to be taken

now, and y

corresponds to the operational decisions

that will be taken when the scenario s is realized, and

is the probability that scenario s will occur. The

objective function is sum of the costs of strategic de-

cisions and the weighted average of the cost of oper-

ational decisions for all scenarios.

When the unknown parameters become known

in multiple stages over a period of time, the corre-

sponding optimization problem is called a multistage

stochastic program. In a two-stage stochastic pro-

gram, all the unknown parameters become known at

the same time. We propose our work on two-stage

stochastic programs but the strategy is easily general-

izable to multi-stage stochastic programs. Moreover,

multistage stochastic programs can be solved as a se-

quence of two-stage stochastic programs.

Equation 2 and 3 shows the ﬁrst and second stage

programs of the two-stage stochastic program, respec-

tively.

Stage 1 Program:

min cx +

∑

(x, y

)

s.t. Ax ≤ b (2)

Stage 2 Program:

min Q

(x, y

)

≤ h

− T

x (3)

In this work, we focus on the stochastic linear pro-

grams, that is, problems that have linear variables and

constraints both in Stage 1 and Stage 2.

The usual method of solving stochastic linear pro-

gram uses Bender’s decomposition (Benders, 1962).

In this method, a candidate Stage 1 solution is ob-

tained by optimizing the Stage 1 program. The candi-

date Stage 1 solution is evaluated against all the sce-

narios in Stage 2. Stage 2 optimization gives the sce-

nario costs for the given Stage 1 solution, and opti-

mality/feasibility cuts that are fed back to Stage 1.

218

Langer A. and Palekar U..

Split-and-Merge Method for Accelerating Convergence of Stochastic Linear Programs.

DOI: 10.5220/0005287902180223

In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 218-223

ISBN: 978-989-758-075-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Stage 1 is re-optimized with the addition of new set

of cuts to obtain another candidate solution. The it-

erative Stage 1-Stage 2 optimization continues until

the optimal solution is found which is determined by

a convergence criteria. A Stage 1 optimization fol-

lowed by a Stage 2 optimization is called an iteration.

There are two variants of the Bender’s approach.

In one, a single cut using a weighted combination of

Stage 2 dual objective function is added to the Stage 1

in each iteration. This method is called the L-shaped

method (Van Slyke and Wets, 1969). In the other,

in an iteration a cut constraint is added to Stage 1

for each scenario. This multicut method (Birge and

Louveaux, 1988) has the advantage that the set of

cuts in each iteration dominates a single L-shaped cut.

However, the number of cuts can become very large

quickly, particularly for problems with large number

of scenarios.

In most real world applications, the number of un-

certain parameters are large, and therefore the num-

ber of scenarios are also very large. In addition to the

complexity of the focal application, factors such as

the number of Stage 2 evaluations, number of rounds

it takes to converge to optimality (within the user-

speciﬁed convergence criteria), and the size of the

Stage 1 linear program which increases with the in-

crease in number of scenarios, add to the computa-

tional complexity of the stochastic programs.

Our research focuses on multicut Bender’s

method. Equation 4 shows the Stage 1 program af-

ter r rounds.

min cx +

∑

s.t. Ax ≤ B

∀s and l ∈ [1, r], E

x + θ

≤ e

(4)

where, E

+ θ

≤ e

are the cut constraints obtained

from Stage 2 optimization and θ

is the cost of sce-

nario s.

Because of the large number of cuts in the mul-

ticut method, it is imperative that the cuts gener-

ated in each round are strong cuts in the sense that

they allow the Bender’s program to converge quickly.

This paper considers a scenario split-and-merge ap-

proach to accelerate the convergence of multicut Ben-

der’s method. In Section 2, we do a literature review

on stochastic optimization methods and their conver-

gence properties. In Section 3, we propose a split-

and-merge method for accelerating the convergence

of multicut L-shaped method. We corroborate our

ideas with some initial results in Section 4. Finally,

we conclude the paper with the ongoing work and fu-

ture work in Section 5.

2 RELATED WORK

Magnanti and Wong in their seminal paper (Magnanti

and Wong, 1981), proposed a method for accelerating

Bender’s decomposition by selecting good cuts to add

to the master problem. A cut θ ≤ π

∗

h + π

∗

T x domi-

nates or is stronger than the cut, θ ≤ π

∗

h + π

∗

T x, if

∗

h + π

∗

T x ≤ π

∗

h + π

∗

T x for all x ∈ X with a strict

inequality for at least one x ∈ X, where π

∗

and π

∗

are any two dual optimal solutions of the degenerate

Stage 2 problem. They deﬁne a cut as pareto optimal

if it has no dominating cut. The corresponding Stage

2 dual optimal solution is called the pareto optimal

solution. Given the set of Stage 2 dual optimal solu-

tion set S(x

∗

), the pareto optimal solution (π

) solves

the problem:

min

π∈S(x

∗

)

πh + πT x

where, x

is a core point of X i.e.

∈ relative interior of X and S(x

∗

) =

{π|π maximizes Q(x

∗

)}. The downside of this

approach is that it requires solving additional op-

timization problem to identify pareto optimal cuts

in every iteration which can trade-off the beneﬁt of

reduction in total number of iterations.

Linderoth et al (Linderoth and Wright, 2003) de-

veloped asynchronous algorithms for stochastic opti-

mization on computational grids. They use a multicut

method and add a cut of a particular scenario to the

master program only if it changes the objective value

of the proposed model function corresponding to that

scenario. This requires solving several additional op-

timization problems at each iteration to determine the

usability of each cut, which can be prohibitive.

Initial iterations in the multicut method are often

inefﬁcient because the solution tends to oscillate be-

tween different feasible regions of the solution space.

Ruszczy

nski (Ruszczy

nski, 1986) proposed a regu-

larized decomposition method that adds a quadratic

penalty term to the objective function to minimize

the movement of the candidate solution. Linderoth

and Wright (Linderoth and Wright, 2003) use a lin-

earized approach to this idea by binding the solution

in a box called the trust region. Trust region method

is used to decide the major iterates that signiﬁcantly

change the value of the objective function in each it-

eration. This requires doing several minor iterations

at each major iteration to come-up with a good can-

didate solution x

. Trust-region method at minor it-

erations limits the step-size by adding constraints of

the form ||x −x

∞

≤ ∆. Heuristics are used to decide

and update ∆. The cuts generated during the minor

iterations can be discarded without affecting the con-

vergence of the problem.

Split-and-MergeMethodforAcceleratingConvergenceofStochasticLinearPrograms

219

The Progressive Hedging algorithm proposed by

Rockafellar and Wets (Rockafellar and Wets, 1991)

solves each scenario independently by introducing la-

grangean multipliers for the Stage 1 variables in the

objective function of the individual problems. This

approach requires search for the optimal lagrangean

multipliers which can be computationally prohibitive.

Langer et al (Langer et al., 2012) propose cluster-

ing schemes for solving similar scenarios in succes-

sion that signiﬁcantly reduces the Stage 2 scenario op-

timization times by use of advanced/warm start. How-

ever, this does not address the slow convergence rate

of the problem.

3 PROPOSED APPROACH

In each iteration of the multicut method, as many cut

constraints are added to the Stage 1 program as there

are scenarios. In the initial iterations of the multicut

Bender’s method, all the scenario cut constraints are

not active in the Stage 1 linear program optimization.

This is because few cuts are needed to perturb the pre-

vious Stage 1 solution and provide a new candidate

solution. Therefore, the cuts from the Stage 2 evalua-

tion of most of the scenarios remain inactive in Stage

1 during the initial iterations of the Bender’s method.

For such scenarios, similar cuts will be generated in

successive iterations, and hence a lot of computation

is wasted.

We propose a split-and-merge (SAM) algorithm

(Algorithm 1) that divides the scenarios into N clus-

ters (S

, S

, ...., S

In SAM, n stochastic programs (P

, P

, ..., P

) are

created and each of these is assigned one cluster of

scenarios (lines 3-4). Probabilities of the scenarios in

each of these subproblems are scaled up so that they

add up to 1 (lines 5-6). We then apply the Bender’s

multicut method to these n stochastic programs inde-

pendently of each other (lines 8-16). For multicore

machines, these problems can be solved in parallel on

multiple cores by adding a simple OpenMP (Dagum

and Menon, 1998) parallel construct to parallelize

the for loop that iterates over each of these subprob-

lems (line 8). Bender’s decomposition is applied to

these subproblems for a ﬁxed number of rounds (r)

or till the subproblem has converged to optimality,

whichever is the earliest (line 12). Once this crite-

ria has been met for all the subproblems, the cut con-

straints from these problems are collected (lines 21-

22). The cuts from subproblems are also valid for the

original problem with all the scenarios. These cuts are

used as the initial set of cut constraints for applying

the multicut Bender’s method to the original stochas-

Algorithm 1: Split-and-Merge (SAM).

abovecaptionskipabovecaptionskipxleftmargin

1 Input: S (set of scenarios), Original Stochastic

Program (P)

2 Divide S into n clusters, S

, S

, ...., S

3 Generate n stochastic programs, P

, P

, ...., P

, with

4 scenarios from S

, S

, ...., S

, respectively

5 Scale scenario probabilities in each of these

subproblems

6 such that they sum up to 1

8 #pragma omp parallel for

9 for i in range(1,n):

10 scosts

= [] #scenario costs

11 cuts

= [] #scenarios cut constraints

12 while r

< r or hasConverged(i):

13 x

= solveStage1(P

, scosts

, cuts

)

14 scosts

, cuts

= solveStage2(x

)

15 r

+ 1

16 end while

18 #wait until all the subproblems have returned

19 cuts = []

20 scosts = []

21 for i in range(1,n):

22 cuts.add(getCutConstraints(P

))

24 #now solve the original problem

25 while not hasConverged(P):

26 x = solveStage1(P, scosts, cuts)

27 scosts, cuts = solveStage2(x)

28 end while

tic linear program.

There are several beneﬁts of this approach. The

chances of a scenario having active cuts is higher in

the subproblems because of the smaller number of

scenarios present in the subproblems. Scenario cut

activity helps in generating newer and different cuts

for those scenarios, and thus doing more useful work,

as compared to the original problem in which most of

the scenarios remain inactive in the initial iterations.

Stage 1 optimization is often a serial bottleneck

in Bender’s decomposition, especially when the num-

ber of scenarios is large. In the decomposition ap-

proach, the number of scenarios per subproblem are

much smaller than the original problem, which speeds

up the Stage 1 optimization and thus the candidate so-

lutions for Stage 2 evaluation become available much

earlier. Additionally, this also gives an opportunity to

have parallelism in Stage 1, in addition to the obvious

Stage 2 parallelization available in stochastic linear

programs. These subproblems being independent of

each other, can be optimized in parallel in Stage 1.

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

220

4 INITIAL RESULTS

Our initial experiments of the proposed SAM ap-

proach are based on a military aircraft allocation

problem. The U.S. Tanker Airlift Control Cen-

ter (TACC) has to allocate aircraft to various mis-

sions and wings one month in advance to the ac-

tual scheduling of those aircraft. The demands of

these missions and wings are not known in advance

and are subject to enormous uncertainty even during

peacetime. We formulated the problem as a two-stage

stochastic program in which aircraft are allocated to

different wings and missions in Stage 1. In Stage

2 these allocations are evaluated by scheduling these

aircraft for various missions once the demands are re-

alized in a scenario. More details of the problem and

its stochastic formulation can be found in (Langer,

2011; Baker et al., 2012).

For our experiments, we took a problem that al-

locates aircraft for a period of 10 days. We consider

120 scenarios. For this problem, Stage 1 has 270 vari-

ables and 180 constraints, while Stage 2 has 25573

variables and 16572 constraints per scenario. All the

experiments were done on the same number of cores,

on a machine with Intel HP X5650 2.66Ghz 6C Pro-

cessor.

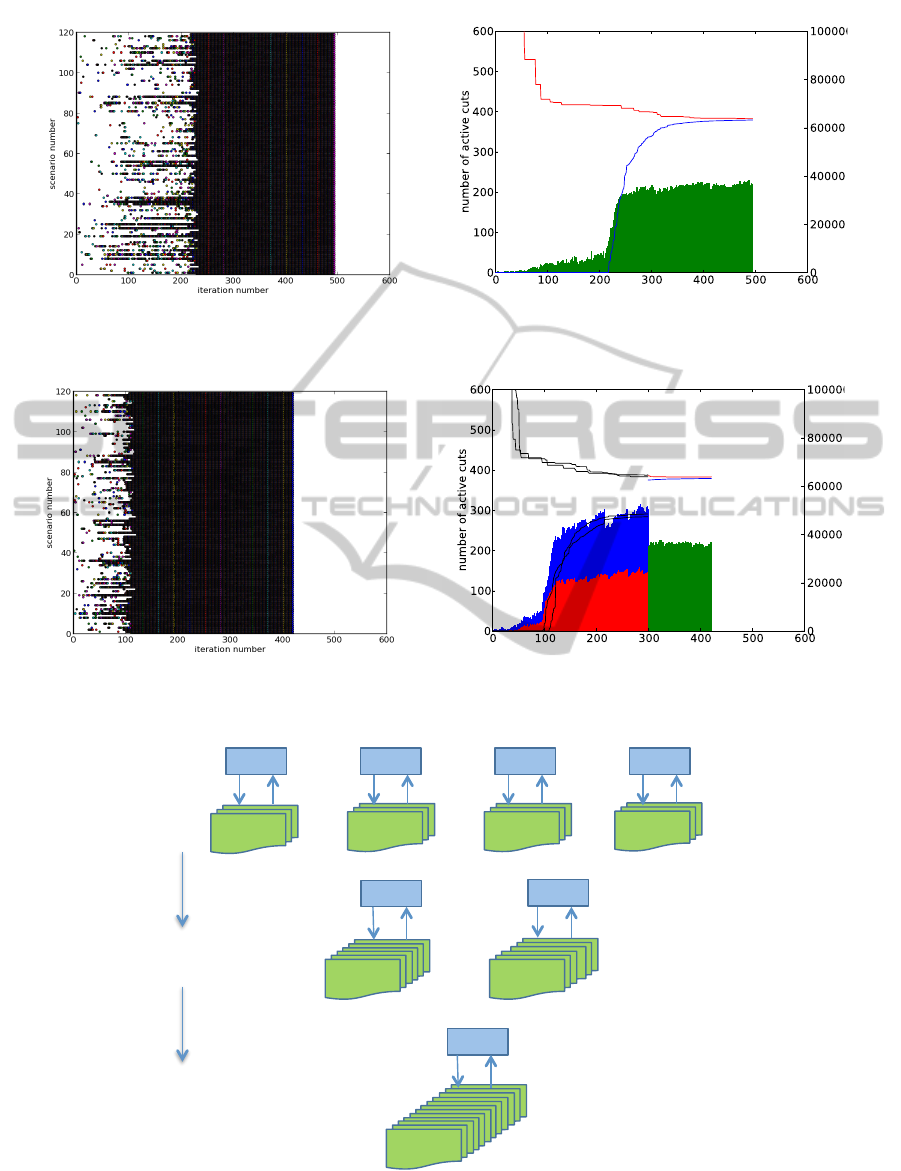
In Figure 1(a), we show the scenarios that have

active cuts in Stage 1 in each iteration of the Bender’s

multicut method. The x-axis is the iteration number,

and y-axis is the scenario number. In the vertical line

corresponding to any iteration number, a dot in the

horizontal line corresponding to a scenario number

means that a cut obtained from the Stage 2 optimiza-

tion of that scenario was active in that iteration. As

can be seen in the ﬁgure (Figure 1(a)), very few sce-

narios have active cuts in the initial few rounds. As

the optimization progresses, the number of scenarios

with active cuts increases with the increase in the it-

eration number. And eventually, after approximately

220 iterations, all the scenarios have active cuts in

Stage 1. The total number of active cuts in each iter-

ation are shown in Figure 1(b). Red color line shows

the upper bound, and the blue color line shows the

lower bound as the number of iterations increase.

For testing the proposed SAM algorithm, we di-

vided the original problem with 120 scenarios into

two subproblems each with 60 scenarios. The sub-

problems are solved for a maximum of 300 rounds,

after which the cut constraints are collected from both

of them and these cut constraints are used as the ini-

tial set of constraints for solving the original problem

with 120 scenarios. Figure 2(a) shows the scenario ac-

tivity for this method. As can be seen in the ﬁgure, the

overall scenario activity is much higher in the initial

iterations of the SAM approach than in the original

Bender’s method. Figure 2(b) shows the number of

cuts that were active in each of the subproblems. Red

bars correspond to P

, and blue bars correspond to

. The bars are stacked on top of each other to show

the total number of active cuts in both the subprob-

lems. Green bars show the number of active cuts for

the original problem (P), which begins optimization

at iteration 301. Black lines correspond to the lower

and upper bounds of the subproblems, and as in Fig-

ure 1(b) blue, red lines correspond to the lower, upper

bounds of the original problem, respectively. Total

time to optimization is 784 seconds with the SAM ap-

proach as compared to 1190 seconds with the original

Bender’s method.

We have extended our algorithm to split-and-

hierarchical-merge (SAHM) algorithm, in which the

merging of the subproblems into the original problem

is done in stages instead of at once as in the SAM

algorithm. Figure 3 shows a schematic diagram of

the SAHM approach. We tested the SAHM approach

by dividing the original problem into 6 subproblems

each with 20 scenarios. In the ﬁrst stage, a set of 2

subproblems combine to form one subproblem, giv-

ing a total of 3 subproblems. In the second stage,

these three subproblems are combined into the orig-

inal problem. Each of these stages is executed for 150

rounds, after which optimization of the original prob-

lem begins. Figure 4 shows the cut activity for this

setup. Total time to solution using SAHM was 507

seconds, giving us an improvement of 58% over the

Bender’s method.

5 FUTURE WORK

We plan to evaluate and extend the proposed scenario

decomposition schemes in the following ways:

• Try decomposing the problem into different num-

ber of subproblems, and determine the optimal

subproblem size.

• Exhaustively study the SAHM scheme.

• Currently, the number of rounds for which the

subproblems are executed before they are merged

is hard-coded by the user/programmer. An impor-

tant milestone is to dynamically determine during

the execution of the program, the optimal time to

merge the subproblems into the original problem.

This could be based on the cut activity of the sub-

problems.

• Use distributed computing to solve the stochas-

tic linear programs. As discussed in Section 3

Split-and-MergeMethodforAcceleratingConvergenceofStochasticLinearPrograms

221

(a) Scenario Activity

Iteration number

(b) Cut Activity

Figure 1: Multicut Benders Method. Total Iterations = 495, Time to Solution = 1190s.

(a) Scenario Activity

Iteration number

(b) Cut Activity

Figure 2: SAM with decomposition into 2 subproblems for 300 iterations. Total Iterations = 415, Time to Solution = 784s.

Stage&2&

Scenarios&

Stage&2&

Scenarios&

Stage&2&

Scenarios&

Stage&2&

Scenarios&

Stage&1& Stage&1& Stage&1& Stage&1&

Stage&2&

Scenarios&

Stage&2&

Scenarios&

Stage&1&

Stage&2&

Scenarios&

Stage&1&

Figure 3: Hierarchical Scenario Decomposition Scheme.

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

222

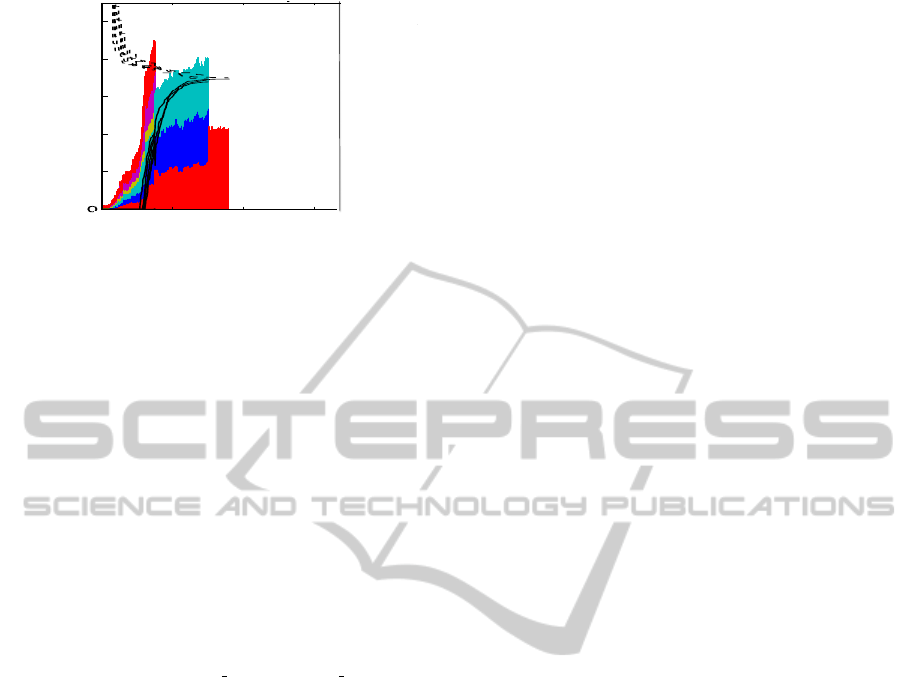
Number'of'ac,ve'cuts'

500

400

300

200

100

0 100 200 300 400 500 600

iteration number

100000

80000

60000

40000

20000

Figure 4: SAHM with decomposition into 6 subproblems

for 150 iterations followed by 3 subproblems for 150 itera-

tions. Total Iterations = 360, Time to Solution = 507s.

scenario decomposition gives us Stage 1 paral-

lelism in addition to the Stage 2 parallelism al-

ready available in stochastic linear programs. This

can be used to increase the parallel efﬁciency of

stochastic linear programs.

REFERENCES

Baker, S., Palekar, U., Gupta, G., Kale, L.,

Langer, A., Surina, M., and Venkataraman,

R. (2012). Parallel Computing for DoD Air-

lift Allocation. MITRE Technical Report, 2012.

www.mitre.org/work/tech papers/2012/11 5412/.

Benders, J. (1962). Partitioning Procedures for Solving

Mixed Variables Programming Problems. Numerische

Mathematik 4, pages 238–252.

Birge, J. and Louveaux, F. (1988). A Multicut Algorithm

for Two-stage Stochastic Linear Programs. European

Journal of Operational Research, 34(3):384–392.

Dagum, L. and Menon, R. (1998). OpenMP: An

Industry-Standard API for Shared-Memory Program-

ming. IEEE Computational Science & Engineering,

5(1).

Langer, A. (2011). Enabling Massive Parallelism for Two-

Stage Stochastic Integer Optimizations: A Branch

and Bound Based Approach. Master’s thesis, De-

partment of Computer Science, University of Illinois.

http://hdl.handle.net/2142/29700.

Langer, A., Venkataraman, R., Palekar, U., Kale, L. V.,

and Baker, S. (2012). Performance Optimization of

a Parallel, Two Stage Stochastic Linear Program: The

Military Aircraft Allocation Problem. In Proceedings

of the 18th International Conference on Parallel and

Distributed Systems (ICPADS 2012), Singapore.

Linderoth, J. and Wright, S. (2003). Decomposition algo-

rithms for stochastic programming on a computational

grid. Computational Optimization and Applications,

24(2):207–250.

Magnanti, T. L. and Wong, R. T. (1981). Accelerating

Benders Decomposition: Algorithmic Enhancement

and Model Selection Criteria. Operations Research,

29(3):464–484.

Rockafellar, R. T. and Wets, R. J.-B. (1991). Scenar-

ios and Policy Aggregation in Optimization Under

Uncertainty. Mathematics of operations research,

16(1):119–147.

Ruszczy

nski, A. (1986). A regularized decomposition

method for minimizing a sum of polyhedral functions.

Mathematical programming, 35(3):309–333.

Van Slyke, R. M. and Wets, R. (1969). L-shaped Linear

Programs with Applications to Optimal Control and

Stochastic Programming. SIAM Journal on Applied

Mathematics, 17(4):638–663.

Split-and-MergeMethodforAcceleratingConvergenceofStochasticLinearPrograms

223