TextTrail

A Robust Text Tracking Algorithm In Wild Environments

Myriam Robert-Seidowsky

, Jonathan Fabrizio

and S´everine Dubuisson

LRDE-EPITA, 14-16, rue Voltaire, F-94276, Le Kremlin Bicˆetre, France

CNRS, UMR 7222, ISIR, F-75005, Paris, France

Keywords:

Text Tracking, Particle Filter, Likelihood Function, Tangent Distance.

Abstract:

In this paper, we propose TextTrail, a new robust algorithm dedicated to text tracking in uncontrolled envi-

ronments (strong motion of camera and objects, partial occlusions, blur, etc.). It is based on a particle ﬁlter

framework whose correction step has been improved. First, we compare some likelihood functions and in-

troduce a new one which integrates tangent distance. We show that this likelihood has a strong inﬂuence on

the text tracking performances. Secondly, we compare our tracker with a similar one and ﬁnally an example

of application is presented. TextTrail has been tested on real video sequences and has proven its efﬁciency.

In particular, it can track texts in complex situations starting from only one detection step without needing

another one to reinitialize the model.

1 INTRODUCTION

With the increasing amount of videos, automatic text

extraction has become an essential topic in the com-

puter vision application ﬁeld. Whereas many works

have already been published on text detection and its

extraction in single images, video context has been

still little investigated. To extend detection process

from an image to a video sequence, a simple way is

to apply a detector on each frame. However, this is

not optimal. First, because the detection process may

be very time consuming, especially for high textured

frames. Secondly, because this “naive” approach does

not provide the matching information between detec-

tions in consecutive frames. However, these associa-

tions are needed for some applications.Visual tracking

algorithms are a solution for such purpose: they at-

tempt to predict the position of text areas at each time

step by using previous information and then provide

some stability of detections or estimations with time.

We could cite a lot of target applications for which

text tracking is important, such as automatic text ex-

traction for indexation, text-to-speech (for example

for visually-impaired persons) or online text transla-

tion (for example for tourists). In these cases, tracking

can improve the ﬁnal transcription through redundant

information and provides only one transcription per

text area. It can also be fundamental in online text re-

moval: if one speciﬁes a text to erase within a frame, a

removalprocess can be automatically propagated over

the whole sequence by using inpainting algorithms.

Thus, the main goal of text tracking is to collect a list

of associated text regions throughout a sequence by

minimizing the number of detection steps, as this step

can be very time consuming.

State of the art about text tracking is quite re-

stricted. Phan et al. (Phan et al., 2013) used the

Stroke Width Transform to estimate a text mask in

each frame. SIFT descriptors in keypoints from

the mask are extracted and matched between two

frames. Because only text pixels are tracked, it

is robust to background changes but, unfortunately,

only handles static or linear motions. Most of re-

cent approaches (Tanaka and Goto, 2008; Merino and

Mirmehdi, 2007; Minetto et al., 2011) use a particle

ﬁlter. Merino et al. (Merino and Mirmehdi, 2007)

proposed a method for text detection and tracking

of outdoor shop signs or indoor notices, that han-

dles both translations and rotations. Here, SIFT de-

scriptors are computed in each component of a de-

tected word (that is supposed to be a letter). Tanaka et

al. (Tanaka and Goto, 2008) suggested two schemes

for signboard tracking: (i) a region-based matching

using RGB colors, and (ii) a block-based matching.

In all prior algorithms, also known as tracking-by-

detection, text is ﬁrst detected in each frame, then

“tracked” between frames, by using a matching step

that associates detected text areas. However, a recent

algorithm, Snoopertrack (Minetto et al., 2011), de-

268

Robert-Seidowsky M., Fabrizio J. and Dubuisson S..

TextTrail - A Robust Text Tracking Algorithm In Wild Environments.

DOI: 10.5220/0005292002680276

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 268-276

ISBN: 978-989-758-091-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

tects text every 20 frames, and tracks it between them,

using HOGs as feature descriptors.

In this paper, we focus on text tracking. Our al-

gorithm, called TextTrail relies on the particle ﬁlter

framework, well known to handle potential erratic and

fast motion. Our tracker is initialized using our pre-

vious work on text localization in single images (Fab-

rizio et al., 2013). This detector is restricted to block

letters text in a Latin alphabet, but could easily be ex-

tended to other alphabet by adapting its learning pro-

cess. Compared to the state of the art, our algorithm

TextTrail can accurately track text regions during a

long time (hundreds of frames) without needing to

reinitialize the model(s) with new detections. We in-

troduce a new likelihood used in the correction step of

the particle ﬁlter which uses the tangent distance be-

tween grayscale patches. This likelihood function has

been studied and compared with other ones including

common ones relying on Bhattacharyya distance be-

tween HOG descriptors (Medeiros et al., 2010; Tuong

et al., 2011; Breitenstein et al., 2009). Our tests

show that the tangent distance is really suitable for

text tracking purposes. The paper is organized as fol-

lows. In Section 2 we quickly introduces the particle

ﬁlter and the tangent distance. Then, in Section 3, we

expose different likelihoods for text tracking before

proposing a new one (the one we use in TextTrail).

We compare them in Section 4 and evaluate TextTrail

performances. We also compare our approach with a

similar one. In addition we illustrate its interest by

integrating it into a complete scheme of application.

Concluding remarks are ﬁnally given in Section 5.

2 BACKGROUND

2.1 Particle Filter

The particle ﬁlter (PF) framework (Gordon et al.,

1993) aims at estimating a state sequence {x

}

t=1,...,T

whose evolution is given, from a set of observations

}

t=1,...,T

. From a probabilistic point of view, it

amounts to estimate for any t, p(x

1:t

). This can be

computed by iteratively using Eq. (1) and (2), which

are respectively referred to as a prediction step and a

correction step.

p(x

1:t−1

) =

t−1

p(x

t−1

)p(x

t−1

1:t−1

)dx

t−1

(1)

p(x

1:t

) ∝ p(y

)p(x

1:t−1

) (2)

In this case, p(x

t−1

) is the transition and p(y

)

the likelihood. PF aims at approximating the above

distributions using weighted samples {x

(i)

, w

(i)

} of N

possible realizations of the state x

(i)

called particles.

In its basic scheme, PF ﬁrst propagates the particle set

(i)

t−1

, w

(i)

t−1

} (Eq. (1)), then corrects particles’ weights

using the likelihood, so that w

(i)

∝ p(y

(i)

), with

∑

i=1

(i)

= 1 (Eq. (2)). The estimation of the pos-

terior density p(x

1:t

) is given by

∑

i=1

(i)

where δ

(i)

are Dirac masses centered on particles x

(i)

A resampling step can also be performed if necessary.

2.2 Tangent Distance

Tangent Distance (TD) allows to robustly compare

two patterns against small transformations. It was

ﬁrst introduced by Simard et al. (Simard et al.,

1992) and was mostly used for character recogni-

tion (Schwenk and Milgram, 1996), but also for face

detection and recognition (Mariani, 2002), speech

recognition (Macherey et al., 2001) and motion com-

pensation (Fabrizio et al., 2012).

To compare two patterns I and J, the Euclidean

distance is not efﬁcient as these two patterns may un-

dergo transformations. With TD, a set of potential

transformations is modeled. As these transformations

are not linear, we consider an approximation with lin-

ear surfaces. Here, the Euclidean distance is not com-

puted between the two patterns, but between the two

linear surfaces. Obviously, amplitudes of these trans-

formations are unknown. In our case, we model trans-

formations only on one pattern (in this example J). If

we note d

(., .) the Euclidean distance, the TD is:

min(d

(I, J +

∑

i=1

)) (3)

with V

the tangent vector of i-th modeled transfor-

mation and λ

its contribution. In this minimization

scheme, I and J are known. Tangent vectors can be

computed numerically or analytically. On the con-

trary, all coefﬁcients λ

are unknown: the result of the

minimization gives their optimal values.

3 PROPOSED APPROACH

3.1 Framework

We propose an algorithm which robustly tracks mul-

tiple text areas in video sequences using a PF. For the

initialization step, text regions are detected in the ﬁrst

frame using the detector proposed in (Fabrizio et al.,

2013), and used as models in the rest of the sequence

without any update. We use one PF per model to

TextTrail-ARobustTextTrackingAlgorithmInWildEnvironments

269

track. Note that we initialize once our tracker in or-

der to see how long the algorithm can track text areas

without needing updating their models: we can then

not detect text that appears over time. The dimension

of the box surrounding each text area is supposed to

be constant: the state vector x

of each PF contains

the coordinates (x, y) of its top left corner. Because

no prior knowledge on motion is taken into account,

particles are propagated within a very large search

space (circle of radius 40 pixels). Each particle x

(i)

i = 1, . . . , N (with N = 200) is here an hypothetical

state (i.e. a possible position for the tracked text area

top left corner). Its weight is given by w

(i)

= e

−αd

with d a distance between the description of the par-

ticle and the one of the model, and the correction pa-

rameter α a positivevalue to ﬁx (see Section 4). When

the region of a particle is partially outside the image,

its description is computed only into its visible part

and ditto for the model. Note that, at each iteration

of a PF, a basic multinomial resampling is performed

from the discrete distribution given by the normalized

weights w

(i)

One of the main challenges in tracking algorithms

is to ascertain which feature descriptors and distance

d between them best discriminate the tracked object

from the rest of the frame. The particles’ weights

should be the most relevant possible. Below, we com-

pare two distances (Bhattacharyya distance (Bhat-

tacharyya, 1943) and TD previously exposed) inte-

grating different descriptors.

3.2 Bhattacharyya Distance between

HOGs and Extension

As feature descriptors for text area(s) to track, an

HOG (Dalal and Triggs, 2005) is computed into each

text area by quantizing gradient orientations into 9

bins (8 orientations plus an extra bin for counting

the negligible gradient amplitudes i.e. homogeneous

zones). A particle and the model can be compared by

computing the Bhattacharyya distance (BD) noted d

between their corresponding normalized HOG.

If we consider two normalized histograms P and Q

with p

(resp. q

) the i

bins of P (resp. Q), i =

1, . . . , B with B the number of bins in the histograms,

the BD between P and Q is given by:

1−

∑

i=1

P(p

)Q(q

) (4)

The particles’ weights are given by w

(i)

= e

−αd

One of the drawback of HOG is that it does not in-

tegrate spatial information, and then not the shape of

letters. To overcome this limitation, we extend HOG

to Revisited Histogram of Oriented Gradient (RHOG)

by:

1. Computing HOG in the mask provided by the seg-

mented letters of the model given by the algorithm

in (Fabrizio et al., 2013) (Fig. 1) ;

2. Dividing the text area into 3× 3 blocks and com-

puting HOG in each block.

BDs are separately computed (on the 9 blocks and

on segmented letters) then averaged. If computing

BD between RHOGs permits to reﬁne the likelihood

function, it can however not handle rotations or scale

changes for example. That is why, to be robust to

small transformations, we introduce the TD into the

PF.

(a) Examples of particles with the mask used to

restrict the computation of HOG (b)

(b) Position of particles and

model in the current frame

the deduced mask

Figure 1: For each particle (a), HOG is computed into the

area restricted to the mask provided by the segmented letters

of the model (c).

3.3 Tangent Distance between Gray

Level Patches

Let J be the text area model and I the particle area

(both corresponding to gray level image patches). We

here consider M = 3 possible transformations of J:

horizontal and vertical stretching and rotation. First,

tangent vectors V

, i = 1, . . . , M are computed from

each model text areas only once in the algorithm.

Then, by minimizing the difference between I and

J (Section 2.2), we get contributions λ

for each

transformation. Applying these coefﬁcients λ

to the

model provides a prediction area noted K. Finally, the

TD noted d

is the difference pixel per pixel between

prediction K and particle I. The particles’ weights are

then computed so that w

(i)

= e

−αd

. The usage of TD

allows the tracker to handle small rotations and small

scale changes. We could have considered other trans-

formations such as illumination changes for example

but it would have been more time consuming.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

270

(a) (b)

Figure 2: Distance surfaces (c-e) computed between each area and the model ((a) magenta) in each pixel of the search space

((b) red). Surfaces are obtained with (c) BD(RHOG), (d) TD and, (c) combination of BD(RHOG) and TD.

3.4 BD and TD Combination

To compare the two previous distances i.e. BD and

TD, we have generated 3D surfaces deﬁned as fol-

lows. A text model was extracted in the ﬁrst frame of

a sequence (magenta rectangle and contours of seg-

mented letters, Fig. 2.(a)). The search space is deﬁned

in frame 6 as the square of 40× 40 pixels centered on

the previous top left corner estimation of the tracked

text area (red square, Fig. 2.(b)). We have chosen this

example because some text areas are visually simi-

lar to the model in this search space (the text epicerie

to track had similar color and shape to kebbab, pizza

and boissons). The distances are computed in each

pixel of this search space, giving surfaces shown in

Fig. 2.(c-e). These distance surfaces should have a

global minimum around the solution (close to the top

left corner location of the tracked text area) and a

slope to reach it. In such cases, w

(i)

= e

−αd

should

have high values.

Fig. 2.(c) shows the surface given by BD between

RHOGs: (BD(RHOG)). We can see that further par-

ticles have a high distance but this surface has no

peaked global minimum but rather presents a valley

along the text direction (horizontal). Then, all parti-

cles located in this latter have a high weight, even if

they are far from the solution. PF will provide an es-

timation in any point along the bottom of this valley.

That is not satisfactory because too much imprecise.

Fig. 2.(d) shows the surface given by TD between

gray level patches. It presents good properties to pre-

cisely localize the solution into a global minimum.

Unfortunately, the region around this global minimum

is too peaked. As this region is too narrow, only few

particles with high weight will contribute to the esti-

mation (weighted sum) of the tracked text. Elsewhere

TD gives approximately the same high values which

means that particles’ weights are low and irrelevant.

As (BD(RHOG)), TD seems not to be reliable be-

cause, integrated into PF, it requires that at least a few

particles are drawn near the solution. If not, PF will

diverge and then fail.

To take advantage of both presented conﬁgura-

tions, we propose to combine (multiply) BD(RHOG)

and TD. The usage of this combination (noted

BD(RHOG)×TD) in a particle ﬁlter gives a robust

text tracker. It is our selected solution called TextTrail.

The result of the combination is shown in Fig. 2.(e).

This surface has both the property of BD(RHOG) to

converge to the solution (valley), and the precision of

its localization (peak of TD surface). Thus, particles’

weights will be computed so that w

(i)

= e

−α(d

×d

)

TextTrail-ARobustTextTrackingAlgorithmInWildEnvironments

271

4 EXPERIMENTAL RESULTS

In this section, we evaluate TextTrail, our text track-

ing algorithm. First, we compare several likelihood

functions used in the framework of the PF: common

ones and new ones we build. We especially focus

on the impact of the TD on tracking performances to

validate the likelihood function we have introduced.

We have created a batch of video to prove the robust-

ness of our method. Secondly, we intended to com-

pare TextTrail with other algorithms but unfortunately

only a few are dedicated to text tracking and none

provides source codes. Nevertheless, performances

of Snoopertrack (Minetto et al., 2011) are given, and

datasets are online available, so we can compare our

method with their. Finally, to illustrate an interest of

our method, we integrate our text tracker into a com-

plete framework dedicated to online text removing in

video sequences.

4.1 Likelihood Evaluation

4.1.1 Our Challenging Dataset

To test the robustness of several likelihood functions,

the dataset must be as challenging as possible. Our

dataset contains seven 1280 × 720 pixel video se-

quences, captured in wild environment i.e. under un-

constrained conditions in natural scenes (indoor and

outdoor environments). These video and their associ-

ated ground truth (GT) are in the same XML format

as in ICDAR (ICDAR, 2013) and publicly available

Note that texts in those video are affected by many

and varied difﬁculties such as: translations, rotations,

noise, stretching, changing in point of view, partial

occlusions, cluttered backgrounds, motion blur, low

contrast, etc. Moreover, same texts can be close to

each others and share visual similarities, thus perturb

trackers. Fig. 4 shows some frame examples for each

video used in our experiment part.

4.1.2 Comparison of Conﬁgurations

We compare the efﬁciency of 5 trackers relying on

different conﬁgurations: BD(HOG), BD(RHOG),

TD, BD(HOG)×TD and BD(RHOG)×TD). For all

of them, the model(s) is(are) initialized in the ﬁrst

frame from their corresponding GT, then tracked

during 100 to 200 frames without any update of

model(s). To evaluate and compare the different con-

ﬁgurations, we compute the Fscore which combines

precision and recall, given by:

https://www.lrde.epita.fr/∼myriam

Precision =

Overlap

Sur f ace

Track

Recall =

Overlap

Sur f ace

Fscore =

2×(Precision×Recall)

Precision+Recall

This measure depends on the spatial overlap between

the non-rectangular areas of GT and prediction from

the tracker. Sur f ace

Track

is the number of pixels in

the predicted region and Sur face

is the number of

pixels in the GT. Overlap is the number of pixels in

both previous surfaces. Note that, because no one

of our proposed conﬁgurations handles size change

while GT does, it is impossible to reach a Fscore of

100% even if, visually the tracking seems to be cor-

rect. Due to the stochastic nature of PF, each tracker’s

Fscore is an average over 50 runs. Note that the cor-

rection parameter α used for weight computation has

a strong inﬂuence on the performance of the tracker:

it reshapes the proﬁle of the likelihood (Lichtenauer

et al., 2004) (Fontmarty et al., 2009) (Brasnett and

Mihaylova, 2007). Therefore, for a fair comparison

between each conﬁguration, we tuned its α so that it

yields best tracking results.

50 100 150 200 250 300 350 400

Fscore (%)

Number of particles

BD(HOG)

BD(RHOG)

BD(HOG)xTD

BD(RHOG)xTD

Figure 3: Convergence curves.

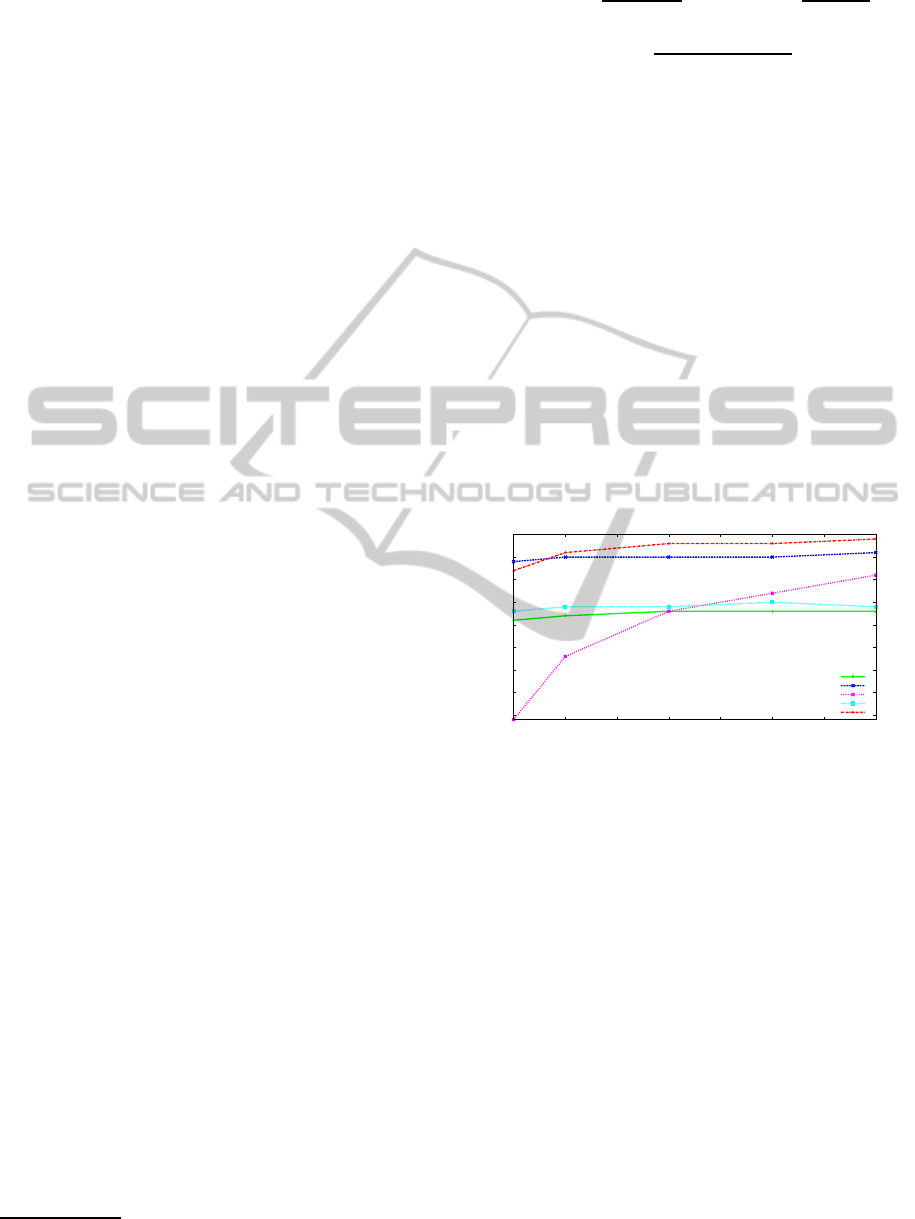
4.1.3 Likelihood Selection

Fig. 3 shows evolutions of Fscore values (aver-

age over 50 runs for each tracked text areas in

all test sequences) when number of particles N in-

creases. One can note that TD needs a lot of

particles to achieve a high Fscore. BD(HOG),

BD(RHOG) and BD(HOG)×TD are more stable

since they quickly converge. Best Fscores are pro-

vided by BD(RHOG)×TD (red curve) from N = 100

and are still slowly increasing with N. As most Fs-

cores are stabilized from N = 200, we have chosen to

perform our tests with this number of particles.

Table 1 presents Fscores (average over 50 runs

for each tracked text areas in all test sequences) with

N = 200. For each Fscore, the standard deviation over

the 50 runs is given in square bracket.

We can observe that TD often gives best Fscore

results, combined with BD(RHOG) or not. Because

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

272

Table 1: Fscores for all trackers with their optimal α value and N = 200. Max Fscores per text are represented in bold and

max average Fscores and min standard deviations in red.

Tracked texts

BD(HOG)

BD(RHOG)

BD(HOG)×TD

BD(RHOG)×TD

# Frames

Fig.3.1. LAVERIE 76.49 [0.60] 89.98 [1.70] 96.45 [0.36] 77.51 [1.02] 95.00 [0.84] 71

Fig.3.1. LIBRE 59.64 [1.88] 77.12 [1.06] 79.02 [7.71] 67.77 [7.08] 84.16 [7.61] 71

Fig.3.1. SERVICE 46.42 [2.34] 46.02 [10.29] 52.34 [13.27] 46.24 [2.65] 47.90 [9.2] 71

Fig.3.1. WASH 58.85 [1.22] 64.61 [1.36] 73.08 [8.14] 64.92 [2.84] 74.50 [3.90] 71

Fig.3.1. SERVICE 31,31 [2.07] 44,93 [7.88] 53,44 [4.81] 32,88 [1.79] 51,74 [10.59] 71

Fig.3.2. DEFENSE 82.69 [0.90] 86.35 [1.39] 72.73 [12.29] 82.73 [0.91] 87,55 [4.75] 207

Fig.3.2. FUMER 37.61 [8.46] 78.24 [4.68] 48.51 [28.09] 53.97 [5.21] 84.61 [6.71] 207

Fig.3.3. THERMOS 58.10 [2.76] 78.29 [0.11] 87.59 [0.04] 62.04 [4.57] 78.15 [0.34] 134

Fig.3.4. RESTAURANT 83.40 [0.62] 88.93 [0.20] 47.46 [3.98] 61.10 [15.46] 81.75 [0.54] 201

Fig.3.5. CONTROL 75.83 [0.25] 78.76 [0.40] 83.32 [0.19] 78.11 [0.44] 83.47 [0.11] 131

Fig.3.6. VOYAGE 86.50 [0.81] 95.34 [1.38] 9.37 [7.97] 84.04 [0.56] 92.44 [1.50] 159

Mean 63.35 75.32 63.94 64.66 78.30

Std 19.18 16.90 24.72 15.94 15.24

of the too much peaked global minimum of TD (see

Section 3), its results are not stable: Fscores can be

either high (Laverie) or low (Voyage). Its standard

deviation is higher than other ones. Therefore, the

unreliability of TD makes it unusable alone. When

it low-performs, its combination with BD(RHOG) al-

lows to reach an higher Fscore (see for example the

case of words Fumer or Voyage).

Notice also, that the RHOG always improves re-

sults compared to HOG (except for Service) when it

is used alone or combined with the TD. This conﬁrms

that the addition of the computation of the HOG on

the boundaries of letters is a powerful improvement.

On words Service, all results are poor. In fact,

the two occurrences of word Service (Fig. 4.1) affect

all trackers because these words are swapped while

tracking. This explains also the high standard devia-

tion of trackers.

Over all tracked texts, our text tracker (called Text-

Trail) with BD(RHOG)×TD combination, gives on

average the higher Fscore (78.3%) on our challenging

video sequences. These experiments have shown that

it is efﬁcient and outperformsa classical approach like

BD(HOG). It takes advantages of both approaches,

the global coarse solution of the BD(RHOG) and the

local and precise solution of the TD.

4.2 Comparison with Another

Approach

Here, we compare our TextTrail with Snooper-

Track (Minetto et al., 2011) in terms of scores and

computation times. Algorithm SnooperTrack re-

lies on detection steps processed every 20 frames:

model(s) of their tracked text(s) are then regularly up-

dated. On the contrary, our method only initializes

models by detecting text areas in the ﬁrst frame and

keeps the corresponding model(s) constant during the

whole sequence. These approaches are not “fairly

comparable” but SnooperTrack seems to be the most

similar online available algorithm. The comparison is

done on their dataset which is publicly available using

evaluation protocol described in (Lucas, 2005). Note

that our algorithm has been executed on a machine In-

tel i5-3450



, 3.1GHz, 8GB of RAM, coded in C++

with our library Olena (Levillain et al., 2010) without

optimization.

Table 2 gives for each video of the dataset, recalls,

precisions, Fscores and average processing times per

frame obtained by TextTrail and SnooperTrack.

One can see that in average on these 5 sequences,

TextTrail reaches the higher Fscore (0.67) and the

higher precision (0.74) rates. Moreover, it is on aver-

age more than two times faster (0.21 sec. per frame)

than the other method (0.44 sec. per frame). Note

that we do not know if computation times of Snoop-

erTrack also include detection times or just tracking.

Apart for the video “Cambronne”, our average com-

putation times are 5.5 times faster (0.0775 sec. per

frame). Note that “Cambronne” sequence is partic-

ular as it contains many text areas localized on the

frame borders: models, restricted to the visible part

of the particle, have to be recomputed. We have not

optimized this part of our algorithm, which explains

the higher computation times obtained for this video.

Our precision rates are always higher (0.74 vs.

TextTrail-ARobustTextTrackingAlgorithmInWildEnvironments

273

1 2 3

4 5 6

Figure 4: Our challenging video sequences. 1-2: motion blur, 3-4: partial occlusion, 5: rotation, 6: cluttered background.

Zoom on text models to track (extracting from the ﬁrst frame) are given above each frame.

Table 2: Comparison of performances and execution times between our tracker

TextTrail and the tracker with detection (every

20 frames)

SnooperTrack. Max recall, precision and Fscores per video in bold and minimum average computation times (in

seconds) per frame in bold.

Recall Precision Fscore T(s)

Video

SnooperTrack TextTrail SnooperTrack TextTrail SnooperTrack TextTrail SnooperTrack TextTrail

v01-Bateau 0.80 0.80 0.55 0.80 0.63 0.80 0.19 0.03

v02-Bistro 0.74 0.67 0.57 0.77 0.64 0.72 0.45 0.15

v03-Cambronne 0.53 0.51 0.60 0.67 0.56 0.58 0.88 0.73

v04-Navette 0.70 0.39 0.73 0.74 0.71 0.51 0.15 0.05

v05-Zara 0.70 0.71 0.60 0.73 0.63 0.72 0.55 0.08

Mean 0.69 0.62 0.61 0.74 0.63 0.67 0.44 0.21

0.61). This shows our prediction areas most of times

is included in the GT. However, our recall rate is lower

(0.62 vs. 0.69). As our model size is ﬁxed over time,

even if TD handle small size changes, our predicted

text area size does not change. This is why our recall

rates are smaller. Our predictions of text areas are

then well localized but the scale is not well adapted to

the GT to get higher recall rates.

Furthermore, “v04-Navette” sequence shows an

explicit example of limitation of our approach. In

this video, text area sizes are hardly changing with

time. Our algorithm succeeds to track text up the TD

reaches its limits i.e. when it can not manage high

scale changes. This is why we added a simple cri-

terion (based on the difference of prediction scores

in successive frames i.e. weight(s) of predicted text

area(s)) to stop our tracker(s) in such cases.

Thanks to the TD, robust to small transformations,

this is not necessary to include the corresponding

transformation parameters (scale, for example) into

the state. The state space dimension is then reduced

and we need fewer particles to get an efﬁcient track-

ing.

Without updating the model, TextTrail can track

during hundreds of frames, that prove its robustness.

In practice, to manage apparitions or high changes

in the model (occlusions, illumination, etc.), a detec-

tion step can be launched more often. But, compared

to SnooperTrack, we can track during more than 20

frames without needing to restart tracking from new

detections.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

274

Figure 5: Example of application of our text tracker. First column presents a series of frames (33, 68, 96, 136) with embedded

text. Second column gives binarized text area provided by a tracking and binarization process. Third column shows results of

“inpainted” frames.

4.3 Application: Text Removal

This section is dedicated to an example of applica-

tion of our text tracker. Our goal is to remove text

superimposed on frames of a video sequence. Text-

Trail can locate the text to remove in each frame. This

text is then removed using a classical inpainting algo-

rithm (Bertalmio et al., 2001). In practice, we manu-

ally select a text area in the ﬁrst frame of the video se-

quence, which is automatically tracked during the se-

quence. A binarization process then provides a mask

which precisely cutouts the text letters. The inpaint-

ing is automatically processed in each frame using

this mask.

Fig. 5 presents different frames of a video from

our dataset: frames with superimposed texts, after the

tracking and binarization process and ﬁnally results

of the inpainting procedure. One can see that the text

is correctly localized and then removed. Even if the

result is not “visually perfect”, no one can identify

that something was erased.

5 CONCLUSIONS

In this article, we have presented TextTrail, a new al-

gorithm for multiple text tracking in complex video

sequences relying on a particle ﬁlter framework. Even

if the particle ﬁlter framework is well known, the

novel idea here, is to combine the Bhattacharyya and

tangent distances in order to increase the efﬁciency

of the correction step which leads to a more robust

text tracker. According to our experiments, tangent

distance on gray level patches gives a good preci-

sion of the text and Bhattacharyya distance between

“revisited” HOGs adds information on the shape of

letters. High likelihood areas are well localized and

sufﬁciently smooth for the particle ﬁlter to keep a di-

versity of its state representation (i.e. position of the

tracked text area) via the particle set. Unlike clas-

sical approaches from the literature, we show that

our method can track text areas during long times in

video sequences containing complex situations (mo-

tion blur, partial occlusion, etc.) starting from only

TextTrail-ARobustTextTrackingAlgorithmInWildEnvironments

275

one detection step, that is less time consuming. In-

deed, our tracker is initialized by a detection step

and models are never updated, proving the efﬁciency

of the method. We also show our tracking can be

embedded into a complete framework dedicated to

text removal. If future works, we plan to overcome

the limitation of our approach and allow to manage

stronger transformations. A simple solution is to add

frequent detections to update the model(s). Another

solution is to extend the state space (add scale param-

eters for example). Usually, increasing the state space

means increasing the number of particles to achieve

good tracking performances. But, because tangent

distance can also handle small transformations, state

space should be sampled more coarsely, then using

fewer particles. We think that, even if we increase the

state space dimension, we probably will need fewer

particles to achieve lower tracking errors, and then

also reduce the computation times.

REFERENCES

Bertalmio, M., Bertozzi, A. L., and Sapiro, G. (2001).

Navier-stokes, ﬂuid dynamics, and image and video

inpainting. In CVPR, pages 355–362.

Bhattacharyya, A. (1943). On a measure of divergence

between two statistical populations deﬁned by their

probability distributions. Bulletin of Cal. Math. Soc.,

35(1):99–109.

Brasnett, P. and Mihaylova, L. (2007). Sequential monte

carlo tracking by fusing multiple cues in video se-

quences. Image and Vision Computing, 25(8):1217–

1227.

Breitenstein, M. D., Reichlin, F., Leibe, B., Koller-Meier,

E., and Gool, L. V. (2009). Robust tracking-by-

detection using a detector conﬁdence particle ﬁlter. In

ICCV, pages 1515–1522.

Dalal, N. and Triggs, B. (2005). Histograms of oriented

gradients for human detection. In CVPR, pages 886–

893.

Fabrizio, J., Dubuisson, S., and B´er´eziat, D. (2012). Motion

compensation based on tangent distance prediction for

video compression. Signal Processing: Image Com-

munication, 27(2):153–171.

Fabrizio, J., Marcotegui, B., and M.Cord (2013). Text de-

tection in street level image. Pattern Analysis and Ap-

plications, 16(4):519–533.

Fontmarty, M., Lerasle, F., and Danes, P. (2009). Likelihood

tuning for particle ﬁlter in visual tracking. In ICIP,

pages 4101–4104.

Gordon, N., Salmond, D., and Smith, A. (1993). Novel ap-

proach to nonlinear/non-Gaussian Bayesian state esti-

mation. IEE Proc. of Radar and Signal Processing,

140(2):107–113.

ICDAR (2013). ICDAR 2013 robust reading competition,

challenge 3: text localization in video.

http://dag.

cvc.uab.es/icdar2013competition/?ch=3

Levillain, R., Geraud, T., and Najman, L. (2010). Why and

howto design a generic and efﬁcient image processing

framework: The case of the milena library. In ICIP,

pages 1941–1944.

Lichtenauer, J., Reinders, M., and Hendriks, E. (2004). In-

ﬂuence of the observation likelihood function on ob-

ject tracking performance in particle ﬁltering. In FG,

pages 227–233.

Lucas, S. M. (2005). Text locating competition results. In

Proceedings of the Eighth International Conference

on Document Analysis and Recognition, ICDAR ’05,

pages 80–85.

Macherey, W., Keysers, D., Dahmen, J., and Ney, H.(2001).

Improving automatic speech recognition using tangent

distance. In ECSCT, volume III, pages 1825–1828.

Mariani, R. (2002). A face location and recognition sys-

tem based on tangent distance. In Multimodal inter-

face for human-machine communication, pages 3–31.

World Scientiﬁc Publishing Co., Inc.

Medeiros, H., Holgun, G., Shin, P. J., and Park, J. (2010).

A parallel histogram-based particle ﬁlter for object

tracking on simd-based smart cameras. Computer Vi-

sion and Image Understanding, (11):1264–1272.

Merino, C. and Mirmehdi, M. (2007). A framework towards

real-time detection and tracking of text. In CBDAR,

pages 10–17.

Minetto, R., Thome, N., Cord, M., Leite, N. J., and Stolﬁ, J.

(2011). Snoopertrack: Text detection and tracking for

outdoor videos. In ICIP, pages 505–508.

Phan, T. Q., Shivakumara, P., Lu, T., and Tan, C. L. (2013).

Recognition of video text through temporal integra-

tion. In ICDAR, pages 589–593.

Schwenk, H. and Milgram, M. (1996). Constraint tangent

distance for on-line character recognition. In ICPR,

pages 515–519.

Simard, P., LeCun, Y., Denker, J., and Victorri, B. (1992).

An efﬁcient algorithm for learning invariances in

adaptive classiﬁers. In ICPR, pages 651–655.

Tanaka, M. and Goto, H. (2008). Text-tracking wearable

camera system for visually-impaired people. In ICPR,

pages 1–4.

Tuong, N. X., M¨uller, T., and Knoll, A. (2011). Robust

pedestrian detection and tracking from a moving vehi-

cle. In Proceedings of the SPIE, volume 7878, pages

1–13.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

276