Non-Invasive Estimation of Blood Pressure through Genetic

Programming

Preliminary Results

Giovanna Sannino

1,2

, Ivanoe De Falco

and Giuseppe De Pietro

ICAR- CNR, Via P. Castellino 111, 80131 Naples, Italy

University of Naples Parthenope, Department of Technology, Naples, Italy

Keywords: Blood Pressure, Wearable Sensors, Heart Rate Variability, Plethysmography, Regression, Genetic

Programming.

Abstract: The hypothesis underlying this paper is that a nonlinear relationship exists between Electrocardiography

(ECG) and Heart Related Variability (HRV) parameters, plethysmography (PPG), and blood pressure (BP)

values. If this hypothesis is true, rather than continuously measuring the patient’s BP, a wearable wireless

PPG sensor can be applied to patient’s finger, an ECG sensor to his/her chest, HRV parameter values can be

computed and, through regression, both systolic and diastolic BP values can be indirectly measured. Genetic

Programming (GP) automatically both evolves the structure of the mathematical model and finds the most

important parameters in it. Therefore, it is perfectly suited to perform regression task. As far as it can be

found in the scientific literature of this field, until now nobody has ever investigated the use of GP to relate

parameters derived from HRV analysis and PPG to BP values. Therefore, in this paper we have carried out

preliminary experiments on the use of GP in facing this regression task. GP has been able to find a

mathematical model expressing a nonlinear relationship between heart activity, and thus ECG and HRV

parameters, PPG and BP values. The approximation error involved by the use of this method is lower than 2

mmHg for both systolic and diastolic BP values.

1 INTRODUCTION

Arterial blood pressure can be continuously

measured in real time and with no patient’s body

cannulation by means of the continuous non-

invasive arterial pressure (CNAP) method.

This method shows the positive features of two

clinical “gold standards”: firstly, blood pressure

(BP) is continuously measured in real time as it

takes place in the invasive arterial catheter system

(IBP), secondly it is non-invasive as it is the case for

the standard procedure based on upper arm

sphygmomanometer (NBP). Recently, results have

been promising in this field as concerns the features

of ease of use, accuracy, and clinical acceptance.

Currently a high demand exists for accurate and

easy-to-use CNAP-systems. Because of this, there is

an increasing focus on these devices by researchers,

practitioners and the related industry of medical

devices. The development of efficient BP

measurement instruments is facilitated by the use of

small yet powerful microcomputers, and by that of

digital signal processors as well. Small, cheap

devices of this kind allow for an easy processing of

complex and computationally intensive

mathematical functions. Researchers (Maguire,

2011) (von Skerst, 2008) have reported that invasive

catheters are used to continuously measure BP in

only a small fraction, between 15% and 18%, of

inpatient surgeries. The practical standard of care for

all the remaining inpatient surgeries, and for

outpatient surgeries as well, is, instead, constituted

by intermittent, non-invasive blood pressure

monitoring. Unfortunately, this latter monitoring

type has the feature of being discontinuous, which

implies possibly missing some dangerous

hypotensive episodes. As an example, when

monitoring women undergoing Caesarean section,

hypotensive phases were detected by CNAP in 39%

of the cases, but only in 9% by non-invasive

methods. As a further example, (Ilies, 2012) reports

that, when CNAP was used to measure systolic BP

values higher than 100mmHg, dangerous foetal

acidosis did not occur. Moreover, (Dueck, 2006)

241

Sannino G., De Falco I. and De Pietro G..

Non-Invasive Estimation of Blood Pressure through Genetic Programming - Preliminary Results.

DOI: 10.5220/0005318002410249

In Proceedings of the International Conference on Biomedical Electronics and Devices (SmartMedDev-2015), pages 241-249

ISBN: 978-989-758-071-0

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

reports that more than 22% of hypotensive episodes

were missed, thus leading to delayed treatments or

even no treatments at all.

Of course, it is very difficult to detect in-artery

pressure changes from outside the arteries

themselves, while it is quite easy to measure changes

in artery volume and flow. This can be accomplished

through the use of e.g. echography, light,

impedance, and so on. The problem is that there is

no linear correlation between these changes in

volume and the arterial pressure, especially when the

measurement takes place in the periphery, where it is

easier to access the arteries.

As a consequence, non-invasive devices must be

able to transform the volume signal measured at the

periphery into a corresponding for the arterial

pressure. Some techniques are based on vascular

unloading, tonometry, pulse transit time (PTT). This

latter relies on the fact that, each time a heart ejects

stroke volume towards arteries, the BP wave reaches

the periphery after a given transit time. PTT has an

indirect dependence on BP, namely it is known that

the higher the pressure, the faster PTT is. The non-

invasive detection of blood pressure changes can be

carried out thanks to this phenomenon (Sotera

wireless). The method has to be calibrated in order

to get absolute values. PTT-based techniques are

good examples of indirect ways for continuously

measuring blood pressure. In them, a measure is

continuously taken of other parameters, and a non-

linear relationship is hypothesized.

In the knowledge discovery area any problem as

this latter, in which a relationship between some

variables, called independent, and another one,

called dependent, is supposed, and the aim is to

search for the explicit form of the mathematical

model connecting them, is termed as a regression

problem. The term “independent” simply means that

these variables are the input variables to the

problem, and this does by no way imply that they are

not correlated one another. In traditional regression

analysis the user must specify the structure of the

mathematical model. Hypothesizing or

experimentally finding a good model is a very

laborious and time-consuming trial-and-error

procedure, and human minds may experience

difficulties in guessing which the most important

independent variables affecting the dependent one

are, and which the best formula relating them is.

Genetic Programming (GP) (Koza, 1992),

instead, automatically both evolves the structure of

the mathematical model and finds the most

important parameters in it. Therefore, it is perfectly

suited to perform regression task.

Nowadays wearable sensors are becoming more

and more widespread and cheap. Among them, chest

sensors able to capture electrocardiographic (ECG)

signals are frequently used. Starting from an ECG

signal, Heart Rate Variability (HRV) analysis can

easily extract a wide set of parameters describing

ECG activity of a patient. Moreover, wearable

wireless sensors can be applied to a patient’s finger

to compute plethysmography (PPG) values.

The hypothesis underlying this paper is that a

nonlinear relationship exists between PPG and heart

activity (and thus ECG and HRV parameters), and

blood pressure. If this hypothesis is true, rather than

continuously measuring the patient’s blood pressure,

a wearable wireless PPG sensor can be applied to

patient’s finger, a wearable wireless ECG sensor to

his/her chest, HRV parameter values can be

computed and, through regression, systolic and

diastolic blood pressure can be indirectly measured.

As far as it can be found in the literature of this

field, until now nobody has ever investigated the use

of GP to relate parameters derived from HRV

analysis and PPG to BP values. Therefore, in this

paper we carry out some preliminary experiments on

the use of GP in facing this regression task.

2 RELATED WORKS

Some papers exist in which the aim is the

investigation of the relationship between the blood

pressure and some other variables. In the following,

some of those papers are shortly described.

In (Meigas, 2007) the BP estimation method

relies on the hypothesis that a relationship exists

between the pulse wave velocity (PWV) in the

arteries and BP. Measuring PWV requires

registering two time markers. The first marker

depends on ECG R peak detection, whereas the

second on detecting the pulse wave in peripheral

arteries. Their experimental device for BP

monitoring is made of two analogue modules for the

acquisition of signals, namely one for ECG and

another for PPG signal. Namely, the ECG electrodes

are positioned on patient’s wrists, while a pulse

oximetry finger to register PPG is placed on a finger.

In (Najjar, 2008) the aim was the evaluation of

whether PWV can reliably predict the longitudinal

changes in systolic BP (SBP), and the incident

hypertension. The authors measured PWV at

baseline in 449 volunteers, partly normotensive and

partly untreated hypertensive. Their average age was

53±17. BP measurements were repeatedly carried

out during an average follow-up of 4.9 ± 2.5 years.

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

242

By considering covariates such as body mass index,

age, and mean arterial pressure, the authors applied

linear mixed effects regression models, and

concluded that PWV can independently determine

the longitudinal SBP increase.

In (Inajima, 2012) an attempt was made to

design and build a wearable sensor for BP

measurement. This sensor should have the features

of placing a lower burden on the examinees, of

being less influenced by patient’s physical

movements, and of being usable to continuously

measure BP. They modified the existing Moens-

Korteweg BP equation by hypothesizing that the

following relation exists: P

= b

/ T

PTT

+ b

where TPTT is the pulse-wave transit time, Ps is the

systolic BP, and coefficients b1 and b2 can be

derived by using measured values of an examinee’s

BP and measured values of T

PTT

. They implemented

a new system for the calculation of patient’s systolic

BP. This system made use of electrocardiography

and ear-lobe pulse waves. Through this system they

were able to estimate patients’ BP, and to also

directly measure patient’s arterial pressure. They

found that their methodology was able to correctly

capture trends in the variations in BP.

In (Gesche, 2012) the aim was the creation of a

function able to link SBP and PWV, and the testing

of its reliability in determining suitable absolute SBP

values by using a non-linear algorithm and a one-

point calibration. They asked 63 volunteers to

exercise to induce BP increase, and obtained this

nonlinear function: BP

PTT

= P1 * PWV * e

(P3*PWV)

P2 * PWV

– (BP

PTT,cal

- BP

cal

), with P1 = 700, P2 =

766,000, P3 = -1, and P4 = 9. BP

PTT,cal

is the BP

value, computed from PTT, corresponding to the BP

value measured by the reference method, while BP

cal

is the BP measured by the reference method (cuff) at

experiment beginning. This non-linear function was

used to compute BP values. Comparing SBP values

using the PTT-based method and those measured by

cuff resulted in a significant correlation.

This brief review shows that researchers are

striving to find a suitable relationship between

independent and dependent variables, yet this is

done at a high cost in terms of labour, time, and

experiments to find the values of the coefficients.

3 SIGNAL PROCESSING

The regulation of BP is traditionally described in

terms of homeostasis (Vukovich & Knill, 1980).

This is regulated by the autonomic nervous system

(ANS) due to two opposing divisions:

the sympathetic division and the parasympathetic

division. Heart rate variability (HRV) is a tool that

represents the balance between the sympathetic and

parasympathetic branches of the autonomic nervous

system. As shown in many studies (Berntson et al.,

1997; Electrophysiology et al., 1996; Karapetian,

Evaluation, & Research, 2008), HRV is considered

one of the most studied non-invasive biomarkers of

ANS activities, and it can be extracted by using a

wearable ECG sensor.

Furthermore, as demonstrated in (Golparvar,

Naddafnia, Saghaei, & Mahmood, 2002), the PPG is

a simple and low-cost optical technique that can be

used to detect blood volume changes in the micro-

vascular bed of tissue. The PPG is a physiological

waveform related to the sympathetic nervous system

activity (Allen, 2007), and it can be monitored by

using a wearable non-invasive finger pulse oximeter.

For these reasons we investigate here the

associations among HRV and PPG measurements

and the Systolic BP (SYS) and Diastolic BP (DIA)

to propose a mathematical model to calculate the

SYS and the DIA by using only a wearable ECG

sensor and a pulse oximeter.

To realize the mathematical model, the MIMIC

database (Goldberger et al., 2000), available on

physionet.org, was used. The MIMIC Database

includes data recorded from over 90 ICU patients.

The data include signals and periodic measurements

obtained from a bedside monitor as well as clinical

data obtained from the patient's medical record. The

files include qrs (ECG beat labels, all beats labelled

normal), al (annotations for alarms related to

changes in the patient's status), in (annotations

related to changes in the functioning of the monitor),

abp (arterial blood pressure), pap (pulmonary

arterial pressure), cvp (central venous pressure), and

ple (fingertip plethysmograph) annotations.

3.1 ElectroCardioGraphy

ECG signal is pre-processed by using Kubios

(Niskanen, Tarvainen, Ranta-Aho, & Karjalainen,

2004; Tarvainen, Ranta-Aho, & Karjalainen, 2002),

a Matlab-based software package for event-related

bio-signal analysis developed by the University of

Kuopio, Finland. Kubios is an advanced computer

program to extract and analyse HRV.

Standard linear HRV analysis is performed

according to the guidelines of the European Society

of Cardiology and the North American Society of

Pacing and Electrophysiology (Electrophysiology et

al., 1996). Additionally, nonlinear features are

computed according to the literature (Melillo,

Non-InvasiveEstimationofBloodPressurethroughGeneticProgramming-PreliminaryResults

243

Bracale, & Pecchia, 2011; Rajendra Acharya, Paul

Joseph, Kannathal, Lim, & Suri, 2006). All the

computed measures are summarized in Table 1.

3.2 Plethysmography and Arterial

Blood Pressure Pulse Waveform

PPG signal and the Arterial Blood Pressure (ABP)

pulse waveform are processed using a Matlab script

developed to automatically calculate the minimum

and the maximum values of PPG and the systolic

and diastolic blood pressure values from the ABP

waveform, as shown in Fig. 1.

Figure 1: An example of a record contains the ECG, the

ABP waveform and the PPG. The blue circles indicate the

systolic BP values; the red circles indicate the diastolic BP

values; the pink circles indicate the maximum PPG values;

the green circles indicate the minimum PPG values.

3.3 The Database

Starting from the MIMIC database (Goldberger et

al., 2000) a new dataset has been built to develop the

mathematical model.

The new database contains the HRV measures,

the BP measurements and the PPG measurements.

It is composed by 50 instances for each subject.

Each instance i in the new database is constituted by

the following information:

 sub_id: a number value to identify the subject;

 SYS_BP

: the average of the Systolic BP

computed in the i-th 1-minute time slot;

 DIA_BP

: the average of the Diastolic BP

computed in the i-th 1-minute time slot;

 Pleth_max

: the average of the maximum

values of PPG signal computed in the i-th 1-

minute time slot;

 Pleth_min

: the average of the minimum

values of PPG signal computed in the i-th 1-

minute time slot;

 f : a vector containing the 35 HRV measures

reported in Table 1;

Table 1: Linear and non Linear HRV features.

Measure Description (Unit)

Time Domain

Mean RR The mean of RR intervals (ms)

STD RR Standard deviation of RR intervals (ms)

Mean HR The mean heart rate (1/min)

STD HR Standard deviation of instantaneous heart rate

value (1/min)

RMSS Square root of the mean squared differences

between successive RR intervals (ms)

NN50 Number of successive RR interval pairs that

differ more than 50 m (count)

pNN50 NN50 divided by the total number of RR

intervals (%)

RR tri

index

The integral of the RR interval histogram

divided by the height of the histogram

TINN Baseline width of the RR interval histogram

(ms)

Frequency Domain

Peak freq.

VLF

VLF band peak frequencies (Hz)

Peak freq.

LF band peak frequencies (Hz)

Peak freq.

HF band peak frequencies (Hz)

Absol.

Pow. VLF

Absolute powers of VLF band (ms

)

Absol.

Pow. LF

Absolute powers of LF band (ms

)

Absol.

Pow. HF

Absolute powers of HF band (ms

)

Rel powers

VLF

Relative powers of VLF bands (%)

Rel powers

Relative powers of LF bands (%)

Rel powers

Relative powers of HF bands (%)

Normalized

powers LF

Powers of LF bands in normalized units

Normalized

powers HF

Powers of HF bands in normalized units

Total

power

Total Value for the spectral power (ms

)

LF/HF

ratio

Ratio between LF and HF band powers

EDR Electrocardiogram Derived Respiration (Hz)

NonLinear Domain

SD1 The standard deviation of the Poincarè plot

perpendicular to the line of identity (ms)

SD2 The standard deviation of the Poincarè plot

along to the line of identity (ms)

ApEn Approximate entropy

SampEn Sample entropy

Correlation Dimension

Short-term fluctuation slope in Detrended

Fluctuation Analysis

Long-term fluctuation slope in Detrended

Fluctuation Analysis

Mean line

length

Mean line length in RP (beats)

Max line

length

Maximum line length in RP (beats)

REC Recurrence Rate (%)

DET Determinism (%)

ShEn Shannon Entropy

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

244

Therefore, each instance is defined as follows:

=



;





;





;ℎ





;ℎ





;

In this paper we have considered four patients,

so our database contains 200 instances in total.

4 GENETIC PROGRAMMING

4.1 The General GP Framework

Genetic Programming (GP) (Koza, 1992) is a

heuristic optimization technique based on mimicking

in a computer mechanisms that are typical of the

evolution in natural populations. GP relies on a set,

called population, of solutions to a given problem. In

the population, individuals are programs that are

represented by tree structures, typically differing in

shape and size. In each individual the internal nodes

represent the functions, while the leaves represent

terminals, meaning with this both problem variables

and constant values. The program can be obtained

by reading the tree in pre-order (see Figure 2).

Figure 2: An example of a tree in Genetic Programming.

This example tree encodes for the following in-

order expression: 7.9 + (3.2 *y) –x.

A very delicate issue of GP is the choice of a

fitness function, i.e. a criterion which may represent

quantitatively the degree of goodness of any solution

at solving the problem faced. Of course, the choice

of a type of fitness depends on the problem at hand.

The search procedure executed by a GP tool is

described by the following pseudo-code:

• load the problem data (e.g. regression values);

• generate randomly an initial population of a

number of Pop_size individuals, each of which

represents a regression model;

• evaluate each individual through the use of a

suitable fitness function;

• at each generation repeat the following steps

until a new population is obtained:

o choose an operator among crossover,

mutation, and copy;

o select a number of individuals in current

population suited to the chosen operator;

o apply the operator chosen in order to generate

an offspring;

o insert the offspring in the new population;

o evaluate the new offspring through the use of

the fitness function;

• repeat the above step until a maximum number

of generations Max_gen is reached.

As the number of generations increases, better

and better solutions in terms of better fitness values)

to the original problem will very likely be found.

Selection is a mechanism that chooses the

individuals that will undergo the reproduction

process among those contained in the current

population. It should favour individuals with better

fitness values to be chosen more frequently, yet

allowing also worse individuals to be selected,

though with lower probability. For the experiments

described in this paper, the widely used tournament

selection has been used. In it, a number of tourn_size

individuals contained in the current population is

chosen in a random way, and the best among them in

terms of fitness is the one that is selected.

The three genetic operators work as follows:

Crossover. Two parent individuals are chosen,

are in each of them a subtree is randomly selected.

Then crossover swaps those subtrees from one

parent individual to the other. The respect of the

limit on the maximal depth allowed should be

ensured by this operator. If this condition is not

respected, then the too-deep offspring is discarded,

and one of the two parents, randomly selected,

becomes the new offspring.

Copy. One individual is randomly selected from

the current population and is copied in the new one.

Mutation. A node in the tree is randomly

selected, and starting from it a new subtree is

generated. The check is carried out that the depth

limit is not violated by this replacement. If this takes

place, this new offspring is discarded and the

original tree is copied into the new generation.

Each time an operator must be chosen, this

choice takes place on the basis of three probability

values for them: p_mutate is that for mutation,

p_cross for crossover, and p_copy for the direct

copy. The sum of these three values must be equal to

1. A random real value in [0.0, 1.0] is generated and

its value determines the operator that will be used.

Non-InvasiveEstimationofBloodPressurethroughGeneticProgramming-PreliminaryResults

245

4.2 GP for Regression

The goal of the use of GP for the regression problem

relies in automatically finding the modelling of the

relationship between the independent variables and a

dependent one, in this case the blood pressure. Thus,

given a fitness function, facing the regression

problem by GP consists in searching the model that

best describes the essential characteristics of this

relationship. Of course, an exhaustive search

performed by the complete enumeration of all the

possible models unviable from a computational

point of view. As a consequence, we make reference

here to GP. Being GP a heuristic method, it does not

guarantee that the global optimum will be achieved

yet it typically finds a suboptimal solution in a

computation time that is reasonable for the users.

The evolving population is composed by

‘formulas’, each of which represents one potential

regression model. These models are encoded as trees

with variable depth, and each of them is composed

by elementary functions and terminals. The function

set contains 11 well-known elementary functions,

and is reported in Table 2. In it, Arity is the number

of arguments a function has.

Table 2: The set of the symbols representing the

elementary functions, their description, and their arity.

Symbol Arity Description

+ 2 addition

- 2 subtraction

* 2 multiplication

/ 2 protected division (returns 1 if the

denominator is 0)

psqroot 1 protected square root (returns 0 for

negative operands)

plog 1 protected logarithm (rlog(0) is 0)

sqr square

tanh 1 hyperbolic tangent

sin 1 sine

cos 1 cosine

exp 1 exponential

The terminal set, instead, consists of 37 symbols

(the generic x

represents the i-th independent

variable in the database), plus the Const symbol,

representing a random constant value in a suitable

range. All these terminals have arity equal to 0.

In order to find the model, the available data is

suitably divided into three sets: the train, the test,

and the validation sets. The train set contains the

items onto which the approximation of the actual

output values will be carried out in the learning

phase. The generalization ability of the model

achieved is, instead, evaluated on the test set.

Finally, the real evaluation of algorithm’s

performance is carried out over the validation set.

If we denote by S the model represented by a

generic individual in the GP evolution, and if f is the

function that represents a regression model over n

instances, the fitness function Φ we use in this paper

is the Root Mean Square Error (RMSE), i.e.:

Φ=

∑(

(

)

−())









where S(i) is the value forecasted by the model on

the i-th item of the problem. In this way the

regression becomes a minimization problem.

5 EXPERIMENTS

We have empirically set the GP parameters values

at: Pop_size = 500, Max_gen = 200, tourn_size = 7,

p_mutate = 0.10, p_cross = 0.85, and p_copy =

0.05.

The database described in Section 3.3, composed

by 50 instances for each of the four patients, has

been divided into train, test, and validation sets.

Namely, for each patient, each item has been

randomly and exclusively assigned to one of the

three sets in this way: 44% for the train set, 32% for

the test set, and 24% for the validation set.

GP is a nondeterministic algorithm, which means

that its execution and its results depend on the initial

value assigned to a random seed. In order to get rid

of this feature, the GP algorithm has been run over

the database 25 times. Among the 25 runs, we

consider as the best one that in which the lowest

RMSE value over the validation set has been

achieved. In fact, the model found in that run shows

the best ability to correctly get totally unknown data,

so it has the highest generalization capability.

The formula achieved in the best run for the

systolic blood pressure is:

_

= 0.5064

0.6095



(



)



−0.5947tanh

ℎ_



−

−0.7316

_

0.7316sin

(

ℎ_

)

0.5857sin

(

sin

(

sin

(



)))



_

−sin

(

ℎ_

)

+1.112

Figure 3 reports how this formula allows fitting

the real systolic BP values over the three sets.

Namely, the top pane shows the behaviour over the

train set, the middle pane that over the test set, and

the bottom pane that over the validation set.

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

246

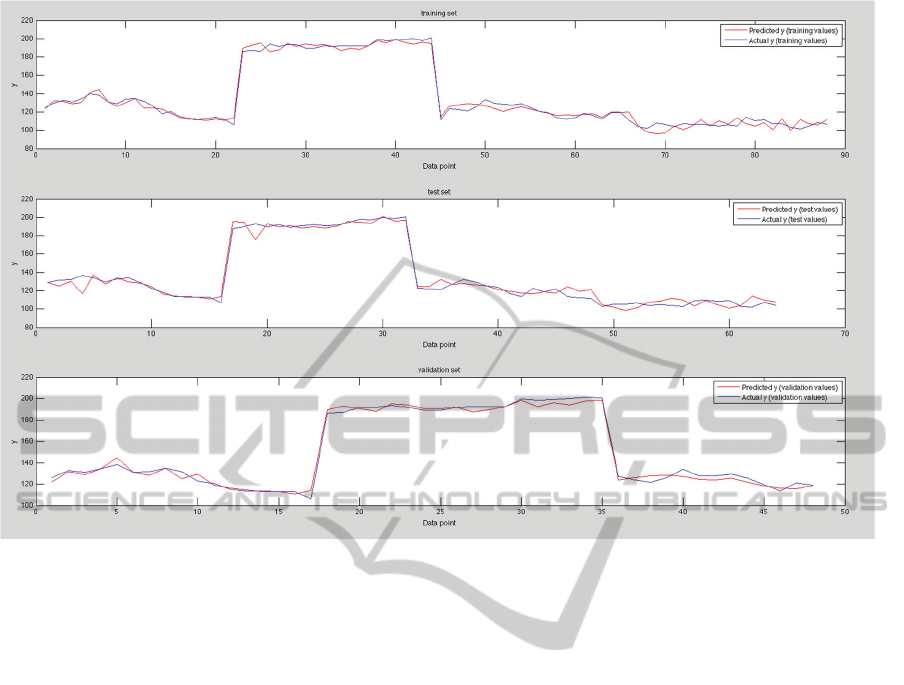
Figure 3: Results for systolic blood pressure.

The results over the validation set, i.e. over data

never learned by the GP algorithm, are very good,

and the RMSE is 3.3679. This means that, on

average, over previously unseen data any actual

systolic blood pressure value and the corresponding

computed one differ by ±√3.3679 = ±1.8352 mmHg,

which is an excellent approximation.

A very important result of the methodology used

is that it has allowed performing the automatic

selection, out of the 37 present in the database, of

the most important parameters for predicting the

values of the systolic blood pressure.

They have turned out to be five: Pleth_min,

Pleth_max, Mean HR, RR tri index, and EDR. This

task is extremely difficult for a human being,

however expert he can be of the field.

Similarly, the formula achieved in the best run

for the diastolic blood pressure is:

_

= 0.3132− 2.142ℎ_

+2.899tanhℎ

(

ℎ_+0.6855

)



+0.8554(sin

(

sin

(



))

+1.829tanh(

_

)−1.386

Figure 4 reports how this formula allows fitting

the real diastolic BP values over the three sets.

Namely, the top pane describes the behaviour over

the train set, the middle pane that over the test set,

and the bottom pane refers to the validation set.

For the diastolic pressure the results over the

validation set, never learned by the GP algorithm,

yield an RMSE value of 2.6692. In this case the

approximation of any actual diastolic blood pressure

value with its corresponding computed value over

previously unseen data is even better than that for

the systolic case, since their difference is now equal

to ±√2.6692 = ±1.6338 mmHg.

Here the automatic selection of the most

important independent parameters has resulted in

three of them, i.e.: Pleth_min, Mean HR, and EDR.

By looking at the two formulae, it can be seen

that some parameters are present in both, so they

strongly influence both pressure values. These

parameters are: Pleth_min, Mean HR, and EDR.

Also Pleth_max and RR tri index are important,

since they are contained in one of the two rules. A

result from these preliminary experiments is that

both PPG values and ECG-related ones are very

important to indirectly estimate BP values.

6 CONCLUSIONS

Continuous blood pressure measurement is an

important issue in the medical field. Of course, a

sphygmomanometer cannot be used to fulfil this

task, and alternative ways should found. One way

Non-InvasiveEstimationofBloodPressurethroughGeneticProgramming-PreliminaryResults

247

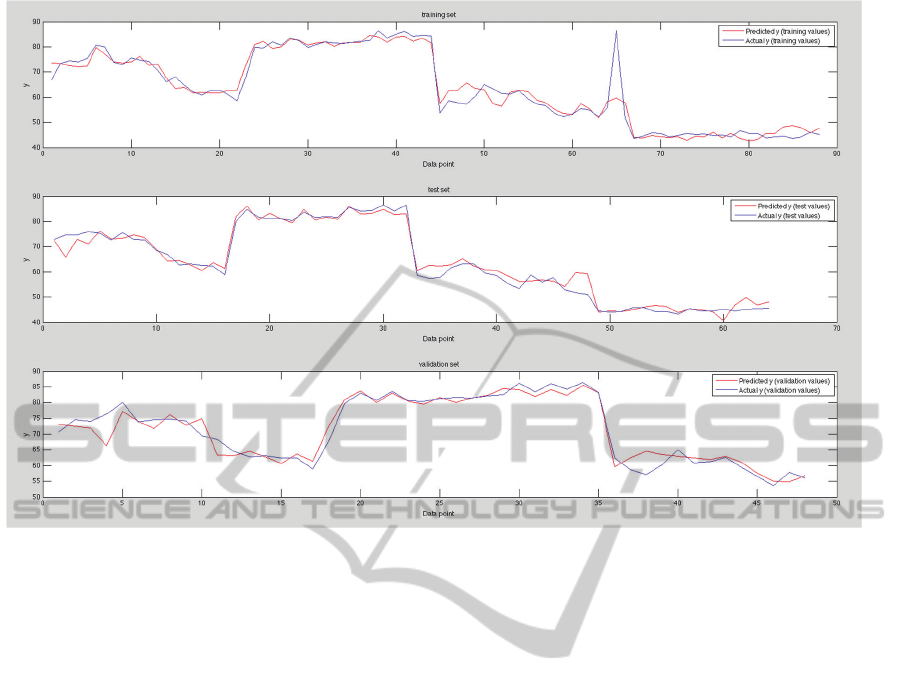
Figure 4: Results for diastolic blood pressure.

consists in indirectly measuring blood pressure

through the measurement of others among the

patient’s vital parameters, if a relationship between

the former and these latter exists.

This paper has tested the hypothesis that a

nonlinear relationship exists between heart activity,

and thus ECG and HRV parameters, PPG and BP

values. Genetic Programming (GP) is able to

automatically both evolve the structure of the

mathematical model and find the most important

parameters in it. Therefore, it is perfectly suited to

perform a regression task such as that involved by

the above hypothesis.

Preliminary experiments on a real-world

database have been performed. The numerical

results achieved have confirmed that this non-linear

relationship indeed exists, and GP has been able to

find a mathematical model expressing it. A result

from these preliminary experiments is that both PPG

values and ECG-related ones are very important to

indirectly estimate BP values. This implies that,

rather than continuously measuring the patient’s BP,

a wearable wireless PPG sensor can be applied to

patient’s finger, a wearable wireless ECG to his/her

chest, HRV parameter values can be computed and,

through regression, both systolic and diastolic BP

values can be indirectly measured. The

approximation error involved by the use of this

method is lower than 2 mmHg for both systolic and

diastolic BP values.

As a future work we will perform an

experimental phase in which 10-fold cross-

validation will be used. Moreover, we will

investigate to determine which the maximal number

of items in the database is, and cases from a much

higher number of patients will be considered in the

creation of the database. Finally, our model will be

compared with other approaches from the literature.

REFERENCES

Allen, J. (2007). Photoplethysmography and its

application in clinical physiological measurement.

Physiological Measurement, 28(3), R1.

Berntson, G. G., Bigger, J. T., Jr., Eckberg, D. L.,

Grossman, P., Kaufmann, P. G., Malik, M., . . . van

der Molen, M. W. (1997). Heart rate variability:

origins, methods, and interpretive caveats.

Psychophysiology, 34(6), 623-648.

Dueck, R., Jameson, L. C. (2006). Reliability of

hypotension detection with noninvasive radial artery

beat-to-beat versus upper arm cuff BP monitoring.

Anesth Analg, 102, Suppl:S10.

Electrophysiology, Task, Force, of, the, European, . . .

Pacing. (1996). Heart Rate Variability: Standards of

Measurement, Physiological Interpretation, and

BIODEVICES2015-InternationalConferenceonBiomedicalElectronicsandDevices

248

Clinical Use. Circulation, 93(5), 1043-1065. doi:

10.1161/01.cir.93.5.1043.

Gesche, H., Grosskurth, D., Kuechler, G., Patzak, A.

(2012). Continuous blood pressure measurement by

using the pulse transit time: comparison to a cuff-

based method. Eur J Appl Physiol, 112, 309-315.

Goldberger, A. L., Amaral, L. A. N., Glass, L., Hausdorff,

J. M., Ivanov, P. C., Mark, R. G., . . . Stanley, H. E.

(2000). PhysioBank, PhysioToolkit, and PhysioNet:

Components of a New Research Resource for

Complex Physiologic Signals. Circulation, 101(23),

e215-e220. doi: 10.1161/01.CIR.101.23.e215.

Golparvar, M., Naddafnia, H., Saghaei, & Mahmood.

(2002). Evaluating the Relationship Between Arterial

Blood Pressure Changes and Indices of Pulse

Oximetric Plethysmography. Anesthesia & Analgesia,

95(6), 1686-1690 1610.1097/00000539-200212000-

200200040.

Ilies, C., Kiskalt, H., Siedenhans, D., Meybohm, P.,

Steinfath, M., Bein, B., Hanss, R. (2012). Detection of

hypotension during Caesarean section with continuous

non-invasive arterial pressure device or intermittent

oscillometric arterial pressure measurement. British

Journal of Anaesthesia, 3-9.

Inajima, T., Imai, Y., Shuzo, M., Lopez, G., Yanagimoto,

S., Iijima, K., Morita, H., Nagai, R., Yahagi, N.,

Yamada, I. (2012). Relation Between Blood Pressure

Estimated by Pulse Wave Velocity and Directly

Measured Arterial Pressure. Journal of Robotics

andMechatronics, 24(5), 811-821.

Karapetian, G. K., Evaluation, W. S. U. E., & Research.

(2008). Heart Rate Variability as a Non-invasive

Biomarker of Sympatho-vagal Interaction and

Determinant of Physiologic Thresholds: Wayne State

University.

Koza, J. (1992). Genetic Programming: On the

Programming of Computers by Means of Natural

Selection: MIT Press, Cambridge, MA.

Maguire, S., Rinehart, J., Vakharia, S., Cannesson, M.

(2011). Technical communication: respiratory

variation in pulse pressure and plethysmographic

waveforms: intraoperative applicability in a North

American academic center. Anesthesia and analgesia,

112(1), 94-96.

Meigas, K., Lass, J., Karai, D., Kattai, R., Kaik, J. (2007).

Pulse Wave Velocity in Continuous Blood Pressure

Measurements. Paper presented at the IFMBE.

Melillo, P., Bracale, M., & Pecchia, L. (2011). Nonlinear

Heart Rate Variability features for real-life stress

detection. Case study: students under stress due to

university examination. Biomed Eng Online, 10, 96.

doi: 10.1186/1475-925x-10-96.

Najjar, S., Scuteri, A., Shetty, V., Wright, J.G., Muller,

D.C:, Fleg, J.L., Spurgeon, H.P., Ferrucci, L., Lakatta,

E.G. (2008). Pulse Wave Velocity Is an Independent

Predictor of the Longitudinal Increase in Systolic

Blood Pressure and of Incident Hypertension in the

Baltimore Longitudinal Study of Aging. J Am Coll

Cardiol, 51(14), 1377-1383.

Niskanen, J. P., Tarvainen, M. P., Ranta-Aho, P. O., &

Karjalainen, P. A. (2004). Software for advanced HRV

analysis. Comput Methods Programs Biomed, 76(1),

73-81. doi: 10.1016/j.cmpb.2004.03.004.

Rajendra Acharya, U., Paul Joseph, K., Kannathal, N.,

Lim, C. M., & Suri, J. S. (2006). Heart rate variability:

a review. Med Biol Eng Comput, 44(12), 1031-1051.

doi: 10.1007/s11517-006-0119-0.

Sotera wireless. http://www.soterawireless.com.

Tarvainen, M. P., Ranta-Aho, P. O., & Karjalainen, P. A.

(2002). An advanced detrending method with

application to HRV analysis. IEEE Trans Biomed Eng,

49(2), 172-175. doi: 10.1109/10.979357.

von Skerst, B. (2008). Market survey, N=198 physicians

in Germany and Austria. Dec.2007 - Mar 2008:

InnoTech Consult GmbH, Germany.

Vukovich, R., & Knill, J. (1980). Blood Pressure

Homeostasis. In D. Case, E. Sonnenblick & J. Laragh

(Eds.), Captopril and Hypertension (pp. 3-13):

Springer US.

Non-InvasiveEstimationofBloodPressurethroughGeneticProgramming-PreliminaryResults

249