
A Closed-form Approximated Expression for the Residual ISI
Obtained by Blind Adaptive Equalizers Applicable for the
Non-Square QAM Constellation Input and Noisy Case
Roy Shevach and Monika Pinchas
Dept. of Electrical and Electronic Engineering, Ariel University of Samaria, Ariel 40700, Israel
Keywords: Blind Equalization, Residual ISI.
Abstract: Recently, closed-form approximated expressions were obtained for the residual Inter-Symbol Interference
(ISI) obtained by blind adaptive equalizers valid for the real or two independent quadrature carrier case such
as the 16 Quadrature Amplitude Modulation (QAM) input. In this paper we propose for the complex and
dependent quadrature carrier case (such as the 32QAM source), a closed-form approximated expression for
the achievable residual ISI which depends on the step-size parameter, equalizer’s tap length, input signal
statistics, channel power and SNR. This approximated expression is applicable for blind adaptive equalizers
where the error is fed into the adaptive mechanism, which updates the equalizer‘s taps and can be expressed
as a polynomial function up to order five of the equalized output. Godard’s algorithm for example, applies a
third order polynomial function to the adaptation mechanism of the equalizer thus belongs to the above-
mentioned type of equalizers. Since the channel power is measurable, or can be calculated if the channel
coefficients are given, there is no need to perform any simulation with various step-size parameters and
different values of SNR to reach the required residual ISI for the dependent quadrature carrier input case.
1 INTRODUCTION
Intersymbol interference (ISI) is a well known
phenomenon in which subsequent symbols at the
receiver are overlapping due to channel
characteristics such as bandwidth limitation or
multipath effects. This distortion makes it difficult
for the decision device at the receiver to recover the
transmitted data. Thus, for bandwidth-efficient
communication systems, operating in high inter-
symbol interference (ISI) environments, adaptive
equalizers have become a necessary component of
the receiver architecture. An accurate estimate of the
amplitude and phase distortion introduced by the
channel is essential to achieve high data rates with
low error probabilities (Abrar, Zerguine and Nandi
2012).
Modern digital communication systems are both
band limited and used to transmit high data rate,
therefore the adaptive equalization method which
relies on training phase is either impractical or very
costly in terms of data throughput. Hence, a blind
adaptive equalization algorithm is the preferable
choice between the three types of equalization
methods (non-blind, semi-blind and blind). Using
these blind algorithms, individual receivers can
begin self-adaptation without transmitter assistance.
This ability of blind startup also enables a blind
equalizer to self-recover from system breakdowns.
This self-recovery ability is critical in broadcast and
multicast systems where channel variation often
occurs (Zhi Ding 2009). The algorithm itself
generates an estimate of the desired response by
applying a non-linear transformation to sequences
involved in the adaptation process (Nikias,
Petropulu, 1993). Since the equalizer performance
depends on the above-mentioned transformation,
equalizer’s tap length, step-size parameter, channel
characteristics, added noise (SNR) and input signal
statistics, therefore tailoring an equalizer for a given
channel (application dependent) was involved with a
long process of simulation to assure the equalizer
will meet the system requirements. For example,
choosing a "big" step-size may lead to fast
convergence time at the expense of a high residual
ISI where the eye diagram is considered to be close
but on the other hand, "small" step-size may
improve the equalizer performance in terms of
residual ISI at the expense of long convergence time.
This expansive time can be spared by a closed-form
217
Shevach R. and Pinchas M..
A Closed-form Approximated Expression for the Residual ISI Obtained by Blind Adaptive Equalizers Applicable for the Non-Square QAM Constellation
Input and Noisy Case.
DOI: 10.5220/0005322202170223
In Proceedings of the 5th International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2015), pages
217-223
ISBN: 978-989-758-084-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

expression for the residual ISI taking into account all
the above mentioned parameters.
Up to now, such an expression was obtained for
real and independent input for the noiseless
(Pinchas, 2010a) and noisy (Pinchas, 2010b) cases
by Pinchas, and for blind adaptive equalizers with
equalized output gain lower or equal to one
(Kupchan and Pinchas, 2014). However none of
those expressions are applicable for the non-square
QAM constellations (such as 32QAM).
Recently, an expression for the non-square QAM
constellations was developed by Pinchas (Pinchas,
2012). But, this expression is only applicable for the
noiseless case and for blind adaptive equalizers
where the error is fed into the adaptive mechanism,
which updates the equalizer‘s taps is expressed as a
polynomial function up to order three of the
equalized output.
In this paper we propose a new closed-form
approximated expression for the residual ISI for the
real as well as for the general case of complex and
dependent input signals such as the 32QAM
constellation applicable also for the noisy case. This
new proposed expression is valid for type of blind
equalizers where the error that is fed into the
adaptive mechanism which updates the equalizer’s
taps can be expressed as a polynomial function of
order five of the equalized output.
This paper is organized as follows: the system
under consideration is depicted in Section 2, the
closed-form approximated expression for the
achievable residual ISI is introduced in Section 3. In
Section 4 simulation results are presented and the
conclusion is presented in Section 5.
2 SYSTEM DESCRIPTION
The system under consideration is similar to the
system presented by Pinchas (Pinchas, 2010b) and
illustrated here in Figure 1.
Figure 1: Block Diagram of a baseband communication
system.
The following assumptions have been taken:
1. The input signal
[]
x
n
is a real or complex
quadrature amplitude modulated (QAM) signal
with variance
2
x
, where for the complex case
the real part and the imaginary part are
dependent.
2. The unknown channel
[]hn is a possibly non-
minimum phase linear time-invariant (LTI)
filter in which the transfer function has no ”deep
zeros”, namely, the zeros lie sufficiently far
from the unit circle.
3. The equalizer
[]cn
is a tap-delay line.
4. The noise
[]wn
is an additive Gaussian white
noise with variance
2
w
.
After that the input signal has been transmitted
through the channel
h
n
, it is corrupted with an
additive Gaussian white noise
[]wn
. Therefore, the
equalizer input may be expressed as:
yn xn hn wn (1)
where the notation "*" refers to the convolution
operation. Following (Pinchas, 2010a), the equalizer
output can be expressed as:
[] [] [] []zn xn pn wn
(2)
where
[]pn
is the convolutional noise produced due
to the error between the actual derived or initial
given value for
[]cn
and the ideal value for
[]cn
and
[] [] []wn wn cn
, namely, the noise passing
through the equalizer. The ISI is defined by:
2
2
max
2
max
()
m
sm s
ISI
s
(3)
where
max
s
is the component of
s
, given by:
[] [] []
s
ncnhn
(4)
having the maximal absolute value (Pinchas, 2010a).
The equalizer adaptive mechanism responsible
for minimizing the convolutional error can be
expressed as:
[]
[1] [] []
[]
eq eq
Fn
cn cn yn
zn
(5)
where
[1]
eq
cn
and
[]
eq
cn
are the equalizer
coefficients at the next and current iteration
respectively,
is the equalizer’s step size,
[]
F
n
is
the cost-function that characterized the ISI and
[]yn
is the input vector
[] []...[ 1]
T
yn yn yn N
,
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
218

where N is the equalizer’s tap length. Note that the
operator
T
represents the transpose function and
*
is the conjugate operator.
3 THE RESIDUAL ISI
In this section we educe a new closed-form
approximated expression for the achievable residual
ISI which depends on the step-size parameter,
equalizer’s tap length, input signal statistics, channel
power and SNR.
Theorem.
Under the following assumptions:
1. The convolutional noise
[]pn
, is a zero mean,
white Gaussian process with variance
2 *
[ [ ]( [n]) ]
p
Epn p
, where []E represents
the expectation operator.
2. The input signal
x
n is a complex and
dependent quadrature amplitude modulated
constellation with known variance and higher
moments (e.g. 32QAM).
3. The convolutional noise
[]pn
and the input
signal are independent.
4.
2
max
1s
, where
s
is defined in (4).
5.
[]
[]
Fn
zn
can be expressed as a polynomial
function of order five of the equalized output
namely as
P
z .
The residual ISI expressed in dB units is defined as:
2
10 10
10log 10log
px
ISI m
(6)
where
2
x
is the variance of the input signal and
p
m
is defined by:
12
min ,
mp mp
p
m Sol Sol
for
1
0
mp
Sol
and
2
0
mp
Sol
or
12
max ,
mp mp
p
m Sol Sol
for
12
0
mp mp
Sol Sol
where
2
1111
1
1
4
2
mp
B
BACB
Sol
A
2
1111
2
1
4
2
mp
B
BACB
Sol
A
22 2 2 2
1133 15
44
22
35 35
66
2
5
44
22 2
5
22
35
(6 27 ( ) 54 ( )
216 ( [ ] [ ]) 864
300 ( [ ] [ ])
2700 ( [ ] [ ] ))
(6 36 ( ))
x
wxw
xw
wx
xw
ABaa a aa
aa E x E w aa
aEx Ew
aEx Ew
aa
222
1113
44
2
3
44
222
315
66
35
44
22
35
88
222
515
66
22 2
5
44
2
5
(8( )
9([ ] [ ])
36 18 ( [ ] [ ])
32 ( [ ] [ ])
288 ( [ ] [ ] )
25 ( [ ] [ ]) 72
400 ( [ ] [ ] )
900 [ ] [ ])
(2
xw
xw
wx
x
w
wx
BBa aa
aEx Ew
aaaExEw
aa E x E w
aa E x E w
aEx Ew aa
aEx Ew
aE x Ew
a
22 22
13 5
44
5
4( )24
6([ ] [ ]))
xw xw
aa
aEx Ew
44
22 2
11 13
66
2
3
66
15
44
22 2
3
88
22
35 13
44
22
15
66
22
35
44
35
2
5
()2([][])
([ ] [ ])
2([][])
9([ ] [ ] )
2([][])8
18 ( [ ] [ ] )
32 ( [ ] [ ] )
72 [ ] [ ]
(
xw
wx
xw
wx
wx
Ca aaEx Ew
aEx Ew
aa E x E w
aEx Ew
aa E x E w aa
aa E x E w
aa E x E w
aaE x E w
aE
10 10
88
22 2
5
64 64
2
5
[][ ])
25 ( [ ] [ ] )
100 [ ] [ ] [ ] [ ]
wx
xEw
aEx Ew
aExEw EwEx
2
1
21
0
kR
x
k
BN hk SNR
2
2
x
w
SNR
(7)
R
is the channel length, N is the equalizer‘s tap
length
[]
x
xn
and
135
,a ,aa are the coefficients of
AClosed-formApproximatedExpressionfortheResidualISIObtainedbyBlindAdaptiveEqualizersApplicableforthe
Non-SquareQAMConstellationInputandNoisyCase
219

the above-mentioned polynomial function
P
z ,
defined as:
2
13
2
2
5
[]
[] [] []
[]
[] []
Fn
P z azn a zn zn
zn
azn zn
(8)
Proof.
We begin our proof by first recalling from (Pinchas,
2012) the expression for
*
[] []Epnpn
:
*
*
*
1
*
0
*
2
11
**
00
[] []
[] [] [] []
[][]
[] []
[][] [][]
mN
m
mN mN
mm
Epnpn
EpnPzn pnPzn
Eynmynm
EPzn Pzn
E ynmynm ynmynm
(9)
where
[]pn
is the convolutional noise and
[]
P
zn
is the polynomial function defined at (8).
Substituting (2) and (8) into (9) yields:
*
5422
11 111 1
[] []
()
pp ppp
Epnpn
BFmEmDmAmBmBC
(10)
where
*
[] []
p
m E pn pn
,
111
,,,
A
BCB are given
in (7), and
111
,,DEF are given by:
2
15
22 2
1355
222
1153 35
22 22
5
2
2
55
22
945
(210 2625 ( ))
(30 15 4
4500 (
80 ( )
(
6
))
000 15)
xw
x
w
xw
xw
FaB
Eaaa B
Daaa aa
B
a
aa
(11)
As was shown in (Pinchas, 2012), at the latter
stages where the algorithm has converged we may
write that
*
[ ([] [] )] 0Epnpn
. For an easy
channel (where the ISI is relatively low but the eye
diagram is still closed) we can neglect the products
of
3
1 p
Dm
,
4
1 p
Em
and
5
1 p
F
m
, thus denoting (10) as:
2
11 1
0
pp
Am Bm BC
(12)
The solution for this second order equation with
respect to
p
m
is given in (7). The relation between
the convolutional noise power
p
m
and ISI was
developed in (Pinchas, 2010a) noted in (6). This
completes our proof.
4 SIMULATION RESULTS
In this section we test the new closed-form
expression for the residual ISI via simulation. In the
simulation we use two equalizers to examine the
benefit of the new expression. The equalizer was
initialized by setting the central equalizer‘s tap to
one and all others to zero. The first equalizer is
based on Godard algorithm (Godard, 1980) (third
order polynomial function) which equalizer's taps
are updated according to:
4
2
2
[]
[1] [] [] [][ ]
[]
mmG
Ex
cn cn zn znynm
Ex
(13)
where
G
is the step-size and
13
,aa are given by:
4
13
2
[]
1,
[]
GG
Ex
aa
Ex
(14)
In order to examine the new expression with an
equalizer of fifth order polynomial function, we are
using an ad hoc equalizer which equalizer's taps are
updated according to:
2
22
13 5
[1] [] [] []
[] [ ]
mmnew
cn cn a azn a zn
zny n m
(15)
where
new
is the step-size and
135
,,aaa are given
by:
13 5
410 68
8610
2
1, 4 , 2 15
[][ ] [][]
([ ]) [ ][ ]
new new new
aaAaA
Ex Ex Ex Ex
A
Ex Ex Ex
(16)
Two input signals were considered: 32QAM
source and 128QAM source, both complex and
dependent signals. Three different channels were
considered.
Channel 1 (initial ISI = 0.44): The channel
parameters were determined according to Shalvi and
Weinstein (Shalvi, Weinstein, 1990):
n
h ={0 for
0n
; -0.4 for
0n
;
1
0.84 0.4
n
}
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
220
Channel 2 (initial lSI = 0.88): The channel
parameters were determined according to Pinchas
(Pinchas, 2010b):
n
h = (0.4851, -0.72765, -0.4851).
Channel 3 (initial lSI = 0.5): The channel
parameters were determined according to Fiori
(Fiori, 2001):
n
h = (-0.0144, 0.0006, 0.0427, 0.0090,
-0.4842, -0.0376, 0.8163, 0.0247, 0.2976, 0.0122,
0.0764, 0.0111, 0.0162, 0.0063) (a sampled
telephonic channel).
The ISI defined in (3) was calculated every
iteration, and compared to the new closed-form
expression that was presented at (6).
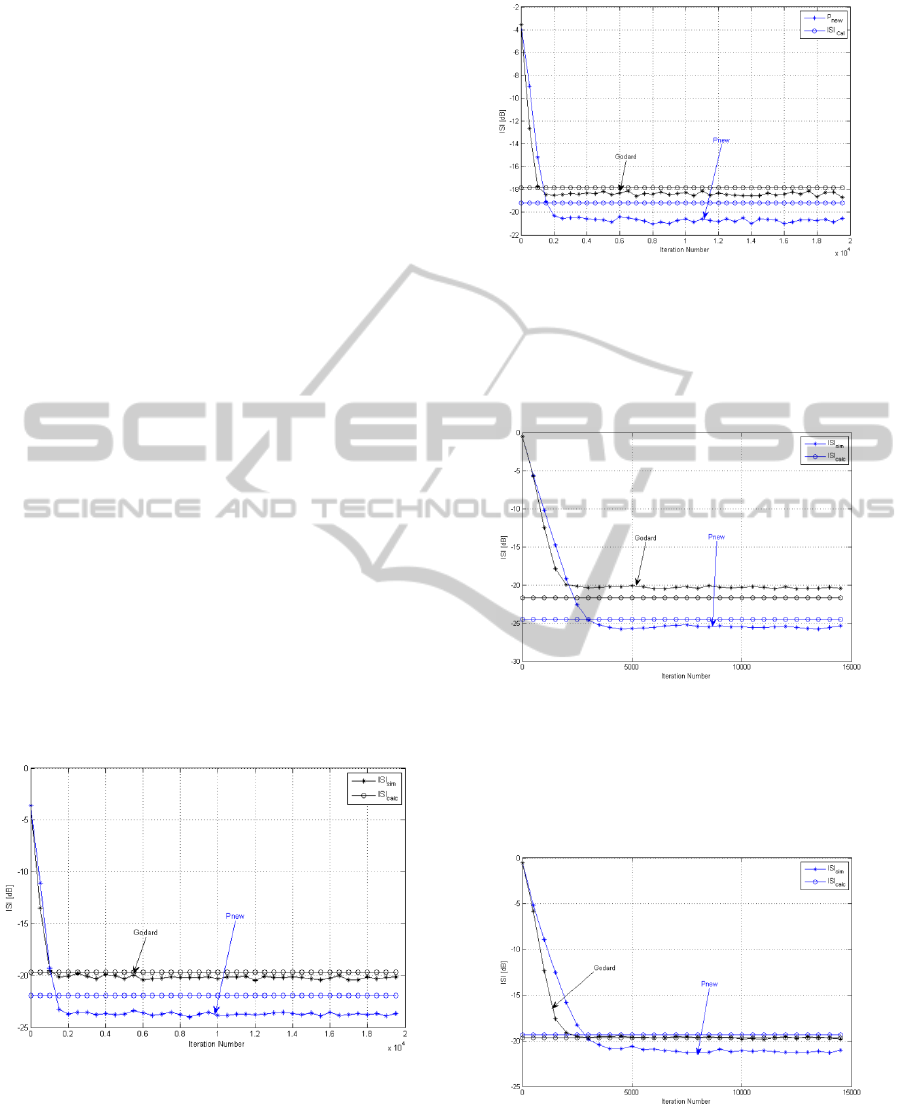
Figures 2-7 present the performance comparison
between the calculated and simulated achievable
residual ISI according to the ad hoc fifth order
equalizer (noted as P
new
) and Godard‘s algorithm for
32QAM input signal, as a function of iteration
number for various step-size parameters (noted as
µ
new
and µ
G
for P
new
and Godard respectively),
channel characteristics, equalizer‘s tap length and
SNR. High correlation was found between the
calculated and simulated achievable residual ISI.
Figures 8-9 present the performance comparison
between the calculated and simulated achievable
residual ISI according to the ad hoc fifth order
equalizer (noted as P
new
) and Godard‘s algorithm
respectively, for 128QAM input signal at SNR of
30dB. Figure 8 (fifth order polynomial equalizer)
shows fine correlation between the calculated and
simulated achievable residual ISI according (3dB
difference) while Figure 9 (Godard) shows very high
correlation.
Figure 2: A comparison between the calculated and
simulated (with Pnew and Godard‘s algorithm) residual
ISI for 32QAM input signal going through channel 1. The
averaged results were obtained in 100 Monte Carlo trials
for 25dB. The equalizer tap length was set to 13, the step-
size parameters µG and µnew were set to 1.5e-5 and -5e-5
respectively.
Figure 3: A comparison between the calculated and
simulated (with Pnew and Godard‘s algorithm) residual
ISI for 32QAM input signal going through channel 1. The
averaged results were obtained in 100 Monte Carlo trials
for 15dB. The equalizer tap length was set to 13, the step-
size parameters µG and µnew were set to 1.5e-5 and -3e-5
respectively.
Figure 4: A comparison between the calculated and
simulated (with Pnew and Godard‘s algorithm) residual
ISI for 32QAM input signal going through channel 2. The
averaged results were obtained in 100 Monte Carlo trials
for 25dB. The equalizer tap length was set to 15, the step-
size parameters µG and µnew were set to 8e-6 and -2.5e-5
respectively.
Figure 5: A comparison between the calculated and
simulated (with Pnew and Godard‘s algorithm) residual
ISI for 32QAM input signal going through channel 2. The
averaged results were obtained in 100 Monte Carlo trials
for 15dB. The equalizer tap length was set to 15, the step-
size parameters µG and µnew were set to 8e-6 and -3e-5
respectively.
AClosed-formApproximatedExpressionfortheResidualISIObtainedbyBlindAdaptiveEqualizersApplicableforthe
Non-SquareQAMConstellationInputandNoisyCase
221
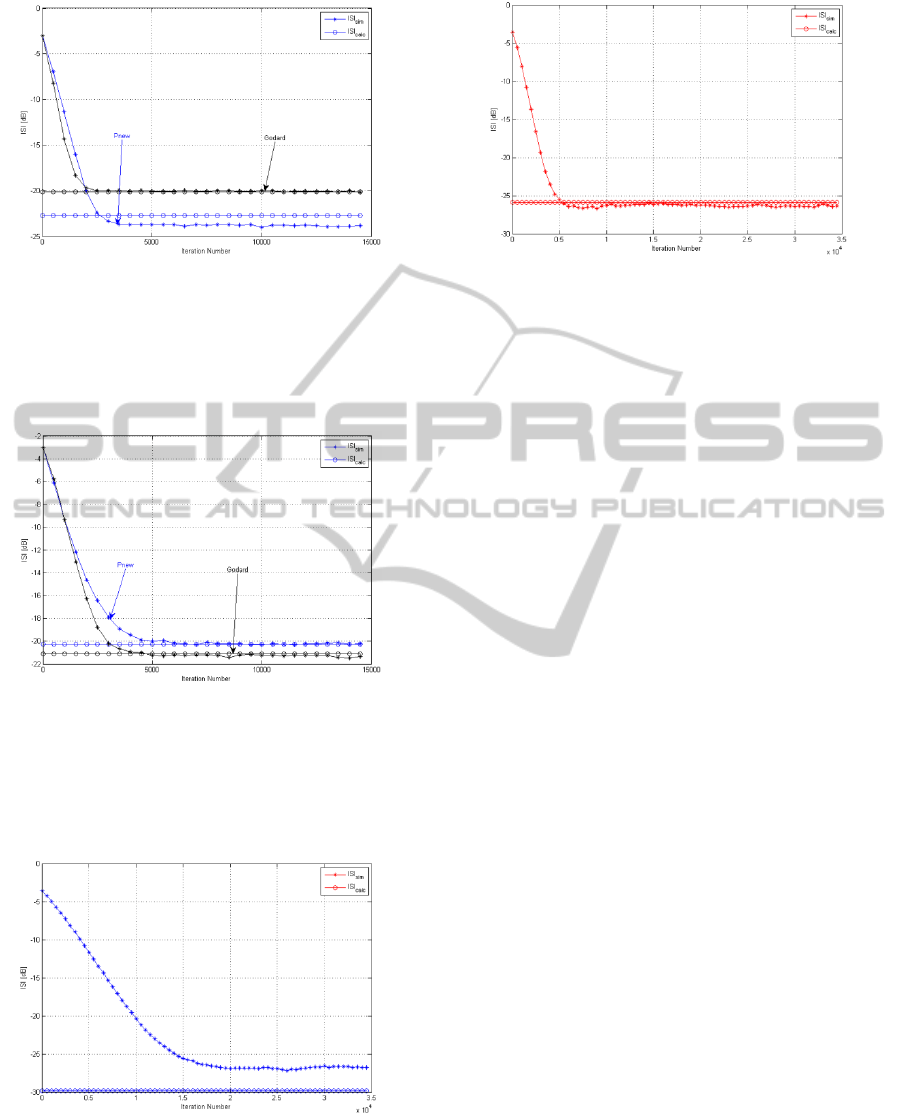
Figure 6: A comparison between the calculated and
simulated (with Pnew and Godard‘s algorithm) residual
ISI for 32QAM input signal going through channel 3. The
averaged results were obtained in 100 Monte Carlo trials
for 25dB. The equalizer tap length was set to 21, the step-
size parameters µG and µnew were set to 8e-6 and -2.5e-5
respectively.
Figure 7: A comparison between the calculated and
simulated (with Pnew and Godard‘s algorithm) residual
ISI for 32QAM input signal going through channel 3. The
averaged results were obtained in 100 Monte Carlo trials
for 15dB. The equalizer tap length was set to 21, the step-
size parameters µG and µnew were set to 4.5e-6 and -1.5e-
5 respectively.
Figure 8: A comparison between the calculated and
simulated (with Pnew) residual ISI for 128QAM input
signal going through channel 1. The averaged results were
obtained in 100 Monte Carlo trials for 30dB. The equalizer
tap length was set to 13, the step-size parameter µ
new
was
set to -1.2e-7.
Figure 9: A comparison between the calculated and
simulated (with Godard‘s algorithm) residual ISI for
128QAM input signal going through channel 1. The
averaged results were obtained in 100 Monte Carlo trials
for 30dB. The equalizer tap length was set to 13, the step-
size parameter µG was set to 2e-7.
5 CONCLUSIONS
In this paper, a new closed-form approximated
expression was developed for the achievable
residual ISI valid for SNR values down to 15 dB for
the complex and dependent quadrature carrier case
applicable for type of blind equalizers where the
error that is fed into the adaptive mechanism which
updates the equalizer’s taps can be expressed as a
polynomial function of order five of the equalized
output. The developed expression for the achievable
residual ISI depends on the channel power (which is
measurable or can be calculated if the channel
coefficients are given), on the step-size parameter,
equalizer’s tap length, input signal statistics and
SNR. The knowledge of these parameters enables
the system designer to use the described evaluation
instead of carrying out multiple simulations with
various step-size parameters and SNR in order to get
the optimal step-size parameter for a required
residual ISI.
ACKNOWLEDGEMENTS
We would like to thank the anonymous reviewers
for their helpful comments.
REFERENCES
Shafayat Abrar, Azzedine Zerguine and Asoke Kumar
Nandi (2012). Adaptive Blind Channel Equalization,
Digital Communication, Prof. C Palanisamy (Ed.),
ISBN: 978-953-51-0215-1, InTech, Available from:
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
222

http://www.intechopen.com/books/digital-
communication/adaptive-blind-channel-equalization.
Zhi Ding, Digital Signal Processing Fundamentals, CRC
Press 2009, Chapter 24. Adaptive Filters for Blind
Equalization.
C.L. Nikias, A.P. Petropulu, Higher-Order Spectra
Analysis A Nonlinear Signal Processing Framework,
Prentice-Hall, Englewood Cliffs, NJ, 1993, pp. 419–
425 (Chapter 9).
Pinchas M. A Closed Approximated formed Expression
for the Achievable Residual Intersymbol Interference
obtained by Blind Equalizers, Signal Processing.
(Eurasip), Jun 2010; Volume 90, Issue 6, pp. 1940-
1962.
Pinchas M. A New Closed Approximated Formed
Expression for the Achievable Residual Intersymbol
Interference obtained by Blind Equalizers for the
Noisy Case, IEEE International Conference, Beijing,
China Jun 2010; pp. 26-30.
Kupchan S., Pinchas M. A Closed-Form Approximated
Expression for the Residual ISI Obtained by Blind
Adaptive Equalizers with Gain Equal or Less than
One, Radioengineering, Sep. 2014, Volume 23, Issue
3, pp. 954.
Pinchas M. The whole story behind blind adaptive
equalizers/blind deconvolution, Bentham Science
Publishers, 2012, (chapter 6).
Godard DN. Self recovering equalization and carrier
tracking in two-dimenional data communication
system. IEEE Trans. Comm. Nov 1980; Volume 28,
Issue 11, pp. 1867-1875.
Shalvi O., Weinstein E. New criteria for blind
deconvolution of nonminimum phase systems
(channels). IEEE Trans. Information Theory Mar
1990; Volume 36, Issue 2, pp. 312-321.
Fiori S. A contribution to (neuromorphic) blind
deconvolution by flexible approximated Bayesian
estimation, Signal Processing (Eurasip) 2001; 81:
2131-2153.
AClosed-formApproximatedExpressionfortheResidualISIObtainedbyBlindAdaptiveEqualizersApplicableforthe
Non-SquareQAMConstellationInputandNoisyCase
223
