
Combination of Characteristic Green’s Function Technique and Rational
Function Fitting Method for Computation of Modal Reflectivity
at the Optical Waveguide End-facet
Abdorreza Torabi and Amir Ahmad Shishegar
Department of Electrical Engineering, Sharif University of Technology, Tehran, Iran
Keywords:
Optical Waveguide End-facet, Guided Mode Reflection Coefficient, Characteristic Green’s Function, Complex
Images Method, Rational Function Fitting Method, VECTFIT Algorithm, Optimization.
Abstract:
A novel method for computation of modal reflectivity at optical waveguide end-facet is presented. The method
is based on the characteristic Green’s function (CGF) technique. Using separability assumption of the struc-
ture and rational function fitting method (RFFM), a closed-form field expression is derived for optical planar
waveguide. The uniform derived expression consists of discrete and continuous spectrum contributions which
denotes guided and radiation modes effects respectively. An optimization problem is then defined to calculate
the exact reflection coefficients at the end-facet for all extracted poles obtained from rational function fitting
step. The proposed CGF-RFFM-optimization offers superior exactness in comparison with the previous re-
ported CGF-complex images (CI) technique due to contribution of all components of field in the optimization
problem. The main advantage of the proposed method lies in its simple implementation as well as precision
for any refractive index contrast. Excellent numerical agreements with rigorous methods are shown in several
examples.
1 INTRODUCTION
Optoelectric devices such as laser amplifier, opti-
cal modulator and coupler are widely used in in-
tegrated optics (IO) circuits. In these applications,
facet reflectivity typically deviates the performance of
the integrated system from its original designed tar-
get. The oldest accepted model for computation of
facet reflectivity is Ikegami’s model (Ikegami, 1972),
which was introduced for double-heterojunction(DH)
GaAs-AlGaAs lasers. In this approach, with the use
of eigenmode expansion, electric and magnetic fields
are matched at the facet. In (Lewin, 1975), an ap-
proximate modal reflectivityis developedby means of
a plane wave Fresnel reflectivity expansion. Derived
expressions are utilized in some other works related
to two-dimensional (2-D) buried DH lasers (Hardy,
1984). These results are quite accurate but are just
useful for low refractive index contrast. Gelin (Gelin
et al., 1981) extended Rozzi’s variational treatment
(Rozzi and Veld, 1980) for end-facet modal reflec-
tivity and proposed an efficient numerical computa-
tion. The main challenge of mode matching based
approach is the computation of time-consuming inte-
grals which usually have singular integrands to con-
tribute radiation modes. Moreover, finite window
Fourier transform could be combined with perturba-
tion series for fast computation of end-facet reflectiv-
ity (Chen et al., 2012).
An efficient way to regard the continuous spec-
trum contribution in mode matching method is using
appropriate set of modes achieved by closing the de-
sired structures with perfectly matched layers (PMLs)
(Derudder et al., 2001). The main disadvantage of
PML method is the considerable number of discrete
modes must be considered to obtain for an appropri-
ate accuracy. A different approach is utilizing itera-
tive based methods. In (Yevick et al., 1991), split-
operator method is utilized and the interface of facet is
divided into segments in such a way that within each
segment the refractive index is nearly constant. The
resulting contribution of each segment to the total re-
flected field is superimposed. Finally a linear iterative
equation is obtained which can be solved by classi-
cal Neumann series or more stably by bi-conjugate
gradient method (Wei and Lu, 2002). In other it-
erative approach, reflection operator is diagonalized
completely or partially (Yevick et al., 1992) using the
known eigenmodes and eigenvectors of square root
operator. A separate class of solution methods em-
14
Torabi A. and Shishegar A..
Combination of Characteristic Green’s Function Technique and Rational Function Fitting Method for Computation of Modal Reflectivity at the Optical
Waveguide End-facet.
DOI: 10.5220/0005332300140021
In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 14-21
ISBN: 978-989-758-093-2
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
ploy Pad´e or complex Pad´e approximations to ratio-
nal approximation of the square root operator (El-
Refaei et al., 2000), (Jamid and Khan, 2007), (Yu and
Yevick, 1997). Stability and convergenceproblem are
the main challenges in this approach. For more rig-
orous solution, integral equation can be used. Parsa
and Paknys (Parsa and Paknys, 2007a) used equiva-
lence principle and image theory and model the trun-
cated semi-infinite dielectric slab waveguide by an
infinite dielectric slab with unknown current density
on a plane just at truncating surface of the end-facet
which is solved by the method of moments (MoM).
Coupling of the guided modes are incorporated in this
method in the form of coupling matrix of end-facet.
In this paper a novel method for computation of
guided modes reflectivity at the waveguide end-facet
is presented. The proposed method is based on the
characteristic Green’s function (CGF) technique com-
bined with rational function fitting method (RFFM)
(Torabi et al., 2014b), (Torabi et al., 2013). Spa-
tial Green’s function of finite dielectric planar waveg-
uide is obtained by separation of the structure into
infinite 1-D layered media. For nonseparable struc-
ture like typical finite dielectric slab waveguide (i.e.
DH laser), using separability assumption, an approx-
imate and closed-form expression for spatial Green’s
function is achieved. The final formulation is utilized
in an efficient optimization problem to find the ex-
act facet reflection coefficients of guided modes. In
contrary to previous reported CGF-complex images
( , )
x y
′ ′
1
r
ε
w
o
x
y
2
r
ε
1
rn
ε
−
rn
ε
0
r
ε
0
r
ε
0
r
ε
1
t
2
t
1
n
t
−
n
t
(a)
t
( , )
x y
′ ′
y
x
2
r
ε
2
r
ε
1
r
ε
w
2
r
ε
o
(b)
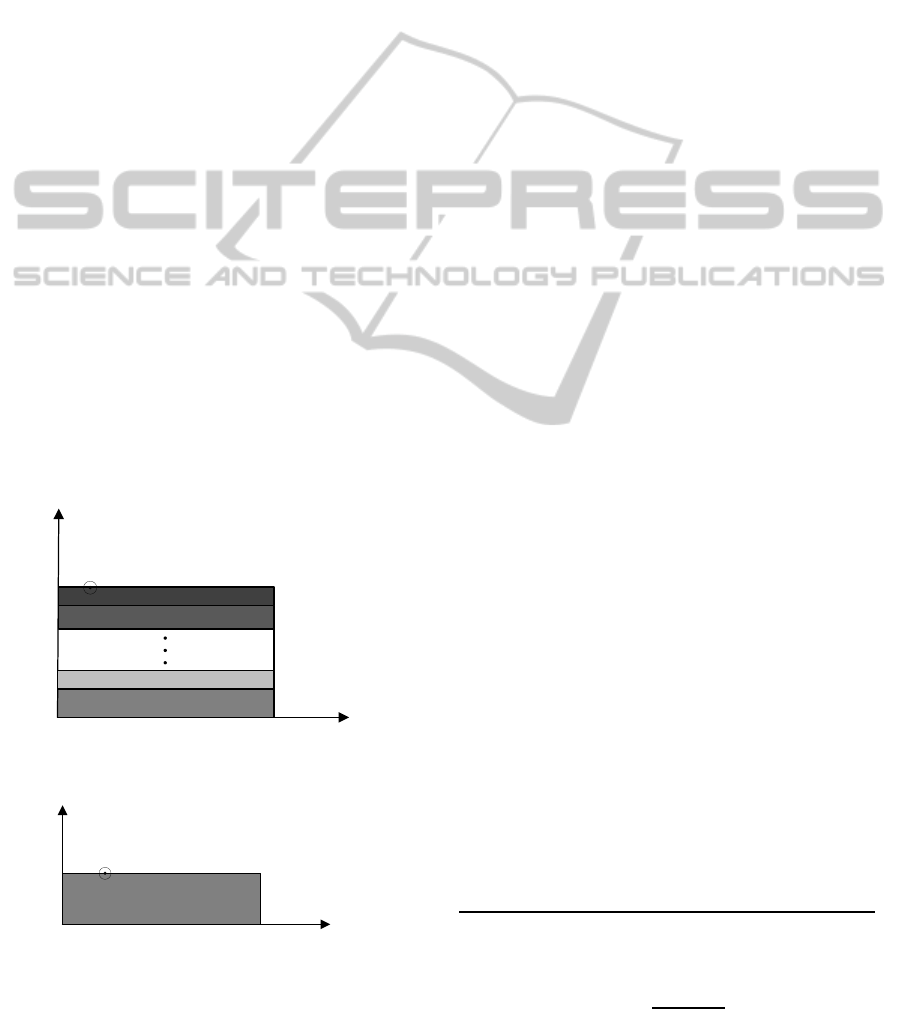
Figure 1: A line source on a truncated (a) multilayered (b)
slab waveguide.
(CI) based method (Torabi et al., 2014a), in the for-
mulation of CGF-RFFM continuous spectrum contri-
bution are presented by some poles similar to guided
modes part. Then unlike CGF-CI, in CGF-RFFM
both discrete and continuous spectrum contributions
are efficiently incorporated in the optimization prob-
lem. Therefore more exact results of guided modes
reflectivity can be obtained. This fact is shown in sev-
eral examples. Simplicity of implementation as well
as precision is the main advantage of the proposed
method. Moreover, this method can be used for any
planar dielectric waveguides with abrupt termination
and also for any refractive index contrasts.
2 CGF-RFFM FORMULATION
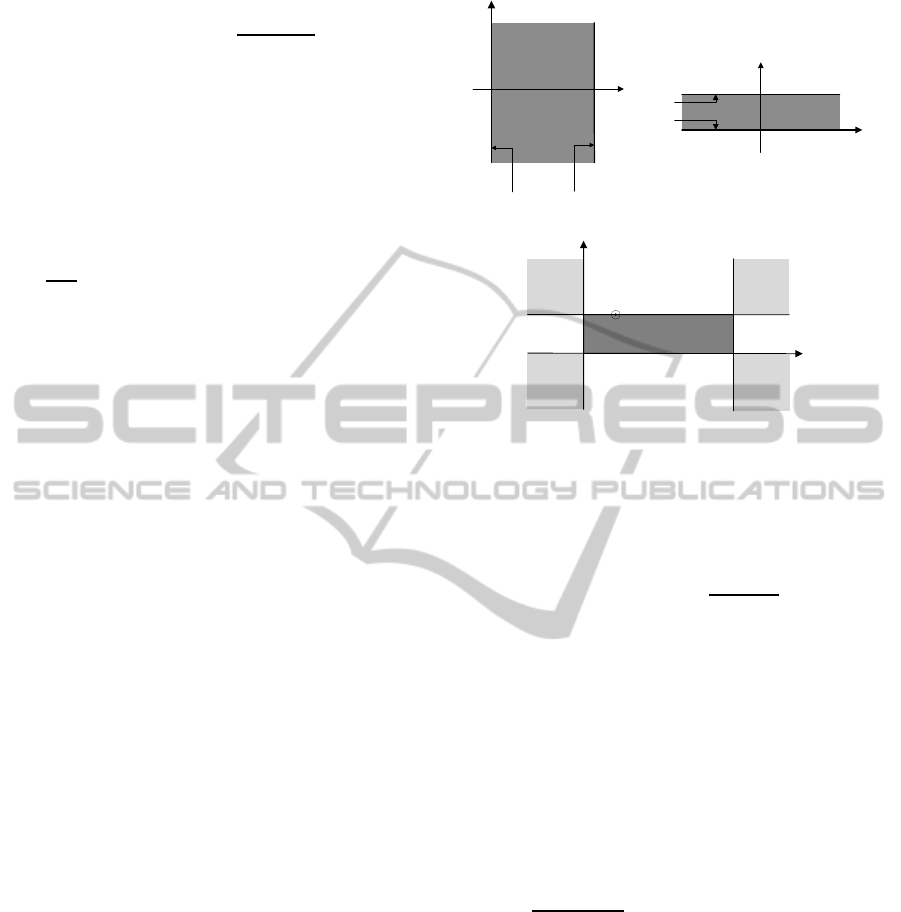
2.1 CGF Technique and Separability
Assumption
The 2-D Helmholtz’s equation should be solved for
Green’s function of magnetic vector potential, A
z
, for
a line source surrounded by layered media as it is
shown in Fig. 1(a). Here for simplicity the derivations
are developed for truncated dielectric slab waveguide
shown in Fig. 1(b) for simplicity while the implemen-
tation for multilayered media (Fig. 1(a)) is straight-
forward. The 2-D Helmholtz’s equation can be sepa-
rated into two 1-D equations if (Faraji-Dana, 1993a),
(Shishegar and Faraji-Dana, 2003)
ε
r
(x,y) = ε
x
(x) + ε
y
(y). (1)
By the assumption of (1), the original structure has
been decomposed into two layered media denoted by
N
x
and N
y
layered media (Fig. 2(a) and Fig. 2(b), N
γ
called normal to γ where γ = x,y), which their relative
dielectric constants are ε
x
(x) and ε
y
(y) respectively.
If this separation is rigorously possible, it means that
the original structure, Fig. 1(b), can be exactly repro-
duced by crossing two 1-D N
x
and N
y
layered me-
dia which is shown in Fig. 2(c). The solutions to
the 1-D Helmholtz’s equations are denoted by G
x
(for
Fig. 2(a)) and G
y
(for Fig. 2(b)) and can be obtained
analytically using usual spectral techniques (Michal-
ski and Mosig, 1997). We will have,
G
γ
(γ,γ
′
) =
(1+ R
γ
e
−j2β
γ1
γ
<
)(1+ R
γ
e
−j2β
γ1
(d
γ
−γ
>
)
)e
−jβ
γ1
(γ
>
−γ
<
)
(2jβ
γ1
)(1−R
2
γ
e
−j2β
γ1
d
γ
)
,
(2)
R
γ
=
β
γ1
−β
γ2
β
γ1
+ β
γ2
, (3)
CombinationofCharacteristicGreen'sFunctionTechniqueandRationalFunctionFittingMethodforComputationof
ModalReflectivityattheOpticalWaveguideEnd-facet
15
where d
γ
is equal to w and t for γ = x and y respec-
tively. γ
>
and γ
<
are greater and smaller values of γ
and γ
′
respectively and β
γi
=
q
ε
γi
k
2
0
+ λ
γ
(i = 1,2).
R
x
and R
y
are the reflection coefficients of a TE wave
at the interfaces (due to the symmetry R
Ax
= R
Bx
= R
x
and R
Ay
= R
By
= R
y
in Fig. 2). Then having G
x
and G
y
, the solution of A
z
for separable structure of
Fig. 2(c) is given by (Faraji-Dana, 1993a), (Shishegar
and Faraji-Dana, 2003)
A
z
(x,y;x
′
,y
′
)
= (
−1
2π j
)
I
C
λ
y
G
x
(x,x
′
,−λ
y
)G
y
(y, y
′
,λ
y
)dλ
y
,
(4)
where the contourC
λ
y
, encloses only the singularities
of G
y
, (including branch cut, branch point and dis-
crete poles singularities), in counterclockwise sense.
For the structure at hand, Fig. 1(b), it can be shown
that the separation of (1), is not rigorously possi-
ble (Shishegar and Faraji-Dana, 2003). If one ig-
nore (1) in four exterior regions in Fig. 2(c), then
an infinite number of solutions for ε
x1
, ε
x2
, ε
y1
and
ε
y2
could be found. It must be noted that the so-
lutions are not physically available relative dielec-
tric constants. They are just mathematical quantities.
One can choose ε
x1
= 0, ε
x2
= ε
r2
−ε
r1
, ε
y1
= ε
r1
,
ε
y2
= ε
r2
for N
x
and N
y
media. For all possible so-
lutions, the corner regions of the original structure
are replaced by ε
x2
+ ε
y2
= 2ε
r1
−ε
r2
(Shishegar and
Faraji-Dana, 2003). This deviation makes the CGF
result in (4) an approximate Green’s function for orig-
inal structure (Fig. 1(b)). It should be noted that for
multilayered truncated waveguide (with n layers) of
Fig. 1(a), after separation, the N
y
layered media would
be a 1-D infinite layered media (with n layers) while
N
x
media would be the same as Fig. 2(a). So it is just
sufficient that G
y
of related N
y
layered media is com-
puted analytically and incorporated in integral repre-
sentation of (4).
2.2 CGF-RFFM
In common optical waveguide structures, t is much
smaller than w. So, with acceptable approxima-
tion, guided modes (surface wave poles) of CGF G
y
(Fig. 2(b)) denote the guided modes of the original
structure in Fig. 1(b). Furthermore, the integration
of (4) in CGF technique is so time consuming and
expensive due to highly oscillatory nature of its in-
tegrand. To circumvent the numerical integration of
(4), rational function fitting method can be used. In
CGF-RFFM the G
y
is first approximated by appropri-
ate set of discrete poles via modified VECTFIT algo-
w
O
x
2
x
ε
1
x
ε
2
x
ε
A x
R
Bx
R
y
(a)
2
y
ε
x
A y
R
t
y
2
y
ε
1
y
ε
By
R
O
(b)
t
w
o
1 1
x y
ε ε
+
( , )
x y
′ ′
y
x
1 2
x y
ε ε
+
1 2
x y
ε ε
+
2 1
x y
ε ε
+
2 2
x y
ε ε
+
2 2
x y
ε ε
+
2 1
x y
ε ε
+
2 2
x y
ε ε
+
2 2
x y
ε ε
+
(c)
Figure 2: (a) N
x
and (b) N
y
layered media, (c) Separable
structure analyzed instead of original structure in CGF tech-
nique.
rithm (Torabi et al., 2014b). Like,
G
y
(y, y
′
,λ
y
) ≈
N
p
∑
m=1
Res
m
λ
y
−λ
ym
(5)
where Res
m
is the residue of G
y
at the mth pole. N
p
is the number of poles used in RFFM for rational fit-
ting. It should be noted that the set of extracted poles
in (5) includes guided modes of the structure. More-
over, some other poles are also extracted that are re-
sponsible to construct the continuous spectrum con-
tribution. Therefore, these poles have similar char-
acteristic to leaky wave poles and so we may call
them quasi leaky wave poles (Torabi et al., 2014b).
Then by substituting (5) in (4) and applying residue
theorem, a closed form series representation for A
z
will be obtained and can be found by (6). In (6),
k
xm
=
q
ε
x1
k
2
0
−λ
ym
is the propagation constant of
the mth mode in the x-direction. Since the rational
function fitting of (5) would have excellent accuracy,
therefore a closed form relation of (6) can approx-
imate the integral of (4) very well. We can sepa-
rate A
z
of (6) in two terms like (7) where A
g
z
denotes
the guided modes part (or discrete spectrum contribu-
tion) and is in series form of (6) in which just guided
modes (surface wave poles) contributes while A
r
z
re-
lated to radiation modes part (or continuous spectrum
contribution) and is in series form of (6) in which the
non surface wave poles (quasi leaky wave poles) con-
tributes.
In (6), R
xm
is the reflection coefficient of modes
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
16

A
z
=
N
p
∑
m=1
−Res
m
(1+ R
xm
e
−j2k
xm
x
<
)(1+ R
xm
e
−j2k
xm
(w−x
>
)
)e
−jk
xm
(x
>
−x
<
)
(2jk
xm
)(1−R
2
xm
e
−j2k
xm
w
)
, (6)
A
z
= A
g
z
+ A
r
z
,
A
g
z
=
N
guided
∑
m=1
−Res
m
(1+ R
xm
e
−j2k
xm
x
<
)(1+ R
xm
e
−j2k
xm
(w−x
>
)
)e
−jk
xm
(x
>
−x
<
)
(2jk
xm
)(1−R
2
xm
e
−j2k
xm
w
)
,
A
r
z
=
N
p
−N
guided
∑
m=1
−Res
m
(1+ R
xm
e
−j2k
xm
x
<
)(1+ R
xm
e
−j2k
xm
(w−x
>
)
)e
−jk
xm
(x
>
−x
<
)
(2jk
xm
)(1−R
2
xm
e
−j2k
xm
w
)
,
(7)
at the N
x
interface shown in Fig. 3(a). But actually,
these modes are reflected from truncated surface of
the substrate shown in Fig. 3(b). This discrepancy
arises from the separability approximation of the orig-
inal structure which also makes the refractive index of
four exterior corners deviate from its exact value. For
low refractive index contrast, ε
r1
≈ ε
r2
, as is common
in optical buried waveguides, the error in A
z
due to ap-
proximate modeling of the corner regions is ignorable
because 2ε
r2
−ε
r1
≈ ε
r2
. But in high refractive index
contrasts, considerable deviation may be imposed on
the Green’s function especially for source and field
points close to the corners. Therefore to have exact
A
z
for truncated dielectric slab waveguide of Fig. 1(b)
both terms A
g
z
and A
r
z
should be corrected. Although
having enough distance from corners for source and
field point makes the deviation in A
r
z
part small but
for more accurate results of reflection coefficients of
guided modes, correction of A
r
z
part along with A
g
z
part
should be considered. Before defining the optimiza-
tion problem, it should be noted that the main dif-
ference between proposed CGF-RFFM and CGF-CI
method (Torabi et al., 2014a) is in the approximation
form of G
y
. In CGF-CI the surface wave poles are first
extracted from G
y
in a similar form of (5) and the re-
maining part is approximated exponentially by GPOF
approach (Hua and Sarkar, 1989). In fact by CGF-
RFFM, unlike CGF-CI, a uniform representation of
G
y
as well as A
z
can be achieved and it will be shown
that it leads to more accurate results of reflection co-
efficients.
3 OPTIMIZATION PROBLEM
Exact values of A
z
for field points (x
i
,y
i
), i =
1,2,...,N
f
can be achieved by CAD tools like COM-
SOL which is fast and accurate and are capable of
solving 2-D problem like Fig. 1. Moreover, exterior-
interior method of moments (MoM) can be used
for problem of Fig. 1 to find exact A
z
(Faraji-Dana,
1993b). Consider the field distribution on the upper
w
1
x
ε
2
x
ε
x
-th guided mode
m
xm
R
(a)
-th guided mode
m
xm
R
x
2
r
ε
1
r
ε
t
y
w
(b)
Figure 3: Reflection of mth SW at the (a) interface of N
x
structure, and (b) end-facet.
surface of the waveguide, y = t, in Fig. 1(b). The line
source is located at x
′
= w/2 and y
′
= t. Suppose that
the exact result of A
z
is denoted by A
exact
z
. If we con-
sider R
xm
, m = 1, 2,...,N
p
in (6) as unknowns, then
a following optimization problem can be defined for
computation of the exact R
xm
at the end-facets of trun-
cated slab shown in Fig. 1
min f
error
(R
x1
,R
x2
,...,R
xN
p
),
R
xm
,
m=1,2,...,N
p
.
(8)
f
error
=
N
f
∑
i=1
A
z
(x
i
,y
i
;x
′
,y
′
;R
x1
,R
x2
,...,R
xN
p
)−
A
exact
z
(x
i
,y
i
;x
′
,y
′
)
2
.
(9)
To solve the optimization problem, subspace trust-
region algorithm is used which is based on the
interior-reflective Newton method described in (Cole-
man and Li, 1996). By increasing the number of field
points, N
f
, more exact R
xm
s will be obtained. For ini-
tial values of R
xm
s, one can use
β
x1
−β
x2
β
x1
+β
x2
λ
y
=λ
ym
for
R
xm
, obtained in CGF method (3). More rapid con-
vergence and rigorous results can be obtained by us-
ing modified initial values of R
xm
such as Marcateli’s
approximation R
xm
=
n
m
−n
2
n
m
+n
2
where n
2
=
√
ε
r2
and the
effective index n
m
is calculated from the propagation
constant of N
y
guided mode. i.e. n
m
=
k
xm
k
0
. More ac-
curate closed-form expression for R
xm
can be found
CombinationofCharacteristicGreen'sFunctionTechniqueandRationalFunctionFittingMethodforComputationof
ModalReflectivityattheOpticalWaveguideEnd-facet
17
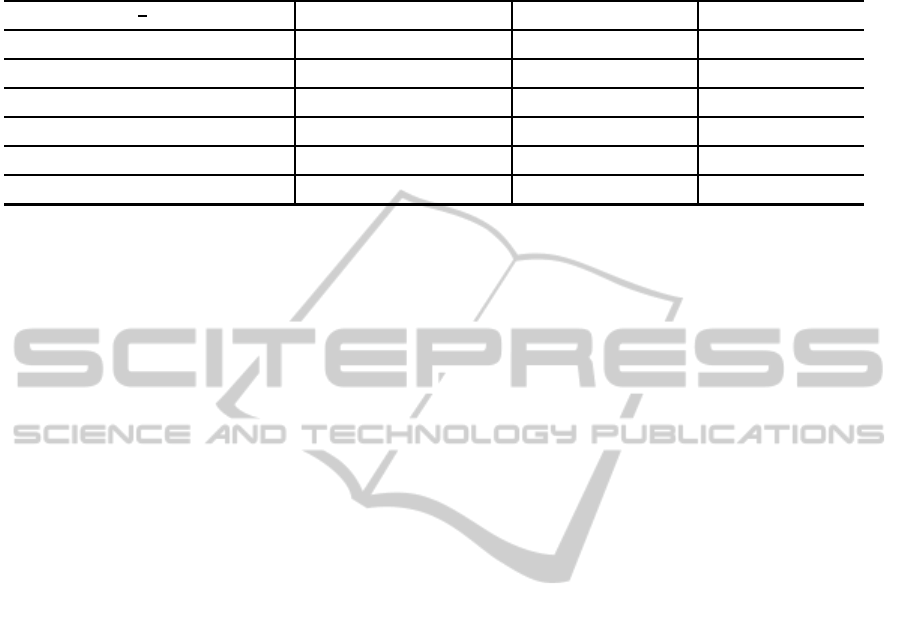
Table 1: R
x1
for low and high refractive index contrast structure shown in Fig. 1(b) with w = 2λ, for N
f
= 200 observation
points using CGF-RFFM-optimization, CGF-CI-optimization with d
s
= w/10, and mode matching methods (Gelin et al.,
1981). Mean time for computation of A
exact
z
by COMSOL is less than 8sec.
t
λ
n
1
n
2
CGF-RFFM-optimization CGF-CI-optimization (Gelin et al., 1981)
Structure 1 0.1 1.46 1.45 -0.760+j0.038 -0.735+j0.088 -0.761+j0.039
Structure 2 0.1 2.6 2.5 -0.468-j0.372 -0.472-j0.379 -0.468-j0.372
Structure 3 0.1 4.472 1 0.688+j0.232 0.672+j0.228 0.688+j0.231
Structure 4 0.166 4.472 1 0.716+j0.151 0.711+j0.142 0.718+j0.155
Structure 5 0.08 5.477 1 0.651+j0.396 0.649+j0.391 0.651+j0.399
Mean time < 5 sec < 2 sec > 8 min
in (Lewin, 1975).
The main advantage of using CGF-RFFM is that
all extracted poles can incorporate in the optimization
problem of (8). While in CGF-CI method (Torabi
et al., 2014a) the part of continuous spectrum con-
tribution (A
CS
z
in (Torabi et al., 2013)) which is re-
lated to approximate separable structure of Fig. 2(c)
is first subtracted by exact A
z
and the remained part
is used to optimized discrete spectrum contribution
to find R
xm
of guided modes. Therefore in (9) both
discrete and continuous spectrum parts would be cor-
rected by optimizing all the R
xm
of extracted poles in-
cluding guided and quazi-leaky wave poles. This is
in fact due to the capability of the rational function
fitting method to obtain uniform expansion of A
z
in
(5). So it is expected that more accurate R
xm
of guide
modes could be found by CGF-RFFM than CGF-CI
method. Although the time of optimization process
would be increased due to more poles incorporated in
(9) but results of next section shows that this is ignor-
able in comparison with the gained accuracy.
4 NUMERICAL RESULTS
To show the efficiency and versatility of the proposed
approach rigorous methods such as mode matching
is utilized (Gelin et al., 1981). More, CGF-CI-
optimization (Torabi et al., 2014a)results are also pro-
vided. RFFM step which includes poles extraction
from G
y
can be so fast. Then, to have exact reflec-
tion coefficients, optimization step should be run for
N
f
sample field points in [0,w] where the exact A
z
are available there. We place the source far from the
corners to have more exact results from CGF-RFFM
in (6). More it should be noted here that in CGF-CI
based method a guard d
s
is considered and the sam-
ples are chosen in [d
s
,w−d
s
]. This is due to the fact
that contribution of continuous spectrum of separa-
ble structure, Fig. 2(c), largely deviates from its orig-
inal value for nonseparable structure, Fig. 1(b), es-
pecially near the corners. But in CGF-RFFM there
is no need for any guard because continuous spec-
trum contribution is also incorporated and corrected
in the optimization process along with discrete spec-
trum contribution. It should be noted that Green’s
function A
z
includes only TE guided modes of the
Fig. 1(b). Therefore by using and incorporating A
z
in
defined optimization problem, reflection coefficients
of TE guided modes can be obtained. To have re-
sults for TM guided modes one can easily use Green’s
function of scalar or vector electric potential and fol-
low the similar steps.
At first, let us consider low refractive index con-
trasts. Results for reflection coefficient of guided
mode for structure 1 and 2 with parameters (n
1
=
1.46, n
2
= 1.45, t = 0.1λ) and (n
1
= 2.6, n
2
= 2.5,
t = 0.1λ) respectively, are shown in Table 1. Sim-
ulation results for higher refractive index contrast
are also reported in Table 1 for structures 3, 4, 5
which have single guided mode. We can find excel-
lent agreement between proposed method and rigor-
ous mode matching method (Gelin et al., 1981). For
single guided mode supported waveguide considered
in Table 1, mean simulation time for optimization is
less than 4 sec. Disregarding the time for preprocess-
ing of the structure to find the exact A
z
, our method
is much faster than mode matching method. Further-
more, by adding required time of step 1 (which is ap-
proximately 8 sec in COMSOL for high accuracy), to-
tal CPU-time would still be less than mode matching
method. moreover, it can be seen from Table 1 that
CGF-RFFM leads to more accurate results in com-
parison with CGF-CI results. For rational function
fitting step of (5), N
p
= 14 poles are used in modified
VECTFIT algorithm.
The number of observation points N
f
may be an
important parameter in controlling the speed and ac-
curacy of the method. In Table 2, amplitude of opti-
mized R
xm
for two of considered structures in Table 1
can be found for different N
f
. Small changes in opti-
mized reflection coefficient can be seen, by increasing
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
18
Table 4: Reflection coefficients for structure shown in Fig. 4 with n
1
= 1.132, n
2
= 2.449, n
3
= 3.162, n
0
= 1, t
1
= 0.1λ,
t
2
= 0.2λ, t
3
= 0.4λ, w = 2λ, for N
f
= 200 observation points using CGF-RFFM-optimization, CGF-CI-optimization (Torabi
et al., 2014a) with d
s
= w/10, and mode matching methods (Gelin et al., 1981). Mean time for computation of A
exact
z
by
COMSOL is less than 8sec.
R
xm
CGF-RFFM-optimization CGF-CI-optimization (Gelin et al., 1981)
R
x1
0.295+j0.717 0.286+j0.722 0.293+j0.716
R
x2
0.753+j0.107 0.721+j0.085 0.755+j0.109
Time < 10 sec < 5 sec > 10 min
Table 2: Amplitude of optimized R
x1
for structure 4 and 5
for different number of observation points N
f
N
f
Structure 4 Structure 5
|R
x1
| |R
x1
|
150 0.723 0.759
200 0.726 0.762
250 0.728 0.764
300 0.728 0.765
N
f
. It can be concluded that with small N
f
, quite exact
reflection coefficient with high speed can be obtained.
In Table 3, Reflection coefficients for a structure with
parameter (n
1
= 5.477, n
2
= 1, t = 0.19λ) that has
three guided TE modes are reported. Excellent match
between the results of CGF-RFFM-optimization and
IE-MoM can be found (Parsa and Paknys, 2007b).
Required simulation time for optimization is near to
8 sec which is much less than exact IE-MoM based
method.
To search the versatility of the proposed method
let us consider a problem of modal reflectivity at end-
facet of of three-layer media of Fig. 4. The refrac-
tive indices of layers are n
1
= 1.132, n
2
= 2.449,
n
3
= 3.162, n
0
= 1, with thickness of t
1
= 0.1λ,
t
2
= 0.2λ, t
3
= 0.4λ that leads to two supporting
guided modes. Results for reflection coefficient of
guided modes obtained by CGF-RFFM-optimization
are reported in Table 4 along with the results of
CGF-CI-optimization and mode matching method are
also given. N
p
= 16 poles are considered for ra-
tional function fitting step of (5). In comparison
with CGF-CI-optimization results excellent match be-
tween CGF-RFFM results and exact mode matching
method (Gelin et al., 1981) is evident. Moreover,
from Table 1 and Table 2, increasing in simulation
time of CGF-RFFM due to incorporation of more
poles in optimization step is ignorable.
The number of observation points N
f
has marginal
effects on the speed and accuracy of the method. In
Fig. 5(a) and Fig. 5(b) magnitude and phase of the op-
timized R
x1
and R
x2
for structure of Fig. 4 (described
Table 3: Reflection coefficients for structure shown in Fig. 1
with n
1
= 5.477, n
2
= 1, t = 0.19λ, w = 2λ, N
f
= 200.
R
xm
CGF-RFFM IE-MoM
-optimization (Parsa and Paknys, 2007b)
R
x1
-0.263+j0.654 -0.263+j0.752
R
x2
0.443+j0.758 0.443+j0.759
R
x3
0.315+j0.841 0.315+j.841
Time < 8 sec > 6 min
3
t
w
o
0
r
ε
2
t
1
t
1
r
ε
2
r
ε
3
r
ε
0
r
ε
Figure 4: Three layer truncated dielectric slab waveguide.
in Table 4) are depicted for N
f
. Good convergence
can be seen in the optimized reflection coefficients,
by increasing N
f
.
5 CONCLUSION
A novel method for reflection of guided mode at the
end-facet of optical waveguide is presented. The
method is based on the formulation of characteris-
tics Green’s function which is combined with rational
function fitting method. In the closed-form derivation
for spatial Green’s function of finite dielectric slab
waveguide, discrete and continuous spectrum contri-
bution are expressed in appropriate forms which can
be imported in optimization problem to obtain an ex-
act reflection coefficients of guided modes. The main
CombinationofCharacteristicGreen'sFunctionTechniqueandRationalFunctionFittingMethodforComputationof
ModalReflectivityattheOpticalWaveguideEnd-facet
19

50 100 150 200 250 300 350 400
0.3
0.31
0.32
0.33
0.34
0.35
0.36
N
f
Magnitude
50 100 150 200 250 300 350 400
0.49
0.5
0.51
0.52
0.53
0.54
0.55
Phase (rad)
Magnitude
Phase
(a)
50 100 150 200 250 300 350 400
0.65
0.7
0.75
0.8
N
f
Magnitude
50 100 150 200 250 300 350 400
0.1
0.15
0.2
0.25
Phase (rad)
Phase
Magnitude
(b)
Figure 5: Convergence of magnitude and phase of opti-
mized a) R
x1
and b) R
x2
, for different N
f
for structure of
Table 4.
advantages of this method lie in its rapidity as well
as accuracy. By using COMSOL for exact results of
spatial Green’s function for optimization, total CPU-
time is much less than rigorous methods. In gen-
eral, for all planar multilayered waveguide the for-
mulation can be easily derived for all components of
dyadic Green’s function to have reflection coefficients
of guided modes at the end-facet of truncation.
REFERENCES
Chen, Y., Lai, Y., Chong, T. C., and Ho, S.-T. (2012). Exact
solution of facet reflections for guided modes in high-
refractive-index-contrast sub-wavelength waveguide
via a fourier analysis and perturbative series summa-
tion: Derivation and applications. J. Lightw. Technol.,
30(15):2455–2471.
Coleman, T. F. and Li, Y. (1996). An interior trust region ap-
proach for nonlinear minimization subject to bounds.
SIAM journal on optimization, 6(2):418–445.
Derudder, H., Olyslager, F., De Zutter, D., and van den
Berghe, S. (2001). Efficient mode-matching analysis
of discontinuities in finite planar substrates using per-
fectly matched layers. IEEE Trans. Antennas Propag.,
49(2):185 –195.
El-Refaei, H., Betty, I., and Yevick, D. (2000). The appli-
cation of complex Pade approximants to reflection at
optical waveguide facets. IEEE Photon. Technol. Lett.,
12(2):158–160.
Faraji-Dana, R. (1993a). An Efficient and Accurate Green’s
Function Analysis of Packaged Microwave Integrated
Circuits. Thesis (Ph.D.)–University of Waterloo.
Faraji-Dana, R. (1993b). An Efficient and Accurate Green’s
Function Analysis of Packaged Microwave Integrated
Circuits. Thesis (Ph.D.)–University of Waterloo.
Gelin, P., Petenzi, M., and Citerne, J. (1981). Rigorous anal-
ysis of the scattering of surface waves in an abruptly
ended slab dielectric waveguide. IEEE Trans. Microw.
Theory Techn., 29(2):107 – 114.
Hardy, A. (1984). Formulation of two-dimensional
reflectivity calculations for transverse-magnetic-like
modes. J. Opt. Soc. Am. A., 1(7):760–763.
Hua, Y. and Sarkar, T. (1989). Generalized pencil-of-
function method for extracting poles of an EM sys-
tem from its transient response. IEEE Trans. Antennas
Propag., 37(2):229 –234.
Ikegami, T. (1972). Reflectivity of mode at facet and oscil-
lation mode in double-heterostructure injection lasers.
IEEE J. Quantum Electron., 8(6):470–476.
Jamid, H. and Khan, M. (2007). 3-D full-vectorial anal-
ysis of strong optical waveguide discontinuities us-
ing Pade approximants. IEEE J. Quantum Electron.,
43(4):343–349.
Lewin, L. (1975). A method for the calculation of the
radiation-pattern and mode-conversion properties of a
solid-state heterojunction laser. IEEE Trans. Microw.
Theory Techn., 23(7):576–585.
Michalski, K. and Mosig, J. (1997). Multilayered media
Green’s functions in integral equation formulations.
IEEE Trans. Antennas Propagat., 45(3):508 –519.
Parsa, A. and Paknys, R. (2007a). Interior Green’s function
solution for a thick and finite dielectric slab. IEEE
Trans. Antennas Propag., 55(12):3504 –3514.
Parsa, A. and Paknys, R. (2007b). Interior Green’s function
solution for a thick and finite dielectric slab. IEEE
Trans. Antennas Propag., 55(12):3504 –3514.
Rozzi, T. and Veld, G. (1980). Variational treatment of the
diffraction at the facet of d.h. lasers and of dielectric
millimeter wave antennas. IEEE Trans. Microw. The-
ory Techn., 28(2):61–73.
Shishegar, A. A. and Faraji-Dana, R. (2003). A closed-form
spatial Green’s function for finite dielectric structures.
Electromagnetics, 23(7):579–594.
Torabi, A., Shishegar, A. A., and Faraji-Dana, R. (2013).
Application of the characteristic Green’s function
technique in closed-form derivation of spatial Green’s
function of finite dielectric structures. In Compu-
tational Electromagnetics Workshop (CEM), 2013,
pages 54–55.
Torabi, A., Shishegar, A. A., and Faraji-Dana, R. (2014a).
Analysis of modal reflectivity of optical waveguide
end-facets by the characteristic Green’s function tech-
nique. J. Lightw. Technol., 32(6):1168–1176.
Torabi, A., Shishegar, A. A., and Faraji-Dana, R. (2014b).
An efficient closed-form derivation of spatial Green’s
function for finite dielectric structures using character-
istic Green’s function-rational function fitting method.
IEEE Trans. Antennas Propagat., 62(3).
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
20

Wei, S.H. and Lu, Y. Y. (2002). Application of Bi-CGSTAB
to waveguide discontinuity problems. IEEE Photon.
Technol. Lett., 14(5):645–647.
Yevick, D., Bardyszewski, W., Hermansson, B., and Glas-
ner, M. (1991). Split-operator electric field reflection
techniques. IEEE Photon. Technol. Lett., 3(6):527–
529.
Yevick, D., Bardyszewski, W., Hermansson, B., and Glas-
ner, M. (1992). Lanczos reduction techniques for elec-
tric field reflection. J. Lightw. Technol., 10(9):1234–
1237.
Yu, C. and Yevick, D. (1997). Application of the bidirec-
tional parabolic equation method to optical waveguide
facets. J. Opt. Soc. Am. A., 14(7):1448–1450.
CombinationofCharacteristicGreen'sFunctionTechniqueandRationalFunctionFittingMethodforComputationof
ModalReflectivityattheOpticalWaveguideEnd-facet
21
