
Robust Interest Point Detection by Local Zernike Moments
Gökhan Özbulak and Muhittin Gökmen
Department of Computer Engineering, Istanbul Technical University, Istanbul, Turkey
Keywords: Interest Point Detection, Feature Extraction, Object Detection, Local Zernike Moments, Scale-Space.
Abstract: In this paper, a novel interest point detector based on Local Zernike Moments is presented. Proposed
detector, which is named as Robust Local Zernike Moment based Features (R-LZMF), is invariant to scale,
rotation and translation changes in images and this makes it robust when detecting interesting points across
the images that are taken from same scene under varying view conditions such as zoom in/out or rotation.
As our experiments on the Inria Dataset indicate, R-LZMF outperforms widely used detectors such as SIFT
and SURF in terms of repeatability that is main criterion for evaluating detector performance.
1 INTRODUCTION
In computer vision, general object detection
framework is based on i) extracting interesting
points in images, ii) describing regions around these
points as feature vectors and iii) matching feature
vectors in order to find corresponding points of the
images. For instance, if there are two images of one
scene containing a black car, by detecting interesting
points that qualify the car itself in both images and
searching for similarity between feature vectors
extracted around these points through some distance
metrics such as Euclidean or Mahalanobis, it's
possible to say that the black car in first image exists
in the second image as well. This point
correspondence is also important for stereo vision,
motion estimation, image registration and stitching
applications to be able to match corresponding
regions in images.
Searching for corresponding points between
images is a hard problem when these images are
scaled, rotated and/or translated versions of each
other. Under these geometric transformations,
interesting points still need to be detected and
matched with high repeatability score that is the
correspondence rate of the interesting points
detected between the images.
A good interest point detector is expected to be
invariant to geometric and photometric
transformations, and also robust to background
clutters and occlusions in image. Changes in scale,
rotation and translation between the images are
examples of geometric transformations whereas
illumination change is an example of photometric
transformations. Scale invariance problem is
handled by building scaled samples of the image
with Gaussian blurring and then applying the interest
point detector to these samples. This stack of images
is named as scale-space and it's widely used by well-
known methods such as Scale Invariant Feature
Transform (SIFT) (Lowe, 2004) and Speeded-Up
Robust Features (SURF) (Bay et al., 2008). Local
characteristics of interest points make them invariant
to background clutters and occlusions (Mikolajczyk
and Schmid, 2004). The locality also provides
translational invariance for interest point detectors
because local regions move together in the image
and thus information in a local region is preserved in
case of image translation.
In this paper, by extending our previous rotation-
invariant detector named as Local Zernike Moment
based Features (LZMF) (Özbulak and Gökmen,
2014), we propose a robust interest point detector
that is invariant under scale, rotational and
translational changes. Proposed method uses
rotation-invariant Zernike moments locally in the
bility scores for “Zoom&Rotationn order to detect
interesting points and thus exhibits rotation and
translation-invariant characteristics. For scale
invariance, a scale-space is constructed from given
image and interest point detector is applied to
images in spatial and scale-space in order to detect
interest points/keypoints. We name our interest point
detector as Robust Local Zernike Moment based
Features or R-LZMF shortly.
644
Özbulak G. and Gökmen M..
Robust Interest Point Detection by Local Zernike Moments.
DOI: 10.5220/0005343506440651
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 644-651
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK
In the literature, most of interest point detection
schemas are based on corner or blob detectors
because they are good candidates to be interesting
points. One of the earliest interest point detector was
developed by Harris et al. and named as Harris
corner detector (Harris and Stephens, 1988). It
searches for large intensity changes in spatial-space
by sliding a window and detects such locations as
corners. Harris detector is rotation-invariant but not
scale-invariant.
Andrew Witkin introduced the scale-space
theory in his seminal work (Witkin, 1983) and
showed that convolving an image with Gaussian
filters of increasing sigma repeatedly exposes the
structures in different scales and thus gives scale
invariance characteristic to the detector building it.
Lindeberg extended the work of Witkin and
proposed automatic scale selection mechanism with
scale normalized Laplacian-of-Gaussian (LoG)
operator to detect blob-like structures in an image
(Lindeberg, 1998). Lowe, in (Lowe, 2004), showed
that LoG can be approximated by Difference-of-
Gaussian (DoG) that is the difference of two images
convolved with Gaussian filters of consecutive
sigma values. Lowe built DoG space for interest
point detection and he presented a complete schema
(detector and descriptor) named as Scale Invariant
Feature Transform (SIFT).
Mikolajczyk et al. proposed Harris-Laplace
detector, which combines Harris detector with LoG
operator, in (Mikolajczyk and Schmid, 2001). They
used Harris detector to localize interest points in 2D
(spatial-space) and LoG operator to find local
maximum in 3D (scale-space). The reason of using
Laplacian instead of Harris function in 3D is that
Harris function can't reach to maximum in scale-
space frequently and this causes a few numbers of
keypoints to be generated. Harris-Laplace detector
was then extended in (Mikolajczyk and Schmid,
2002, 2004) by determining the shape of the
elliptical region with the second moment matrix.
This schema was named as Harris-Affine detector.
Hessian-Affine detector, which detects interest
points based on the Hessian matrix in 2D space, was
also proposed in (Mikolajczyk and Schmid, 2002,
2004). Both Harris-Affine and Hessian-Affine
detectors have significant invariance to affine
transformations when compared with Harris-Laplace
detector.
Bay et al., in their schema named as Speeded-Up
Robust Features (SURF) (Bay et al., 2008), used
Hessian-based detector instead of Harris-based
counterpart because Hessian function is more stable
and repeatable. They preferred building scale-space
of approximated LoG filters rather than image itself
as opposed to SIFT and Harris-Laplace. Up-scaling
the filters instead of down-scaling the image
prevents aliasing problems occurred when sub-
sampling the image and this approach is also faster
than SIFT because up-scaled filters are implemented
with efficient integral image method.
Rosten et al. developed a fast interest point
detector and named it as Features from Accelerated
Segment Test (FAST) in (Rosten and Drummond,
2006). FAST tests each image pixel for cornerness
by looking its 16 pixel-circular neighborhood and if
some contiguous pixels in this neighborhood are
brighter/darker than the pixel in test then it's
detected as corner. This method also learns from
image pixels by applying decision tree to increase its
accuracy. Interest points detected by FAST are not
multi-scale features, in other words, FAST is not
scale-invariant. Oriented FAST and Rotated Brief
(ORB), proposed in (Rublee et al., 2011), is a
combination of FAST keypoint detector and BRIEF
descriptor (Calonder et al., 2010). ORB modifies
FAST to work with image pyramid for scale
invariance and it also modifies BRIEF descriptor to
make it rotation-invariant. Center Surround Extrema
(CenSurE) is another scale and rotation-invariant
interest point detector proposed in (Agrawal et al.,
2008). In CenSurE, a center-surround filter is
applied to the image at all locations and scales, and
Harris function is used for eliminating weak corner
points. Leutenegger et al. proposed a rotation and
scale-invariant key point detector named as Binary
Robust Invariant Scalable Keypoints (BRISK) in
(Leutenegger et al., 2011). BRISK uses a novel
scale-space FAST-based detector for scale-invariant
interest point detection and considers a saliency
criterion by using quadratic function fitting in
continuous domain.
In (Özbulak and Gökmen, 2014), we proposed a
rotation-invariant interest point detector by applying
Zernike moment of
to the image locally in order
to measure cornerness and sweeping up nearby
edges by dividing Zernike moments
to
. We
named it as Local Zernike Moment based Features
(LZMF). Performance evaluation of LZMF with
“Rotation” sequence of the Inria Dataset showed that
our method outperforms well-known interest point
detectors such as SIFT, SURF, CenSurE and
BRISK. In this study, we extend our rotation-
invariant detector to be scale-invariant by building
scale-space with optimal parameter settings.
RobustInterestPointDetectionbyLocalZernikeMoments
645

3 ROBUST INTEREST POINT
DETECTION
In this section, we introduce our robust and local
Zernike Moment (LZM) based interest point
detector schema, R-LZMF. Zernike moments are
described in Section 3.1 and Section 3.2 includes a
general overview of the proposed detector. In
Section 3.3, we show how the scale-space is built in
order to yield the best scale-invariance performance
with our detector.
3.1 Zernike Moments
In (Zernike, 1934), Fritz Zernike introduced a
complete set of complex polynomials, named as
Zernike polynomials, that are orthogonal on the unit
disk
+
≤1. Zernike polynomials are defined
as:
(
,
)
=
(
,
)
=
()
(1)
Where
(
)
is the radial polynomial, is the
order of polynomial, is the number of iteration,
is the length of vector from origin to (x,y) and is
the angle between and x-axis in counter-clockwise
direction. There are some constraints on n and m
parameters such as ≥0, n−|m|=even and
|m|<=n.
(
)
is defined as:
(
)
=
(
−1
)
(
−
)
!
!
|
|
!
|
|
!
|
|
(2)
Teague introduced using Zernike polynomials as
orthogonal image moments in (Teague, 1980) for
two-dimensional pattern recognition. Given an
image function of f(x,y), Zernike moment of order
and repetition is defined as:
=
+1
(
,
)
∗
(
,
)
(3)
Where ∗ in
∗
(,) denotes the complex
conjugate. The formula in (3) is discretized in order
to work with digital images of size MxN as:
=
+1
(,)
∗
(
,
)Δ
Δy
(4)
Where
,
∈[−1,1],
=
+
,
=tan
⁄
and Δ
=Δ
=2/
√
2.
As seen from (4), a Zernike moment,
, is a
measurement about the intensity profile of the whole
image. It's also possible to project the local intensity
profiles on to Zernike polynomials by fitting the unit
circle on the pixels of the image. The image
moments using Zernike moments in this way are
named as local Zernike moments or LZM shortly.
LZM presents a powerful description of local image
region as it's successfully applied to face recognition
problem in (Sariyanidi et al., 2012) and used for
detection of low-level features such as step edges
and gray-level corners in (Ghosal and Mehrotra,
1997). In this paper, we use LZM representation to
detect gray-level corners by convolving the image
with LZM based operator,
.
is a
convolutional filter for Zernike moment of order
and repetition and defined as:
(
,
)
=
(
,
)
(5)
An image is convolved with
as below:
(
,
)
=
(−,−)
(,)
,
(6)
There is one real filter denoted as [
] and
one imaginary filter denoted as [
] for a
Zernike moment of order and repetation
because Zernike moments are complex. However,
imaginary filter is discarded when there is no
repetition (m=0) and the image is only convolved
with real filter.
The magnitude of Zernike moments is
unchanged when an image is rotated by an angle of
w.r.t. x-axis. This property gives Zernike moments
rotation-invariant characteristic under image
rotations, see (Khotanzad and Hong, 1990). The
magnitude of Zernike moment is defined as:
|
|
=
([
])
+([
])
(7)
Where [
] and [
] are local Zernike
moment representations obtained by convolving an
image with real and imaginary Zernike filters,
[
] and [
], respectively. As a note,
[
] is zero and discarded when =0.
3.2 Interest Point Detection by LZM
Our interest point detection method is applied in
spatial (2D) and scale-space (3D). In spatial-space,
input image is first converted to gray-scale and then
-normalization is applied on the gray-scaled image
to make proposed detector more robust to noise as
we showed in (Özbulak and Gökmen, 2014).
Before convolving the image with Zernike filter,
a second normalization procedure is locally applied
to the region where unit circle is fitted. The local
intensity profile under this circle is fitted to standard
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
646

normal distribution with =0 and =1 in order to
make proposed detector more robust to local
illumination changes. This is similar to
normalization procedure in Normalized Cross-
Correlation (NCC) and feature vector normalization
in SIFT (Lowe, 2004).
The input image is then convolved with Zernike
filters,
and
. Ghosal, in (Ghosal and
Mehrotra, 1997), used Zernike filters with order of
2,
and
, for his corner detection schema. In
the experiments, however, we found that working
with more complex orders such as 4 yields better
results in terms of repeatability. In our method, the
magnitude of Zernike moment of
, |
|, is used
to measure the cornerness. A pre-defined corner
threshold is applied to |
| response and the pixels
that are higher than this threshold are considered as
candidate interest points. The drawback of using
Zernike moment of
is that it may respond to
edges closer to corners. We suppress these nearby
edges by dividing |
| to |
| as
|
|
|
|
and then
thresholding
|
|
|
|
with a pre-defined nearby edge
threshold. Candidate interest points passing this
thresholding test are retained for further processing
and the rest is discarded. So, in this way, interest
points/keypoints, which are corners but not nearby
edges, are considered. For proposed detector, corner
threshold value of 0.51 and nearby-edge threshold
value of 5, which were determined in our previous
work by using “Rotation” sequence of the Inria
Dataset, are used throughout the experiments.
A further refinement procedure by Non
Maximum Suppression is also applied to the
detected interest points in spatial domain as follows:
i) a 5x5 window is centered on each interest point,
ii) the interest point is compared based on |
| with
detected interest points in its 5x5 neighborhood, iii)
the interest point is retained if its |
| response is
the maximum or discarded otherwise. In this way,
redundant interest points are swept out and more
consistent interest points are retained.
Candidate interest points detected in spatial-space
are then examined in scale-space to eliminate weak
ones, which don't reach local maximum in scale-
space, and to figure out characteristic scales of
strong ones (see Section 3.3 for details). This
analysis is realized in each octave of the scale-space
as follows: For outermost scale levels of an octave,
candidate interest points detected as a result of
spatial analysis are directly retained without any
scale analysis. For inner scale levels of an octave, a
candidate interest point is compared with interest
points detected in lower and upper scale levels based
on |
|. This comparison again falls in 5x5
neighborhood of the point in interest for adjacent
scale levels. If |
| response of the interest point is
the maximum among all interest points detected in
lower and upper scale levels then the candidate
interest point is considered as a real interest point.
This kind of approach is also named as 3D Non
Maximum Suppression. Here, R-LZMF has
5x5x3=75-1=74 comparisons at most in spatial and
scale-space and this check doesn't take time because
it only compares the point in interest with detected
interest points in 2D and 3D space, and stops
comparison if one interest point in the neighborhood
has higher |
|.
3.3 Scale-Space
Andrew Witkin introduced the scale-space concept
in his seminal work (Witkin, 1983) to represent
signals in different scale levels in order to show how
signal behaviour changes from fine to coarse scales.
He also showed that smoothing an image with
Gaussian filters of increasing sigma has ability to
suppress fine details and expose coarse structures.
Koenderink, in (Koenderink, 1984), showed that
Gaussian filter is the unique filter for building scale-
space. Lindeberg verified this uniqueness and
proposed an automatic scale selection mechanism in
order to find the characteristic scale of an interesting
point in an image (Lindeberg, 1998). Characteristic
scale is the scale level where an interest point
detection function reaches local extremum in the
scale-space. This is the moment an image point
exhibits most interesting characteristic (cornerness,
blobness etc.) in the scale-space. A description
extracted from an interest point with characteristic
scale size would be independent of same interest
points detected in different scaled images.
In this study, we build a scale-space for our
rotation-invariant interest point detector proposed in
our previous work to make it scale-invariant as well.
The input image is repeatedly convolved with
Gaussian filters of increasing sigma size for blurring
and each blurred image constitutes a scale level,
(,,), in the scale-space. (,,) is defined
as:
(
,,
)
=
(
,,
)
∗(,)
(8)
Where (,) is the input image and (,,) is
the 2D Gaussian function defined as:
(
,,
)
=
1
2
(
)/
(9)
We divide scale-space into octaves for efficient
computation. An octave is a stack of scale
RobustInterestPointDetectionbyLocalZernikeMoments
647
levels/layers, (,,), with same resolution and
sigma for each scale level is a constant factor of
previous scale layer's sigma. An image in one octave
is a sub-sampled version of an image in previous
octave. When sigma in an octave is doubled, the
image convolved with Gaussian filter of this sigma
is halved in size and used as first scale layer of next
octave. Here, sub-sampling is the key factor for
computational gain.
(a)
(b)
(c)
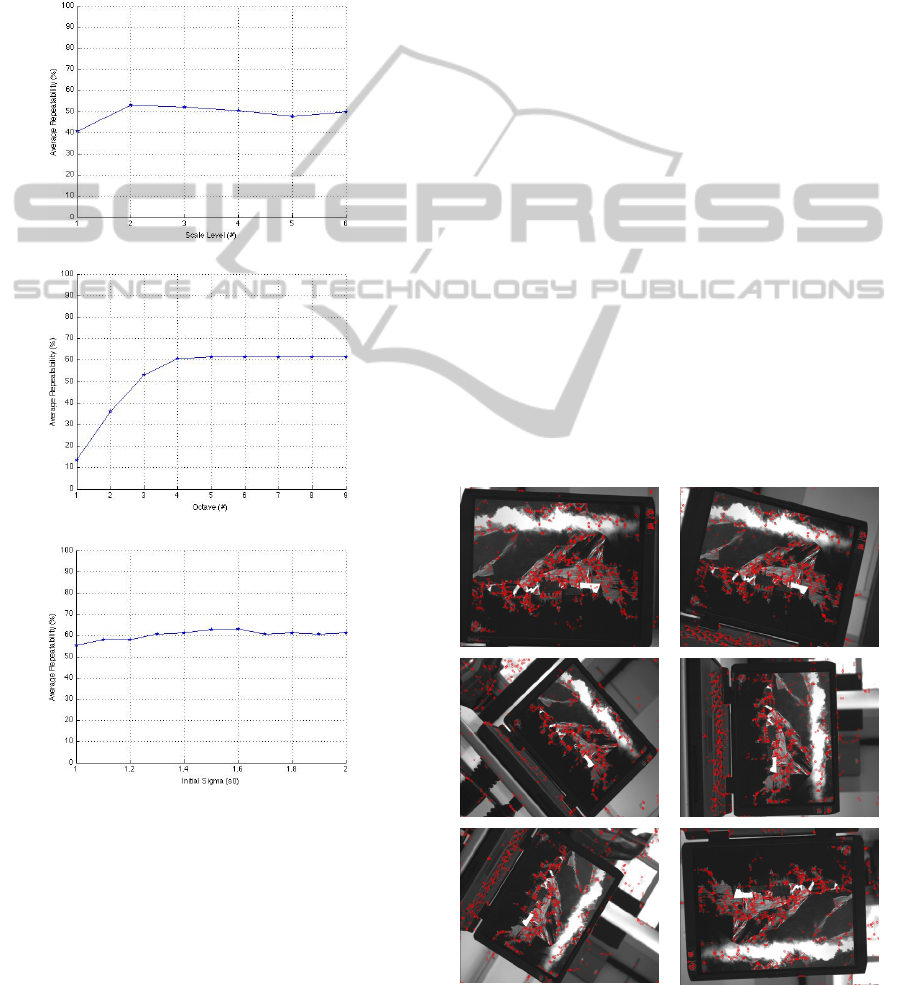
Figure 1: Parameter evaluation for scale-space based on
average repeatability: (a) Number of scale level
performance for =3,
=1.7. (b) Number of octave
performance for =2,
=1.7. (c) Initial sigma
performance for =4, =2.
There are some parameters that should be fine-
tuned in order to have a full coverage of scale-space.
These are the number of scale levels in one octave
(), the number of octaves in scale-space () and
initial sigma for first scale level of the first octave
(
). We used Belledonnes images from “Zoom”
sequence of the Inria Dataset to figure out the
optimum parameters for our detector. We first
determined the number of scale layer under
assumptions of =3 and
=1.7 and got the best
average repeatability by using two scale levels (=
2), see Figure 1-a. In this case, however, 3D Non
Maximum Suppression is not applied because
outermost scale layers are the only scale layers to be
used. We then searched for the optimum number of
octaves with =2 under assumption of
=1.7
and as seen from Figure 1-b working with 4 octaves
(=4) yields the best result in terms of average
repeatability. As noted, using more than 4 octaves
doesn't affect the performance. For initial sigma
value, under =4 and =2, although the best
repeatability performance is obtained with value of
1.6 as seen in Figure 1-c, we had better performance
with value of 1.8 (
=1.8) in the experiments, so
we use this value as initial sigma value. Thus, final
parameter settings were determined as =4, =2
and
=1.8.
In Figure 2, the interest points detected by R-
LZMF can be seen as red circles in some Laptop
images of “Zoom&Rotation” sequence. In this
figure, most of the interesting points detected in one
image can be observed in other images as an
indicator of how our detector is accurate in terms of
repeatability.
Figure 2: Interest points detected by R-LZMF for some
Laptop images from “Zoom&Rotation” sequence.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
648
4 EXPERIMENTAL RESULTS
The Inria Dataset is used for performance evaluation
of proposed detector. We used Asterix, Crolles,
VanGogh image sets from "Zoom" sequences, and
East_park, Laptop, Resid image sets from
"Zoom&Rotation" sequences. "Zoom" sequence
contains only scaled image sets and
"Zoom&Rotation" image sets have scaled and
rotated images. Image sets in both sequences have
their own transformation matrices for repeatability
evaluation although scale and rotation information
about image sets are not provided. Therefore, x-axis
in Figure 3 and Figure 4 show the image index
instead of scale value or rotation angle. One can
think of larger image index as larger scale and
rotation angle.
As proposed in (Schmid et al., 1998), the
repeatability score is main criterion to evaluate
performance of interest point detectors. The
repeatability is a measurement of the point
correspondence between two images that are
transformed form (scaled, rotated or translated) of
each other. A robust interest point detector is
expected to detect the most of the same structures in
two images even they are scaled, rotated or
translated versions of each other. The repeatability
score is evaluated as:
,
=
(
,
)
min(
,
)
(10)
Where (
,
) is the number of corresponding
points detected in both images,
and
are the
numbers of the keypoints detected in first and
second images respectively.
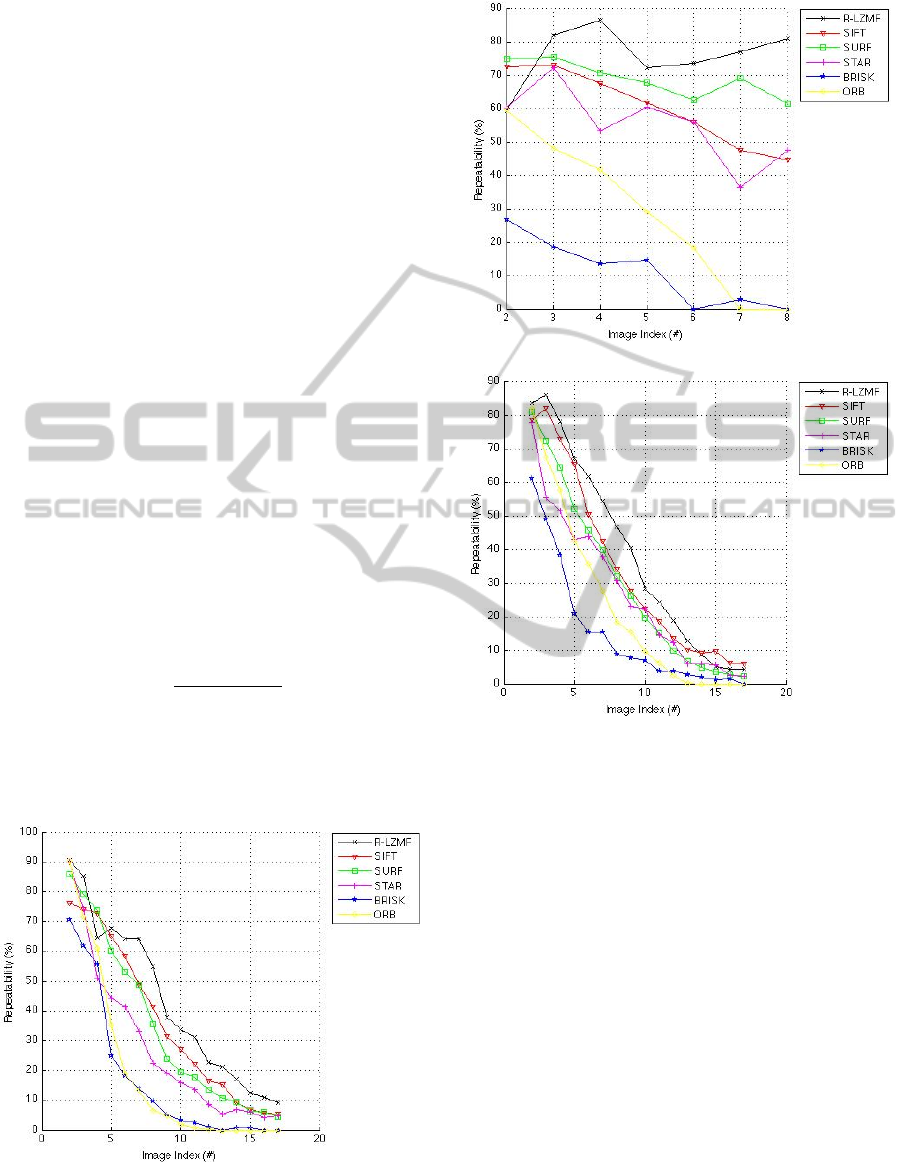
(a)
Figure 3: Repeatability scores for “Zoom” sequence: (a)
Asterix. (b) Crolles. (c) VanGogh.
(b)
(c)
Figure 3: Repeatability scores for “Zoom” sequence: (a)
Asterix. (b) Crolles. (c) VanGogh (cont.).
Repeatability performance of R-LZMF with
image sets used for evaluation is plotted in Figure 3
for “Zoom” sequence and in Figure 4 for
“Zoom&Rotation” sequence. As seen from plots, R-
LZMF outperforms well-known detectors such as
SIFT, SURF, CenSurE (STAR), BRISK and ORB
for all image sets. We used OpenCV v2.4.8 to work
with these detectors and applied them on the image
sets with default parameter settings. As a note,
throughout the experiments, we used our detector
with same parameter settings as well: corner
threshold=0.51, nearby-edge threshold=5, =4,
=2,
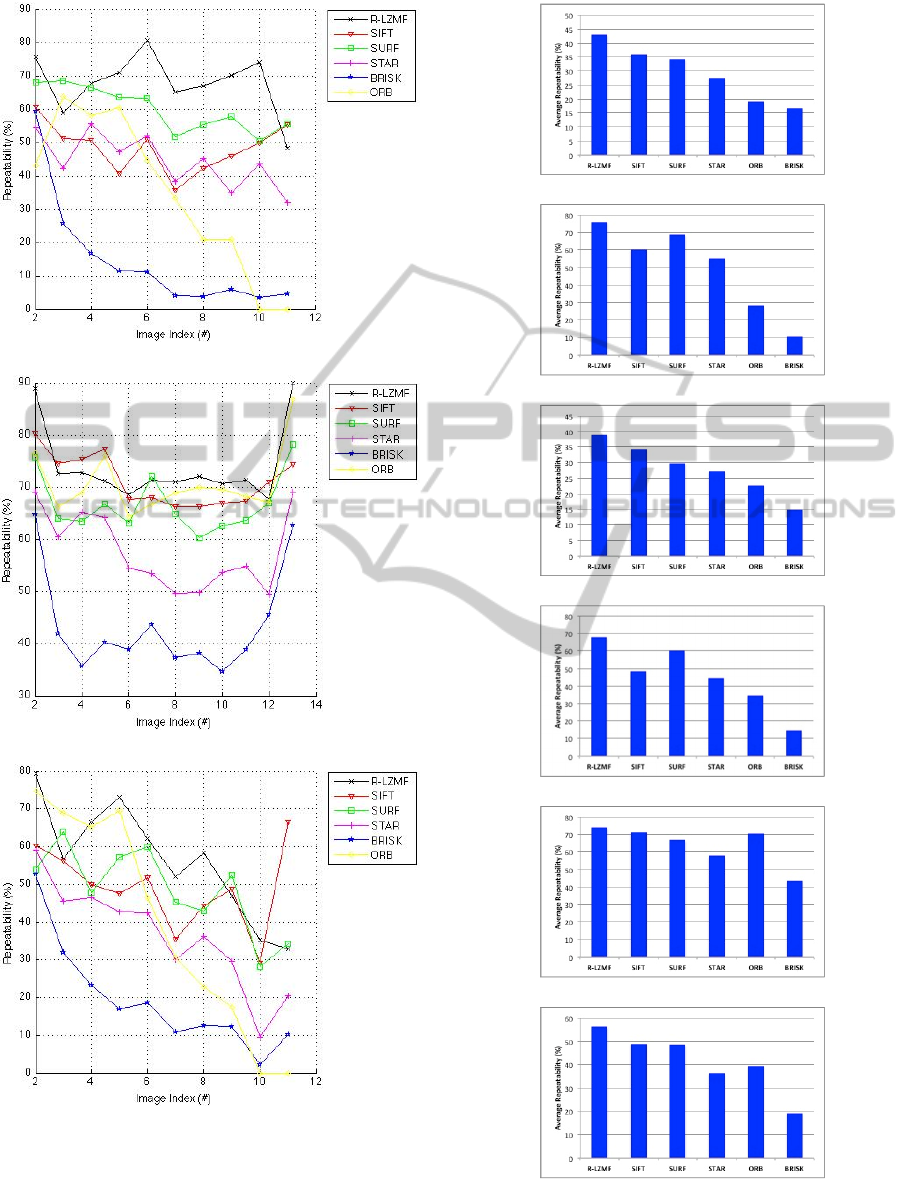
=1.8. From the bar charts in Figure 5, it
can be seen that R-LZMF has also the best
performance in terms of average repeatability when
compared with all other detectors.
RobustInterestPointDetectionbyLocalZernikeMoments
649
(a)
(b)
(c)
Figure 4: Repeatability scores for “Zoom&Rotation”
sequence: (a) East_park. (b) Laptop. (c) Resid.
(a)
(b)
(c)
(d)
(e)
(f)
Figure 5: Average repeatability scores for: (a) Asterix. (b)
Crolles. (c) VanGogh. (d) East_park. (e) Laptop. (f) Resid.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
650

5 CONCLUSIONS
In this paper, we proposed a novel interest point
detector named as Robust Local Zernike Moment
based Features or R-LZMF. This detector is based
on local Zernike moments and invariant to geometric
transformations such as scale, rotation and
translation. We validated its robustness to these
transformations by testing it with the Inria Dataset
and reported that R-LZMF outperforms SIFT,
SURF, CenSurE (STAR), BRISK and ORB for all
image sets in the experiments. As a future work, we
plan to analyse the performance of R-LZMF for
affine transformation as well. Furthermore, we will
extend R-LZMF to have a descriptor by using LZM
again to utilize from its descriptive power so that it
will be a complete schema (detector and descriptor)
as in SIFT and SURF.
REFERENCES
Agrawal, M., Konolige, K., Blas, M. R., 2008. CenSurE:
Center surround extremas for realtime feature
detection and matching. In European Conference on
Computer Vision, pp. 102-115.
Bay, H., Ess, A., Tuytelaars, T., Gool, L.V., 2008. SURF:
Speeded Up Robust Features. In Computer Vision and
Image Understanding, vol. 110, no. 3, pp. 346-359.
Calonder, M., Lepetit V., Strecha, C., Fua, P., 2010.
BRIEF: Binary Robust Independent Elementary
Features. In European Conference on Computer
Vision, pp. 778-792.
Ghosal, S., Mehrotra, R., 1997. A moment based unified
approach to image feature detection. In IEEE Trans.
Image Processing, vol. 6, no. 6, pp. 781-793.
Harris, C., Stephens, M., 1988. A combined corner and
edge detector. Alvey Vision Conference, pp. 147-151.
Khotanzad, A., Hong, Y. H., 1990. Invariant image
recognition by Zernike moments. In IEEE
Trans.Pattern Analysis and Machine Intelligence, vol.
12, pp. 489-497.
Koenderink, J.J., 1984. The structure of images.
Biological Cybernetics, 50:363–396.
Leutenegger, S., Chli, M., Siegwart R., 2011. BRISK:
Binary Robust Invariant Scalable Keypoints. In
International Conference on Computer Vision, pp.
2548-2555.
Lindeberg, T., 1998. Feature detection with automatic
scale selection. In International Journal of Computer
Vision, 30(2):79-116.
Lowe, D.G., 2004. Distinctive image features from scale-
invariant keypoints. In International Journal of
Computer Vision, vol. 60, no. 2, pp. 91-110.
Mikolajczyk, K., Schmid, C., 2001. Indexing based on
scale invariant interest points. In International
Conference on Computer Vision, pp. 525-531.
Mikolajczyk, K., Schmid, C., 2002. An affine invariant
interest point detector. In European Conference on
Computer Vision, pp. 128-142.
Mikolajczyk, K., Schmid, C., 2004. Scale and affine
invariant interest point detectors. In International
Journal of Computer Vision, vol. 60, no. 1, pp. 63-86.
Özbulak, G., Gökmen, M., 2014. A rotation invariant local
Zernike moment based interest point detector. In Proc.
SPIE of International Conference on Machine Vision.
Rosten, E., Drummond, T., 2006. Machine learning for
high-speed corner detection. In European Conference
on Computer Vision, pp. 430-443.
Rublee, E., Rabaud, V., Konolige, K., Bradski, G., 2011.
ORB: an efficient alternative to SIFT or SURF. In
Internatioanl Conference on Computer Vision, pp.
2564-2571.
Sariyanidi, E., Dagli, V., Tek, S.C., Tunc, B., Gokmen,
M., 2012. Local Zernike Moments: A new
representation for face recognition. In International
Conference on Image Processing, pp. 585-588.
Schmid, C., Mohr, R., Bauckhage, C., 1998. Comparing
and evaluating interest points. In IEEE International
Conference on Computer Vision, pp. 230-235.
Teague, M.R., 1980. Image analysis via the general theory
of moments, In J. Optical Soc. Am., Vol. 70, pp. 920-
930.
The Inria Dataset, http://lear.inrialpes.fr/people/
mikolajczyk/Database.
Witkin, A.P., 1983. Scale-space filtering. In International
Joint Conference on Artificial Intelligence, Karlsruhe,
Germany, pp. 1019–1022.
Zernike, F., 1934. Physica, vol. 1.
RobustInterestPointDetectionbyLocalZernikeMoments
651
