Antennas’ Correlation Inﬂuence on the GMD-assisted MIMO Channels

Performance

C´esar Benavente-Peces

, Andreas Ahrens

, Francisco Javier Ortega-Gonz´alez

and Jos´e Manuel Pardo-Mart´ın

Universidad Polit´ecnica de Madrid, ETS de Ingenier´ıa y Sistemas de Telecomunicaci´on,

Department of Signal Theory and Communications, Ctra. Valencia km. 7, 28031 Madrid, Spain

Hochschule Wismar, University of Technology, Business and Design, Faculty of Engineering, Department of Electrical

Engineering and Computer Science, Philipp-M¨uller-Straße, PO box 1210, 23952 Wismar, Germany

Keywords:

Multipe-Input Multile-Output (MIMO), Geometric Mean Decompositioin, Trasnmission Mode, Bit Alloca-

tion, Power Allocation.

Abstract:

The use of multiple antennas in MIMO (multiple-input multiple-output) systems at both the transmit and re-

ceive sides produces the effect known as antennas correlation which impact the overall channel performance,

throughput and bit-error rate (BER). The geometric mean decomposition (GMD) is a signal processing tech-

nique which can be used to process transmit and receive signals in MIMO channels. The GMD pre- and

post-procesing in conjunction with dirty-paper precoding shows some advantages over the popular singular

value decomposition (SVD) technique which provides GMD-assisted MIMO systems a superior performance

particularly when the channel is affected by antennas correlation. This paper analyses the impact of antennas

correlation on the performance of GMD-assisted wireless MIMO channels highlighting the advantages over

SVD-assisted ones.

1 INTRODUCTION

In the last decades researchers and engineers are fac-

ing the uphill to obtain higher transmission data rates

and wider bandwidths required for the current and

future high-speed services demanded by the indus-

try and society, as video streaming, video-conference,

massive data transference, multi-user services, etc. In

this context multiple-input multiple-output (MIMO)

systems are playing a key role due to their capability

to increase the channel throughput and performance

compared with single-input single-output (SISO) sys-

tems (Foschini and Gans, 1998), (Ozgur et al., 2013).

Due to their potential capabilities MIMO wireless

communication systems have attracted a lot of atten-

tion from the research community. The use of spatial

diversity in MIMO systems can considerably increase

data rate and signiﬁcantly improve the system robust-

ness, reliability and coverage (Yang et al., 2011).

The use of multiple transmit and receive antennas

causes effects which affect the channel performance.

First, due to the multi-antenna conﬁguration and the

multi-path transmission inter-antennas interferences

disturb the channel behaviour. MIMO systems beneﬁt

from multipath by using additional signal processing

in order to improve the channel performance. Sec-

ond, due to physical limitations the antennas at each

side are really close compared to the wavelength and

the correlation effectappears negativelyimpacting the

MIMO channel performance (Janaswamy, 2002).

As stated above, in order to beneﬁt the MIMO

channels capabilities additional signal processing

is required. The SVD is a popular technique

widely used to improve MIMO channels performance

(Haykin, 2002). Given perfect channel state infor-

mation (PCSI) is available at both the transmit and

receive link sides, the SVD is used to perform pre-

and post-processing on the transmit and receive sig-

nals (respectively) to completely eliminate the ex-

isting inter-antennas interferences. As a result the

MIMO channel is transformed into several parallel,

independent and non-interfering single-input single-

output (SISO) unequally weighted channels.

GMD-assisted signal processing seems to be an

advantageous alternative to SVD-assisted signal pro-

cessing in MIMO systems. The GMD can be used

to process transmit and receive signals decomposing

the MIMO channel into several SISO channels with

325

Benavente-Peces C., Ahrens A., Pardo-Martín J. and Ortega-González F..

Antennas’ Correlation Inﬂuence on the GMD-assisted MIMO Channels Performance.

DOI: 10.5220/0005363603250334

In Proceedings of the 5th International Conference on Pervasive and Embedded Computing and Communication Systems (AMC-2015), pages 325-334

ISBN: 978-989-758-084-0

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

remaining inter-antennas interferences which must be

eliminated by using additional signal processing (e.g.,

Tomlinson-Harashima pre-coding) to obtain the best

channel performance. Along the investigation the

Tomlinson-Harashima pre-coding is used in a fre-

quency non-selectiveGMD-assisted MIMO system to

perfectly cancel the inter-antenna interferences (Kinjo

and Ohno, 2013).

In order to improve the SVD-assisted MIMO sys-

tem performance, where the resulting SISO channels

have different particular layer gains, bit and power al-

location techniques based on the varying channel con-

dition can be used (Zhou et al., 2005), which is syn-

onymous of adaptive modulation. One of the main

advantages of using the GMD is that the resulting in-

dependent layers have the same particular SISO chan-

nel gain coefﬁcient (the geometric mean of the sin-

gular values), assuming that the inter-antenna inter-

ferences are perfectly eliminated by dirty-paper pre-

coding. Hence, power allocation doesn’t make sense

in GMD-assisted MIMO systems (a priori) avoiding

the required computational overhead.

Antennas correlation is characterized by the an-

tennas’ correlation coefﬁcients which affect the chan-

nel matrix and hence its behaviour (Lee, 1973). The

higher the antennas’ correlation the lower the chan-

nel scatter richness condition (required by MIMO sys-

tems to get a better behaviour) and the lower the over-

all performance. The correlation effect affects the ge-

ometric mean PDF which impacts the channel perfor-

mance. The geometric mean PDF and the CCDF can

be used to predict and optimize the MIMO channel

performance by activating a proper number of layers

which deﬁne different transmission modes conﬁgura-

tions.

In (Benavente-Peces et al., 2013) the authors fo-

cused the investigation on the analysis of the singular

values CCDF to evaluate the receiver-side antennas

correlation effect on the channel performance and the

outcomes of the appropriate antennas usage in a SVD-

assisted MIMO system.

The noveltyof this contribution is that a frequency

non-selective MIMO link is studied independently of

the antennas electrical properties to analyse the im-

pact of antennas’ correlation on the performance of

GMD-assisted MIMO systems. The effects on the

channel matrix are highlighted and the resulting ge-

ometric mean PDF and CCDF are studied.

Additionally the beneﬁts of having equal values of

layer-speciﬁc weighting factors (i.e. gain coefﬁcients)

in GMD-based MIMO systems are remarked against

the SVD-assisted ones using different number of ac-

tive layers, highlighting the effect of correlation com-

pared to classical uncorrelated channels. The geomet-

ric mean CCDF curves are used to analyse and pre-

dict the behaviour of the MIMO channel. The BER

is computed for various active layers and the effect

of antennas’ correlation is remarked to ﬁnd the best

transmission mode. A 4×4 MIMO system transmit-

ting QAM signals along the active layers is consid-

ered as an example.

The remaining part of this paper is structured as

follows. Section 1 shows the computation of the

geometric mean of the channel matrix singular val-

ues. Section 3 describes the channel model for the

GMD-assisted MIMO system, including the anten-

nas’ correlation model. The analysed transmission

modes are introduced in Section 4. Section 5 com-

pares the GMD-assisted MIMO system versus the

SVD-assisted one. In Section 6 the main results of the

investigation are introduced including the geometric

mean PDF and CCDF analysis, the antennas’ corre-

lation effects and the considered transmission modes.

Finally, Section 7 summarizes and highlightsthe main

outcomes.

2 THE GEOMETRIC MEAN

The GMD with remaining interference elimination

decomposes the MIMO channel into several indepen-

dent SISO channels with equal performance. The

main advantage that GMD-assisted MIMO systems

present over the SVD-assisted ones is that those inde-

pendent layers have the same gain coefﬁcient which is

the geometric mean of the singular values of the chan-

nel matrix. Hence, the additional computational load

required to perform bit and power allocation to im-

prove and optimize the MIMO channel performance

is reduced. The geometric mean can be computed

from the channel matrix singular values as:

µ =

∏

i=1

1/L

, (1)

where L is the number of activated layers (with L ≤

min(n

), n

and n

are the number of transmit and

receive antennas respectively) and

(singular val-

ues) states for the positive square roots of the eigen-

values ξ

of H· H

, where H is the channel matrix

and (·)

is the hermitian operator.

3 CHANNEL MODEL

The MIMO channel can be described in general terms

y = H· c+ n (2)

PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

326

where c is the (n

× 1) transmit data vector, H is the

×n

) channel matrix, n is the (n

×1) noise vector

at the receive antennas and y is the (n

× 1) receive

data vector (with n

the number of transmit antennas

and n

the number of receive antennas). By using the

GMD the channel matrix can be decomposed as:

H = Q · R· P

(3)

where R is an upper triangular matrix and Q and P

are unitary matrices whose rows are orthonormal. As-

suming the PCSI condition at both the transmit and

receive sides, pre (P) and post (Q

) processing can

be performed at the transmit and receive sides result-

ing in

y = R· c+

n, (4)

where R is an upper triangular matrix whose elements

in the main diagonal equal the geometric mean of the

singular values and the upper non-zero elements de-

scribe the remaining inter-antenna interferences,

n is

the post-processed noise vector and

y is the resulting

receive data vector. By using perfect interference can-

cellation (e.g. Tomlinson-Harshima pre-coding) the

remaining interference can be removed and the chan-

nel can be ﬁnally described as

y =

R· c+

n (5)

where

R is a diagonal matrix whose non-zero ele-

ments equal the geometric mean of the singular val-

ues. In order to improve the channel performance it

is possible to select the appropriate number of active

layers obtaining an extra gain in the geometric mean

computation as only the largest singular values are

considered (Jiang et al., 2005).

3.1 Singular Values vs. Geometric Mean

The SVD decomposes the channel matrix as H = S·

V· D

, where V is a diagonal matrix containing the

singular values of H in descending order, and S and D

are unitary matrices. After pre- and post-processing

the transmit and receive data vectors with matrices D

and S

respectively, the resulting receive data vector

is givenby

y = V·c+

n, where

n is the post-processed

noise vector, described a system composed of several

independent layers (SISO channels).

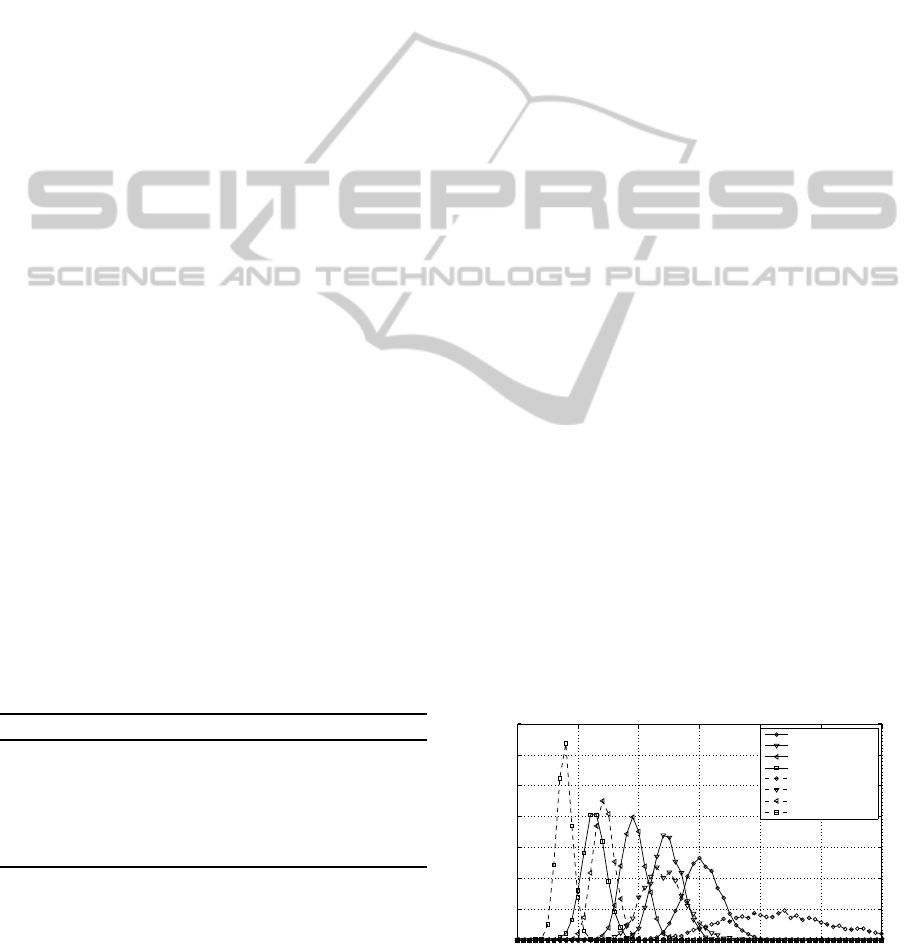
Figure 1 represents and compares the matrices V

(containing the singular values), R (containing the ge-

ometric mean and remaining inter-antenna interfer-

ences) and

R (containing the geometric mean) for an

exemplary (4 × 4) MIMO channel. Independently of

the number of active layers the value of the singular

values doesn’t change. On the other hand the value of

the geometric mean depends on the number of active

layers as shown in Fig. 1(b)-(f). For one active layer

((a) and (f)) the systems behave in the same way as the

layer coefﬁcient is the same in both cases. For four

active layers the SVD-assisted MIMO system shows

a weak layer which drops the overall system perfor-

mance and the GMD-assisted one shows a higher per-

formance. The cases concerning two and three active

layers requires a more detailed analysis as different

transmission modes can be considered and the ﬁnal

results depend on the real channel status.

3.2 Antennas’ Correlation

Antennas correlation is characterized by the correla-

tion matrix which is composed of the correlation coef-

ﬁcients describing the dependencies of the multipath

transmission. The correlation between antennas k and

ℓ is denoted as ρ

kℓ

. Given a set of n

antennas, the

correlation matrix is a (n

× n

) one. As an example,

the receiver side correlation matrix for a four receive

antennas is given by

(4×4)







1 ρ

(RX)

1 ρ

(RX)

1 ρ

(RX)







. (6)

Therein, the correlation coefﬁcient ρ

(RX)

k,ℓ

de-

Figure 1: Singular values vs. geometric mean: (a) Matrix V,

(b) Matrix R, (c) Matrix

R (4 active layers), (d) Matrix

(3 active layers), (e) Matrix

R (2 active layers), (f) Matrix

R (1 active layer).

Antennas'CorrelationInfluenceontheGMD-assistedMIMOChannels

Performance

327

scribes the receiver side correlation between the trans-

mit antenna k and ℓ. It can be demonstrated that

(RX)

ℓ,k

= ρ

∗(RX)

k,ℓ

and the matrix in (6) can be simpliﬁed.

The transmit correlation matrix R

can be described

in a similar way. In the case of uncorrelated antennas,

the off-diagonal elements are zero.

According to (Ahrens et al., 2013) the (n

× n

)

channel matrix H

which models a MIMO system af-

fected by antennas’ correlation can be obtained from

the channel matrix of an uncorrelated MIMO system

and the matrix modelling the antennas’ correlation as:

vec(H

) = R

1/2

· vec(H) , (7)

where H is a (n

× n

) uncorrelated channel matrix

with independent, identically distributed complex val-

ued Rayleigh elements, vec(·) is the vector operator

which stacks the matrix H into a vector column-wise

and R

is the correlation matrix which includes both

the transmit and receive antennas’ correlation. Taking

into consideration the common assumption that the

correlation between the various antennas composing

the transmitter side array is independent from the cor-

relation between the differentantennas composing the

receiver side array, the correlation matrix R

can be

described by the Kronecker product of the transmit-

ter side correlation matrix R

and the receiver side

correlation matrix R

as:

= R

⊗ R

. (8)

4 TRANSMISSION MODES

In this investigationa 4 × 4 MIMO system with QAM

modulation and a constant data rate with an over-

all throughput of 8 bits/s/Hz is considered. Hence,

the possible transmission modes deﬁned by the active

layers are those shown in Table 1.

Table 1: Investigated QAM transmission modes.

throughput layer 1 layer 2 layer 3 layer 4

8 bit/s/Hz 256 0 0 0

8 bit/s/Hz 64 4 0 0

8 bit/s/Hz 16 16 0 0

8 bit/s/Hz 16 4 4 0

8 bit/s/Hz 4 4 4 4

The different transmission modes are deﬁned by

the transmission of distinct QAM constellation sizes

along the available (active) layers.

5 GEOMETRIC MEAN VS.

SINGULAR VALUES

In order to improve the SVD-assisted MIMO systems

performance bit and power allocation strategies can

be used by selecting the appropriate number of active

layers, the modulation order and the transmit power

per layer in order to obtain the best performance, re-

quiring additional computational load and transmis-

sion overhead. In GMD-assisted MIMO systems all

the active layers have the same gain coefﬁcient (the

geometric mean) performing with the same quality,

and hence power allocation is not required to improve

the overall MIMO channel performance.

A concrete number of active layers can be selected

to compute the geometric mean using (1) resulting

in different MIMO channel performances. By se-

lecting just one layer the geometric mean coincides

with the singular value of that layer (the one with

the largest value). Activating more layers with dif-

ferent singular values results in a geometric mean

whose value is lower than the largest singular value.

Even so the GMD-assisted MIMO performance is not

lower than the SVD-assisted one given there are lay-

ers with low valued singular values. In fact GMD-

assisted MIMO systems are (in general) more robust

than SVD-assisted without requiring power allocation

techniques. Nonetheless, the appropriate selection of

the number of active layers (which is synonymous of

bit allocation) can lead to the best performance, par-

ticularly under antennas’ correlation effect.

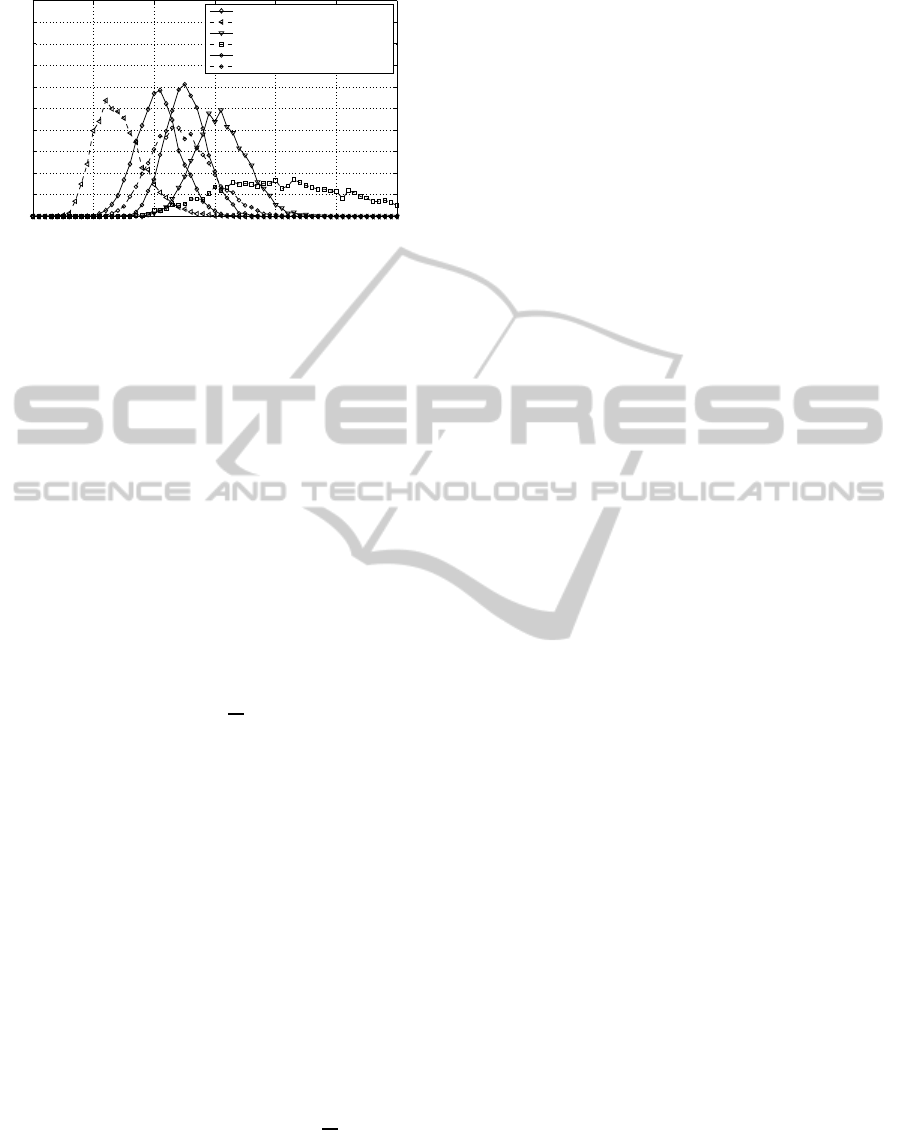
Fig. 2 represents the geometric mean PDF for un-

correlated (solid lines) and correlated (dashed lines)

4×4 GMD-assisted MIMO channels for a different

number of active layers. The analysis reveals that

the geometric mean decreases with the number of ac-

tive layers, which is event more evident under an-

tennas’ correlation effect. As the considered number

0 1 2 3 4 5 6

0.05

0.1

0.15

0.2

0.25

0.3

0.35

layer gain coefficient

PDF

Geometric mean PDF for 1 to 4 layers

uncorrelated, 1 layer

uncorrelated, 2 layers

uncorrelated, 3 layers

uncorrelated, 4 layers

correlated, 1 layer

correlated, 2 layers

correlated, 3 layers

correlated, 4 layers

Figure 2: Geometric mean PDF representation for uncorre-

lated (solid line) and correlated (dashed line) 4×4 MIMO

channels activating 1-4 layers.

PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

328

0 1 2 3 4 5 6

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

0.2

layer gain coefficient

PDF

2 layers MIMO: singular values vs. geometric mean

layer #2 singular value (uncorrelated)

layer #2 singular value (correlated)

layer #1 singular value (uncorrelated)

layer #1 singular value (correlated)

2 layers geometric mean (uncorrelated)

2 layers geometric mean (correlated)

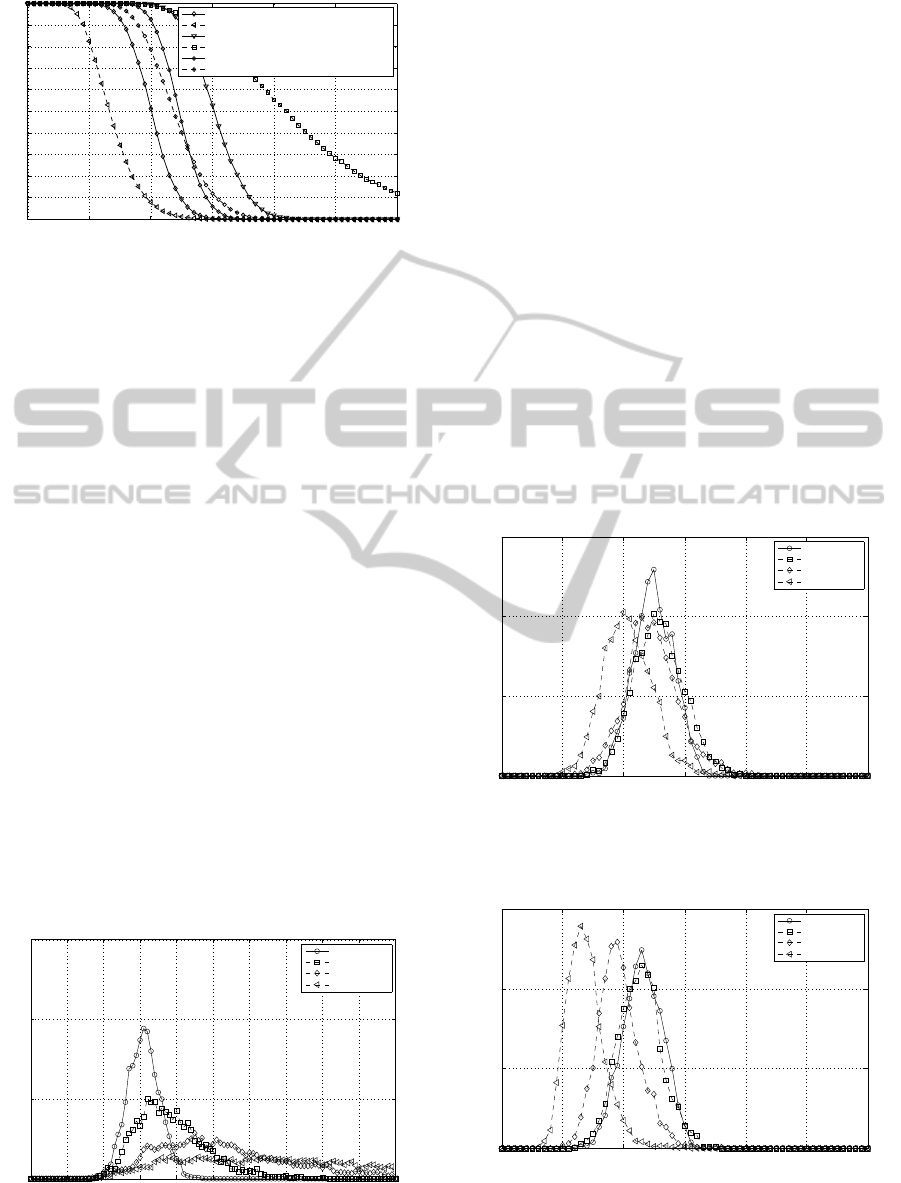
Figure 3: Singular values vs. geometric mean PDF for a

two active layers MIMO channel.

of active layers increases lower valued singular val-

ues (weak layers) are used to compute the geomet-

ric mean through equation (1) obtaining a lower layer

gain coefﬁcient (geometric mean). In conclusion, due

to antennas’ correlation weak layers results in lower

singular values and the geometric mean drops and

wider spreads when various layers are activated.

A key different between SVD-assisted and GMD-

assisted MIMO systems is that in the ﬁrst ones re-

ducing the number of active layers doesn’t change the

singular values and the individual layer gain isn’t al-

tered. In contrast, in the second ones (i.e. GMD) se-

lecting a lower number of active layers results in a

larger geometric mean, which is the layer coefﬁcient

gain.

Fig. 3 depicts the PDF of the gain coefﬁcients

for a two active layers SVD-assisted MIMO sys-

tem (with singular values

) and GMD-assisted

one (geometric mean µ) for uncorrelated (solid lines)

and correlated (dashed lines) cases. In the SVD-

assisted MIMO channel the antennas’ correlation ef-

fect favours the existence of strong (layer # 1) and

weak (layer #2) layers as the active layers singu-

lar values PDF curves become more spaced and

smoothed. Hence power and bit allocation is required

to optimize the performance. Conversely, in the

GMD-assisted MIMO channel the geometric mean

wider spreads with correlation but the mean value

doesn’t signiﬁcantly change (it slightly diminishes its

value). In consequence it can be concluded that the

GMD-assisted MIMO system behaves more robustly

than the SVD-assisted one under the effect of the an-

tennas’ correlation. SVD-assisted MIMO systems

are more sensitive to antennas’ correlation. In these

systems, as the correlation increases the strongest

layer becomes indeed stronger (larger

) and the

weakest gets a lower singular value. Therein the over-

all MIMO channel performance drops due to the ex-

istence of low quality layers. In the GMD-assisted

one, as the correlation increases the geometric mean

decreases but in a reduced percentage and the overall

performance slightly drops.

6 RESULTS

This section analysis the results of the simulation

of the GMD-assisted MIMO channel under different

conditions. The goal is determining how the anten-

nas’ correlation affects the geometric mean of the

singular values (layer gain coefﬁcient) for different

transmission modes and correlation indexes as well

how the channel performance is affected. For conve-

nience the correlation coefﬁcients have been chosen

to be the same for all the pairs of antennas.

6.1 Geometric Mean PDF and CCDF

Analysis

In GMD-assisted MIMO systems (with pre-coding)

bit- and power allocation make no sense as all the ac-

tive layers perform with the same quality (BER) given

the layers coefﬁcients gain are the same. Neverthe-

less the selection of the appropriate number of active

layers leads to different overall performances as the

geometric mean differs. The larger the number of se-

lected layers the lower the geometric mean and the

lower the transmit QAM constellation size per layer

at a given quality.

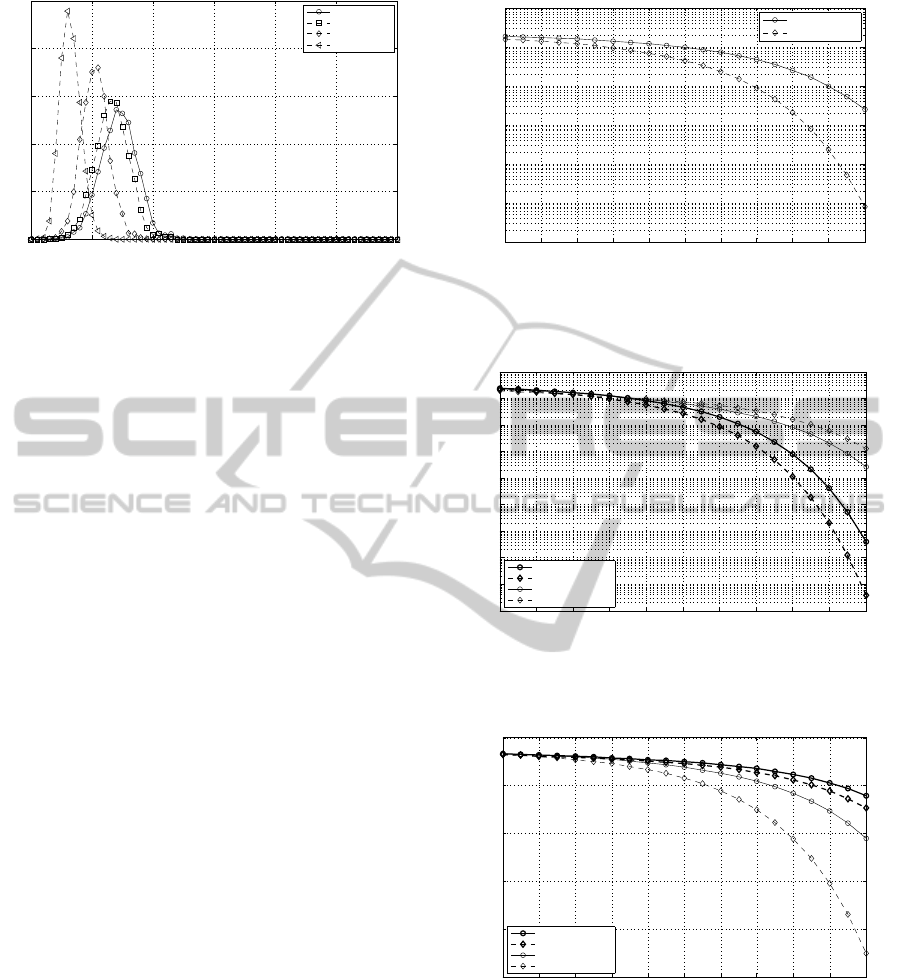
Fig. 4 shows the CCDF of the two largest singular

values and the geometric mean of a 4×4 MIMO chan-

nel when the two best layers are selected (two active

layers). Under antennas’ correlation effect the sin-

gular value CCDF curve of the strongest layer shifts

right while the weak layer one shifts left. In conse-

quence the overall SVD-assisted MIMO system per-

formance diminishes. In the GMD-assisted one the

geometric mean CCDF doesn’t signiﬁcantly vary with

antennas’ correlation and the overall channel perfor-

mance is approximately the same. Then, the conclu-

sion is drawn that the GMD-assisted MIMO system

is more robust against the antennas’ correlation effect

than the SVD-assisted one.

The separation between the CCDF curves pro-

vides information to anticipate the system perfor-

mance. When the CCDF curves are more spaced it

seems to be more convenient the activation of a re-

duced number of layers to reach a better performance.

This is because the weakest layer drops the computed

geometric mean. Comparing the CCDF curves for

uncorrelated and correlated MIMO channels, the last

ones spread wider showing that for correlated MIMO

channels choosing a reduced number of layers is more

Antennas'CorrelationInfluenceontheGMD-assistedMIMOChannels

Performance

329

0 1 2 3 4 5 6

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

layer gain coefficient

CCDF

2 layers MIMO: singular values vs. geometric mean CCDF

layer #2 singular value CCDF (uncorrelated)

layer #2 singular value CCDF (correlated)

layer #1 singular value CCDF (uncorrelated)

layer #1 singular value CCDF (correlated)

2 layers geometric mean CCDF (uncorrelated)

2 layers geometric mean CCDF (correlated)

Figure 4: Singular values and geometric mean CCDF for a

two active layers MIMO channel: uncorrelated (solid lines)

and correlated (dashed lines) cases.

appropriate. This effect is event larger in systems with

antennas’ correlation.

Figures 5 to 8 depict the geometric mean PDF

for a different number of active layers and distinct

correlation indexes. For simplicity, in the investiga-

tion the same correlation coefﬁcient is considered for

each pair of antennas. Figure 5 represents the PDF

when just one active layer is active for uncorrelated

and correlated conditions, considering different cor-

relation degrees (ρ={0.0, 0.2, 0.4, 0.6}). In this case

the geometric mean takes the value of the largest sin-

gular value (the stronger layer) of the resulting chan-

nel matrix. Increasing the correlation index augments

the probability of having larger values, i.e., antennas’

correlation causes the strongest layer become even

stronger because the singular value increases (and in

this case the geometric mean).

The analysis of ﬁgures 6 to 8 gives different con-

clusions. Comparing the geometric mean PDF when

2, 3 and 4 layers are active for uncorrelated and corre-

lated cases with a correlation index ρ=0.2 (weak cor-

relation) it can be observed that the geometric mean

PDF doesn’t signiﬁcantly change. As outcome, it

can be concluded that GMD-assisted MIMO systems

0 1 2 3 4 5 6 7 8 9 10

0.05

0.1

0.15

layer gain coefficient (geometric mean)

PDF

Geometric mean PDF for 1 layer and various correlation indexes (ρ)

uncorrelated

correlated, ρ=0.2

correlated, ρ=0.4

correlated, ρ=0.6

Figure 5: Geometric mean PDF for 1 active layer MIMO

and various correlation indexes (ρ=0, 0.2, 0.4, 0.6).

seem to be robust against antennas’correlation. When

two active layers are active the GMD-assisted MIMO

seems to robustly behave under the antennas’ corre-

lation effect. For the correlation indexes considered

in our analysis the geometric mean PDF curves ap-

proximately centre in the same value. As the two

weakest values are discarded the impact of the cor-

relation index on the geometric mean is not quite re-

markable and the system performance doesn’t notice-

ably change, except for the highest correlation index.

Figures 7 and 8 show the results when activating

three and four layers respectively. Now the geometric

mean value is more sensitive to correlation. This is

due to the activation of the weakest layers (three and

four) with low valued singular values which tend to

take lower values as the correlation index increases.

The ﬁrst case shows to be more robust for low cor-

relation indexes while the second one is more sensi-

tive to correlation because the weakest layer (with the

lowest singular value) is much more sensitive to the

correlation effect, i.e., the singular value remarkably

decreases with the increment of the correlation index.

0 1 2 3 4 5 6

0.05

0.1

0.15

layer gain coefficient (geometric mean)

PDF

Geometric mean PDF for 2 layers and various correlation indexes (ρ)

uncorrelated

correlated, ρ=0.2

correlated, ρ=0.4

correlated, ρ=0.6

Figure 6: Geometric mean PDF for 2 active layers MIMO

and various correlation indexes (ρ=0, 0.2, 0.4, 0.6).

0 1 2 3 4 5 6

0.05

0.1

0.15

layer gain coefficient (geometric mean)

PDF

Geometric mean PDF for 3 layers and various correlation indexes (ρ)

uncorrelated

correlated, ρ=0.2

correlated, ρ=0.4

correlated, ρ=0.6

Figure 7: Geometric mean PDF for 3 active layers MIMO

and various correlation indexes (ρ=0, 0.2, 0.4, 0.6).

PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

330

0 1 2 3 4 5 6

0.05

0.1

0.15

0.2

0.25

layer gain coefficient (geometric mean)

PDF

Geometric mean PDF for 4 layers and various correlation indexes (ρ)

uncorrelated

correlated, ρ=0.2

correlated, ρ=0.4

correlated, ρ=0.6

Figure 8: Geometric mean PDF for 4 active layers MIMO

and various correlation indexes (ρ=0, 0.2, 0.4, 0.6).

6.2 The Effect of Correlation on the

System Performance

Figures 9 to 13 show the effect of the antennas’ cor-

relation on the performance of GMD-assisted MIMO

systems for the transmission modes considered in Ta-

ble 1. As reference, the BER for the equivalent SVD-

assisted MIMO transmission mode is depicted. In

the case in which just one active layer is active the

GMD- and SVD-assisted MIMO systems show the

same behaviour. The analysis of ﬁgures 8 to 12,

where a reduced number of available layers are ac-

tivated, reveals that the GMD-assisted MIMO system

performance increases with correlation (for low val-

ues). The reduction of the number of active layers dis-

cards weak layers in the computation of the geomet-

ric mean. Hence, the geometric mean is higher with

a lower number of active layers. Under the anten-

nas’ correlation effect, weak layers take indeed lower

singular values and strong layers become stronger

(higher singular values). As a result, the geometric

mean takes higher values in correlated systems with a

reduced number of active layers. This behaviour re-

verses when all layers are active. The increase in the

correlation coefﬁcient changes the described perfor-

mance behaviourfor an intermediate number of active

layers.

6.3 Transmission Modes Comparison

Figures 14 to 16 represent the GMD-assisted MIMO

channel performance (BER) for the analysed trans-

mission modes described in Table 1 for different an-

tennas’ correlation degrees. Power allocation is not

considered in the different transmission modes and

the same power is transmitted along the active lay-

ers. Figure 14 compares the performances obtained

by the GMD-assisted MIMO system for the different

transmission modes when affected by antennas’ cor-

0 2 4 6 8 10 12 14 16 18 20

−6

−5

−4

−3

−2

−1

SNR (dB)

BER

BER for GMD−assisted MIMO with 1 active layer (256−0−0−0)

uncorrelated

correlated, ρ=0.2

Figure 9: BER for a GMD-assisted MIMO system with 1

active layer (TM 256-0-0-0): uncorrelated (solid line) vs.

correlated with ρ=0.2 (dashed line).

0 2 4 6 8 10 12 14 16 18 20

−9

−8

−7

−6

−5

−4

−3

−2

−1

SNR (dB)

BER

BER for GMD− vs. SVD−assisted MIMO with 2 active layers (16−16−0−0)

GMD uncorrelated

GMD correlated, ρ=0.2

SVD uncorrelated

SVD correlated, ρ=0.2

Figure 10: BER for a GMD- vs. SVD-assisted MIMO

system with 2 active layers (TM 16-16-0-0): uncorrelated

(solid line) vs. correlated with ρ=0.2 (dashed line).

0 2 4 6 8 10 12 14 16 18 20

−10

−8

−6

−4

−2

SNR (dB)

BER

BER for GMD− vs. SVD−assisted MIMO with 2 active layers (64−4−0−0)

uncorrelated

correlated, ρ=0.2

SVD uncorrelated

SVD correlated, ρ=0.2

Figure 11: BER for a GMD- vs. SVD-assisted MIMO sys-

tem with 2 active layers (TM 64-4-0-0): uncorrelated (solid

line) vs. correlated with ρ=0.2 (dashed line).

relation with a factor ρ = 0.2 (weak correlation). The

results reveal that the transmission mode 16-16-0-0

(with two active layers) is the one showing the best

performance.

The increase in the correlation coefﬁcient affects

the MIMO performance as described above. Figure

15 represents the performance for the various trans-

Antennas'CorrelationInfluenceontheGMD-assistedMIMOChannels

Performance

331

0 2 4 6 8 10 12 14 16 18 20

−6

−5

−4

−3

−2

−1

SNR (dB)

BER

BER for GMD− vs. SVD−assisted MIMO with 3 active layers (16−4−4−0)

GMD uncorrelated

GMD correlated, ρ=0.2

SVD uncorrelated

SVD correlated, ρ=0.2

Figure 12: BER for a GMD- vs. SVD-assisted MIMO sys-

tem with 3 active layers (TM 16-4-4-0): uncorrelated (solid

line) vs. correlated with ρ=0.2 (dashed line).

0 2 4 6 8 10 12 14 16 18 20

−5

−4

−3

−2

−1

SNR (dB)

BER

BER for GMD− vs. SVD−assisted MIMO with 4 active layers (4−4−4−4)

GM uncorrelated

GMD correlated, ρ=0.2

SVD uncorrelated

SVD correlated, ρ=0.2

Figure 13: BER for a GMD- vs. SVD-assisted MIMO sys-

tem with 4 active layers (TM 4-4-4-4): uncorrelated (solid

line) vs. correlated with ρ=0.2 (dashed line).

mission modes and a correlation factor ρ = 0.4 (mod-

erate). Now the effect of the correlation is noticed.

The best performance is obtained with the transmis-

sion mode 256-0-0-0, i.e., activating just one layer.

Finally, ﬁgure 16 depicts the BER performance for a

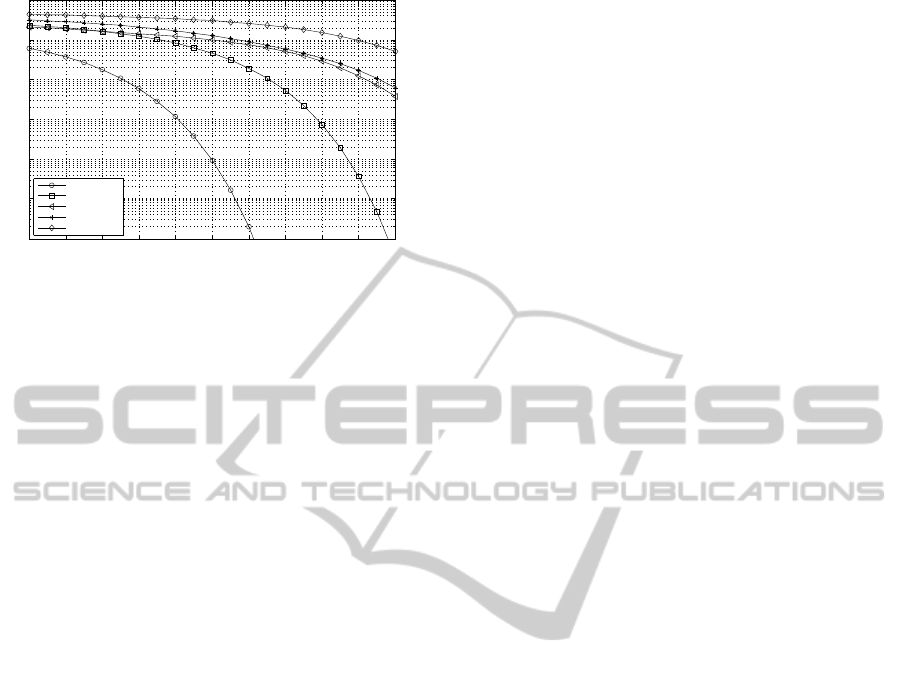
correlation factor Figure ρ = 0.6 (strong). Now the an-

tennas’ correlation effect is noticeable and the trans-

mission mode with the best performance is (TM 256-

0-0-0), i.e., the case in which just one layer is active.

The analysis of the three ﬁgures provides clear

conclusions. The transmission mode 4-4-4-4 with

four active layers shows the worst performance in all

the cases. This is because in the computation of the

geometric mean we are considering the layer fourth,

the one with the lowest singular value. Moreover, the

correlation effect favours the appearance of weak lay-

ers which negatively affects the resulting geometric

mean of the singular values. Furthermore, the correla-

tion also favours the appearance of very strong layers.

In this case, the lower the number of active layers the

higher the resulting geometric mean. This is because

the transmission mode 256-0-0-0 shows the best per-

formance for moderate and strong correlation.

A key point in this discussion is the comparison

between transmission mode 16-4-4-0 (with three ac-

tive layers) and transmission modes 64-4-0-0 and 16-

16-0-0 (with two active layers). For moderate correla-

tion transmission mode 16-4-4-0 performs better than

64-4-0-0. As correlation increases the third active

layer shows a lower singular value and the geomet-

ric mean drops resulting in a worse performance (as

shown for ρ=0.4 and ρ=0.6). Furthermore, the trans-

mission mode 16-16-0-0 show a better performance

than 64-4-0-0 (in this example). The equal distribu-

tion of bits along the active layers seems to be better

than the unequal distribution given by transmission

mode 64-4-0-0. Nevertheless this is not a general rule

and depends on the resulting geometric mean.

0 2 4 6 8 10 12 14 16 18 20

−6

−5

−4

−3

−2

−1

SNR (dB)

BER

BER for correlated GMD−assisted MIMO with various active layers (1 to 4), ρ=0.2

TM 256−0−0−0

TM 16−16−0−0

TM 64−4−0−0

TM 16−4−4−0

TM 4−4−4−4

Figure 14: BER comparison for a GMD-assisted MIMO

system with various active layers and a Tx/Rx correlation

factor ρ=0.2.

0 2 4 6 8 10 12 14 16 18 20

−6

−5

−4

−3

−2

−1

SNR (dB)

BER

BER for correlated GMD−assisted MIMO with various active layers (1 to 4), ρ=0.4

TM 256−0−0−0

TM 16−16−0−0

TM 64−4−0−0

TM 16−4−4−0

TM 4−4−4−4

Figure 15: BER comparison for a GMD-assisted MIMO

system with various active layers and a Tx/Rx correlation

factor ρ=0.4.

7 CONCLUSIONS

This paper analyses the performance of exemplary

4×4 GMD-assisted MIMO systems affected by an-

tennas’ correlation focussing on the geometric mean

PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

332

0 2 4 6 8 10 12 14 16 18 20

−6

−5

−4

−3

−2

−1

SNR (dB)

BER

BER for correlated GMD−assisted MIMO with various active layers (1 to 4), ρ=0.6

TM 256−0−0−0

TM 16−16−0−0

TM 64−4−0−0

TM 16−4−4−0

TM 4−4−4−4

Figure 16: BER comparison for a GMD-assisted MIMO

system with various active layers and a Tx/Rx correlation

factor ρ=0.6.

PDF and CCDF of the singular values as well as the

BER, comparing with the uncorrelated one. Several

transmission modes have been deﬁned by the acti-

vation of a different number of layers. The analy-

sis takes into consideration various antennas’ correla-

tion indexes to show the robustness of GMD-assisted

MIMO systems against correlation.

The simulations outcomes demonstrate that an-

tennas’ correlation affects the SVD-assisted MIMO

channel performance by decreasing its throughput

and increasing the BER. This behaviour is caused by

the existence of predominant weak and strong lay-

ers with corresponding small and large valued singu-

lar values respectively, which are the particular layer

gain coefﬁcient. In the case of GMD-assisted MIMO

systems the number of active layers leads to differ-

ent conclusions. The PDF and CCDF of the singu-

lar values and their geometric mean seems to be a

proper way to anticipate the SVD-assisted and GMD-

assisted MIMO systems performance.

As shown, for a given number of active lay-

ers, antennas’ correlation signiﬁcantly spreads the

singular values CCDF curves dropping the overall

channel performance. Nevertheless the geometric

mean CCDF curves don’t signiﬁcantly change with

correlation. As the separation between the singu-

lar values CCDF curves increases, the overall SVD-

assisted MIMO channel performance drops due to

the poor performance of weak layers (with low val-

ued gain coefﬁcients). Conversely, the geometric

mean CCDF curve for a given number of active layers

doesn’t remarkably change with correlation, conclud-

ing that GMD-assisted MIMO systems are more ro-

bust against antennas’ correlation than SVD–assisted

ones. Then, in general terms GMD-assisted MIMO

systems performs better than SVD-assisted ones, spe-

cially when weak layers exist (particularly in corre-

lated channels).

The activation a different number of layers results

in distinct transmission modes which show different

performances as shown in the results. In order to

minimize the overall BER the same constellation size

as well as the same transmit power per layer should

be used. Although individual layers in GMD-assisted

MIMO systems perform in the same way as the gain

coefﬁcient is the same, the appropriate usage of dif-

ferent constellations per layer can improve the overall

MIMO channel performance.

Activating a larger number of layers takes into ac-

count weak layers. In consequence, due to the low

valued singular values of weak layers the computed

geometric mean diminishes and the GMD-assisted

MIMO system performance drops. This outcome is

much more remarkable as the antennas’ correlation

increases. At the opposite side, activating just one

layer leads to the largest geometric mean value. Nev-

ertheless the best performance is not reached because

a high order constellation is transmitted. An interme-

diate number of active layers seems to be the most

appropriate solution which depends on the particular

correlation index.

REFERENCES

Ahrens, A., Cano-Broncano, F., and Benavente-Peces, C.

(2013). Power distribution for svd-aided mimo trans-

mission with receiver-side antennas correlation. In

10th IASTED International Conference on Signal Pro-

cessing, Pattern Recognition, and Applications (SP-

PRA), Innsbruck (Austria).

Benavente-Peces, C., Cano-Broncano, F., Ahrens, A.,

Ortega-Gonzalez, F., and Pardo-Martin, J. (2013).

Analysis of singular values pdf and ccdf on receiver-

side antennas correlated mimo channels. Electronics

Letters, 49(9):625–627.

Foschini, G. J. and Gans, M. J. (1998). On limits of wire-

less communications in a fading environment when

using multiple antennas. Wireless Personal Commu-

nications, 6:311–335.

Haykin, S. S. (2002). Adaptive Filter Theory. Prentice Hall,

New Jersey.

Janaswamy, R. (2002). Effect of element mutual coupling

on the capacity of ﬁxed length linear arrays. Antennas

and Wireless Propagation Letters, IEEE, 1(1):157–

160.

Jiang, Y., Li, J., and Hager, W. W. (2005). Joint transceiver

design for mimo communications using geometric

mean decomposition. Signal Processing, IEEE Trans-

actions on, 53(10):3791–3803.

Kinjo, S. and Ohno, S. (2013). A tomlinson-harashima pre-

coding for correlated mimo channels. In Intelligent

Signal Processing and Communications Systems (IS-

PACS), 2013 International Symposium on, pages 257–

262.

Antennas'CorrelationInfluenceontheGMD-assistedMIMOChannels

Performance

333

Lee, W.-Y. (1973). Effects on correlation between two mo-

bile radio base-station antennas. IEEE Transactions

on Vehicular Technology, 22(4):130140.

Ozgur, A., Leveque, O., and Tse, D. (2013). Spatial de-

grees of freedom of large distributed mimo systems

and wireless ad hoc networks. Selected Areas in Com-

munications, IEEE Journal on, 31(2):202–214.

Yang, P., Xiao, Y., Yu, Y., and Li, S. (2011). Adaptive spa-

tial modulation for wireless mimo transmission sys-

tems. IEEE Communications Letters, 15:602–604.

Zhou, Z., Vucetic, B., Dohler, M., and Li, Y. (2005). Mimo

systems with adaptive modulation. IEEE Transactions

on Vehicular Technology, 54:1828 – 1842.

PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

334