
A Mathematical Programming Approach to Multi-cloud Storage
Makhlouf Hadji
Technological Research Institute SystemX, Palaiseau, Saclay, France
Keywords:
Cloud Computing, Distributed Storage, Data Replication, Encryption, Broker, Optimization.
Abstract:
This paper addresses encrypted data storage in multi-cloud environments. New mathematical models and
algorithms are introduced to place and replicate encrypted data chunks and ensure high availability of the
data. To enhance data availability, we present two cost-efficient algorithms based on a complete description
of a linear programming approach of the multi-cloud storage problem. Performance assessment results, using
simulations, show the scalability and cost-efficiency of the proposed multi-cloud distributed storage solutions.
1 INTRODUCTION
Cloud storage has emerged as a new paradigm to host
user and enterprize data in cloud providers and data
centers. Cloud storage providers (such as Amazon,
Google, etc.) store large amounts of data and vari-
ous distributed applications (AWS, 2014) with differ-
entiated prices. Amazon provides for example stor-
age services at a fraction of a dollar per Terabyte per
month (AWS, 2014)). Cloud service providers pro-
pose also different SLAs in their storage offers. These
SLAs reflect the different cost of proposed availabil-
ity guarantees. End-users interested in more reliable
SLAs, must pay more, and this leads to cause high
costs when storing large amounts of data. The cloud
storage providers to attract users do not charge for
initial storage or put operations. Retrieval becomes
unfortunately a hurdle, a costly process and users are
likely to experience data availability problems. A way
to avoid unavailability of data is to rely on multiple
providers by replicating the data and actually chunk
the data and distribute it across the providers so none
of them can actually reconstruct the data to protect it
from any misuse. This paper aims at improving this
type of distributed storage across multiple providers
to achieve high availability at reasonable (minimum)
storage service costs by proposing new scalable and
efficient algorithms to select providers for distributed
storage. The objective is to optimally replicate data
chunks and store the replicates in a distributed fash-
ion across the providers. In order to protect the data
even further, the chunks are encrypted.
1.1 Paper Contributions and Structure
We propose data chunk placement algorithms to
tradeoff data availability and storage cost and pro-
vide some guarantees on the performance of the dis-
tributed storage. We assume end-users involved in
PUT (write) and GET (read) operations of data ob-
jects stored in an encrypted manner and distributed
optimally in different data centers require a specified
level of data availability during data retrieval. More
specifically, after data encryption and partition oper-
ations which consist to split the data into encrypted
chunks to be distributed across multiple data centers,
our main work focuses on improving and optimizing
two operations:
• Data Chunks Placement Optimization: through
a novel, efficient, scalable algorithm that mini-
mizes placement cost and meets data availability
requirements given probabilities of failure (or un-
availability) of the storage systems and hence the
stored data.
• Chunk Replication: to meet a required high level
of availability of the data using optimal replica-
tion of chunks to reduce the risk of inaccessibility
of the data due to data center failures (or storage
service degradations).
To realize these objectives, we derive a number of
mathematical models to be used by a broker (real or
logical broker) to select the storage service providers
leading to cost-efficient and reliable data storage. The
proposed broker collaborates with the providers hav-
ing different storage costs and reliability (storage ser-
vice availability), as depicted in detail in Figure 1.
17
Hadji M..
A Mathematical Programming Approach to Multi-cloud Storage.
DOI: 10.5220/0005412000170029
In Proceedings of the 5th International Conference on Cloud Computing and Services Science (CLOSER-2015), pages 17-29
ISBN: 978-989-758-104-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

We assume that the providers propose storage ser-
vices to the broker and to end-users with same reli-
ability but with different prices (prices for a real bro-
ker for instance will be lower than those proposed to
end-users).
It is consequently assumed that there exist ben-
efits for a storage service brokerage that optimally
distributes encrypted data across the most appropriate
providers. Thus, the aim of this paper consists to pro-
pose a scalable and polynomial algorithm spanning a
cost efficient chunk placement model that can achieve
optimal solutions, when guaranteeing high data avail-
ability to end-users.
Section 2 presents related work on cloud storage
and optimization. In Section 3, we use the well known
Advanced Encryption Standard (AES) algorithm (Se-
ungmin et al., 2014) to encrypt end-user data and
divide them into |N | chunks. In the same section,
we propose mathematical models to deal with chunk
placement and replication in an optimal manner for
given server costs and availabilities. Performance as-
sessments and results are reported in Section 4. Con-
clusion and future work are reported in Section 5.
2 RELATED WORK
Data storage and data replication has received a lot of
attention at the data management, distribution and ap-
plication level since the distribution of original data
objects and their replicas is crucial to overall sys-
tem performance, especially in the cloud environment
where data are supposed to be protected and highly
available in different data centers. The current liter-
ature concerns essentially the cloud storage problem
in tandem with replication techniques to improve data
availability, but to our knowledge, does not consider
data transfer in/out costs, or migration costs, etc. We
will nevertheless cite some of the related work even if
it can not be directly compared to the proposed algo-
rithms in this paper.
In (Mansouri et al., 2013), authors dealt with the
problem of multi-cloud storage with a focus on avail-
ability and cost criteria. The authors proposed a first
algorithm to minimize replication cost and maximize
expected availability of objects. The second algo-
rithm has the same objective subject to budget con-
straints. However, this paper did not embed security
aspects apart from dividing the data into chunks or ob-
jects. In our work, we propose to divide data into en-
crypted chunks, that will be optimally stored and dis-
tributed through various data centers with minimum
costs while satisfying the QoS required by end-users.
Moreover, the proposed algorithm in (Mansouri et al.,
2013) is a simple heuristic without any convergence
guarantee to the optimal solution. Our proposed algo-
rithm converges in few seconds to optimal solutions
benchmarked by the Bin-Packing algorithm.
In (Thanasis et al., 2012), authors present Scalia,
a system to deal with the problem of multi cloud data
storage under availability and durability requirements
and constraints. The authors note the NP-Hardness
of the considered problem, and propose algorithms to
solve small instances of the problem. In our work, we
propose a new efficient and scalable solution capable
of handling large instances in a few seconds. Clearly,
the proposed solution in (Thanasis et al., 2012) suffers
from scalability challenges to handle on with larger
instances, when our algorithms are able to quickly
solve large instances of the defined problem.
To avoid failure and achieve higher availability
when storing data in the cloud, reference (Yanzhen
and Naixue, 2012) proposes a distributed algorithm to
better replicate data objects in different virtual nodes
instantiated in physical servers. According to the traf-
fic load of all considered nodes, the authors consid-
ered three decisions or actions as replicate, migrate,
or suicide to better meet end-user requirements and
requests. However, the proposed approach consists
only in checking the feasibility of migrating a virtual
node, performs suicide actions or replicating a copy
of a virtual node, without optimizing the system. In
our work, we propose optimization algorithms based
on a complete description of the convexe hull of the
defined problem, leading to reach optimal solutions
even for large instances.
Reference (Srivastava et al., 2012) proposes a sim-
ple heuristic to give stored data greater protection and
higher availability by splitting a file (data) into sub-
files to be placed in different virtual machines belong-
ing to the physical resources (data centers for exam-
ple) of one provider or different providers. The paper
dealt with PUT and GET operations to distribute and
retrieve the required subfiles (data) without encrypt-
ing them. The proposed heuristic in (Srivastava et al.,
2012) can only reach suboptimal solutions, leading to
considerable gaps compared to the optimal solutions.
We propose a new scalable and cost efficient solution
to deal with the multi-cloud storage problem.
Aiming to provide cost-effective availability and
improve performance and load balancing of cloud
storage, the authors of reference (Qingsong et al.,
2010) propose CDRM as a cost-effective dynamic
replication management scheme. CDRM consists in
maintaining a minimal number of replica for a given
availability requirement, and proposes a replica place-
ment based on the blocking probability of data nodes.
Moreover, CDRM allows us to dynamically adjust the
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
18

replica number according to changing workload and
node capacities. However, the paper focuses only on
the relationship between availability and replica num-
ber, and there is no proposal to deal with the optimal
placement of replicas.
To achieve high performance and reduce data loss
when we require storage services in the cloud, dif-
ferent papers in the literature propose various algo-
rithms that are useful only for small instances due to
the NP-Hardness of the problem. In (Bonvin et al.,
2010), the authors propose a key-value store named
Skute, which consists in dynamically allocating the
resources of a data cloud to several applications in
a cost effective and fair way using game theoretical
models. To guarantee cloud object storage perfor-
mance, the authors of (Jindarak and Uthayopas, 2012)
propose a dynamic replication scheme to enhance the
workload distribution of cloud storage systems. The
authors of (Chia-Wei et al., 2012) conduct a study
based on a dynamic programming approach, to deal
with the problem of selecting cloud providers offer-
ing storage services with different costs and failure
probabilities.
Reference (Abu-Libdeh et al., 2010) proposes
a distributed storage solution named RACS, to
avoid vendor lock-in, reduce the cost of switch-
ing providers, and better tolerate provider outages.
The authors applied erasure coding (see references
(Weatherspoon and Kubiatowicz, 2002), (Li and Li,
2013) and (Rodrigo and Liskov, 2005)) to design the
proposed solution RACS. In the same spirit, refer-
ences (Ford et al., 2010), (Myint and Thu, 2011), (Ne-
gru et al., 2013) and (Zhang et al., 2012) addressed the
cloud storage problem described above, under differ-
ent constraints including energy consumption, budget
limitation, limited storage capacities, and the avail-
ability of the stored data.
In (Varghese and Bose, 2013), authors propose
a new solution to guarantee the data integrity when
stored in a cloud data center. The proposed solution is
based on homomorphic verifiable response and hash
index hierarchy. This kind of solutions can be inte-
grated to our work to reenforce data security and pri-
vacy for reticent users. An other reference on secured
multi cloud storage can be found in (Balasaraswathi
and Manikandan, 2014). Authors presented a crypto-
graphic data splitting with dynamic approach for se-
curing information. The splitting approach of the pro-
posed solution is not deeply studied. This may lead to
not select cost efficient providers.
3 SYSTEM MODEL
To store encrypted data in multiple DCs belonging
to various cloud providers system, while optimizing
storage costs and failure probabilities, we separate
the global problem into a number of combinatorial
optimization sub-problems. To derive the model we
make a simplifying assumption regarding the pricing
scheme between cloud service providers, the broker
and end-users. We assume that the proposed stor-
age price by a service cloud provider to end-users is
higher than that proposed to the broker. This can be
explained by the large amount of demands that will
be required by the broker aggregating the demands
of a finite set of end-users seeking to avoid vendor
lock-in and higher availability. One can assume that
prices proposed by cloud providers are smaller as the
volume of data is larger. Note that the broker will
guarantee a minimum storage cost meeting end-users
requirements, ensuring that the proposed cost to end-
users can never exceed a certain threshold.
We first propose to use the well known AES (Ad-
vanced Encryption Standard) algorithm (Seungmin
et al., 2014) for efficient data encryption. This will
generate different encrypted chunks to be distributed
in the available storage nodes or data centers. This en-
cryption ensures the confidentiality of the stored data.
Moreover, the used solution permits to construct di-
verse chunks (with small sizes) to facilitate PUT and
GET requests as is shown in Figures 1 and 2.
We derive two algorithms to handle encrypted data
chunk placement and replication to guarantee data
high availability, and storage cost efficiency. This can
be summarized as follows:
• Data Chunk Placement: The first important ob-
jective of our paper consists in guaranteeing the
availability of all chunks of stored data by opti-
mally distributing them to a cost-efficient set of
selected data centers (see Figure 1). This avoids
user lock-in, and reduces the total cost of the stor-
age service. This optimization is performed under
end-user or data owner constraints and require-
ments such as the choice of a minimum number of
data centers to be involved in storing the chunks
of the data. This can reinforce the availability of
data for given data centers failure probabilities.
• Data Chunk Replication: After optimally stor-
ing the encrypted chunks of a data, we determine
a replication algorithm based on bipartite graph
theory, to derive optimal solutions of the problem
of storing replica chunks. This ensures high data
availability since content can be retrieved even if
some servers or data centers are not available.
Once all data chunk are placed in different data
AMathematicalProgrammingApproachtoMulti-cloudStorage
19
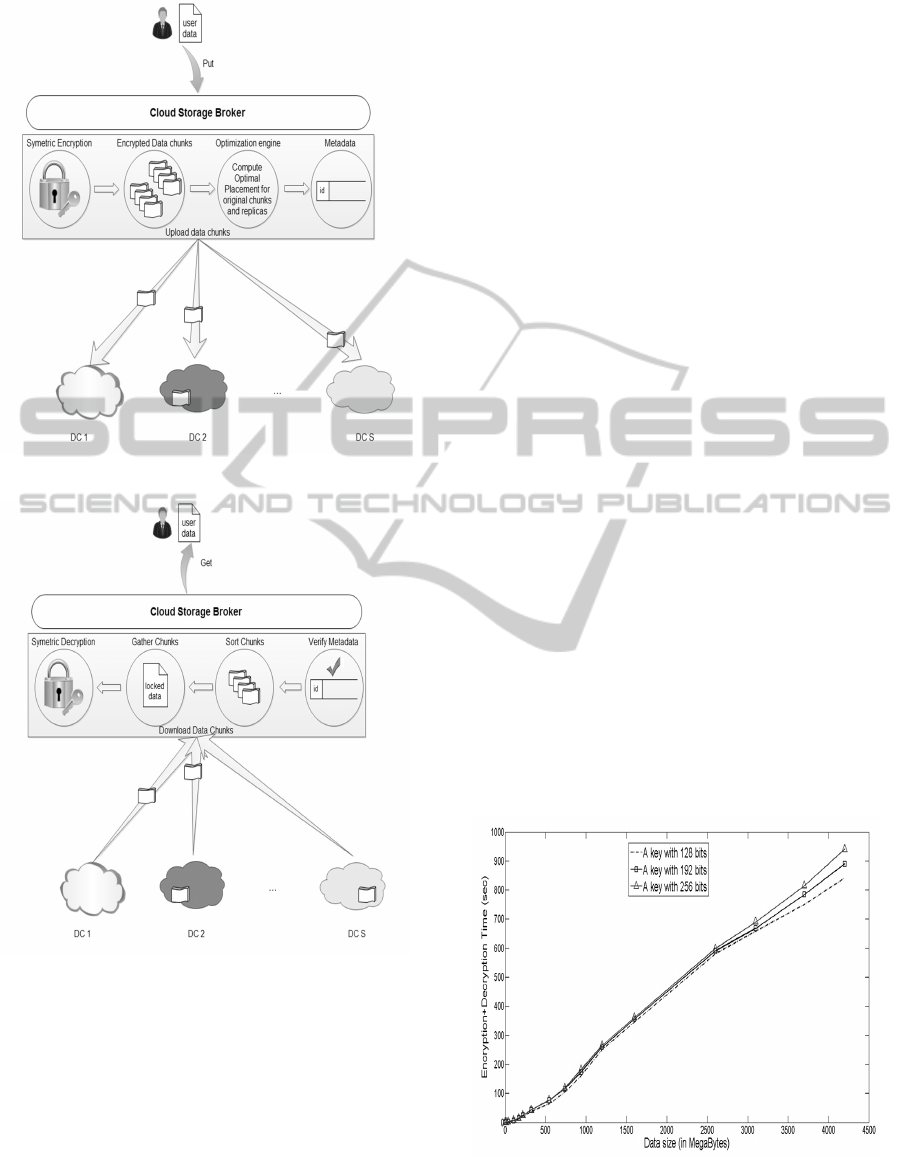
Figure 1: The system model: PUT requests.
Figure 2: The system model: GET requests.
centers, end-users may solicit the data by GET re-
quests (download data). The broker needs to gather
all the data chunks, sort them, decrypt them, and fi-
nally deliver the entire data to the end-user. Figure 2
gives more details on GET operations.
In the following, we suppose that each data object
(chunk) has r replicas. Finding the optimal number
of replicas of each chunk, is not in the scope of this
paper. A well-known example on the choice of r is
the Google storage solution based on r = 3 replicas of
each stored data chunk (Ghemawat et al., 2003).
3.1 Data Encryption Algorithm
While consumers have been willing to trade privacy
for the convenience of cloud storage services, this is
not the case for enterprises and government organi-
zations. To achieve high data security and privacy,
we propose to divide the requested user data to store
into encrypted chunks. This facilitates PUT and GET
requests by considering small files (chunks), and rein-
forces the security of data (thanks to the encryption)
in the same time.
To preserve the confidentiality of data, we seek
algorithms that can encrypt and decrypt multiple
chunks in a small time. To deal with this problem, we
propose to use the symmetric encryption algorithm
noted AES for Advanced Encryption Standard (Se-
ungmin et al., 2014). The AES algorithm is a fast
solution to handle with large amount of data as it is
shown in Figure 3 where three different keys (128
bits, 192 bits and 256 bits) are used to encrypt and
decrypt data sizes ranging from 1 Megabyte to 4 Gi-
gabytes in a time interval ranging from 200 seconds
to 800 seconds.
The key sizes are chosen by end-users depending
on the privacy level of their data. In our proposal,
we suppose that the broker proposes an encryption
solution in which generated private keys are well kept
within end-users with a key size of 128 bits.
Note that more details on the encryp-
tion/decrytpion algorithms used in this paper,
can be found in the literature (see for example
(Seungmin et al., 2014) and (NIST, 2014)). A deep
study of these solutions is not in the scope of this
paper.
Figure 3: Encryption and decryption’s time evolution with
data size.
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
20

3.2 Data Placement Cost Minimization:
b-Matching Formulation
We start data chunks placement model by consider-
ing each data D of a user u, as a set of chunks (noted
by N ), resulting from the AES algorithm. Let S be
the set of all available data centers able to host and
store end-user data. We investigate an optimal place-
ment by storing all the chunks in the ”best” available
data centers. Each cloud provider with a data center
s ∈ S proposes a storage cost per Gigabyte and per
month noted by µ
s
. This price varies for different
reasons: varying demands and workloads, data cen-
ter reliability, geographical constraints, etc. End-user
requests are submitted to the broker which will relay
them to cloud service providers, in an encrypted form
with optimized storage costs. The broker guarantees
end-users high data availability with minimum cost
by choosing a set of cloud providers (or DCs) meet-
ing the requirements (see Figure 1 for more details).
In the following, we will address chunks place-
ment optimization model based on different con-
straints as the probability of failure of a data center or
a provider, and a limited storage capacity. Each data
center (or provider) has a probability of data avail-
ability (according to the number of nines in the pro-
posed SLA), and a failure probability ( f ) is then equal
to 1−probability of data availability. Moreover, the
limited storage capacity is given by a storage quota
proposed by the provider to the broker according to a
negotiated pricing menue.
Our optimization problem is similar to a classical
Bin-Packing formulation, in which bins can be repre-
sented by the different Data Centers, and the items can
be seen as the data chunks. Reference (Korte and Vy-
gen, 2001) has shown a while ago the NP-Hardness
of the Bin-Packing problem. Thus, we deduce the
complexity (NP-Hardness) of our chunks’ placement
problem.
For this reason, and the fact that workloads and re-
quests to store date arrive overtime, the broker seeks a
dynamic chunk placement solution that will be regu-
larly and rapidly updated to remain cost-effective and
ensure data high availability.
Each data chunk i ∈ N has a certain volume noted
by ν
i
. We graphically represent the storage of a chunk
i in a data center k as an edge e = (i, k) (with the ini-
tial extremity (i = I(e)) of e corresponding to a chunk,
and the terminal extremity (k = T (e)) of e) represent-
ing the data center (see Figure 4).
Based on this configuration, one can construct a
new weighted bipartite graph G = (N ∪ S,E), where
N is the set of vertices representing encrypted chunks
to be stored, and S is the set of all available data cen-
Figure 4: Complete bipartite graph construction.
ters (see Figure 4). E is the set of weighted edges
between N and S constructed as described:
there is an edge e = (i, k) between each encrypted
chunk i and each available data center k, and the
weight of e is given by µ
k
ν
i
.
We now introduce the well known ”minimum
weight b-matching problem” to build a combinato-
rial optimization solution. The b-matching is a gen-
eralization of the minimum weight matching problem
and can be defined as follows (see (Korte and Vygen,
2001) for more details):
Definition Let G be an undirected graph with inte-
gral edge capacities: u : E(G) → N ∪ ∞ and numbers
b : V (G) → N. Then a b-matching in G is a func-
tion f : E(G) → N with f (e) ≤ u(e), ∀e ∈ E(G), and
∑
e∈δ(v)
f (e) ≤ b(v) for all v ∈ V (G).
In the above, δ(v) represents the set of incident edges
of v. To simplify notation, with no loss in generality,
we use E and V for the edges and vertices of G. That
is we drop the G in E(G) and V (G).
From the definition, finding a minimum weight b-
matching in a graph G consists in identifying f such
that
∑
e∈E
γ
e
f (e) is minimum, where γ
e
is an associ-
ated cost to edge e. This problem can be solved in
polynomial time since the full description of its con-
vex hull is given in (Korte and Vygen, 2001).
Proposition 3.1. Let G = (N ∪ S, E) be a weighted
complete bipartite graph built as described in Figure
4. Then, finding an optimal chunk placement solution
is equivalent to an uncapacitated (u ≡ ∞) minimum
weight b-matching solution, where b(v) = 1 if v ∈ N
(v is a chunk) and for all vertices v ∈ S , we put b(0) =
0, and for v ≥ 1, we have
AMathematicalProgrammingApproachtoMulti-cloudStorage
21

b(v) =
&
|N | −
∑
v−1
k=0
b(k)
β
'
(1)
where β is the minimum number of data centers to
be used to store the data chunks. This parameter is
required by end-users to avoid vendor lock-in.
To mathematically formulate our model, we asso-
ciate a real decision variable x
e
to each edge e in the
bipartite graph. As shown in Figure 4, each edge links
a chunk to a data center. After optimization, if the de-
cision is x
e
= 1 then chunk i (i = I(e) initial extrem-
ity) will be stored in data center j ( j = T (e) terminal
extremity). Since the solution of a b-matching prob-
lem is based on solving a linear program, an integer
solution of the minimum weight b-matching is found
in polynomial time. This is equivalent to the optimal
solution of the chunk placement problem described in
this section.
According to the storage costs listed previously and
by defining the probability of failure of a data cen-
ter (or a provider) noted by f , we assign each chunk
to the best data center with minimum cost. We note
by Cost
plac
the total cost of placing |N | chunks in an
optimal manner. We can formulate the objective func-
tion as follows:
minCost
plac
=
∑
e∈E,e=(i, j)
µ
j
1 − f
j
ν
i
x
e
(2)
where ν
i
is the volume of chunk i, and (1 − f ) is
the probability of data center availability (or provider
availability).
This optimization is subject to a number of linear
constraints. For instance, the broker has to consider
the placement of all data chunks, and each chunk will
be assigned to one and only one data center (the chunk
replication problem will be discussed in the next sec-
tion). This is represented by (3):
∑
e∈δ(v)
x
e
= 1, ∀v ∈ N (3)
Each data center s has a capacity Q
s
. This leads to
the following constraints:
|N |
∑
C=1
ν
C
x
Cs
≤ Q
s
, ∀s ∈ S (4)
According to end-user requirements and to guar-
antee high data availability, chunks will be deployed
in different data centers to avoid vendor lock-in. This
is given by the following inequality:
|N |
∑
C=1
x
Cs
≤ b(s), ∀s ∈ S (5)
Using the b-matching model with constraints (4),
enables the use of the complete convex hull of b-
matching and makes the problem easy in terms of
combinatorial complexity theory.
Reference (Korte and Vygen, 2001) gives a com-
plete description of the b-matching convex hull ex-
pressed in constraints (3), (4) and (5). These families
of constraints are reinforced by blossom inequalities
to get integer optimal solutions with continuous vari-
ables:
∑
e∈E(G(A))
x
e
+ x(F) ≤
∑
v∈A
b
v
+ |F|
2
, ∀A ∈ N ∪S,
(6)
where F ⊆ δ(A) and
∑
v∈A
b
v
+ |F| is odd, and
δ(A) =
∑
i∈A, j∈A
x
(i j)
. E(G(A)) represents a subset of
edges of the subgraph G(A) generated by a subset of
vertices A. An in depth study of blossom constraints
(6) is out of the scope of this paper, but more details
can be found in (Grotschel et al., 1985).
Based on the bipartite graph G, we constructed a
polynomial time approximation scheme of the data
chunks placement problem by identifying the b-
matching formulation. The blossom constraints (6)
are added to our model to get optimal integer solu-
tions of the placement problem whose model is finally
given by:
minCost
plac
=
∑
|S|
s=1
∑
|N |
C=1
µ
s
1− f
s
ν
C
x
Cs
S.T. :
∑
|S|
s=1
x
Cs
= 1, ∀C ∈ N
∑
|N |
C=1
ν
C
x
Cs
≤ Q
s
, ∀s ∈ S
∑
|N |
C=1
x
Cs
≤ b(s), ∀s ∈ S
∑
e∈E(G(A))
x
e
+ x(F) ≤
j
∑
v∈A
b
v
+|F|
2
k
, ∀A ∈ N ∪S
F ⊆ δ(A),
∑
v∈A
b
v
+ |F| is odd
x
Cs
∈ R
+
, ∀C ∈ N , ∀s ∈ S
(7)
The variables and constants used in the final
model are summarized as follows:
3.3 Data Replication Algorithm
To enhance performance and availability of end-user
stored data, we propose a replication model of data
chunks depending on data center failure probabilities,
and expected availability (noted by A
expec
) required
by each user. The objective consists in finding the
optimal trade-off between data center availability and
storage costs. This leads to avoiding expensive data
centers with high failure probability.
We assume that each data chunk is replicated r
times, and reconstituting a file data needs to get one
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
22

Table 1: Variables and constants of the model.
Variables Meaning
N set of data chunks
S set of data centers
ν
C
volume of a data chunk C
µ
j
storage cost per Gigabyte/month of
provider j
x
e
real variable indicating if e is so-
licited or not
b
v
upper bound of the degree of v
δ(A) =
∑
i∈A, j∈A
x
(i j)
δ(v) set of incident edges to v
β minimum number of providers
copy of all chunks (i.e. |N | chunks among r × |N |
are necessary to reconstruct a data). Figure 5 gives
more details and shows chunks replication procedure.
It is important to note that initially, each en-
crypted chunk will be replicated by the selected host-
ing providers within their data centers, and the bro-
ker can reinforce this mechanism by proposing to add
more replicas guaranteeing higher data availability.
Figure 5: Data replication.
In the following, we would like to replicate |N |
chunks into |S| data centers according to various
costs (storage costs) and performance requirements
such as the data availability. We suppose that S =
s
1
, s
2
, . . . , s
|S|
and for the sake of simplicity (due to
the problem NP-Hardness), we suppose w.l.o.g. each
data center has a large amount of storage resources
able to host data chunks and replicas. We associate
each data center s ∈ S with a probability of failure f
s
.
We suppose (as cited above) that each data chunk
C (C = 1, |N |) has r replicas to place in r data centers
that do not contain the chunk C. Thus we ask the
following question: How do we replicate data chunks
through available data centers so that the total cost of
storage is optimal (minimal) and data availability is
maximal?
Thus, for each chunk C, the problem consists in
selecting a subset ϕ
C
of r available data centers that
do not contain C, leading to a minimum storage cost
and a high probability of data availability.
We note by P(C) the probability of chunk C avail-
ability (respect. P(C) is the probability of non-
availability of a chunk C). P(D) is the probability
of data availability (respect. P(D) is the probability
of non-availability of data D). Note that a chunk C
is not available if all of its copies are not available
(see Figure 5). In other words, a block in Figure 5
with r replicas is non available if all of the data cen-
ters storing this block are non available. By supposing
the data centers are independent, we get the following
proposition:
Proposition 3.2. P(C) =
∏
s∈ϕ
C
f
s
Proof.
P(C) = P(C
1
and C
2
and . . . and C
r
)
= P(C
1
) × P(C
2
) × . . . × P(C
r
)
=
∏
s∈ϕ
C
f
s
Proposition 3.3. P(D) =
∏
|N |
C=1
1 −
∏
s∈ϕ
C
f
s
Proof. A data D with r × |N | chunks, is entirely
available if all chunks are available. According to
Proposition (3.2), the probability of data file availabil-
ity (i.e. P(D)) is then given by:
P(D) =
|N |
∏
C=1
P(C)
=
|N |
∏
C=1
1 −
∏
s∈ϕ
C
f
s
!
The QoS requirement for end-users is presented
by the data availability. This is noted by A
expect
(as
used in (Mansouri et al., 2013) for example). Thus,
to meet end-user QoS requirement, the broker should
replicate each D in a selected sub-set of data centers
that satisfies:
|N |
∏
C=1
1 −
∏
s∈ϕ
C
f
s
!
≥ A
expect
(8)
AMathematicalProgrammingApproachtoMulti-cloudStorage
23
We derive a mathematical model to efficiently re-
duce the replication costs noted by Cost
rep
, under the
QoS requirements described by the inequality (8). As
the number of replicas of each chunk is supposed to
be r, we seek an optimal sub-set of data centers of
size r to store the replicas of each chunk. Moreover,
our solution should not put all the chunks within the
same data center to avoid vendor lock-in. Thus, in
the following, we address a mathematical optimiza-
tion model to efficiently replicate all the chunks of a
data D.
min
ϕ
C
Cost
rep
=
∑
|N |
C=1
∑
s∈ϕ
C
µ
s
ν
C
S.T. :
(
∏
|N |
C=1
1 −
∏
s∈ϕ
C
f
s
≥ A
expect
, ;
|ϕ
C
| = r, ∀C = 1, |N |;
(9)
To solve the model (9), we can resort to dynamic
programming approach as the objective function of
(9) is separable and monotone. As these methods re-
sort to recursion technique, they can prove to be ex-
pensive in certain cases due to the exponential number
of data centers subsets to enumerate. For this reason,
and for the sake of scalability, we prefer to address a
simple, scalable and succinct algorithm to reach near
optimal solutions for large instances in few seconds.
Solving the model (9) is equivalent to find a sub-
set of data centers able to host chunks in a cost ef-
ficient manner, and that satisfies the requirement (8).
We propose a simple and scalable algorithm to solve
(9) in few seconds for large number of data centers
and data chunks. Without loss of generality, we
assume that minimizing a function Z is approxima-
tively equivalent to minimize ln(Z). Thus, for each
chunk C, we seek a subset of data centers that min-
imizes ln(
∏
s∈ϕ
C
f
s
). This is equivalent to minimize
∑
s∈ϕ
C
ln( f
s
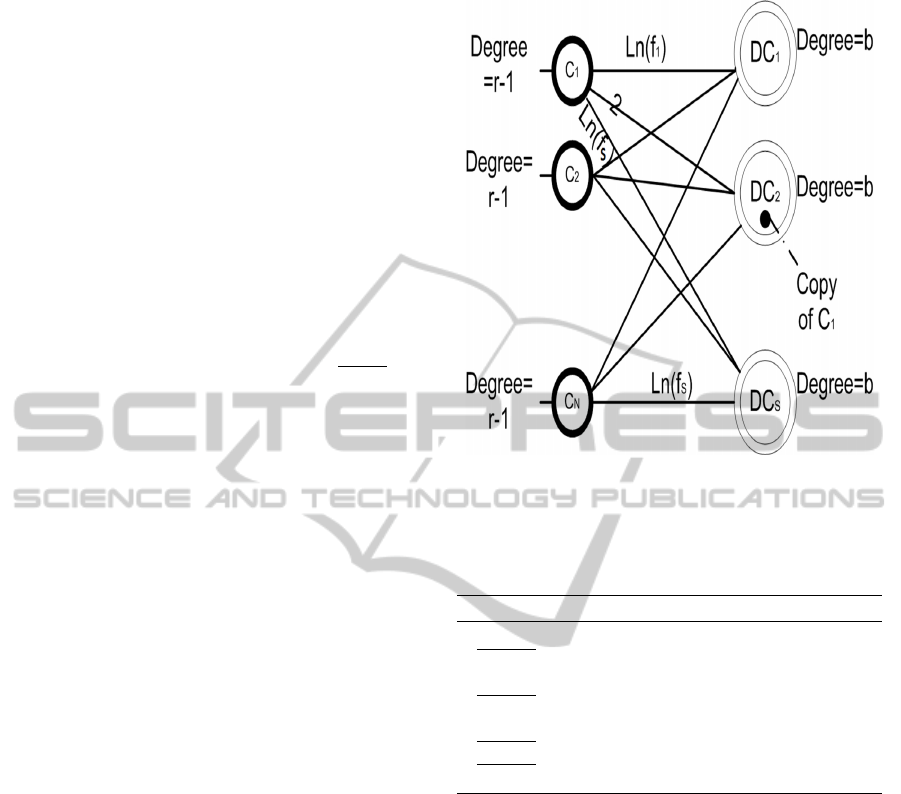
). Moreover, We construct a new bipar-
tite graph G
2
= (V
2
∪ S
2
, E
2
), where V
2
is the set of
chunks to be stored and S
2
is the set of all available
data centers (see Figure 6). E
2
is the set of weighted
edges between the two parts of vertices of G
2
. There
is an edge between each chunk C and each data center
s (not containing a copy of chunk C) with a weight
given by ln( f
s
). If a data center s has already stored a
copy of chunk C, then the weight of the edge (C, s) is
equal to 2. Figure 6 gives more details.
From graph G
2
, we identify a minimum weight b-
matching with a given vector b as follows :
• for each v ∈V
2
, degree of v is equal to b(v) = r −1,
• the degree of each vertex v ∈ S
2
is equal to b(v)
given by (1).
To summarize, we give the following algorithm,
Figure 6: New bipartite graph G
2
to replicate chunks.
leading to find the best subset of data centers to repli-
cate all the chunks in a cost efficient manner, verifying
condition (8).
Algorithm 1: Data replication algorithm.
Step 0: Construct the bipartite graph G
2
(see Fig-
ure 6);
Step 1: Compute a b-Matching with a minimum
cost solution using the vector b;
Step 2: Check if (8) is satisfied;
Step 3: If (8) is not satisfied, GOTO Step 0, by in-
crementing the degrees of vertices in S
2
;
The algorithm 1 is deployed to replicate efficiently
r − 1 copies of each chunk C of a data D.
3.4 Data Chunk Splitting
In this section, we discuss the rational number of
chunks (|N
∗
|) to be used to split the data according to
data center failure probabilities ( f
s
for a DC s), num-
ber of replicas (r) of each chunk, and the data avail-
ability expected by end-users (A
expect
).
According to Proposition (3.3), we seek a ratio-
nal number of encrypted chunks to get after splitting
the data when satisfying end-users QoS represented
by data availability A
expect
. We get the following in-
equality :
P
D
=
|N |
∏
C=1
P
C
=
|N |
∏
C=1
1 −
∏
s∈ϕ
C
f
s
!
≥ A
expect
(10)
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
24

As A
expect
< 1 and
∏
|N |
C=1
1 −
∏
s∈ϕ
C
f
s
< 1, in-
equality (10) leads to the following one:
ln
|N |
∏
C=1
1 −
∏
s∈ϕ
C
f
s
!!
≤ ln(A
expect
) (11)
We also note that for each chunk indexed by C,
we have r replicas and then |ϕ
C
| = r. For the sake of
simplicity, we also suppose that the failure probabil-
ity of each data center is close to the average failure
probability given by f . This allows us to deduce :
∏
s∈ϕ
C
f
s
=
f
r
(12)
And following inequality (11), we get:
|N | × ln
1 − f
r
≤ ln(A
expect
) (13)
According to (13), we deduce the number of data
chunks as follows :
|N
∗
| ≥
ln(A
expect
)
ln
1 − f
r
(14)
4 NUMERICAL RESULTS
To evaluate and assess performance, our algorithms
have been implemented and evaluated using simula-
tions and an experimental platform managed by an
instance of OpenStack (Openstack, 2014). The lin-
ear programming solver CPLEX (CPLEX, 2014) was
used to derive the b-matching solution and the Bin-
Packing solution used to benchmark our heuristic.
As our goal in this paper is to analyze and discuss
the applicability and the interest of storage brokering
services in interaction with multiple data centers or
cloud providers, we devote some numerical results to
cross validating our proposed algorithms and assess-
ing their cost efficiency and scalability for large data
sizes. It is obvious to remark that the Bin-Packing
model used to place data chunks invokes a branch and
bound approach leading to explore the entire space of
all the existing solutions. This leads to find ”optimal”
solutions for small data sizes serving as a benchmark
for other approaches and algorithms. As the data size
increases, the optimal solution for data chunk place-
ment can only be found in exponential time. Thus, for
large data, we resort to our heuristic solution based on
graph theory and the b-matching approach.
In addition, our performance evaluation seeks to
identify the limits of the discussed problem in terms
of algorithmic complexity, and its suitability for op-
timizing real life instances. We will also determine
the gap between the suboptimal heuristic solutions
and the optimal solution provided by the Branch and
Bound model when it can be reached in acceptable
times.
4.1 Simulation Environment
The proposed algorithms in this paper were evaluated
using a 1.70 GHz server with 6 GBytes of available
RAM. We used data files with sizes ranging from 100
Megabytes to 4 Gigabytes. These data were stored in
a distributed manner over a number of available data
centers or providers ranging from 10 to 50. We asso-
ciate with each data center, a data price per Gigabyte
and per month, uniformly generated between 0 $ and
1 $. Each data is splitting multiple chunks and each
chunk size is equal to 1 Megabyte. This configura-
tion leads to construct a full mesh bipartite graph as
described above. The number of generated bipartite
graphs was set to 100 in our simulations yielding an
average value reported in the following curves and ta-
bles. Without loss of generality, we suppose that each
data center has an unlimited storage capacity.
In addition, we also used a platform of 20 servers
running a Havana instance of OpenStack (Openstack,
2014) in a multi-node architecture. Each server (as-
similated to a data center in real life) proposes Swift
containers (Swift, 2014) to store data chunks. We as-
sociate a storage cost to each container (or DC) as
described above. It is important to note that we used
Swift API only to guarantee PUT and GET operations
from and to the broker by intercepting and hosting en-
crypted chunks, without considering Swift replication
policy. To improve our broker functionalities, we will
add an S3 compatible interface allowing end-users to
request the broker storing their data within Amazon
S3.
4.2 Performance Evaluation
The first experiment consists in comparing the Bin-
Packing and b-Matching (heuristic) approaches in
terms of delay to derive the optimal and suboptimal
solutions, respectively. We report different scenarios
in Table 2, varying the number of data centers able
to store end-users data (from 12 to 700 DCs), and the
number of chunks ranging from 50 chunks to 2000
chunks, which is equivalent to store data size of 50
Megabytes to 2000 Megabytes, as each chunk is of 1
Megabyte.
To get a better grasp of the relative performance
of the two algorithms, we generate 100 runs and take
the average value of each instance, as reported.
The performance of the heuristic algorithm com-
AMathematicalProgrammingApproachtoMulti-cloudStorage
25
pared to the optimal solution is represented by a gap
defined as the percentage difference between the cost
of the optimal and the heuristic solutions:
Gap(%) = 100 ×
bM
sol
− BP
sol
BP
sol
(15)
where BP
sol
is the cost of the exact solution pro-
vided by the Bin-Packing algorithm (to use as a ref-
erence or benchmark) and bM
sol
is the cost of the b-
Matching solution.
Table 2 reports the results of the evaluation and
clearly shows the difficulty to reach optimal solutions
using the Bin-Packing (Branch and Bound) algorithm
whose resolution times become prohibitive for the
scenarios of a data file of 2 Gigabytes to be distributed
on a selected set of data centers among 300, 500 and
700 providers or data centers. Our heuristic solution
performs close to optimal with Gap not exceeding 6%
for the evaluated cases. More specifically the gap is
in the interval [0.65%; 5.93%].
The results shown in Table 2 illustrate the diffi-
culty to optimally solve the data chunks placement
problem (see case of a data of 50 Mb with 25 DCs).
At the same time, they demonstrate that the heuris-
tic approach can find good and near-optimal solutions
whose cost is quite close to the optimum (see case
of data with 2000 MB and 700 DCs). Our algorithm
provides an excellent trade-off between convergence
time, optimality, scalability and cost. With respect to
convergence time as seen in the third column of Table
2, it converges in a few seconds for the scenario with
2000 chunks and 700 DCs (54 secs compared to more
than 3 hours for Bin-Packing).
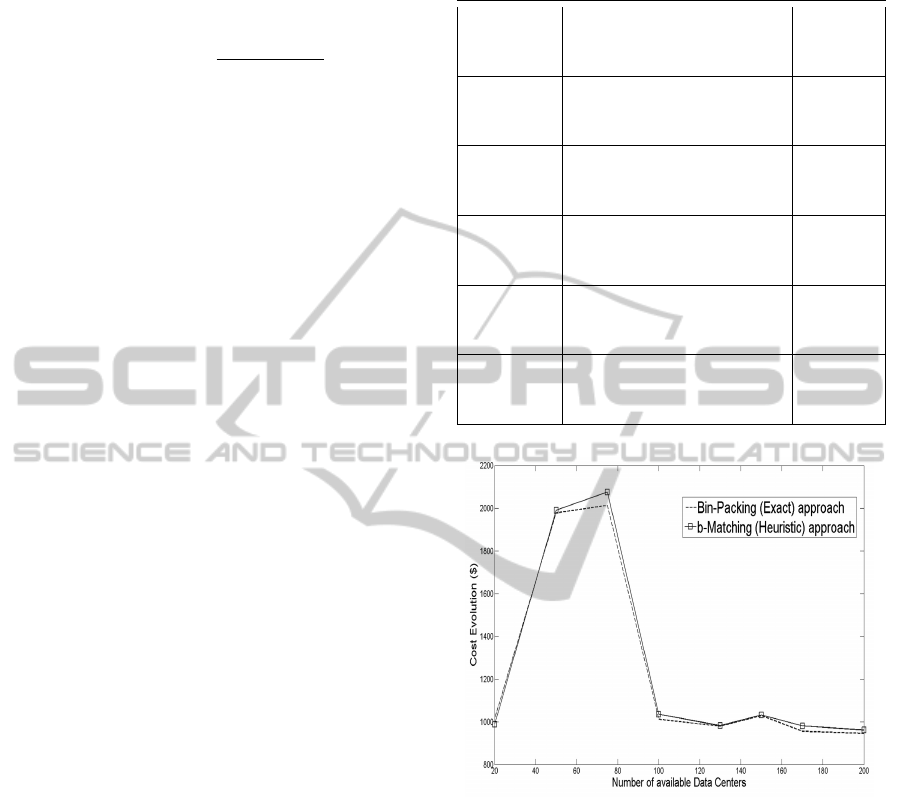
To get a better grasp of the relative performance
of the two algorithms used in this paper, a data file of
100 Megabytes is used and split into 100 encrypted
chunks to be stored in a number of data centers rang-
ing from 20 to 200. Figure 7 shows the characteristics
of the algorithms. The b-matching algorithm achieves
the best cost performance since it has consistently in-
curred the smallest cost, very close to the Bin-Packing
which does not scale (as seen in Table 2). Exception-
ally, one can remark in Figure 7 (the scenario with
20 to 40 available DCs), the cost found by the b-
Matching is slightly lower than the cost of the Bin-
Packing leading to negligible SLA violations caused
by the quality of the upper bound given by equation
(1) which should be enhanced in a future work. This
is explained by the difficulty to optimally store and
place all the data chunks in different data centers.
Another experiment consists in evaluating the pro-
posed heuristic solution to determine the trade-off be-
tween storage cost and data availability. We associate
with each user a required percentage of its data avail-
ability, denoted by A
expect
. We reformulate A
expect
in
Table 2: Encrypted data chunks placement: b-Matching al-
gorithm performances.
|N | |S| b-
Matching
Time (sec)
Bin-
Packing
Time (sec)
Gap (%)
50
12 0.15 0.16 2.24
25 0.15 0.16 5.93
40 0.17 0.18 2.06
100
25 0.17 0.20 3.08
50 0.18 0.20 0.65
75 0.20 0.22 2.98
500
100 1.10 2.11 1.94
250 1.27 3.68 4.37
350 1.33 4.20 0.97
1000
200 7.22 12.7 5.36
400 8.5 17.5 1.37
700 10.4 22.6 3.66
2000
300 30.7 > 3H 1.45
500 45.2 > 3H 4.3
700 54.8 > 3H 0.81
Figure 7: Storage cost gap.
terms of the number of nines required by a user. We
simulated a cloud storage market of 15 data centers
belonging to different providers having different fail-
ure rates. For example, Amazon S3 (AWS, 2014) of-
fers two levels of services: ”Standard Storage” witch
has 11 nines of storage availability for 0.03$ per Giga-
byte per month, while ”Amazon S3 Reduced Redun-
dancy Storage (RRS)” has 4 nines of data availability
for 0.024$ per GB per month. The simulated market
is summarized in Table 3.
We consider a user data of 100 Gigabytes, and we
investigate four methods to find the trade-off between
a maximum data availability and a minimum price
(cost). We use the following scenarios:
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
26
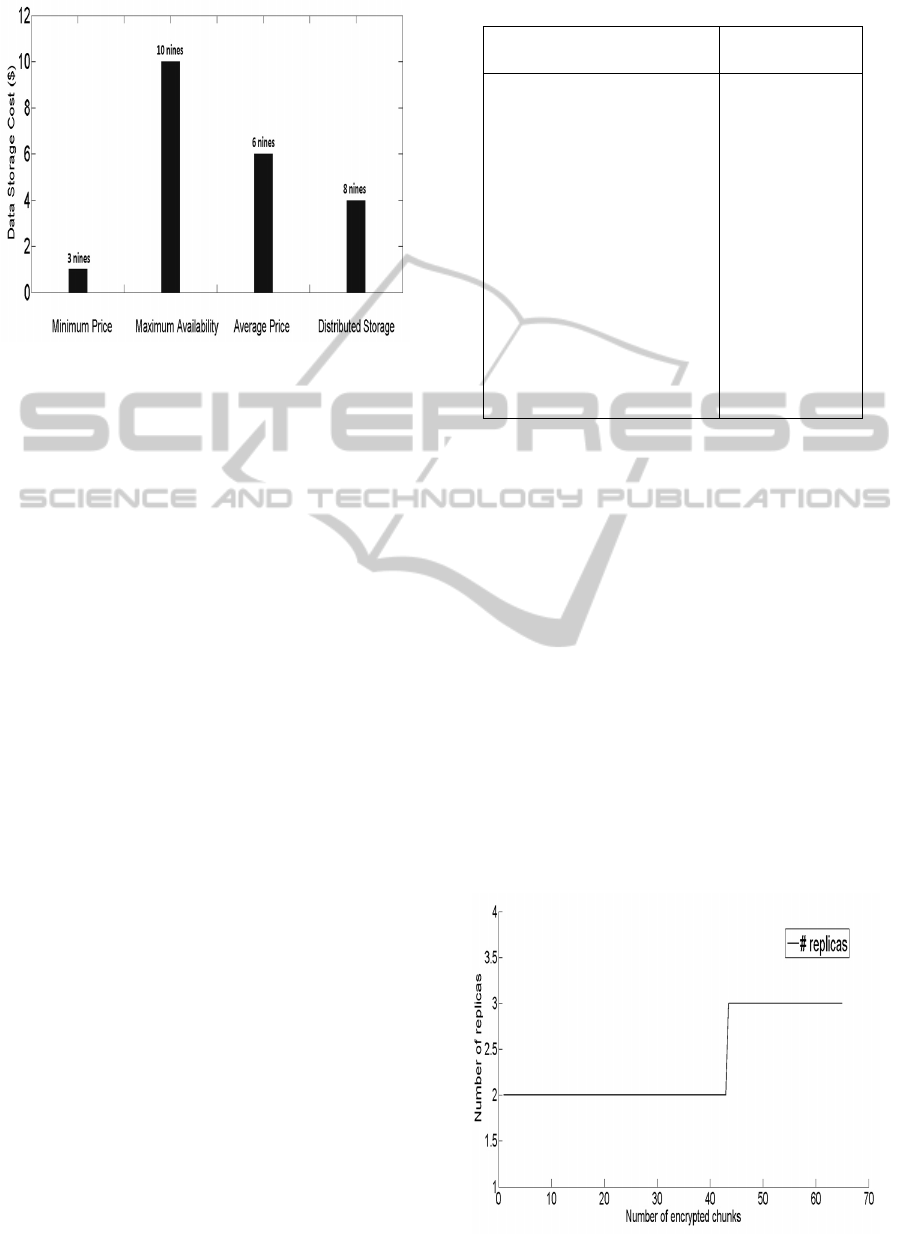
Figure 8: Data storage cost and availability trade-off.
• Minimum Price: A user selects simply the
cheapest provider in the market (Provider 15
proposing a price of $0.01 per Gigabyte and per
month in Table 3) without concerns on data avail-
ability (3 nines). Following this approach, the
data will be stored with a total minimum costs of
1$ and a weak data availability (3 nines in Fig-
ure 8). Moreover, the user is locked-in within one
cloud provider with a weak data availability. This
can lead to disrupting services and loss of data.
• Maximum Availability: A user selects the
provider with high availability in the simulated
market (Provider 1 with 10 nines in Table 3). Ac-
cording to pricing proposal of Provider 2, the total
storage cost is higher than the cost of the first sce-
nario (10 $ in Figure 8). This may also lead to
users’ lock-in within the same provider.
• Average Price: In this case, we use the average
price of the market, and we store the data within
the provider with equivalent price (Provider 9
with 0.06$ per Gigabyte per month in Table 3).
The total data cost in this case is equal to 6$ with
6 nines of data availability (according to the pro-
posal of Provider 6). This scenario presents higher
data availability than scenario 1 with a consider-
able cost increase. In this case, we also solicited
one provider to store the data, which may cause
user lock-in.
• Distributed Storage: We used our proposed ap-
proach (Algorithm 1) to find the trade-off between
data availability and price. As depicted in Fig-
ure 8, our solution reaches a maximum availabil-
ity of 8 nines with a minimum cost of 4$. This
is due to data distribution over a set of selected
providers with high availability and reasonable
prices, avoiding user lock-in at the same time.
Table 3: Storage market costs and data availability.
Providers Price
($/GB/month)
Data Avail-
ability
Prov 1 0.1 99.99999999%
Prov 2 0.095 99.99999995%
Prov 3 0.09 99,9999999%
Prov 4 0.085 99,9999995%
Prov 5 0.08 99,999999%
Prov 6 0.075 99,999995%
Prov 7 0.07 99.99999%
Prov 8 0.065 99,99995%
Prov 9 0.06 99,9999%
Prov 10 0.055 99,9995%
Prov 11 0.05 99,999%
Prov 12 0.04 99,995%
Prov 13 0.03 99.99%
Prov 14 0.02 99.95%
Prov 15 0.01 99.9%
A last experiment consists in evaluating the be-
havior of the number of replicas (noted by r) of
each chunk with the evolution of the number of data
chunks (|N
∗
|) identified in (14) for example. We sup-
posed that the average value of data centers failure
probability is equal to 10
−3
, when the expected data
availability required by cloud consumers is equal to
99.9999%.
Figure 9 depicts the evolution of r for different
chunks number ranging from 1 to 60. Thus, we re-
mark that for a number of chunks |N
∗
| ≤ 43, the
number of required replicas is equal to 2, and for
|N
∗
| ≥ 44 chunks, the number of replicas converges
to 3 and there is no need to replicate more even for
larger number of chunks. This may lead to store large
data volumes with reduced costs when satisfying the
required QoS (data availability). Note that this result
is very similar than that determined by the Google
File System solution (Ghemawat et al., 2003).
Figure 9: Data chunks replication behavior.
AMathematicalProgrammingApproachtoMulti-cloudStorage
27

5 SUMMARY AND FUTURE
WORK
In this paper we considered an encrypted and dis-
tributed solution allowing to store users’ data in dif-
ferent providers’ data centers offering storage ser-
vices with different prices and SLAs. To eliminate
user lock-in and to liberate user data from a unique
provider, we proposed a new efficient and scalable
solution based on b-Matching theory to optimize the
storage cost and the data failure at the same time. The
b-Matching algorithm works in tandem with a replica-
tion solution allowing to efficiently increase the data
availability of end-users. This replication algorithm is
based on a simple and fast approach giving near opti-
mal solutions even for large problem instances.
In future work, we will reinforce our mathematical
model of data chunk placement based on b-Matching
theory, to consider network constraints when users are
involved in PUT and GET operations. This may lead
cloud consumers to combine requests of compute (as
EC2 instances (EC2, 2014)) services with storage ser-
vices (as Google Drive (Google, 2014)) at the same
time. Thus, we will reinforce our broker’s function-
alities to give cloud consumers various means to con-
sume proposed cloud resources in a more secure man-
ner with reduced cost.
REFERENCES
Abu-Libdeh, H., Princehouse, L., and Weatherspoon, H.
(2010). Racs: A case for cloud storage diversity.
In Proceedings of the 1st ACM Symposium on Cloud
Computing, SoCC ’10, pages 229–240, New York,
NY, USA. ACM.
AWS (2014). http://aws.amazon.com/fr/s3/pricing/.
Balasaraswathi, V. and Manikandan, S. (2014). Enhanced
security for multi-cloud storage using cryptographic
data splitting with dynamic approach. In Advanced
Communication Control and Computing Technologies
(ICACCCT), 2014 International Conference on, pages
1190–1194.
Bonvin, N., Papaioannou, T., and Aberer, K. (2010). A
self-organized, fault-tolerant and scalable replication
scheme for cloud storage. In Proceedings of the 1st
ACM Symposium on Cloud Computing, SoCC ’10,
pages 205–216, New York, NY, USA. ACM.
Chia-Wei, C., Pangfeng, L., and Jan-Jan, W. (2012).
Probability-based cloud storage providers selection al-
gorithms with maximum availability. In Parallel Pro-
cessing (ICPP), 2012 41st International Conference
on, pages 199–208.
CPLEX (2014). http://www-01.ibm.com/software/
commerce/optimization/cplex-optimizer/.
EC2 (2014). http://aws.amazon.com/fr/ec2/.
Ford, D., Labelle, F., Popovici, F., Stokely, M., Truong,
V., Barroso, L., Grimes, C., and Quinlan, S. (2010).
Availability in globally distributed storage systems. In
Proceedings of the 9th USENIX Symposium on Oper-
ating Systems Design and Implementation.
Ghemawat, S., Gobioff, H., and Leung, S. (2003). The
google file system. SIGOPS Oper. Syst. Rev.,
37(5):29–43.
Google (2014). drive.google.com/.
Grotschel, M., Lovsz, L., and Shrijver, A. (1985). Ge-
ometric algorithms and combinatorial optimization.
Springer.
Jindarak, K. and Uthayopas, P. (2012). Enhancing cloud
object storage performance using dynamic replication
approach. In Parallel and Distributed Systems (IC-
PADS), 2012 IEEE 18th International Conference on,
pages 800–803.
Korte, B. and Vygen, J. (2001). Combinatorial optimiza-
tion: theory and algorithms. Springer.
Li, J. and Li, B. (2013). Erasure coding for cloud storage
systems: A survey. Tsinghua Science and Technology,
18(3):259–272.
Mansouri, Y., Toosi, A., and Buyya, R. (2013). Brokering
algorithms for optimizing the availability and cost of
cloud storage services. In Proceedings of the 2013
IEEE International Conference on Cloud Computing
Technology and Science - Volume 01, CLOUDCOM
’13, pages 581–589, Washington, DC, USA. IEEE
Computer Society.
Myint, J. and Thu, N. T. (2011). A data placement algo-
rithm with binary weighted tree on pc cluster-based
cloud storage system. In Cloud and Service Comput-
ing (CSC), 2011 International Conference on, pages
315–320.
Negru, C., Pop, F., Cristea, V., Bessisy, N., and Jing, L.
(2013). Energy efficient cloud storage service: Key
issues and challenges. In Emerging Intelligent Data
and Web Technologies (EIDWT), 2013 Fourth Inter-
national Conference on, pages 763–766.
NIST (2014). Announcing the advanced encryption stan-
dard (aes).
Openstack (2014). https://www.openstack.org/.
Qingsong, W., Veeravalli, B., Bozhao, G., Lingfang, Z., and
Dan, F. (2010). Cdrm: A cost-effective dynamic repli-
cation management scheme for cloud storage cluster.
In Cluster Computing (CLUSTER), 2010 IEEE Inter-
national Conference on, pages 188–196.
Rodrigo, R. and Liskov, B. (2005). High availability in
dhts: Erasure coding vs. replication. In Peer-to-Peer
Systems IV 4th International Workshop IPTPS 2005,
Ithaca, New York.
Seungmin, K., Bharadwaj, V., and KhinMiMi, A. (2014).
Espresso: An encryption as a service for cloud storage
systems. Monitoring and Securing Virtualized Net-
works and Services, pages 15–28.
Srivastava, S., Gupta, V., Yadav, R., and Kant, K. (2012).
Enhanced distributed storage on the cloud. In Com-
puter and Communication Technology (ICCCT), 2012
Third International Conference on, pages 321–325.
Swift (2014). http://docs.openstack.org/developer/swift/.
Thanasis, G. P., Bonvin, N., and Aberer, K. (2012). Scalia:
An adaptive scheme for efficient multi-cloud storage.
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
28

In Proceedings of the International Conference on
High Performance Computing, Networking, Storage
and Analysis, SC ’12, pages 20:1–20:10, Los Alami-
tos, CA, USA. IEEE Computer Society Press.
Varghese, L. and Bose, S. (2013). Integrity verification in
multi cloud storage. In Proceedings of International
Conference on Advanced Computing.
Weatherspoon, H. and Kubiatowicz, J. (2002). Erasure cod-
ing vs. replication: A quantitative comparison. In Re-
vised Papers from the First International Workshop
on Peer-to-Peer Systems, IPTPS ’01, pages 328–338,
London, UK, UK. Springer-Verlag.
Yanzhen, Q. and Naixue, X. (2012). Rfh: A resilient,
fault-tolerant and high-efficient replication algorithm
for distributed cloud storage. In Parallel Processing
(ICPP), 2012 41st International Conference on, pages
520–529.
Zhang, Q., Xue-zeng, P., Yan, S., and Wen-juan, L. (2012).
A novel scalable architecture of cloud storage sys-
tem for small files based on p2p. In Cluster Com-
puting Workshops (CLUSTER WORKSHOPS), 2012
IEEE International Conference on, pages 41–47.
AMathematicalProgrammingApproachtoMulti-cloudStorage
29
