A 3D Feature for Building Segmentation based on Shape-from-Shading

Dimitrios Konstantinidis

, Vasileios Argyriou

, Tania Stathaki

and Nikos Grammalidis

Communications and Signal Processing, Imperial College London, London, U.K.

Computing and Information Systems, Kingston University, London, U.K.

CERTH-ITI, Thessaloniki, Greece

Keywords:

Building Segmentation, Satellite Images, 3D Reconstruction, Shape-from-Shading, Kmeans, Quaternions.

Abstract:

An important cue that can assist towards an accurate building detection and segmentation is 3D information.

Because of their height, buildings can easily be distinguished from the ground and small objects, allowing

for their successful segmentation. Unfortunately, 3D knowledge is not always available, but there are ways

to infer 3D information from 2D images. Shape-from-shading techniques extract height and surface normal

information from a single 2D image by taking into consideration knowledge about illumination, reﬂectance

and shape. In this paper, a novel feature is proposed that can describe the 3D information of reconstructed

images based on a shape-from-shading technique in order to successfully acquire building boundaries. The

results are promising and show that such a 3D feature can signiﬁcantly assist in a correct building boundary

detection and segmentation.

1 INTRODUCTION

3D reconstruction is considered as the task of infer-

ring a 3D model of a scene from 2D or 3D data. It

is a well-studied and analyzed problem, applied in a

wide range of ﬁelds that require 3D information of a

scene. In urban environments, 3D reconstruction can

assist in the 3D mapping of areas, allowing govern-

ments and municipalities to visualize the current 3D

model of the earth’s terrain and compare it with older

models. Such an urban model comparison could play

a signiﬁcant role in the analysis and study of changes

that have occurred in the time intervals between the

3D models, allowing social sciences to investigate a

population’s prosperity as it is depicted in the build-

ing expansion/destruction.

Combined with the detection of buildings, 3D re-

construction can greatly assist in the identiﬁcation and

segmentation of building areas. Buildings are tall

structures and can easily be distinguished from small

objects, such as cars and low vegetation. As a result,

the extracted 3D information can play a signiﬁcant

role to an accurate building detection and extraction.

Moreover, the appropriate identiﬁcation of building

boundaries can allow an accurate and robust satellite

image registration, as buildings are static objects that

can be used as reference for image registration.

Although 3D modeling of urban areas can easily

be achieved from appropriate 3D sensors, the high

cost of such sensors poses a serious problem to the

acquisition of 3D data. As a result, other techniques

have been developed that attempt to infer 3D infor-

mation from 2D data. Photometric stereo algorithms

belong to a large category of 3D reconstruction tech-

niques and they are widely employed to solve the

problem of 3D reconstruction from 2D data. To this

end, such methodologies attempt to infer the shape of

a scene from the knowledge or computation of illumi-

nation and reﬂectance that describe the scenery.

In this paper, a 3D feature is proposed based on

the result of a 3D reconstruction technique applied on

a satellite image. There are two main reasons for the

use of the proposed 3D feature. Firstly, such a feature

can assist in the identiﬁcation of building boundaries

and contribute towards an accurate pixel-based build-

ing segmentation. Secondly, this feature will make

the creation of 3D building models in an urban area

possible, laying the foundations for a 3D mapping of

an entire urban environment.

The rest of the paper is organized as follows. In

Section 2, a review on state-of-the-art 3D reconstruc-

tion algorithms is provided, while in Section 3 the

proposed and implemented methodologyis described.

In Section 4 some preliminary results on 3D recon-

struction of buildings are presented. Finally, conclu-

sions and future work are presented in section 5.

595

Konstantinidis D., Argyriou V., Stathaki T. and Grammalidis N..

A 3D Feature for Building Segmentation based on Shape-from-Shading.

DOI: 10.5220/0005456305950602

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (MMS-ER3D-2015), pages 595-602

ISBN: 978-989-758-090-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

There is an extensive literature available with ways

to tackle the problem of 3D reconstruction. The se-

lection of a speciﬁc methodology depends to a large

degree on the type of data available. As a result,

3D reconstruction techniques can be split on method-

ologies that employ already acquired 3D data, multi-

view stereo matching methods that are based on two

or more 2D images or video and shape from shad-

ing methodologies that employ a single 2D image.

An overview of 3D reconstruction algorithms is pre-

sented in (Kordelas et al., 2010).

3D reconstruction methods based on 3D data are usu-

ally the fastest and most accurate methods available

that create a 3D model of a scene. These techniques

mainly depend on 3D point clouds acquired from 3D

laser scanners or LiDAR (LIght Detection And Rang-

ing) sensors to get the necessary information for the

3D model computation. Since point clouds are usu-

ally unstructured, there are techniques that attempt to

group them in meaningful shapes (Kim and Li, 2006;

Kolluri et al., 2004). Such methods usually rely on

triangularization techniques to get an initial 3D mesh

from the point clouds. Optimization techniques, such

as the Stokes’ theorem, can then be applied to reﬁne

the 3D model and reduce the number of the initially

formed triangles (Kim et al., 2003). Unfortunately,

3D information from radar/laser sensors is not always

available, due to the high cost of acquisition.

Multi-view stereo techniques attempt to infer the 3D

model of a scene from multiple 2D images captur-

ing the same scene from different viewing angles. A

successful approach to 3D reconstruction from mul-

tiple views has been achieved by the method of vi-

sual hull and voxels (Seitz and Dyer, 1997; Eisert

et al., 1999). The whole scene is assumed to be a

large 3D cube that consists of a number of smaller

cuboids, known as voxels. These voxels are removed,

based on whether they are seen from a point of view.

This method is a curving process, where parts of the

scene are removed to accurately describe the underly-

ing original scene. However, visual hull reconstruc-

tion’s performance suffers from the need of multiple

cameras, capturing the scene from different views and

the existence of occluded objects.

One of the most common ways to achieve 3D recon-

struction from two or more images is with the use

of stereo matching techniques (Baillard et al., 1999;

Geiger et al., 2011). Distinctive and invariant to ro-

tation and illumination image features are extracted

from a pair of overlapping images, using algorithms

such as SIFT (Lowe, 2004) or SURF (Bay et al.,

2008). Afterwards, these features are transformed

into 3D points by applying optimization techniques,

such as bundle adjustment (Lourakis and Argyros,

2009) and RANSAC (Fischler and Bolles, 1981).

Since these points are usually sparse in the 3D space,

smoothing functions can be employed to ﬁll the gaps

among the points (Agarwal et al., 2011). An alterna-

tive method for context-based clustering of 2D im-

ages in order to infer 3D information is presented

in (Makantasis et al., 2014). The accuracy of stereo

matching techniques increase as more images of the

same scene become available.

Another approach to 3D reconstruction from multi-

ple images is by employing photometric stereo tech-

niques. These methods estimate the surface normals

of a scene by observing the scene under different

lighting conditions. Woodham was the ﬁrst to intro-

duce photometric stereo, when he proposed a method

to obtain surface gradients by using two photomet-

ric images, assuming that the surface albedo is known

for each point on the surface (Woodham, 1980). His

method, although simple and efﬁcient, only dealt with

Lambertian surfaces and was sensitive to noise. Cole-

man and Jain extended photometric stereo to four

light sources, where specular reﬂections were dis-

carded and estimation of surface shape could be per-

formed by means of diffuse reﬂections and the use of

the Lambertian model (Coleman Jr. and Jain, 1982).

A photometric approach to obtain the shape and re-

ﬂectance information for a surface was developed in

(Nayar et al., 1990). Barsky and Petrou presented

an algorithm for estimating the local surface gradient

and real albedo by using four source colour photomet-

ric stereo in the presence of highlights and shadows

(Petrou and Barsky, 2001; Barsky and Petrou, 2003;

Barsky and Petrou, 2006). Other approaches to the

photometric stereo problem in the presence of high-

lights and shadows worth mentioning (Argyriou and

Petrou, 2008; Argyriou et al., 2013).

Finally, given that a single image is available, 3D

reconstruction can be achieved by employing shape-

from-shading methodologies. Shape-from-shading is

considered a special case of photometric stereo and

was initially formulated by (Horn, 1970). Shape-

from-shading can be expressed as a minimization

problem that attempts to reconstruct scenes by mea-

suring the reﬂectance and illumination of a surface

(Frankot and Chellappa, 1988; Bors et al., 2003).

Many different approaches have been proposed to

solve this problem in an attempt to infer both the

height and the surface normals for each pixel in an im-

age. A review on some popular shape-from-shading

techniques is performed in (Zhang et al., 1999), while

the different numerical approaches to the problem

of shape-from-shading are analyzed in (Durou et al.,

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

596

2008). A signiﬁcant problem that can severely limit

the applicability of shape-from-shading techniques is

their high computational complexity.

Our technique is based on the shape from shading

methodology developed in (Barron and Malik, 2013).

His method, named SIRFS, can be considered as an

extension to the classical shape from shading prob-

lem (Horn, 1970), since not only shape, but also re-

ﬂectance and illumination are unknown. With the ac-

quisition of 3D information, we expect to enhance the

classiﬁcation performance of a building detection al-

gorithm by allowing a more accurate and robust build-

ing boundary segmentation. Moreover, the 3D recon-

structed buildings can be the basic components for the

construction of a 3D model that characterizes the en-

tire urban area. The advantagesof our approach lies in

the fact that the 3D reconstruction will be based on a

single 2D image, without the need of multiple images

capturing the same scene and the fact that the SIRFS

algorithm works without any prior knowledge of the

location of the sun the time the image was captured.

3 METHODOLOGY

Before any methodology is applied, it is assumed

that only a single 2D satellite image, depicting an ur-

ban environment exists and therefore, no reconstruc-

tion strategies that depend on multiple images or al-

ready acquired 3D data can be applied. Furthermore,

the satellite images are assumed to be orthorectiﬁed,

meaning that distortions caused from the sensor and

the earth’s terrain have been geometrically removed

and an accurate measurement of angles and distances

is possible. Moreover, since the main goal is to use

the 3D representation of an urban area as an additional

cue for building detection and segmentation purposes,

the assumption that a building detection algorithm has

already been applied is made. Therefore, some ini-

tial candidate areas where buildings exist havealready

been identiﬁed and extracted.

Our proposed methodology attempts to reconstruct

only the candidate building areas that a building de-

tector outputs. Such an approach will not only re-

duce the computational burden of a 3D reconstruc-

tion procedure applied in the entire image, but also

allow for an accurate 3D representation of the can-

didate building areas since only a few objects are in-

volved, leaving limited space for errors. The extracted

3D information from these areas will enable the cre-

ation of coarse 3D building models and assist towards

a precise and robust building detection and segmen-

tation. Buildings, being tall structures, can easily be

distinguished from ground objects. As a result, ar-

eas that do not contain buildings can be discarded,

leading to an increase in the classiﬁcation accuracy

of an object-based building detection algorithm. Fur-

thermore, building boundaries can be identiﬁed and

segmented based on height and surface normals, al-

lowing the reﬁnement of the initial computed candi-

date building areas and increasing the performance of

a pixel-based building detection algorithm.

To achieve the desired 3D representation of the ur-

ban areas, the proposed approach relies on the work

of Barron (Barron and Malik, 2013). The authors

present the SIRFS algorithm as an extension of a clas-

sical shape-from-shading algorithm, capable of com-

puting all the unknown parameters (i.e. shape, re-

ﬂectance and illumination). The shape-from-shading

problem is formulated by the following maximization

function:

max

R,Z,L

P(R)P(Z)P(L) (1)

subject to I = R+ S(Z, L) (2)

where I is the image for which the 3D representa-

tion is sought, R is the log-reﬂectance image, Z is the

depth map, and L is a spherical harmonic model of

illumination. P(R), P(Z) and P(L) are the priors on

reﬂectance, shape and illumination respectively and

S(Z, L) linearizes Z into a set of surface normals, pro-

ducing a log-shading image from these normals and

the illumination L (Barron and Malik, 2013).

Every candidate building area is processed separately

so as to successfully extract its 3D information. As a

preprocessing step, the illumination of each image is

histogram equalized so as details in the image become

more apparent. This is achieved by transforming the

RGB color space to another color space, where the

color and the illumination component of the image is

separated. The HSV color space can achieve this dif-

ferentiation. Afterwards, the V channel of the HSV

color space, representing illumination, is histogram

equalized. Histogram equalization distributes an im-

age’s pixel values uniformly, allowing objects that are

barely seen to be distinguished. Then, the HSV color

space, having the V channel histogram equalized is

transformed back to the RGB color space.

To successfully extract 3D information, the SIRFS al-

gorithm requires a mask, which deﬁnes where the ob-

ject of interest is. As a result, an initial image seg-

mentation should be performed and the pixels that be-

long to the building class should be highlighted. Since

such knowledge is not available, a kmeans algorithm

is employed to partition image pixels to k number of

classes according to their values. A kmeans algorithm

is a clustering algorithm that given k number of clus-

ters, it deﬁnes the initial positions of the cluster cen-

ters randomly and then iteratively moves the cluster

A3DFeatureforBuildingSegmentationbasedonShape-from-Shading

597

centers in new positions that best describe the data

distribution (MacQueen, 1967). Given that a satellite

image contains n channels, each pixel is described by

a tuple of n values and according to these values, each

candidate area is segmented. The number of clusters

k for the kmeans algorithm is selected to be equal to

2, since the problem can be considered as a binary

classiﬁcation task with two classes, the building and

the non-building class. The result of the segmenta-

tion is afterwards reﬁned with morphological opening

and closing operations, so that pixels with no adjacent

neighbors belonging to the same class are reversed to

the other class. These morphological operations are

performed in order to avoid small islands or holes of

pixels that can cause problems in the correct estima-

tion of height and surface normals.

Since there is no prior knowledge of which cluster of

pixels corresponds to the building class, the SIRFS al-

gorithm is applied twice, once for each cluster of pix-

els, assuming each time that the tested cluster is the

one that corresponds to the building class. The output

of the SIRFS method is used to describe only the clus-

ter of pixels for which the algorithm was executed,

although the SIRFS method computes an output for

every pixel of the provided image. The output of the

SIRFS algorithm is for each pixel p of the image, a

height value H

, and the coordinates of the surface

normal vector in the 3D space (N

, N

Given the result of the 3D reconstruction procedure

that was previously described, a 3D feature is pro-

posed that is based on the aforementioned values of

the height and the surface normals computed for each

pixel of a candidate building area. In order to de-

ﬁne this new feature, the quaternion algebra that was

ﬁrst described in (Hamilton, 1844) is employed. A

quaternion is a special complex number in the 3D

space and it can be described by the equation q =

a+ b ∗i+ c∗ j + d ∗k. The reasons behind the selec-

tion of a quaternion to characterize the proposed 3D

feature lie in the fact that a quaternion can describe a

4-tuple value, while being able to represent a structure

in the 3D sphere. Furthermore, being an expansion of

a complex number, a quaternion possesses some inter-

esting properties, such as the fact that its multiplica-

tion is not commutative (ij = k, while ji = −k), while

its norm is computed in the same way as the norm of

a vector (kqk=

√

+ b

+ c

+ d

). Such properties

may be proved useful for the tasks of building seg-

mentation and 3D reconstruction. Therefore, the 3D

representation of each pixel is approached as a quater-

nion of the following form:

= H

+ N

∗i+ N

∗ j + N

∗k (3)

Equation (3) describes the novel 3D feature that is

proposed for building extraction and segmentation.

Such a 3D feature will be able to not only charac-

terize the 3D representation of an urban area, but also

identify and segment buildings that are present in the

area. The reason behind the deﬁnition of such a 3D

feature lies in the fact that this feature can afterwards

be used as an input to another machine learning al-

gorithm that attempts to locate and segment building

boundaries based on the height information and the

surface normals. Furthermore, such 3D knowledge

can assist in the elimination of false alarms building

detection algorithms produce, by acknowledging the

lack of buildings in an extracted candidate building

area. The methodology for the creation of the pro-

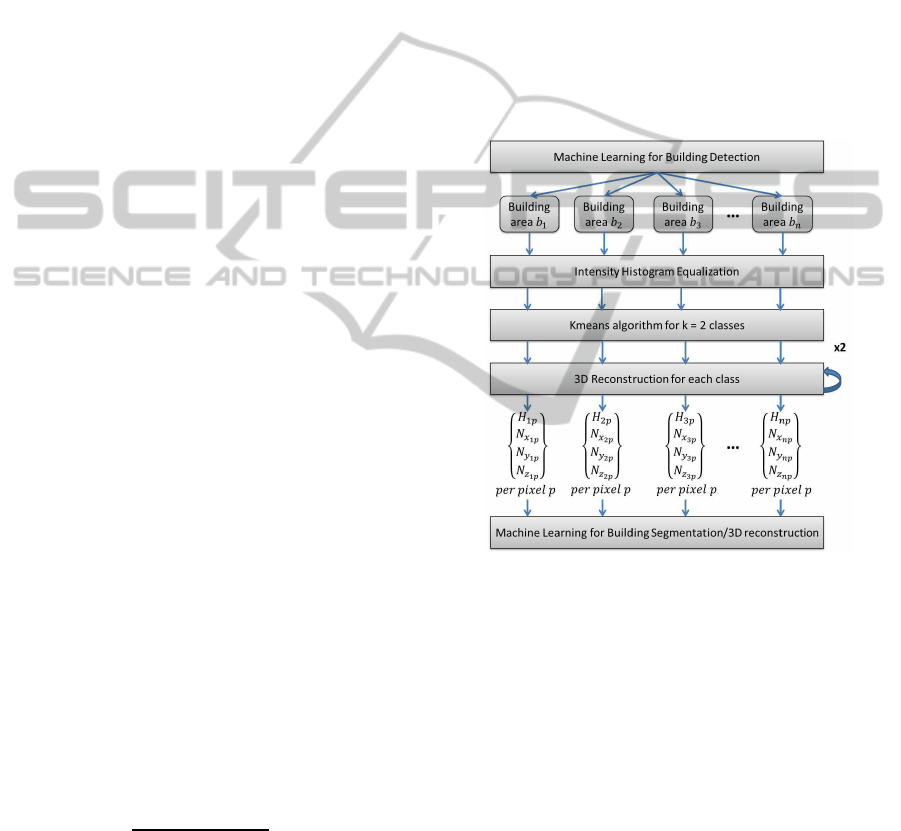
posed 3D feature is summarized in Figure 1.

Figure 1: Our proposed 3D feature extraction procedure.

4 EXPERIMENTS AND RESULTS

In this section, the results of employing the proposed

methodology in a set of image patches extracted from

a QuickBird satellite image will be presented. The

output of the SIRFS algorithm in the form of height

and surface normals computed for every pixel of the

tested image patches will be visualized and the value

and importance of the extracted 3D information in or-

der to achieve a successful building segmentation will

be demonstrated.

To identify the potential of the proposed method-

ology to correctly describe building regions and lead

to their accurate and robust segmentation. For this

purpose, ﬁve image patches where buildings exist and

three image patches with no buildings present were

employed. The reason behind the selection of the last

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

598

three non-building image patches is to demonstrate

the ability of the proposed methodology to not only

extract building boundaries, but also identify when

buildings are not present, leading to rejection of false

positives, given our methodology is applied in con-

junction with a building detector algorithm. Figure 2

presents the tested image patches, the results of their

binary segmentations by employing the kmeans algo-

rithm and the output of the SIRFS algorithm in the

form of height information and surface normals.

The ﬁrst row of Figure 2 shows the ﬁve tested satel-

lite image patches after being preprocessed with his-

togram equalization. As it is already mentioned, his-

togram equalization allows objects that are barely

seen to be distinguished by uniformly distributing the

illumination in an image patch. The eight tested and

preprocessed images are shown in the ﬁrst row of Fig-

ure 2, where only the RGB channels are shown for vi-

sualization purposes.

The second row of Figure 2 shows the result of

the kmeans algorithm applied on the tested image

patches. The masks are binary since the kmeans al-

gorithm is executed for k = 2 classes. Although the

segmentation is not too accurate, it provides satisfac-

tory results for the SIRFS algorithm that is then em-

ployed. The better the object of interest is segmented,

the more accurate the results of the 3D reconstruction

achieved from the SIRFS algorithm are. Segmenting

an image patch into more than 2 classes may produce

slightly better results, but it would signiﬁcantly in-

crease the execution time of the methodology, since

the SIRFS algorithm, which is quite a computation-

ally heavy operation, would then have to be executed

k times, where k is the number of classes.

The third row of Figure 2 shows the height in-

formation that is derived from the execution of the

SIRFS algorithm. The images are slightly rotated for

better visualization. As one may observe, the differ-

ences in the height of buildings with respect to the

ground is correctly captured in the 3D reconstruc-

tion of the image patches, while inaccuracies intro-

duced by the kmeans clustering are to some degree

rectiﬁed. As expected, buildings can be easily dis-

tinguished from ground objects based on their height,

and therefore, the extracted height information is an

important cue towards an accurate and robust build-

ing detection and segmentation. A drawback of the

employed 3D reconstruction procedure is that inaccu-

racies of the computed height are present, especially

close to the borders of an image patch.

Another observation concerns the computed

height of the roads. The height of roads is relatively

low, with respect to the ground, thus the SIRFS algo-

rithm can correctly capture the surface of the tested

terrain. However, there are cases where roads are

shown a little elevated overthe ground. In these cases,

the shape of the roads can be an important cue towards

their identiﬁcation as non-building objects. These ob-

servations showthat the 3D representation of an urban

environment can be used to reduce the false positives

that a building detection algorithm produces, thus in-

creasing the classiﬁcation accuracy of a building de-

tector and allowing an accurate and successful pixel-

based building segmentation. Moreover, the potential

of the 3D representation to describe roads can be used

for the development of an accurate and robust road

segmentation algorithm.

The fourth row of Figure 2 presents the results

of the surface normals based on the SIRFS algorithm

that are computed for each pixel of the image patch.

The surface normals are vectors in the 3D space that

describe the orientation of the surface of a 3D repre-

sentation. Surface normals are expected to be really

valuable features that indicate the existence of build-

ings, since building rooftops are usually ﬂat or have

a uniform slope. Such an attribute of buildings is ex-

pected to be reﬂected to the surface normals, which

should have slight variations on the building area, but

high variations close to the building boundaries, since

the height of terrain close to the building boundaries

is changed abruptly. The values of the 3D surface

normal vectors are mapped to the RGB color space

and are presented in the fourth row of Figure 2. One

may observe that the SIRFS algorithm produces sur-

face normals with the same or similar orientation for

ﬂat areas. As a result, the information extracted from

the surface normals can play a signiﬁcant role to-

wards the identiﬁcation and segmentation of building

boundaries.

In order to demonstrate how valuable the 3D infor-

mation extracted from the SIRFS algorithm is for the

task of building segmentation, some preliminary re-

sults are presented. To this end, the buildings shown

in the ﬁrst row of Figure 2 were manually segmented

so as to consist the ground truth masks of the tested

image patches. Afterwards, these ground truth masks

were compared to the kmeans segmentation before

the 3D reconstruction procedure, as presented on the

second row of Figure 2. Furthermore, the kmeans al-

gorithm was employed once again to compute a re-

ﬁned segmentation, where except for the color infor-

mation, each pixel is also represented by the 3D in-

formation computed from the SIRFS algorithm, in the

form of height and surface normals. Since the height

information is relative to the tested image patch, the

height values of each patch are normalized to the

range [0, 1]. What is more, two multipliers are em-

ployed to give a certain weight to the height and

A3DFeatureforBuildingSegmentationbasedonShape-from-Shading

599

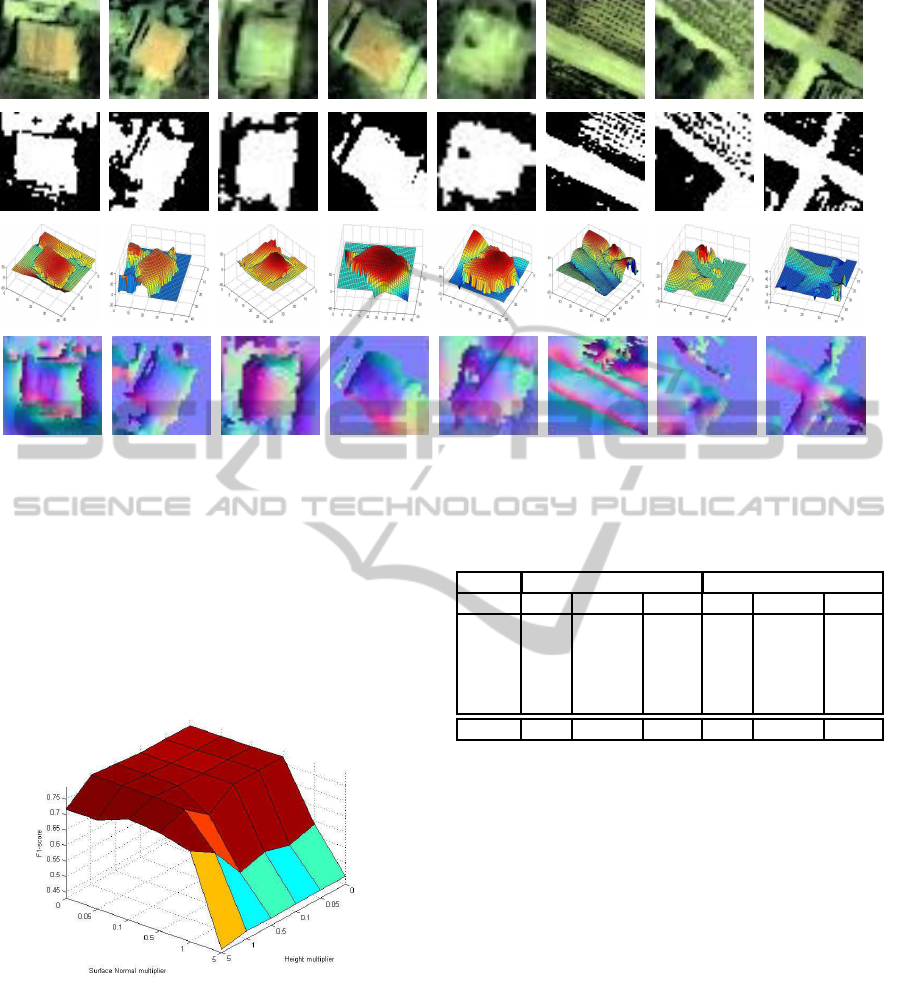
Figure 2: Results from SIRFS algorithm. Original images after preprocessing shown in ﬁrst row. Results from kmeans

algorithm shown in second row. Height information extracted from SIRFS algorithm shown in third row. Surface normals

extracted from SIRFS algorithm shown as RGB images in fourth row.

surface normal information, in order to test how the

weighted 3D information affects building segmenta-

tion. The values chosen for both the height and the

surface normal multipliers are [0, 0.05, 0.1, 0.5, 1, 5].

Figure 3 presents the F1-score of the pixel-based com-

parison between the ground truth masks and the re-

ﬁned building segmentations.

Figure 3: Results of building segmentation based on various

values of height and surface normal multipliers.

There is a single combination of height and surface

normal multipliers’ values that give the best possi-

ble results with respect to the F1-score. These val-

ues are 1 and 0 for the height and surface normal

multiplier respectively. These values demonstrate the

importance of the height information for the build-

ing detection and segmentation task. On the other

hand, it seems that the surface normals decrease the

performance of the building segmentation based on

Table 1: Segmentation results of the ﬁve tested building im-

age patches.

Before Reconstruction After Reconstruction

Image Recall Precision F-score Recall Precision F-score

1 0.902 0.57 0.698 0.905 0.599 0.721

2 0.992 0.514 0.677 0.989 0.548 0.705

3 0.928 0.669 0.778 0.928 0.669 0.778

4 0.906 0.714 0.798 0.902 0.743 0.815

5 0.968 0.793 0.872 0.971 0.852 0.908

Average 0.939 0.652 0.765 0.939 0.682 0.785

the kmeans algorithm. This can be attributed to the

fact that all ﬂat areas tend to have normals pointing

upwards and thus, a building cannot be easily dis-

tinguished using surface normals. Of signiﬁcant im-

portance is also the fact that giving strong weight to

the height information leads to a drop in the results

of the building segmentation. This happens because

there are inaccuracies in the height computed from

the SIRFS algorithm close to the boundaries of the

image patches. The results in the form of recall, preci-

sion and F1-score achieved on the pixel-based build-

ing segmentation of the ﬁve image patches, depicting

buildings before and after the introduction of the 3D

information are presented on Table 1.

The numbers in the ﬁrst column of Table 1 correspond

to the order of the ﬁve tested image patches as they

appear in the ﬁrst row of Figure 2 from left to right.

From Table 1, one can conclude that the building seg-

mentation achieved from the kmeans algorithm and

that is based both on color and on the height and sur-

face normal information is more accurate than with-

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

600

out the 3D knowledge. More speciﬁcally, the preci-

sion of the pixel-based building segmentation is sig-

niﬁcantly increased by a measure of 4.6% when 3D

information is introduced, while recall remains unal-

tered. Overall, the increase in the measure of F1-score

by 2.6% shows that the introduction of 3D informa-

tion can signiﬁcantly assist towards an accurate and

robust building segmentation. A visualization of the

best building segmentation results of Table 1, along

with the initial segmentation results and the ground

truth masks is presented in Figure 4.

5 CONCLUSIONS

A methodology to extract 3D information using a

shape-from-shading algorithm, named SIRFS (Bar-

ron and Malik, 2013) is proposed. Furthermore, a 3D

feature to describe the 3D representation of an urban

environment is deﬁned. The proposed feature can not

only allow for a 3D reconstruction of an urban en-

vironment, but also improve the classiﬁcation accu-

racy of a building detection algorithm by identifying

buildings and rejecting image regions with no build-

ings present. Moreover, the extracted 3D information

can lead to an accurate pixel-based building bound-

ary extraction, thus assisting to a successful building

boundary identiﬁcation and segmentation.

The experimental results on the 3D reconstruction

of buildings and roads can be used as a qualitative

measurement of the importance and usefulness of the

proposed 3D feature. The height information and the

extracted surface normals can be proved valuable fea-

tures to a machine learning algorithm that attempts to

segment buildings in an urban environment. Table 1

presents with a quantitative manner the signiﬁcance

of the 3D information to an accurate and robust pixel-

based building segmentation.

In the future, the proposed 3D feature will be em-

ployed in order to demonstrate the signiﬁcance of the

height and normal information in the building extrac-

tion task. The goal would be to create a machine

learning algorithm that accepts as input the candi-

date building areas detected from a building detection

methodology. Along with the extracted 3D informa-

tion from the proposed methodology of this thesis, the

machine learning algorithm would be capable of facil-

itating the building detection task by discarding areas

that do not contain buildings and allowing for an ac-

curate building segmentation by correctly identifying

the building boundaries. In addition, such an algo-

rithm could be used to successfully solve the build-

ing change detection task, by taking into considera-

tion both 2D and 3D information and overcoming the

Figure 4: Results from the kmeans building segmentation.

Ground truth masks of buildings shown in ﬁrst column.

Kmeans building segmentation employing only color infor-

mation shown in second column. Kmeans building segmen-

tation employing color and 3D information shown in third

column.

limitations of algorithms that operate only on 2D or

3D data.

ACKNOWLEDGEMENTS

This research has been co-ﬁnanced by the European

Union (European Social Fund-ESF) and Greek na-

tional funds through the Operational Program ”Ed-

ucation and Lifelong Learning” of the National

Strategic Reference Framework (NSRF): THALIS-

NTUA-UrbanMonitor project and by the Operational

Programme ”Competitiveness and Entrepreneurship

(OPCE II)(EPAN II) of the National Strategic Ref-

erence Framework (NSRF)”- Greece-Israel Bilat-

eral R&T Cooperation 2013-2015: 5 Dimensional

Multi-Purpose Land Information System (5DMu-

PLIS) project.

A3DFeatureforBuildingSegmentationbasedonShape-from-Shading

601

REFERENCES

Agarwal, S., Furukawa, Y., Snavely, N., Simon, I., Curless,

B., Seitz, S., and Szeliski, R. (2011). Building Rome

in a Day. Communications of the ACM, 54(10):105–

112.

Argyriou, V. and Petrou, M. (2008). Recursive photomet-

ric stereo when multiple shadows and highlights are

present. In IEEE Conference on Computer Vision and

Pattern Recognition (CVPR), pages 1–6.

Argyriou, V., Zafeiriou, S., Villarini, B., and Petrou, M.

(2013). A sparse representation method for determin-

ing the optimal illumination directions in Photometric

Stereo. Signal Processing, 93(11):3027–3038.

Baillard, C., Schmid, C., Zisserman, A., and Fitzgibbon,

A. (1999). Automatic line matching and 3d recon-

struction of buildings from multiple views. In ISPRS

Conference on Automatic Extraction of GIS Objects

from Digital Imagery, volume 32, Part 3-2W5, pages

69–80.

Barron, J. and Malik, J. (2013). Shape, Illumination,

and Reﬂectance from Shading. Technical Report

UCB/EECS-2013-117, EECS, UC Berkeley.

Barsky, S. and Petrou, M. (2003). The 4-source photomet-

ric stereo technique for three-dimensional surfaces in

the presence of highlights and shadows. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

25(10):1239–1252.

Barsky, S. and Petrou, M. (2006). Design Issues for a

Colour Photometric Stereo System. Journal of Math-

ematical Imaging and Vision, 24(1):143–162.

Bay, H., Ess, A., Tuytelaars, T., and Van Gool, L. (2008).

Speeded-up robust features (SURF). Computer Vision

and Image Understanding, 110(3):346–359.

Bors, A., Hancock, E., and Wilson, R. (2003). Terrain anal-

ysis using radar shape-from-shading. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

25(8):974–992.

Coleman Jr., North, E. and Jain, R. (1982). Obtaining 3-

dimensional shape of textured and specular surfaces

using four-source photometry. Computer Graphics

and Image Processing, 18(4):309 – 328.

Durou, J., Falcone, M., and Sagona, M. (2008). Numeri-

cal Methods for Shape-from-shading: A New Survey

with Benchmarks. Computer Vision and Image Un-

derstanding, 109(1):22–43.

Eisert, P., Steinbach, E., and Girod, B. (1999). Multihy-

pothesis volumetric reconstruction of 3-d objects from

multiple calibrated camera views. In Proceedings of

International Conference on Acoustics, Speech, and

Signal Processing (ICASSP), pages 3509–3512.

Fischler, M. and Bolles, R. (1981). Random Sample Con-

sensus: A Paradigm for Model Fitting with Applica-

tions to Image Analysis and Automated Cartography.

Communications of the ACM, 24(6):381–395.

Frankot, R. and Chellappa, R. (1988). A method for enforc-

ing integrability in shape from shading algorithms.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 10(4):439–451.

Geiger, A., Ziegler, J., and Stiller, C. (2011). StereoScan:

Dense 3d reconstruction in real-time. In Intelligent

Vehicles Symposium (IV), pages 963–968.

Hamilton, W. (1844). On quaternions, or on a new system

of imaginaries in algebra. Philosophical Magazine,

25(3):489–495.

Horn, B. K. (1970). Shape from Shading: A method for

obtaining the shape of a smooth opaque object from

one view. Technical report, MIT.

Kim, N., Yoo, S., and Lee, K. (2003). Polygon reduction of

3D objects using Stokes’ theorem. Computer Methods

and Programs in Biomedicine, 71(3):203–210.

Kim, S.-I. and Li, R. (2006). Complete 3D surface re-

construction from unstructured point cloud. Journal

of Mechanical Science and Technology, 20(12):2034–

2042.

Kolluri, R., Shewchuk, J., and O’Brien, J. (2004). Spec-

tral Surface Reconstruction from Noisy Point Clouds.

In Symposium on Geometry Processing, pages 11–21.

ACM Press.

Kordelas, G., Perez-Moneo Agapito, J. D., Vegas Hernan-

dez, J. M., and Daras, P. (2010). State-of-the-art Al-

gorithms for Complete 3D Model Reconstruction. In

Summer School ENGAGE-Immersive and Engaging

Interaction with VH on Internet.

Lourakis, M. and Argyros, A. (2009). SBA: a software

package for generic sparse bundle adjustment. ACM

Transactions on Mathematical Software, 36(1):1–30.

Lowe, D. (2004). Distinctive image features from scale in-

variant keypoints. International Journal of Computer

Vision, 60(2):91–110.

MacQueen, J. (1967). Some Methods for classiﬁcation

and Analysis of Multivariate Observations. In Pro-

ceedings of 5th Berkeley Symposium on Mathematical

Statistics and Probability, pages 281–297. University

of California Press.

Makantasis, K., Doulamis, A., Doulamis, N., and Ioan-

nides, M. (2014). In the wild image retrieval and clus-

tering for 3D cultural heritage landmarks reconstruc-

tion. Multimedia Tools and Applications, pages 1–37.

Nayar, S., Ikeuchi, K., and Kanade, T. (1990). Determin-

ing shape and reﬂectance of hybrid surfaces by photo-

metric sampling. IEEE Transactions on Robotics and

Automation, 6(4):418–431.

Petrou, M. and Barsky, S. (2001). Shadows and highlights

detection in 4-source colour photometric stereo. In

International Conference on Image Processing, vol-

ume 3, pages 967–970.

Seitz, S. and Dyer, C. (1997). Photorealistic scene re-

construction by voxel coloring. In IEEE Conference

on Computer Vision and Pattern Recognition (CVPR),

pages 1067–1073.

Woodham, R. (1980). Photometric Method For Determin-

ing Surface Orientation From Multiple Images. Opti-

cal Engineering, 19(1):139–144.

Zhang, R., Tsai, P., Cryer, J., and Shah, M. (1999). Shape

from Shading: A Survey. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 21(8):690–

706.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

602