
Experimental Modal Analysis based on a Gray-box Model of Flexible
Structures
Alberto Cavallo
1
, Giuseppe De Maria
1
, Michele Iadevaia
2
, Ciro Natale
1
and Salvatore Pirozzi
1
1
Seconda Universit`a di Napoli, Dip. di Ingegneria Industriale e dell’Informazione, Via Roma 29, 81031 Aversa, Italy
2
Dynamic Design Solutions (DDS) NV, Leuven, Belgium
Keywords:
Experimental Modal Analysis, Subspace Identification, Flexible Structures.
Abstract:
The main objective of this paper is to propose an experimental modal analysis procedure, based on the use of
a gray-box model for flexible structures. The described approach presents interesting advantages with respect
to commercial solutions: ease of use due to the low number of parameters to set for an identification session;
no need for expert users, even in the presence of particular cases such as double modes, since it does not use
a stabilization diagram to be elaborated; use of a gray-box model whose unknown parameters have a clear
physical meaning. All these characteristics are discussed in the paper, and the performance of the proposed
procedure has been evaluated by using experimental data available from a non-trivial standard benchmark.
The results have been compared with those obtained by using a commercial tool.
1 INTRODUCTION
Experimental modal analysis has become a key tech-
nology in structural dynamic analysis and in mechan-
ical products development. Modal analysis is the pro-
cess of extracting the dynamics characteristics of a vi-
brating system from experimental data (Ewins, 1984).
When all of these parameters have been obtained, a
complete mathematical model of the system can be
defined. The mathematical model may then be used
in computer simulations to predict the response of the
system when it is modified, so that a designer can
evaluate different design modifications without build-
ing prototypes (Ewins, 1984; Heylen et al., 1995) or
to design an active vibration and noise control for a
flexible structure (Cavallo et al., 2008; Cavallo et al.,
2010).
This paper presents a new frequency domain pro-
cedure for experimental modal analysis, based on the
use of a gray-box model of flexible structures. The
main objective of the paper is to show how, with the
proposed approach, it is possible to obtain experimen-
tal results similar to those obtained with the commer-
cial solutions, but with some advantages in terms of
experience required to the user and physical mean-
ing of the model unknown parameters. The procedure
uses the results of the identification method proposed
in (Cavallo et al., 2007). Differently from (Cavallo
et al., 2007), where the identification procedure was
developed only for model-based control applications,
in this paper for the first time the same procedure has
been adapted, as regards the estimation of the mode
shapes, for experimental modal analysis. The pro-
posed procedure is compared with the polyreference
Least Squares Complex Frequency domain method
(pLSCF) (Guillaume et al., 2003). The comparison
is made with this algorithm since the pLSCF is one of
newest approach presented in literature and moreover
there are some papers in which the pLSCF is com-
pared with the others classical methods (Guillaume
et al., 2003; Peeters et al., 2004), obtaining an indirect
comparison also with these last ones. The pLSCF al-
gorithm has been applied by using the modal analysis
estimator module integrated in the commercial soft-
ware FEMtools
TM
(FEMtools Version 3.6, 2012).
The proposed procedure, similarly to the pLSCF
method, separates the estimation of the system poles
from the mode shapes. However, the pLSCF method
uses a polynomial form and generally it starts with a
model order very high, trying to fit models that con-
tain much more modes than those actually present in
the experimental data. Then, the true physical modes
are separated from the spurious ones by interpret-
ing the so-called ”stabilization diagram” by an expert
user. The poles corresponding to a certain model or-
der are compared to the poles of a one order lower
model and if their differences are minor than pre-set
limits, the pole is labelled as a stable one. The spu-
439
Cavallo A., De Maria G., Iadevaia M., Natale C. and Pirozzi S..
Experimental Modal Analysis based on a Gray-box Model of Flexible Structures.
DOI: 10.5220/0005504304390447
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 439-447
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

rious poles will not be stable during this comparison
and will be sorted out of the modal parameters. Fi-
nally, an eigenvalue decomposition of the companion
matrix, associated with the polynomial coefficients
identified, is implemented to compute the real modal
parameters (Guillaume et al., 2003). The number of
parameters to set by the user before starting the op-
timization procedure is high and can lead to wrong
results if the user experience is not adequate.
Differently from the commercial solutions, the
procedure here proposed estimates the eigenvalues by
using a subspace approach, and the user is required
only to fix the number of modes to identify and to
select the frequency range in which to perform the
identification. Spurious modes outside the frequency
range of interest are not extracted. Moreover, the pro-
posed approach does not use a stabilization diagram
to select stable poles in the selected frequency range,
since the stability of the estimated poles is guaran-
teed by the identification procedure of the dynamic
matrix detailed in (Cavallo et al., 2007). As a conse-
quence, the interaction of an expert user is not nec-
essary, even in the presence of particular cases such
as double modes. This feature makes the proposed
approach very interesting to be automated for applica-
tions where iterative modal analysis is necessary (e.g.,
health monitoring, model-based control, optimal po-
sitioning of actuators and sensors for control).
Another advantage of the proposed procedure is
the use of a gray-box model whose unknown param-
eters have a clear physical meaning. In particular, for
all the applications where a numerical–experimental
correlation between a finite element model and exper-
imental data is necessary, the use of a gray-box model
can simplify the user task of tuning the numeric pa-
rameters in order to match the experimental data.
2 MODELLING OF FLEXIBLE
STRUCTURES
Consider a n−degree-of-freedom mechanical system
whose generalized coordinates are represented by a
n× 1 vector q and with n×n mass matrix M and stiff-
ness matrix K; both matrices are positive definite and
symmetric. The equation of motion can be written in
the form (Cavallo et al., 2010)
M ¨q+ Kq = f (1)
where f is the n× 1 vector of generalized forces. It is
evident that the state of this dynamic system is con-
stituted by the 2n × 1 vector z = (q
T
˙q
T
)
T
. With this
choice, the state space representation of the system is
˙z =
0 I
−M
−1
K 0
z+
0
M
−1
u
y = (0 I)z
if the observed output is the velocity ˙q. Since the ma-
trix M
−1
K have all real and positive eigenvalues, it
can be diagonalized by solving the following eigen-
value problem
M
−1
KU = UΩ (2)
where Ω = diag{ω
2
n
1
,... ,ω
2
n
n
} is the diagonal matrix
of the eigenvaluesof M
−1
K andU is the matrix whose
columns are the eigenvectors of M
−1
K, the so-called
“mode shapes”. It is well-known that the eigenvectors
are orthogonal with respect to the mass matrix and
thus they can be normalized so as
U
T
MU = I (3)
Now, define the transformation in the state space
z =
U 0
0 U
x, (4)
where x are the so-called “modal coordinates”, and
consider a number m of input forces f
i
, i ∈ F ⊆
{1,. .. ,m} applied to the structure along a set of de-
grees of freedom, so that, defining the unit vector e
i
as the vector with 1 at entry i and 0 elsewhere, a se-
lection matrix S can be defined whose rows are e
T
i
,
i ∈ F . Assuming to observe the velocity along the
same degrees of freedom, the state space representa-
tion assumes the form
˙x = Ax + Bu =
0 I
−Ω −Λ
x+
0
U
T
S
T
f (5)
y = Cx = (0 SU)x (6)
where the diagonal matrix Λ =
diag{2ζ
1
ω
n
1
,... ,2ζ
n
ω
n
n
}, being ζ
i
∈ (0,1) the
damping coefficient of the i−th mode, has been
introduced to take into account the unavoidable
damping present in the physical system. Notice, that
this corresponds to add in Eq. (1) the friction forces
d = D ˙q acting in the material, with a proportional
damping matrix D = α
1
K + α
2
M. This choice to add
a proportional damping in the model Eq. (1) changes
the finite-dimensional, complex eigenvalue problem.
In particular, the solution yields n pairs of complex
conjugate eigenvalues, named “modes”
λ
i
= −ζ
i
ω
n
i
± jω
n
i
q
1− ζ
2
i
i = 1, ...,n (7)
where λ
i
is the i−th complex eigenvalue of the struc-
ture. The Eq. (7) represents the relation between the
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
440

complex eigenvalue, the damping coefficient ζ
i
and
the natural frequency ω
n
i
of the i−th mode.
Furthermore, this choice for the viscous damping
has also the following implications: it does not affect
the mode shapes that are the eigenvectors (ψ
i
∈ C
n
)
of the matrix M
−1
K; the mode shapes are real and or-
thonormal; each mode shape is described by a stand-
ing wave that contains fixed stationary node points.
In contrast, if the matrix D is not representative of a
proportional damping, the mode shape are complex
valued and results in modes, which are described as
complex modes, having different characteristics; each
mode shape is described by a travelling wave and ap-
pears to contain a moving node point on the struc-
ture; in such a case, the mode shape from the un-
damped case does not diagonalise the damping matrix
D. Since in the typical case of experimental modal
analysis the available data are Frequency Response
Functions (FRFs), also the relations between the gray-
box model and the FRFs data are useful. In particu-
lar, applying the Fourier transform, the frequency re-
sponse matrix corresponding to the model (5)–(6), is
symmetric and has the form
G( jω) = UΦ( jω)U
T
(8)
with Φ( jω) = diag{φ
1
( jω),. .. , φ
n
( jω)} and
φ
l
( jω) = jω/(ω
2
n
l
− ω
2
+ j2ζ
l
ω
n
l
ω), l = 1,. .., n
and thus for an applied force at a spatial position k
(as input) and a velocity measurement at a spatial
position h (as output), the FRF g
hk
( jω) in physical
coordinates is
g
hk
( jω) =
n
∑
l=1
φ
l
( jω)ψ
h
l
ψ
k
l
(9)
where ψ
h
l
is the h-th column of the matrix U of the
mode shape corresponding to the l-th mode.
3 MODAL PARAMETERS
ESTIMATION
The objective of experimental modal analysis (Ewins,
1984) is to derive natural frequencies and damping
coefficients as well as mode shapes. In the proposed
approach, the unknown parameters to identify are ex-
plicitly present in the gray-box model reported in
Eqs. (5)–(6) and used in the identification procedure.
Note that if the number of excitation inputs is differ-
ent from the number of measured outputs, the selec-
tion matrix in Eq. (5) is different from the one in the
Eq. (6). In particular, if the number of inputs is equal
to m and the number of outputs is p (p > m is the typi-
cal case of experimental modal analysis) the gray-box
model can be rewritten as
˙x =
0 I
−Ω −Λ
x+
0
B
2
u (10)
y =
0 C
2
x (11)
where Λ,Ω ∈ R
n×n
, B
2
∈ R
n×m
and C
2
∈ R
p×n
have
to be estimated. With this choice, the rows of B
2
represent spatial samples of the mode shapes corre-
sponding to excitation points, while the columns of
C
2
represent spatial samples of the mode shapes cor-
responding to measurement points.
All the parameters to be identified for the
model (10)–(11) can be estimated by using the pro-
cedure detailed by the same authors in (Cavallo et al.,
2007). The only choices that the user has to do, as dis-
cussed in the introduction, are: to select the frequency
range in which to perform the identification and to fix
the number of modes to identify.
The selection of the working frequency range
[ f
1
, f
2
]Hz, in which to extract the modes of interest,
has to take into account that the real system is infi-
nite dimensional. In fact, for flexible structures the
FRFs in a given frequency range depend not only on
the modes with natural frequencies within the con-
sidered range but also on the lower and higher fre-
quency modes. This means that near the extremes
of the range the experimental data are not sufficient
for an accurate identification of modal parameters and
thus the FRFs should be measured on a working fre-
quency range [ f
′
1
, f
′
2
]Hz wider than the interesting one
[ f
′
1
, f
′
2
] ⊃ [ f
1
, f
2
]. Fixed the frequency range, denote
with G
i
∈ C
p×m
, i = 1, .. .,M the experimentalmea-
sured samples of the frequency response matrix in the
frequency range [ f
′
1
, f
′
2
]Hz (not necessarily uniformly
spaced). The choice of M depends on the modal
density of the flexible structure and obviously on the
width of the frequency range of interest. The num-
ber of the modes to be identified (n) can be fixed on
the basis of a classical indicator used in experimental
modal analysis (Ewins, 1984), i.e.
H(ω
i
) =
p
∑
h=1
m
∑
k=1
|g
hk
( jω
i
)|, i = 1,. .., M (12)
by counting (approximately and lightly overestimat-
ing) its number of peaks by simple inspection.
By following the procedure in (Cavallo et al.,
2007), in a first step, the M measured samples of the
FRFs are used to construct the matrices detailed in
the cited paper, from which, via a subspace identifica-
tion technique, the eigenvalues of the dynamic matrix
A are estimated. At the end of this step, the n fixed
modes are completely estimated in terms of natural
frequencies and damping ratios. The second stage
consists in determining an estimate of B
2
and C
2
. In
ExperimentalModalAnalysisbasedonaGray-boxModelofFlexibleStructures
441

particular, in view of (9), the frequency response ma-
trix can be written as
G( jω) =
n
∑
l=1
φ
l
( jω)c
l
b
T
l
=
n
∑
l=1
φ
l
( jω)R
l
(13)
where R
l
= c
l
b
T
l
∈ R
p×m
is the residue matrix corre-
sponding to the l-th mode, with c
l
and b
T
l
the l-th col-
umn of C
2
and the l-th row of B
2
, respectively. From
Eq. (13) it is evident that the unknown parameters R
l
can be easily computed by resorting to a least mean
square technique, being G( jω) the measured data and
the generic φ
l
( jω) known from the first step. From
the estimated R
l
residues it is possible to construct the
matrices B
2
and C
2
in different ways. The interested
reader can refer to (Cavallo et al., 2007) and (Cavallo
et al., 2010) for more details. For the experimental
modal analysis, objective of this paper, the estima-
tion of residues is sufficient. In fact, the estimated
residues allows an easy estimation of the so called
modal constants from which any normalization can
be chosen to estimate the mode shapes (details can be
found in any textbook on experimental modal analy-
sis, e.g., (Ewins, 1984; Heylen et al., 1995)). Recall-
ing that the modal constants are the constant matrices
A
l
appearing in the following decomposition of the
FRF matrix
G( jω)=
n
∑
l=1
φ
l
( jω)R
l
= jω
n
∑
l=1
A
l
jω − λ
l
+
A
∗
l
jω − λ
∗
l
,
(14)
it is straightforward to see that the modal constants
are related to the residues as
A
l
=
1
2jω
n
l
q
1− ζ
2
l
R
l
. (15)
Equation (15) shows the classical property that modal
constants are purely imaginary for flexible structures
exhibiting only stationary waves. For the evaluation
of the experimental results in the remainder of the pa-
per, the normalization selected to compute the nor-
malized mode shape from the modal constant, corre-
sponding to the l-th mode, is
φ
l
=
Im(A
l
)
max|(A
l
)|
. (16)
4 EXPERIMENTAL RESULTS
The proposed approach for the experimental modal
analysis has been tested by using data for the Modal
Parameter Estimation (MPE) Round Robin. This
round robin is an initiative of the Michigan State
Technical University (MTU) and was presented at the
Figure 1: Lumped parameter model used to generate cali-
bration data set for IMAC MPE Round Robin.
recent IMAC XXIX conference. More than twenty
participants from several countries has taken part in
the exercise, performed on simulated and experimen-
tal data. The data are available for research activities
on the web (IMAC website, 2011). In particular, the
calibration data set with proportional damping and the
experimental data of the plexiglass plate available on-
line have been considered for this work. For each data
set a comparison with the FEMtools
TM
commercial
solution is also presented.
4.1 The Calibration Data
The calibration data sets, available from IMAC MPE
Round Robin, were generated using a lumped pa-
rameters model, constituted by 6 masses, 10 springs
and 10 dampers. The details about the model are re-
ported in Fig. 1 (see also the web site (IMAC website,
2011)). As detailed above, the proposed approach is
based on a gray-box model with proportional damp-
ing. According to this hypothesis, the data set with
D = 0.0001K + 0.05M has been selected. As de-
scribed above, the only choice, that the proposed ap-
proach asks the user, is to set the number n of modes
to identify. For a lumped parameter model the num-
ber of mode is finite, and in particular is n = 6 for
the selected model. With this choice of n, the pro-
posed approach has been applied, starting from the
FRF samples of the considered calibration data set, to
estimate the modal parameters of the lumped param-
eter model. The results are reported in Table 1, where
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
442

Table 1: Calibration data with proportional damping: modes extracted by using the proposed approach.
Mode # ω
a
n
[Hz] ω
e
n
[Hz] E
ω
n
[%] ζ
a
[%] ζ
e
[%] E
ζ
[%] MAC
1
alias [%] MAC
2
[%]
1 3.395 3.506 3.269 0.224 0.224 0 3.25 99.67
2 5.238 5.493 4.868 0.240 0.245 2.083 2.72 98.13
3 6.423 6.427 0.062 0.264 0.264 0 3.05 99.84
4 7.547 7.552 0.066 0.290 0.290 0 0.51 99.86
5 8.305 8.388 0.999 0.309 0.311 0.647 3.25 98.78
6 12.639 12.641 0.016 0.428 0.429 0.234 1.03 99.98
the natural frequencies and the damping ratios of the
estimated modes are compared to the actual ones, an-
alytically obtained by the numeric matrices M, K and
D. The percentage errors for the estimated natural fre-
quencies have been quantified as
E
ω
n
=
|ω
a
n
− ω
e
n
|
ω
a
n
100, (17)
where ω
a
n
and ω
e
n
are the actual and the estimated val-
ues of the natural frequencies, respectively. Similarly,
for the damping ratios the following percentage error
has been evaluated
E
ζ
=
|ζ
a
− ζ
e
|
ζ
a
100, (18)
where ζ
a
and ζ
e
represent the actual and the estimated
values of the damping ratios, respectively. The re-
sults, reported in Table 1, show the good estimation
obtained for all the 6 modes of the considered model.
The percentage errors are always less than 5% and of-
ten less than 1%. For the mode shapes, the results
have been evaluated by using the classical Modal As-
surance Criterion (MAC). The MAC index between
two modes ψ
i
and ψ
j
is defined as:
MAC =
|ψ
H
i
ψ
j
|
2
(ψ
H
i
ψ
i
)(ψ
H
j
ψ
j
)
100, (19)
where the symbol (·)
H
indicates the transpose con-
jugate. The MAC index can be used to evaluate the
correlation between: two mode shapes of the same
estimated model; an estimated mode shape with the
corresponding actual mode shape; two corresponding
1
2
3
4
5
6
1
2
3
4
5
6
0
50
100
Mode #
Mode #
MAC [%]
Figure 2: Calibration data with proportional damping:
MAC
1
for the modes extracted with the proposed approach.
mode shapes estimated by using two different proce-
dures. Based on this observations, the first signifi-
cant analysis is the evaluation of the correlation be-
tween the mode shapes of the estimated model. In
particular, since the mode shapes define an orthogo-
nal basis, they are uncorrelated and the correspond-
ing MAC value should be zero. As a consequence,
computing the MAC values for a set of mode shapes
of the same model should, in theory, provide a diag-
onal matrix, i.e. diagonal elements with a value of
100 and zero-valued off-diagonal elements. Hence,
the MAC
1
index values have been computed by using
Eq. (19), where ψ
i
and ψ
j
(with i, j = 1, .. .,6) are the
normalized mode shape obtained from Eq. (16). The
results are reported in Fig. 2, where the off-diagonal
elements are clearly very low. The maximum MAC
1
alias, which is the highest off-diagonal value for the
considered modes, is reported in Table 1 to simplify
its evaluation. The comparison of the estimated mode
shapes with the actual ones, analytically obtained by
the numeric matrices M, K and D, has been carried
out by computing the MAC
2
index values by using
Eq. (19). In particular, the correlation between the es-
timated ψ
i
and the corresponding actual ψ
j
normal-
ized mode shapes (with i = j = 1, ...,6) has been
computed for the 6 modes of the considered model.
The excellent results are reported in the last column
of Table 1. In order to better appreciate the results
obtained with the proposed approach, the MPE has
been also carried out by using the commercial solu-
tion FEMtools
TM
. The same calibration data have
been used to implement the same analysis. Hence, the
same experimental results are reported to allow a fair
1
2
3
4
5
6
1
2
3
4
5
6
0
50
100
Mode #
Mode #
MAC [%]
Figure 3: Calibration data with proportional damping:
MAC
1
for the modes extracted by using FEMtools.
ExperimentalModalAnalysisbasedonaGray-boxModelofFlexibleStructures
443

Table 2: Calibration data with proportional damping: modes extracted by using FEMtools.
Mode # ω
a
n
[Hz] ω
e
n
[Hz] E
ω
n
[%] ζ
a
[%] ζ
e
[%] E
ζ
[%] MAC
1
alias [%] MAC
2
[%]
1 3.395 3.506 3.269 0.224 0.224 0 3.21 99.67
2 5.238 5.493 4.868 0.240 0.245 2.083 2.69 98.14
3 6.423 6.427 0.062 0.264 0.264 0 3.06 99.84
4 7.547 7.552 0.066 0.290 0.290 0 0.49 99.86
5 8.305 8.388 0.999 0.309 0.311 0.647 3.21 98.78
6 12.639 12.641 0.016 0.428 0.428 0 1.00 99.99
comparison. The estimated natural frequencies and
damping ratios have been compared with the actual
ones and the mode shapes have been evaluated by us-
ing the MAC indices. The corresponding results are
reported in Table 2 and Fig. 3. The obtained results
are practically identical. These results, obtained in a
standard benchmark, allow to conclude that the pro-
posed method is technically sound and with the same
performance of a well assessed method, but with the
advantage that the number of parameters to set for an
identification procedure is lower than a commercial
solution since this procedure does not use a stabiliza-
tion diagram.
4.2 The Plexiglass Plate
The plexiglass plate data, available from IMAC MPE
Round Robin, were acquired from a plexiglas plate
that measures 53 × 32× 1.5cm. The plexiglass mate-
rial has been chosen in order to obtain high damped
modes. The plate has been designed to have a dou-
ble mode at the first resonance peak in order to obtain
non-trivial experimental data. The identification of
these double mode is the greater difficulty on which
to assess the performance of the proposed approach.
The plate was tested in a free-free boundary condi-
tion. The measurements were made by using triaxial
accelerometers, mounted with the wax and a random
excitation signal as source. Hence, the available FRF
data have accelerations as outputs and forces as in-
puts. Since the proposed approach uses a gray-box
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
50
100
Mode #
Mode #
MAC [%]
Figure 4: Plexiglass plate data: MAC
1
for the modes ex-
tracted by using the proposed approach.
model with velocities as outputs, a preliminary divi-
sion by jω has been applied to the data in order to
compute the necessary FRF samples. The proposed
approach has been applied by fixing the number of
modes n = 20, by using the indicator in Eq. (12). The
first 10 extracted modes are reported in Table 3. In
particular the natural frequencies and the damping ra-
tios are reported in the first two columns. Concerning
the mode shapes, as made for the calibration data, the
MAC
1
index has been evaluated for the 10 identified
modes and the results are reported in Fig. 4, while the
MAC
1
alias values are reported in the 4-th column of
the Table 3. In this case, since no actual values are
available, only a comparison with the results carried
out by using FEMtools is possible. The results about
the first 10 modes extracted with the commercial tool
are reported in Table 4 and in Fig. 5. In this experi-
mental case, the differences between the proposed ap-
proach and the commercial solution are very low, in
terms of natural frequencies and damping ratios for
the extracted modes. Concerning the mode shapes,
separate discussions for the first two modes, that rep-
resent the double mode, and the remaining ones have
to be done. In particular, Fig. 4 shows that the mode
shapes associated to the first two modes, evaluated
by using the proposed approach, are clearly two dis-
tinct modes, since the MAC
1
index between mode 1
and mode 2 is about 7%. Instead, from Fig. 5, it is
evident that the first two modes, evaluated by using
FEMtools, are more similar to each other, showing a
MAC
1
index between them of about 28%. For the re-
Table 3: Plexiglass plate: first 10 modes extracted by using
the proposed approach.
Mode # ω
e
n
[Hz] ζ
e
[%] MAC
1
alias [%] MAC
3
[%]
1 99.660 4.85 7.8 69.23
2 99.717 6.07 14.7 71.25
3 226.792 3.66 10.7 97.88
4 279.570 3.53 3.3 92.30
5 291.574 3.48 8.5 94.30
6 356.267 3.25 8.6 96.77
7 417.760 3.36 14.7 93.81
8 502.296 3.03 25.9 82.95
9 569.037 3.01 11.2 88.72
10 667.035 4.07 34.34 56.10
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
444

1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
0
50
100
Mode #
Mode #
MAC [%]
Figure 5: Plexiglass plate data: MAC
1
for the modes ex-
tracted by using FEMtools.
maining modes, the differences between the proposed
approach and FEMtools in terms of MAC
1
and MAC
1
alias, are not significant since the MAC index values
are sometimes in favor of the proposed approach and
other in favor of the commercial tool, but always suf-
ficiently low. It is important to remark that the ex-
traction of the double mode, by using FEMtools, has
required iterated attempts by an expert user. With-
out the expertise there is the risk of confusing, dur-
ing the identification procedure, the double mode with
a simple mode. On the contrary, with the proposed
approach, there are not differences due to the pres-
ence/absence of double modes. An additional MAC
3
index has been computed by using Eq. (19) to evaluate
the correlation between the ψ
i
and the corresponding
ψ
j
normalized mode shapes (with i = j = 1,. ..,10),
estimated with the proposed approach and the com-
mercial tool, respectively. These correlation index
values, computed for the first estimated 10 modes, are
reported in the last column of the Table 3. The results
show that the mode shapes #1, #2 and #10 have dis-
crete differences.
To further highlight the quality of the results
obtained, the spatial reconstruction of some mode
shapes are reported, both for the proposed approach
Table 4: Plexiglass plate: first 10 modes extracted by using
FEMtools.
Mode # ω
e
n
[Hz] ζ
e
[%] MAC
1
alias [%]
1 99.917 4.53 28.18
2 100.130 4.80 28.18
3 226.633 3.71 12.2
4 279.301 3.70 28.2
5 290.900 3.44 6.1
6 355.853 3.40 34.3
7 417.651 3.24 35.1
8 503.163 3.25 4.5
9 568.682 2.93 10.1
10 672.990 3.17 23.3
0
0.1
0.2
0.3
0.4
0
0.1
0.2
−2
−1
0
1
2
x [m]
y [m]
normalized z
−1
−0.5
0
0.5
1
Figure 6: Plexiglass plate data: normalized mode shape
at 99.660 Hz (Mode #1), estimated with the proposed ap-
proach.
and the commercial solution. First off all, the mode
shapes associated to the double mode are reported,
since they represent the more interesting problem for
the considered experimental data. In particular, Fig. 6
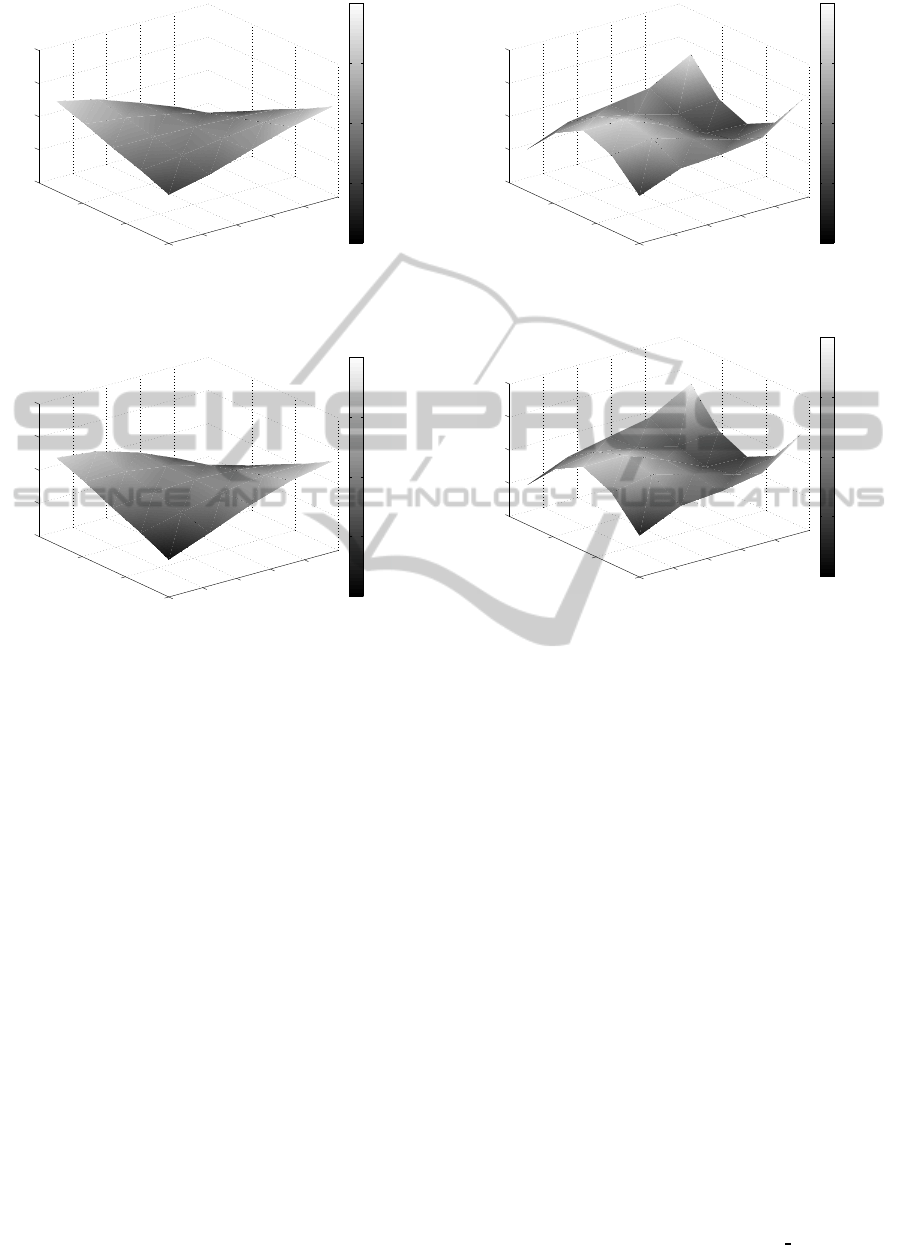
and 8 reports the normalized mode shapes for the dou-
ble mode, obtained with the proposed approach, while
Fig. 7 and 9 the corresponding mode shapes, obtained
with FEMtools
TM
.
An additional mode shape for the remaining
modes is reported for completeness of the work. In
particular, Fig. 10 and 11 show the normalized mode
shapes corresponding to mode #6. From the MAC in-
dex values reported in previous tables it is evident that
the quality of all other modes is very similar to that of
the mode #6 here plotted.
5 CONCLUSIONS
In this paper an experimental modal analysis, based
on the use of a gray-box model, has been presented.
A first advantage of the proposed approach is the low
number of parameters needed to be set: the user is
required only to fix the number of modes to identify
0
0.1
0.2
0.3
0.4
0
0.1
0.2
−2
−1
0
1
2
x [m]
y [m]
normalized z
−1
−0.5
0
0.5
1
Figure 7: Plexiglass plate data: normalized mode shape at
99.917 Hz (Mode #1), estimated by using FEMtools.
ExperimentalModalAnalysisbasedonaGray-boxModelofFlexibleStructures
445
0
0.1
0.2
0.3
0.4
0
0.1
0.2
−2
−1
0
1
2
x [m]
y [m]
normalized z
−1
−0.5
0
0.5
1
Figure 8: Plexiglass plate data: normalized mode shape at
99.717 Hz (Mode #2), estimated by using the proposed ap-
proach.
0
0.1
0.2
0.3
0.4
0
0.1
0.2
−2
−1
0
1
2
x [m]
y [m]
normalized z
−1
−0.5
0
0.5
1
Figure 9: Plexiglass plate data: normalized mode shape at
100.130 Hz (Mode #2), estimated by using FEMtools.
and to select the frequency range in which to perform
the identification. Moreover, the proposed approach
does not use a stabilization diagram to select stable
poles in the selected frequency range and, as a con-
sequence, the interaction of an expert user is not nec-
essary, even in the presence of particular cases such
as double modes. Another advantage of the proposed
procedure is the use of a gray-box model whose un-
known parameters have a clear physical meaning: for
all the applications where a numerical–experimental
correlation between a finite element model and exper-
imental data is necessary, the use of a gray-box model
can simplify the user task of tuning the numeric pa-
rameters in order to match the experimental measure-
ments. The experimental results, obtained in a stan-
dard benchmark, are practically identical to those ob-
tained with commercial solutions, with some advan-
tages for double mode identification. These results
allow to conclude that the proposed method is techni-
cally sound and with the same performance, of a well
assessed method, but with the advantages just summa-
rized. Future activities are planned in order to test the
proposed approach to more complex flexible systems.
0
0.1
0.2
0.3
0.4
0
0.1
0.2
−2
−1
0
1
2
x [m]
y [m]
normalized z
−1
−0.5
0
0.5
1
Figure 10: Plexiglass plate data: normalized mode shape at
356.267 Hz estimated by using the proposed approach.
0
0.1
0.2
0.3
0.4
0
0.1
0.2
−2
−1
0
1
2
x [m]
y [m]
normalized z
−1
−0.5
0
0.5
1
Figure 11: Plexiglass plate data: normalized mode shape at
355.853 Hz estimated by using FEMtools.
REFERENCES
Cavallo, A., De Maria, G., Natale, C., and Pirozzi, S.
(2007). Gray-box identification of continuous-time
models of flexible structures. IEEE Trans Contr Syst
Tech, 15:967–981.
Cavallo, A., De Maria, G., Natale, C., and Pirozzi, S.
(2008). Robust control of flexible structures with sta-
ble bandpass controllers. Automatica, 44:1251–1260.
Cavallo, A., De Maria, G., Natale, C., and Pirozzi, S.
(2010). Active Control of Flexible Structures–From
modelling to implementation. Springer, London.
Ewins, D. (1984). Modal Testing: Theory and Practice.
Research Studies Press LTD, Baldock.
FEMtools Version 3.6 (2012). Dynamic Design Solutions.
(www.femtools.com), Leuven, Belgium.
Guillaume, P., Verboven, P., Vanlanduit, S., Van der Auwer-
aer, H., and Peeters, B. (2003). A poly-reference im-
plementation of the least-squares complex frequency-
domain estimator. In Proc. of International Modal
Analysis Conference (IMAC XXI), Kissimmee, FL.
Heylen, W., Lammens, S., and Sas, P. (1995). Modal Anal-
ysis Theory and Testing. Department of Mecanical
Engineering, Katholike Universiteit Leuven, Leuven.
IMAC website (2011). www.me.mtu.edu/imac
mpe/. Modal
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
446

Parameter Estimation Round Robin, Int. Modal Anal-
ysis Conf. (IMAC XXIX), Jacksonville, FL.
Peeters, B., Guillaume, P., Van der Auweraer, H.,
Cauberghe, B., Verboven, P., and Leuridan, J. (2004).
Automotive and aerospace applications of the poly-
max modal parameter estimation method. In Int.
Modal Analysis Conf. (IMAC XXII), Dearborn, MI.
ExperimentalModalAnalysisbasedonaGray-boxModelofFlexibleStructures
447
