
A 2 Dimensional Dynamical Model of Asphalt-roller Interaction
during Vibratory Compaction
Syed Asif Imran
1
, Sesh Commuri
1
and Musharraf Zaman
2
1
School of Electrical and Computer Engineering, University of Oklahoma, W. Boyd St, Norman, Oklahoma, U.S.A.
2
School of Civil Engineering and Environmental Science, University of Oklahoma, W. Boyd St, Norman, Oklahoma, U.S.A.
Keywords: Intelligent Compaction, Vibration Analysis, Asphalt Pavements, Roller Dynamics, Construction Engineering.
Abstract: The quality and longevity of an asphalt pavement is influenced by several factors including, the design of the
mix and environmental factors at the time of compaction. These factors are difficult to control during the
construction process and often result in inadequate compaction of the pavement. Intelligent Compaction (IC)
technologies address this issue by providing continuous real-time estimation of the compaction level achieved
during construction. This information can then be used to address quality issues during construction and
improve the overall quality of the pavement. One of the goals of IC is the dynamic adjustment of the
compaction effort of the vibratory roller in order to achieve uniform density and stiffness of the pavement.
However, complex dynamics of the compaction process and lack of computationally tractable dynamical
models hamper the development of such controllers of vibratory rollers. In this study, the interaction between
the vibratory roller and the underlying pavement is studied. A two-dimensional lumped element model that
can replicate the compaction in the field is developed and its parameters are determined using the visco-elastic
plastic properties and the shear deformation properties of the asphalt mix. Numerical simulation results show
that the model is capable of capturing the coupled vibration dynamics of the asphalt-roller system in both the
vertical and longitudinal direction. Comparison of numerical studies with the field compaction data also
indicates that the model can be helpful in the development of control algorithms to improve the quality of
pavements during their construction.
1 INTRODUCTION
Asphalt pavements constitute an important part of the
transportation infrastructure. The long term
performance of these pavements depends largely on
the quality of compaction achieved during their
construction. Compaction is a process of reducing the
volume of air in hot mix asphalt (HMA) by using
external forces and vibrations to reorient the
constituent aggregate particles into a more closely
spaced arrangement. This reduction of air volume in
a mixture produces a corresponding increase in HMA
unit weight, or density. Several studies have indicated
compaction to be the greatest determining factor in
dense graded pavement performance (Brown, 1984;
Scherocman and Martenson, 1984). Proper and good
quality compaction increases the service life of
pavement by improving its load bearing capacity,
temperature stability and fatigue life.
The compaction of an asphalt pavement is influenced
by numerous factors related to the properties of
asphalt mixture, environmental effect and
construction process (Lenz, 2011). The mechanistic
properties of the asphalt mixture such as viscosity and
stiffness are largely affected by its temperature. The
volumetric properties such as gradation, size,
angularity of aggregates and chemical property of the
binder also affect the compaction. The environmental
factors include temperature and stiffness of the
underlying layer, ambient temperature, wind speed,
and solar radiation etc. Several construction related
factors such as rolling pattern, applied vibratory force
and speed of the roller, thickness of the lift being
compacted also play significant roles during
compaction process. Therefore any change in the
influential factors during construction can result in a
variation in the compaction characteristics of asphalt
pavement and can require different compaction effort
to achieve the same level of compaction everywhere.
In the traditional construction process, it is assumed
that the environmental and material properties do not
vary during compaction. Therefore, a roller operating
533
Asif Imran S., Commuri S. and Zaman M..
A 2 Dimensional Dynamical Model of Asphalt-roller Interaction during Vibratory Compaction.
DOI: 10.5220/0005536405330540
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 533-540
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

at constant speed and frequency is used during
compaction of the pavement along a pre-determined
path. However, material and environmental
variability results in non-uniform compaction of the
mix. Investigations carried out during field
compaction have shown as much as 2% variation in
density in locations less than a meter apart from each
other (Beainy et al., 2011). Intelligent Compaction
(IC) technologies attempt to address this variability in
compaction quality by providing continuous real-
time quality control by monitoring the level of
compaction of the pavement and adjusting the amount
of compaction energy applied by the roller in order to
obtain uniform density.
IC solutions have been developed by Original
Equipment Manufacturers (OEMs) with the goal of
providing real-time estimation of the level of
compaction (Arasteh, 2007; Briaud and Seo, 2003;
Rakawoski, 2008). However, these approaches were
hampered by limited understanding of the roller
dynamics and the lack of adequate mathematical
models and have met with limited success.
Several attempts have been made in recent years
to study the dynamical interaction between the roller
and the underlying material. Huerne (2004)
developed a constituent model of asphalt mixture
using critical state theory adopted from the soil
mechanics and used this model to study compaction
using a static roller. Koneru et al. (2008) developed a
constitutive model using a thermodynamic
framework to study the compaction of asphalt mixes.
In this method, the notion of multiple natural
configurations assumed by a body was used to
analyze compaction of asphalt mixes using laboratory
equipment. Masad et al (2010) used a
thermodynamics based nonlinear viscoelastic model
of the asphalt mix. A finite element based numerical
scheme was developed to simulate the response
during laboratory and field compaction. The
developed model was able to predict the influence of
material properties such as binder viscosity,
aggregate shape characteristics, and aggregate
gradation during the static compaction of asphalt
specimen. Chen (2011) formulated a Discrete element
Method based model of asphalt compaction taking
into account the viscoelastic property of the mix as
well as the slippage and interlocking of the aggregates
during compaction. While these results are
encouraging, significant work is still required to
develop a simple and computationally tractable
model to implement and study real-time closed loop
control algorithms.
Researchers have also studied analytical models
such as Maxwell, generalized Maxwell, Kelvin–
Voigt, generalized Kelvin, Huet–Sayegh, and Burger
models to represent asphalt pavement as a
combination of simple mechanical elements such as
spring and damper (Nillson et al., 2002; Pronk, 2005;
Xu and Solaimanian, 2009). These models are used
mostly to study the long term behavior of the
pavement under traffic loads. Their ability in
representing the pavement during field compaction is
not studied. Among the analytical models, Burger’s
model is simple and can represent the viscoelastic
behavior of an asphalt pavement (Liu and You, 2009;
Liu et al., 2009). Beainy et al. (2013) used Burger’s
model to represent the dynamical properties of
asphalt pavement in his model for studying the
asphalt-roller interaction during compaction. The
model captures the coupled dynamics of the static
vibratory interaction between the roller and asphalt
pavement in the direction normal to the surface of the
pavement. The movement of the roller along the
pavement and the vibration of the roller drum in the
longitudinal or lateral direction are not taken into
account. Imran et al. (2014) incorporated the motion
of roller to the Beainy’s model to demonstrate its
applicability in emulating the field compaction
process that uses a conventional rolling pattern. In
their study, the asphalt pavement was considered to
be a collection of small independent blocks of
Burger’s material. At any given time, the roller was
assumed to be interacting with one set of blocks. This
model also was limited to study the vibration in the
vertical direction only. The effect of shear resistance
of the asphalt pavement was not taken into account.
This paper extends the work of Imran et al. (2014) by
incorporating the effect of shear strength between the
adjacent blocks in the longitudinal direction. The
model is aimed to capture the dynamics of the
vibratory compaction in both the vertical and the
longitudinal direction.
2 DEVELOPMENT OF THE
MODEL
The work of Beainy et. al (2013) and Imran et. al
(2014) is extended in this study for the development
of a model that can represent the asphalt-roller
interaction during compaction process. In this model,
the vibratory roller drum and the underlying
pavement are considered to form a coupled system.
The roller is considered to be in continuous contact
with the asphalt pavement. The dynamics due to
bouncing or loss of contact is not taken into account.
The vibration dynamics in both the vertical and
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
534

longitudinal directions are studied. No lateral
movement due to vibration is considered.
The asphalt mat is assumed to be placed on top of
a rigid base. The pavement is modelled as a collection
of small blocks of Burger’s material placed in a grid
wise manner adjacent to each other. At any given
cycle of vibration the roller interacts with only one
block. The dimensions of each block depend on the
geometry of the drum and asphalt layer, and, the
velocity of the roller. Its height is equal to the
thickness of the pavement layer. The width
corresponds to the width of the drum. The length is
the distance the roller travels along the pavement
while making one impact. At the beginning of each
impact cycle the drum moves on top of a new block.
The interaction between the roller and the block
continues for one cycle of the vibration. Then in the
next cycle the roller moves to the next block (Figure
1). The blocks along the direction of roller motion
(longitudinal) are assumed to be connected to each
other through a spring indicating the shear stiffness of
the asphalt mat. The blocks in the lateral direction are
considered to be independent of one other. The
parameter values of each block are dependent on the
density and temperature of the block.
A vibratory roller uses a combination of static
forces (drum and frame weights) and impact force
(drum eccentric vibrations) to compress the asphalt
mix. The eccentric force is directly related to the mass
of the rotating weight and to the rotational speed. It
acts radially and can be expressed as
(1)
Where,
is the moment of the eccentric mass
and
is the angular frequency of rotation.
The eccentric force can be divided into two
components, a vertical force that acts normal to the
asphalt surface and a horizontal component that acts
tangentially to it. The vertical component of the
eccentric force is expressed as
sin
,
(2)
and the horizontal component is expressed as
cos
.
(3)
The coupling between the drum and the fame of the
roller is modelled as a parallel combination of a linear
spring and a linear dashpot element.
The underlying asphalt pavement is modelled as a
collection of blocks of Burger’s material arranged in
a grid wise manner. The Burger’s material
encompasses the viscoelastic, instantaneous and
permanent deformation experienced by the asphalt
mat during compaction. They are represented as a
combination of linear spring and damper elements
and shown in Figure 2.
Figure 1: Block representation of asphalt pavement.
Vertical Vibration
The total vertical deformation occurring in each (th)
block of the asphalt pavement due to stress
applied
by the roller consist of an instantaneous elastic
deformation ‘
’, a delayed viscoelastic deformation
‘
’, and a permanent deformation ‘
’. The
constitutive equation of the vertical strain can be
expressed as
(4)
Here,
and
indicate the stiffness of the spring
elements and,
and
indicate the damping
coefficient of the dampers used in the th asphalt
block.
, and
are constants that represent the
boundary conditions.
The interaction between the roller and the
underlying asphalt block due to the vertical
component of vibration can be formulated as follows.
Drum Vibration:
sin
(5)
Frame Vibration:
A2DimensionalDynamicalModelofAsphalt-rollerInteractionduringVibratoryCompaction
535
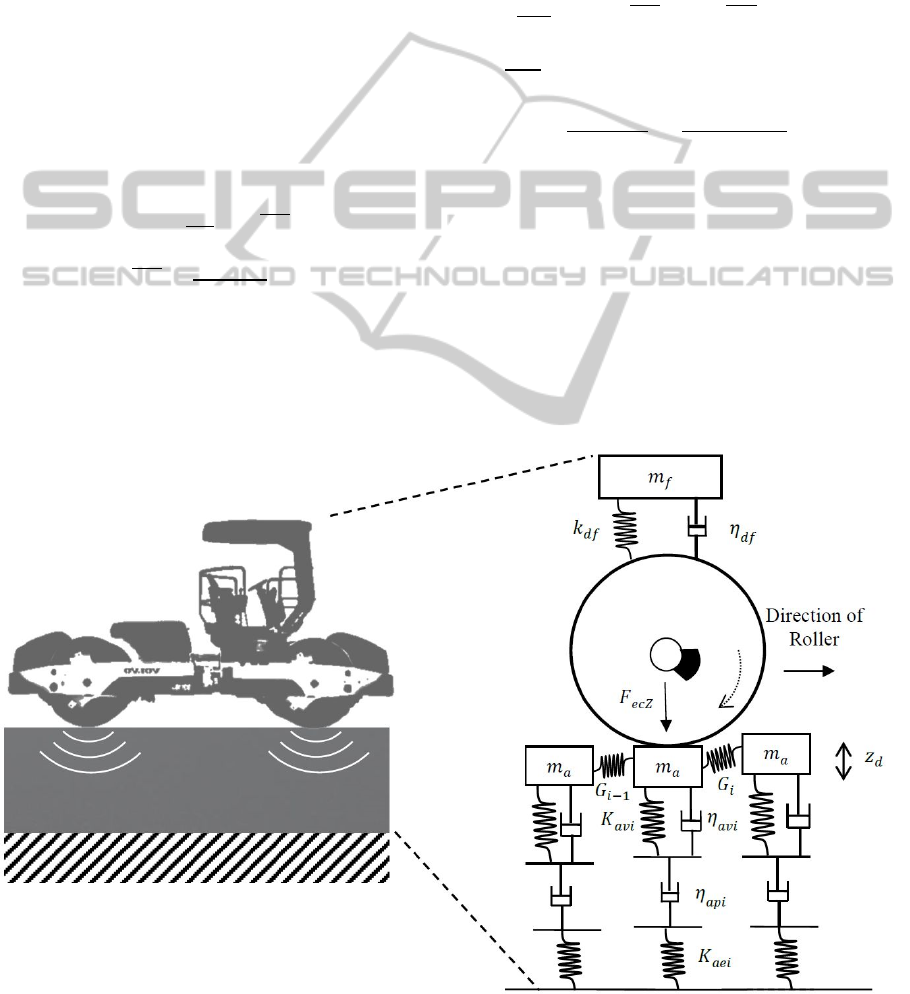
(6)
where
is the displacement of the asphalt layer;
is the vertical reaction force of the asphalt block;
is the reaction force due to shear component;
is
the displacement of the drum;
is the displacement
of the frame;
is the drum-frame stiffness
coefficient;
is the velocity of the drum;
is the
velocity of the frame;
is the drum-frame damping
coefficient;
is the asphalt weight;
is the vertical
acceleration of the drum;
is the vertical
acceleration of the asphalt block;
is the
acceleration of the frame.
The vertical reaction force of the asphalt block
is the force exerted by each block opposing the
compaction force of the roller. It can be expressed as
(7)
is the force generated by the shear spring
component
between the current block and the
block next to it and can be represented as,
(8)
Boundary Conditions:
In the th cycle of vibration, the shear spring
component will generate an equal amount of force
to the next block that will be compacted in the 1
th cycle. For simplicity of calculation, if we consider
to be a constant force in the th cycle, then, the
constants
and
can be determined as follows,
1
(9)
Horizontal Vibration:
The dynamics of interaction between the roller and
the asphalt mat in the longitudinal direction can be
formulated as
Figure 2: Interaction between vibratory roller and asphalt pavement in the vertical direction.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
536
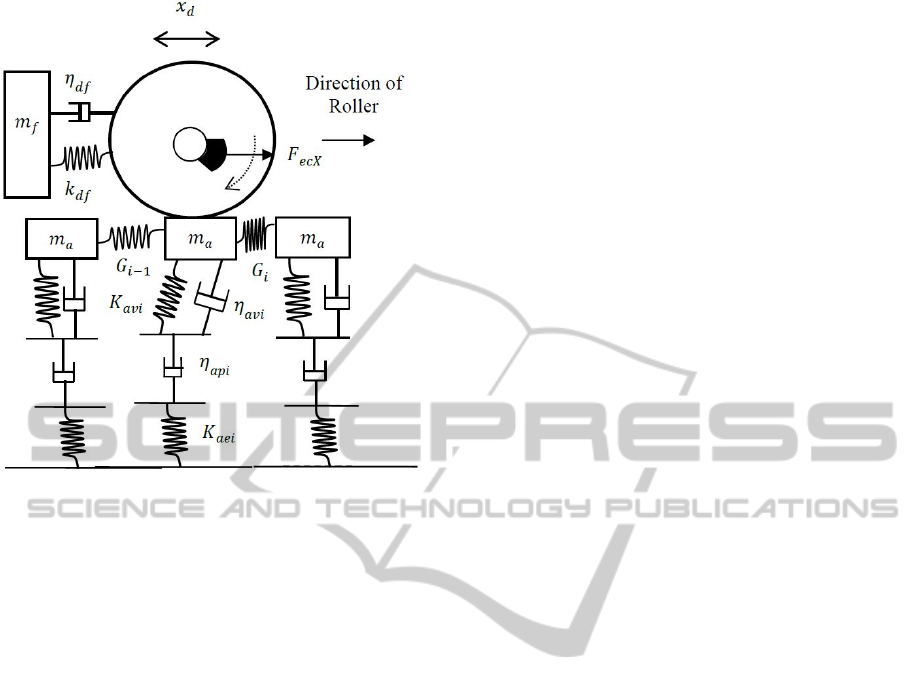
Figure 3: Asphalt-roller interaction in horizontal direction.
Drum Vibration:
cos
(10)
Frame Vibration:
(11)
Where,
,
and
are the displacement, velocity
and acceleration of the drum in the longitudinal
direction respectively.
,
and
are the
corresponding displacement, velocity and
acceleration of the frame.
3 MODEL PARAMETERS
The model parameters can be divided into two sets,
the asphalt material parameters and the roller
parameters. Asphalt material parameters mostly
include the stiffness and damping coefficients of the
Burger’s material. They are dependent on the type
and gradation of the mixture, type of the binder used,
temperature and air void contents of the pavement
during compaction. They also depend on the
dimension and velocity of the drum and the frequency
of vibration. A systematic procedure was developed
in previous studies to estimate these parameters from
the laboratory complex modulus test. A detailed
information regarding the estimation of these
parameters can be found elsewhere (Beainy et al.,
2013a; Imran et al., 2014). The parameters are
adjusted according to the dimension of each block.
The height of each block is equal to the depth of the
asphalt layer. Its length is equal to the length of the
drum and the width is assumed to be equal to the
distance the roller covers during one cycle of
vibration.
One important inclusion of this model from the
previous study (Imran et. al., 2014) is the
incorporation of shear component. Unfortunately,
due to limited resources, it was not possible to
estimate the shear stiffness as a function of asphalt
material properties for this research. However, it is
found in the literature is the shear modulus values are
approximately 30-40% of the dynamic modulus
values for asphalt cores (Pellinen and Xiao, 2006). In
this research, the shear stiffness is considered to be
30% of the Burger’s material stiffness at the
compaction temperature.
The roller parameters include mass of the drum
and frame, width and diameter of the drum, stiffness
coefficient and damping coefficient of drum-frame
coupling, rotational frequency of eccentrics and the
eccentric moment. These parameters can be
determined from some previous studies and the
manufacturer’s specifications of the roller.
4 NUMERICAL SIMULATION
Simulations are performed to study and evaluate the
ability of the model in replicating the field response.
The compaction of a 76.2 mm thick layer of asphalt
mix with a nominal maximum aggregate size of
12.5mm and PG 76 -28 binder is studied. An IR
DD118HF smooth drum vibratory roller is considered
for compaction of the asphalt mix. The roller is
assumed to be operating at a rated frequency of 56 Hz
and moving at a constant speed of 6.4km/h
throughout the simulation process. The compaction of
a single pass on the asphalt pavement with an initial
density of 90% of the maximum theoretical density is
simulated. The model is developed and simulated in
Matlab/Simulink environment for this study.
The parameters of the asphalt block depend on the
density and temperature of asphalt mix, as well as the
operating frequency of the roller. At each simulation
step, the roller operating frequency, the temperature
and air void content of the pavement for each block is
monitored and the parameter values are adjusted
accordingly. The temperature of the asphalt mix is
considered to be constant at 150
0
C during simulation.
A2DimensionalDynamicalModelofAsphalt-rollerInteractionduringVibratoryCompaction
537
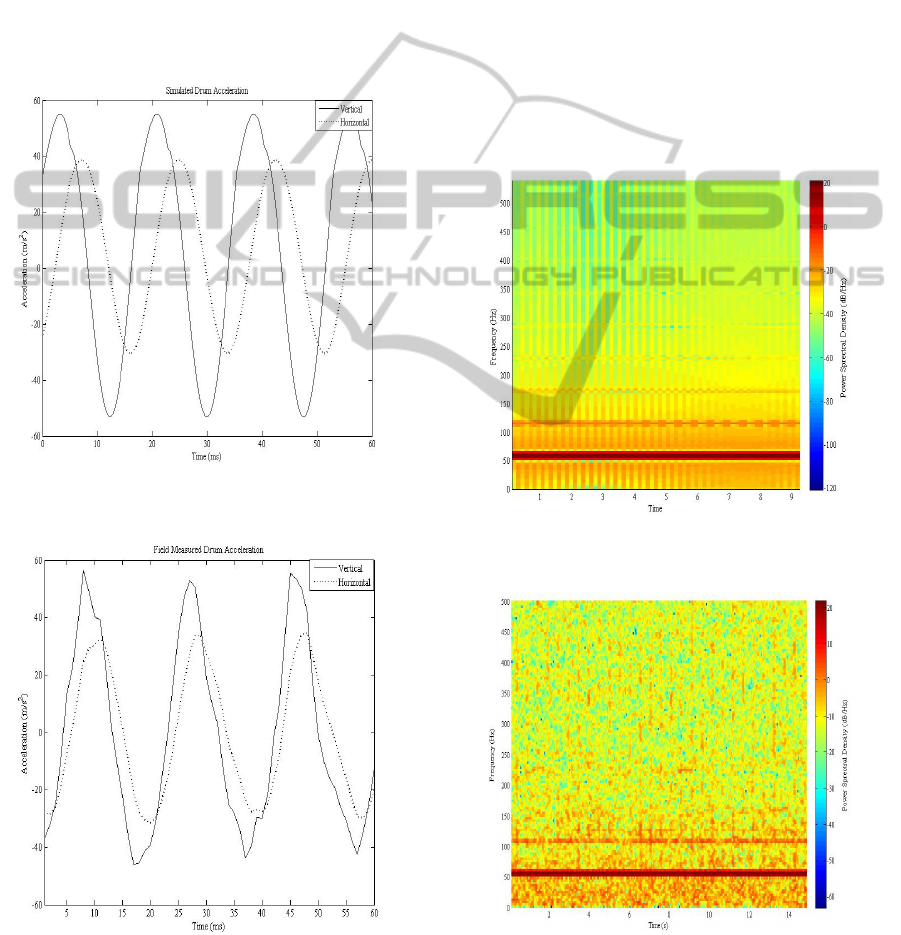
Figure 4 show the simulated drum acceleration in the
vertical and horizontal direction. The simulation
results are compared with the data measured during
field construction. A Crossbow CXL10HF3 triaxial
accelerometer is used to measure the vibration of an
IR DD 118HF roller during construction of US 77 in
Noble, Oklahoma. Both the vertical and the
horizontal vibration were measured. Figure 5 show
the drum acceleration measured during field
compaction. The field data is filtered in order to
reduce the high frequency noise. Comparison
between the model vibration data and the field
vibration data show that the model is able to capture
Figure 4: Simulated drum acceleration in vertical and
longitudinal direction.
Figure 5: Drum acceleration in vertical and longitudinal
direction collected from field.
the response of the roller drum in both the vertical and
horizontal direction.
From the field data, it is evident that, the
amplitude of the horizontal vibration is less than that
of the vertical vibration. Besides, the horizontal
vibration lags its vertical counterpart. This is due to
the effect of rotating radial force exerted by the
eccentric masses. The model is capable of addressing
this dynamics. However, the phase difference
between the vibrations is found higher in the
simulated results than in the field data. This can be
attributed to the fact that the shear component of the
asphalt pavement is represented by a spring in the
model. The viscous behavior of asphalt in the
horizontal direction is not taken into consideration.
This results in variation in the delayed response from
the actual field data.
Figure 6: Simulated roller vibration spectrum
(longitudinal).
Figure 7: Field measured roller vibration spectrum
(longitudinal).
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
538
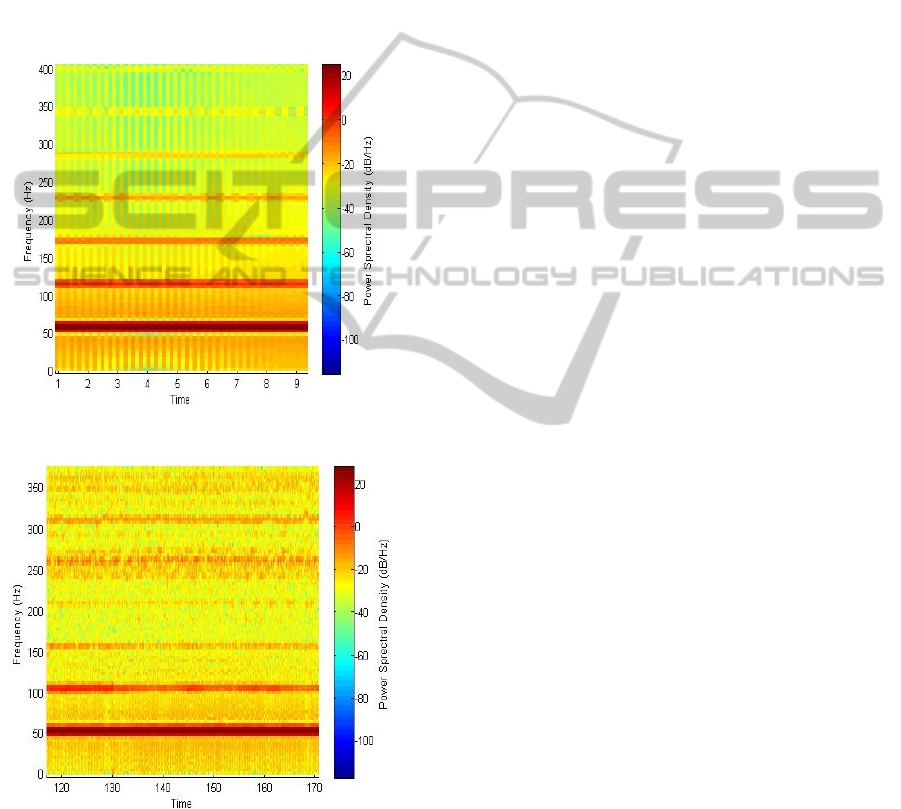
The spectrogram of the vibrations obtained using
numerical simulations is shown in Figure 6 and
Figure 8. Figure 7 and Figure 9 show the
corresponding spectrogram of the vibrations of the
roller observed during field compaction. The power
spectral density of the drum accelerations in each
frequency band is presented in these figures using a
color-coded map. The comparison of the spectral
analysis show that the model presented in this paper
captures not only the response of the roller at the
fundamental frequency (frequency of the eccentrics),
but also the response at the harmonics.
Figure 8: Simulated roller vibration spectrum (vertical).
Figure 9: Field measured roller vibration spectrum
(vertical).
5 CONCLUSIONS
A dynamical model of asphalt-roller interaction
during compaction is presented in this paper. The
dynamics of vibration in both the vertical and
horizontal direction is incorporated in the model. The
2 dimensional coupled dynamics between a moving
vibratory roller and the underlying asphalt pavement
is studied for the first time to the best of the
knowledge of the authors. The visco-elastic property
as well as the shear resistance of the asphalt pavement
is taken into account. The model parameters are
derived considering some important properties that
affect the compaction process. These are the
temperature and density of the mixture during
compaction, gradation of the mix, type of the binder,
layer thickness, frequency of the vibratory force and
several roller properties etc.
The ability of the model in emulating the real time
compaction process is studied. Comparison between
simulations results and field measured compaction
data showed that the model is capable of capturing the
coupled vibration dynamics between the roller and
the asphalt mat in both the vertical and horizontal
direction. The results indicate that the model can be a
simple and tractable mathematical representation of
the complex compaction dynamics. The model can
also serve as a preliminary step towards the
development closed loop control algorithms for the
compaction process.
The model was developed based on certain
assumption such as rigid base, fixed contact area
between roller drum and asphalt pavement, and
constant speed of the roller during compaction. The
effect of shear resistance is considered for
longitudinal direction only. The lateral shear flow of
asphalt is not taken into account. Future research is
aimed at relaxing these assumptions.
REFERENCES
Arasteh, M. 2007. Innovations in Compaction Control and
Testing. Intelligent Compaction 2007 Construction
Conference, Federal Highway Administration,
Bishmark, ND.
Beainy, F., Commuri, S., and Zaman, M. 2011. Quality
assurance of hot mix asphalt pavements using the
intelligent asphalt compaction analyser. ASCE Journal
of Construction Engineering and Management, 138(2),
178-187.
Beainy, F., Commuri, S., Zaman, M., & Imran, S. 2013.
Viscoelastic-Plastic Model of Asphalt-Roller
Interaction. ASCE International Journal of
Geomechanics, 13(5), 581-594.
Briaud, J. L.; and Seo, J. 2003. Intelligent compaction:
Overview and research needs. Texas A&M Univ.,
College Station, TX.
Brown, E. R. 1984.Experiences of Corps of Engineers in
Compaction of Hot Asphalt Mixtures. Placement and
A2DimensionalDynamicalModelofAsphalt-rollerInteractionduringVibratoryCompaction
539

Compaction of Asphalt Mixtures, F.T. Wagner, Ed.
ASTM Special Technical Publication 829. American
Society for Testing and Materials. Philadelphia, PA.
Chen, J. 2011. Discrete Element Method (DEM) Analyses
for Hot-Mix Asphalt (HMA) Mixture Compaction.
PhD Dissertation, University of Tennessee.
Huerne, H. L. 2004. Compaction of Asphalt Road
Pavements. PhD Dissertation, University of Twente,
Netherlands.
Imran, S., Beainy, F., Commuri, S., and Zaman, M. 2014.
Dynamical Model of Asphalt-Roller Interaction During
compaction. 11th International Conference on
Informatics in Control, Automation and Robotics, 559-
567.
Koneru, S., Masad, E., and Rajagopal, K. R. 2008. A
thermo-dynamical framework for modeling the
compaction of asphalt mixes. Mechanics of Materials,
40(10), 846–864.
Lenz, R. 2011. Pavement Design Guide. Texas Department
of Transportation.
Liu, Y., and You, Z. 2009. Determining Burger’s Model
Parameters of Asphalt Materials using Creep-recovery
Testing Data. Pavements and Materials: Modeling,
Testing, and Performance. ASCE Geotechnical Special
Publication, 184, 26-36.
Liu, Y., Qingli, D., and You, Z. 2009. Viscoelastic Model
for Discrete Element Simulation of Asphalt Mixtures.
ASCE Journal of Engineering Mechanics, 135(4), 324-
333.
Masad, E., Koneru, S., Scarpas, T., Kassem, E., and
Rajagopal, K. 2010. Modeling of Hot-Mix Asphalt
Compaction: A Thermodynamics-Based Compressible
Viscoelastic Model. Texas Transportation Institute,
Office of Acquisition Management, Federal Highway
Administration, Washington, D.C.
Nillson, R., Hopman, P., and Isacsson, U. 2002. Influence
of different rheological models on predicted pavement
responses in flexible pavements. Road Materials and
Pavement Design: An International Journal, 3, 117-
149.
Pellinen, T. K., and Xiao, S. 2006. Stiffness of Hot-Mix
Asphalt. Publication FHWA/IN/JTRP-2005/20. Joint
Transportation Research Program, Indiana Department
of Transportation and Purdue University, West
Lafayette, Indiana.
Pronk, A. 2005. The Huet–Sayegh model: a simple and
excellent rheological model for master curves of
asphaltic mixes. Lytton Symposium on Mechanics of
Flexible Pavements, Baton Rouge, LA.
Rakowski, S. 2008. Intelligent Compaction CCV IC.
Presentation, Sakai, Dallas, TX: Transportation Pooled
Fund Intelligent Compaction Systems initial-Task
Working Group meeting.
Scherocman, J. A. and Martenson, E. D. 1984. Placement
of Asphalt Concrete Mixtures. Placement and
Compaction of Asphalt Mixtures, F.T. Wagner,
Ed. ASTM Special Technical Publication
829. American Society for Testing and
Materials. Philadelphia, PA. 3-27.
Xu, Q., and Solaimanian, M. 2009. Modelling linear
viscoelastic properties of asphaltconcrete by the Huet–
Sayegh model. International Journal of Pavement
Engineering, Taylor & Francis, 10(6), 401-422.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
540
