
Semantic Secure Public Key Encryption with Filtered Equality Test
PKE-FET
Kaibin Huang
1
, Yu-Chi Chen
2
and Raylin Tso
1
1
Department of Computer Science, National Chengchi University, Taipei, Taiwan
2
Institute of Computer Science, Academic Sinica, Taipei, Taiwan
Keywords:
Cloud Storage, Equality Test, Filtered Equality Test, Public Key Encryption, Secret Sharing, Semantic
Security.
Abstract:
Cloud storage allows users to outsource their data to a storage server. For general security and privacy con-
cerns, users prefer storing encrypted data to pure ones so that servers do not learn anything about privacy.
However, there is a natural issue that servers have worked some analyses (i.e. statistics) or routines for en-
crypted data without losing privacy. In this paper, we address the basic functionality, equality test, over
encrypted data, which at least can be applied to specific analyses like private information retrieval. We in-
troduce a new system, called filtered equality test, which is an additional functionality for existing public key
encryption schemes. It satisfies the following scenario: a ciphertext-receiver selects several messages as a set
and produces its related warrant; then, on receiving this warrant, an user is able to perform equality test on
the receiver’s ciphertext without decryption when the hidden message belongs to that message set. Similar
to the attribute based encryption, ABE. In ABE schemes, those ones who match the settled conditions could
get the privilege of decryption. In FET schemes, those ‘messages inside selected set’ can be equality tested.
Combining PKE schemes and filtered equality test, we propose a framework of public key encryption scheme
with filtered equality test, abbreviated as PKE-FET. Then, taking ElGamal for example, we propose a concrete
PKE-FET scheme based on secret sharing and bilinear map. Finally, we prove our proposition with semantic
security in the standard model.
1 INTRODUCTION
With the development of cloud computing, users can
carry on devices with weak computational abilities in-
stead of powerful ones, since computational resource
and power come from the cloud server. In particu-
lar, cloud storage (an application of cloud services)
provides space which users can store data on cloud
and retrieve their data when they need. For example,
Dropbox, Google Drive, and iCloud, are well-known
cloud storage services, but these systems only allow
users to access their own data. In this case, users
must trust the server without doubt. Straightly, there
is a natural privacy issue − the server can see data in
the clear. For privacy, data encryption is employed
to overcome this issue. Finally, servers receive large
amount of encrypted data everyday, but they cannot
do any statistical analysis because data is encrypted.
Complicated data analysis may not be realized for
encrypted data, but it is plausible to obtain data equal-
ity which is the easiest analysis to check whether two
encrypted data are the same or not. For this purpose,
encrypted data with equality test extracts significant
attention in cloud storage applications. In the origi-
nal equality testable setting like (Peng et al., 2005),
it allows the storage server to play the tester role who
has the ability to work equality test on two ciphertexts
of the same receiver. To make PKE-ET more flex-
ible, Yang et al. add the multi-user setting (Bellare
et al., 2000)(Fouque et al., 2014) to propose the pub-
lic key encryption with equality test, PKE-ET (Yang
et al., 2010), which the tester can check ciphertexts
of different receivers. However, PKE-ET (both in the
multi-user setting or single-user setting) has a draw-
back that all users including adversaries can play the
tester role to arbitrarily test ciphertexts, since this is
the main goal of PKE-ET. Public key encryption with
authenticated equality test, PKE-AET, (Huang et al.,
2015) is presented to overcome above issue by lim-
iting the availability of being a tester. In PKE-AET,
an user becomes a tester after obtaining the warrant
from the corresponding ciphertext-receiver. The war-
327
Huang K., Chen Y. and Tso R..
Semantic Secure Public Key Encryption with Filtered Equality Test - PKE-FET.
DOI: 10.5220/0005550303270334
In Proceedings of the 12th International Conference on Security and Cryptography (SECRYPT-2015), pages 327-334
ISBN: 978-989-758-117-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
c
S
R
S’
R’
Filtered
Equality Test
warrant w warrant w’
pass
fail
or
Tester
c’
Figure 1: Public key encryptions with filtered equality test.
rant is referred to an authority that allows the tester to
perform equality test.
1.1 Related Works
In the literature, the notion of PKE-ET was first in-
troduced by Yang et al. (Yang et al., 2010). Based
on bilinear map, they constructed the framework in
which everyone is able to perform equality test on
two ciphertexts encrypted under different public keys.
Generally speaking, it is impossible to achieve stan-
dard semantic security or IND-CPA security due to
equality testability. However, Tang partially fixed
the above security issue by adding the authority of
equality testability (Tang, 2012b)(Tang, 2012a). The
receiver gives warrants to trusted testers, and these
testers can perform equality test on ciphertexts of this
receiver. Therefore, Tang’s method provides IND-
CCA security against outsider attacker (not the tester)
and one-way security against the testers. Tang de-
fined Type-I/II adversary as the party with/without the
warrant. Later, Ma et al. propose an efficient pub-
lic key encryption with delegated equality test in a
multi-user setting, PKE-DET (Ma et al., 2014). Both
of Tang and Ma et al.’s schemes make testers able to
perform equality test on all ciphertexts of the receiver
who gives the warrant. Recently, Huang et al. intro-
duced a new PKE-ET with ciphertext-binded author-
ities (Huang et al., 2014) which makes testers only
able to work equality test on a specific ciphertext. The
receiver takes ciphertexts as input to generate war-
rants, and the functionality of warrants is rigorously
restricted.
1.2 Contributions
In this paper, we present a new notion called filtered
equality test, it provides additional functionality to ex-
isting public key encryption schemes: in a selected
message set, it makes equality tests work. There
are three entities, sender, equality tester (server), and
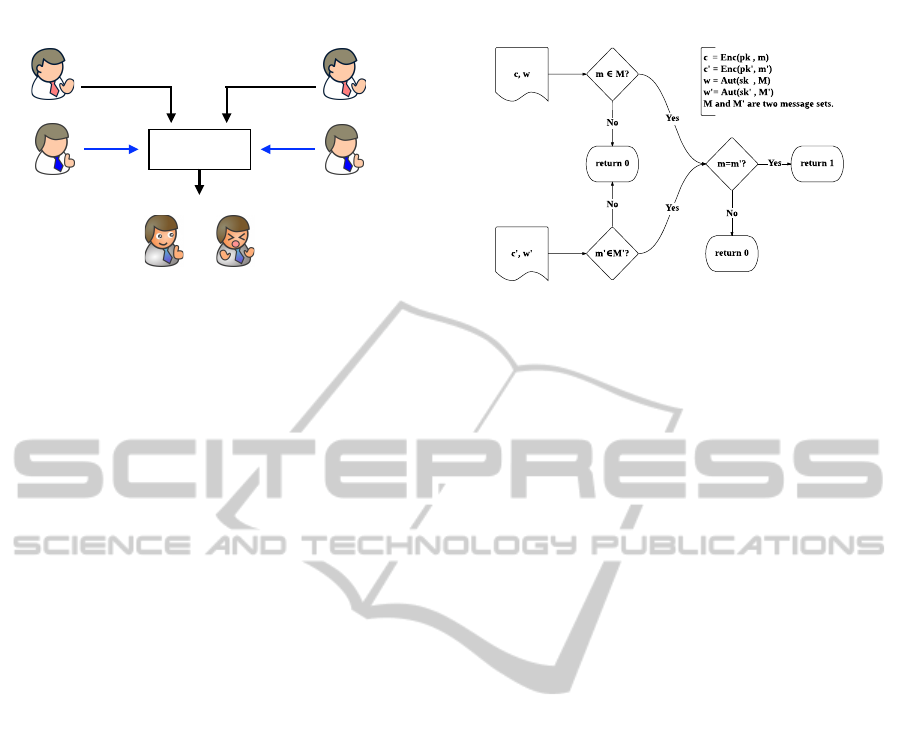
Figure 2: Flow chart of filtered equality test.
receiver. The sender uses the receiver’s public key
to produce encrypted data, and delivers them to the
tester (server). The receiver designates a set of mes-
sages to generate its warrant, and delivers to the tester.
Once the tester holds warrants and ciphertexts, it does
the check in Figure 1 without decryption; the detail
data flow is described in Figure 2. To help under-
standing, we take attribute-based encryption (ABE)
schemes for example. In ABE schemes, those quanti-
fied users who match settled conditions can decrypt
the ciphertexts. In FET schemes, those quantified
‘messages’ can be equality tested.
We construct the framework of PKE-FET , and its
security model. Taking ElGamal (Gamal, 1985) for
instance, we propose an efficient PKE-FET scheme
based on the properties of secret sharing and bilinear
map, and then prove the its semantic security in the
standard model.
The rest of paper is organized as follows. In Sec-
tion 2, some preliminaries are briefly introduced, i.e.
bilinear map, secret sharing, and hardness assump-
tions. In Section 3, we show the notion of PKE-FET
in details. We present our PKE-FET scheme in Sec-
tion 4 and its security proof in Section 5. Finally, the
conclusions of this paper are given in Section 6.
2 PRELIMINARIES
Now we will introduce some preliminaries, including
the bilinear map, a well-defined primitive, and then
review the concept of secret sharing. Moreover, we
attach some hardness assumptions which will be used
to analyze the security of the proposed scheme.
2.1 Bilinear Map (A.K.A Pairing)
The bilinear map (Chatterjee and Menezes, 2011)
works as follows. Let G
1
, G
2
and G
T
be three mul-
tiplicative cyclic groups with the same prime order
q. Define the mapping as a function e : G
1
× G
2
→
SECRYPT2015-InternationalConferenceonSecurityandCryptography
328

G
T
. If G
1
= G
2
, it is called Type-I pairing in (Gal-
braith et al., 2008). Otherwise, it is called asym-
metric pairing while G
1
6= G
2
. In asymmetric pair-
ing setting, if there is an efficiently-computable iso-
morphism ψ : G
2
→ G
1
, it is called Type-II pairing.
However, if it is in asymmetric setting without an
efficiently-computable isomorphism ψ : G
2
→ G
1
, it
is called Type-III pairing.
Let g
1
∈ G
1
and g
2
∈ G
2
be generators respec-
tively. e : G
1
× G
2
→ G
T
holds the following proper-
ties.
1. Bilinear: for all x, y ∈ Z
∗
q
, we have
e(g
x
1
,g
y
2
) = e(g
1
,g
2
)
xy
2. Non-degenerate: let I be the identity of group G
T
;
for all generators g
1
and g
2
, we have
e(g
1
,g
2
) 6= I
3. Computable: e(g
1
,g
2
) can be computed in poly-
nomial run-time.
2.2 Secret Sharing
The notion of secret sharing (Shamir, 1979) is intro-
duced to share a secret data D to n users. In secret
sharing, sufficient k (1 ≤ k ≤ n) users can reconstruct
the secret D on receiving their sharing fragments; on
the other hand, any less than k −1 pieces reveal no in-
formation about D. In the following, there is a simple
k-out-of-n secret sharing scheme provided in (Shamir,
1979).
For sharing a secret D to n users, a dealer (trusted
party who holds the secret) first picks k − 1 ran-
dom numbers, r
1
to r
k−1
, to form k points on a 2-
dimensional plane, which are {(0,D),(1,r
1
),...,(k −
1,r
k−1
)}. Then, along with these points, there should
be one and only one polynomial function ψ with
k − 1 degree determined. Next, he computes follow-
ing points (i, ψ(i)) for user i ∈ [k,n]. Now there are
total n points which all of them satisfy y = ψ(x). By
distributing these points, it formalizes a k-out-of-n se-
cret sharing scheme. As a result, k users are able to
rebuild the polynomial function ψ by linear combi-
nation, and then compute D = ψ(0) to acquire the
secret. However, if there are less than k users, they
cannot recover ψ so that the secret D is perfectly pro-
tected. Hence, secret sharing is perfect secure.
2.3 Hardness Assumptions
In this section, some hardness assumptions will be in-
troduced since we will use them to argue the security
of the proposed PKE-FET scheme. In general, we as-
sume the probability of breaking these assumptions is
negligible. We describe the universal one-way hash
function (Diffie and Hellman, 1976)(Naor and Yung,
1989) as follows.
Universal One-way Hash Function. A function
F is one-way if a random input x, given F(x), it is hard
to compute x. In other words, a one-way hash func-
tion F is easy to find F(x) given an input x, but it is
computational difficult to extract x from F(x). Based
on one-way hash function, an universal one-way hash
function is proposed by Naor and Yung (Naor and
Yung, 1989). It address on the problem that find
x,y in the domain such that y 6= x and F(x) = F(y).
Let A be an polynomial-time adversary to solve the
one-way hash function. We define A ’s advantage as
Adv
OW
A,F
= Pr[x ← A(F(x))].
Besides, there are a series of computationally
hardness assumptions.
• Discrete Logarithm Problem (DLP). given
g,y ∈ G it is hard to output an integer x such that
y = g
x
where G can be G
1
or G
2
. Let A be an
polynomial-time adversary to solve DLP. We de-
fine A’s advantage as Adv
DLP
A,G
= Pr[x ← A (g,g
x
)].
• Computational Diffie-Hellman (CDH) Prob-
lem. given g
x
∈ G and g
y
∈ G it is hard to out-
put g
xy
. Let A be an polynomial-time adversary to
solve the CDH problem. We define A’s advantage
as Adv
CDH
A,G
= Pr[g
xy
← A(g
x
,g
y
)]. According to
(Sakurai and Shizuya, 1995), the only known so-
lution to solve CDH problem is to solve DL prob-
lem.
• Decisional Diffie-Hellman (DDH) Problem.
given g
x
∈ G, g
y
∈ G, and Z ∈ G, it is hard to
decide whether Z = g
xy
or not. Let c ∈ {0, 1} be
a fair coin, both c = 1 and c = 0 appear with half
probability; if c = 1, Z = g
xy
; otherwise, Z is a
random number. Let A be an polynomial-time
adversary to break the DDH problem. We define
A’s advantage as Adv
DDH
A,G
= Pr[c
∗
← A(g
x
,g
y
,Z) :
c
∗
= c] −
1
2
.
• Symmetric External Diffie-Hellman (SXDH).
By the definition of (Ghadafi et al., 2010), the
DDH problem in G
1
or G
2
in the type-III pairing
environment is called SXDH problem; and SXDH
problem is as hard as DDH problem.
3 MODELS OF PKE-FET
PKE-FET is composed of a PKE scheme and FET
functionality, which FET denotes the following sce-
nario: the receiver picks n messages (denoted as a set
M = {m
1
,···m
n
}) from message space M; then she
SemanticSecurePublicKeyEncryptionwithFilteredEqualityTest-PKE-FET
329

generates a warrant w using these n messages and her
private key. Following, she can delegate the equal-
ity testability to someone by delivering the warrant w.
When one user gets the warrant, he can run equality
tests on the receiver’s ciphertexts if the messages in-
side the ciphertexts belong M . For security issues,
we have to limit n << |M|. The formal description of
PKE-FET is listed below:
3.1 Framework
Let PKE-FET be a public key encryption with filtered
equality test. Formally, PKE-FET is composed of fol-
lowing polynomial-time algorithms:
• Setup: on input a secure parameter λ, it generates
a series of public parameters pp.
• Key generation: on input the public key pp, it re-
turns the receiver’s key pair (sk, pk).
• Encryption: on input a public key pk and a mes-
sage m, the encryption algorithm, run by the
sender, generates a probabilistic ciphertext c =
Enc(pk,m).
• Decryption: on input a ciphertext c and the se-
cret key sk, the decryption algorithm, run by the
receiver, outputs the message m hidden in the ci-
phertext.
• Authorization: on input the secret key sk and a
set of n messages, m
1
,...,m
n
∈ M , it generates
a warrant w for the message set M . Let w =
Aut(sk, M ). The receiver will give the warrant w
to a trusted tester, and thus the tester is able to per-
form the filtered equality test on those ciphertext
encrypted under the receiver’s public key.
• Filtered equality test: (see Figure 2) on in-
put two ciphertexts c = Enc(pk, m) and c
0
=
Enc(pk
0
,m
0
) and two warrants w = Aut(sk,M )
and w
0
= Aut(sk
0
,M
0
), this algorithm returns 1 ←
FET (c, c
0
,w,w
0
) if and only if all of the following
three conditions hold:
m ∈ M , m
0
∈ M
0
, and m = m
0
Otherwise, it returns 0.
3.2 Properties of PKE-FET
Define ε(λ) as a negligible probability based on
the secure parameter λ. Referring to (Yang et al.,
2010)(Huang et al., 2014)(Huang et al., 2015), a
PKE-FET scheme is considered to be valid if and
only if it satisfies correctness, perfect consistency, and
computational soundness.
• Correctness: PKE-FET is a public key encryption
scheme in which the receiver can recover the cor-
rect message m. That is, for all m,
Pr[Dec(sk, Enc(pk,m)) = m] = 1
• Perfect consistency: for three true conditions, m ∈
M , m
0
∈ M
0
, and m = m
0
, FET (c,c
0
,w,w
0
) must
return 1.
• Computational soundness: with at least
one false condition, the probability
Pr[1 ← FET (c, c
0
,w,w
0
)] is bounded at most
ε(λ).
3.3 Semantic Security
To discuss about security issues of PKE-FET , first we
recall the definition of semantic security, or so called
indistinguishability (IND) style of security, which
composed of an adversary A and a challenger.
On input a public key pk selected by the chal-
lenger, the probabilistic polynomial time (PPT) ad-
versary A is allowed to access decryption oracle D
1
for polynomial times, then it outputs two messages
m
0
and m
1
. The challenger randomly picks one of
them (m
b
, b ∈ {0, 1}) and encrypts it as a challenge
c
b
= Enc(pk, m
b
). A is still allowed to access decryp-
tion oracle D
2
, then it has to output a guess of b. If it
successfully guesses with a non-negligible probabil-
ity in advance, then A breaks this game; otherwise,
this encryption scheme achieves semantic security, or
called indistinguishability styles of security.
Decryption oracle D
1
and D
2
differ from differ-
ent attack models, where: in the chosen-plaintext at-
tack (CPA) model, neither D
1
nor D
2
works; in the
chosen-ciphertext attack (CCA) model, D
1
works, but
D
2
does not; and in the adaptive chosen-ciphertext
attack (CCA2) model, they both work, but the chal-
lenge c
b
= Enc(pk,m
b
) is forbidden to be requested
to D
2
. Along with the IND game, semantic secure is
classified into IND-CPA, IND-CCA and IND-CCA2
secure.
3.4 Semantic Security for PKE-FET
Schemes
Extending from above section, we define semantic se-
curity for PKE-FET schemes. In the beginning, the
challenger generates a legal key pair (sk, pk) and a
warrant w ← Aut(sk,M ) which M is randomly se-
lected from message space M; and meanwhile, M
is unknown to A . Then, pk and w are delivered to
A to start a semantic secure game. With the aid of
decryption oracle D
1
, A outputs his two messages
SECRYPT2015-InternationalConferenceonSecurityandCryptography
330

m
0
and m
1
selected in M. The challenger picks one
of them (m
b
, b ∈ {0,1}) and encrypts it into a chal-
lenge c
b
= Enc(pk,m
b
). Along with the help of de-
cryption oracle D
2
, A outputs a guess b
∗
to terminate
this game. Let Adv
IND
A,FET
be the probability of A wins
the game in advance (more than universally guessing).
If Adv
IND
A,FET
is non-negligible, then we say A breaks
this game; otherwise, we say a PKE-FET scheme is
semantic secure. We say a PKE-FET scheme is se-
mantic secure if Adv
IND
A,FET
is negligible, where it is
defined as follows:
Pr
(sk, pk) ← KeyGen(λ);M ←
R
M;
w ← Aut(sk, M );
(m
0
,m
1
) ← A
D
1
(pk, w);
b ←
R
{0,1};c
b
← Enc(pk,m
b
);
b
∗
← A
D
2
(pk, w, c
b
) : b
∗
= b
−
1
2
≤ ε(λ)
4 PROPOSED PKE-FET SCHEME
In this section, we will describe the proposed
PKE-FET scheme from secret sharing to realize fil-
tered equality test over encrypted data. Taking ElGa-
mal as a building block, we construct our PKE-FET
scheme below.
4.1 Construction
• Setup: Let e : G
1
× G
2
→ G
T
be a Type-III bi-
linear map operation which are mentioned in Sec-
tion 2.1. Then, G
1
, G
2
, and G
T
are three multi-
plicative cyclic group with the same prime order
q. Randomly choose g ∈
R
G
1
and g
2
∈
R
G
2
as
two generators respectively. The message space
M is set to be a subgroup of G
1
; i.e., M ⊆ G
1
.
H
1
: M → G
T
and H
2
: {0,1}
∗
→ Z
∗
q
are two uni-
versal one-way hash functions. Here, the auxiliary
information n = n(λ) is needed, and we empha-
size that n << |M|. The public parameter is com-
posed of pp = {G
1
,G
2
,G
T
,e,q,g, g
2
,H
1
,H
2
,n}.
• Key generation: Sample (u,v, s
0
,s
1
,...,s
n
) ←
R
Z
∗
q
as sk. Compute U = g
u
, V = e(g,g
2
)
uv
and
S
i
= g
s
i
for all i ∈ [0,n]; then publish pk =
(U,V, S
0
,S
1
,...S
n
).
• Encryption: Taking a message m ∈ M, the sender
first randomly selects r ←
R
Z
∗
q
, then computes h =
H
2
(m) and c = (A,B,C, D) where
A = g
r
,B = m ·U
r
,C = V
r
· H
1
(m)
D = ((S
0
)
r
,(S
1
)
rh
,(S
2
)
rh
2
,...,(S
n
)
rh
n
) (1)
• Decryption: The receiver computes m = B/A
u
.
Let D = (D
0
,D
1
,...,D
n
) and h = H
2
(m), he ver-
ifies both C = e(A, g
2
)
uv
· H
1
(m) and D
i
= A
s
i
h
i
for all i ∈ [0,n]. If they both hold, it returns m;
otherwise, it returns ⊥ as decryption failed.
• Authorization: on input M = {m
1
,...,m
n
} and the
secret key sk = (u, v,s
0
,s
1
,...,s
n
), the authoriza-
tion algorithm computes a n-degree polynomial
function f (x) following:
f (x) =
n
∏
i=1
(x − H
2
(m
i
)) + uv =
n
∑
i=0
a
i
x
i
. (2)
Furthermore, the receiver computes w
i
= g
a
i
/s
i
2
for
all i ∈ [0,n]; and then, he destroys (a
0
,...,a
n
) and
sends the warrant w = (w
0
,w
1
,...,w
n
).
Note that the message set M is hidden in the gen-
erated warrant, which is unknown for all users
even he or she gets the warrant.
• Filtered equality test: upon receiving two ci-
phertexts c = Enc(pk,m) and c
0
= Enc(pk
0
,m
0
)
and two warrants w = Aut(sk,M ) and w
0
=
Aut(sk
0
,M
0
), the filtered equality test algorithm
works the following steps.
1. Parse c = (A,B,C,D), D = (D
0
,D
1
,...,D
n
) and
w = (w
0
,w
1
,...,w
n
).
2. Compute
z = C/
n
∏
i=0
e(D
i
,w
i
) (3)
3. Compute z
0
from (c
0
,w
0
) following Steps 1 and
2.
4. Check whether z = z
0
or not. If z = z
0
, then it
returns 1, which means m ∈ M , m
0
∈ M
0
, and
m = m
0
. If not, it returns 0 instead.
4.2 Analysis
We now verify our scheme to satisfy three significant
properties mentioned in Section 3.2.
• Correctness: The decryption algorithm computes
B/A
u
= mg
ur
/g
ur
= m
Then, let h = H
2
(m), it checks both
e(A,g
2
)
uv
· H
1
(m) = e(g
r
,g
2
)
uv
· H
1
(m)
= e(g,g
2
)
uvr
· H
1
(m)
= V
r
· H
1
(m) = C
and
∀i ∈ [1,n],D
i
= (S
i
)
rh
i
= g
s
i
rh
i
= A
s
i
h
i
It is straightforward that the correctness holds
along with the decryption algorithm.
SemanticSecurePublicKeyEncryptionwithFilteredEqualityTest-PKE-FET
331

Table 1: Comparison with previous works.
(Yang et al., 2010) (Ma et al., 2014) (Huang et al., 2014) Proposed
Efficiency KeyGen O(1) O(1) O(1) O(n)
Enc O(1) O(1) O(1) O(n)
Dec O(1) O(1) O(1) O(n)
Aut - O(1) O(1) O(n)
Test O(1) O(1) O(1) O(n)
Storage Key O(1) O(1) O(1) O(n)
Cipher O(1) O(1) O(1) O(n)
Warrant - O(1) O(1) O(n)
Testable messages M M 1 n
Security With Aut - OW-CCA OW-CCA IND-CCA
W/O Aut OW-CCA IND-CCA IND-CCA IND-CCA
• Perfect consistency: On input (c,w) and (c
0
,w
0
),
the filtered equality test algorithm obtains z by
computing equation (3).
z = C/Π
n
i=0
e(D
i
,w
i
)
= C/Π
n
i=0
e(g
s
i
rH
2
(m)
i
,g
a
i
/s
i
2
)
= C/Π
n
i=0
e(g,g
2
)
ra
i
H
2
(m)
i
= C/e(g,g
2
)
r
∑
n
i=0
a
i
H
2
(m)
i
= C/e(g,g
2
)
r f (H
2
(m))
If m 6∈ M , z will be a random number locates sta-
tistically random in G
T
because f (H
2
(m)) is sta-
tistically random in Z
∗
q
. Otherwise, in case that m
is in the message set M , then we have
f (H
2
(m)) =
n
∑
i=0
a
i
H
2
(m)
i
= uv (4)
Therefore, equation (3) will be
z = C/e(g,g
2
)
uvr
= V
r
· H
1
(m)/V
r
= H
1
(m)
Analogously, it returns z
0
= H
1
(m
0
) if m
0
∈ M
0
through the same computations. Finally, it veri-
fies whether z = z
0
or not. It returns 1 if and only
if the m ∈ M , m
0
∈ M
0
and m = m
0
, and therefore
the perfect consistency holds.
• Computational soundness: We consider the fol-
lowing two conditions.
1. m ∈ M and m
0
∈ M
0
: By the inference of con-
sistency, z and z
0
will be computed as z = H
1
(m)
and z
0
= H
1
(m
0
) respectively. We can reduce
computational soundness to the universal prop-
erty of hash function H
1
. If collision happens
with negligible probability, then the probability
of 1 ← FET (c,c
0
,w,w
0
) in this condition is also
negligible.
2. m 6∈ M or m
0
6∈ M
0
: At least one of z and z
0
will be close to a uniformly random number in
G
T
, so the probability of 1 ← FET (c,c
0
,w,w
0
)
in this condition is definitely 1/q (negligible).
The computational soundness holds due to the
negligible probability.
We compare PKE-FET to some existing protocols
and record them on Table 1. It is clear that PKE-FET
performs not good on considering the efficiency and
storage space. Nevertheless, it provides the ‘filtered
equality test’ functionality; and meanwhile, it is se-
mantic secure against those adversaries who own war-
rants. The security analysis will be discussed in the
next section.
5 SECURITY PROOF
In this section, we are going to prove the security
of our PKE-FET scheme through a series of hybrid
games in the standard model. We claim that if there is
a polynomial time adversary can break our PKE-FET
with non-negligible probability, then the challenger is
able to take advantage of A to break SXDH problem
with non-negligible probability. First, we define game
0 which is equal to our PKE-FET scheme, and then it
will be inferred step by step.
Game 0:
The challenger works key generation and autho-
rization algorithms to generate a key pair (sk, pk) =
KeyGen(λ) and a warrant w = Aut(sk,M ), which M
is randomly selected from message space M. Then,
he delivers pk and w to the adversary A . With the
aid of decryption oracle D
1
, A outputs m
0
and m
1
af-
ter polynomial times of decryption requests. Then,
the challenger picks one of two messages (m
b
, b ∈
{0,1}), encrypts it into c
b
= Enc(pk,m
b
), and then
returns c
b
to A. With polynomial times requests to
decryption oracle D
2
, A finally outputs a guess b
∗
.
Decryption oracles D
1
and D
2
are defined as follows:
on receiving a decryption query Dec(sk, c), the chal-
SECRYPT2015-InternationalConferenceonSecurityandCryptography
332

lenger returns m = Dec(sk,c) to A. Only c
b
is forbid-
den to be requested. Let Pr[game
0
] be the probability
to break the semantic security in game 0, it is oblivi-
ous that Adv
IND
A,FET
= Pr[game
0
] −
1
2
.
Game 1:
All settings in game 1 is identical to those in game
0 except for the following condition. If m
0
∈ M
or m
1
∈ M , the challenger terminates and claims
fail; otherwise, game 1 works as game 0 does. Ac-
cording to difference lemma (Shoup, 2004), we have
Pr[game
0
] ≤ Pr[game
1
] +
2n
|M|
; where
2n
|M|
is negligible
in Pr[game
1
] since n << |M|.
Game 2:
Extends from game 1, we import the SXDH prob-
lem defined in section 2 to help proof. The challenger
runs (sk, pk) = KeyGen(λ) and w = Aut(sk,M ) (M
is randomly picked from M). Following, he replaces
S
0
= g
y
and
V = e(g,g
2
)
uv−a
0
· e(g
y
,g
2
)
a
0
/s
0
= e(g,g
2
)
uv−a
0
+a
0
y/s
0
Then, pk = (U,V,S
0
,S
1
,...,S
n
) and w are sent to A .
After polynomial times of decryption queries to D
1
,
A returns two messages m
0
and m
1
. After that, the
challenger randomly picks message m
b
, b ∈
R
{0,1},
then he computes h = H
2
(m
b
) and c
b
= (A,B,C,D),
where
A = g
x
, C = (e(g
x
,g
2
)
uv−a
0
· e(Z, g
2
)
a
0
/s
0
) ⊕ H
1
(m
b
),
B = m
b
g
ux
, D = (Z, g
xs
1
h
,g
xs
2
h
2
,...g
xs
n
h
n
)
After receiving c
b
and polynomial times of decryption
queries to D
2
, A outputs a guess b
∗
. If b
∗
= b, the
challenger guesses c = 1; otherwise, he guesses c = 0.
Theorem 1. Game 2 is indistinguishable from game
1.
Proof. There are two major differences between
game 1 and game 2: the first one comes from the sub-
stitution of S
0
and V; and the second one is Z in part
C or D of challenge c
b
. S
0
is originally g
s
0
, and it
becomes g
y
. It is oblivious that S
0
is still in the cor-
rect form, but y becomes unknown to the challenger;
moreover, since secret key v is unknown in A’s view-
point, any V belongs to G
T
is considered as a regular
parameter. On the hand, both two substitutions of Z
in c
b
are distinguishable because of the intractable of
SXDH problem. The probability that A can distin-
guish game 2 from game 1 is estimated as Adv
SXDH
A,G
1
.
Theorem 2. Pr[game
2
] can be polynomially reduced
to the SXDH problem.
Proof. Let A has a non-negligible probability ε in
advance to break PKE-FET scheme (total
1
2
+ ε prob-
ability). We discuss game 2 on considering whether
Z = g
xy
or not. The first case, when c = 1, scenario
in game 2 is actually a PKE-FET scheme so that A
has
1
2
+ ε probability to break PKE-FET scheme. The
second case, c = 0, scenario in game 2 is different
from PKE-FET scheme; the probability that A break
game 2 is estimated as
1
2
. After plenty of games,
considering on those games that A has won, first
case must be more than second case; and their rate
will be (1/2 + ε) : 1/2. It means when A wins the
game, the challenger has more probability on answer-
ing Z = g
xy
. The accurate advanced probability of
breaking SXDH problem is estimated as:
Adv
SXDH
A,G
1
=
1/2 + ε
1/2 + ε + 1/2
−
1
2
=
ε
2 + 2ε
In other words, if A has non-negligible advanced
probability ε to break PKE-FET scheme; then, the
challenger can take advantage of A to break SXDH
problem with non-negligible advanced probability
ε
2+2ε
, which is a little smaller than
ε
2
, but it is still
non-negligible. Therefore, we can say Pr[game
2
] is
close to but a little bigger than 2Adv
SXDH
A,G
1
+
1
2
. Then,
Adv
IND
A,FET
is inferred as follows:
Adv
IND
A,FET
= Pr[game
0
] −
1
2
≤ Pr[game
1
] +
2n
|M|
−
1
2
≤ Pr[game
2
] + Adv
SXDH
A,G
1
+
2n
|M|
−
1
2
Combining Pr[game
2
], Adv
IND
A,FET
is esti-
mated bounded by a real number d, which
d ≈ 3Adv
SXDH
A,G
1
+
2n
|M|
is negligible in λ. We say
PKE-FET is semantic secure or IND-CCA2 secure
based on the intractability of SXDH problem.
6 CONCLUSIONS
Computations over ciphertext has extracted research
attention. In this paper, a new notion of filtered equal-
ity test has been presented. We show a framework
and some security requirements of filtered equality
test as an additional functionality to existing encryp-
tion protocols; and then propose an instantiation, the
PKE-FET scheme, from secret sharing and bilinear
map. In addition, we prove its semantic security in the
standard model. Finally, the efficiency of PKE-FET is
not well due to massive bilinear mapping operations.
We keep the efficiency improvement as an open prob-
lem.
SemanticSecurePublicKeyEncryptionwithFilteredEqualityTest-PKE-FET
333

ACKNOWLEDGEMENTS
This research is supported by the Ministry of Science
and Technology, Taiwan, R.O.C., under Grant MOST
103-2221-E-004-009. We appreciate the anonymous
reviewers for their valuable suggestions.
REFERENCES
Bellare, M., Boldyreva, A., and Micali, S. (2000). Public-
key encryption in a multi-user setting: Security proofs
and improvements. In EUROCRYPT, pages 259–274.
Chatterjee, S. and Menezes, A. (2011). On crypto-
graphic protocols employing asymmetric pairings -
the role of revisited. Discrete Applied Mathematics,
159(13):1311–1322.
Diffie, W. and Hellman, M. E. (1976). New directions in
cryptography. IEEE Transactions on Information The-
ory, 22(6):644–654.
Fouque, P., Joux, A., and Mavromati, C. (2014). Multi-user
collisions: Applications to discrete logarithm, even-
mansour and PRINCE. In Advances in Cryptology -
ASIACRYPT 2014 - 20th International Conference on
the Theory and Application of Cryptology and Infor-
mation Security, Kaoshiung, Taiwan, R.O.C., Decem-
ber 7-11, 2014. Proceedings, Part I, pages 420–438.
Galbraith, S. D., Paterson, K. G., and Smart, N. P. (2008).
Pairings for cryptographers. Discrete Applied Mathe-
matics, 156(16):3113–3121.
Gamal, T. E. (1985). A public key cryptosystem and a sig-
nature scheme based on discrete logarithms. IEEE
Transactions on Information Theory, 31(4):469–472.
Ghadafi, E., Smart, N. P., and Warinschi, B. (2010). Groth-
sahai proofs revisited. In Public Key Cryptography
- PKC 2010, 13th International Conference on Prac-
tice and Theory in Public Key Cryptography, Paris,
France, May 26-28, 2010. Proceedings, pages 177–
192.
Huang, K., Tso, R., Chen, Y., Li, W., and Sun, H. (2014). A
new public key encryption with equality test. In Net-
work and System Security - 8th International Confer-
ence, NSS 2014, Xi’an, China, October 15-17, 2014,
Proceedings, pages 550–557.
Huang, K., Tso, R., Chen, Y.-C., Rahman, S. M. M., Almo-
gren, A., and Alamri, A. (2015). Pke-aet: Public key
encryption with authorized equality test. The Com-
puter Journal, page bxv025.
Ma, S., Zhang, M., Huang, Q., and Yang, B. (2014). Public
key encryption with delegated equality test in a multi-
user setting. The Computer Journal.
Naor, M. and Yung, M. (1989). Universal one-way hash
functions and their cryptographic applications. In Pro-
ceedings of the 21st Annual ACM Symposium on The-
ory of Computing, May 14-17, 1989, Seattle, Washig-
ton, USA, pages 33–43.
Peng, K., Boyd, C., Dawson, E., and Lee, B. (2005). Ci-
phertext comparison, a new solution to the millionaire
problem. In ICICS, pages 84–96.
Sakurai, K. and Shizuya, H. (1995). Relationships among
the computational powers of breaking discrete log
cryptosystems. In EUROCRYPT, pages 341–355.
Shamir, A. (1979). How to share a secret. Commun. ACM,
22(11):612–613.
Shoup, V. (2004). Sequences of games: a tool for tam-
ing complexity in security proofs. IACR Cryptology
ePrint Archive, 2004:332.
Tang, Q. (2012a). Public key encryption schemes support-
ing equality test with authorisation of different granu-
larity. IJACT, 2(4):304–321.
Tang, Q. (2012b). Public key encryption supporting plain-
text equality test and user-specified authorization. Se-
curity and Communication Networks, 5(12):1351–
1362.
Yang, G., Tan, C. H., Huang, Q., and Wong, D. S. (2010).
Probabilistic public key encryption with equality test.
In CT-RSA, pages 119–131.
SECRYPT2015-InternationalConferenceonSecurityandCryptography
334
