A Comparison of Learning Rules for Mixed Order Hyper Networks
Kevin Swingler
Computing Science and Maths, University of Stirling, FK9 4LA Stirling, Scotland, U.K.
Keywords:
High Order Networks, Learning Rules.
Abstract:
A mixed order hyper network (MOHN) is a neural network in which weights can connect any number of
neurons, rather than the usual two. MOHNs can be used as content addressable memories with higher capacity
than standard Hopfield networks. They can also be used for regression, clustering, classification, and as fitness
models for use in heuristic optimisation. This paper presents a set of methods for estimating the values of the
weights in a MOHN from training data. The different methods are compared to each other and to a standard
MLP trained by back propagation and found to be faster to train than the MLP and more reliable as the error
function does not contain local minima.
1 INTRODUCTION
For a long time, the multi layer perceptron (MLP)
has been a very popular choice for performing non-
linear regression on functions of multiple inputs. It
has the advantage of being easy to apply to problems
where there is little or no knowledge of the struc-
ture of the function to be learned, particularly con-
cerning the interactions between input variables. The
weight learning algorithm (back propagation of error,
for example) simultaneously discovers features (inter-
actions between inputs) in the function that underlies
the training data and the correct values for the regres-
sion coefficients, given those features. This leads to
two significant and well known disadvantages of the
MLP, namely the so called ‘black box problem’ that
means it is very difficult for a human analyst to learn
much about the structure of the underlying function
from the structure of the network and the problem of
local minima in the error function that are a result of
the hidden units failing to encode the correct interac-
tions between input variables.
These problems are addressed by Mixed Order
Hyper Networks (MOHNs) (Swingler and Smith,
2014a), which make the structure of the function ex-
plicit, meaning that human readability is greatly im-
proved and there are no local minima in the error
function. This paper presents and compares a num-
ber of methods for calculating the correct weight val-
ues for a MOHN of fixed structure. Different learning
rules have different strengths and weaknesses. Some,
for example may be carried out in an on line mode,
meaning that the data need not be all stored in mem-
ory at one time. On line learning also allows partially
learned networks to be updated in light of new data or
as part of an algorithm to discover the correct connec-
tion structure. Standard regression techniques such
as ordinary least squares (OLS) and Least Absolute
Shrinkage and Selection Operator (LASSO) may be
applied when on line learning is not required. This has
the added advantage that confidence intervals may be
calculated for the network weights. LASSO also has
the advantage that weights that do not contribute to
the function end up with values equal to zero.
MOHNs have been shown to be useful as fitness
function models if used as part of a metaheuristic con-
straint satisfaction (or combinatorial optimisation) al-
gorithm (Swingler and Smith, 2014b). In such cases,
it is not always necessary to learn the whole func-
tion space correctly, but sufficient to build a model
where the attractors in the energy function correspond
to turning points (local optima) in the fitness func-
tion. A simpler learning rule is sufficient to build such
models, and is presented in this paper.
2 MIXED ORDER HYPER
NETWORKS
A Mixed Order Hyper Network is a neural network
in which weights can connect any number of neurons.
A MOHN has a fixed number of n neurons and ≤ 2
n
weights, which may be added or removed dynami-
cally during learning. Each neuron can be in one of
Swingler, K..
A Comparison of Learning Rules for Mixed Order Hyper Networks.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 3: NCTA, pages 17-27
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
17
three states: u
i
∈ {−1, 1,0} where a value of 0 in-
dicates a wild card or unknown value. The state of
the MOHN is determined by the values of the vector,
u = u
0
...u
n−1
. The structure of a MOHN is defined
by a set, W of real valued weights, each connecting
0 ≤ k ≥ n neurons. The weights define a hyper graph
connecting the elements of u. Each weight, w
j
has an
integer index that is determined by the indices of the
neurons it connects:
W ⊆ {w
j
: j = 0 .. . 2
n−1
} w
j
∈ R (1)
The weights each have an associated order, de-
fined by the number of neurons they connect. There
is a single zero-order weight, which connects no neu-
rons, but has a weight all the same. There are n first
order weights, which are the equivalent of bias inputs
in a standard neural network. In general, there are
n
k
possible weights of order k in a network of size
n. For convenience of notation, the set of k neurons
connected to weight w
j
is denoted Q
j
, meaning that
the index j defines a neuron subset. This is done by
creating an n bit binary number, where bit i is set to
one to indicate that neuron i is part of the subset and
zero otherwise. The resulting binary number, stated
in base 10 becomes the weight index. For example,
the weight connecting neurons {0,1, 2} is w
7
as set-
ting the bits 0,1,2 in a four bit number gives 0111,
which is 7 in base 10. Consequently, we can write
Q
7
= {u
0
,u
1
,u
2
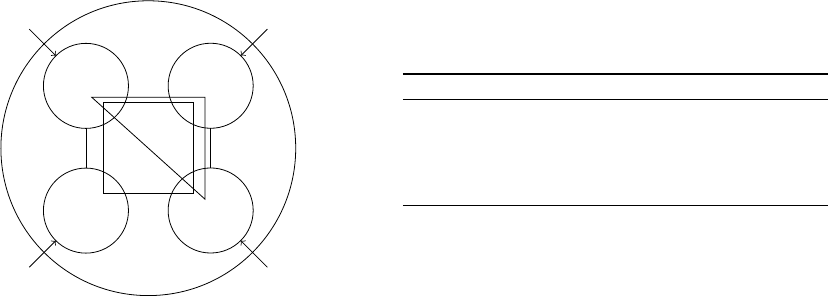
}. Figure 1 shows an example MOHN
where n = 4.
u
0
u
1
u
3
u
2
w
9
w
6
w
1
w
2
w
8
w
4
w
0
w
15
w
7
Figure 1: A four neuron MOHN with some of the weights
shown. w
7
is the triangle and w
15
is the square.
2.1 Using a MOHN
MOHNs can be applied to a number of different
computational intelligence tasks such as building a
content addressable memory, performing regression,
clustering, classification, probability distribution es-
timation and as fitness function models for use in
heuristic optimisation. These different tasks involve
different methods of use and require different ap-
proaches to estimating the values on the weights.
3 THE WEIGHT ESTIMATION
RULES
This section presents the different methods for es-
timating the weights needed to allow a MOHN to
perform a particular task. Although, in theory the
weights can be designed by hand, all of the methods
described here are based on learning from data. In
what follows, a single training example consists of a
vector of input variables and a real valued output de-
noted (x, y). The training data as a whole is denoted
D.
3.1 Hebbian Learning
The simplest of the MOHN learning rules is an exten-
sion to the Hebbian rule employed by a Hopfield net-
work to allow it to work with higher order weights. In
this case, the training data consists only of input pat-
terns, x and no function output is specified. Learning
involves setting u
i
= x
i
for each neuron and the weight
update is then:
w
j
= w
j
+
∏
u∈Q
j
u (2)
The Hebbian learning rule allows the MOHN to
be used as a content addressable memory (CAM). The
CAM learning algorithm is given in algorithm 1.
Algorithm 1: Loading Pattern x into a MOHN CAM.
u
i
= x
i
∀i Set the neuron outputs to equal the
pattern to be learned
w
j
= w
j
+
∏
u∈Q
j
u ∀w
j
∈ W Update the weights
according to equation 2
For a network that is fully connected at order two,
algorithm 1 is the same as loading patterns into a stan-
dard Hopfield network. When the MOHN contains
higher order weights, the capacity of the network is
increased. Patterns are recalled as they are in a Hop-
field network, by setting the neuron values to a noisy
or degraded pattern and allowing the network to set-
tle using a neuron update rule that first calculates an
activation value for each neuron, a
i
using equation 3
and then applies a threshold using equation 4.
a
i
=
∑
j:u
i
∈Q
j
w
j
∏
k∈Q
j
\i
u
k
!
(3)
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
18

where j : u
i
∈ Q
j
makes j enumerate the index of each
weight that connects to u
i
and k ∈ Q
j
\ i indicates the
index of every member of Q
j
, except neuron i itself. A
neuron’s output is then calculated using the threshold
function in equation 4.
u
i
=
1, if a
i
> 0
−1, otherwise
(4)
An attractor state is a pattern across u from which
the application of equation 3 results in no change to
any of the neuron outputs. A trained MOHN settles to
an attractor point by repeated application of the acti-
vation rules 3 and 4, choosing neurons in random or-
der. Algorithm 2 describes the algorithm for settling
from a pattern to an attractor:
Algorithm 2: Settling a trained MOHN to an attractor point.
repeat
ch ← FALSE Keep track of whether or not a
change has been made
visited ← {} Keep track of which neurons
have been visited
repeat
i ← rand(i : i /∈ visited) Pick a random
unset neuron
temp ← u
i
Make a note of its value for
later comparison
Update(u
i
) Update the neuron’s output
using equations 3 and 4
if u
i
6= temp then
ch ← T RUE
end if If a change was made to the
neuron’s output, note the fact
visited ← {visited ∪ i} Add the neuron’s
index to the visited set
until kvisitedk = n Loop until all neurons
have been updated
until ch = FALSE Loop if any neuron value has
changed
The dynamics of algorithm 2 have an underlying
Lyapunov function, just as they do in a standard HNN
and will always settle to a local minimum of the asso-
ciated energy function. (Venkatesh and Baldi, 1991)
report a capacity for binary valued order k networks
of the order of n
k
/ln n, a figure that is also reported
by (Kubota, 2007). In fact, as described below, such
networks are capable of representing any arbitrary
Lyaponov function and therefore a network with the
right structure will be able to represent any possible
number of turning points.
3.2 Weighted Hebbian Learning
Let f (x) be a multi-modal function where each lo-
cal maximum represents a pattern of interest. These
patterns might be local optima in an optimisation
task, archetypes in a clustering task or examples of
a satisfaction of multiple constraints, for example. A
MOHN can be trained as a CAM in which the attrac-
tors are the local maxima of the function. The learn-
ing rule is a weighted version of the Hebbian rule:
w
j
=
∑
x∈D
1
|D|
f (x)
∏
u∈Q
i
u (5)
Previous work (Swingler and Smith, 2014b) has
shown that the weighted Hebbian rule is capable of
learning the local maxima of a function from sam-
ples of x, f (x) and that the capacity of the resulting
networks for storing such attractors was equal to the
capacity of a CAM trained using equation 2. The dif-
ference between equations 2 and 5 is that the target
patterns are known in the first case, but unknown in
the second, where they are local maxima of y in a
function that is learned from a sample of (x, y) pairs.
Note also that experiments have shown that the train-
ing data need not contain a single example of any of
the attractor patterns for the method to work.
3.2.1 Parity Count Learning
When the inputs (both single variables and products
of variable subsets) are uncorrelated (i.e. orthogonal)
and each input has an even distribution of values, the
weighted Hebbian rule produces the correct weight
values in a single pass of the data. When the distribu-
tion of values across each variable is uneven, a better
estimate of weight values may be made by taking into
account how often the input product on each weight
is positive or negative during learning. Each weight is
set to equal the difference between the average of the
output y when the weight’s input is positive and when
it is negative.
Let D
+
j
be the set of sub-patterns learned by w
j
that contain values whose product is positive and D
−
j
be the set of sub-patterns learned by w
j
that contain
values whose product is negative. Now let hy
+
i be the
average value of y associated with the members of D
+
j
and hy
−
i be the average value of y associated with the
members of D
−
j
:
hy
+
i =
1
|D
+
j
|
∑
x∈D
+
j
f (x) (6)
Similarly, hy
−
i is calculated as a sum over
x ∈ D
−
j
. The weight calculation is simply
A Comparison of Learning Rules for Mixed Order Hyper Networks
19

w
j
=
1
2
hy
+
i − hy
−
i
(7)
The averages may be maintained online so that the
weight values are always correct at any time during
learning (rather than summing and dividing at the end
of a defined training set). W
0
is set in a similar way.
The Weighted Hebbian calculation, w
0
= hyi means
that w
0
is just the average of the output, y across the
training sample. This can be improved by taking into
account the distribution of patterns across each input.
w
0
= hyi −
∑
j:w
j
∈W
w
j
∏
x∈w
j
x
(8)
where x ∈ w
j
indicates the neurons connected to
weight w
j
and
∏
x∈w
j
x
is the average value across
all input patterns of the product of the values of x con-
nected to w
j
.
3.3 Regression Rules
The weighted Hebbian update rule is capable of cap-
turing the turning points in a function, but cannot ac-
curately reproduce the output of the function itself
across all of the input space. Such networks have an
energy function
1
and this can be used as a regression
function for estimating ˆy = f (x) in the form
ˆy =
∑
i
w
j
∏
u∈Q
i
u (9)
The weight values for the regression may be cal-
culated either in a single off line calculation or using
an on line weight update rule.
3.3.1 Off Line Regression
To use ordinary least squares (OLS) (Hastie et al.,
2009) to estimate the weights offline, a matrix X is
constructed where each row represents a training ex-
ample and each column represents a weight. The first
column represents W
0
and always contains a 1. The
remaining columns contain the product of the val-
ues of the inputs connected by the column’s weight,
∏
x∈Q
i
x. A vector Y takes the output values associ-
ated with each of the input rows and the parameters
are calculated using singular value decomposition:
β = (X
T
X)
−1
X
T
y (10)
where X
T
is the transpose of X, X
−1
is the inverse
of X and β becomes a vector from which the weights
of the MOHN may be directly read so that w
0
= β
0
1
The regression equation 9 is actually the negative of
the energy function, which is minimised by applying the
settling algorithm 2.
and the remaining weights take values from β in the
same sequence as they were inserted into the matrix
X.
3.3.2 LASSO Learning Rule
The LASSO algorithm (Tibshirani, 1996) may also be
used to learn the values on the weights of the MOHN.
Each input vector is set up in the same way as de-
scribed for OLS, by calculating the product of the
input values connected to each weight and the coef-
ficients generated by LASSO are read back into the
weights of the MOHN in the same order. LASSO per-
forms regression with an additional constraint on the
L
1
norm of the weight vector. The learning algorithm
minimises the sum:
∑
x∈D
( f (x) −
ˆ
f (x)) + λ
∑
w∈W
|w| (11)
where λ controls the degree of regularisation. When
λ = 0, the LASSO solution becomes the OLS solu-
tion. With λ > 0 the regularisation causes the sum of
the absolute weight values to shrink such that weights
with the least contribution to error reduction take a
value of zero. This not only allows LASSO to re-
ject input variables that contribute little, but also to re-
ject higher order weights that are not needed. LASSO
can be used as a simple method for choosing network
structure by over-connecting a network and then re-
moving all the zero valued weights after LASSO re-
gression has been performed.
3.3.3 On Line Learning
The weights of a MOHN can also be estimated on
line (where the data is streamed one pattern at a time,
rather than being available in a matrix as in equation
10) using a linear version of the delta learning rule,
the Linear Delta Rule (LDR):
w
i
= w
i
+ α( f (x) −
ˆ
f (x))
∏
u∈Q
i
u (12)
where α < 1 is the learning rate. Experimental re-
sults have suggested that one divided by the number
of weights in the network is a good value for α, i.e
α =
1
|W |
. This allows the correction made in response
to each prediction error to be spread across all of the
weights.
The online learning algorithm is very similar to
the perceptron (or MLP) learning algorithm. The iter-
ative nature of the algorithm allows for early stopping
to be used to control for overfitting with reference to
an independent test set. Algorithm 3 describes the
learning process.
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
20

Algorithm 3: On Line MOHN Learning with the Linear
Delta Rule.
Let D
r
be a subset of the available data to be used
for training the network
Let D
s
be a subset of the available data to be used
for testing the network
for all (x, f (x)) ∈ D
r
do
Initialise the weights in the network using the
parity rule of equation 7
end for
repeat
for all x ∈ D
r
do
Update the weights in the network using the
delta learning rule of equation 12
Let e be the root mean squared error that
results from evaluating every member of D
s
with
the model
end for
until e is sufficiently low or starts to increase con-
sistently
Note that the weights are initialised with the par-
ity count learning rule, not to random values as with
an MLP. This is because there are no local minima in
the error function and so no need for random starting
points. In cases where the entire input,output space
of the function may be noiselessly sampled, the ini-
tialisation step will produce the correct weights imea-
diately, without the need for additional error descent
learning. The learning algorithm will work without
the initialisation (the weights can be set to zero) but
then requires more iterations of the learning cycle.
4 ANALYSIS OF LEARNING
RULES
This section begins with a summary of the abilities
and limitations of the different learning rules pre-
sented in this paper. It then goes on to analyse the
rules and the resulting networks. Table 1 summarises
some of the differences between the methods. Due
to the structure of the MOHN, all of the learning rules
are capable of reproducing the maximal turning points
of the learned function, but the Hebbian based rules
do not minimise the error elsewhere in the function
space. The Hebbian rules learn in a single presenta-
tion of the data, so can operate in an on line mode
without the need to iterate through the data set more
than once. The others require either on line iterations
or the entire data set to be present off line.
The weighted Hebbian rule is accurate only when
a full sample of the input/output space is available,
Table 1: Comparing four different MOHN learning rules in
terms of the learning mode, any regularisation that is pos-
sible, whether or not the training error is minimised, and
whether the training data is presented as input,output pairs
(IO) or as patterns to store in a content addressable memory
(CAM).
Method Mode Reg. Min. Err. Data
Hebbian One shot None No CAM
Weighted Hebb One shot None No IO
LDR On line Early Stop Yes IO
OLS Off line None Yes IO
LASSO Off line L
1
-norm Yes IO
so is of limited practical use as the parity counting
method gives more accurate estimates operating on
weights independently with a single pass through the
data. The parity counting method provides good start-
ing weights for the linear delta rule.
The following sections investigate different net-
work structures in more detail.
4.1 Second Order Networks
When a MOHN has only second order connections,
it is equivalent to a Hopfield Neural Network (HNN)
(Hopfield, 1982) and the Hebbian learning rule of
equation 2 is the standard learning rule for a HNN.
It is well known that HNNs are able to learn patterns
as content addressable memories, but that they suffer
from the presence of spurious attractors too. These
spurious attractors may be removed (or their presence
avoided) by defining an energy function for the net-
work in which the patterns to be stored as memories
are local maxima. This may be done using a Ham-
ming distance based function and (Swingler, 2012),
(Swingler and Smith, 2014b) have shown that using
the weighted Hebbian update rule of equation 5 and
such a function on a second order MOHN (or equiv-
alently, a HNN) is sufficient to produce a content ad-
dressable memory in which the turning points of the
function are the memories to be stored. The capac-
ity of a HNN for storing patterns is the same if the
patterns are loaded directly with the Hebbian learn-
ing rule as it is when the patterns are learned from a
Hamming distance based function.
To build the Hamming distance based function,
denote the set of patterns to be stored as T:
T = {t
1
,... ,t
s
} (13)
and define a set of sub-functions, f (x|t
j
) as a
weighted Hamming distance between x and each tar-
get pattern t
j
in T as
f (x|t
j
) =
∑
δ
x
i
,t
ji
n
(14)
A Comparison of Learning Rules for Mixed Order Hyper Networks
21
where t
ji
is element i of target j and δ
x
j
,t
ji
is the Kro-
necker delta function between pattern element i in t
j
and its equivalent in x. The function output given an
input pattern, f (x) is the maximal output across all
the sub-functions given an input of f (x).
f (x|t) = max
j=1...s
( f (x|t
j
)) (15)
By generating random input patterns, evaluating
each using equation 15 and then using the LDR of
equation 12 to learn each input,output pair sampled,
a network with attractors at each member of T is
learned. The network has the additional quality that
as the number of samples learned increases, the num-
ber of spurious attractors in the network decreases.
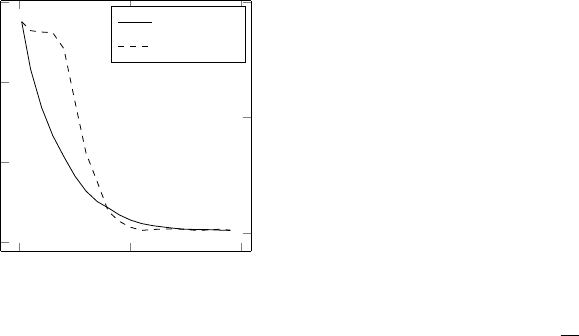
To test this claim, experiments were run in which
a 100 neuron MOHN was trained on a function that
contained four true attractor states. Figure 2 shows
the average results of running 100 trials in which the
number of spurious attractors and the error of the net-
work were measured for each iteration of the training
data, which was a random sample of size 20,000 from
the Hamming distance based function 15. In each
case, the number of spurious attractors was reduced
to zero as the training error approached zero.
0
50
100
0
0.1
0.2
0.3
Training Epoch
Training Error
0
500
1,000
Spurious Attractors
Error
Attractors
Figure 2: As the number of learning iterations increases,
the training error decreases as does the number of spurious
attractors in the model.
Researchers have shown how the weights of a
HNN can be designed to represent the travelling sales-
man problem (Hopfield and Tank, 1985), (Wilson
and Pawley, 1988) and other problems such as graph
colouring (Caparr
´
os et al., 2002). These approaches
are limited by the fact that the weights must be cho-
sen by hand to reflect the constraints of the problem
to be solved. By training a HNN (or a MOHN) by
sampling from a fitness function, it is now possible to
build a network to represent any problem with a fit-
ness function that can be evaluated, not just those that
are amenable to having their weights set by hand.
4.2 Full Networks
When the data are noise free, a network is fully con-
nected and the data sample is exhaustive (i.e. it covers
every possible input pattern once), the weighted Heb-
bian rule of equation 5 (with |D| = 2
n
) will produce
weights which reproduce the target function perfectly.
In such cases, the product
∏
u∈Q
i
u provides a basis
function for f : {−1, 1}
n
→ R. This basis function
is very similar to the well know Walsh basis (Walsh,
1923), (Beauchamp, 1984).
A Walsh representation of a function f (x) is de-
fined by a vector of parameters, the Walsh coeffi-
cients, ω = ω
0
...ω
2
n
−1
. Each ω
j
is associated with
the Walsh function ψ
j
. The Walsh representation of
f (x) is constructed as a sum over all ω
j
. In the sum,
each ω
j
is either added to or subtracted from the total,
depending on the value of the Walsh function ψ
j
(x)
which gives the function for the Walsh sum:
f (x) =
2
n−1
∑
j=0
ω
j
ψ
j
(x) (16)
A Walsh function, ψ
j
(x) returns +1 or -1 depend-
ing on the parity of the number of 1 bits in shared
positions across x and j where j is the binary repre-
sentation of the integer j. Using logical notation, a
Walsh function is derived from the result of an XOR
(parity count) of an AND (agreement of bits with a
value of 1):
ψ
j
(x) = ⊕
n
i=1
(x
i
∧ j
i
) (17)
where ⊕ is a parity operator, which returns 1 if the
argument list contains an even number of 1s and -1
otherwise. The Walsh transform of an n-bit function,
f (x), produces 2
n
Walsh coefficients, ω
j
, indexed by
the 2
n
combinations across f (x). Each Walsh coeffi-
cient, ω
j
is calculated by
ω
j
=
1
2
n
2
n
−1
∑
x=0
f (x)ψ
j
(x) (18)
The weight values in a fully trained MOHN are
equal in magnitude to the Walsh coefficients of the
same index, but that they differ in sign when the
weight order is an odd number. That is,
ω
j
= p(ω
j
)w
j
∀w
j
∈ W (19)
where p(ω
j
) is the parity of the order of ω
j
such that:
p(ω
j
) =
(
1 if the order of i is even
−1 otherwise
(20)
This is because the Walsh function returns a value
based on a parity count of the number of variables set
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
22

to one across the input variables that are connected to
a given coefficient, as shown in equation 17. The par-
ity function returns 1 if the number of variables with
a value of one is even and -1 otherwise. The MOHN
uses the product of those same values, which evalu-
ates to -1 whenever there is an odd number of inputs
set to -1. The MOHN indices match the Walsh coeffi-
cient indices because they both use the same method
of deriving the index number from the binary repre-
sentation of the connections described in section 2.
As a fully connected MOHN provides a basis for
all possible functions in f : {−1,1}
n
→ R, then it fol-
lows that any function with coefficient values of zero
may be perfectly represented by a less than fully con-
nected MOHN so providing the correct structure can
be found, a MOHN may represent any arbitrary func-
tion.
4.3 Discovering Network Structure
The structure of a MOHN is defined by W , which
is a subset of all possible 2
n
weights. As noted
above, a fully connected second order network im-
plements a HNN and a fully connected network at all
orders forms a basis of all functions f : {−1, 1}
n
→ R.
Any other pattern of connectivity is also possible, for
example a first order only network is equivalent to
a perceptron, or a multiple linear regression model.
Adding higher order weights increases the power of
the model to represent more complex functions.
Discovering the correct structure for the network
is both challenging and instructive, compared to the
same task when using an MLP, which is quite straight
forward, but done in the dark. The question of dis-
covering structure in functions from samples of data
is of particular importance in the field of metaheuris-
tic optimisation, where it is called linkage learning
(see (Pelikan et al., 2000), (Heckendorn and Wright,
2004)).
The correct structure for a function may be dis-
covered from the training data using an iterative ap-
proach of adding and removing weights as training
progresses. The basics of the structure discovery al-
gorithm are to train a partial network, test the signif-
icance of the weights it contains, remove those that
are not significant, then add new weights according
to some criteria. The weight picking criteria chosen
for this work are based on maintaining a probability
distribution over the possible weights, which is up-
dated on each round of learning so that connection
orders and neurons that have proved useful in previ-
ous rounds have a higher probability of being picked
in subsequent rounds. The process is described in al-
gorithm 4.
Algorithm 4: Probability distribution based structure dis-
covery algorithm.
Start with an empty network with weight set W =
/
0
Initialise a distribution over possible weights, P(w)
repeat
Sample new weights from the distribution P(w)
Calculate the values for all weights
Remove any insignificant weights from the net-
work
Update the weights distribution, P(w)
Calculate the test error
until The test error is sufficiently low or doesn’t
change
The probability distribution over W is based on
the order of a weight and the neurons it connects. The
sampling process involves first picking an order, k for
the weight to be added from a distribution, Pk() over
all possible orders (1... n) and then picking k neu-
rons to connect from a distribution, Pn() over the n
available neurons. The choice made for the algorithm
described here is to impose an exponential distribu-
tion on the choice of weight order, centred at order
c where initially c = 1 and c is incremented as lower
order weights are either used or discarded.
Pk(k) = λe
−λ|c−k|
(21)
where λ controls the width of the distribution. In the
early iterations of the algorithm where c = 1, there
is a high probability of picking first order weights
and an exponentially decreasing probability of pick-
ing weights of higher order. In subsequent itera-
tions, Pk(k) is updated in two ways. Firstly, c is
incremented to allow the algorithm to pick weights
with higher orders and secondly the values of existing
weights are used to shape the distribution to guide the
algorithm towards orders that have yielded high value
weights already.
The weight order probability distribution, Pk(k) is
updated by counting the proportion of weights in the
current network that are of each order. Let this vector
of proportions be p = p
1
... p
n
where p
i
is the number
of weights at order i divided by the total number of
weights in the network. These proportions are then
used to update Pk() as follows along with an updated
version of the exponential distribution:
Pk(i) ← (1 − (α + β))Pk(i) + αp
i
+βλe
−λ|c−k|
(22)
where α and β are update rates such that 0 ≤ α ≤ 1,
0 ≤ β ≤ 1 and 0 < α + β ≤ 1.
The neuron distribution update rule sets the prob-
ability of a neuron being picked to be proportionate
A Comparison of Learning Rules for Mixed Order Hyper Networks
23

to the sum of the absolute values of the weights con-
nected to it. The contribution of neuron i is C(i)
C(i) =
∑
x
i
∈w
|w| (23)
and the probability of picking neuron i is
Pn(i) =
C(i)
∑
n−1
j=0
C( j)
(24)
As each new set of weights is added, another
phase of learning cycles is required to update the new
network. The existing weight values will be close
to their correct value, but need to change slightly to
accommodate the newly added weights. The new
weights also need to be learned. This is requires an on
line learning approach as the existing weights need to
be moved from their current values, rather than cal-
culated from scratch, making the delta rule the ideal
choice. Weights may be identified for removal by per-
forming a t-test on their values, looking for significant
difference from zero in order to keep a weight. Al-
ternatively, each new structure may be learned from
scratch using LASSO, which has the advantage of au-
tomatically identifying the weights to remove as those
with a coefficient of zero.
This approach to growing a neural network differs
from the many previously reported methods in that it
only adds weights, not neurons. Generally, grow-and-
learn neural network algorithms proceed by adding
neurons to the existing hidden layer or by introduc-
ing new layers. For example the Netlines algorithm
(Torres-Moreno and Gordon, 1998) adds binary hid-
den units one at a time in an incremental approach to
learning classifier functions. The Upstart algorithm
(Frean, 1990), on the other hand, produces deeper tree
structured networks by adding pairs of hidden units
between the input layer and the current first hidden
layer. As a MOHN contains no hidden units, it is only
weights, not neurons that are added at each iteration
of the growth algorithm.
The MOHN may also be compared to other sta-
tistical models. By introducing a link function, a
MOHN becomes a generalised linear model (GLM)
(Dobson and Barnett, 2011). A link function is usu-
ally a non-linear function that is applied to the output
of a linear regression to allow a wider range of proba-
bility distributions to be modelled. The general form
is
g(x) = ˆy (25)
where ˆy is the energy function of the network from
equation 9 and g(x) is the link function. If the in-
verse of g (x) is known, then the learning rules may
all be used with the simple replacement of f (x)
with g
−1
( f (x)). For example, setting g(x) = e
x
and
g
−1
(x) = ln(x) constructs a Boltzmann distribution if
the target values, f (x) are proportional to the prob-
ability of pattern x. This is the approach taken in
(Shakya et al., 2012) who use a Markov Random
Field to model the distribution of solutions to opti-
misation problems by training a mixed order network
with an exponential link function using OLS.
5 EXPERIMENTAL RESULTS
In this section, the learning rules described in this pa-
per are compared with each other and with a standard
multi layer perceptron (MLP) for the speed at which
they learn. The Hamming distance based function of
equation 15 was used for these tests as it is possible to
generate arbitrary functions containing a chosen num-
ber of turning points at random locations. This allows
the different methods to be tested across thousands of
different functions of varying degrees of complexity.
5.1 Speed Against Complexity
One way to vary the complexity of a function is to
vary the number of turning points it contains. This
section describes a set of experiments designed to
measure the speed of learning of each of the MOHN
learning rules and an MLP as the complexity of the
function to be learned varies. Each single experiment
involved training a MOHN and an MLP on a data set
generated from a function with a random number of
turning points. The same data was used to train three
different MOHNs, one with each learning rule from
OLS, LASSO and LDR. The function had 15 inputs
and the MOHNs were fully connected up to order
three, giving them 576 weights. The MLP has only
10 hidden units, giving it only 176 weights.
A sample of 580 random points was used for train-
ing each network. For the iterative learning methods
(all except OLS) a target error of 0.01 was used as a
stopping criteria, hence the measure of interest was
time taken to reach a training error of 0.01. This pro-
cess was repeated 1000 times, each with a new func-
tion with a number of turning points between 1 and
30.
Figure 3 shows the results. All methods except
the MLP learned the function in a constant time, re-
gardless of the degree of complexity. The MLP was
able to learn the single turning point function (i.e. lin-
ear function) in less time than it was able to learn the
more complex functions. The function with two turn-
ing points was also faster than those with more. After
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
24
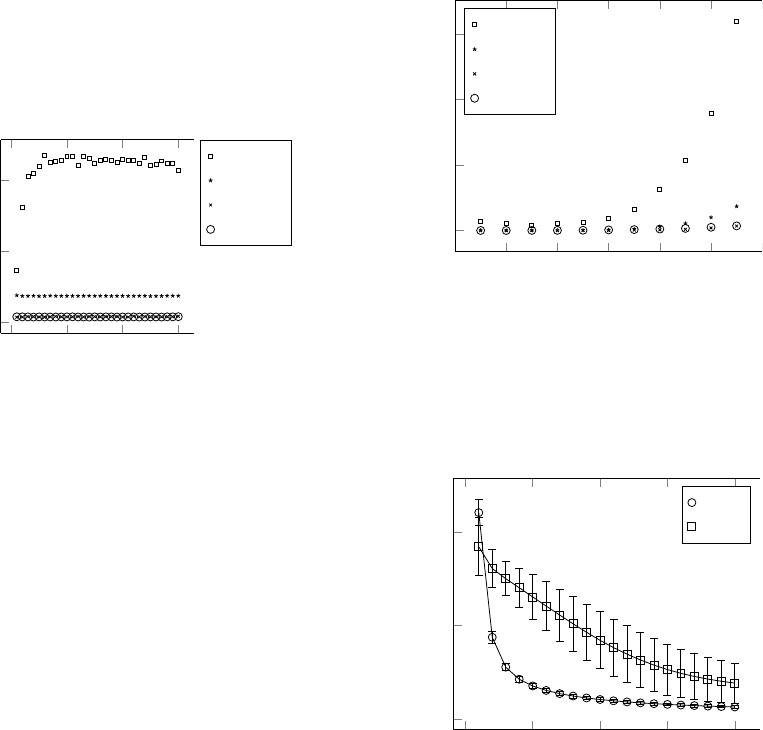
two turning points, the learning time for the MLP be-
came constant. Regardless of the complexity of the
function, the MLP always took considerably longer,
followed by OLS. The LDR and LASSO algorithms
took similar amounts of time and were the fastest.
0 10 20 30
0
1,000
2,000
Turning Points
Training Time
Learning Time by Complexity
MLP
OLS
LASSO
LDR
Figure 3: Average learning time in milliseconds by function
complexity for different MOHN learning rules and an MLP.
The LASSO and LDR values are almost equal and can be
seen along the bottom of the graph.
5.2 Speed By Network Size
Another set of similar experiments related the training
speed of each method to the size of the network. The
number of inputs to a network was varied from 5 to
15 and 1000 trials were run. The mean squared error
of the result of performing OLS was used as the stop-
ping criteria for the MLP and the MOHN as it was
trained with LDR, ensuring that all models had the
same level of accuracy. Figure 4 shows the results.
OLS is known to have a time complexity of O(np
2
)
where n is the number of data points and p is the num-
ber of variables. LASSO and LDR were of the same
order, but the algorithms ran in less time. The MLP’s
training time grew exponentially with the number of
variables in these particular experiments. As before
the MOHN models all reached the target training er-
ror faster than the MLP.
5.2.1 Error Descent Rate
The difference in training speed between the MOHN
and an MLP was investigated further by recording the
average error by training epoch for the first twenty
passes through the training data. Figure 5 shows the
average error on each pass of the training data from
1000 repeated trials on functions of varying complex-
ity. The error bars show 1 standard deviation from
the mean. Note that the MOHN error drops faster and
that there is far less variation across trials (the error
4
6
8 10 12 14
16
0
1,000
2,000
3,000
Input Variables
Training Time
Learning Time by Network Size
MLP
OLS
LASSO
LDR
Figure 4: Average learning time in milliseconds by number
of inputs for different MOHN learning rules and an MLP.
bars for the MOHN are sufficiently short that they sit
inside the marks).
0
5
10
15
20
0
0.2
0.4
Training Epochs
Training Error
Training Error by Epoch
LDR
MLP
Figure 5: The mean and standard deviation of training error
as it descends over twenty training epochs, comparing an
MLP with the Linear Delta Rule training a MOHN.
The improved learning speed of the MOHN and
the slower, more varied speed of the MLP may be
explained by the fact that the MLP combines fitting
parameter values with feature selection. Recently,
(Swingler, 2014) provided an insight into the phases
of MLP training, showing that early training cycles
are taken up with fixing the role of the hidden units
and later cycles then fit the parameters within the con-
straints of the features encoded by those hidden units.
The MOHN does not have hidden units and so only
needs to fit parameter values to its fixed structure. Of
course, that structure needs to be discovered, but the
task of structure discovery and parameter fitting are
separated, unlike the case for the MLP.
Another consequence of the MLP’s dual learning
A Comparison of Learning Rules for Mixed Order Hyper Networks
25
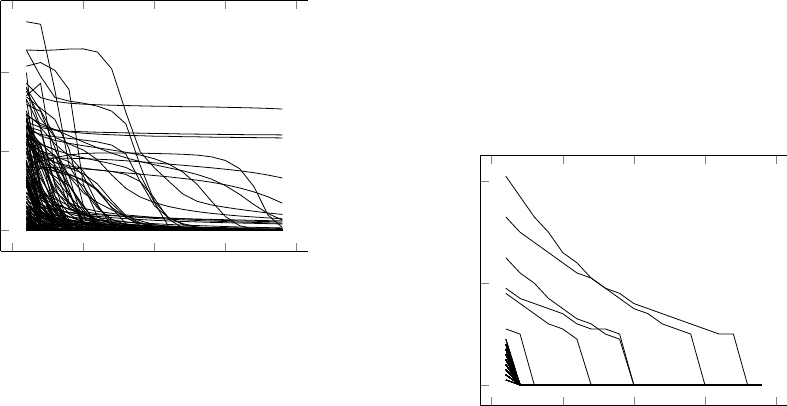
0
500
1,000
1,500
2,000
0.00
0.05
0.10
Training Epoch
Training Error
Training Error Descent for MLP
Figure 6: Traces of training error over 200 different at-
tempts at training an MLP on a concatenated XOR function.
Note the variation in convergence time and the presence of
a number of failed attempts after 2000 epochs.
task of fitting both function structure and regression fit
is that the error function contains local minima. These
occur when the hidden units encode a suboptimal set
of features and the network fits weight values to them.
This is commonly solved by re-starting the training
process from a different random set of initial weight
values. The MOHN error function does not contain
local minima, so the weights do not need to be ran-
domised before learning, as shown in algorithm 3. To
illustrate this point, a final set of experiments com-
pared an MLP trained with error back propagation to
a MOHN trained with the LDR on a function designed
to contain local minima in its cost function. The func-
tion to be learned was a concatenation of XOR pairs
such that each x
i
where i is even is paired with x
i+1
to form an XOR function. The function output is the
normalised sum of the XOR of the pairs, so 101010
would produce an output of one and 110011 would
produce zero. Figure 6 shows the traces of 200 MLPs
started with random weights, each trained for 2000
cycles through the training data. The variation in er-
ror descent is clear, with some networks converging
quickly, some taking many training epochs to con-
verge, and some still stuck in local minima after 2000
epochs.
For functions of small numbers of inputs, it was
possible to exhaustively sample the function space
and so use the weighted Hebb rule to allow the
MOHN to learn the function fully in a single pass of
the data. For networks where the number of inputs is
too large for an exhaustive sample, a random sample
was taken. Figure 7 shows the trace of the training
error during 200 attempts at learning the same XOR
based function as that in figure 6 using a MOHN with
the LDR. The variation is not due to random starting
points—all networks start with weights at zero—but
is due to the fact that the training data is a small ran-
dom subset of the full input space. Note that there are
no traces that indicate a local minimum; all go to zero
error.
0
50
100
150
200
0.000
0.002
0.004
Training Epoch
Training Error
Training Error Descent for MOHN
Figure 7: Traces of training error over 200 different at-
tempts at training a MOHN on a concatenated XOR func-
tion. Compare both the scale of the error and the number of
training epochs involved with the same plot for the MLP in
figure 6.
6 SUMMARY AND FUTURE
DIRECTIONS
Mixed Order Hyper Networks are universal function
approximators over f : {−1,1}
n
→ R. They may be
trained from a sample of data to act as either a re-
gression function that attempts to fit the function that
underlies the data across the entire function space or
just to capture the function’s turning points as energy
minima. Learning may be off line, in which case all
of the data needs to be available at one time, or on
line in situations where data is streamed or the net-
work structure is changing and existing weights need
to be updated. This paper presented five learning rules
designed to cover both on line and off line learning,
and both regression and content addressable memory
learning. Other learning methods might also be con-
sidered such as ridge regression or LARS, but that is
left for future work.
This paper has only presented networks for func-
tion learning, but they may also be used as classifiers.
As a MOHN has only one output, binary classifica-
tions are straight forward. Further work is required
to discover the best way to learn multi-class models.
Learning a classifier will also introduce the possibility
NCTA 2015 - 7th International Conference on Neural Computation Theory and Applications
26
of using alternative learning algorithms such as Min-
imerror (Torres-Moreno et al., 2002), which is a per-
ceptron learning rule with a cost function designed to
reduce the number of classification errors rather than
mean squared error. The MOHN and its learning rules
would also be usefully compared to deep networks as
they present a start contrast in approach.
The issue of MOHN structure discovery was also
raised, but the detail is left for future work. The exper-
iments presented in this paper worked on the assump-
tion that the networks in question contained weights
of sufficient order to capture the functions on which
they were trained. This becomes increasingly difficult
as the number of inputs grows. Problems with large
numbers of inputs require a structure discovery phase
to be carried out as part of the training process.
With a given network structure, training a MOHN
is faster and has less error variance across trials than
training with an MLP. Additionally, the training al-
gorithm has no local minima when training a fixed
structure MOHN, making training more reliable than
that of an MLP. Of course, any algorithm used to dis-
cover the correct structure for the MOHN may well
have local optima, but that (again) is a matter for fu-
ture work.
REFERENCES
Beauchamp, K. (1984). Applications of Walsh and Related
Functions. Academic Press, London.
Caparr
´
os, G. J., Ruiz, M. A. A., and Hern
´
andez, F. S.
(2002). Hopfield neural networks for optimization:
study of the different dynamics. Neurocomputing,
43(1-4):219–237.
Dobson, A. J. and Barnett, A. (2011). An introduction to
generalized linear models. CRC press.
Frean, M. (1990). The upstart algorithm: A method for con-
structing and training feedforward neural networks.
Neural computation, 2(2):198–209.
Hastie, T., Tibshirani, R., Friedman, J., Hastie, T., Fried-
man, J., and Tibshirani, R. (2009). The elements of
statistical learning, volume 2. Springer.
Heckendorn, R. B. and Wright, A. H. (2004). Efficient link-
age discovery by limited probing. Evolutionary com-
putation, 12(4):517–545.
Hopfield, J. J. (1982). Neural networks and physical sys-
tems with emergent collective computational abili-
ties. Proceedings of the National Academy of Sciences
USA, 79(8):2554–2558.
Hopfield, J. J. and Tank, D. W. (1985). Neural computa-
tion of decisions in optimization problems. Biological
Cybernetics, 52:141–152.
Kubota, T. (2007). A higher order associative memory with
Mcculloch-Pitts neurons and plastic synapses. In Neu-
ral Networks, 2007. IJCNN 2007. International Joint
Conference on, pages 1982 –1989.
Pelikan, M., Goldberg, D. E., and Cant
´
u-paz, E. E.
(2000). Linkage problem, distribution estimation,
and bayesian networks. Evolutionary Computation,
8(3):311–340.
Shakya, S., McCall, J., Brownlee, A., and Owusu, G.
(2012). Deum - distribution estimation using markov
networks. In Shakya, S. and Santana, R., editors,
Markov Networks in Evolutionary Computation, vol-
ume 14 of Adaptation, Learning, and Optimization,
pages 55–71. Springer Berlin Heidelberg.
Swingler, K. (2012). On the capacity of Hopfield neural
networks as EDAs for solving combinatorial optimi-
sation problems. In Proc. IJCCI (ECTA), pages 152–
157. SciTePress.
Swingler, K. (2014). A walsh analysis of multilayer percep-
tron function. In Proc. IJCCI (NCTA), pages –.
Swingler, K. and Smith, L. (2014a). Training and making
calculations with mixed order hyper-networks. Neu-
rocomputing, (141):65–75.
Swingler, K. and Smith, L. S. (2014b). An analysis of
the local optima storage capacity of hopfield network
based fitness function models. Transactions on Com-
putational Collective Intelligence XVII, LNCS 8790,
pages 248–271.
Tibshirani, R. (1996). Regression shrinkage and selection
via the lasso. Journal of the Royal Statistical Society.
Series B (Methodological), pages 267–288.
Torres-Moreno, J.-M., Aguilar, J., and Gordon, M.
(2002). Finding the number minimum of errors in n-
dimensional parity problem with a linear perceptron.
Neural Processing Letters, 1:201–210.
Torres-Moreno, J.-M. and Gordon, M. B. (1998). Efficient
adaptive learning for classification tasks with binary
units. Neural Computation, 10(4):1007–1030.
Venkatesh, S. S. and Baldi, P. (1991). Programmed inter-
actions in higher-order neural networks: Maximal ca-
pacity. Journal of Complexity, 7(3):316–337.
Walsh, J. (1923). A closed set of normal orthogonal func-
tions. Amer. J. Math, 45:5–24.
Wilson, G. V. and Pawley, G. S. (1988). On the stability of
the travelling salesman problem algorithm of hopfield
and tank. Biol. Cybern., 58(1):63–70.
A Comparison of Learning Rules for Mixed Order Hyper Networks
27
