Multi-Strategy Genetic Algorithm for Multimodal Optimization
Evgenii Sopov
Department of Systems Analysis and Operations Research, Siberian State Aerospace University, Krasnoyarsk, Russia
Keywords: Multimodal Optimization, Self-Configuration, Genetic Algorithm, Metaheuristic, Niching.
Abstract: Multimodal optimization (MMO) is the problem of finding many or all global and local optima. In recent
years many efficient nature-inspired techniques (based on ES, PSO, DE and others) have been proposed for
real-valued problems. Many real-world problems contain variables of many different types, including
integer, rank, binary and others. In this case, the weakest representation (namely binary representation) is
used. Unfortunately, there is a lack of efficient approaches for problems with binary representation. Existing
techniques are usually based on general ideas of niching. Moreover, there exists the problem of choosing a
suitable algorithm and fine tuning it for a certain problem. In this study, a novel approach based on a
metaheuristic for designing multi-strategy genetic algorithm is proposed. The approach controls the
interactions of many search techniques (different genetic algorithms for MMO) and leads to the self-
configuring solving of problems with a priori unknown structure. The results of numerical experiments for
classical benchmark problems and benchmark problems from the CEC competition on MMO are presented.
The proposed approach has demonstrated efficiency better than standard niching techniques and comparable
to advanced algorithms. The main feature of the approach is that it does not require the participation of the
human-expert, because it operates in an automated, self-configuring way.
1 INTRODUCTION
Many real-world problems have more than one
optimal solution, or there exists only one global
optimum and several local optima in the feasible
solution space. Such problems are called
multimodal. The goal of multimodal optimization
(MMO) is to find all optima (global and local) or a
representative subset of all optima.
Evolutionary and genetic algorithms (EAs and
GAs) demonstrate good performance for many
complex optimization problems. EAs and GAs are
also efficient in the multimodal environment as they
use a stochastic population-based search instead of
the individual search in conventional algorithms. At
the same time, traditional EAs and GAs have a
tendency to converge to the best-found optimum
losing population diversity.
In recent years MMO have become more
popular, and many efficient nature-inspired MMO
techniques were proposed. Almost all search
algorithms are based on maintaining the population
diversity, but differ in how the search space is
explored and how optima basins are located and
identified over a landscape. The majority of
algorithms and the best results are obtained for real-
valued MMO problems (Das et al., 2011). The main
reason is the better understanding of landscape
features in the continuous search space. Thus many
well-founded heuristics can be developed.
Unfortunately many real-world MMO problems
are usually considered as black-box optimization
problems and are still a challenge for MMO
techniques. Moreover, many real-world problems
contain variables of many different types, including
integer, rank, binary and others. In this case, usually
binary representation is used. Unfortunately, there is
a lack of efficient approaches for problems with
binary representation. Existing techniques are
usually based on general ideas of niching and fitness
sharing. Heuristics from efficient real-valued MMO
techniques cannot be directly applied to binary
MMO algorithms because of dissimilar landscape
features in the binary search space.
In this study, a novel approach based on a
metaheuristic for designing multi-strategy MMO GA
is proposed. Its main idea is to create an ensemble of
many MMO techniques and adaptively control their
interactions. Such an approach would lead to the
self-configuring solving of problems with a priori
unknown structure.
The rest of the paper is organized as follows.
Section 2 describes related work. Section 3 describes
Sopov, E..
Multi-Strategy Genetic Algorithm for Multimodal Optimization.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 55-63
ISBN: 978-989-758-157-1
Copyright
c
2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
55
the proposed approach. In Section 4 the results of
numerical experiments are discussed. In the
Conclusion the results and further research are
discussed.
2 RELATED WORK
The problem of MMO has exists since the first EAs.
The first MMO techniques were applied in EAs and
GAs for improvement in finding the global optimum
in the multimodal environment.
The MMO, in general, can have at least 3 goals
(Preuss, 2014):
to find a single global optimum over the
multimodal landscape only;
to find all global optima;
to find all optima (global and local) or a
representative subset of all optima.
It is obvious that the second and the third goals
are more interesting from both a theoretical and a
practical point of view.
Over the past decade interest for this field has
increased. The recent approaches are focused on the
goal of exploring the search space and finding many
optima to the problem. Many efficient algorithms
have been proposed. In 2013, the global completion
on MMO was held within IEEE CEC'13 (Li et al.,
2013a).
The list of widespread MMO techniques includes
(Das et al., 2011; Liu et al., 2011; Deb and Saha,
2010):
1. General techniques:
Niching (parallel or sequential)
Fitness sharing, Clearing and Cluster-based
niching
Crowding and Deterministic crowding
Restricted tournament selection (RTS)
Mating restriction
Species conservation
2. Special techniques:
Niching memetic algorithm
Multinational EA
Bi-objective MMO EA
Clustering-based MMO EA
Population-based niching
Topological algorithms
3. Other nature-inspired techniques:
PSO, ES, DE, Ant Colony Optimization and
others
Binary and binarized MMO problems are usually
solved using the GA based on general techniques.
Also special techniques are applied, but some of
their features can be lost in the binary space.
Unfortunately, many efficient nature-inspired MMO
algorithms have no binary version and cannot be
easily converted to binary representation.
As we can see from many studies, there is no
universal approach that is efficient for all MMO
problems. Many researches design hybrid
algorithms, which are generally based on a
combination of search algorithms and some heuristic
for niching improvement. For example, here are four
top-ranked algorithms from the CEC’13 competition
on MMO: Niching the CMA-ES via Nearest-Better
Clustering (NEA2), A Dynamic Archive Niching
Differential Evolution algorithm (dADE/nrand/1),
CMA-ES with simple archive (CMA-ES) and
Niching Variable Mesh Optimization algorithm (N-
VMO) (Li et al., 2013b).
Another way is combining many basic MMO
algorithms to run in parallel, migrate individuals and
combine the results. In (Bessaou et al., 2000) an
island model is applied, where islands are iteratively
revised according to the genetic likeness of
individuals. In (Yu and Suganthan, 2010) four MMO
niching algorithms run in parallel to produce
offspring, which are collected in a pool to produce a
replacement step. In (Qu et al., 2012) the same
scheme is realized using the clearing procedure.
The conception of designing MMO algorithms in
the form of an ensemble seems to be perspective. A
metaheuristic that includes many different MMO
approaches (different search strategies) can deal
with many different MMO problems. And such a
metaheuristic can be self-configuring due to the
adaptive control of the interaction of single
algorithms during the problem solving.
In (Sopov, 2015) a self-configuring multi-
strategy genetic algorithm in the form of a hybrid of
the island model, competitive and cooperative
coevolution was proposed. The approach is based on
a parallel and independent run of many versions of
the GA with many search strategies, which can deal
with many different features of optimization
problems inside the certain optimization class. The
approach has demonstrated good results with respect
to multi-objective and non-stationary optimization.
3 MULTI-STRATEGY MMO GA
In the field of statistics and machine learning,
ensemble methods are used to improve decision
making. On average, the collective solution of
multiple algorithms provides better performance
than could be obtained from any of the constituent
algorithms. This concept can be also used in the
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
56
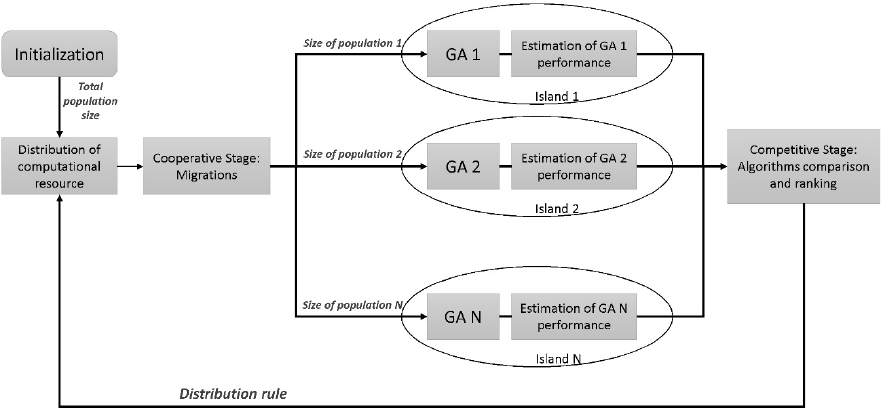
Figure 1: The Self*GA structure.
field of EA. The main idea is to include different
search strategies in the ensemble and to design
effective control of algorithm interaction. Our
hypothesis is that different EAs are able to deal with
different features of the optimization problem, and
the probability of all algorithms failing with the
same challenge in the optimization process is low.
Moreover, the interaction of algorithms can provide
the ensemble with new options for optimization,
which are absent in stand-alone algorithms.
The general structure of the self-configuring
multi-strategy genetic algorithm proposed in (Sopov,
2015) is called Self*GA (the star sign corresponds to
the certain optimization problem) and it is presented
in Figure 1.
The total population size (or the sum of
populations of all stand-alone algorithms) is called
the computational resource. The resource is
distributed between algorithms, which run in parallel
and independent over the predefined number of
iterations (called the adaptation period). All
algorithms have the same objective and use the same
encoding (solution representation). All populations
are initialized at random. After the distribution, each
GA included in Self*GA has its own population
which does not overlap with populations of other
GAs. At the first iteration, all algorithms get an
equal portion of the resource. This concept
corresponds to the island model, where each island
realizes its own search strategy.After the adaptation
period, the performance of individual algorithms is
estimated with respect to the objective of the
optimization problem. After that algorithms are
compared and ranked. Search strategies with better
performance increase their computational resource
(the size of their populations). At the same time, all
algorithms have a predefined amount of resource
that is not distributed to give a chance for algorithms
with low performance. This concept corresponds to
the competitive coevolution scheme.
Finally, migrations of the best solutions are set to
equate the start positions of algorithms for the run
with the next adaptation period. According to the
optimization problem, such a migration can be
deterministic, selection-based or random. This
concept corresponds to cooperative coevolution.
Such a technique eliminates the necessity to
define an appropriate search strategy for the problem
as the choice of the best algorithm is performed
automatically and adaptively during the run.
Now we will discuss the design of a Self*GA for
MMO problems that can be named SelfMMOGA.
At the first step, we need to define the set of
individual algorithms included in the SelfMMOGA.
In this study we use six basic techniques, which are
well-studied and discussed (Singh and Deb, 2006;
Das et al., 2011), and they can be used with binary
representation with no modification. Algorithms and
their specific parameters are presented in Table 1.
All values for radiuses and distances in Table 1 are
in the Hamming metric for binary problems and in
the Euclidean metric for continuous problems.
The motivation of choosing certain algorithms is
that if the SelfMMOGA performs well with basic
techniques, we can develop the approach with more
complex algorithms in further works.
The adaptation period is a parameter of the
SelfMMOGA. Moreover, the value depends on the
Multi-Strategy Genetic Algorithm for Multimodal Optimization
57

Table 1: Algorithms include in the SelfMMOGA.
Algorithm Parameters
Alg1 Clearing
Clearing radius, Capacity of
a niche
Alg2 Sharing
Niche radius, α
Alg3 Clustering
Number of clusters, min
distance to centroid, max
distance to centroid
Alg4
Restricted
Tournament
Selection (RTS)
Window size
Alg5
Deterministic
Crowding
-
Alg6
Probabilistic
Crowding
-
limitation of the computational resource (total
number of fitness evaluations).
The key point of any coevolutionary scheme is
the performance evaluation of a single algorithm.
For MMO problems performance metrics should
estimate how many optima were found and how the
population is distributed over the search space.
Unfortunately, good performance measures exist
only for benchmark MMO problems, which contain
knowledge of the optima. Performance measures for
black-box MMO problems are still being discussed.
Some good recommendations can be found in
(Preuss and Wessing, 2013). In this study, the
following criteria are used.
The first measure is called Basin Ratio (BR). The
BR calculates the number of covered basins, which
have been discovered by the population. It does not
require knowledge of optima, but an approximation
of basins is used. The BR can be calculated as
=
(1)
=1,,
∈
,
=
1,∈
0,
where pop is the population, k is the number of
identified basins by the total population, l is the
indicator of basin coverage by a single algorithm, b
is a function that indicates if an individual is in basin
z.
To use the metric (1), we need to define how to
identify basins in the search space and how to
construct the function b(x,z).
For continuous MMO problems, basins can be
identified using different clustering procedures like
Jarvis-Patrick, the nearest-best and others (Preuss et
al., 2011). In this study, for MMO problems with
binary representation we use the following approach.
We use the total population (the union of
populations of all individual algorithms in the
SelfMMOGA). For each solution, we consider a
predefined number of its nearest neighbours (with
respect to the Hamming distance). If the fitness of
the solution is better, it is denoted as a local optima
and the centre of the basin. The number of
neighbours is a tunable parameter. For a real-world
problem, it can be set from some practical point of
view. The simplified basin identification procedure
is described using a pseudo-code as follows:
Z=∅;
for all (x ∈ total population)
{
for i=1,..,S
y
i
=define nearest neighbour(x);
for all y
i
if (fitness(x) > fitness(y
i
))
{
Z=Z+x;
};
};
The function b(x,z) can be easily evaluated by
defining if individual x is in a predefined radius of
basin centre z. The radius is a tunable parameter. In
this study, we define it as
=
(2)
where k is the number of identified basins (=
|
|
).
The second measure is called Sum of Distances
to Nearest Neighbour (SDNN). The SDNN penalizes
the clustering of solutions. This indicator does not
require knowledge of optima and basins. The SDNN
can be calculated as
=
,
(3)
,
=min
∈\
,
where d
nn
is the distance to the nearest neighbour,
dist is the Hamming distance.
Finally, we combine the BR and the SDNN in an
integrated criterion K:
=∙1∙
(4)
where
is a normalized value of ,
defines weights of the BR and the SDNN in the sum
(∈0,1.
Next, we need to design a scheme for the
redistribution of computational resources. New
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
58

population sizes are defined for each algorithm. In
this study, all algorithms give to the “winner”
algorithm a certain percentage of their population
size, but each algorithm has a minimum guaranteed
resource that is not distributed. The guaranteed
resource can be defined by the population size or by
problem features.
At the coopearative stage, in many
coevolutionary schemes, all individual algorithms
begin each new adaptation period with the same
starting points (such a migration scheme is called
“the best displaces the worst”). For MMO problems,
the best solutions are defined by discovered basins
in the search space. As we already have evaluated
the approximation of basins (Z), the solutions from Z
are introduced in all populations replacing the most
similar individuals.
Stop criteria in the SelfMMOGA are similar to
those in the standard GA: maximum number of
objective evaluations, the number of generations
with no improvement (stagnation), etc.
4 EXPERIMENTAL RESULTS
To estimate the approach performance we have used
the following list of benchmark problems:
Six binary MMO problems are from (Yu and
Suganthan, 2010). These test functions are based
on the unitation functions, and they are
massively multimodal and deceptive.
Eight real-valued MMO problems are from
CEC’2013 Special Session and Competition on
Niching Methods for Multimodal Function
Optimization (Li et al., 2013b).
Table 2: Test suite.
Problem
Number of desirable
optima
Problem
dimensionality*
binaryF11 32 global 30
binaryF12 32 global 30
binaryF13 27 global 24
binaryF14 32 global 30
binaryF15 32 global 30
binaryF16 32 global 30
cecF1 2 global + 3 local 9, 12, 15, 19, 22
cecF2 5 global 4, 7, 10, 14 ,17
cecF3 1 global + 4 local 4, 7, 10, 14 ,17
cecF4 4 global 14, 22, 28, 34, 42
cecF5 2 global + 2 local 11, 17, 24, 31, 37
cecF6 18 global + 742 local 16, 22, 30, 36, 42
cecF7 36 global 14, 20, 28, 34, 40
cecF8 12 global 8, 14, 20, 28, 34
* Real-valued problems have been binarized using the
standard binary encoding with 5 accuracy levels.
We have denoted the functions as in the source
papers. Some details of the problems are presented
in Table 2.
In all comparisons, all algorithms have equal
maximum number of the objective evaluations, but
may differ in population sizes.
The following criteria for estimating the
performance of the SelfMMOGA over the
benchmark problems are used for continuous
problems:
Peak Ratio (PR) measures the percentage of all
optima found by the algorithm (Equation 5).
Success Rate (SR) measures the percentage of
successful runs (a successful run is defined as a
run where all optima were found) out of all runs.
=
|
∈|
,
|
(5)
where =
,
,…,
is a set of known optima,
is accuracy level.
The maximum number of function evaluation
and the accuracy level for the PR evaluation are the
same as in CEC completion rules (Li et al., 2013b).
The number of independent runs of the algorithm is
50.
In the case of binary problems, we cannot define
the accuracy level in the PR, thus the exact points in
the search space have to be found. This is a great
challenge for search algorithms, thus we have
substituted the SR measure with Peak Distance
(PD). The PD indicator calculates the average
distance of known optima to the nearest individuals
in the population (Preuss and Wessing, 2013).
=
1
,
(6)
To demonstrate the control of algorithm
interaction in the SelfMMOGA, we have chosen an
arbitrary run of the algorithm on the cecF1 problem
and have visualized the distribution of the
computational resource (see Figure 2). The total
population size is 200 and the minimal guaranteed
amount of the computational recourse is 10. The
maximum number of generations is 200 and the size
of the adaptation period is 10, thus the horizontal
axis contains numeration of 20 periods.
As we can see, there is no algorithm that wins all
the time. At the first two periods, Sharing (Alg2) and
Clearing (Alg1) had better performance. The highest
amount of the resource was won by Clustering
(Alg3) at the 10th period. At the final stages,
Deterministic Crowding showed better performance.
The results of estimating the performance of the
SelfMMOGA with the pack of binary problems are
Multi-Strategy Genetic Algorithm for Multimodal Optimization
59
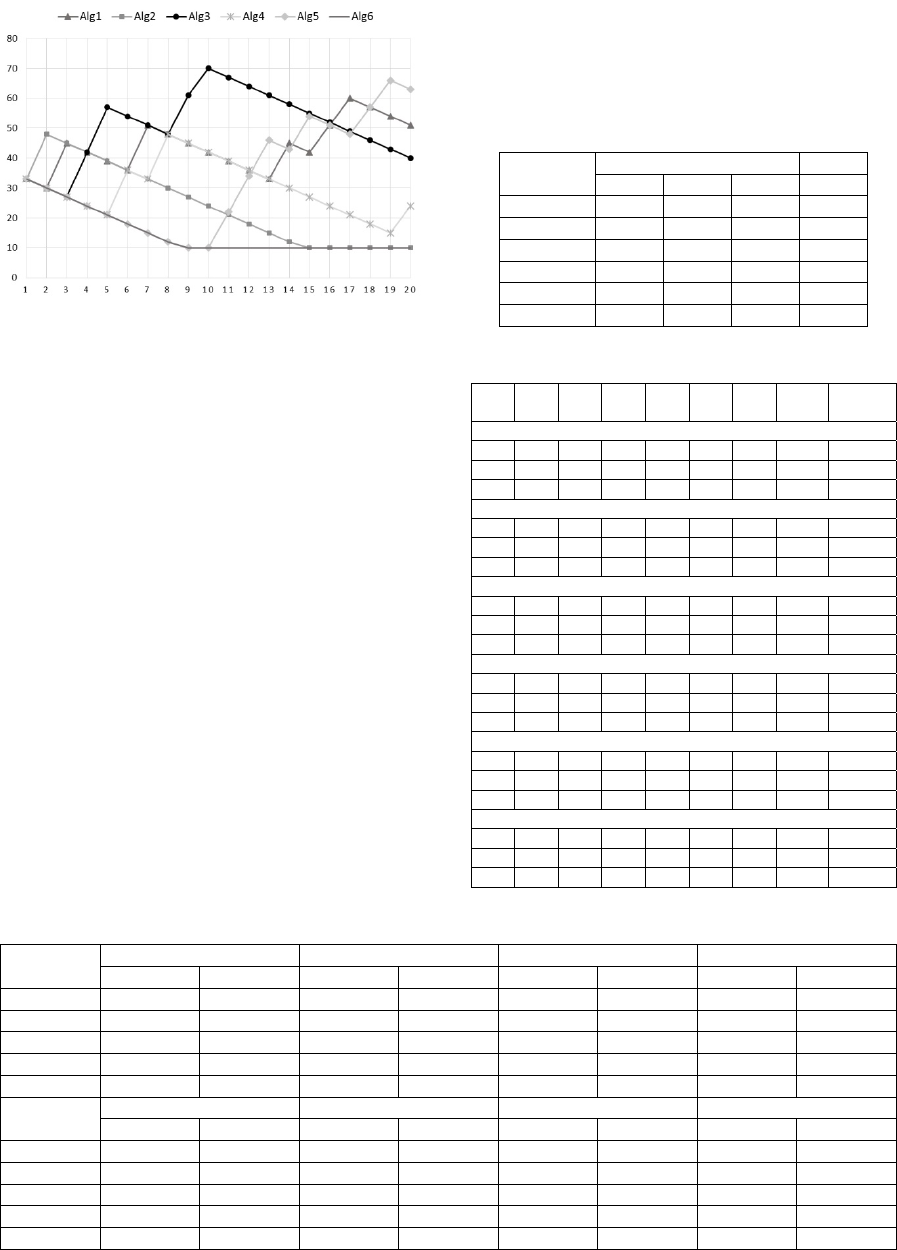
Figure 2: Example of the SelfMMOGA run.
presented in Table 3. The table contains the values
of the PR, the SR and the PD averaged over 50
independent runs. We also have compared the
results with Ensemble of niching algorithms (ENA)
proposed in (Yu and Suganthan, 2010). There is
only the SR value for the ENA.
The setting for the SelfMMOGA are:
Maximum number of function evaluation is
50000 (as for the ENA);
Total population size is 200 (the ENA uses 500);
Adaptation period is 10 generations (25 times);
All specific parameters of individual algorithms
are self-tunable using the concept from
(Semenkin and Semenkina, 2012).
As we can see, binary problems are not too
complex for the SelfMMOGA and the ENA.
Therefore we will analyze the results in details. In
Table 4, the results for stand-alone algorithms, the
average of 6 stand-alone algorithms and the
SelfMMOGA (6 algorithms ensemble) are
presented. The average value (“Mean” column) can
be viewed as the average performance of a randomly
chosen algorithm. Such an estimate is very useful for
black-box optimization problems, because we have
no information about problem features and,
consequently, about what algorithms to use. If the
performance of the SelfMMOGA is better that the
Table 3: Results for binary problems.
Problem
SelfMMOGA ENA
PR SR PD SR
binaryF11 1.00 1.00 0.00 1.00
binaryF12 1.00 1.00 0.00 1.00
binaryF13 1.00 1.00 0.00 1.00
binaryF14 1.00 1.00 0.00 1.00
binaryF15 1.00 1.00 0.00 1.00
binaryF16 1.00 1.00 0.00 0.99
Table 4: Detailed results for binary problems.
Alg1 Alg2 Alg3 Alg4 Alg5 Alg6 Mean
Self-
MMOGA
Problem: binaryF11
PR
0.94 0.84 0.91 1.00 0.97 0.78 0.91 1.00
SR
0.90 0.84 0.88 1.00 0.94 0.80 0.89 1.00
PD
2.40 3.37 2.40 0.00 2.33 3.30 2.30 0.00
Problem: binaryF12
PR
0.97 0.97 1.00 1.00 0.97 0.84 0.96 1.00
SR
0.96 0.98 1.00 1.00 0.94 0.84 0.95 1.00
PD
2.00 1.00 0.00 0.00 1.67 3.62 1.38 0.00
Problem: binaryF13
PR
1.00 0.96 0.96 0.93 0.96 0.89 0.95 1.00
SR
1.00 0.96 0.94 0.90 0.94 0.84 0.93 1.00
PD
0.00 2.50 2.67 2.80 2.67 3.37 2.34 0.00
Problem: binaryF14
PR
0.91 0.81 0.91 1.00 0.94 0.75 0.89 1.00
SR
0.92 0.92 0.90 1.00 0.94 0.80 0.91 1.00
PD
3.25 2.50 2.60 0.00 2.67 3.20 2.37 0.00
Problem: binaryF15
PR
0.88 0.88 0.84 0.88 0.88 0.72 0.84 1.00
SR
0.88 0.86 0.84 0.86 0.84 0.64 0.82 1.00
PD
2.33 2.57 2.62 2.71 2.37 3.06 2.61 0.00
Problem: binaryF16
PR
0.84 0.75 0.84 0.88 0.78 0.56 0.78 1.00
SR
0.84 0.80 0.86 0.84 0.76 0.66 0.79 1.00
PD
3.25 2.80 3.00 2.87 3.08 3.47 3.08 0.00
Table 5: The SelfMMOGA results (PR and SR) for continuous problems.
Accuracy
level ε
cecF1 cecF2 cecF3 cecF4
PR SR PR SR PR SR PR SR
1e-01 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
1e-02 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
1e-03 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
1e-04 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
1e-05 1.000 1.000 1.000 1.000 1.000 1.000 0.887 0.623
Accuracy
level ε
cecF5 cecF6 cecF7 cecF8
PR SR PR SR PR SR PR SR
1e-01 1.000 1.000 0.843 0.540 0.851 0.540 1.000 1.000
1e-02 1.000 1.000 0.834 0.536 0.792 0.223 1.000 1.000
1e-03 1.000 1.000 0.814 0.378 0.762 0.029 0.966 0.775
1e-04 1.000 1.000 0.560 0.140 0.731 0.000 0.964 0.753
1e-05 1.000 1.000 0.000 0.000 0.687 0.000 0.954 0.670
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
60
Table 6: Average PR and SR for each algorithm.
ε
SelfMMOGA DE/nrand/1/bin cDE/rand/1/bin N-VMO dADE/nrand/1
PNA-
NSGAII
PR SR PR SR PR SR PR SR PR SR PR SR
1e-01 0.962 0.885 0.850 0.750 0.963 0.875 1.000 1.000 0.998 0.938 0.945 0.875
1e-02 0.953 0.845 0.848 0.750 0.929 0.810 1.000 1.000 0.993 0.828 0.910 0.750
1e-03 0.943 0.773 0.848 0.748 0.847 0.718 0.986 0.813 0.984 0.788 0.906 0.748
1e-04 0.907 0.737 0.846 0.750 0.729 0.623 0.946 0.750 0.972 0.740 0.896 0.745
1e-05 0.816 0.662 0.792 0.750 0.642 0.505 0.847 0.708 0.835 0.628 0.811 0.678
Average 0.916 0.780 0.837 0.750 0.822 0.706 0.956 0.854 0.956 0.784 0.893 0.759
Table 7: Algorithms ranking over cecF1-cecF8 problems.
Rank by
PR criterion
Algorithm
Rank by
SR criterion
Algorithm
1 N-VMO and dADE/nrand/1 1 N-VMO
2 SelfMMOGA 2 dADE/nrand/1
3 PNA-NSGAII 3 SelfMMOGA
4 DE/nrand/1/bin 4 PNA-NSGAII
5 cDE/rand/1/bin 5 DE/nrand/1/bin
- - 6 cDE/rand/1/bin
average of its component, we can conclude that on
average the choice of the SelfMMOGA will be
better.
As we can see from Table 4, the SelfMMOGA
always outperforms the average of its stand-alone
component algorithms for binary problems.
Moreover, for problems F15 and F16 no stand-alone
algorithm has a SR value equal to 1, but the
SelfMMOGA does.
The results of estimating the performance of the
SelfMMOGA with the pack of continuous problems
are presented in Tables 5-6. Table 5 shows detailed
results, Table 6 shows a comparison of average
values with other techniques and Table 7 contains
ranks of algorithms by separate criteria.
All problems and settings are as in the rules of
the CEC’13 competition on MMO. For each
problem there are 5 levels of accuracy of finding
optima (={1e-01, 1e-02,…, 1e-05}). Thus, each
problem have been binarized 5 times. The
dimensionalities of binarized problems are presented
in Table 2.We have also compared the results of the
SelfMMOGA runs with some efficient techniques
from the competition. The techniques are
DE/nrand/1/bin and Crowding DE/rand/1/bin (Li et
al., 2013b), N-VMO (Molina et al., 2013),
dADE/nrand/1 (Epitropakis et al., 2013), and PNA-
NSGAII (Bandaru and Deb, 2013).
The settings for the SelfMMOGA are:
Maximum number of function evaluation is
50000 (for cecF1-cecF5) and 200000 (for cecF6-
cecF8);
Total population size is 200;
Adaptation period is 10 generations 25 times (for
cecF1-cecF5) and 25 generations 40 times
(cecF6-cecF8);
All specific parameters of individual algorithms
are self-tunable.
As we can see from Tables 5-7, the
SelfMMOGA shows results comparable with
popular and well-studied techniques. It yields to
dADE/nrand/1 and N-VMO, but we should note that
these algorithms are specially designed for
continuous MMO problems, and have taken 2nd and
4th places, respectively, in the CEC competition. At
the same time, the SelfMMOGA has very close
average values to the best two algorithms, and
outperforms PNA-NSGAII, CrowdingDE and DE,
which have taken 7th, 8th and 9th places
respectively.
In this study, we have included only basic MMO
search techniques in the SelfMMOGA.
Nevertheless, it performs well due to the effect of
collective decision making in the ensemble. The key
feature of the approach is that it operates in an
automated, self-configuring way. Thus, the
SelfMMOGA can be a good alternative for complex
black-box MMO problems.
5 CONCLUSIONS
In this study, a novel genetic algorithm (called
SelfMMOGA) for multimodal optimization is
proposed. It is based on self-configuring
metaheuristic, which involves many different search
Multi-Strategy Genetic Algorithm for Multimodal Optimization
61
strategies in the process of MMO problem solving
and adaptively control their interactions.
The SelfMMOGA allows complex MMO
problems to be dealt with, which are the black-box
optimization problems (a priori information about
the objective and its features are absents or cannot
be introduces in the search process). The algorithm
uses binary representation for solutions, thus it can
be implemented for many real-world problems with
variables of arbitrary (and mixed) types.
We have included 6 basic MMO techniques in
the SelfMMOGA realization to demonstrate that it
performs well even with simple core algorithms. We
have estimated the SelfMMOGA performance with
a set of binary benchmark MMO problems and
continuous benchmark MMO problems from
CEC’2013 Special Session and Competition on
Niching Methods for Multimodal Function
Optimization. The proposed approach has
demonstrated a performance comparable with other
well-studied techniques.
Experimental results show that the SelfMMOGA
outperforms the average performance of its stand-
alone algorithms. It means that it performs better on
average than a randomly chosen technique. This
feature is very important for complex black-box
optimization, where the researcher has no possibility
of defining a suitable search algorithm and of tuning
its parameters. The proposed approach does not
require the participation of the human-expert,
because it operates in an automated, self-configuring
way.
In further works, we will investigate the
SelfMMOGA using more advanced component
techniques.
ACKNOWLEDGEMENTS
The research was supported by President of the
Russian Federation grant (MK-3285.2015.9). The
author expresses his gratitude to Mr. Ashley
Whitfield for his efforts to improve the text of this
article.
REFERENCES
Bandaru, S. and Deb, K., 2013. A parameterless-niching-
assisted bi-objective approach to multimodal
optimization. Proc. 2013 IEEE Congress on
Evolutionary Computation (CEC’13). pp. 95-102.
Bessaou, M., Petrowski, A. and Siarry, P., 2000. Island
Model Cooperating with Speciation for Multimodal
Optimization. Parallel Problem Solving from Nature
PPSN VI, Lecture Notes in Computer Science, Volume
1917. pp. 437-446.
Das, S., Maity, S., Qub, B.-Y. and Suganthan, P.N., 2011.
Real-parameter evolutionary multimodal optimization:
a survey of the state-of-the art. Swarm and
Evolutionary Computation 1, pp. 71–88.
Deb, K. and Saha, A., 2010. Finding Multiple Solutions
for Multimodal Optimization Problems Using a Multi-
Objective Evolutionary Approach. Proceedings of the
12th Annual Conference on Genetic and Evolutionary
Computation, GECCO 2010. ACM, New York. pp.
447-454.
Epitropakis, M.G., Li, X. and Burke, E.K., 2013. A
dynamic archive niching differential evolution
algorithm for multimodal optimization. Proc. 2013
IEEE Congress on Evolutionary Computation
(CEC’13). pp. 79-86.
Li, X., Engelbrecht, A. and Epitropakis, M., 2013a.
Results of the 2013 IEEE CEC Competition on
Niching Methods for Multimodal Optimization.
Report presented at 2013 IEEE Congress on
Evolutionary Computation Competition on: Niching
Methods for Multimodal Optimization.
Li, X., Engelbrecht, A. and Epitropakis, M.G., 2013b.
Benchmark functions for CEC’2013 special session
and competition on niching methods for multimodal
function optimization. Evol. Comput. Mach. Learn.
Group, RMIT University, Melbourne, VIC, Australia.
Tech. Rep.
Liu, Y., Ling, X., Shi, Zh., Lv, M., Fang. J. and Zhang, L.,
2011. A Survey on Particle Swarm Optimization
Algorithms for Multimodal Function Optimization.
Journal of Software, Vol. 6, No. 12. pp. 2449-2455.
Molina, D., Puris, A., Bello, R. and Herrera, F., 2013.
Variable mesh optimization for the 2013 CEC special
session niching methods for multimodal optimization.
Proc. 2013 IEEE Congress on Evolutionary
Computation (CEC’13). pp. 87-94.
Preuss, M. and Wessing, S., 2013. Measuring multimodal
optimization solution sets with a view to
multiobjective techniques. EVOLVE – A Bridge
between Probability, Set Oriented Numerics, and
Evolutionary Computation IV. AISC, vol. 227,
Springer, Heidelberg. pp. 123–137.
Preuss, M., 2014. Tutorial on Multimodal Optimization. In
the 13th International Conference on Parallel
Problem Solving from Nature, PPSN 2014, Ljubljana,
Slovenia.
Preuss, M., Stoean, C. and Stoean, R., 2011. Niching
foundations: basin identification on fixed-property
generated landscapes. Proceedings of the 13th Annual
Conference on Genetic and Evolutionary
Computation, GECCO 2011. pp. 837–844.
Qu, B., Liang, J., Suganthan P.N. and Chen, T., 2012.
Ensemble of Clearing Differential Evolution for Multi-
modal Optimization. Advances in Swarm Intelligence
Lecture Notes in Computer Science, Volume 7331. pp.
350-357.
Semenkin, E.S. and Semenkina, M.E., 2012. Self-
ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications
62
configuring Genetic Algorithm with Modified
Uniform Crossover Operator. Advances in Swarm
Intelligence. Lecture Notes in Computer Science 7331.
Springer-Verlag, Berlin Heidelberg. pp. 414-421.
Singh, G. and Deb, K., 2006. Comparison of multi-modal
optimization algorithms based on evolutionary
algorithms. In Proceedings of the Genetic and
Evolutionary Computation Conference, Seattle. pp.
1305–1312.
Sopov, E., 2015. A Self-configuring Metaheuristic for
Control of Multi-Strategy Evolutionary Search. ICSI-
CCI 2015, Part III, LNCS 9142. pp. 29-37.
Yu, E.L. and Suganthan, P.N., 2010. Ensemble of niching
algorithms. Information Sciences, Vol. 180, No. 15.
pp. 2815-2833.
Multi-Strategy Genetic Algorithm for Multimodal Optimization
63
