Ranking of Interval Type-2 Fuzzy Numbers based on Centroid Point
and Spread
Ahmad Syafadhli Abu Bakar, Ku Muhammad Naim Ku Khalif and Alexander Gegov
University of Portsmouth, School of Computing, PO1 3HE, Portsmouth, Hampshire, U.K.
Keywords: Interval Type-2 Fuzzy Numbers, Standardised Generalised Interval Type-2 Fuzzy Numbers, Ranking,
Centroid Point, Spread.
Abstract: A concept of interval type-2 fuzzy numbers is introduced in decision making analysis as this concept is
capable to effectively deal with the uncertainty in the information about a decision. It considers two types of
uncertainty namely inter and intra personal uncertainties, in enhancing the representation of type-1 fuzzy
numbers in the literature of fuzzy sets. As interval type-2 fuzzy numbers are crucial in decision making, this
paper proposes a methodology for ranking interval type-2 fuzzy numbers. This methodology consists of two
parts namely the interval type-2 fuzzy numbers reduction methodology as the first part and ranking of type-
1 fuzzy numbers as the second part. In this study, established reduction methodology of interval type-2
fuzzy numbers into type-1 fuzzy numbers is extended to reduction into standardised generalised type-1
fuzzy numbers as the extension complements the capability of the methodology on dealing with both
positive and negative data values. It is worth adding here that this methodology is analysed using thorough
empirical comparison with some established ranking methods for consistency evaluation. This methodology
is considered as a generic decision making procedure, especially when interval type-2 fuzzy numbers are
applied to real decision making problems.
1 INTRODUCTION
Fuzzy set theory serves as the basis of formal
decision making analysis when uncertainty factors
are involved in human decision making. This is
expressed through ability of human in making
logical decisions using imprecise and incomplete
information which leads to uncertainty in terms of
decision informativeness. Fuzzy number or type-1
fuzzy number is the first numerical representation of
fuzzy sets (or type-1 fuzzy sets) introduced in the
literature of fuzzy sets (Zadeh, 1965). Among
decision making situations that considered type-1
fuzzy numbers in the evaluations are fuzzy risk
analysis by Chen et al. (2012), supply chain
management (Wu et al., 2013), fuzzy portfolio
(Bermudez et al., 2012), selection of construction
project (Ebrahimnejad et al., 2012) and decision
making on water resources (Morais and Almeida,
2012). Main reason of those authors utilised type-1
fuzzy numbers in their chosen decision making
situations is due to the capabilities of type-1 fuzzy
numbers to appropriately deal with imprecise
numerical quantities and subjective preferences of
decision makers (Deng, 2014). Although, type-1
fuzzy numbers are appropriate for decision making
purposes, it is not easy to clearly determine which
type-1 fuzzy number is larger or smaller than
another (Kumar et al., 2010). This is because type-1
fuzzy numbers are represented by possibility
distributions which indicate that they potentially
overlap with each other (Zimmermann, 2000; Kumar
et al., 2010). Thus, decision makers need to compare
or ranking them correctly so that an effective
outcome of a decision making is obtained.
In the literature of fuzzy sets, a concept of
ranking type-1 fuzzy numbers is introduced by Jain
(1976) as a way to differentiate type-1 fuzzy
numbers effectively. In order to do so, several
ranking methods are recently suggested in literature
of ranking type-1 fuzzy numbers namely ranking
method based on different heights and spreads (Chen
and Chen, 2009), method using similarity measure
with centroid (Bakar et al., 2010), ranking based on
area of fuzzy numbers (Chen and Sanguatsan, 2011),
ranking of fuzzy numbers based on distance (Bakar
et al., 2012), centroid based ranking method (Dat et
al., 2012) and ranking method using epsilon degree
(Yu et al., 2013). Based on these ranking methods,
two common processes involve when ranking type-1
Bakar, A., Khalif, K. and Gegov, A..
Ranking of Interval Type-2 Fuzzy Numbers based on Centroid Point and Spread.
In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 2: FCTA, pages 131-140
ISBN: 978-989-758-157-1
Copyright
c
 2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
131

fuzzy numbers are identified. They are evaluation of
each type-1 fuzzy number considered and
comparison among type-1 fuzzy numbers under
consideration.
In a recent research work by Bakar and Gegov
(2014), a new ranking of type-1 fuzzy numbers
method is proposed where the method utilises two
intuition based approaches namely the centroid point
and spread (CPS). The capabilities of this method in
ranking type-1 fuzzy numbers are shown when the
method effectively solved many main problems of
type-1 fuzzy numbers faced by recently established
ranking methods of Kumar et al. (2010), Chen and
Chen (2009), Chen and Sanguatsan (2011) and Dat
et al. (2012) in embedded fuzzy numbers of different
spread, ranking embedded fuzzy numbers of
different shapes but having same centroid and
embedded normal and non-normal fuzzy numbers
respectively. Even though, the CPS ranking method
capable to solve all shortcomings faced by the
established ranking methods, limitation of type-1
fuzzy number to adequately representing the
uncertainty affects the role played by methods
developed for ranking type-1 fuzzy numbers,
including the CPS ranking method when dealing
with complex decision making.
Due to this, issue regarding the representation
adequacy of type-1 fuzzy numbers on the
uncertainty becomes one of the crucial problems in
decision making environment (Zadeh, 1975;
Wallsten and Budescu, 1995). According to Zadeh
(1975) and Wallsten and Budescu (1995), there are
two kinds of uncertainties that are supposedly
related to linguistic characteristics which are often
used in human decision making namely the intra-
personal uncertainty and inter-personal uncertainty.
Nonetheless, only one kind of uncertainty which is
the intra-personal uncertainty is considered in the
representation of type-1 fuzzy numbers. Thus, a
concept of type-2 fuzzy sets is introduced by Zadeh
(1975) in the literature of fuzzy sets as the extension
of type-1fuzzy sets with capability of representing
both kinds of uncertainty appropriately.
If the numerical representation for type-1 fuzzy
set is called type-1 fuzzy number (Tsoukalas and
Urigh, 1997), then the numerical representation for
type-2 fuzzy set is known as type-2 fuzzy number
(Coupland and John, 2003). As far as the
investigations on utilising type-2 fuzzy numbers are
concerned, many decision making problems are
solved such as radiographic tibia image clustering
(John, 2000), signal processing problem (Nagy and
Takács, 2008), pattern recognition (Wu and Mendel,
2009) and oversea minerals investment problem (Hu
et al., 2013).
Even though, type-2 fuzzy number is better than
type-1 fuzzy number in terms of uncertainty
representation (Agüero and Vargas, 2007), less
coverage on type-2 fuzzy numbers are given in the
literature of fuzzy sets. Therefore, this paper
suggests a methodology for ranking interval type-2
fuzzy numbers where the first part covers on the
reduction of interval type-2 fuzzy numbers into type-
1 fuzzy numbers and the second part is on the
application of the CPS ranking method (Bakar and
Gegov, 2014). It is worth mentioning here that
interval type-2 fuzzy numbers is used in this
methodology, instead of type-2 fuzzy number as it is
viewed as a special case and requires less
computational works (Hu et al., 2013). Along with
this study, an extension of interval type-2 fuzzy
numbers into standardised generalised interval type-
2 fuzzy numbers is introduced for the first time in
the literature of fuzzy sets due to the fact that the
extension creates generic representation for
established interval type-2 fuzzy numbers which are
suitable for generic decision making purposes.
The remainder of the paper is organised as
follows: Section 2 discusses the theoretical prelim-
naries, Section 3 views on the proposed work.
Validation of the proposed work is given in Section
4 and at last, a conclusion is made in section 5.
2 THEORETICAL
PRELIMINARIES
2.1 Type-1 Fuzzy Sets
A type-1 fuzzy set A
i
in a universe of discourse X is
characterised
by a membership function
() x
i
A
μ
which
maps each element
x
in X such that
x
is real
number
in the interval [0, 1] (Cheng, 1998)
.
Membership function for A
i
,
() x
i
A
μ
is given as
()
()
() []
{
}
XxxxxA
ii
AAi
∈∀∈= 1,0, μμ
(1)
When type-1 fuzzy set is in the numerical
representation, hence it is called as type-1 fuzzy
numbers with membership function shown as
follows.
() ()
1
12
21
23
1234
4
34
43
1
,,,
0
i
i
ii
ii
ii
Aiiii
i
ii
ii
xa
if a x a
aa
if a x a
xaaaa
ax
if a x a
aa
otherwise
μ
−

≤≤

−

≤≤

==

−

≤≤

−


FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
132

Figure 1: Type-1 trapezoidal fuzzy number.
For a type-1 trapezoidal fuzzy numbers as in
Figure 1, if a
i2
= a
i3
, then the type-1fuzzy number is
in the form of type-1triangular fuzzy number.
Whereas, if a
i1
= a
i2
= a
i3
= a
i4
for both type-1
triangular and type-1 trapezoidal fuzzy numbers,
then both type-1 fuzzy numbers are said to be in the
form of type-1 singleton fuzzy number. Length
between a
i1
and a
i4
is known as the support of the
type-1fuzzy numbers (Chen and Chen, 2009).
2.2 Standardised Generalised Type-1
Fuzzy Numbers
If type-1 fuzzy number A
i
has the property such that
11
4321
≤≤≤≤≤−
iiii
aaaa
, then
i
A
~
is called a
standardised generalised type-1 trapezoidal fuzzy
number (Chen and Chen, 2009) and is denoted as
(
)
i
A
iiiii
waaaaA
~
4321
;
~
,
~
,
~
,
~
~
=
Furthermore, if
32
~
~
ii
aa =
then
i
A
~
is known as a
standardised generalised type-1 triangular fuzzy
number. Any type-1 fuzzy numbers are transformed
into a standardised generalised type-1 fuzzy
numbers by normalisation step which is described in
(2).








=
i
A
iiii
i
w
k
a
k
a
k
a
k
a
A
~
4321
;,,,
~
(
)
i
A
iiii
waaaa
~
4321
;
~
,
~
,
~
,
~
=
(2)
where
()
.,,,max
4321 iiii
aaaak =
It should be noted here that the normalisation
process in equation (2), only the components of
type-1 fuzzy numbers are changed where a
i1
, a
i2
, a
i3
,
a
i4
are changed to
4321
~
,
~
,
~
,
~
iiii
aaaa
while the height of
the type-1 fuzzy number remains unchanged (Chen
and Chen, 2009).
2.3 Type-2 Fuzzy Sets
If
() UP
is the set for fuzzy set U, then a type-2
fuzzy set
i
A
′
in universe of discourse X is
characterised by membership grades which are fuzzy
(Zadeh, 1975). This implies that
() x
i
A
′
μ
is a fuzzy
set in U for all x given as
()
()
() ( )
{
}
XxUPxxxA
ii
AAi
∈∀∈=
′
′′
μμ ,
(3)
This follows that
UJXx
x
⊆∃∈∀
such that
() UJx
xA
i
→
′
:
μ
. Using equation (1), the following is
obtained.
() ()() () ()()
{
}
UJuUuxuxux
xAAA
iii
⊆∈∀∈=
′′′
μμμ ,
(4)
where X and
x
J
are the primary domain and primary
membership of x respectively while U and
() x
i
A
′
μ
are
the secondary domain and secondary membership of
x (Greenfield and Chiclana, 2013).
Using (3) and (4), the following is obtained.
()() ()() ()()
{
}
UJuXxUuxuxuxA
xAAi
ii
⊆∈∀∧∈∀∈=
′
′′
,,, μ
(5)
2.4 Interval Type-2 Fuzzy Sets
According to Greenfield and Chiclana (2013), an
interval type-2 fuzzy set is a type- 2 fuzzy set whose
secondary membership grades are all 1. Thus, in the
case of interval, equation (5) can be reduced to the
following equation (6).
()(){} UJuXxuxA
xi
⊆∈∀∧∈∀=
′
,1,,
(6)
Therefore, based on equations (1) and (3), the
interval type-2 fuzzy set is called a trapezoidal
interval type-2 fuzzy set when upper membership
function (secondary) and lower membership
function (primary) are depicted as
(
)
(
)
(
)
[
]
L
a
L
i
L
i
L
i
L
i
U
i
U
i
U
i
U
ii
i
waaaaaaaaA
ˆ
43214321
;
ˆ
,
ˆ
,
ˆ
,
ˆ
,1;
ˆ
,
ˆ
,
ˆ
,
ˆ
ˆ
=
(7)
where
4,3,2,1,
ˆ
=ja
U
ij
and 4,3,2,1,
ˆ
=ja
L
ij
are secondary
and primary membership functions values for
i
A
ˆ
.
Therefore, the numerical domain representation
of trapezoidal interval type-2 fuzzy number is
illustrated as follows,
(
)
x
i
A
μ
i
A
x
(
)
i
Aiiiii
waaaaA ;,,,
4321
=
i
A
w
Ranking of Interval Type-2 Fuzzy Numbers based on Centroid Point and Spread
133

x
()
x
i
A
ˆ
μ
i
A
ˆ
(
)
(
)
(
)
[
]
L
a
L
i
L
i
L
i
L
i
U
i
U
i
U
i
U
ii
i
waaaaaaaaA
ˆ
43214321
;
ˆ
,
ˆ
,
ˆ
,
ˆ
,1;
ˆ
,
ˆ
,
ˆ
,
ˆ
ˆ
=
Figure 2: An interval type-2 fuzzy number.
3 PROPOSED METHODOLOGY
In this section, details with regard to procedure
involved in the proposed methodology are described.
Full descriptions on the methodology are as follows.
This study first proposes a concept of
standardised generalised interval type-2 fuzzy
numbers in replacing the interval type-2 fuzzy
numbers for easy computation. This is because the
proposed concept provides generic representation of
interval type-2 fuzzy numbers that are suitable for
decision making purposes such as consideration of
both positive and negative values. Thus, the
definition of standardised generalised interval type-2
fuzzy number introduced in this study is given as the
following.
If an interval type-2 fuzzy number
i
A
ˆ
has the
property such that – 1<
U
i
a
1
ˆ
<
U
i
a
2
ˆ
<
U
i
a
3
ˆ
<
U
i
a
4
ˆ
< 1 and –
1<
L
i
a
1
ˆ
<
L
i
a
2
ˆ
<
L
i
a
3
ˆ
<
L
i
a
4
ˆ
<1, then
i
A
′
is called as a
standardised generalised interval type-2 fuzzy
number denoted as
(
)
(
)
[
]
L
a
L
i
L
i
L
i
L
i
U
i
U
i
U
i
U
ii
i
waaaaaaaaA ;,,,1;,,,
43214321
′′′′′′′′
=
′
(8)
Any interval type-2 fuzzy numbers are
transformed into a standardised generalised interval
type-2fuzzy numbers by normalisation process
shown as follows.
































=
′
L
a
L
i
L
i
L
i
L
i
U
i
U
i
U
i
U
i
i
i
w
k
a
k
a
k
a
k
a
k
a
k
a
k
a
k
a
A
ˆ
43214321
;
ˆ
,
ˆ
,
ˆ
,
ˆ
,1;
ˆ
,
ˆ
,
ˆ
,
ˆ
(
)
(
)
(
)
[
]
L
a
L
i
L
i
L
i
L
i
U
i
U
i
U
i
U
i
i
waaaaaaaa ;,,,,1;,,,
43214321
′′′′′′′′
=
(9)
where
(
)
U
i
U
i
U
i
U
i
aaaak
4321
ˆ
,
ˆ
,
ˆ
,
ˆ
max=
It should be noted here that the normalisation
process only changes the components of interval
type-2 fuzzy numbers where
U
i
U
i
U
i
U
i
aaaa
4321
ˆ
,
ˆ
,
ˆ
,
ˆ
and
L
i
L
i
L
i
L
i
aaaa
4321
ˆ
,
ˆ
,
ˆ
,
ˆ
are changed to
U
i
U
i
U
i
U
i
aaaa
4321
,,,
′′′′
and
L
i
L
i
L
i
L
i
aaaa
4321
,,,
′′′′
respectively while the heights
of interval type-2 fuzzy number remain unchanged.
After the interval type-2 fuzzy numbers are
transformed into standardized generalised interval
type-2 fuzzy numbers, the standardized generalised
interval type-2 fuzzy numbers obtained are then
ranked using the following procedure.
 Reduce the standardised generalised interval
type-2 fuzzy number using Nie and Tan (2008)
reduction method.
 Extend the CPS ranking method (Bakar and
Gegov, 2014) to ranking the reduced
standardised generalised interval type-2 fuzzy
number.
3.1 Part One
According to Greenfield and Chiclana, 2013), the
reduction algorithm is a process of reducing type-2
fuzzy sets into type-1 fuzzy sets. The process
generalises the operations defined for crisp numbers
to type-1 fuzzy sets mathematically which is in line
with the Extension Principle developed by Zadeh
(1965). In an analysis on accuracy by Greenfield and
Chiclana (2013), Nie and Tan (2008) reduction
method outperforms Wu and Mendel (2002) and
Enhanced Iterative Algorithm with Stop Condition,
EIASC(Wu and Nie, 2011) methods.
Since, it is shown that equation (6) is obtained
from equation (5), hence the reduction algorithm
developed for type-2 fuzzy sets by Nie and Tan
(2008) is also applicable to interval type-2 fuzzy
sets. In this case, the numerical representation of
interval type-2 fuzzy sets which is the interval type-
2 fuzzy numbers is reduced into type-1 fuzzy
numbers. Therefore, without loss of generality, the
reduction of standardised generalised interval type-2
fuzzy numbers into type-1 fuzzy numbers using Nie
and Tan (2008) is as follows.
()
U
A
L
AA
iii
′′′
+= μμμ
2
1
()






′
+
′′
+
′′
+
′′
+
′
=
L
i
U
i
U
i
L
i
L
i
U
i
L
i
U
i
aaaaaaaa
44332211
,,,
2
1
(10)
where
[] 1,1,,,,,,,
44332211
−∈
′′′′′′′′
L
i
U
i
U
i
L
i
L
i
U
i
L
i
U
i
aaaaaaaa
.
Note that, Nie andTan (2008) reduction method
in equation (10) neglects the non-normal interval
type-2 fuzzy sets in their analysis as the work
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
134

assumes that the heights for both primary and
secondary components are always 1,
1, =
′′
U
A
L
A
ii
μμ
.
However, Wu and Mendel (2009) indicate that the
height of secondary component is 1,
1=
′
L
A
i
μ
but the
height of the primary component can be between 0
and 1,
[] 1,0∈
′
U
A
i
μ
. Therefore, based on this reason,
this study extends the work by Nie andTan (2008)
where the extension is as follows.
()
U
A
L
AA
iii
′′′
+= μμμ
2
1
()






+
′
+
′′
+
′′
+
′′
+
′
=
′
L
A
L
i
U
i
U
i
L
i
L
i
U
i
L
i
U
i
i
waaaaaaaa 1;,,,
2
1
44332211
(11)
where
[]
1,1,,,,,,,
44332211
−∈
′′′′′′′′
L
i
U
i
U
i
L
i
L
i
U
i
L
i
U
i
aaaaaaaa
[]
1,0∈
′
L
A
i
w
It is worth mentioning here that, the main
different between equations (10) and (11) is the
latter considers the height in the reduction process
while this is neglected by the former. This extension
is introduced in this study as it provides a more
generic valuation for the height of the primary
component and standardised generalised interval
type-2 fuzzy numbers. This process is crucial for
evaluating standardised generalised interval type-2
fuzzy numbers, especially when they are applied for
decision making. It is worth mentioning here that the
extension is introduced in accordance to equation (6)
given by Wu and Nie (2011). Note that, the
reduction process in equation (11) reduces
standardised generalised interval type-2 fuzzy
numbers and not the interval type-2 fuzzy numbers.
3.2 Part Two
As mentioned in the introduction section, the CPS
ranking method introduced by Bakar and Gegov
(2014) caters limitations faced by existing
established methods in ranking type-1 fuzzy
numbers. Effectiveness of this method in ranking
various type-1 fuzzy numbers cases proves this
method is applicable for practical usage. Note that,
as standardised generalised interval type-2 fuzzy
numbers are used in previous part, the reduction step
in (11) reduces standardised generalised interval
type-2 fuzzy numbers into standardised generalised
type-1 fuzzy numbers. Therefore, the
CPS ranking
method proposed by Bakar and Gegov (2014) is
extended to the
CPS
2
ranking method to indicate that
the
CPS
2
ranking method is utilised for ranking
standardised generalised type-1 fuzzy numbers after
reduction from standardised generalised interval
type-2 fuzzy numbers. Details on the procedure in
the
CPS
2
ranking method are as follows.
Let
A be standardised generalised type-1 fuzzy
numbers
after reduction using equation (11)
described as
A = (a
1
, a
2
, a
3
, a
4
; w
A
),
Step 1: Compute the centroid point value for
standardised generalised type-1 fuzzy
number
A using Shieh (2007) formula
such that the horizontal –
x centroid value
of
A, x
A
is calculated as
(12)
and vertical – y cenrtroid of A, yA is


=
A
A
w
w
A
dA
dA
y
0
0
α
αα
α
α
(13)
where
α
A
is length of
α
– cuts of standardised generalised
type-1 fuzzy number
A, x
A
∈
[–1 , 1] and y
A
∈
[0 ,w
A
].
Step 2: Calculate the spread value for standardised
generalised type-1 fuzzy number
A by
considering the distance along
x – axis
from
x
A
defines as
i
A
= dist(a
4
– a
1
) =
14
axxa
AA
−+−
14
aa −=
(14)
and the distance along vertical
y – axis defines as
ii
A
= y
A
(15)
Therefore, the spread of
A, s
A
is defined as
s
A
= i
A
x ii
A
(16)
where
i
A
and ii
A
are dist(a
4
– a
1
) and y
A
respectively.
s
A
, i
A
, ii
A
, dist(a
4
– a
1
)
∈
[0 ,1].
Step 3: Determine the ranking value for
standardised generalised type-1 fuzzy
number
A using the following equation as
() ( )
AAA
syxACPS −××= 1
2
(17)
where
A
x
is the horizontal – x centroid for A
A
y
is the vertical – y centroid for A
A
s is the spread for A


∞
∞−
∞
∞−
=
dxxf
dxxxf
x
A
)(
)(
Ranking of Interval Type-2 Fuzzy Numbers based on Centroid Point and Spread
135

() ∈ACPS
2
[–1 , 1]
If
() () BCPSACPS
22
> , then
B
A

(i.e.
A
is
greater than
B
).
If
() ()
BCPSACPS
22
< , then
B
A

(i.e.
A
is
lesser than
B
).
If () () BCPSACPS
22
= , then
B
A
≈
(i.e.
A
and
B
are equal).
4 VALIDATION OF RESULTS
In this validation, relevant benchmarking examples
of standardised generalised interval type-2 fuzzy
numbers are introduced for the first time in the
literature of fuzzy sets. It has to be noted here that
validation in this section is a comparative – based
analysis which compares the
CPS
2
ranking method
with some established ranking methods of ranking
type-1 fuzzy numbers to ranking standardised
generalised interval type-2 fuzzy numbers. This is
because there are inadequate methods for ranking
standardised generalised interval type-2 fuzzy
numbers in the literature of fuzzy sets. Moreover,
the standardised generalised interval type-2 fuzzy
numbers are reduced into standardised generalised
type-1 fuzzy numbers, thus established ranking
methods considered in this study are suitable for
ranking standardised generalised type-1 fuzzy
numbers
Benchmarking examples developed in this study
involve cases that are related with decision making
problems. If a ranking method produces correct
ranking result such that the result is consistent with
human intuition, then the ranking result is signified
as consistent (Y), otherwise, it is inconsistent (N).
As mentioned, all established existing ranking
methods used in this section are methods established
for ranking standardised generalised type-1 fuzzy
numbers. Thus, these established methods are added
‘2’ (e.g. 2-Cheng (1998)) to signify that they are
methods for ranking standardised generalised type-1
fuzzy numbers but are extended to ranking
standardised generalised interval type-2 fuzzy
number for the first time. Note that, these methods
are applicable to ranking standardised generalised
interval type-2 fuzzy numbers only if all
standardised generalised interval type-2 fuzzy
numbers considered in this validation are reduced
standardised generalised type-1 fuzzy numbers using
equation (11). Therefore, cases of standardised
generalised interval type-2 fuzzy numbers
considered in this study that are potentially appeared
in decision making environment are as follows.
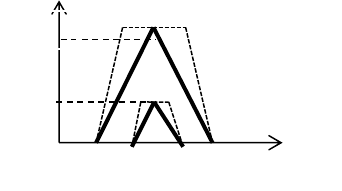
Case 1: Embedded standardised generalised
interval type-2 fuzzy numbers of different shapes.
Consider two standardised generalised interval
type-2 fuzzy numbers
1i
A
′
and
2i
A
′
shown in Figure
3. The correct ranking order such that the ranking
result is consistent with human intuition for this case
is
1i
A
′

2i
A
′
because the centroid point of
1i
A
′
is
greater than
2i
A
′
. Using Chen and Chen (2009)
ranking method, an unreasonable ranking order is
produced such that the result is inconsistent with
human intuition
2i
A
′

1i
A
′
as they treat type-2 fuzzy
numbers with smaller centroid point as greater than
the other. Kumar et al. (2010) and Chen and
Sanguatsan (2011) ranking methods on the other
hand treat both type-2 fuzzy numbers as equal (
1i
A
′
≈
2i
A
′
) which is also incorrect such that the result is
inconsistent with human intuition. It is also shown in
Table 1 where ranking methods by Cheng (1998)
and Chu and Tsao (2002) unable to give any ranking
result for this case as they are only applicable to
normal case of standardised generalised interval
type-2 fuzzy numbers. Using the
CPS
2
ranking
method, the ranking order produced is the same as
Dat et al. (2012) ranking method where both ranking
methods produce correct ranking order for this case
such that the result is consistent with human
intuition by ranking the standardised generalised
interval type-2 fuzzy numbers with higher centroid
point as higher ranking order.
()( )() []
7.0;7.0;4.0,35.0,25.0,2.0,1;1;5.0,4.0,2.0,1.0
1
=
′
i
A
()( )() []
7.0;7.0;4.0,3.0,3.0,2.0,1;1;5.0,3.0,3.0,1.0
2
=
′
i
A
Figure 3: Standardised generalised interval type -2 fuzzy
numbers
1i
A
′
and
2i
A
′
of Case 1.
Case 2: Embedded standardised generalised
interval type-2 fuzzy numbers of different spreads
Consider two standardised generalised interval type-
2 fuzzy numbers
1i
A
′
and
2i
A
′
shown in Figure 4.
The correct ranking order such that the ranking
2
i
A
′
0.7
0.1 0.3 0.5
x
1.0
1
i
A
′
)( x
μ
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
136

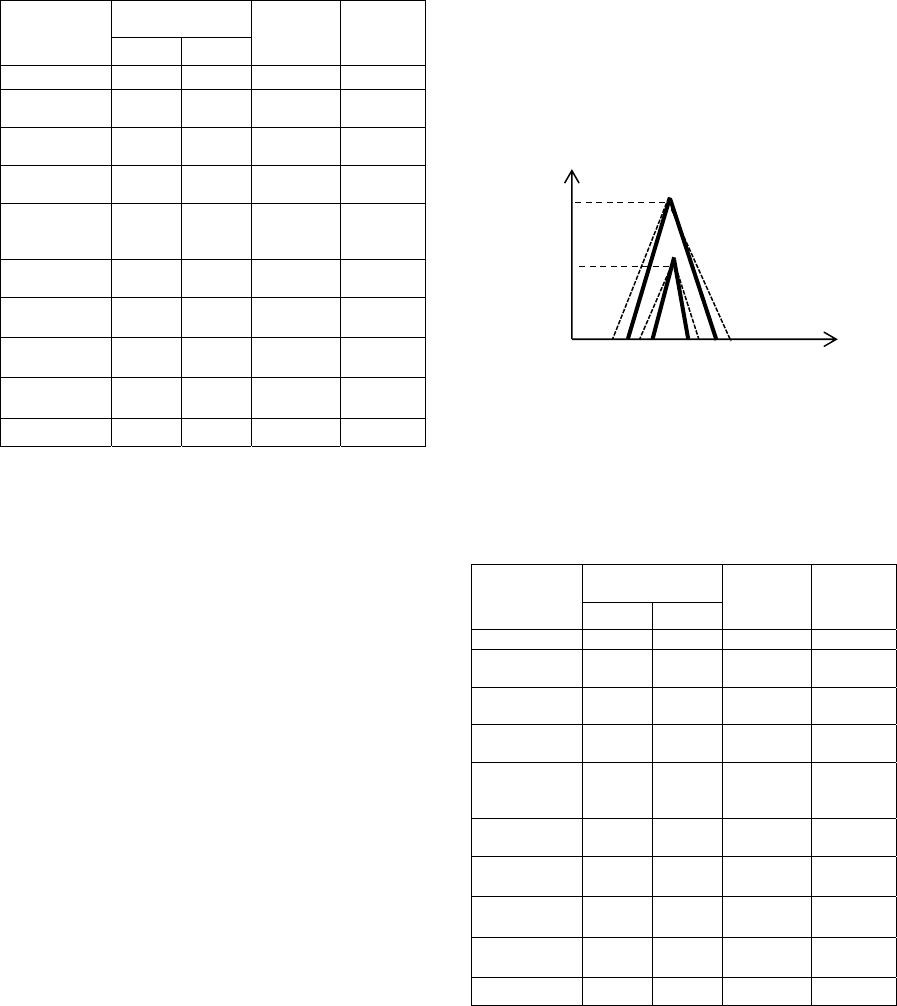
Table 1: Comparative results for Case 1.
Methods
Type-2 fuzzy
numbers
Ranking
Results
Evaluation
1i
A
′
2i
A
′
2-Cheng (1998) - - x N
2-Chu and Tsao
(2002)
- - x N
2-Chen and
Chen (2009)
0.2243 0.2272
1i
A
′

2i
A
′
N
2-Kumar et al.
(2010)
0.2400 0.2400
1i
A
′
≈
2i
A
′
N
2-(Chen and
Sanguatsan,
2011)
0.3000 0.3000
1i
A
′
≈
2i
A
′
N
2-Dat et al.
(2012)
0.3333 0.2220
1i
A
′

2i
A
′
Y
2-Yu et al.
(2013),
α
= 0
1.0000 1.0000
1i
A
′

2i
A
′
N
2-Yu et al.
(2013),
α
= 0.5
1.0000 1.0000
1i
A
′
≈
2i
A
′
N
2-Yu et al.
(2013),
α
= 1
1.0000 1.0000
1i
A
′

2i
A
′
Y
CPS
2
0.0136 0.0077
1i
A
′

2i
A
′
Y
‘x’ denotes ranking method as unable to rank the standardised
generalised interval type-2 fuzzy numbers
‘-‘ denotes no ranking result are obtained.
‘Y’ denotes the ranking result is consistent
‘N‘ denotes the ranking result is inconsistent.
result is consistent with human intuition for this case
is
2i
A
′

1i
A
′
. This is due to ranking order for any
standardised generalised interval type-2 fuzzy
numbers with lower spread value is greater than
others provided that the centroid point value of each
standardised generalised interval type-2 fuzzy
number under considerationis the same. In this case,
Kumar et al. (2010), Chen and Sanguatsan (2011)
and Dat et al. (2012) ranking methods are unable to
differentiate the standardised generalised interval
type-2 fuzzy numbers where they produce equal
ranking
()
21 ii
AA
′
≈
′
such that the result is inconsistent
with human intuition. Cheng (1998) and Chu
andTsao (2002) ranking methods in this case
produce no ranking result as they both are not
applicable when dealing with non – normal
standardised generalised interval type-2 fuzzy
numbers. Ranking method by Yu et al. (2013) on the
other hand, captures the actual decision makers’
preference by utilising the degree of optimisms in
obtaining the ranking order for the standardised
generalised interval type-2 fuzzy numbers. Thus,
this method produces many ranking result for this
case. Another incorrect ranking order such that the
result is inconsistent with human intuition is
produced by Chen and Chen (2009) ranking method
where it gives
1i
A
′

2i
A
′
. Based on Table 2, only the
CPS
2
ranking method produces correct ranking
order such that the result is consistent with human
intuition by giving priority towards standardised
generalised interval type-2 fuzzy numbers with
lower spread as higher ranking. It is also shown in
this case where most of the latest presented ranking
methods are unable to solve this case appropriately.
()( )()
[]
5.0;5.0;6.0,5.0,5.0,4.0,1;1;8.0,5.0,5.0,2.0
1
=
′
i
A
()( )()
[]
5.0;5.0;55.0,5.0,5.0,45.0,1;1;75.0,5.0,5.0,25.0
2
=
′
i
A
Figure 4: Standardised generalised interval type-2 fuzzy
numbers
1i
A
′
and
2i
A
′
of Case 2.
Table 2: Comparative results for Case 2.
Methods
Type-2 fuzzy
numbers
Ranking
Results
Evaluation
1i
A
′
2i
A
′
2-Cheng (1998) - - x N
2-Chu and Tsao
(2002)
- - x N
2-Chen and
Chen (2009)
0.3819 0.4770
1i
A
′

2i
A
′
N
2-Kumar et al.
(2010)
0.5000 0.5000
1i
A
′
≈
2i
A
′
N
2-(Chen and
Sanguatsan,
2011)
0.3000 0.3000
1i
A
′
≈
2i
A
′
N
2-Dat et al.
(2012)
0.1111 0.1111
1i
A
′
≈
2i
A
′
N
2-Yu et al.
(2013),
α
= 0
1.0000 1.0000
1i
A
′

2i
A
′
N
2-Yu et al.
(2013),
α
= 0.5
1.0000 1.0000
1i
A
′
≈
2i
A
′
N
2-Yu et al.
(2013),
α
= 1
1.0000 1.0000
1i
A
′

2i
A
′
Y
CPS
2
0.0135 0.0115
1i
A
′

2i
A
′
Y
‘x’ denotes ranking method as unable to rank the standardised
generalised interval type-2 fuzzy numbers
‘-‘ denotes no ranking result are obtained.
‘Y’ denotes the ranking result is consistent
‘N‘ denotes the ranking result is inconsistent.
Case 3: Reflection of standardised generalised
interval type-2 fuzzy numbers.
Consider two standardised generalised interval
type-2 fuzzy numbers
1i
A
′
and
2i
A
′
shown in Figure
1
i
A
′
2
i
A
′
0.5
0.2 0.5 0.8
1.0
x
)( x
μ
Ranking of Interval Type-2 Fuzzy Numbers based on Centroid Point and Spread
137

5. It is obvious that
2i
A
′
is situated on the farthest
right of
1i
A
′
, where the correct ranking order such
that for this case such that the result is consistent
with human intuitions is
2i
A
′

1i
A
′
. Cheng (1998)
and Chu and Tsao (2002) ranking methods again
produce no ranking result for this case while Kumar
et al. (2010) ranking method is incapable to
differentiate both standardised generalised interval
type-2 fuzzy numbers, hence produces incorrect
ranking result such that the result is inconsistent
()( )()
[]
7.0;7.0;4.0,35.0,25.0,2.0,1;1;5.0,4.0,2.0,1.0
1
=
′
i
A
()( )() []
7.0;7.0;2.0,25.0,35.0,4.0,1;1;1.0,2.0,4.0,5.0
2
−−−−−−−−=
′
i
A
Figure 5: Standardised generalised interval type-2 fuzzy
numbers
1i
A
′
and
2i
A
′
of Case 3.
Table 3: Comparative results for Case 3.
Methods
Type-2 fuzzy
numbers
Ranking
Results
Evaluation
1i
A
′
2i
A
′
2-Cheng (1998) - - x N
2-Chu and Tsao
(2002)
- - x N
2-Chen and
Chen (2009)
– 0.2272 0.2272
1i
A
′

2i
A
′
Y
2-Kumar et al.
(2010)
0 0
1i
A
′
≈
2i
A
′
N
2-(Chen and
Sanguatsan,
2011)
– 0.3000 0.3000
1i
A
′

2i
A
′
Y
2-Dat et al.
(2012)
0.1333 0.1500
1i
A
′

2i
A
′
Y
2-Yu et al.
(2013),
α
= 0
1.0000 1.0000
1i
A
′

2i
A
′
N
2-Yu et al.
(2013),
α
= 0.5
1.0000 1.0000
1i
A
′
≈
2i
A
′
N
2-Yu et al.
(2013),
α
= 1
1.0000 1.0000
1i
A
′

2i
A
′
Y
CPS
2
– 0.0077 0.0077
1i
A
′

2i
A
′
Y
‘x’ denotes ranking method as unable to rank the standardised
generalised interval type- 2 fuzzy numbers
‘-‘ denotes no ranking result are obtained.
‘Y’ denotes the ranking result is consistent
‘N‘ denotes the ranking result is inconsistent.
with human intuition. While for the CPS
2
ranking
method, the ranking order obtained is the same as
Chen and Chen (2009), Chen and Sanguatsan (2011)
and Dat et al. (2012) where the ranking order is
correct such that consistent with human intuitions.
Case 4:
Non – overlapping standardised genera-
lised interval type-2 fuzzy numbers of different
shapes.
Consider different shape case of two non –
overlapping standardised generalised interval type-2
fuzzy numbers
1i
A
′
and
2i
A
′
shown in Figure 6.
Using the same explanation in Case 3, the correct
ranking order such that the ranking result is
consistent with human intuition is
2i
A
′

1i
A
′
. This is
because a crisp value is always treated greater than
any standardised generalised interval type-2 fuzzy
numbers as it represent the actual value. Based on
Table 4, only some ranking methods are capable to
rank this case correctly such that the result is
consistent with human intuitions. They are Chen and
Chen (2009), Chen and Sanguatsan (2011), Dat et al.
(2012) and the
CPS
2
ranking method. While, for
other remaining ranking methods under considera-
tion, they are incapable to give any ranking order for
this case. Therefore, this case indicates that the
CPS
2
ranking method not only capable to give consistent
ranking order towards standardised generalised
interval type-2 fuzzy numbers but also to crisp
value.
It is notable that each presented method of
ranking standardised generalised interval type-2
fuzzy numbers has its own strengths and
weaknesses. Although, all methods use for
comparing standardised generalised interval type-2
fuzzy numbers in this section are actually methods
for ranking type-1 fuzzy numbers, the above
analysis is provided to illustrate the capability of the
established ranking methods in ranking standardised
generalised interval type-2 fuzzy numbers rather
than ranking type-1 fuzzy numbers only. Based on
the analysis provided, there are some methods deals
with cases of fuzzy numbers effectively while some
produce irrelevant results for certain cases.
Nevertheless, in each case examined above, the
CPS
2
ranking method is the most effective ranking
method compared to other ranking methods under
consideration where it provides correct ranking
order such that the result is consistent with human
intuition in all cases of standardised generalised
interval type-2 fuzzy numbers considered in this
study.
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
138

()( )() []
7.0;7.0;4.0,35.0,25.0,2.0,1;1;5.0,4.0,2.0,1.0
1
=
′
i
A
()( )() []
7.0;7.0;0.1,0.1,0.1,0.1,1;1;0.1,0.1,0.1,0.1
2
=
′
i
A
Figure 6: Standardised generalised interval type-2 fuzzy
numbers
1i
A
′
and
2i
A
′
of Case 4.
Table 4: Comparative results for Case 4.
Methods
Type-2 fuzzy
numbers
Ranking
Results
Evaluation
1i
A
′
2i
A
′
2-Cheng (1998) x x - N
2-Chu and Tsao
(2002)
x x - N
2-Chen and
Chen (2009)
0.2243 0.8500
1i
A
′

2i
A
′
Y
2-Kumar et al.
(2010)
x x - N
2-(Chen and
Sanguatsan,
2011)
0.3000 1.000
1i
A
′

2i
A
′
N
2-Dat et al.
(2012)
x x - N
2-Yu et al.
(2013),
α
= 0
1.0000 1.0000
1i
A
′

2i
A
′
N
2-Yu et al.
(2013),
α
= 0.5
1.0000 1.0000
1i
A
′
≈
2i
A
′
N
2-Yu et al.
(2013),
α
= 1
1.0000 1.0000
1i
A
′

2i
A
′
Y
CPS
2
0.0136 0.283
1i
A
′

2i
A
′
Y
‘x’ denotes ranking method as unable to rank the standardised
generalised interval type-2 fuzzy numbers
‘-‘ denotes no ranking result are obtained.
‘Y’ denotes the ranking result is consistent
‘N‘ denotes the ranking result is inconsistent.
Since, the proposed methodology have been
analysed through empirical validations proposed in
this study, hence this implies that the proposed
methodology is relevant and reliable for solving any
real decision making problems involving
standardised generalised interval type-2 fuzzy
numbers.
5 CONCLUSION
This study proposes a novel method for ranking
standardised generalised interval type-2 fuzzy
numbers which consists of centroid point and spread
approaches,
CPS
2
. In this paper, it is shown that the
CPS
2
ranking methodology is analysed and
produced results that are correct such that the results
are consistent with human intuition. Furthermore,
the introduction of the standardised generalised
interval type-2 fuzzy numbers in replacing
conventional interval type-2 fuzzy numbers
improves the capability of interval type-2 fuzzy
numbers when being applied to decision making
problems. In conclusion, the proposed method
possesses intuitional concepts for ranking
standardised generalised interval type-2 fuzzy
numbers as well as for decision making analysis.
Therefore, it is expected that this method can be
further improved for decision making purposes.
REFERENCES
Agüero, J. R., Vargas, A. 2007. Inferring the Operative
Configuration of Distribution Networks Through
Type-2 Fuzzy Logic Systems for Implementing Outage
Management and State Estimation, Proceedings of
XXI Pan American Congress of Mechanical,
Electrical, and Industrial Engineering, Lima, Peru.
Bakar, A. S. A., Gegov, A. 2014. Ranking of fuzzy
numbers based centroid point and spread, Journal of
Intelligent and Fuzzy Systems, vol. 27.
Bakar, A. S. A., Mohamad, D., Sulaiman, N. H.
2010.Ranking fuzzy numbers using similarity measure
with centroid, IEEE International Conference on
Science and Social Research, Kuala Lumpur.
Bakar, A. S. A., Mohamad, D., Sulaiman, N. H. 2012.
Distance-based ranking fuzzy numbers, Advances in
Computational Mathematics and Its Applications, vol.
1(3).
Bermudez, J. D., Segura, J. V., Vercher, E. 2012. A multi –
objective genetic algorithm for cardinality constrained
fuzzy portfolio selection, Fuzzy Sets and Systems, vol.
188 (1).
Chen, S. M., Chen, J. H. 2009.Fuzzy risk analysis based
on ranking generalized fuzzy numbers with different
heights and different spreads, Expert Systems with
Applications, vol. 36.
Chen, S. M., Munif, A., Chen, G – S., Liu H – S. and Kuo,
B – C. 2012. Fuzzy risk analysis based on ranking
generalized fuzzy numbers with different heights and
different spreads, Expert Systems with Applications,
vol. 39.
Chen, S. M., Sanguansat, K. 2011. Analyzing fuzzy risk
based on a new fuzzy ranking method between
2
A
′
0.1
0.3
1.0
1.0
0.5
)(x
μ
1
A
′
0.7
Ranking of Interval Type-2 Fuzzy Numbers based on Centroid Point and Spread
139

generalized fuzzy numbers”, Expert System with
Applications, vol. 38.
Cheng, C. H. 1998. A new approach for ranking fuzzy
numbers by distance method, Fuzzy Sets and System,
vol. 95.
Chu C. T., Tsao, C. T. 2002.Ranking fuzzy numbers with
an area between the centroid point and original point,
Computer and Mathematics with Applications, vol. 43.
Coupland, S., John, R. 2003.An approach to type-2 fuzzy
arithmetic, Proceeding U.K. Workshop Computational
Intelligent.
Dat, L. Q., Yu, V. F., Chou, S. Y. 2012. An improved
ranking method for fuzzy numbers based on the
centroid index, International Journal of Fuzzy
Systems, vol. 14(3).
Deng, H. 2014. Comparing and ranking fuzzy numbers
using ideal solutions, Applied Mathematical
Modelling, vol. 38.
Ebrahimnejad, S., Mousavi, S. M., Moghaddam, R. T.,
Hashemi, H., Vahdani, B. 2012.A novel two – phase
group decision making approach for construction
project selection in a fuzzy environment, Applied
Mathematical Modelling, vol. 36 (9).
Greenfield, S., Chiclana, F. 2013.Accuracy and complexity
evaluation of defuzzification strategies for the
discretised interval type – 2 fuzzy se”, International
Journal of Approximate Reasoning, vol. 54(8).
Hu, J., Zhang, Y., Chen X., Liu, Y. 2013. Multi-criteria
decision making method based on possibility degree of
interval type-2 fuzzy number, Knowledge-Based
Systems, vol. 43.
Jain, R. 1976. Decision-making in the presence of fuzzy
variable, IEEE Transactions on Man and Cybernetic,
vol. 6.
John, R. I., Innocent, P. R., Barnes, M. R. 2000. Neuro-
fuzzy clustering of radiographic tibia image data using
type-2 fuzzy sets, Information Sciences, vol. 125.
Kumar, A., Singh, P., Kaur, P., Kaur, A. 2010. A new
approach for ranking generalized trapezoidal fuzzy
numbers”, World Academy of Science, Engineering
and Technology, vol. 68.
Mendel J. M., John, R. I. 2002. Type-2 fuzzy sets made
simple, IEEE Trans. Fuzzy Syst., vol. 10.
Mendel, J. M. 2001. Uncertain Rule-Based Fuzzy Logic
Systems .Introduction and New Directions. Upper
Saddle River, N J: Prentice-Hall.
Morais D. C., Almeida, A. T. 2012. Group decision
making on water resources based on analysis of
individual rankings, Omega, vol. 40 (1).
Nagy, K., Takács, M. 2008. Type-2 fuzzy sets and SSAD as
a possible application, Acta Polytechnica Hungarica,
vol. 5.
Nie, M., Tan, W. W. 2008. Towards an efficient type-
reduction method for interval type-2 fuzzy logic
systems, Proceedings of FUZZ-IEEE 2008, Hong
Kong.
Shieh, B. S. 2007. An approach to centroids of fuzzy
numbers, International Journal of Fuzzy Systems,
vol.9.
Tsoukalas, L. H., Urigh, R.E. 1997. Fuzzy and Neural
Approaches in Engineering.New York: Wiley.
Wallsten, T. S., Budescu, D.V. 1995. A review of human
linguistic probability processing: general principles
and empirical evidence, The KnowledgeEngineering
Review, vol. 10(1).
Wu, D., Mendel, J-M. 2009. A comparative study of
ranking methods, similarity measures and uncertainty
measures for interval type-2 fuzzysets, Information
Sciences, vol. 179.
Wu, D., Wu D. D., Zhang, Y, Olson, D. L. 2013.Supply
chain outsourcing risk using integrated stochastic -
fuzzy optimization approach, Information Sciences,
vol. 235.
Yu, V. F., Chi, H. T. X, Shen, C. W. 2013.Ranking fuzzy
numbers based on epsilon-deviation degree, Applied
Soft Computing, vol. 13(8).
Zadeh, L. A. 1965. Fuzzy sets, Information Control, vol. 8.
Zadeh, L. A. 1975.The concept of a linguistic variable and
its application to approximate reasoning, part 1, 2 and
3, Information Sciences, vol. 8.
Zimmermann, H-J. 2000. An application – oriented view
of modelling uncertainty, European Journal of
Operational Research, vol. 122.
FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications
140