An Evolutionary and Graph-Rewriting based Approach to Graph

Generation

Aaron Barry, Josephine Grifﬁth and Colm O’Riordan

Computational Intelligence Research Group, NUI, Galway, Ireland

Keywords:

Graph Rewriting, Evolutionary Computation, Graph Generation.

Abstract:

This paper describes an evolutionary computation based graph rewriting approach to generating classes of

graphs that exhibit a set of desired global features. A set of rules are used to generate, in a constructive

manner, classes of graphs. Each rule represents a transformation from one graph to another. Each of these

transformations causes local changes in the graph. Probabilities can be assigned to the rules which govern the

frequency with which they will be applied. By assigning these probabilities correctly, one can generate graphs

exhibiting desirable global features. However, choosing the correct probability distribution to generate the

desired graphs is not an easy task for certain graphs and the task of ﬁnding the correct settings for these graphs

may represent a difﬁcult search space for the evolutionary algorithms. In order to generate graphs exhibiting

desirable features, an evolutionary algorithm is used to ﬁnd the suitable probabilities to assign to the rules.

The ﬁtness function rewards graphs that exhibit the desired properties. We show, using a small rule base, how

a range of graphs can be generated.

1 INTRODUCTION

Graphs are used in a large range of domains in com-

puter science and mathematics and in a range of ap-

plications of these ﬁelds. Many problems can be

elegantly and intuitively modelled or abstracted as

graph problems. Popular classes of graph problems

include path ﬁnding (Pohl, 1970), graph colouring

(Wood, 1969) and graph partitioning (Kernighan and

Lin, 1970).

Many problem domains such as simulation in spa-

tial game theory or modelling the spread of informa-

tion in a population involve the need to create classes

of graphs that exhibit speciﬁc features. Often the

question of interest relates to exploring the potential

impact of certain features in a graph. In these scenar-

ios, analysis can be facilitated by generating graphs

that exhibit those features.

One approach that has been used to create these

classes of graphs is to sample data from the real prob-

lem domain and build graphs from these samples.

There have been many attempts to undertake such

a task in a range of domains; for example

Alvarez-

Garc

ıa build multi-partite graphs from given data

(

Alvarez-Garc

ıa et al., 2014). Oftentimes, such data

is prohibitively expensive or impossible to obtain. In

such domains, global features of these graphs can be

observed and measured and one can then build graphs

exhibiting these features.

Many approaches have been used to generate ar-

tiﬁcial graphs that exhibit various features. There

have been a range of approaches to generating ran-

dom graphs including Erd

os-R

enyi graphs (Erd

os and

enyi, 1961), (Gilbert, 1959) and random geometric

graphs (Penrose, 2003) and a number of techniques

to generate graphs that exhibit the scale free property

(Barab

asi and Albert, 1999), small world properties

(Newman, 2000) and other properties such as a de-

sired clustering coefﬁcient (Li and O’Riordan, 2013)

and community structure (Seshadhri et al., 2012).

These approaches generate a class of graphs that ex-

hibit a set of features.

A graph rewriting system represents a more gen-

eral approach to generating graphs. Graph rewrit-

ing systems involve transforming a graph by apply-

ing rewrite rules; a component of the original graph is

replaced with a new component. Many existing tech-

niques such as preferential attachment (Barab

asi and

Albert, 1999), the Chung-Lu model (Chung and Lu,

2002) forest ﬁre model (Leskovec et al., 2005b) can

be viewed as graph-rewriting system where an origi-

nal graph is transformed by the application of a num-

ber of transformations. The type of graphs generated

depends on both the set of rules to be applied and

Barry, A., Grifﬁth, J. and O’Riordan, C..

An Evolutionary and Graph-Rewriting based Approach to Graph Generation.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 237-243

ISBN: 978-989-758-157-1

237

the frequency with which they are applied. Other ap-

proaches that have been adopted include generating

graphs using evolutionary computation and then ap-

plying noise to the graphs (Bach et al., 2013), using

multiplication of Kronecker matrics (Leskovec et al.,

2005a), (Leskovec et al., 2010).

The contributions of this work are two-fold: ﬁrst,

we introduce an approach that combines evolutionary

computation and re-writing rules to generate graphs

that exhibit desired global features and second, we il-

lustrate the approach by generating classes of graphs

that display desired global features (in our case, a de-

sired clustering coefﬁcient and a ﬁxed set of nodes),

using a small set of rewriting rules.

The paper is laid out as follows. Some prelim-

inary concepts are introduced and then we discuss

the proposed model. We then discuss some simple

rules and demonstrate the ability of the evolution-

ary algorithm to generate a class of graphs exhibit-

ing pre-deﬁned properties. We compare the approach

with existing graph generation techniques. Finally,

we present some conclusions and suggest future di-

rections for the research.

2 BACKGROUND CONCEPTS

A graph, G, comprises a set, V, of nodes (or vertices)

and a set E of edges such that each edge e in E com-

prises an unique pair (v

, v

) of nodes in V . A graph

rewriting system comprises a set of rules of the form

α → β which transform a graph G to a new graph G

In these rules, α represents an existing construct in

the graph (α ∈ G(V, E)) and β represents a new con-

struct which replaces α. Typically, the construct β is

bigger than the construct α and results in the graph

growing in terms of the number of vertices, number

of edges, or both. The re-write rules to be applied can

be selected based on probabilities assigned to them.

Many previous graph creation approaches have

led to the creation of graphs with speciﬁc features

(low average degree, small world property, commu-

nity structure etc.). Depending on the domain, dif-

ferent properties may be of interest. These include,

among others, the following features:

• Degree Distribution: the degree distribution of a

graph is the fraction of nodes in the network with

a given degree.

• Diameter: the diameter of a graph is the length of

the longest path between any pairs of nodes.

• Clustering Coefﬁcient: the clustering coefﬁcient

of a graph is a measure of how closely clustered

together vertices on the graph are. The local clus-

tering coefﬁcient of a node is deﬁned as the num-

ber of edges between a node’s neighbours divided

by the possible number of edges between a node’s

neighbours. The global clustering coefﬁcient is

the average of the local clustering coefﬁcient over

all nodes.

• Centrality Measures: centrality measures are used

to quantify how central or important a given

node is. There are many measures of centrality

that have been proposed in the literature includ-

ing degree centrality (the higher the degree of a

node, the higher this measure), closeness central-

ity (measures how close the node is to other nodes

in the graph) and betweenness centrality (mea-

sures how often a node is a member of the shortest

path between two pairs of nodes).

3 GRAPH CREATION MODEL

The approach contains two distinct components—

ﬁrst, a graph generation component which repeatedly

applies a number of transformation rules to create a

new graph from an original graph (outlined in Al-

gorithm 1), and second, an evolutionary component

which, for a set of speciﬁed desired features, learns

the best probabilities to assign to the rules (outlined

in Algorithm 2).

The graph generation model comprises the fol-

lowing components: an initial state which comprises

an initial graph G

, E

), a set of re-write rules

{R}, which can transform a graph G to a new graph

, a probability distribution {P

} over these rules

and the number of times (NumSteps), to select and

apply a rule.

Algorithm 1: Generate.

Graph Generation Algorithm(G

, E

), {R}, {P

}, NumSteps)

G ← G

for i ← 1 to NumSteps

Choose R

with probability P

Apply R

to G to create G

G ← G

return(G)

The evolutionary component uses a genetic algo-

rithm over a population of size m where the chromo-

somes are of length n + 1 when there are n rules; the

ﬁnal n + 1

gene, Num Steps, is used to determine

how many rules are to be applied.

Genecode =< P

, P

, . . . P

n−1

, P

, NumSteps >

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

238

A set of predeﬁned features are used to guide the

search; the overall ﬁtness function is deﬁned by how

close the graph is to having these features. If a user

speciﬁes k features, the following ﬁtness function is

used:

Fitness =

∑

i=1

× closeness

(G, f

)

∑

i=1

The set of closeness

functions measure how well

the graph G exhibits each feature f

. The ω

values

allow the user to give higher priority to some features

over others. The overall ﬁtness is effectively a linear

combination of a number of closeness measures.

Algorithm 2: Evolution Algorithm.

Evolution Algorithm(Gen, G

, PopSize, Samplesize)

Create a population of chromosomes, {C

}, each of

length m

G ← G

for g ← 1 to Gen

for p ← 1 to PopSize

for s ← 1 to Samplesize

NumSteps ← C

[m]

← Generate(G

, {R},C

[0. . . m −

1], NumSteps)

for i ← 1 to NumberFeatures

Measure presence of feature f

in G

Calculate overall ﬁtness of G

Calculate average ﬁtness over graphs from the

sample

Tournament Selection

Mutation

Crossover

Due to the stochasticity in the graph generation al-

gorithm, samples of graphs are created to evaluate

each chromosome; the features are measured for each

graph in the sample and the ﬁtness assigned to the

chromosome is calculated as the average of these ﬁt-

ness values. Tournament selection is adopted to select

chromosomes for the next generations; these selected

chromosomes are then subjected to potential mutation

and crossover.

Mutation has two aspects. If the gene to be mu-

tated represents the NumSteps, creep mutation is used

to increase or decrease this value by an amount cho-

sen randomly from a pre-deﬁned range. If the gene

chosen represents a probability associated with a spe-

ciﬁc rule, then that probability is modiﬁed using creep

mutation. To ensure correctness, the change and its

magnitude is reﬂected across the other probabilities

equally to ensure the resulting probabilities sum to

unity. Crossover is one-point and similar considera-

tion is given to ensuring correctness.

4 SAMPLE GRAPH

GENERATION USING

RE-WRITING RULES

4.1 Sample Rule Set

In this illustrative example, we include three rather

simple rules. The semantics of these rules are for-

malised in Tables 1 to 3. The rules are used to trans-

form an existing graph into a new graph. The ﬁrst rule

adds a new vertex and a new edge; the new vertex is

connected together to an existing vertex. This exist-

ing vertex is chosen randomly. This can be viewed as

a rewriting rule where a vertex is replaced by a vertex

connected to a new vertex.

The second rule attempts to add an edge between

two existing vertices in the graph where one does not

already exist. This has the effect of increasing the

density of the graph. The vertices to connect together

are chosen randomly. If no such pair of vertices exist

(i.e. on a complete graph), the rule is not applied.

The third and ﬁnal rule included was one that re-

places an existing vertex with a ‘triangle’, i.e two new

vertices are added to the graph; these vertices are both

connected to an existing vertex; ﬁnally an edge is

added to these two vertices. This rule can be seen

as a re-writing rule that changes an existing node to

a ‘triangle’ of nodes. This new ‘triangle’ will contain

some vertices with a high local clustering coefﬁcient.

Each of these rules transforms a graph G(V, E) to

another graph G

, E

). For all our rules V

⊇ V and

⊇ E and so the graph grows monotonically.

Table 1: Conditions for Rule 1.

Name Add a vertex

Pre-condition v

∈ V, v

6∈ V

Post-condition v

∈ V

, v

∈ V

, e(v

, v

) ∈ E

Table 2: Conditions for Rule 2.

Name Add an edge

Pre-condition v

∈ V, v

∈ V, e(v

, v

) 6∈ E

Post-condition v

∈ V

, v

∈ V

, e(v

, v

) ∈ E

Table 3: Conditions for Rule 3.

Name Add a triangle

Pre-condition v

∈ V, v

, v

6∈ V

Post-condition 1 v

, v

∈ V

Post-condition 2 e(v

, v

), e(v

, v

), e(v

, v

) ∈ E

An Evolutionary and Graph-Rewriting based Approach to Graph Generation

239

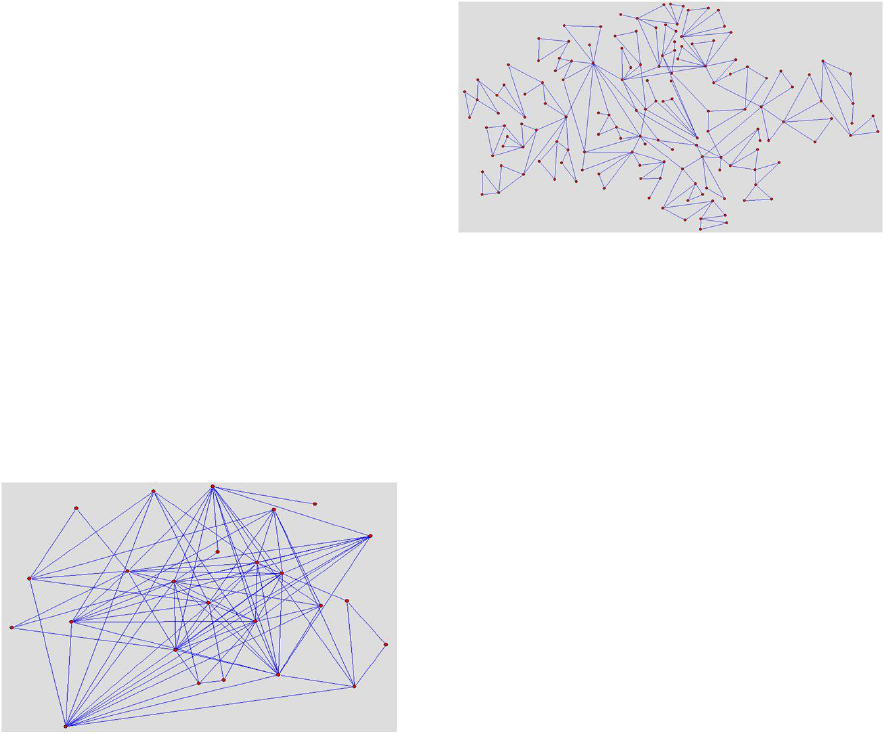
4.2 Illustration of Graph Generation

By assigning probabilities to the rules and specifying

the number of times to apply the rules, we can gen-

erate a large set of graphs. Depending on the prob-

abilities assigned, the graphs generated may exhibit

different global properties. We now show two such

examples.

For the ﬁrst example, we assigned the probabili-

ties 0.1, 0.8 and 0.1 to the ﬁrst, second and third rules

respectively. We apply the rules 100 times starting

with a simple original graph of two vertices connected

with an edge. Given the high probability associated

with the second rule, we expect to generate graphs

with a high number of edges and a high density. The

graph shown in Fig. 1 has been generated with this

probability distribution over the rules. As expected,

the graph displays a high density. The graph has 28

vertices, 117 edges, an average degree of 8.357, and a

clustering coefﬁcient of 0.56.

Figure 1: An illustrative graph generated with probabilities

0.1, 0.8, 0.1.

The second example involves generating a graph

using a different probability distribution. The graph

in Fig. 2 shows a graph generated with the same three

simple rules and probabilities 0.1, 0.1 and 0.8 respec-

tively. In this case, the graph should have more ‘tri-

angles’ and hence more nodes and a higher clustering

coefﬁcient. The resulting graph has 158 vertices, 235

edges, an average degree of 2.97 and a clustering co-

efﬁcient of 0.698.

These examples illustrate the graph generation ap-

proach using a set of simple graph rewriting rules.

By choosing, different distributions we can generate

classes of graphs that exhibit substantially different

global phenomena. It is worth noting, that due to the

stochastic nature of the process, we can generate a

large set of graphs with the same probability distribu-

tion over the rule set which will exhibit similar global

phenomena.

Figure 2: An illustrative graph generated with probabilities

0.1, 0.1, 0.8.

5 SAMPLE EVOLUTION AND

GRAPH GENERATION

5.1 Evolutionary Settings

In the evolutionary setting, the desirable global fea-

tures must be speciﬁed. In order to facilitate search,

some mechanism is needed to measure their presence

in the graph in order to deﬁne the closeness func-

tions needed in the ﬁtness function. The genetic algo-

rithm, outlined in Algorithm 2, evolves a population

of weightings and converges towards settings that al-

low the generation of graphs with the desired features.

To illustrate its performance, we adopt a small set

of features as the desirable global features: namely

the number of vertices and the clustering coefﬁcient.

The genetic algorithm parameters are as follows:

population size 100, number of generations 30, mu-

tation 1%, no crossover, tournament size 10. For the

ﬁtness function, we give equal credence to both the

desirable functions, i.e., ω

= 1, ∀ω

We illustrate the evolutionary process with three

different settings for the features representing three

ﬁtness landscapes for the evolutionary process to

search:

1. No. of vertices = 100; Clustering coefﬁcient = 0.0

2. No. of vertices = 100; Clustering coefﬁcient = 0.4

3. No. of vertices = 100; Clustering coefﬁcient = 0.7

5.2 Illustration of Graph Evolution

For the ﬁrst ﬁtness function, with minimal clustering

of nodes, the evolutionary algorithm quickly evolves

to ﬁnding such a graph with the ideal number of nodes

and ideal clustering coefﬁcient according to the ﬁt-

ness function. The chromosome selected by the evo-

lutionary algorithm is as follows: < 100, 0, 0, 100 >,

indicating that the second and third rule were never

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

240

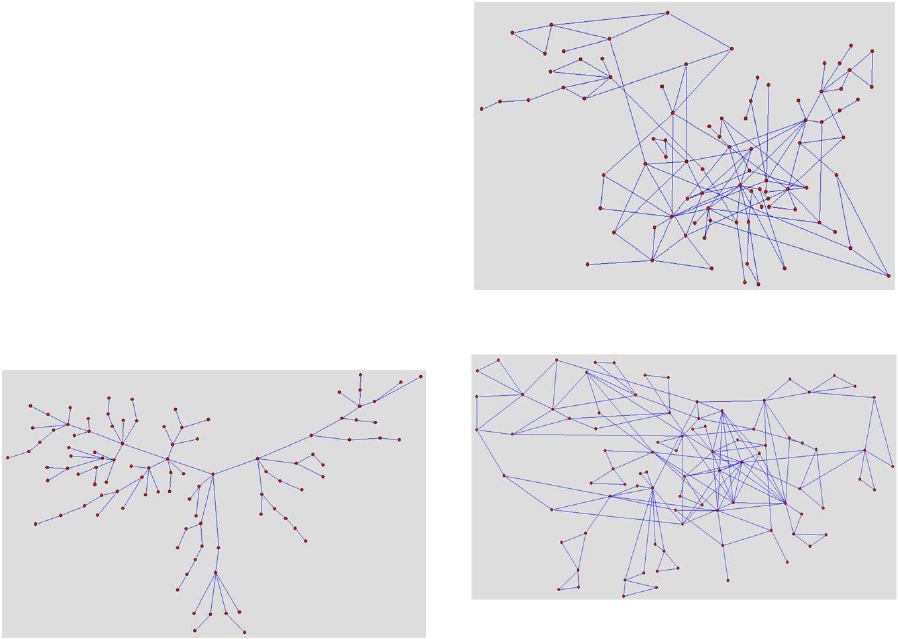
applied and rule 1 (adding a new vertex to an exist-

ing vertex) is applied 100 times. Figure 3 illustrates a

graph generated using these evolved values.

We see a tree like structure emerge. It is worth

noting, that other graphs can be formed that are not

strictly trees but that can have a low or zero level of

clustering. However, given the set of rules, it would

seem that the less one applies the rule involving add

‘triangles’, the lower the clustering coefﬁcient. Simi-

larly, in applying the second rule involving adding an

edge, there is a probability of forming triangles in the

graph which would increase the clustering coefﬁcient.

The best rule to apply in creating a graph with mini-

mal clustering coefﬁcient is the rule that adds a node

connected to an existing node.

Figure 3: Desired features: number of nodes 100, clustering

coefﬁcient= 0.0.

For the second ﬁtness function, the genetic algo-

rithm quickly ﬁnds a chromosome with a set of val-

ues that captures the balance between applying the

three rules and the correct number of time steps. A

chromosome found by the genetic algorithm is as fol-

lows: < 44, 25, 21, 86 >. Figure 4 illustrates a graph

generated with these rules. The illustrated graph has

just less than 100 nodes and clustering coefﬁcient of

0.403.

For the third and ﬁnal ﬁtness function, a much

higher clustering coefﬁcient is required. This takes

longer to ﬁnd and a greater variance is witnessed in

applying the evolved rules. An illustrative chromo-

some found was as follows: < 1, 61, 38, 83 > which

was used to generate the graph in Figure 5.

In summary, these examples show that we can

search the space of possible probability values to as-

sign to the rules and ﬁnd suitable settings in order to

generate graphs exhibiting the desirable global fea-

tures. It is worth noting that for any evolutionary run,

we may ﬁnd a number of settings that generate suit-

able graphs (this will depend on the landscape and

whether it is unimodal or not), and for each setting,

we can generate a family of graphs.

Figure 4: Desired feature - number of nodes 100, clustering

coefﬁcient= 0.4.

Figure 5: Desired feature - number of nodes 100, clustering

coefﬁcient= 0.7.

5.3 Evolutionary Algorithm

For each of the problem cases, we run the algorithm

twenty times. In all cases, the evolutionary algo-

rithm ﬁnds suitable graphs in each run with little vari-

ation in the number of generations taken per individ-

ual cases. For the intermediate case with a cluster-

ing coefﬁcient of 0.4, the genetic algorithm converged

to good graphs quickly; the genetic algorithm found

very good solutions (ﬁtness value less than 0.005)

within a small number of generations (5-7). This is

not surprising given that there are many graphs with

such a value for the clustering coefﬁcient.

For the problem where graphs with a clustering

coefﬁcient of 0.7 of required; the genetic algorithm

never reached solutions with as low ﬁtness function

values as for the previous case. Runs typically con-

verged in 10 to 15 generations to a reasonably good

set of rules to generate graphs with the desirable fea-

tures. The stochastic nature of the problem domain

meant that ﬁtness values of between 0.05 and 0.1 were

found and maintained through the evolutionary run.

For the third case involving attempting to evolve a

graph with a clustering coefﬁcient of zero had a sim-

ilar trajectory to the previous case with convergence

An Evolutionary and Graph-Rewriting based Approach to Graph Generation

241

happening in the ﬁrst 10-15 generations and a ﬁtness

value of between 0.05 and 0.1 achieved.

6 DISCUSSION

Bach et al. (Bach et al., 2013) discuss an approach

to generating graphs with evolutionary algorithms.

Their approach involves using motif generators which

create speciﬁed topological patterns and a module that

introduces noise to the graph. Of the works encoun-

tered, this work is most similar to ours in that an

evolutionary algorithm is used to guide the search.

There are also parallels in that a level of abstraction is

adopted in both approaches; we adopt rules to trans-

form graphs whereas in the work of Bach et. al. mo-

tifs are used as building blocks. The work differs from

ours in that they extend the basic approach to allow

user feedback also guide the evolution.

Another well-known evolutionary approach to

generate graphs has been described by Stanley and

Miikkulainen and others (e.g. (Stanley and Miikku-

lainen, 2002), (Stanley et al., 2003)) where evolution-

ary approaches are used to evolve neural networks.

The focus in this work is less on producing graphs or

networks with speciﬁc topological features, but rather

on the resulting neural network’s ability to learn a par-

ticular task.

Many existing graph generator models can pro-

duce graphs that guarantee speciﬁc statistical proper-

ties (diameter, average degree). As argued by Shuail

et. al (Shuai et al., 2013), it can be difﬁcult to main-

tain other properties. They report on their work which

allows the generation of very large graphs that pre-

serve other patterns that may be important given the

semantics of a particular domain. Our approach can

capture succinctly the requirements of a particular do-

main by incorporating speciﬁc rules to produce de-

sired local properties; the required local and global

properties can be ensured via the genetic algorithm.

The application problem tackled in this paper of

generating graphs with a predeﬁned clustering coefﬁ-

cient is one that been addressed by other researchers;

for example, Herrera et al (Herrera and Zuﬁria, 2011),

(Heath and Parikh, 2011) and Holme et al (Holme and

Kim, 2002) present techniques to generate different

types of graphs with a tunable clustering coefﬁcient.

Graphs with different levels of clustering have been

explored in the domain of evolutionary game theory

in order to explore the effect of clustering on the emer-

gence of cooperation (Gang et al., 2008), (O’Riordan

et al., 2008); in order to pursue research in a similar

vein it is important to be able to generate graphs with

particular features.

We have shown with a small example rule set and

a small set of features how this approach can be used

to generate classes of graphs exhibiting these features.

For simulation domains, one often wishes to generate

a large potentially diverse set of graphs that exhibit

similar global features. Adopting an evolutionary ap-

proach, a set of chromosomes with similar ﬁtness can

be evolved. Each chromosome can be used to gen-

erate a set of graphs that will include some level of

variation. This is a useful beneﬁt of the approach.

Another beneﬁt is the level of abstraction af-

forded. Given the ability to specify the desirable

graph features and some means to measure these fea-

tures, the approach can be applied. Furthermore,

if domain knowledge is available about useful local

properties, we can augment our set of rules accord-

ingly.

One caveat worth noting is that genetic algorithms

are a suitable approach where a non-binary measure

can be assigned to the solution. This is true for many

features of graphs of interest in social science and so-

cial simulation. For example, for the features con-

sidered in this paper (clustering coefﬁcient, degree),

we can calculate how close the graph is to exhibiting

these features. For other graph features, deﬁning such

a measure may be computationally expensive or even

intractable.

On a related note, the speciﬁed desirable proper-

ties may conﬂict with each other in some way; for ex-

ample adding an edge will increase the average degree

but it might also have another effect (introducing a

cycle, increasing the clustering coefﬁcient etc.). Sim-

ilarly, one or more rules may partially cover another

rule. In these cases, an alternative type of ﬁtness func-

tion may be reasonable. Adopting a multi-objective

ﬁtness function and returning a range of graphs may

be suitable.

7 CONCLUSIONS AND FUTURE

WORK

We have shown that graph rewriting rules can be used

in conjunction with genetic algorithms to generate

classes of graphs that exhibit speciﬁed global features.

While the approach discussed and presented in this

paper has been successful in generating graphs exh-

biting certain properties, further work is needed to test

the approach on more complex graph generation. In

order to further motivate and justify this approach, it

is necessary to illustrate its ability on a wider range of

graphs types and properties.

Proposed future work includes applying the ap-

proach to a wider range of graph properties to further

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

242

explore the applicability of this approach. We aim to

show that graphs generated by other approaches can

be generated adopting this approach. It would also

be interesting to discover if there are graph genera-

tion approaches that we cannot replicate with this ap-

proach.

Another strand of future work is to explore an ex-

tended set of rules that includes rules of a different

type. Currently all our rules are like those in a regular

grammar; the right hand side of the rules are merely

graph constructs. One could include non-terminals in

the right hand side which would in turn trigger an-

other rule.

REFERENCES

Alvarez-Garc

ıa, S., Baeza-Yates, R., Brisaboa, N. R.,

Larriba-Pey, J.-L., and Pedreira, O. (2014). Auto-

matic multi-partite graph generation from arbitrary

data. Journal of Systems and Software, 94:72–86.

Bach, B., Spritzer, A., Lutton, E., and Fekete, J.-D. (2013).

Interactive random graph generation with evolution-

ary algorithms. In Graph Drawing, pages 541–552.

Springer.

Barab

asi, A.-L. and Albert, R. (1999). Emergence of scal-

ing in random networks. science, 286(5439):509–512.

Chung, F. and Lu, L. (2002). The average distances in ran-

dom graphs with given expected degrees. Proceedings

of the National Academy of Sciences, 99(25):15879–

15882.

Erd

os, P. and R

enyi, A. (1961). On the evolution of random

graphs. Bull. Inst. Internat. Statist, 38(4):343–347.

Gang, W., Kun, G., Han-Xin, Y., and Bing-Hong, W.

(2008). Role of clustering coefﬁcient on cooperation

dynamics in homogeneous networks. Chinese Physics

Letters, 25(6):2307.

Gilbert, E. N. (1959). Random graphs. The Annals of Math-

ematical Statistics, pages 1141–1144.

Heath, L. S. and Parikh, N. (2011). Generating random

graphs with tunable clustering coefﬁcients. Phys-

ica A: Statistical Mechanics and its Applications,

390(23):4577–4587.

Herrera, C. and Zuﬁria, P. J. (2011). Generating scale-

free networks with adjustable clustering coefﬁcient

via random walks. arXiv preprint arXiv:1105.3347.

Holme, P. and Kim, B. J. (2002). Growing scale-free net-

works with tunable clustering. Physical review E,

65(2):026107.

Kernighan, B. W. and Lin, S. (1970). An efﬁcient heuristic

procedure for partitioning graphs. Bell system techni-

cal journal, 49(2):291–307.

Leskovec, J., Chakrabarti, D., Kleinberg, J., and Faloutsos,

C. (2005a). Realistic, mathematically tractable graph

generation and evolution, using kronecker multiplica-

tion. In Knowledge Discovery in Databases: PKDD

2005, pages 133–145. Springer.

Leskovec, J., Chakrabarti, D., Kleinberg, J., Faloutsos, C.,

and Ghahramani, Z. (2010). Kronecker graphs: An

approach to modeling networks. The Journal of Ma-

chine Learning Research, 11:985–1042.

Leskovec, J., Kleinberg, J., and Faloutsos, C. (2005b).

Graphs over time: densiﬁcation laws, shrinking diam-

eters and possible explanations. In Proceedings of the

eleventh ACM SIGKDD international conference on

Knowledge discovery in data mining, pages 177–187.

ACM.

Li, M. and O’Riordan, C. (2013). The effect of clustering

coefﬁcient and node degree on the robustness of co-

operation. In Evolutionary Computation (CEC), 2013

IEEE Congress on, pages 2833–2839. IEEE.

Newman, M. E. (2000). Models of the small world. Journal

of Statistical Physics, 101(3-4):819–841.

O’Riordan, C., Cunningham, A., and Sorensen, H. (2008).

Emergence of cooperation in n-player games on small

world networks. In ALIFE, pages 436–442.

Penrose, M. (2003). Random geometric graphs, volume 5.

Oxford University Press Oxford.

Pohl, I. (1970). Heuristic search viewed as path ﬁnding in a

graph. Artiﬁcial Intelligence, 1(3):193–204.

Seshadhri, C., Kolda, T. G., and Pinar, A. (2012). Commu-

nity structure and scale-free collections of erd

os-r

enyi

graphs. Physical Review E, 85(5):056109.

Shuai, H.-H., Yang, D.-N., Yu, P. S., Shen, C.-Y., and Chen,

M.-S. (2013). On pattern preserving graph genera-

tion. In Data Mining (ICDM), 2013 IEEE 13th Inter-

national Conference on, pages 677–686. IEEE.

Stanley, K. O., Bryant, B. D., and Miikkulainen, R. (2003).

Evolving adaptive neural networks with and with-

out adaptive synapses. In Evolutionary Computa-

tion, 2003. CEC’03. The 2003 Congress on, volume 4,

pages 2557–2564. IEEE.

Stanley, K. O. and Miikkulainen, R. (2002). Evolving neu-

ral networks through augmenting topologies. Evolu-

tionary computation, 10(2):99–127.

Wood, D. (1969). A technique for colouring a graph appli-

cable to large scale timetabling problems. The Com-

puter Journal, 12(4):317–319.

An Evolutionary and Graph-Rewriting based Approach to Graph Generation

243