The Reverse Doubling Construction

Jean-Franc¸ois Viaud

, Karell Bertet

, Christophe Demko

and Rokia Missaoui

Laboratory L3i, University of La Rochelle, La Rochelle, France

University of Qu

ebec in Outaouais, Gatineau, Canada

Keywords:

Concept Lattice, Congruence Relation, Factor Lattice, Arrow Relation, Arrow Closed Subcontext, Compatible

Subcontext, Doubling Convex.

Abstract:

It is well known inside the Formal Concept Analysis (FCA) community that a concept lattice could have an

exponential size in the data. Hence, the size of concept lattices is a critical issue in the presence of large

real-life data sets. In this paper, we propose to investigate factor lattices as a tool to get meaningful parts of the

whole lattice. These factor lattices have been widely studied from the early theory of lattices to more recent

work in the FCA ﬁeld. This paper contains two parts. The ﬁrst one gives background about lattice theory

and formal concept analysis, and mainly compatible sub-contexts, arrow-closed sub-contexts and congruence

relations. The second part presents a new decomposition called “reverse doubling construction” that exploits

the above three notions used for the doubling convex construction investigated by Day. Theoretical results and

their proofs are given as well as an illustrative example.

1 INTRODUCTION

During the last decade, the computation capabilities

have promoted Formal Concept Analysis (FCA) with

new methods based on concept lattices. Though they

are exponential in space/time in worst case, concept

lattices of a reasonable size enable an intuitive repre-

sentation of data expressed by a formal context that

links objects to attributes through a binary relation.

Methods based on concept lattices have been devel-

oped in various domains such as knowledge discovery

and management, databases or information retrieval

where some relevant concepts, i.e. possible corre-

spondences between objects and attributes are con-

sidered either as classiﬁers, clusters or representative

object/attribute subsets.

With the increasing size of data, a set of meth-

ods have been proposed in order to either generate

a subset (rather than the whole set) of concepts and

their neighborhood in an on-line and interactive way

(Ferr

e, 2014; Visani et al., 2011) or better display lat-

tices using nested line diagrams (Ganter and Wille,

1999). Such approaches become inefﬁcient when

contexts are huge. However, the main idea of lat-

tice/context decomposition into smaller ones is still

relevant when the classiﬁcation property of the ini-

tial lattice is maintained. Many lattice decomposi-

tions have been deﬁned and studied, either from an

algebraic point of view (Demel, 1982; Mih

ok and

Semani

sin, 2008) or from an FCA point of view

(Ganter and Wille, 1999; Funk et al., 1995). We

can cite the Unique Factorisation Theorem (Mih

and Semani

sin, 2008), the matrix decomposition (Be-

lohlavek and Vychodil, 2010), the Atlas decomposi-

tion (Ganter and Wille, 1999), the subtensorial de-

composition (Ganter and Wille, 1999), the subdirect

decomposition (Demel, 1982; Freese, 2008; Freese,

1997; Freese, 1999; Wille, 1969; Wille, 1976; Wille,

1983; Wille, 1987; Funk et al., 1995), or the doubling

convex construction. The doubling convex construc-

tion has also been widely studied (Day, 1994; Na-

tion, 1995; Geyer, 1994; Bertet and Caspard, 2002),

mainly from a theoretical point of view in order to

characterize lattices that can be obtained by such de-

composition.

In this paper, we investigate a new method named

reverse doubling construction to reduce the size of

data. In other words, we propose a new method to

construct a smaller lattice from a given one. It is

based on the previous work of Day about the dou-

bling convex construction (Day, 1977; Day, 1994).

Such a method has then be generalized (Geyer, 1994)

and further widely studied (Day et al., 1989; Nation,

1995; Bertet and Caspard, 2002). Intuitively, this con-

struction consists in doubling into a lattice L a convex

subset C of nodes of L. In this paper, we propose a

“reverse doubling construction” which aims at remov-

ing from a lattice L a doubled convex set until no du-

350

Viaud, J., Bertet, K., Demko, C. and Missaoui, R..

The Reverse Doubling Construction.

In Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2015) - Volume 1: KDIR, pages 350-357

ISBN: 978-989-758-158-8

plicated convex set exists. However, there may be no

convex to remove and hence no changes in the initial

lattice structure. When the reverse doubling construc-

tion successively applied to an assumed ﬁnite lattice L

and a convex set C, and following the Day’s doubling

construction, the initial lattice L is recovered without

any loss of information.

Studies about the doubling convex construction

can be organized according to the following chrono-

logical sequence of events:

• The ﬁrst one corresponds to the original work of

Day (Day, 1977; Day, 1994; Day et al., 1989; Na-

tion, 1995), who introduced the construction. At

the very beginning, only intervals were doubled.

• Further generalizations were developed that lead

to the general doubling convex method (Geyer,

1994).

• In parallel, characterizations of lattices obtained

by iterating the doubling convex construction we-

re investigated (Day, 1977; Day, 1994; Day et al.,

1989; Nation, 1995; Bertet and Caspard, 2002).

• In this paper, we deﬁne a reverse construction

which removes a convex from a lattice whenever

it is possible.

Being able to recover the full lattice from the

smaller one and a convex inside, means that all the

information is contained in the small lattice. Thus we

only need to consider the sub-context that deﬁnes the

small lattice. In other words, only a part of the data

is relevant. Consequently, one needs only to access

or even keep a smaller part of the data. This is obvi-

ously an interesting way to manage big data that are

nowadays ubiquitous in many real-life applications.

This paper is organized as follows. The next sec-

tion as well as the appendix give the background

needed to understand the rest of the article. Then,

Section 3 presents the decomposition method while

an example serves as an illustration in Section 4. Con-

clusion and future work are given in Section 5.

2 STRUCTURAL FRAMEWORK

Throughout this paper all sets (and thus lattices) are

considered to be ﬁnite.

This work takes place in the framework of Formal

Concept Analysis (FCA) (Ganter and Wille, 1999)

which deals with formal contexts, i.e. data repre-

sented as binary matrices. From a formal context, a

concept lattice is deduced. An example of a formal

context is given in Table 1 and its associated concept

lattice is given in Figure 1.

Figure 1: A lattice with its irreducible nodes.

2.1 Lattices and Formal Concept

Analysis

2.1.1 Algebraic Lattice

Let us ﬁrst recall that a lattice (L,≤) is an ordered set

in which every pair (x,y) of elements has a least upper

bound, called join x ∨ y, and a greatest lower bound,

called meet x ∧ y. As we are only considering ﬁnite

structures, every subset A ⊂ L has a join and meet (e.

g. ﬁnite lattices are complete).

2.1.2 Concept or Galois Lattice

A (formal) context (O,A, R) is deﬁned by a set O of

objects, a set A of attributes, and a binary relation R ⊂

O × A, between O and A. Two operators are derived:

• for each subset X ⊂ O, we deﬁne X

= {m ∈

A, j R m ∀ j ∈ X} and dually,

• for each subset Y ⊂ A, we deﬁne Y

= { j ∈

O, j R m ∀m ∈ Y }.

Table 1 is an example of a formal context where X

in a cell ( j,m) means that object j has the attribute m.

A(formal) concept represents a maximal objects-

attributes correspondence by a pair (X ,Y ) such that

= Y and Y

= X . The sets X and Y are respectively

called extent and intent of the concept. The set of

concepts derived from a context is ordered as follows:

) ≤ (X

) ⇐⇒ X

⊆ X

⇐⇒ Y

⊆ Y

(1)

The whole set of formal concepts together with

this order relation form a complete lattice, called the

concept lattice of the context (O,A,R).

Different formal contexts can provide isomorphic

concept lattices, and there exists a unique one, named

the reduced context, deﬁned by the two sets O and A

of the smallest size.

This particular context is introduced by means of

The Reverse Doubling Construction

351

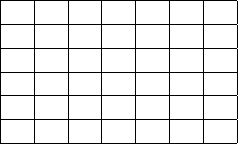
Table 1: The reduced context of the lattice in Figure 1.

b c d f g j

2 x x x x x

3 x x x x

5 x x x

6 x x x

9 x x

special concepts or elements of the lattice L, namely

irreducible elements.

An element j ∈ L is join-irreducible if it is not a

least upper bound of a subset not containing it. The

set of join irreducible elements is noted J

. Meet-

irreducible elements are deﬁned dually and their set

is M

. As a direct consequence, an element j ∈ L is

join-irreducible if and only if it has only one immedi-

ate predecessor denoted j

−

. Dually, an element m ∈ L

is meet-irreducible if and only if it has only one im-

mediate successor denoted m

In Figure 3, nodes with with a number above are

meet-irreducible while nodes with a number below

are join-irreducible.

2.1.3 Fundamental Bijection

A fundamental result (Barbut and Monjardet, 1970)

establishes that any lattice (L,≤) is isomorphic to the

concept lattice of the context (J

,≤), where J

and M

are the join and meet irreducible concepts of

L, respectively. Moreover, this context is a reduced

one.

As a direct consequence, there is a bijection be-

tween lattices and reduced contexts where objects of

the context are associated with join-irreducible con-

cepts of the lattice, and attributes are associated with

meet-irreducible concepts.

Table 1 in the appendix shows the reduced context

of the lattice in Figure 1.

When needed, operators •

introduced in subsec-

tion 2.1.2 will be written •

to stress the fact that they

are used with the reduced context of the lattice L.

A sub-context consists of a binary relation be-

tween a subset of objects and a subset of attributes

in the initial data. In this paper we consider particular

sub-contexts for which three different equivalent def-

initions can be given. More details can be found in

(Viaud et al., 2015).

• Compatible sub-contexts,

• Arrow-closed sub-contexts,

• Sub-contexts deﬁning factor lattices and congru-

ence relations.

In conjunction with Day’s doubling construction

(Day, 1977; Day, 1994), these particular sub-contexts

enable us to introduce a new construction, namely the

reverse doubling construction.

3 REVERSE DOUBLING

CONVEX

In this section, we describe the reverse doubling con-

struction which itself uses congruence relations.

Given a lattice L, we recall that we are looking for

a lattice L

containing a convex C such that L = L

[C].

3.1 Main Steps

Before giving details about this decomposition, let us

provide the main steps of our construction.

3.1.1 Main Steps of the Proof

Given a ﬁnite lattice L, we are searching a lattice L

and a convex set C ⊂ L

such that L is isomorphic to

[C].

1. We ﬁrst use following result of Day (Day, 1994):

Theorem 1. Let L be a congruence normal lattice

and Θ a congruence relation which is an atom, i.e.

a successor of the bottom element. Then, there

exists a convex set C such that L is isomorphic to

L/Θ[C].

From this theorem 1, we know that good candi-

dates can be obtained from factor lattices, spanned

by a congruence relation which is an atom.

It is important to note that we only get good candi-

dates because we do not use the congruence nor-

mality hypothesis.

2. We next use the following equivalence whose

proof can be found in (Ganter and Wille, 1999):

Theorem 2. Given a lattice L, the set of congru-

ence relations on L corresponds bijectively with

the set of arrow-closed subcontexts of the reduced

context of L.

KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval

352

From this Theorem 2, we know that these con-

gruence relations correspond to arrow-closed sub-

contexts.

3. Then the following theorem 3 of Geyer is used:

Theorem 3. Let L = L

[C] be a lattice obtained

by doubling the convex set C of the lattice L

Note K = (O,A,R) the reduced context of L, then

the reduced context K

= (J,M,R ∩ J × M) is an

arrow-closed subcontext of K such that:

R ∩ ((O\J) × (A\M)) =

0 (2)

We only need to check if the arrow-closed sub-

contexts that are just good candidates satisfy the

Geyer’s condition 2.

4. If none of these sub-contexts is valid, the decom-

position is not possible. Otherwise, each one of

these sub-contexts generates a lattice L

that is

appropriate.

3.1.2 Main Steps of the Construction

The principal steps are as follows:

1. The ﬁrst step of our construction is to compute

atoms of the lattice of congruence relations.

2. Then we select the arrow-closed sub-contexts sat-

isfying the Geyer’s condition. Each one of these

sub-contexts generates a lattice L

that is appro-

priate.

3. The last step consists in identifying the convex set

C in L

3.2 The Lattice of Congruence

Relations

A reduced context (O, A,R) of a lattice L is supposed

to be given.

Recall that congruence relations are equivalence

relations compatible with the lattice structure. As a

particular kind of binary relation, the set of congru-

ence relations inherits a structure of lattice: it is a

sublattice of the lattice of binary relations which is

ordered by inclusion. Using Theorem 2, this lattice

is also the lattice of arrow-closed sub-contexts. As

explained previously, we aim at ﬁnding the atoms of

that lattice. To that end, we introduce a new con-

text, namely the context of arrow-closed subcontexts,

which is deﬁned and computed as follows. We ﬁrst

compute one-generated arrow-closed sub-contexts.

Deﬁnition 1. A context (J,M, R) is one-generated if it

can be obtained by arrow-closing a context with only

one j ∈ J. Thus (J, M,R) is the smallest arrow-closed

subcontext containing j ∈ J.

The set of such one-generated sub-contexts con-

tains all join-irreducible arrow-closed sub-contexts of

the lattice of arrow-closed sub-contexts. Thus, the set

of one-generated sub-contexts generates the lattice of

arrow-closed sub-contexts. The one-generated sub-

contexts are stored as observations of a new context

in the following way: an arrow-closed is character-

ized by its set of attributes, since it is closed. Thus

the newly generated context has the same set of at-

tributes, namely A. Since one-generated sub-contexts

are computed by closing one j ∈ O, they can be iden-

tiﬁed with that j. The set of observations of the newly

generated context is still O. Finally, there is a cross

in the new context between object j and attribute a if

and only if the arrow-closed sub-context generated by

j contains the attribute a.

From this context, we can deduce the lattice of

arrow-closed sub-contexts and in particular its atoms.

3.3 The Factor Lattice

We are now given a list of arrow-closed sub-contexts,

which correspond to atom congruence relations.

The second step is to remove from this list the fol-

lowing contexts:

• The empty context. In the particular case where

the initial lattice has only two congruence rela-

tions, there is only one atom, namely the bottom

element. This case is excluded since it gives rise

to a trivial decomposition.

• Any context that does not satisfy Geyer’s Condi-

tion.

After this removal process, our list could be emp-

ty. Since the Geyer’s condition is necessary and sufﬁ-

cient, we can conclude that the original lattice can not

be processed through the reverse doubling construc-

tion.

On the opposite side, any remaining context gen-

erates a lattice L

such that there exists a convex set

C so that the initial lattice L satisﬁes L = L

[C].

3.4 Finding the Convex

Given a lattice L

satisfying the previous conditions

of Subsection 3.3, the last step is to identify in L

nodes of a convex set C such that L = L

[C].

Using Theorem 3 which gives a necessary and suf-

ﬁcient condition, we already know that L is obtained

by the doubling construction from L

. Thus, each

concept of L

gives rise to one concept in L if and

only if it is not in C and two concepts in L if and only

if it is in C.

The Reverse Doubling Construction

353

Let us be more precise about these two concepts,

and ﬁrst let us recall some notations: (O,A, R) is

the reduced context of the lattice L. We consider

(J, M,R ∩ J × M) an atom in the lattice of arrow-

closed sub-contexts which satiﬁes the Geyer’s condi-

tion. From this context, we can deduce L

the lat-

tice from which a convex has been removed. Let c

be a concept of L

. Recall from (Ganter and Wille,

1999) that arrow-closed sub-contexts are also com-

patible ones. Since (J,M,R ∩ J × M) is a compat-

ible sub-context, using this result, c can be written

as c = (H ∩ J,N ∩ M) with (H,N) a concept of L.

Since c is a concept, we have (H ∩ J)

= N ∩ M and

(N ∩ M)

= H ∩ J. Recall, from the end of Subsec-

tion 2.1.3, that these operations are written •

in the

reduced context (O,A, R) of L; thus we also have

= N and N

= H. Now, we can conclude that,

if c = (H ∩ J, N ∩ M) is not in the convex, it comes

from the unique concept of L, namely (H, N) and

thus we must have ((H ∩ J)

,(H ∩ J)

) = (H,N) =

((N ∩ M)

,(N ∩ M)

). In the other case, we have

((H ∩ J)

,(H ∩J)

) 6= ((N ∩ M)

,(N ∩ M)

From this point, we can state a simpler condition

for a concept to be in the convex set:

Theorem 4. A concept c = (H ∩ J, N ∩ M) is in the

convex if and only if

(H ∩ J)

⊆ (N ∩ M) or (N ∩ M)

⊆ (H ∩ J) (3)

Proof. We have previously seen that if c is in the con-

vex then:

((H ∩ J)

,(H ∩J)

) = (H,N) (4)

= ((N ∩ M)

,(N ∩ M)

) (5)

So both inclusions are true and actually are equal-

ities.

Suppose, reciprocally, that we have the ﬁrst one:

(H ∩ J)

⊂ (N ∩ M) (6)

We obtain the same result dually in the second

case.

First we prove that the inclusion is an equality.

Indeed, since (J, M, R ∩ J × M) is a subcontext of

(O,A, R), we have:

(H ∩ J)

⊂ (H ∩ J)

(7)

However (H ∩ J)

= (N ∩ M), so:

(N ∩ M) ⊂ (H ∩ J)

(8)

and dually

(H ∩ J) ⊂ (N ∩ M)

(9)

Therefore, we deduce that (H ∩ J)

= (N ∩ M),

and then (N ∩ M)

= (H ∩ J)

Moreover:

(H ∩J) ⊂ (N ∩M)

=⇒ (N ∩M)

⊂ (H ∩J)

(10)

and with (N ∩ M) = (H ∩ J)

, we deduce that:

(N ∩ M) = (N ∩ M)

(11)

since (N ∩ M) ⊂ (N ∩ M)

Now from (H ∩ J)

= (N ∩ M) = (N ∩ M)

and

(N ∩ M)

= (H ∩ J)

, we get:

((H ∩J)

,(H ∩ J)

) = ((N ∩M)

,(N ∩M)

) (12)

This means that a concept ((H ∩ J),(N ∩ M)) in

the small lattice L

that satisﬁes the condition (H ∩

⊂ (N ∩ M) or (N ∩ M)

⊂ (H ∩ J) comes from a

unique concept in the lattice L, namely the concept:

((H ∩ J)

,(H ∩J)

) = (H,N) (13)

= ((N ∩ M)

,(N ∩ M)

)

(14)

Conversely, if ((H ∩ J),(N ∩M)) does not satisfy

the previous condition, it comes from two concepts in

((H ∩J)

,(H ∩ J)

) 6= ((N ∩M)

,(N ∩M)

) (15)

Thus to get L from L

, one needs to double these

concepts and then these concepts are exactly the ones

of the convex.

4 EXAMPLE

To illustrate the reverse doubling convex construction,

we will use the lattice given in Figure 2 and its re-

duced context given by Table 2 already ﬁlled with ar-

rows. Nodes in light grey and dark grey correspond

to the two occurrences of the doubled convex.

From the lattice shown in Figure 2, we compute

Table 3 of one-generated arrow-closed sub-contexts

and then we get the lattice of congruence relations

given in Figure 4. Notice that Table 3 has been re-

duced after computation. In this particular case, there

are two atoms.

Since the two atoms identiﬁed in Figure 4 satisfy

Geyer’s condition, the lattice given in Figure 2 has

two decompositions.

Using only one of these atoms, namely the one

containing observation 25, we get the arrow-closed

KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval

354

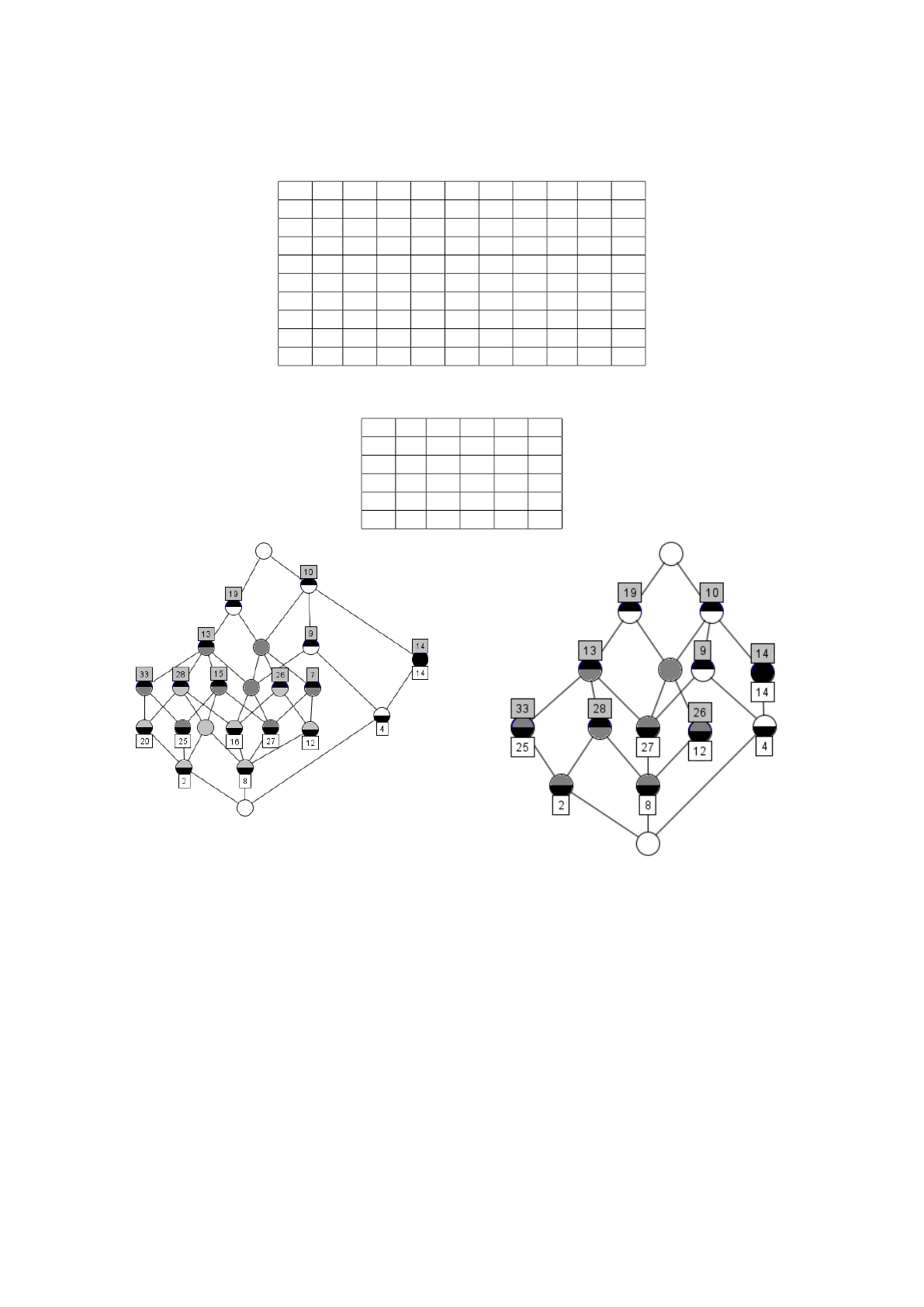
Table 2: The reduced context of the lattice in Figure 2 ﬁlled with arrows.

9 10 14 19 33 15 28 7 26 13

2 ↓ l ↓ × × × × ↓ ↓ ×

4 × × × l ↓ ↓ ↓ ↓ ↓ ↓

8 × × l × l × × × × ×

12 l × ↑ × ◦ ↓ ↓ × × l

14 l × × ↑ ◦ ◦ ◦ ◦ ◦ ◦

25 ◦ ↑ ◦ × × × l ◦ ◦ ×

20 ◦ ↑ ◦ × × l × ◦ ◦ ×

27 × × ↑ × ↑ × l × l ×

16 × × ↑ × ↑ l × l × ×

Table 3: The reduced context computed to get the lattice of congruence relations (Figure 4).

9 10 19 15 28

2 ×

4 ×

8 × ×

25 × × × ×

20 × × × ×

Figure 2: The lattice of Figure 3 with the convex set dou-

bled. Nodes of each convex are colored in light grey and

dark grey.

subcontext of Table 4, which satisﬁes Geyer’s condi-

tion. Then, its concept lattice, which is also the fac-

tor lattice of the selected congruence relation, can be

computed and visualized on Figure 3.

In Figure 3, nodes of the convex C are in grey, and

when the doubling construction is applied on that lat-

tice, with this convex set, the lattice from Figure 2 is

obtained. Nodes in light grey and dark grey corre-

spond to the two occurrences of the doubled convex.

This lattice is obtained from the reduced context given

in Table 4, which is one of the two atoms of the lattice

in Figure 4.

In order to test our decomposition method with re-

Figure 3: A lattice with its irreducible nodes. Nodes with a

number above are meet-irreducible while nodes with a num-

ber below are join-irreducible.

spect to its ability to reduce the lattice size, a ﬁrst ex-

periment has been done. A series of 500 random con-

texts with 20 observations, 10 attributes and a density

of 75% was generated. Only 42 of them (8.4%) had a

non trivial decomposition. However, 17 of these con-

texts (40%) led to reduced lattices with a ratio of 50%

while the rest (60%) of contexts led to a lattice size

reduction higher than 50%. Table 5 reﬂects such ra-

tios where the ﬁrst column represents the lattice size

reduction (i.e., the number of nodes of the reduced

lattice over the number of nodes in the initial lattice)

The Reverse Doubling Construction

355

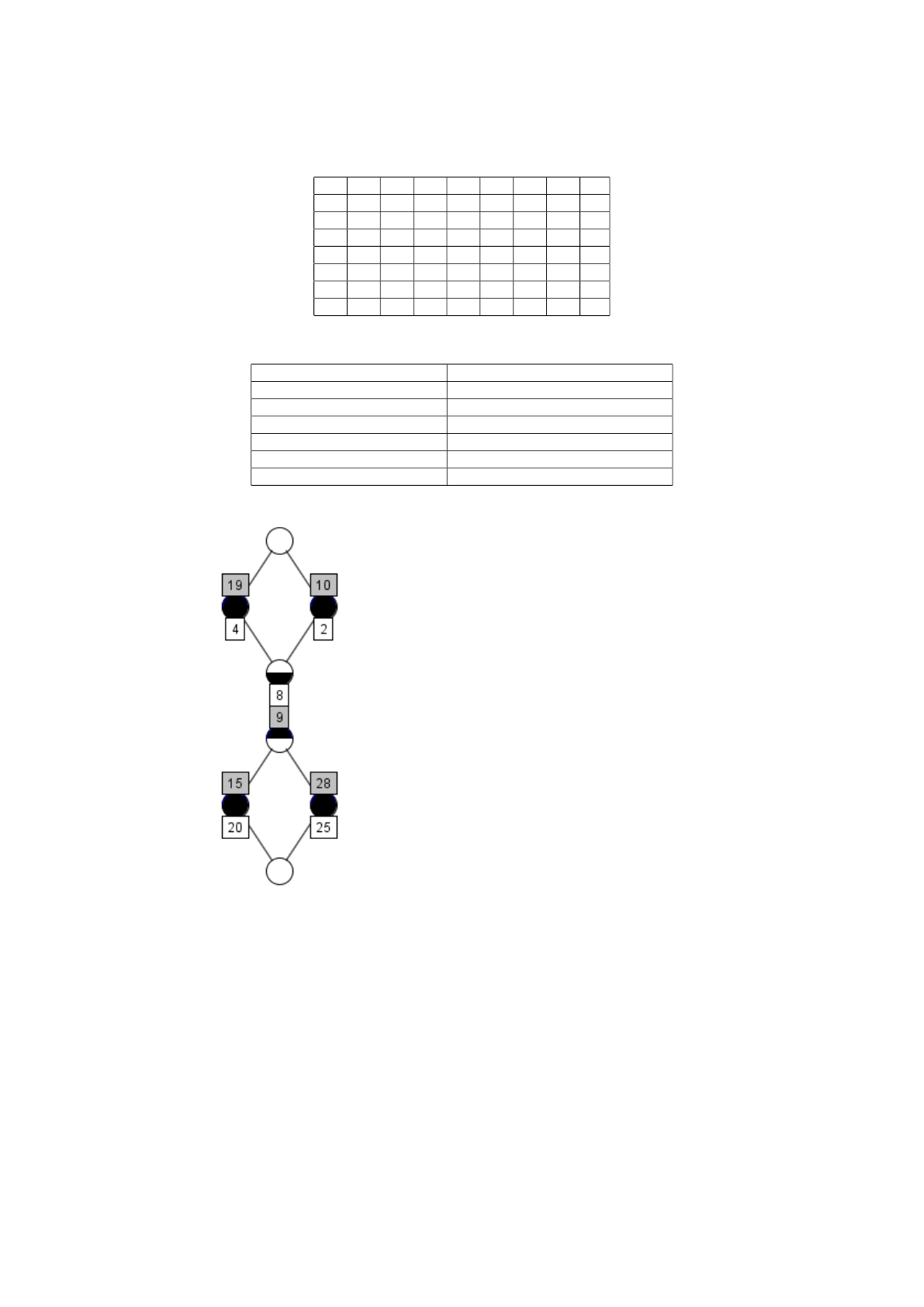
Table 4: The reduced context of the factor lattice given in Figure 3.

10 13 14 19 26 28 33 9

12 × × ×

14 × ×

2 × × × ×

25 × × ×

27 × × × ×

4 × × ×

8 × × × × ×

Table 5: Lattice size reduction ratio and proportion of reduced lattices.

Ratio of the numbers of nodes Number and proportion of contexts

50% 17 - 40%

50% to 60% 9 - 21%

60% to 70% 6 - 14%

70% to 80% 5 - 12%

80% to 90% 4 - 10%

90% to 100% 1 - 3%

Figure 4: The lattice of congruence relations of the lattice

given in Figure 2.

while the second column indicates the number and

proportion of contexts for which the reduction ratio

is in the interval given in the ﬁrst column. We can

then conclude that the decomposition is rarely possi-

ble, but when it occurs, it often leads to a signiﬁcant

reduction in the lattice size.

All computations were done using the Galac-

tic project available at http://thegalactic.github.io/

while the lattices were drawn with ConExp (see

http://conexp.sourceforge.net/).

5 CONCLUSION AND FUTURE

WORK

In this paper, a new decomposition based on Day’s

construction was given which uses congruence rela-

tions. Although Day’s doubling construction has been

widely studied, the reverse doubling construction we

are investigating is, to the best of our knowledge, a

new decomposition method that could be helpful in

dealing with large contexts and their visualization.

To further investigate the reverse doubling con-

struction, it would be interesting to conduct large-

scale experiments on very large real-life data, not only

to test the potential of decomposition for lattice reduc-

tion but also its performance and scalability for such

large data sets. Since noisy data occur frequently in a

process of data analysis, we plan to carefully perform

a preprocessing step in which efﬁcient data cleaning

techniques will be identiﬁed and used.

Since the empirical study in (Snelting, 2005)

shows that many real-life contexts do not contain non-

trivial congruence relations, we plan to formally iden-

tify cases in which the reverse doubling construction

can either be used or not.

Our future work consists to study, compare and

combine other decompositions with the one descri-

bed in this paper. In particular the Fratini congruence

(Duquenne, 2010) which exploits again a congruence

relation, and Atlas decomposition (Ganter and Wille,

1999) which uses tolerance relations.

KDIR 2015 - 7th International Conference on Knowledge Discovery and Information Retrieval

356

REFERENCES

Barbut, M. and Monjardet, B., editors (1970). L’ordre et

la classiﬁcation. Alg

ebre et combinatoire, tome II.

Hachette.

Belohlavek, R. and Vychodil, V. (2010). Discovery of op-

timal factors in binary data via a novel method of ma-

trix decomposition. Journal of Computer and System

Sciences, 76(1):3–20.

Bertet, K. and Caspard, N. (2002). Doubling convec sets in

lattices: characterizations and recognition algorithms.

Technical Report TR-LACL-2002-08, LACL (Labo-

ratory of Algorithms, Complexity and Logic), Univer-

sity of Paris-Est (Paris 12).

Day, A. (1977). Splitting lattices generate all lattices. alge-

bra universalis, 7(1):163–169.

Day, A. (1994). Congruence normality: The characteriza-

tion of the doubling class of convex sets. algebra uni-

versalis, 31(3):397–406.

Day, A., Nation, J., and Tschantz, S. (1989). Doubling con-

vex sets in lattices and a generalized semidistributivity

condition. Order, 6(2):175–180.

Demel, J. (1982). Fast algorithms for ﬁnding a subdirect de-

composition and interesting congruences of ﬁnite al-

gebras. Kybernetika (Prague), 18(2):121–130.

Duquenne, V. (2010). Lattice drawings and morphisms. In

Formal Concept Analysis, 8th International Confer-

ence, ICFCA 2010, Agadir, Morocco, March 15-18,

2010. Proceedings, pages 88–103.

Ferr

e, S. (2014). Reconciling expressivity and usability in

information access from ﬁle systems to the semantic

web. Rapport hdr, University Rennes 1.

Freese, R. (1997). Computing congruence lattices of ﬁnite

lattices. Proceedings of the American Mathematical

Society, 125(12):3457–3463.

Freese, R. (1999). Algorithms in ﬁnite, ﬁnitely presented

and free lattices. Preprint, July, 22:159–178.

Freese, R. (2008). Computing congruences efﬁciently. Al-

gebra universalis, 59(3-4):337–343.

Funk, P., Lewien, A., and Snelting, G. (1995). Algorithms

for concept lattice decomposition and their applica-

tions. Technical report, TU Braunschweig.

Ganter, B. and Wille, R. (1999). Formal concept analysis -

mathematical foundations. Springer.

Geyer, W. (1994). The generalized doubling construction

and formal concept analysis. algebra universalis,

32(3):341–367.

Mih

ok, P. and Semani

sin, G. (2008). Unique factorization

theorem and formal concept analysis. In Yahia, S.,

Nguifo, E., and Belohlavek, R., editors, Concept Lat-

tices and Their Applications, volume 4923 of Lecture

Notes in Computer Science, pages 232–239. Springer

Berlin Heidelberg.

Nation, J. (1995). Alan day’s doubling construction. alge-

bra universalis, 34(1):24–34.

Snelting, G. (2005). Concept lattices in software analysis.

In Formal Concept Analysis, Foundations and Appli-

cations, pages 272–287.

Viaud, J.-F., Bertet, K., Demko, C., and Missaoui, R.

(2015). Subdirect decomposition of contexts into sub-

directly irreducible factors. Formal Concept Analysis

and Applications FCA&A 2015, page 49.

Visani, M., Bertet, K., and Ogier, J.-M. (2011). Navi-

gala: an Original Symbol Classiﬁer Based on Navi-

gation through a Galois Lattice. International Jour-

nal on Pattern Recognition and Artiﬁcial Intelligence

(IJPRAI).

Wille, R. (1969). Subdirekte produkte und konjunkte sum-

men. Journal f

ur die reine und angewandte Mathe-

matik, 0239 0240:333–338.

Wille, R. (1976). Subdirekte Produkte vollst

andiger Ver-

ande. J. reine angew. Math., 283/284:53–70.

Wille, R. (1983). Subdirect decomposition of concept lat-

tices. Algebra Universalis, 17:275–287.

Wille, R. (1987). Subdirect product construction of concept

lattices. Discrete Mathematics, 63(2-3):305–313.

The Reverse Doubling Construction

357