Investigation into Mutation Operators for Microbial Genetic Algorithm

Samreen Umer

University College Cork, Western Road, Cork, Ireland

Keywords:

Microbial Genetic Algorithm, Evolutionary Algorithms, Mutation.

Abstract:

Microbial Genetic Algorithm (MGA) is a simple variant of genetic algorithm and is inspired by bacterial con-

jugation for evolution. In this paper we have discussed and analyzed variants of this less exploited algorithm

on known benchmark testing functions to suggest a suitable choice of mutation operator. We also proposed a

simple adaptive scheme to adjust the impact of mutation according to the diversity in population in a cost ef-

fective way. Our investigation suggests that a clever choice of mutation operator can enhance the performance

of basic MGA signiﬁcantly.

1 INTRODUCTION

The idea of using evolutionary principles for auto-

mated problems was ﬁrst originated in the middle of

20th century. Dr. L.J Fogel, known as father of evo-

lutionary programming, presented ﬁrst evolutionary

technique in his dissertation (Fogel et al., 1966). Later

on, this area got signiﬁcant attention and different di-

alects of this technology were evolved. Since then

swarm based optimization and nature inspired algo-

rithms marked their signiﬁcance in computational sci-

ences. In recent decades these techniques have gain

much popularity in terms of optimization applica-

tions, system design and scheduling operations. Ge-

netic algorithms are evolutionary computation tech-

niques which mimics the evolution process to gener-

ate useful solutions for optimization problems (John,

1992). Many variants for genetic algorithms have

been introduced to satisfy different constraints ac-

cording to different situations. Here we will discuss

about one of the variants of genetic algorithm called

Microbial Genetic Algorithm (MGA).

Harvey introduced the idea of bacterial recom-

bination or infection as a substitute to inheritance

from parents in genetic algorithm (McCarthy, 2007)

and called it as microbial genetic algorithm (Harvey,

2011). Motivation behind this variant was to produce

a minimalist algorithm still containing all the char-

acteristics of a true genetic algorithm. Since then,

bacterial or microbial evolution based algorithms

have been used successfully by many researchers and

scientists. However any investigation on MGA’s per-

formance or its operators is not available in literature.

We conducted this study to verify the behaviour of

basic MGA and MGA with newer mutation operators

to solve unconstrained optimization problems. We

introduced a simple adaptive mutation scheme and

results conclude that a clever selection of MGA

operators can improve its performance notably.

2 MICROBIAL GENETIC

ALGORITHM

MGA is a simpler variant of GA. Main difference

between these two is different recombination opera-

tor. In MGA, initially parents are selected from gen-

erated population using a selection scheme and, are

then evaluated on the basis of their ﬁtness to mark a

loser and winner. Unlike basic GA, MGA crossover

genes in such a way that the winner is left intact and

some genes are transferred to the loser with a deﬁned

crossover probability. In this way the elitism is main-

tained and assumingly good genes are transferred to

the next generation. Mutation is then carried out on

infected loser to keep the diversity in the population.

The whole routine can be repeated until the desired

results are achievedor up to maximum number of iter-

ations allowed. Figure 2.1 illustrates one tournament

or life cycle of MGA.

2.1 Generating Population

Like in any other evolutionary algorithm, the ﬁrst step

is to generate a potential population within domain

Umer, S..

Investigation into Mutation Operators for Microbial Genetic Algorithm.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 299-305

ISBN: 978-989-758-157-1

299

Figure 1: One MGA Cycle.

of the problem. Size and diversity of the popula-

tion plays a crucial role in the performance of any

algorithm. Larger the population ensures greater di-

versity but more computations.Small population can

converge in less time but can also lead to premature

convergence. Many studies have been conducted to

generalize an optimal population size but mostly it

depends on the dimension of the problem and number

of maximum iterations allowed. Generally the popu-

lation is generated from a uniform distribution within

prescribed range and is unbiased.

2.2 Selecting Parents

A variety of selection technique is available for ge-

netic algorithms. Some possibilities are stochas-

tic universal sampling (Baker, 1985), Ranked selec-

tion (Whitley et al., 1989), Roulette wheel selection,

and Truncation selection (Goldberg and Deb, 1991).

However we have used ranked roulette selection as

our selection scheme in experiments.

2.2.1 Ranked Roulette Selection

Roulette scheme of selection is one of the commonly

used scheme among the researchers. In this method,

the probability of selection P

is assigned to the mem-

ber i of population size n in accordance to their ﬁtness

value f

such that

∑

j=1

(1)

For ﬁnding optimal minimums this formula can be

manipulated as

∑

f − f

∑

(2)

But in case of non positive values unfortunately

this equation can not work leaving us with the im-

plication of some kind of scaling or scoring of ﬁt-

ness values. One possible solution to such problem

was proposed by (Al Jadaan and Rao, 2008) as an

improved selection operator. The population is ﬁrst

evaluated and sorted in accordance to the rank based

on ﬁtness value and then the probabilities are assigned

using following formula

Pop(Pop+ 1)

(3)

Where P

is the probability of individual i with

rank R

from population with with population size

Pop for being selected as a parent. A simple ranking

scheme can be where rank of a member is its position

in sorted population according to ﬁtness.

The above scheme is used to select parents for

each cycle or tournament. Parents are then evaluated

and assigned as winner and loser for their survivabil-

ity in next generation.

2.3 Recombination

In each cycle the population is replaced with new gen-

eration. The selection scheme mentioned above gives

the parents to breed for children who will be intro-

duced in population to make new generation. In con-

ventional GA this has been the normal way of each

life/death cycle where the parents are replaced with

the children and thus genes are transferred vertically

down to the next generation. However in Microbes,

breeding is not in similar fashion. The organisms or

microbes reproduce by binary ﬁssion and further ex-

change their genetic material via a process called bac-

terial conjugation. What happens in this phenomenon

is that the ﬁttest bacteria most commonly the one who

has developed resistance to the antibiotics makes a

contact with the weaker vulnerable bacteria and trans-

fer its resistance in terms of plasmid to it. MGA

uses this concept of parallel gene transfer to evolve

instead of horizontal gene transfer in conventional

GA. The ﬁttest among the parents transfer its genes

to the weaker thus the new chromosome is actually

the weaker parent with some of its genes replaced by

genes from the winner.

2.4 Mutation

Mutation is responsible for maintaining the diver-

sity in population and preventing premature conver-

gence. Extensive research and studies have been done

already to provide different mutation operators and

proved to be useful in most cases. Following oper-

ators are reviewed here for further use in experimen-

tation ahead.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

300

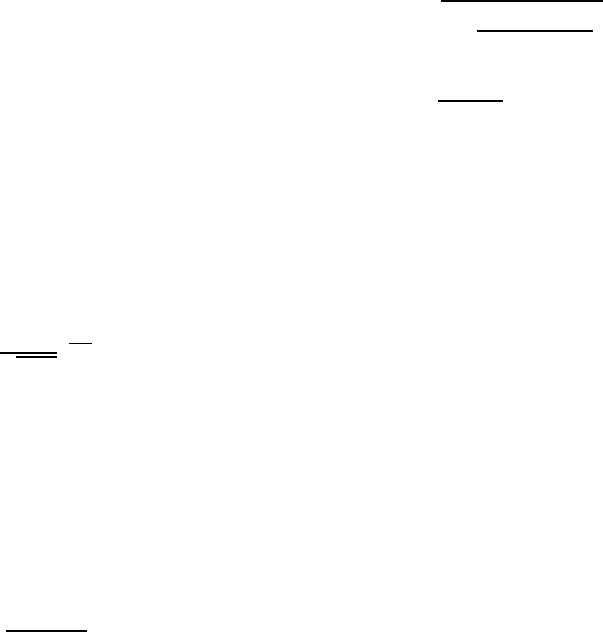
2.4.1 Uniform One Point Mutation

One random gene from the member which in this case

is the infected loser, is replaced with a new gene. In

case of binary MGA the gene is a bit so mutation

means just ﬂipping the bit. However in case of real

number or integers, a new gene is generated from the

possible range randomly. Uniform one point mutation

is a technique in which at one random locus, the gene

is replaced by a new one generated randomly from a

uniform distribution.

2.4.2 Gaussian One Point Mutation

Instead of uniform distribution other distributions like

Gaussian can be used for generating the new gene. A

classical Gaussian mutation operator was developed

by Rechenberg and Schwefel in which a scaled Gaus-

sian normally distributed number is added to the pre-

vious value of gene (Back and Schwefel, 1993) . This

method requires information about mean and vari-

ance of desired distributionto produce a random gene.

Generally value of mean is set to be 0 with variance of

0.2 to 0.8. the formula for Gaussian density function

with mean µ = 0 and δ variance is given by

f(x) =

√

2πδ

−x

2δ

(4)

2.4.3 Cauchy One Point Mutation

For some functions with relative minima that are far

apart the small mutations of uniform or Gaussian dis-

tributions may lead to premature convergence to local

minima. For this reason (Yao et al., 1999) devised

an alternative to the Gaussian mutation by using a

Cauchy distributed random number instead. Cauchy

distribution with mean µ = 0 is deﬁned as

f(x) =

π(t

+ x

)

(5)

Where t is the scaling factor and usually set as 1.

This allows for larger mutation and can help prevent

premature convergence and search the search space

faster. However there is less probability of smaller

mutations in the neighbourhood of the parent leading

to a less accurate local search.

2.4.4 Forced Adaptive Guassian Mutation

Experiments suggest that MGA converges faster in

earlier stages but with time as population tends to be

more similar, the same mutation operator does not re-

main as effective. Many researchers have proposed

adaptive or forced mutation operators for enhancing

its over all performance. In (Hatwagner and Horvath,

2012) a new forced mutation operator has been intro-

duced for bacterial evolutionary algorithm based on

relationship between diversity of population and vari-

ance of mutation operator. Howevercalculating diver-

sity in each iteration incurs additional computational

overhead and delays. Inspired by their technique, we

designed a mutation operator where we set thresholds

to calculate diversity in the population and adjust mu-

tation accordingly. The diversity of population is cal-

culated using formula given in (Miller and Goldberg,

1995).

i, j

∑

k=1

(

i,k

−x

j,k

k,max

−X

k,min

) (6)

D =

Pop −1

Pop

∑

i=1

i,best

(7)

Any mutation scheme can be coupled with this

technique however we used gaussian scheme where

the variance is controlling parameter of mutation. Ob-

jective for designing this operator is to improve the

diversity D in earlier evaluations and tune to ﬁne po-

sition in the later stages. So when the population is

generated it usually has higher diversity at that point

we can directly relate the variance σ with D allowing

MGA routine to get variety in its early generations.

With higher variance we observed no improvement in

this situation where as low variance in such condition

showed better reﬁne. Using following formula where

Variance σ increases with diversity up to a threshold

value lets say D = 0.5 and then start decreasing lin-

early .

σ = α.min(D, 1−D) (8)

α is the scaling constant with values 0 ≤ alpha ≤ 1

. σ obtained is then used in equation (4) to facilitate

gaussian mutation.

2.5 Replacing Previous Generation with

New One

Now comes the turn to introduce the infected and mu-

tated member into the population to proceed for next

cycle. In basic original GA, usually either both of the

selected parents are replaced with new crossed and

mutated offsprings or the worst of whole population

is replaced with the new offsprings. Howeverto main-

tain the elitism by keeping the winner intact and also

avoid losing all of the genes from loser, in basic MGA

loser chromosome is replaced with the new infected

and mutated version of loser. This is easy to imple-

ment and effective as well. This keeps in consistency

with the underlying intuition of microbial evolution

where evolution is brought without death of parents.

Investigation into Mutation Operators for Microbial Genetic Algorithm

301

3 EVALUATION

Performance of any optimization algorithm is mea-

sured through some characteristic features like its ro-

bustness and precision. A set of standard benchmark

problems are usually used to analyze these features

for any algorithm. These functions are well known in

literature, and their qualitative properties and global

extremes are also known. The notion of robustness

may refer to a set of characteristics itself. This tells

how good the algorithm can perform with increas-

ing number of dimensions and difﬁculty as well as

how timely it can converge to optimal solution. The

term convergence may be interpreted in two mean-

ings, either all the population becoming just uniform

at any suboptimal location or when the evaluation hits

the desired optimal results. Both these situations are

closely related but different from each other. Preci-

sion of the algorithm tells how close the results are to

desired optimal solution. A fast, robust and, precise

algorithm is an objective of optimization researcher.

A number of simulations are carried out to testify the

proposed suggestions. These simulations are run on

MATLAB 7.1 to give numerical results and graph-

ical representation of algorithm performances. We

have used a set of standard benchmark from literature

(Ortiz-Boyer et al., 2005) for our simulations catego-

rized under three subsets as follows.

• Unimodal multidimensional convex problems

• Multimodal two dimensional problems

• Multimodal multidimensional problems

Unimodal multidimensional convex problems include

some cases causing poor or slow convergenceto a sin-

gle global extreme. Multimodal problems may have

large number of local extremes making a multidimen-

sional problem harder to locate the global optima. In-

creasing number of dimensions further increases the

hardness of the problem but most of the real practical

problems desired to be modelled usually are multidi-

mensional. For evaluation, we run monte carlo sim-

ulations to ﬁnd suitable controlling parameters like

probabilities and constants and then average the re-

sults from 100 simulations for each problem and vari-

ant of MGA.

3.1 Simulations Results

In this section, we have presented simulation plots

for MGA with different mutation operators. We have

used ranked roulette selection scheme in all simula-

tions and different mutation operators for each opti-

mization problem. The results plotted are mean val-

ues of 100 simulations for each evaluation. Proba-

bility of mutation and infection have been chosen af-

ter extensive experimental investigation. Table 1 pro-

vides chosen values for probabilities of infection Pi

and probability of mutation Pm for each problem and

also states the best solution achieved over 10000 it-

erations and n = 2, 30. MGA with adaptive mutation

is also compared with basic GA over 5000 iterations

using MATLAB GA toolbox with suggested values

of parameters from literature and ranked roulette se-

lection scheme as in MGA. Comparison with GA is

given in table 3 in appendix and shows that MGA

with adaptive mutation is highly comparable with ba-

sic GA and even outperforms GA in many problems

in terms of ﬁnding better minima specially in prob-

lems with less variables or dimensions.

Table 1: Chosen Parameters and Best Achieved Solutions

in 5000 iterations.

Problem Best Minima Pi Pm

DeJong First 0.0002 0.7 0.7

Axis Parallel Ellipsoid 0.0025 0.7 0.7

Rotated Hyper Ellipsoid 0.0020 0.7 0.7

Sum of Different Powers 0.0092 x10

−4

0.7 0.7

Rosenbrok Valley 0.1081 0.7 0.7

Rastrigins 0.0329 0.7 0.7

Schwefel -1256.9 0.6 0.8

Griewangk 0.0566x10

−6

0.7 0.8

Ackley 0.0104 0.6 0.8

Branin 0.3978 0.5 0.75

Goldstein Price 3 0.6 0.4

Six Hump Camel Back -1.036 0.6 0.75

DeJong Fifth 0.998 0.6 0.75

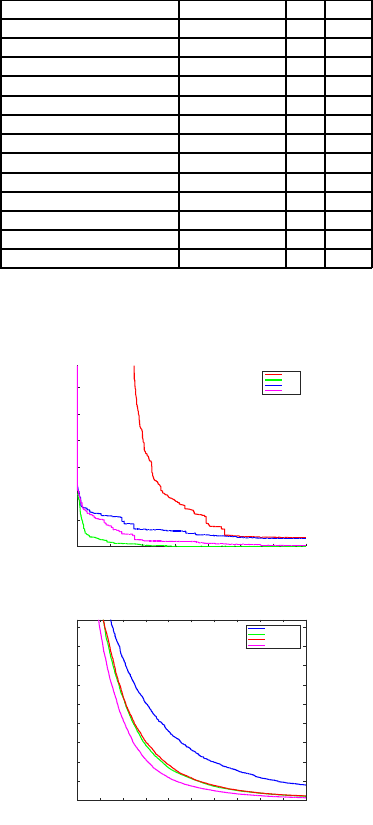
3.1.1 Unimodal Multidimensional Problems

No. of Iterations

0 1000 2000 3000 4000 5000 6000 7000

Minima

×10

-3

0.5

1.5

2.5

Sum of Different Powers function

MGA

MGA-G

MGA-C

MGA-A

Figure 2: Sum of different powers function.

iterations

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

optima

Axis Parallel Hyper Ellipsoid Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 3: Axis parallel hyper ellipsoid function.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

302

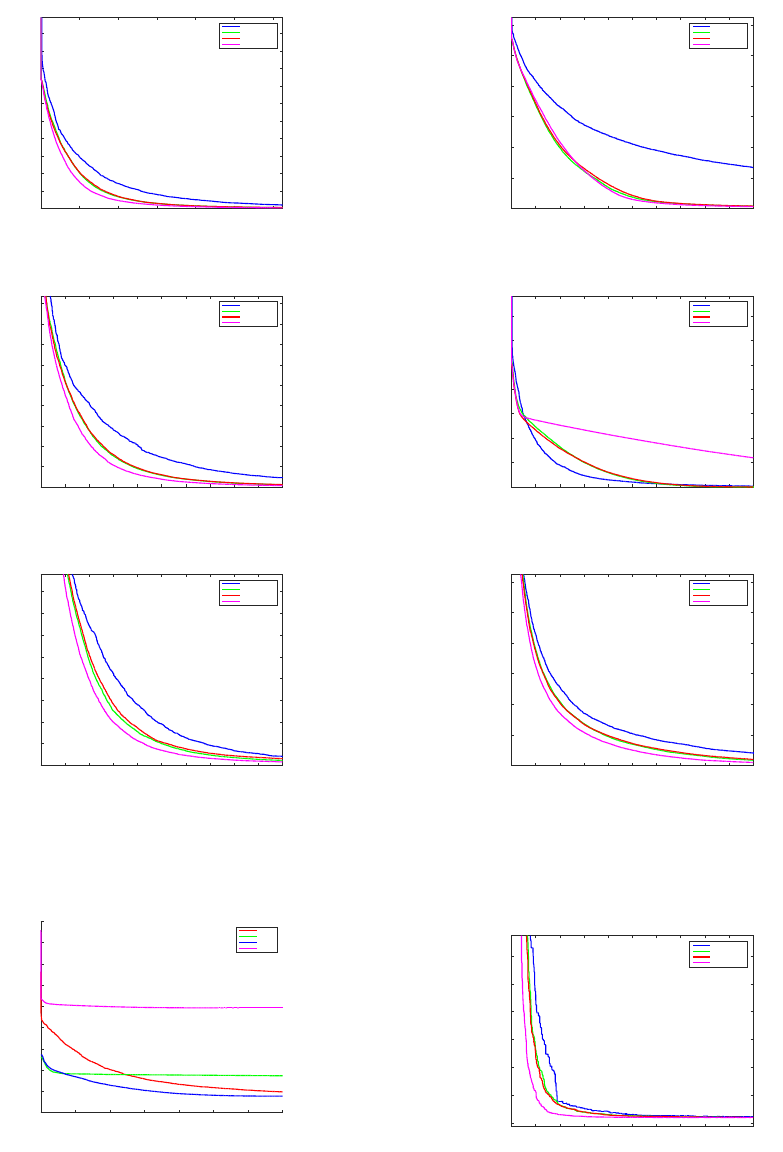
iterations

0 1000 2000 3000 4000 5000 6000

optima

Dejong First Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 4: Dejong ﬁrst function.

iterations

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

optima

Rotated Hyper Ellipsoid Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 5: Rotated hyper ellipsoid function.

iterations

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

optima

Rosenbrok Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 6: Rosenbrok valley function.

3.1.2 Multimodal Multidimensional Problems

No. of Iterations

0 1000 2000 3000 4000 5000 6000 7000

Minima

-14000

-12000

-10000

-8000

-6000

-4000

-2000

2000

4000

Schwefel function

MGA

MGA-G

MGA-C

MGA-A

Figure 7: Schwefel function.

iterations

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

optima

Ackley Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 8: Ackley function.

iterations

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

optima

Griewangk Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 9: Griewangk function.

iterations

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

optima

100

120

Rastrigin Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 10: Rastrigin function.

3.1.3 Two Dimensional Multimodal Difﬁcult

Problems

iterations

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

optima

-1.032

-1.03

-1.028

-1.026

-1.024

-1.022

-1.02

Six Hump Camel Back Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 11: Six hump camel back function.

Investigation into Mutation Operators for Microbial Genetic Algorithm

303

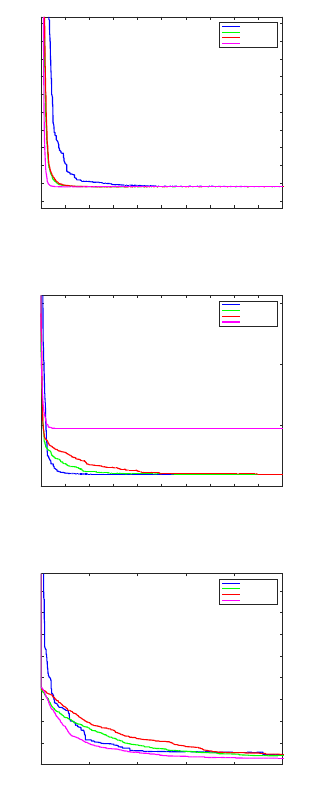
iterations

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

optima

0.39

0.4

0.41

0.42

0.43

0.44

0.45

0.46

0.47

0.48

0.49

Branin Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 12: Branin function.

iterations

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

optima

Dejong fifth Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 13: Dejong ﬁfth function.

iterations

0 500 1000 1500 2000 2500

optima

Goldstein Price Function

MGA-uniform

MGA-Gaussian

MGA-Cauchy

MGA-Adaptive

Figure 14: Goldstein price function.

4 CONCLUSIONS

In this paper, we have analyzed performance of MGA

in minimizing unconstrained complex problems us-

ing commonly used mutation operators. We have also

suggested a simple adjustment to adapt the mutation

according to the diversity in population to be more

effective. Comparison of different variants of MGA

might be helpful for readers in choosing the suitable

variant according to their objective problem. MGA

with our adaptive mutation has shown promising be-

haviour in general and comparison with basic GA ver-

iﬁes its potential as a useful optimization technique.

REFERENCES

Al Jadaan, Omar, L. R. and Rao, C. (2008). Improved selec-

tion operator for genetic algorithm. Theoretical and

Applied Information Technology, (4.4).

Back, T. and Schwefel, H.-P. (1993). An overview of evo-

lutionary algorithms for parameter optimization. Evo-

lutionary computation, 1(1):1–23.

Baker, J. E. (1985). Adaptive selection methods for genetic

algorithms. In Proceedings of an International Con-

ference on Genetic Algorithms and their applications,

pages 101–111. Hillsdale, New Jersey.

Fogel, L. J., Owens, A. J., and Walsh, M. J. (1966). Artiﬁ-

cial intelligence through simulated evolution.

Goldberg, D. E. and Deb, K. (1991). A comparative anal-

ysis of selection schemes used in genetic algorithms.

Foundations of genetic algorithms, 1:69–93.

Harvey, I. (2011). The microbial genetic algorithm. In Ad-

vances in artiﬁcial life. Darwin Meets von Neumann,

pages 126–133. Springer.

Hatwagner, F. and Horvath, A. (2012). Maintaining genetic

diversity in bacterial evolutionary algorithm. Annales

Univ. Sci. Budapest, Sec. Comp, 37:175–194.

John, H. (1992). Holland, adaptation in natural and artiﬁcial

systems: An introductory analysis with applications to

biology, control and artiﬁcial intelligence.

McCarthy, J. (2007). What is artiﬁcial intelligence. URL:

http://www-formal. stanford. edu/jmc/whatisai. html,

page 38.

Miller, B. L. and Goldberg, D. E. (1995). Genetic algo-

rithms, tournament selection, and the effects of noise.

Complex Systems, 9(3):193–212.

Ortiz-Boyer, D., Herv´as-Mart´ınez, C., and Garc´ıa-Pedrajas,

N. (2005). Cixl2: A crossover operator for evolution-

ary algorithms based on population features. J. Artif.

Intell. Res.(JAIR), 24:1–48.

Whitley, L. D. et al. (1989). The genitor algorithm and se-

lection pressure: Why rank-based allocation of repro-

ductive trials is best. In ICGA, pages 116–123.

Yao, X., Liu, Y., and Lin, G. (1999). Evolutionary program-

ming made faster. Evolutionary Computation, IEEE

Transactions on, 3(2):82–102.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

304

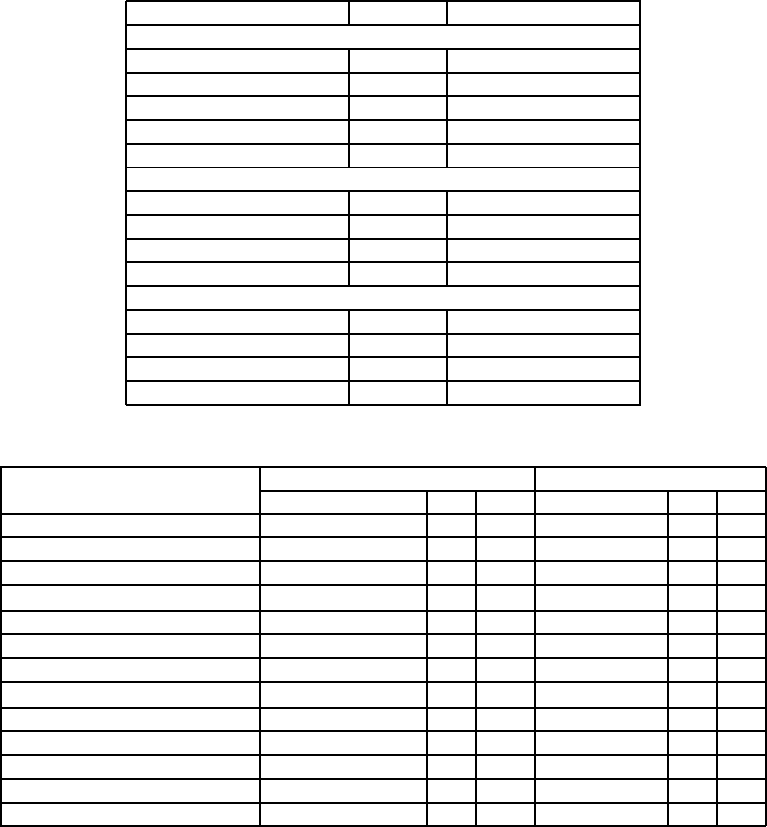
APPENDIX

Table 2: Test Functions Used.

Name Min domain

Unimodal Multidimensional Problems

De Jong First 0 −5.12 ≤ x

≤ 5.12

Axis Parallel Ellipsoid 0 −5.12 ≤ x

≤ 5.12

Rotated Hyper Ellipsoid 0 −65.54 ≤ x

≤ 65.54

Sum of Different Powers 0 −1 ≤ x

≤ 1

Rosenbrocks Valley 0 −2.048 ≤ x

≤ 2.048

Multimodal Multidimensional Problems

Rastrigins 0 −5.12 ≤ x

≤ 5.12

Schwefel -418.98n −500 ≤ x

≤ 500

Grienwangk 0 −600 ≤ x

≤ 600

Ackley 0 −32.76 ≤ x

≤ 32.76

Difﬁcult Two dimensional Multimodal Problems

Branin 0.397887 −5 ≤ x

≤ 15

Goldstein Price 3 −2 ≤ x

≤ 2

Six Hump Camel Back -1.036 −3 ≤ x

≤ 3

De Jong Fifth 0.998 −65.54 ≤ x

≤ 65.54

Table 3: Comparison of GA with MGA-Adaptive over 5000 iterations.

Problem MGA-Adaptive GA

Minima Achieved P

Minima P

DeJong First 0.0002 0.7 0.7 0.0001 0.8 0.2

Axis Parallel Hyper Ellipsoid 0.0025 0.7 0.7 0.0028 0.8 0.2

Rotated Hyper Ellipsoid 0.0020 0.7 0.7 0.0021 0.8 0.2

Sum of Different Powers 0.0092 x10

{−4}

0.7 0.7 0.0009 0.8 0.2

Rosenbrok Valley 0.1081 0.7 0.7 0.0541 0.8 0.2

Rastrigins 0.0329 0.7 0.7 0.004 0.8 0.1

Schwefel -1256.9 0.6 0.8 -1494.0 0.8 0.1

Griewangk 0.0566x10

{−6}

0.7 0.8 1.364x10

{−7}

0.8 0.1

Ackley 0.0104 0.6 0.8 0.0014 0.8 0.1

Branin 0.3960 0.5 0.75 0.3979 0.6 0.2

Goldstein Price 3.0000 0.6 0.4 3.002 0.6 0.2

Six Hump Camel Back -1.0360 0.6 0.75 -1.032 0.6 0.2

DeJong Fifth 0.9980 0.6 0.75 0.998 0.6 0.2

Investigation into Mutation Operators for Microbial Genetic Algorithm

305