
Hubless 3D Medical Image Bundle Registration
R
´
emi Agier, S
´
ebastien Valette, Laurent Fanton, Pierre Croisille and R
´
emy Prost
Universit
´
e de Lyon, CREATIS; CNRS UMR5220; Inserm U1044; INSA-Lyon; CHU Lyon and St-Etienne
Universit
´
e Claude Bernard Lyon 1, Villeurbanne, France
Keywords:
Big Data, Medical Imaging, Points of Interest, Registration.
Abstract:
We propose a hubless medical image registration scheme, able to conjointly register massive amounts of
images. Exploiting 3D points of interest combined with global optimization, our algorithm allows partial
matches, does not need any prior information (full body image as a central patient model) and exhibits very
good robustness by exploiting inter-volume relationships. We show the efficiency of our approach with the
rigid registration of 400 CT volumes, and we provide an eye-detection application as a first step to patient
image anonymization.
1 INTRODUCTION
The increasing availability of digital medical imag-
ing techniques such as Magnetic Resonance Imaging
(MRI), Computed Tomography (CT) and Ultrasound
(US) and the amount of data to process in health-
care networks has grown exponentially, thus illustrat-
ing the Big Data challenge in medecine. To perform
early screening, monitoring or to follow-up thousands
of patients throughout their healing, stress has to be
put on the ability to perform fast and robust image
analysis. This sums up to one question: how to pro-
cess several thousand volumes automatically and ro-
bustly? In this context, we propose a versatile feature-
based co-registration framework which can serve as a
first step towards volume collections processing. The
aim of this paper is to register the volumes altogether.
this paper currently focus on robustness rather than
accuracy, with the belief that the challenge is in inter-
patient variability.
The Picture Archiving and Communication Sys-
tem (PACS) is at the center of image management in
healthcare networks. Medical images are stored in
the Digital imaging and communications in medicine
(DICOM) format which contains, in addition to im-
ages, informations such as acquisition parameters and
patient data. With cohort studies (Bild et al., 2002)
and mass computation, spatial consistency between
images is crucial. Despite the fact that DICOM con-
tains data about spatial positions, we can see in fig-
ure 1 that they are not consistent. So, when one wants
to deal with large medical image datasets, an initial
Figure 1: Mass 3D image registration. (Top) a bundle of
heterogeneous images arranged according to DICOM em-
beded data. This shows that DICOM metadata are gen-
erally not consistent and may hinder subsequent computa-
tions. (Bottom) After mass hubless registration, images are
well aligned and the bundle may be used in further com-
putation. Registration is robust over heterogeneous images,
with, for example, only small body parts like heads. For
visualization purposes, images are distributed over an hori-
zontal grid.
global registration is needed. We propose to solve
this global challenge using a hubless approach. To
our knowledge, this is the first time that an approach
which jointly process medical images is proposed.
This paper is organized as follows : Section 2 gives
a brief overview of related approaches both in Med-
ical Imaging and Computer Vision fields. Section 3
presents our hubless registration proposal. Section 4
shows experimental results and a conclusion follows.
Agier, R., Valette, S., Fanton, L., Croisille, P. and Prost, R.
Hubless 3D Medical Image Bundle Registration.
DOI: 10.5220/0005666702650272
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 267-274
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
267

2 RELATED WORKS
2.1 Points of Interest
During the last decades points of interest (Harris and
Stephens, 1988; Lowe, 2004) have successfully been
exploited for tasks such as object recognition (Lowe,
1999; Lowe, 2004), action recognition, robotic navi-
gation, panorama creation, etc... They aim at being
fast while reducing the amount of data to process,
mainly to deal with realtime processing or tasks in-
volving large amounts of data. Their suitability to
medical imaging has been evaluated in (L
´
opez et al.,
1999), and various applications have been proposed
in this context, like image annotation (Datta et al.,
2005), image retrieval (Zheng et al., 2008). Most
of the applications relate to image registration and
matching. There are some 3D points of interest de-
velopment, like (Knopp et al., 2010), which use ras-
terized meshes to describe 3D shapes.
2.2 Image Registration
Image registration in medical application is a wide
research field (Hill et al., 2001; Sotiras et al., 2013)
where a lot of different approaches have emerged. We
split the approaches in two categories:
• dense -or voxelwise- registration, with minimiza-
tion or maximization of an energy function (for
example mutual information (Pluim et al., 2003)).
The main advantage is to provide a dense regis-
tration, with an information about deformation at
each point of the space. However, voxelwise com-
putation is time-consuming.
• sparse registration, using points of interest (Al-
laire et al., 2008; Cheung and Hamarneh, 2007;
Khaissidi et al., 2009). This approach provides a
less accurate method because points of interest do
not always span the whole space. But if one has
to perform multiple registrations, this approach is
several orders of magnitude faster than dense reg-
istration, because points of interest have to be ex-
tracted only once per image.
Registration can be used directly for medical ap-
plications, as instance for therapy planning (Pelizzari
et al., 1989; Rosenman et al., 1998). It can also be
used as an essential step for other algorithms such as
atlas-based approaches (Gass et al., 2014).
2.3 Bundle Optimization
As first applications in computer vision, points of in-
terest are generally used in the medical field to match
two images. But novel approaches in computer vi-
sion have appeared, using multiple images in order to
tackle problems such as real time 3D reconstruction
(Triggs et al., 2000), efficient tracking using low-end
cameras (Karlsson et al., 2005). More recent works,
like (Frahm et al., 2010), deal with large amount of
data to reconstruct a town.
Bundle optimization is a promising paradigm, that
paved the way to augmented reality and virtual real-
ity (Klein and Murray, 2007), and can contribute to
emerging challenges in medical image processing:
• Large Amounts of Images: nowadays, medical
imaging is a very spread technology and more and
more images are produced each day.
• Multiple Modalities: in order to be more accu-
rate, multiple modalities (CT, MRI, US, etc.) may
be used in order to establish a diagnostic. Algo-
rithms have to follow this trend and manage mul-
tiple modalities.
Note that some papers already have proposed the
use of multiple medical images such as Multi-Atlas
approaches (Gass et al., 2014). But these approaches
most often carry out several applications of one-to-
one matching with a hub model (Bartoli et al., 2013)
and are limited to completely overlapping input im-
ages (Marsland et al., 2008) contrary to image bundle
optimization. We call these approach hub-based, in
contrast with our hubless model (figure 2).
3 HUBLESS REGISTRATION
3.1 Multiple Views vs Multiple Patients
There is a fundamental difference between scene re-
construction and body registration. More precisely,
3D reconstruction assumes a unique scene acquired
with different points of view in contrast with mul-
tiple patients, variability breaks the hypothesis of a
unique scene. The challenge shifts from 3D estima-
tion with 2D data to inter-patient variability handling
among 3D images.
3.2 The ”Hub-based Model” Issue
If one wants to register two images I
1
and I
2
, one
containing an upper body part and one a lower body
part, one faces the overlap limit (August and Kanade,
2005). One solution is to use a third image I
re f
, a full
body image (the hub) and register it with I
1
and I
2
. Af-
terwards, the two registrations are composed in order
to obtain the upper body to lower body registration.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
268
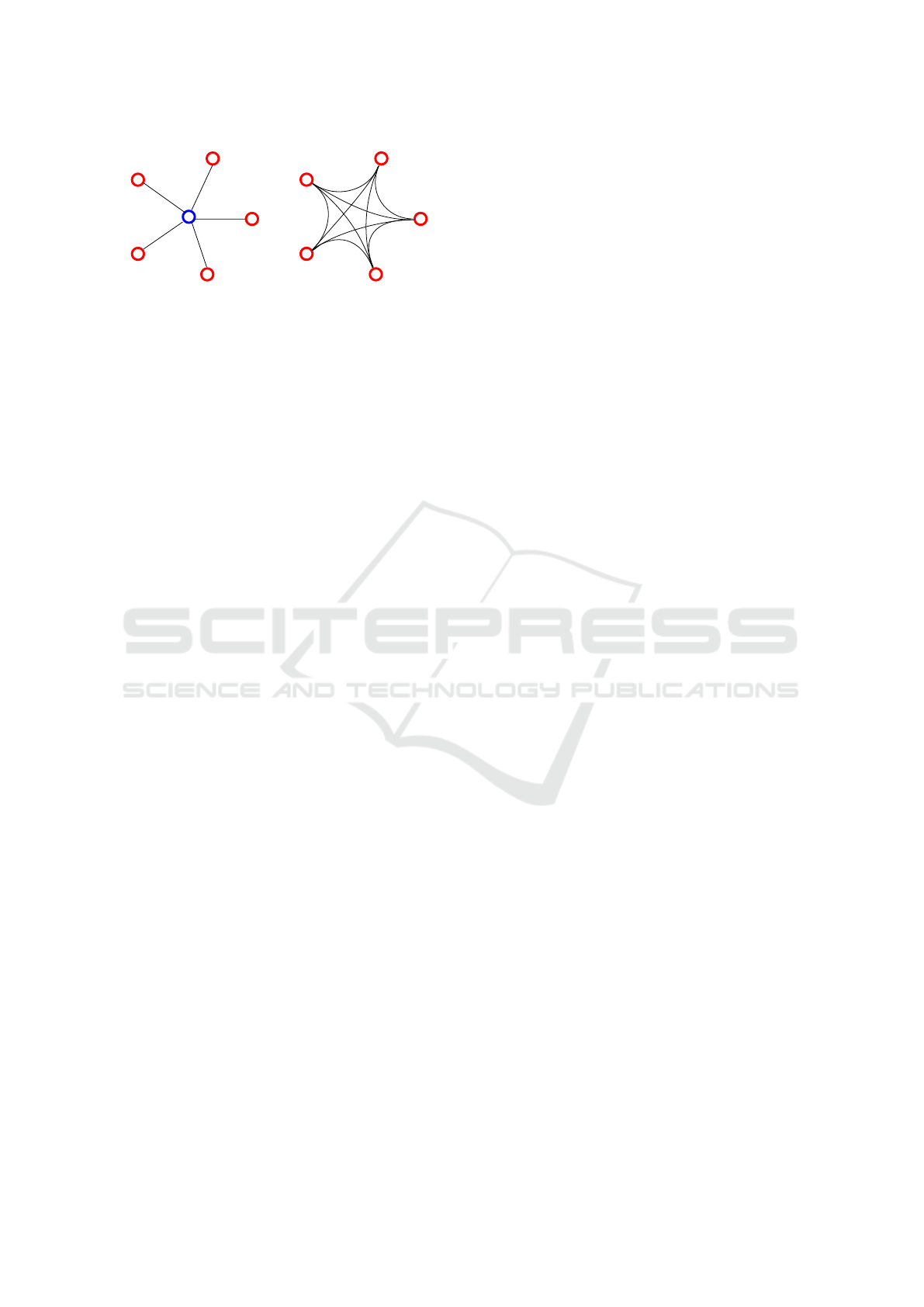
hublesshub-based
Figure 2: Fundamental differences between hub-based and
hubless approaches. Here, 5 images are represented by 5
red dots. (Left) Hub-based approach : one needs an sixth
image as a central model. This approach allows only 5 links
between images, and its efficiency depends on the choice
of the model image. (Right) The hubless approach : no
image is picked as a model. This allows to compute 10
links between the 5 images.
In the case of image bundles, an image used as a
hub to register two images may not be the best hub for
other images. As a result, picking the right hub is a
complex task. Moreover, this ”one size fits all” model
may be difficult to register with some images due to
patient anatomy variability.
3.3 Challenges and Contributions
Our approach of registration is to deal with the whole
image bundle at once, which brings major improve-
ments compared to one-to-one registration. This pa-
per only deals with rigid registration, as a proof of
concept, with the intend to generalize it to non-rigid
registration in future works. A first challenge is to
deal with a big amount of data. In this paper, each im-
age is a scanner acquisition which resolution ranges
between 200
3
and 600
3
, each voxel being encoded
with 16 bits. In the last experimentation, we have a
bundle of 400 images representing more than 100GB
of image data. We overcome this challenge by con-
verting the whole image bundle into a compact repre-
sentation such as Speeded Up Robust Features (SURF
(Bay et al., 2006)) that we extend to 3D in section 3.4.
Moreover, we need to be able to process images
containing not only full-body scans but also body
parts which is usually a problem. Indeed, incomplete
data (body parts) generally hinder the registration pro-
cess, due to the overlap limitation. In our case, we
overcome this difficulty, and use partial matches to
improve our results.
Also, as seen on figure 2, registering a group of
n images with a hub-based approach, is performed
with n registrations. On the other hand, with a hub-
less approach, one can benefit from a much higher
number of registrations. This number can be as high
as n(n − 1)/2, depending on the overlap between im-
ages. The advantage of this difference is the problem
which becomes more and more overdetermined with
the number of images. We exploit this fact to increase
robustness and accuracy of our approach. A second
challenge is to face the overdetemined nature of our
problem, for which we propose a novel solution in
section 3.6.
As a consequence, partially overlapping image
sets can easily be processed with our approach, and
incorrect registrations do not significantly impact ac-
curacy as long as the problem remains overdeter-
mined.
3.4 3D Surf
The SURF approach comes as a fast and efficient
points of interest extractor, but was originally created
for 2D images. We then developed a generalization of
the SURF descriptor to deal with 3D medical images.
3.4.1 Blob-like Structure Detection
The first step is to extend the 3D scale-space of a 2D
image into a 4D function of a 3D image. In spirit
with 2D SURF, we compute a box-filter approximate
Hessian matrix H(x) at each point x = (x,y,z) of the
image. This results in a 3x3 Matrix H. Blob detection
is carried out by analysing the sign of the eigenval-
ues of H. But in contrast with 2D SURF, computing
the determinant of H is not sufficient to check that
its eigenvalues are all negative or positive. In spirit
with what Allaire et al. proposed for 3D SIFT (Al-
laire et al., 2008), we use the trace of the Hessian
tr(H) and the sum of principal second-order minors
∑
det
P
2
(H) in addition to the determinant to have suf-
ficient knowledge on the eigenvalues.
3.4.2 Description
For a 2D image, SURF splits the neighborhood of
each point of interest into smaller 4x4 square sub-
regions. For each sub-region, a set of features is com-
puted using Haar wavelet responses (2 responses per
direction). All responses are concatenated into a 64-
element vector which is normalized to be contrast-
invariant. We apply the same method but take bene-
fit of the third dimension, by splitting neighborhoods
into 2x2x2 cubic-sub-regions, and extracting 3x2 re-
sponses. We build a 48-element vector, which is
smaller compared to 2D SURF but contains more lo-
cal information thanks to the third dimension.
3.4.3 Upright SURF
We chose to not extend the rotation-invariance of 2D
SURF to our case, as with most problems subject to
Hubless 3D Medical Image Bundle Registration
269
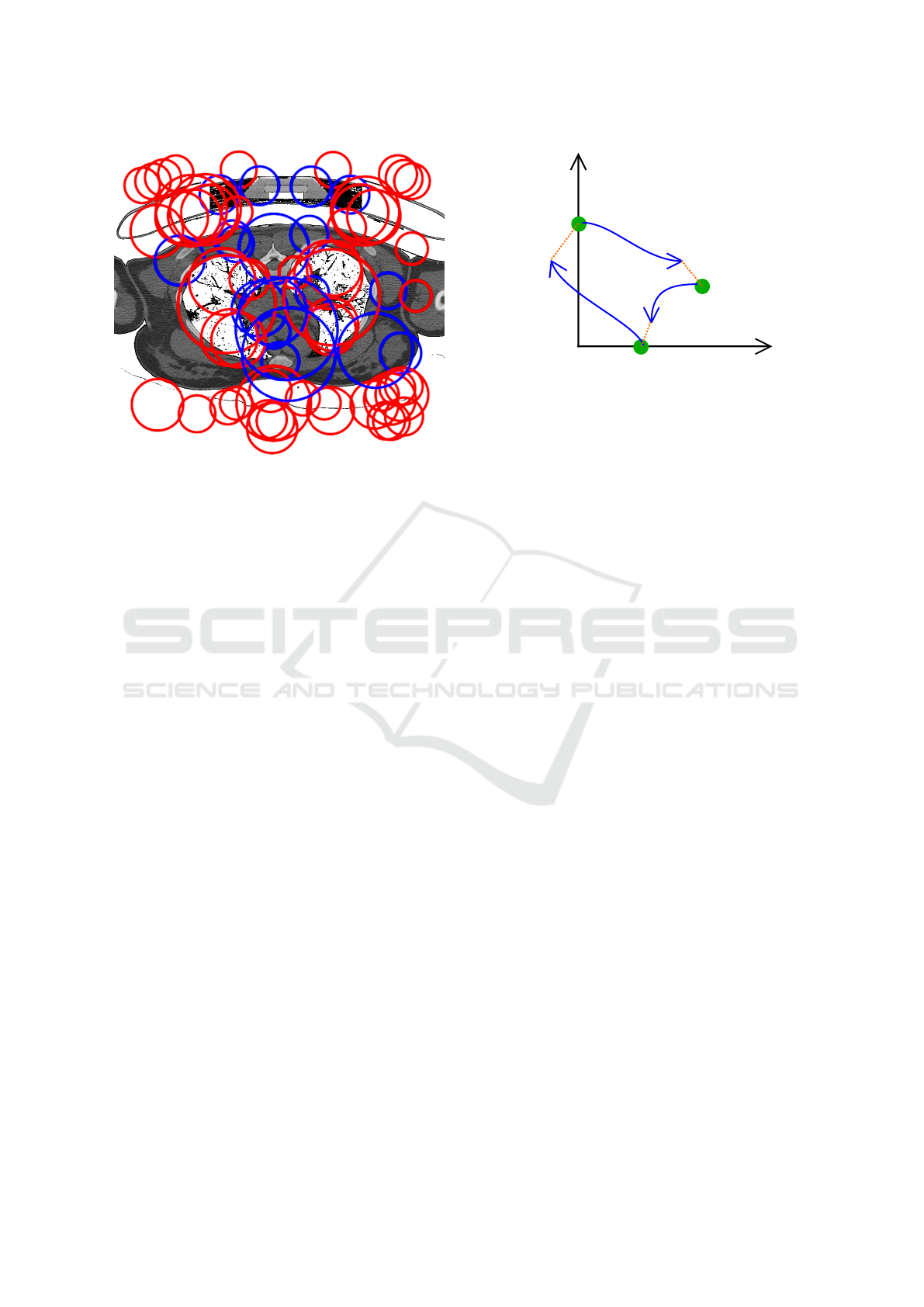
Figure 3: Points of interest extracted from a CT volume.
Clearly, important structures inside the patient such as lungs
are well detected. Blue and red circles represent dark and
light blobs, respectively.
the curse of dimensionality, giving the descriptor in-
variance to rotations would decrease robustness. Vari-
ous invariant solutions exist, as in (Allaire et al., 2008;
Cheung and Hamarneh, 2007). But in our current ap-
plication, we have the prior information that during
image acquisition, the patient is standing, which make
the principal orientation computing unnecessary as
long as inter-patient deformation remains reasonable.
3.5 Pairwise Registration
Once SURF descriptors are extracted from the whole
image bundle, we register all possible image pairs
using RANdom SAmple Consensus (Fischler and
Bolles, 1981). We currently deal with a rigid trans-
form model with 4 degrees of freedom : 3 translations
and 1 isotropic scale.
f : x 7→ s.x + t (1)
The output of this step is a set of n ∗ (n − 1)/2
transforms which link the images altogether. How-
ever this set contains incorrect transforms due to sev-
eral issues:
• non-overlapping images pairs.
• pairs with too few matches due to variability be-
tween patients.
e
Y =
1.5 −1
−1 −0.8
−1 1.8
t
3
2
= [−1, −0.8]
t
1
3
= [−1, 1.8]
t
2
1
= [1.5, −1]
Y =
2 −1
−1 −1
−1 2
n
1
n
2
n
3
Figure 4: A simple problem with 3 volumes (green dots)
and 3 translations: Blue arrows depict observed registra-
tions, orange dotted lines represent registration error. Ma-
trix Y depicts ground truth transforms between all images.
Matrix
e
Y represents estimated transforms.
3.6 Hubless Bundle Registration
3.6.1 Problem Statement
Once we have the set of transforms, we want to be
able to consistently register the images. Note that
we restrict ourselves to using transforms with 3 de-
grees of freedom (translations). Extension to 4 de-
grees of freedom is explained in a subsequent section.
In a slightly more abstract formulation, our problem
is equivalent to compute point positions given only
relative positions between them. Figure 4 shows an
example where 3 nodes n
1
, n
2
and n
3
, have to be lo-
cated given their 3 ∗ (3 − 1)/2 = 3 relative positions
t
2
1
, t
3
2
and t
1
3
.
3.6.2 Solving Laplacian Equations
We propose to solve this problem by writing it as a
Laplace equation (Cohen-Or and Sorkine, 2006), us-
ing the image bundle complete graph. The graph car-
ries several kinds of information:
• Each node n
i
corresponds to one patient image I
i
,
with a local reference frame x
i
which will be ad-
justed consistently with the bundle.
• Each edge e
k
j
carries the translation t
k
j
between the
two images I
j
and I
k
as computed using pairwise
registration (section 3.3). Note that due to the
presence of incorrect registrations (section 3.3),
the set of translations is not always consistent.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
270
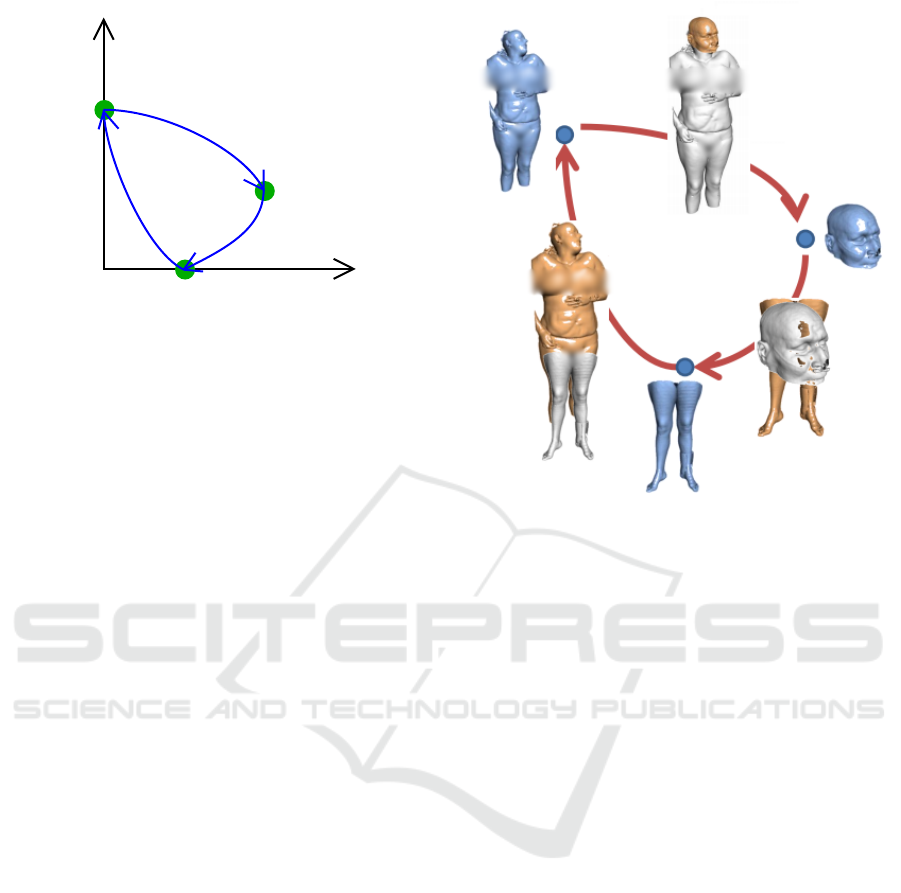
x
1
= [0, 2]
x
2
= [1.67, 1]
x
3
= [0.83, 0.2]
e
P =
0 2
1.67 1
0.83 0.2
P =
0 2
2 1
1 0
n
1
n
2
n
3
Figure 5: Reconstructed positions. Using our algorithm on
the problem shown in figure 4, we can reconstruct the po-
sitions. Blue arrows represent the corrected registrations
between all images. Matrix P depicts ground the truth posi-
tions. Matrix
e
P represents the estimated positions.
The problem now simplifies to finding the best set of
local frames x
i
given the set of translations t
k
j
. In
graph theory, there is an analogy which can be done
in relation with relative / absolute information, based
on a matrix representation of the graph:
E
t
.P = Y (2)
where E is the incidence matrix that shows the rela-
tionship between vertices. P is the local frame matrix
which stores local frames x
i
, each row representing
one vertex, each column referring to one space dimen-
sion. Y refers to the observation matrix, where each
row contains the translation carried by one edge e
k
j
.
In our case, we aim at finding the best estimate of P
given an inconsistent observation matrix Y, which we
propose to solve using a Laplacian equation. Given
a graph, the matrix L = E
t
.E is known as the graph
laplacian operator matrix. This matrix is symmetric,
singular and positive semi-definite.
By left-multiplying equation (2), by E the Lapla-
cian matrix appear as follow :
L
t
.P = E.Y (3)
which cannot be solved as it is because the Lapla-
cian matrix is always singular, of rank n − 1. In a ge-
ometric point-of-view, this result in the fact that abso-
lute reconstruction from relative positions is defined
up to an offset. Applying the same displacement to
all local frames doesn’t change relative positions be-
tween them. To make the Laplacian matrix non singu-
lar, we fix the absolute coordinates of one vertex, re-
ferred to as anchor in (Cohen-Or and Sorkine, 2006).
Figure 6: Example of problem with 3 volumes (legs, head,
body) and 1 impossible registration. To successfully regis-
ter this bundle of 3 volumes, the registration between the
legs and head has to be discarded.
We solve equation 3 using least square minimization.
Figure 5 shows the solution to the problem depicted
in figure 4 with an anchor fixed on vertex n
1
.
3.6.3 Graph Decimation
All possible image pairs are used to perform the
registration and construct the graph. As a conse-
quence, non-overlapping body parts create outliers in
the graph, as shown in figure 6. In other word, some
edges represent a wrong observation. As a reminder,
the breakdown of least square approaches is 0 (Meer
et al., 1991). Then in our case, the error caused by
one outlier edge will not be filtered out but it will be
distributed over all the graph nodes. One solution is
to discard edges representing the worst registrations,
while keeping the graph connected. This requires the
definition of a quality criterion for each individual
transform. For robustness purpose, given two images
and their registration computed using RANSAC, we
simply use the number of inliers found by RANSAC.
We then sequentially remove edges according to this
criterion, avoiding the removal of any edge that would
break the graph connectedness. We chose to remove
edges until the graph contains k ∗ n edges. We experi-
mentally set k to 3.
Hubless 3D Medical Image Bundle Registration
271
3.6.4 Extension to Scale Computation
Our graph approach can only deal with summable val-
ues, allowing us to manage only translations between
images.
But scale information between two images depicts
a multiplicative relationship, as in Equation (1). We
address this problem in a separable way, with, on one
hand, the translation parameters and on the other hand
the scale parameters. Taking the logarithm of equa-
tion (1) changes the scale into an additive value.
We exploit this fact by processing log-scale as a
fourth dimension, supplementary to the three first co-
ordinates.
4 RESULTS
We applied this method to register a bundle of het-
erogeneous Computed Tomography (CT) 3D images.
Images exhibit different dimensions, different reso-
lutions and most importantly may contain different
body parts. All computation have been carried out on
a 24-core workstation with 128 GB of RAM, using
the DESK framework (Jacinto et al., 2012).
In practice, SURF points of interest provide a very
compact representation of the data. As an example,
one image, which weighs from 200 to 600 MB, can
be turned into a 0.1 to 1MB SURF description. Com-
plexity of this part is linear with the number of im-
ages and can be easily parallelized. For a typical
full body acquisition (1.8*0.6*0.6 meters, resized into
an isotropic image with 1.5mm spacing), about 5000
points of interest are extracted in about 2 minutes.
Hubless bundle registration exhibits quadratic
complexity, as we have to register each possible im-
age pair. During RANSAC registration, we perform
6000 iterations with a distance threshold of 40mm.
As our metric reflects natural units, we add a crite-
rion about difference in scale during match computa-
tions: if the scale ratio between two points of inter-
est is larger than 1.5, we forbid the match between
these points. Thanks to a very compact representa-
tion, computing a transformation between two typical
full bodies (with full overlap) is done in a few sec-
onds.
Points of interest approaches were originally used
to register two images with different point of views
of the same scene. A main criterion to evaluate per-
formance of points extraction is repeatability. In our
case, repeatability is less significant because we regis-
ter images from different patients. Moreover we cur-
rently only deal with global translations between im-
ages, as we currently focus on robustness rather than
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
0 50 100 150 200 250 300 350 400
Processing time(s)
Number of volumes
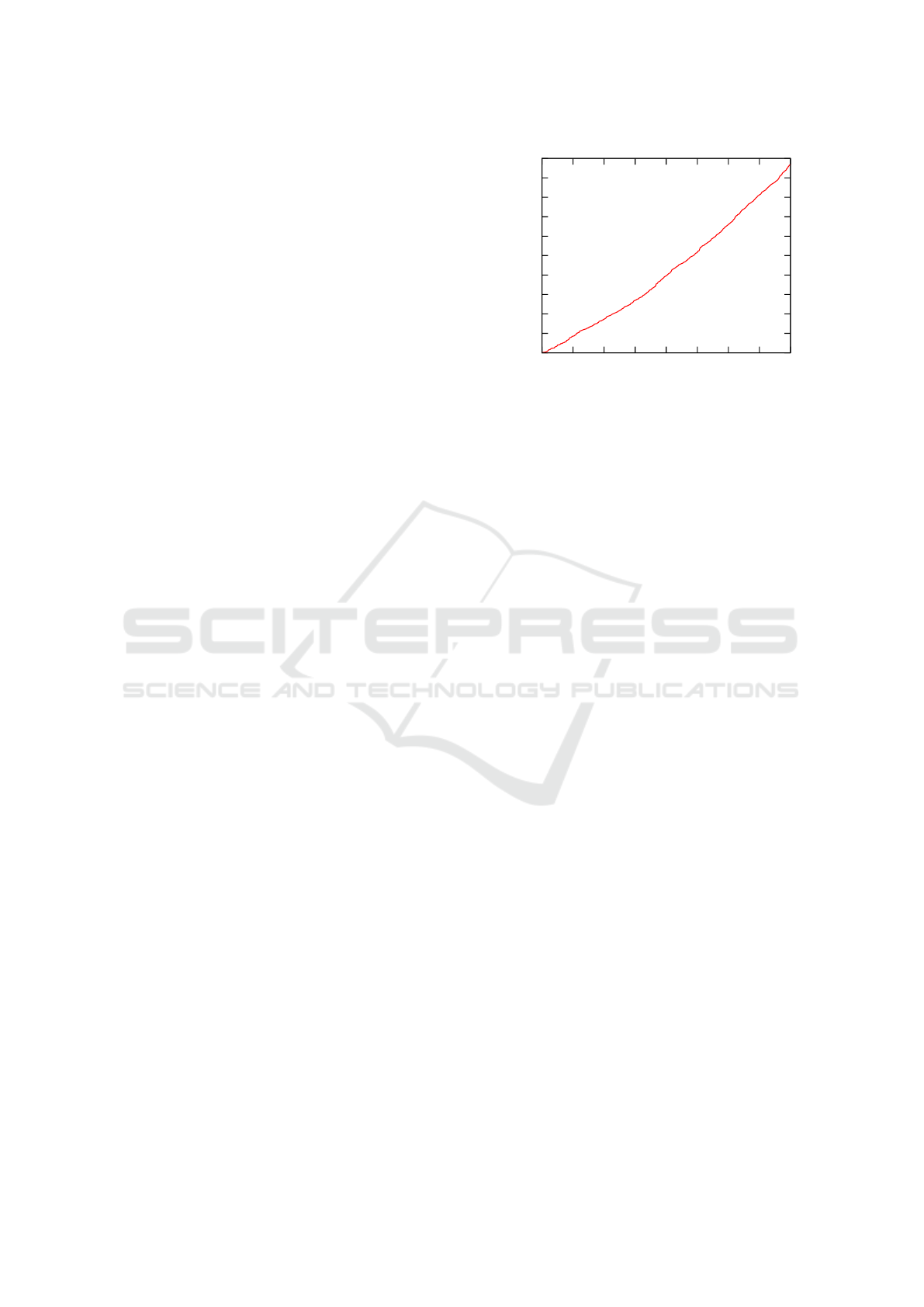
Figure 7: Processing time vs number of volumes.
accuracy. However we experimentally checked that
images containing overlapping body parts are well
registered together.
Figure 1 shows the registration of a bundle of 35
CT images, and figure 8 an example with 400 CT im-
ages. Our approach is able to register both bundles in
a very robust way. Figure 7 shows processing time for
a bundle depending on the number of images it con-
tains. This graph exhibits a slight quadratic behavior,
as computation time is still dominated by the points of
interest extraction stage, which has linear complexity.
Quadratic complexity will be more visible with bun-
dles containing more than 400 images.
A first application of our algorithm is automatic
eye covering for anonymization. The only needed
user input is the head bounding box b
head
in one of
the images, and the eyes bounding box b
eyes
. After-
wards, we perform these steps:
1. compute the hubless bundle registration
2. extract images containing heads, by propagating
a human-made cut out of a head in one image, in
spirit with atlas-based approaches
3. apply a second pass of the whole hubless process,
using only points of interest located in the head.
4. transport the location of the pre-positioned eyes
on every images containing eyes using the previ-
ous registration.
Re-computation using only partial set of points of in-
terest allows the algorithm to be more accurate. Con-
ceptually, this can be considered as a first step towards
deformable registration, with a locally-rigid registra-
tion. First results can be seen in figure 9. One can
note that the eyes are correctly covered except for
cases where the patient head is tilted. Solving these
cases will imply the use of transformation models
with more degrees of freedom than simple transla-
tions.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
272

Figure 8: Mass registration of 400 volumes. (Top Image) A bundle of volumes displayed with raw information about position
contained in DICOM. (Bottom Image) Registered bundle.
Figure 9: Covering eyes on meshes extracted from CT-images. Note that here the surface meshes are solely used for visual-
ization purposes, only the image is used for processing.
5 CONCLUSIONS AND
PERSPECTIVES
We have shown the benefits of computing joint reg-
istrations compared to one-to-one registrations. This
brings robustness in the case of heterogeneous med-
ical datasets which may contain disjoint body parts.
Compact approaches, using point of interest extrac-
tion, allow us to deal with large datasets, in reason-
able time. Our approach provides an efficient way
to background screening of large medical databases,
using a simple translation-and-scale transform model.
Future work may study the extension of this approach
to non-rigid transforms. We also plan to tackle the
complexity issues that will arise when dealing with
even bigger image bundles. Finally, our image graph
is currently connected, but sub-graph extraction is a
promising way to classify the patients, analyzing both
the graph inner properties and patient data.
REFERENCES
Allaire, S., Kim, J. J., Breen, S. L., Jaffray, D. A., and Pekar,
V. (2008). Full orientation invariance and improved
feature selectivity of 3d sift with application to medi-
cal image analysis. In IEEE Computer Vision and Pat-
tern Recognition Workshops, 2008., pages 1–8. IEEE.
August, J. and Kanade, T. (2005). The role of non-overlap
in image registration. In Information Processing in
Medical Imaging, pages 713–724. Springer.
Bartoli, A., Pizarro, D., and Loog, M. (2013). Stratified
generalized procrustes analysis. International Journal
of Computer Vision, 101(2):227–253.
Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:
Speeded up robust features. In Computer vision–
ECCV 2006, pages 404–417. Springer.
Hubless 3D Medical Image Bundle Registration
273

Bild, D. E., Bluemke, D. A., Burke, G. L., Detrano, R.,
Roux, A. V. D., Folsom, A. R., Greenland, P., Jacob-
sJr, D. R., Kronmal, R., Liu, K., et al. (2002). Multi-
ethnic study of atherosclerosis: objectives and design.
American journal of epidemiology, 156(9):871–881.
Cheung, W. and Hamarneh, G. (2007). N-sift: N-
dimensional scale invariant feature transform for
matching medical images. In Biomedical Imaging:
From Nano to Macro, ISBI 2007., pages 720–723.
Cohen-Or, D. and Sorkine, O. (2006). Encoding meshes in
differential coordinates. In SCCG06) Proceedings of
the 22nd Spring Conference on Computer Graphics.
ACM, New York. Citeseer.
Datta, R., Li, J., and Wang, J. Z. (2005). Content-based
image retrieval: approaches and trends of the new age.
In Proceedings of the 7th ACM SIGMM international
workshop on Multimedia information retrieval, pages
253–262. ACM.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: a paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Communications of the ACM, 24(6):381–395.
Frahm, J.-M., Fite-Georgel, P., Gallup, D., Johnson, T.,
Raguram, R., Wu, C., Jen, Y.-H., Dunn, E., Clipp,
B., Lazebnik, S., et al. (2010). Building rome on a
cloudless day. In Computer Vision–ECCV 2010, pages
368–381. Springer.
Gass, T., Szekely, G., and Goksel, O. (2014). Multi-atlas
segmentation and landmark localization in images
with large field of view. In Medical Computer Vision:
Algorithms for Big Data, pages 171–180. Springer.
Harris, C. and Stephens, M. (1988). A combined corner and
edge detector. In Alvey vision conference, volume 15,
page 50. Manchester, UK.
Hill, D. L., Batchelor, P. G., Holden, M., and Hawkes,
D. J. (2001). Medical image registration. Physics in
medicine and biology, 46(3):R1.
Jacinto, H., K
´
echichian, R., Desvignes, M., Prost, R., and
Valette, S. (2012). A web interface for 3d visualization
and interactive segmentation of medical images. In
Web 3D 2012, pages 51–58, Los-Angeles, USA.
Karlsson, N., Di Bernardo, E., Ostrowski, J., Goncalves, L.,
Pirjanian, P., and Munich, M. E. (2005). The vslam al-
gorithm for robust localization and mapping. In IEEE
Robotics and Automation, 2005. ICRA 2005, pages
24–29. IEEE.
Khaissidi, G., Tairi, H., and Aarab, A. (2009). A fast med-
ical image registration using feature points. ICGST-
GVIP Journal, 9(3):19–24.
Klein, G. and Murray, D. (2007). Parallel tracking and map-
ping for small ar workspaces. In Mixed and Aug-
mented Reality, 2007. ISMAR 2007. 6th IEEE and
ACM International Symposium on, pages 225–234.
IEEE.
Knopp, J., Prasad, M., Willems, G., Timofte, R., and
Van Gool, L. (2010). Hough transform and 3d surf for
robust three dimensional classification. In Computer
Vision–ECCV 2010, pages 589–602. Springer.
L
´
opez, A. M., Lumbreras, F., Serrat, J., and Villanueva, J. J.
(1999). Evaluation of methods for ridge and valley
detection. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 21(4):327–335.
Lowe, D. G. (1999). Object recognition from local scale-
invariant features. In Computer vision, 1999. The pro-
ceedings of the seventh IEEE international conference
on, volume 2, pages 1150–1157. Ieee.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International journal of computer
vision, 60(2):91–110.
Marsland, S., Twining, C. J., and Taylor, C. J. (2008).
A minimum description length objective function for
groupwise non-rigid image registration. Image and Vi-
sion Computing, 26(3):333 – 346. 15th Annual British
Machine Vision Conference.
Meer, P., Mintz, D., Rosenfeld, A., and Kim, D. Y. (1991).
Robust regression methods for computer vision: A
review. International journal of computer vision,
6(1):59–70.
Pelizzari, C. A., Chen, G. T., Spelbring, D. R., Weichsel-
baum, R. R., and Chen, C.-T. (1989). Accurate three-
dimensional registration of ct, pet, and/or mr images
of the brain. Journal of computer assisted tomogra-
phy, 13(1):20–26.
Pluim, J. P., Maintz, J. A., and Viergever, M. A. (2003).
Mutual-information-based registration of medical im-
ages: a survey. Medical Imaging, IEEE Transactions
on, 22(8):986–1004.
Rosenman, J. G., Miller, E. P., Tracton, G., and Cullip, T. J.
(1998). Image registration: an essential part of radia-
tion therapy treatment planning. International Journal
of Radiation Oncology* Biology* Physics, 40(1):197–
205.
Sotiras, A., Davatzikos, C., and Paragios, N. (2013). De-
formable medical image registration: A survey. Med-
ical Imaging, IEEE Transactions on, 32(7):1153–
1190.
Triggs, B., McLauchlan, P. F., Hartley, R. I., and Fitzgib-
bon, A. W. (2000). Bundle adjustment – a modern
synthesis. In Vision algorithms: theory and practice,
pages 298–372. Springer.
Zheng, X., Zhou, M., and Wang, X. (2008). Interest point
based medical image retrieval. In Medical Imaging
and Informatics, pages 118–124. Springer.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
274
