Multi-Class Error-Diffusion with Blue-noise Property

Xiaoliang Xiong, Haoli Fan, Jie Feng, Zhihong Liu and Bingfeng Zhou

Institute of Computer Science and Technology, Peking University, 100871, Beijing, China

Keywords:

Sampling, Error-Diffusion, Halftoning, Image Vectorization, Blue-noise.

Abstract:

Existing researches on error-diffusion mainly focus on sampling over a single channel of input signal. But

there are cases where multiple channels of signal need to be sampled simultaneously while keeping their

blue-noise property for each individual channel as well as their superimposition. To solve this problem,

we propose a novel discrete sampling algorithm called Multi-Class Error-Diffusion (MCED). The algorithm

couples multiple processes of error-diffusion to maintain a sampling output with blue-noise distribution. The

correlation among the classes are considered and a threshold displacement is introduced into each process of

error-diffusion for solving the sampling conﬂicts. To minimize the destruction to the blue-noise property, an

optimization method is used to ﬁnd a set of optimal key threshold displacements. Experiments demonstrate

that our MCED algorithm is able to generate satisfactory multi-class sampling output. Several application

cases including color image halftoning and vectorization are also explored.

1 INTRODUCTION

Error-diffusion (ED) is originally a halftoning tech-

nique that quantizes a multi-level image to a binary

one while preserving its visual appearance through

diffusing the quantization error of one pixel to its

neighborhood (Floyd and Steinberg, 1976). It is

widely used in the industry of printing and displaying,

and also an important sampling algorithm working on

discrete domain. Some researchers extend its usage

into digital geometry processing (Alliez et al., 2002).

Previous research mainly focused on the behavior

of error-diffusion sampling over a single channel of

input signal (Ulichney, 1988; Ostromoukhov, 2001;

Zhou and Fang, 2003; Chang et al., 2009). However,

there are cases where multiple channels of input sig-

nal need to be sampled simultaneously, while certain

ideal properties such as blue-noise are also required

for all the sampling output of these channels.

Simply overlapping the output of blue-noise sam-

pling for multiple individual channels can not guaran-

tee the blue-noise property of their superimposition.

Hence, we are aiming to propose a novel Multi-Class

Error-diffusion (MCED) algorithm to solve this prob-

lem. Here, a class refers to the sampling process for a

single channel of input signal as well as its sampling

output. For an ideal multi-class error-diffusion with

This work is partially supported by NSFC grants

#61170206, #61370112.

blue-noise property, the following requirements must

be satisﬁed:

1. The sampling point distribution of each individual

class should possess blue-noise property.

2. When the sampling output of all the classes are

superimposed, no two sampling points from dif-

ferent classes can occupy the same position.

3. When all the sampling points from all the classes

are superimposed and considered as a whole, their

distribution should possess blue-noise property.

The ﬁrst requirement is naturally guaranteed by

the standard ED algorithm. For the second, we

remain only one class with the highest priority and

disable the others when conﬂict occurs. However,

the selection of a certain class may disrupt the point

distribution of other classes which violates the ﬁrst

requirement. To solve this problem, we introduce a

threshold displacement into each process of ED and

they are optimized to minimize the destruction to the

blue-noise property. Since the frequency spectrum

property of each class and the ﬁnal output is consid-

ered during the threshold displacement optimization,

the blue-noise property is promised after all classes

are superimposed (the third requirement). After meet-

ing these requirements, our MCED algorithm gener-

ates satisfactory multi-class sampling output.

Contribution. The contributions of of our work

includes: (1) Proposing a multi-class error-diffusion

Xiong, X., Fan, H., Feng, J., Liu, Z. and Zhou, B.

Multi-Class Error-Diffusion with Blue-noise Property.

DOI: 10.5220/0005677300260036

In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 1: GRAPP, pages 28-38

ISBN: 978-989-758-175-5

framework, the validity of which can be explained

by the commonly used Fourier transform (Knox and

Eschbach, 1993); (2) Giving a parameter optimiza-

tion method to ensure the blue-noise property of

the output. Experiment results using these optimal

parameters show the effectiveness of the method;

(3) Several applications of the MCED are explored,

showing that our algorithm is generic and applicable

in many areas in computer graphics.

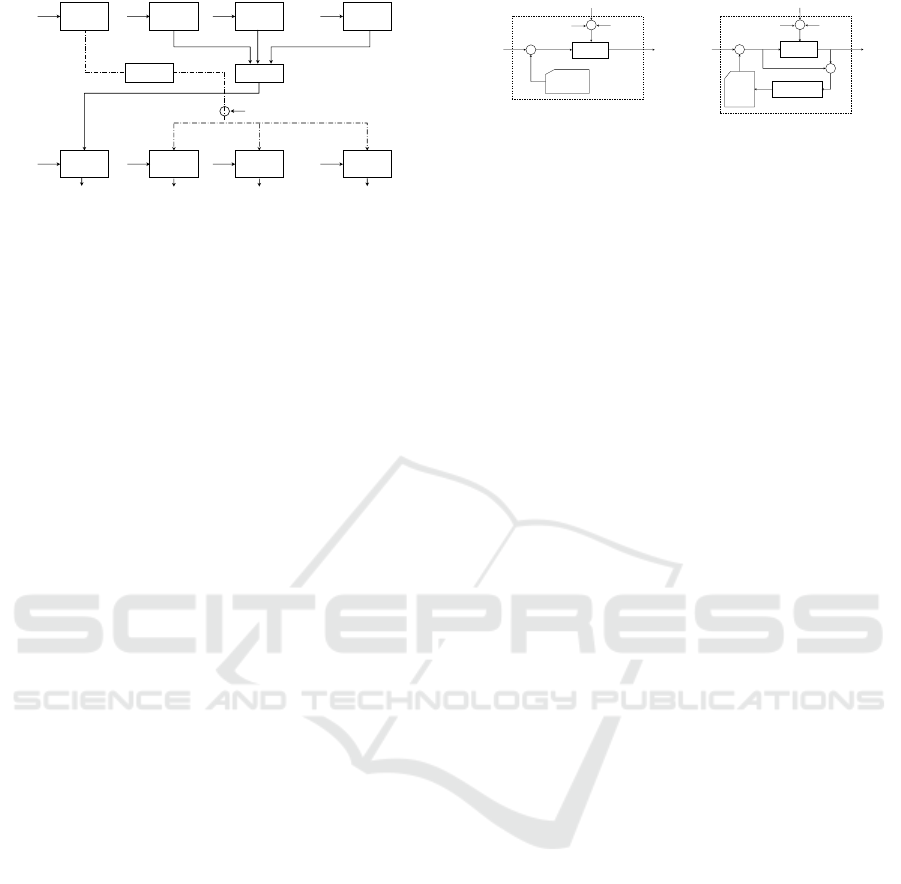
2 RELATED WORK

The original ED is an algorithm invented for gray-

scale image displaying and printing (Floyd and Stein-

berg, 1976). It is also frequently used in many other

areas in computer graphics as a sampling algorithm

(Alliez et al., 2002; Bourguignon et al., 2004; Kim

et al., 2009). Its principle is shown inside the dashed

line of Fig.1. In this algorithm, each pixel p(x,y) ∈

[0,1] in the input image p is parsed with a serpentine

scan line order and quantized by a quantizer:

Q(p

,u) =

(

1, p

> u

0, otherwise

(1)

After that, the quantization error e(x, y) is calculated

and distributed into multiple unparsed pixels by accu-

mulating to an error buffer b(·,·), which is used to

compensate the error. Therefore, for pixel p(x,y),

the actual input p

to the quantizer Q(·,·) is p

p(x,y) + b(x, y). Here, the error ﬁlter a

is a set of

constant coefﬁcients, and the quantization threshold u

in Q(·,·) is also a ﬁxed value, e.g. u = 0.5.

Some important improvements to the original ED

algorithm include the introduction of a variable error

ﬁlter (Ostromoukhov, 2001) and a variable threshold

value (Zhou and Fang, 2003) to ensure the blue-

noise property of the sampling output. In this paper,

we use Zhou and Fang’s threshold modulated ED

algorithm to build our MCED framework. Similar as

in (Chang et al., 2009), we refer to that algorithm as

the standard ED, and its diagram is given by Fig.1 as

a whole. Unlike the original ED, the threshold u and

the error ﬁlter a

here are not constant, but functions

of the input pixel p = p(x,y), that is, u = 0.5 + r(p),

and a

= a

(p). Here, r(p) = δ(p) · λ(x, y) is a

modulated white noise. The modulation strength δ(p)

for the white noise λ(x,y), and the error ﬁlter a

(p)

are pre-optimized so that the output of the standard

ED possesses blue-noise property.

Some mathematical analysis about the behavior of

error-diffusion is given in (Weissbach and Wyrowski,

1992; Knox and Eschbach, 1993), which helps to

explain and predict the result of many techniques

Q(p’, u)p(x, y) c(x, y)

Error filter:a

−

p’

0.5

r(p)

Details of standard E-D 4-1

b(x,y)

(p)

e(x,y)

Original error diffusion

Error

buffer

b(j,k)

Figure 1: The principle of the standard error-diffusion.

derived from the original ED algorithm. Ulichney

ﬁrst proposed the concept of blue-noise (Ulichney,

1988) and used it as a tool to measure the quality of

ED output. For single-class ED, some ideal results

have been achieved for generating sampling points

with such a property (Ostromoukhov, 2001; Li and

Allebach, 2001; Zhou and Fang, 2003).

Using ED to sample multiple channels of input

signals in a coordinated way is not a novel problem. It

traditionally exists in the area of color printing, where

a limited number of colorants are used to reproduce

a continuous-tone color image (Baqai et al., 2005).

Many studies focus on solving this problem using

ED technique, which is called vector error-diffusion

in some literature, because they quantized the input

signals simultaneously by treating them as a vector

(Haneishi et al., 1996; Kang, 1999; Damera-Venkata

et al., 2003). For example, the vector ED algorithm

proposed in (Damera-Venkata and Evans, 2001) uses

an optimum matrix-valued error ﬁlter to take into

account the correlation among color planes. It can

generate sampling output with blue-noise property for

color images, but cannot guarantee this property for

each individual color channel.

Wei extends the traditional Poisson disk sampling

for a single channel of signal into a multi-class blue-

noise sampling algorithm (Wei, 2010). The algorithm

is able to sample a set of input signals in a correlated

way while keeping the blue-noise property of the

whole output. It can also precisely control the number

or density of the generated sampling points. Unlike

the ED which works directly in a discrete domain,

this algorithm is originally designed in a continuous

domain. Hence it is not suitable to be applied

in certain application areas that deal with discrete

domain, such as color image halftoning (Wei, 2012).

3 MULTI-CLASS

ERROR-DIFFUSION

Our MCED algorithm mainly concerns about simul-

taneously sampling on multiple channels of input

signals and maintaining the blue-noise property for all

the classes as well as their superimposition. If simply

performing the standard ED independently on each

Multi-Class Error-Diffusion with Blue-noise Property

...

Disable

control

𝑐

𝑛

Disable

control

Figure 2: The framework of our MCED algorithm, where

|i = 1, ··· , n} are the input signals, and p

∑

i=1

an internal reference signal. After two processing steps of

modiﬁed standard ED, Q

and E

, the framework generates

blue-noise sampling outputs {c

|i = 0, · ·· ,n}. The pseudo

code for the framework can be found in the appendix.

channel of input signal, there may be sampling points

from different classes situated at the same sampling

position when they are superimposed, which is called

sampling conﬂict. Hence, the blue-noise property of

the superimposed output cannot be guaranteed. To

solve this problem, we ﬁrst perform the quantization

on each channel of signal, and produce a set of initial

sampling outputs with sampling conﬂicts. Then, the

conﬂicts are removed by disabling the outputs of

certain classes based on the inter-class correlation. In

this way, the initial outputs are modiﬁed to generate

the ﬁnal sampling points. During the process of quan-

tization and error-diffusion, a threshold displacement

is introduced to decrease the occurrence of sampling

conﬂict and maintain the blue-noise property.

3.1 MCED Framework

Fig.2 illustrates the framework of our MCED algo-

rithm. It takes n channels of signals {p

|i = 1,·· · ,n}

as input, where p

= p

(x,y) is a 2-D discrete function

that satisﬁes p

(x,y) ∈ [0,1] and

∑

i=1

(x,y) ≤ 1.

In fact, it deﬁnes the density of sampling points to

be generated at the spatial position (x,y). Specially,

when p

represents an image, element p

(x,y) is the

intensity of the pixel at position (x, y). Our framework

concerns the processing of individual channels of

signals as well as their correlations, and produces

corresponding sampling point sets {c

|i = 1, · ·· ,n},

where c

(x,y) = 1 indicates a sampling point gener-

ated at (x, y) for signal p

, while 0 means no point

generated. Therefore, the sampling process from the

input p

to the output c

is referred as a class C

To facilitate the inter-class correlation, we deﬁne

a special internal signal p

, whose sampling density

is p

(x,y) =

∑

i=1

(x,y). Sampling to p

with the

standard ED, we can also obtain a blue-noise output,

which is used as a reference for the superimposition

of the sampling output of all the classes. That means

(p’, u)p

(x, y) c

(x, y)

p’

0.5

r(p)

(x,y)

Error buffer

(∙, ∙)

(p’, u)p

(x, y) c

(x, y)

Error filter

−

p’

0.5

r(p)

(x,y)

Error

buffer

(∙, ∙)

Figure 3: Two processing steps of modiﬁed ED: Q

(left)

performs only the quantization and E

(right) complete the

ﬁnal error-diffusion (i = 0,...,n).

the corresponding output of p

, denoted as c

, will be

identical to the superimposition of {c

|i = 1, ··· ,n}.

Hence, we name C

as a reference class.

Our framework parses the elements {p

(x,y)|i =

0,··· ,n} in a serpentine scan line order. All p

(x,y) at

the same position (x,y) are processed simultaneously,

and then the processing moves to the next position.

For each group of {p

(x,y)|i = 0,··· ,n} at (x,y), the

processing of each class includes two steps: Q

and

. Q

performs independent sampling and produces

initial output c

(x,y) for each individual class C

;

while E

modiﬁes the initial output according to the

correlation between the sampling classes and generate

the ﬁnal output c

(x,y).

3.2 Quantization and Error-Diffusion

The work ﬂow of the two processing steps, Q

and E

are shown in Fig.3. Acturally, E

is a modiﬁed version

of the standard ED given in Fig.1. It simply adds one

more variable m

to the latter’s quantization threshold.

This simple modiﬁcation plays an important role in

our framework, because m

will be used to introduce

the inter-class correlation into the sampling, and that

is the key to avoid sampling conﬂict and ensure the

blue-noise property of c

It is notable that Q

produces only the initial sam-

pling output, hence it performs only the quantization

part of E

. Although Q

shares the error buffer b

(·,·)

with E

, it does not modify b

(·,·). This is because

the output of Q

will be modiﬁed in E

and thus the

quantization error made in the latter step is the one

that is to be distributed for the further processing.

3.3 Removing Sampling Conﬂicts

In our framework, the input signal p

, i = 0,··· ,n, of

each class is ﬁrstly processed by Q

, and generates

corresponding uncorrelated blue-noise output c

. In

order to eliminate the conﬂict after superimposition,

the correlation between classes are introduced by the

reference class C

. Based on that, some classes with

sampling conﬂicts will be disabled, i.e. they will be

prohibited to produce a sampling point.

As shown in Fig.4, when Q

of class C

does not

generate a sampling point at current position (x,y),

GRAPP 2016 - International Conference on Computer Graphics Theory and Applications

} have

output?

} have

conflicts?

Disable all E

Disable E

No adjustment

needed

(ideal output)

Outputs of Q

has output?

N Y

Disable some of E

only one remains

Figure 4: Eliminating sampling conﬂicts by disabling some

of the classes.

the output of all {E

|i 6= 0} should be forced to be 0. In

other words, all E

should be disabled from generating

a sampling point at (x, y), for there is no correspon-

dence in the ﬁnal superimposition. Similarly, when

generates sampling point but none of {Q

|i 6= 0}

does, E

should also be disabled because no E

will

provide sampling point to form this superimposition.

The third case, in which {Q

|i 6= 0} generate sampling

points without conﬂicts, is the ideal case that we are

expecting and no modiﬁcation to {c

|i 6= 0} is needed.

Finally, when sampling conﬂicts occur (

∑

j6=0

> 1),

most of the conﬂicting classes must be disabled, and

only one of them with the highest priority is allowed

to remain. Here, we give the priority to the class C

with the highest average sampling density, i.e. k =

argmax

∑

(x,y)

(x,y), for j 6= 0 and c

= 1. Then,

a binary selecting signal s

(i 6= 0) is deﬁned, where

= 0 means E

should be disabled:







∑

j6=0

> 1 and i 6= k;

∑

j6=0

> 1 and i = k;

∑

j6=0

≤ 1.

(2)

To disable a class, we utilize another disabling

signal to modify the quantization threshold. It is

based on an important fact about the ED: If the thresh-

old u in the quantizer Q(p

,u) takes a value larger than

any possible value of input p, the output of Q will be

forced to be 0, and the corresponding class will be

disabled. As shown in Fig.2, the disabling signals are

obtained based on the initial outputs {c

|i = 0,· · · ,n}

by the Disable control, where d

= ¬(c

∨ c

··· ∨ c

)

and d

= ¬(c

). Then, combining with the selecting

signal s

, d

turns into a d

= d

∧ s

for each E

(i 6=

0). Therefore, if d

= 1, a large value (+∞) will

be added to the corresponding quantization threshold,

and the class will be disabled.

In this way, d

, d

and s

facilitate the correlation

described in Fig.4. For example, when c

= 1 and

= 1 (i 6= 0), we have d

= 0 and d

= 0, and

the output of E

will be decided by its priority: if

= 0, E

will be disabled. After the class disabling,

sampling conﬂicts can be removed and no more than

one sampling point will be generated at each position.

3.4 Maintaining Blue-noise Property

Modifying the output of certain Q

to remove the

sampling conﬂicts may cause the destruction of the

blue-noise property of the initial outputs. To solve

this problem, we make use of another important

fact for ED: For a given input signal, a constant

variation of the quantization threshold u will change

the distribution of output sampling points, but will not

affect the average sampling density, as long as u is

not constantly +∞. This fact can be proofed with

the analysis tool provided in (Knox and Eschbach,

1993), which will be brieﬂy described in section

7. Therefore, adding a properly chosen threshold

displacement t

to the threshold u will help to decrease

the chance of the sampling conﬂict occurrence and

restore the blue-noise distribution. The detail of t

will

be discussed in the next section.

Hence, the disabling signals d

, along with

the threshold displacement t

, are ﬁnally added to the

thresholds of E

via the modiﬁcation term m

in the

second step. Then, E

quantizes the input element

(x,y) at current position (x, y), and the quantization

error is distributed and accumulated to the error buffer

b( j, k). The above processing is repeated during the

parsing of the input elements. When all the elements

(x,y) are parsed, the ﬁnal blue-noise MCED output

that satisﬁes all the requirements given in Section 1

can be generated.

4 THRESHOLD DISPLACEMENT

After the ﬁrst step of the MCED, the output of some of

the classes is disabled due to sampling conﬂicts. This

may disrupt the blue-noise property that originally

existed in the standard ED output. We solve this

problem by adding a constant displacement value t

to the quantization threshold for the input p

, since a

shift of the threshold may change the distribution of

sampling points and thus may decrease the chance of

sampling conﬂicts. Therefore, it is possible to ensure

a better blue-noise output with a properly chosen t

4.1 Displacement Optimization

Our goal is to ﬁnd a set of optimal threshold displace-

ments {t

|i = 0,1,··· ,n}, to decrease the probability

Multi-Class Error-Diffusion with Blue-noise Property

of sampling conﬂict occurrence. Since the sampling

conﬂict is a interference among all the classes, the

value of the displacement t

is related to all the

input signals {p

|i = 1,··· ,n}. For each class C

,i =

0,··· ,n, in a n-class MCED, we treat the inﬂuence

from all other sampling classes as a noise, which is

characterized by its strength σ

∑

j6=0∧ j6=i

. We

assume that the same amount of σ

for a given p

will result in similar output. Since σ

can be derived

from σ

= p

− p

, then t

can be simpliﬁed as a

function of p

and p

. As class C

is designed as a

reference for the superimposition of other n classes, t

is related with only the sum of other classes inputs, i.e.

∑

i=1

. Therefore, given an input combination

, p

),i = 1, ··· ,n, in a n-class MCED, we have:

(

= g(p

, p

),i = 1,··· , n,

= f (p

(3)

Then, optimal t

are calculated by solving an op-

timization problem. The optimization target function

is deﬁned according to the Fourier power spectrum of

the sampling output. Based on the existing research

(Ulichney, 1988; Zhou and Fang, 2003), the blue-

noise property of a sampling set can be measured by

the anisotropy and the lower frequency ratio of its

spectrum. In this paper, the sampling output of ED are

affected by both the input signal p

and the threshold

displacement t

. Therefore, the anisotropy α(p

)

and lower frequency ratio β(p

) for the ﬁnal output

can be modiﬁed from their original formulations in

(Zhou and Fang, 2003):

(

α(p

) = Corre(P

),P

)),

β(p

) = L(p

(4)

where Corre(·) is a cross-correlation function; P

(·),

(·) and P

(·) are segmented radially averaged

power spectrums; L(·) is the lower frequency ratio.

Therefore, our target function T to be minimized

in the searching of optimal threshold displacements t

is deﬁned as:

T = ω

∑

i=1

α(p

) + (1 − ω

) ·

∑

i=1

β(p

)

+(1 − ω

) · (ω

· α(p

) + (1 − ω

) · β(p

)),

(5)

where the weights ω

= 0.5 and ω

= 0.7 are taken

in our implementation. A simplex method (Press

et al., 1992) is adopted to automatically search for the

optimal displacement {t

|i = 0,1,·· · ,n}.

Fig.5

demonstrates an example of the displace-

ment optimization. Given p

255

, p

255

, p

Conﬁg the PDF reader with 100% scaling ratio and the

given DPI for best viewing of the details, similar for the

following ﬁgures.

(a) C

(b) C

(d) C

(e) C

(f) C

(g) C

(h) C

(i) C

(j) C

(k) C

(l) C

(m) C

(n) C

(o) C

(p) C

Figure 5: Optimization result for a 7-class ED. (a)-(h)

Sampling outputs of each classes C

. (i)-(p) Corresponding

Fourier power spectra. (Image best viewed at 306 DPI).

255

, p

255

, p

255

, p

255

, p

255

, and

∑

i6=0

100

255

, the optimized threshold displace-

ments are: t

255

, t

255

, t

255

, t

255

, t

255

, t

255

, and t

= −

255

. The

sampling outputs of classes {C

|i = 0, · ·· ,7}, and

their corresponding Fourier power spectra are given in

the ﬁgure. Fig.5(h) is the superimposition of the dots

from the 7 classes, which are colored in red, green,

blue, yellow, magenta, cyan and white, respectively.

The optimization is performed on 256 × 256 patches.

4.2 Displacement Interpolation

To decrease computational costs, we perform dis-

placement optimization only on a set of selected key

input combinations, by minimizing the target function

T in Eq.5. Then, the optimal threshold displacements

for other input combinations can be calculated by

interpolation, where t

= g(p

, p

), i = 1,··· , n, is

implemented with a bilinear interpolation, and t

f (p

) with a 1-D linear interpolation.

The key input combinations and their correspond-

ing optimal threshold displacement values are shown

in the tables contained in Fig.6. The key levels are

selected by an interval of

255

. For convenience, all

the numbers ﬁlled into the table are 255 times of their

real values. The right table gives the correspondence

between the threshold displacement t

and the input

of the reference class C

, as t

= f (p

). The left

table is composed of two parts:

GRAPP 2016 - International Conference on Computer Graphics Theory and Applications

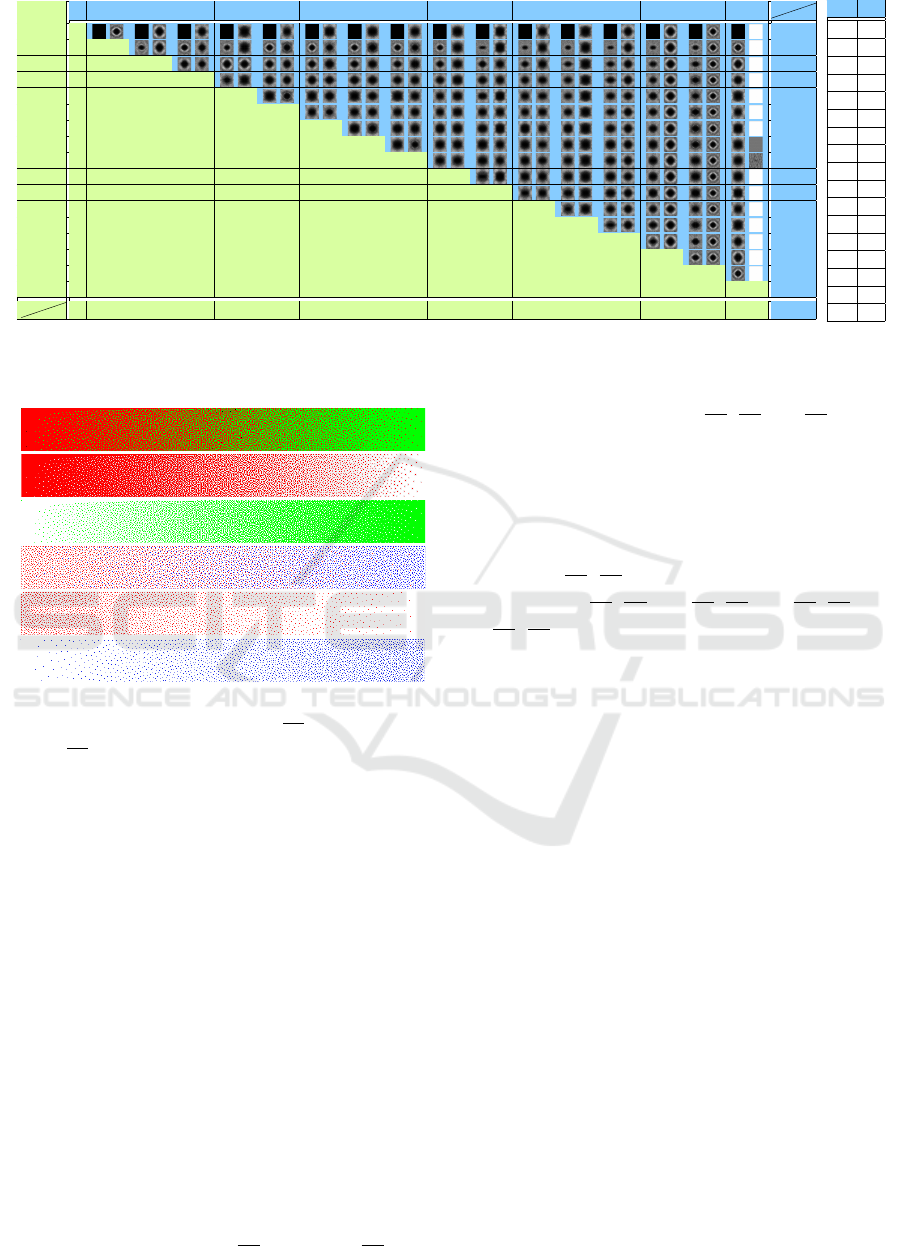
0 16 32 48 64 80 96 112 128 144 160 176 192 208 224 240 255

0 0 0

16 0 0 16

32 0 39 0 32

48 0 49 -3 0 48

64 0 14 51 -23 0 64

80 0 28 35 3 37 0 80

96 0 56 18 43 6 -6 0 96

112 0 49 30 53 96 12 59 0 112

128 0 34 10 11 62 -26 2 93 0 128

144 0 6 26 59 5 -1 12 18 14 0 144

160 0 14 100 106 12 56 44 98 90 22 0 160

176 0 12 43 47 42 48 39 100 52 25 47 0 176

192 0 -46 28 6 0 -7 45 -36 0 25 37 1 0 192

208 0 75 54 -7 71 -33 59 23 -1 13 9 13 0 0 208

224 0 12 18 89 12 -2 75 0 0 0 12 3 0 50 0 224

240 0 16 12 9 9 12 49 -20 -2 14 50 1 9 50 46 0 240

255 0 12 12 20 12 0 29 12 44 50 18 0 50 43 50 86 0 255

0 16 32 48 64 80 96 112 128 144 160 176 192 208 224 240 255

0 0

16 0

32 65

48 -35

64 -39

80 -90

96 -20

112 -15

128 -79

144 0

160 169

176 13

192 61

208 109

224 168

240 166

255 64

Figure 6: Threshold displacement t

and t

with their Fourier analysis results for different key input combinations (p

, p

For convenience, the numbers in this table are all 255 times of the value by their deﬁnition.

(a)

(b)

(c)

(d)

(e)

(f)

Figure 7: Two-class ED with density changing horizontally

in opposite directions: in (a)-(c) from

255

to 0, and in (d)-

(f) from

255

to 0. (a)&(d) are the superimposition, (b)&(c)

and (e)&(f) are the sampling points for the two classes,

respectively. (Image best viewed at 150 DPI).

• The values of the threshold displacement t

g(p

, p

) for the given key input combinations are

enumerated in the lower-left triangle area. They

are obtained by solving the optimization problem

of Eq.5. The indices of p

and p

are given in the

bottom row and the leftmost column, respectively.

• The corresponding power spectra of the sampling

outputs for p

and p

can be found in the upper-

right triangle area, where the left image is for p

and the right for p

. The indices of p

and p

are given in the top row and the rightmost col-

umn. The power spectra show that, for the given

input combinations, our optimization successfully

converges to threshold displacements that can

produce outputs with ideal blue-noise property.

Hence, the threshold displacement of a key input

combination can be read directly from the table.

For example: given p

112

255

and p

255

, the

displacement value t

= g(

112

255

) =

255

can be

found in the cell at the 8th row and the 2nd column

of the left table, and the corresponding power spectra

are in the cell at the 2nd row and 8th column.

Then, for arbitrary combination (p

, p

) that is

not included in Fig.6, we use a bilinear interpolation

to obtain their t

and t

. For example, for an input

, p

) = (

122

255

), its t

is interpolated between four

key values g(

112

255

), g(

112

255

), g(

128

255

) and

128

255

) that exist in the table. The value of t

interpolated in a similar way, but using a 1-d linear

interpolation between the values in the right table.

Fig.7 gives two groups of experiment results of a two-

class MCED using our key values and interpolation

mechanism. It can be seen that the sampling results

meet the requirement of MCED given in Section 1.

5 EXPERIMENTAL RESULTS

We proposed a multi-class ED algorithm that is able

to produce blue-noise sampling points on multiple

input signals as well as their superimposition. Given

k channel of signals, each with n elements, the time

complexity of our algorithm (Alg.1) is O(kn). Some

experimental results have been shown in Section 4.

In this section, we compare our MCED with the

per-channel standard ED (Zhou and Fang, 2003), and

our method achieves results signiﬁcantly better than

the latter. As illustrated in Fig.8(b)-(g), applying

our MCED to three channels of input signal, three

sampling point sets with blue-noise distribution can

be produced (Fig.8(b)(d)(f), colored with red, green

and blue for distinction). The corresponding Fourier

power spectra in Fig.8(c)(e)(g) demonstrate the per-

fect blue-noise property of each class. Fig.8(a) is a

colored superimposition of the three classes. Since

Multi-Class Error-Diffusion with Blue-noise Property

(a) (b) (c) (d) (e)

(f) (g) (h) (i)

Figure 8: A 3-class MCED sampling result. Each individual

class (b-g) and their superimposition (h-i) possess perfect

blue-noise property. (Best viewed at 150 DPI).

(a) (b) (c) (d) (e)

(f) (g) (h) (i) (j)

Figure 9: A 3-class sampling using standard ED. Large

number of conﬂicting sampling points exists (e-h), and the

superimposition does not possess blue-noise property (i-j).

(Best viewed at 150 DPI).

no sampling conﬂicts exist, i.e., none of the sampling

point overlaps with others, there are no color other

then red, green and blue in the image. Fig.8(h)-(i)

show that the superimposed point sets also possesses

blue-noise property.

On the contrary, if applying the standard ED to

each channel of signal separately, though each set of

sampling points has blue-noise distribution, a large

number of sampling conﬂicts will occur when the

three point sets are superimposed. Fig.9(a) is also a

colored superimposition of the sampling point sets,

where each color channel correspond to a class. Then,

in Fig.9(b)-(d) are the sampling points that do not

overlap with others, and Fig.9(e)-(h) show the con-

ﬂicting sampling points, generated by the overlapping

of points from different classes (The colors indicate

the combination). Consequently, the superimposition

set can not maintain blue-noise property (Fig.9(i)-(j)).

The sampling conﬂicts are harmful in certain

application areas, such as color printing. For the per-

channel ED, uncontrollable overlapping of sampling

points will affect the controlling of the maximum ink

amount at each position, and the ﬁnal printing quality.

Our MCED method can help to solve this problem

and hence brings an important improvement.

6 APPLICATIONS

6.1 MCED for Color Image Halftoning

ED algorithm is widely used in grayscale image

halftoning due to its ideal blue-noise property (Os-

tromoukhov, 2001; Zhou and Fang, 2003). For color

image halftoning, a commonly used way is to perform

standard ED independently on each color plane, and

then superimpose the results to create a color halfton-

ing. Since halftoning dots for each color plane are

generated independently, the blue-noise property for

their superimposition can not be guaranteed. This

may result in uncontrolled color appearance in the

generated halftone image (Fig.10(p)).

In this section, we utilize our MCED to generate

color halftone images that meet the requirements: The

distribution of the halftone dots with the same color

should possess blue-noise property; The distribution

of all the dots contained in the halftone image as a

whole should also possess blue-noise property.

6.1.1 15-Class ED for CMYK Color Halftoning

CMYK Color Images. In the state-of-the-art color

printing systems, the device-independent colors are

converted to the densities of the ink dots in four

primary colors: Cyan, Magenta, Yellow and Black.

We denote them as well as their densities as D

, D

, respectively, and they are the input of the

halftoning algorithms. When the output halftoning

image is printed using the four color inks, the dots

generated on paper will appear in totally 15 colors,

corresponding to all possible ink overprints.

∑

i=1

> 1 within a local area in a CMYK

halftone image, there must be dots with different

primary colors placed at the same position, and new

colors will be created. The colors generated by 2

primary colors, namely the 2nd order colors, are

denoted as C

, C

. The subscript

indicate the overprinted primary colors, e.g., C

an overprinting of D

and D

. In the six colors,

, C

and C

correspond to blue, green and red

respectively, and the remaining are very dark colors

because they contain black. Similarly, the 3rd and the

4th order colors generated by 3 or 4 primary colors

are denoted as C

123

, C

124

, C

134

, C

234

, C

1234

. Specially,

the subsets of halftone dots generated by only one

primary color are denote as C

, C

Without ambiguity, we use the same notations for

the dot density and the sampling class for each color.

Hence, there is a total of 15 classes to be sampled

in MCED. Before applying our MCED in CMYK

color halftoning, the densities of the 15 classes need

GRAPP 2016 - International Conference on Computer Graphics Theory and Applications

to decided.

Linear Programming for Dot Densities. For a color

image pixel with

∑

i=1

≤ 1, the dot densities are

simply C

= D

, C

= D

, C

= D

, C

= D

, and the

densities for higher order colors are 0. While for a

pixel with

∑

i=1

> 1, the dot densities must satisfy:











+ C

123

+ C

124

+ C

134

+ C

234

+ C

1234

= 1,

+ C

123

+ C

124

+ C

134

+ C

1234

= D

+ C

123

+ C

124

+ C

234

+ C

1234

= D

+ C

123

+ C

134

+ C

234

+ C

1234

= D

+ C

124

+ C

134

+ C

234

+ C

1234

= D

(6)

Eq.6 is a linear programming problem, which can

be solved by specifying one or more optimization

target to be maximized (Press et al., 1992). In our

experiments, we deﬁne the optimization target h as:

h = C

+ C

123

. (7)

This target function maximizes the colors created by

C, M and Y, and minimizes those mixed with black,

because black always tends to cover the appearance of

other colors. When the densities of each class at each

pixel are obtained, they are sent into our 15-class ED

and produce an output halftone image.

Fig.10 shows an example of our 15-class ED

color halftoning. It is able to create blue-noise dot

distributions for all of the classes (Fig.10(a)-(m),

some empty classes are omitted), as well as their

superimposition (Fig.10(n)). Comparing our result

(Fig.10(o)) with that of the standard ED (Fig.10(p)),

it can be seen that our result demonstrates better blue-

noise property. More CMYK image halftoning results

using our MCED are given in Fig.11.

6.1.2 Comparison with Vector Error-Diffusion

We also compared the performance of our MCED

with the vector error diffusion (VED) (Damera-

Venkata and Evans, 2001) on color image halftoning.

Both algorithms process multiple channels of signals

using ED in a coordinated way. The VED treats the

signals as a vector, and uses an optimum matrix-

valued error ﬁlter to introduce the correlation among

the color planes, hence it can generate good color

halftoning results. However, it does not evaluate

the dot distribution on each color planes and the

conﬂict between them. Thus, the blue-noise property

on each individual color plane cannot be promised.

On the contrary, our MCED can generate blue-noise

outputs on each individual channel of input signal, as

well as their superimposition. Fig.12 demonstrates

a per-channel comparison of the two algorithms on

RGB color image halftoning. It can be seen that our

(a) C

(M) (c) C

(Y) (d) C

(K)

(e) C

(CM) (f) C

(CY) (g) C

(CK) (h) C

(MY)

(i) C

(MK) (j) C

123

(CMY) (k) C

124

(CMK) (l) C

234

(MYK)

(m) C

1234

(CMYK) (n) Superimposition (o) Colored (p) Standard ED

Figure 10: CMYK color image halftoning using our 15-

class MCED. Blue-noise dot distributions are generated for

all classes (a)-(m), as well as their superimposition (n).

(o): colored superimposition. (p): halftoning result by the

standard ED. (Best viewed at 100% scaling ratio, 600 DPI).

Figure 11: More CMYK color image halftoning results

using MCED. (Best viewed at 100% scaling ratio, 300DPI).

MCED produce obviously better sampling results

with smoother distribution and less artiﬁcial textures.

6.2 Multi-tone Error-Diffusion

Multi-toning, also known as multi-level halftoning

(Kang, 1999; Rodrłguez et al., 2008), aims to repro-

duce a continuous tone image with dots of a limited

number of intensities {k

|i = 1,··· ,n} (k

< k

, if i <

j). It is useful in printing with multiple types of inks

or dot sizes. Blue-noise property is also required in

multi-tone images for visually pleasant result, hence

our MCED method is also a solution for multi-tone

image generation.

Given a pixel (x,y) in a continuous tone image

with intensity p(x,y), if k

< p(x,y) < k

i+1

, then

p(x,y) can be simulated with a linear combination of

the halftone patterns with intensity k

and k

i+1

p(x,y) = p

(x,y) · k

+ p

i+1

(x,y) · k

i+1

, (8)

Multi-Class Error-Diffusion with Blue-noise Property

(a) Output (b) Zoom in (c) R (d) G (e) B (f) C (g) M (h) Y

Vector ED

MCED

Vector ED

MCED

Figure 12: Color image halftoning using our MCED method and the Vector ED (Damera-Venkata and Evans, 2001). (a) The

superimposed color halftoning image; (b) Zoom-in viewing of the dot distribution in the red box in (a); (c)-(h) The halftoning

output of the corresponding color plane. (Images best viewed at 100% scaling ratio, 600 DPI).

where p

(x,y) and p

i+1

(x,y) are respectively the den-

sities of the halftone pattern of pixels with intensity

and k

i+1

at (x, y), and p

(x,y) + p

i+1

(x,y) = 1. For

j 6= i and j 6= i +1, we let p

(x,y) = 0.

Therefore, considering p

(x,y) as the input of

class C

in a n-class ED, a n-tone image can be

generated by our MCED algorithm. Fig.13 shows an

example of 7-tone image generated with our method.

The halftone patterns for the given intensities {k

|i =

1,...,7} can be found in Fig.13(a)-(g), and all of them

possess ideal blue-noise property.

6.3 Color Image Vectorization

A typical catalog of color image vectorization meth-

ods (Swaminarayan and Prasad, 2006) build polygon

meshes on the image plane based on a set of sampling

points. Then, by assigning each polygon node the

image color at the same position, the original image

can be converted to a vector form. The colors inside

a polygon is calculated by interpolating between the

colors of its nodes. Hence, the quality of the sampling

point distribution is crucial for the quality of ﬁnal

vectorization results.

Our MCED method can provide ideal sampling

point distribution for such a vectorization task. Here,

the input image is in RGB, and the sampling points

can be generated in the three color planes using our

MCED in a similar way as in Section 6.1.1. After

superimposing the sampling points, a planar triangle

mesh is obtained by Delaunay triangulation, which

can be used as the foundation of the vector image.

To preserve the image features during vectoriza-

tion, we extract a salience map from the gradient of

the original color image. At each pixel, the salience

is deﬁned as the sum of the absolute value of the

gradient components, which is calculated by a Sobel

operator. The salience is separately computed in the

three color planes, and the resulting salience map is

also a RGB image. Hence, sampling on the salience

map instead of the original image, we can obtain a

sampling point set that better preserves the features.

7 ANALYSIS AND CONCLUSION

This paper gives an algorithm for multi-class ED.

The key technique of this algorithm is to use the

optimized threshold displacement to minimize the

distortion to the blue-noise property caused by inter-

class correlation in multi-class error-diffusion. Our

experiment shows that this technique can effectively

maintain the blue-noise property that the standard

error-diffusion possesses. The reason for this can be

explained by Fourier transform-based analysis (Knox

and Eschbach, 1993; Gonzalez and Woods, 2001).

7.1 Analysis

According to (Knox and Eschbach, 1993), for the

original ED, the power spectrum B(u,v) of the Fourier

transform of the output image can be written as:

B(u,v) = I(u, v) + F(u, v)E(u,v), (9)

GRAPP 2016 - International Conference on Computer Graphics Theory and Applications

(a) k

= 0 (b) k

255

(d) k

129

255

(e) k

172

255

(f) k

215

255

(g) k

255

(h) M-tone image

Figure 13: An example of 7-tone ED. For an image with

intensity ranges from 1 to 0 (from center to border), a

multi-tone rendering of the image (h) is generated by our

MCED using 7 intensities (tones) given in the ﬁgure. (a)-

(g) show the distribution of the pixels with these intensities

respectively. (Images best viewed at 300 DPI).

where I(·) and E(·) are the Fourier transform of the

input image and the error map e(x,y) generated dur-

ing error-diffusion; F(·) is a high-pass ﬁlter deﬁned

solely by the diffusion ﬁlter.

For each class C

, our algorithm is based on (Zhou

and Fang, 2003) by adding an extra modulation m

to its threshold, and m

includes the displacement t

which is in nature a noise from other ED classes. Also

according to (Knox and Eschbach, 1993), threshold

modulation is equivalent to sending to the original

ED an equivalent image that is the sum of the original

image and a ﬁltered modulation, where the ﬁlter F(·)

is exactly the one in Eq.9. Therefore we have:

B(u,v) = I(u, v) + F(u, v)(D

(u,v) + M(u, v))

+F(u,v)E

(u,v),

(10)

where D

(u,v) is the Fourier transform of d

, M(u,v)

is the Fourier transform of the threshold modulation

r(p) deﬁned in Fig.1 , E

(u,v) is the Fourier transform

of the error map e(x, y) for the equivalent image.

Note that t

does not appear in Eq.10 because it is a

DC component and is ﬁltered out by F(·). Hence,

threshold displacements do not have inﬂuence on the

average density of the output image of any class.

It is also noted that in Eq.10, only D

(·) and

(·) are decided by the threshold displacement {t

Considering the fact that t

actually has the effect of

decreasing or increasing the amount of slow response

phenomenon at the beginning of the ED, so properly

chosen {t

} are able to minimize the amount of

sampling conﬂict, which in turn can improve the

anisotropy and lower frequency ratio deﬁned in Eq.4.

7.2 Limitation and Future Work

In the experiment results of our paper, smear artifacts

may appear in the sampling classes with low average

(a) (b) (c) (d)

Figure 14: Color image vectorization using our MCED

vs. the standard ED. (a) and (d) are triangulation on

points sampled by Standard ED and MCED, (b) and (c) are

correspong rendering result. The input image is in RGB.

sampling density (Fig.13(g)). This is because we

use s

to choose the class with the highest average

intensity when sampling conﬂict occurs and this may

cause classes with less average intensity to generate

output with lower quality. Hence, the selection of s

is a topic to be investigated.

The optimal threshold displacement t

= g(p

, p

)

has the effect of reducing slow response (Haneishi

et al., 1996), which is also called transient effect in

some literature (Zhou and Fang, 2003). That effect

in our MCED is shown obliviously in Fig.14. At

the top of the image, our sampling result (Fig.14(d))

has very weak slow response than that generated by

the standard ED (Fig.14(a)). In fact, the amount of

slow response directly affects the lower frequency

ratio β(p

) in Eq.4. Our displacement optimiza-

tion automatically guides t

to a proper value to

decrease the anisotropy and lower frequency ratio,

and consequently, reduces the slow response. Hence,

introducing threshold displacement into the single-

class standard ED to further reduce its slow response

is also a future research topic to be explored.

REFERENCES

Alliez, P., Meyer, M., and Desbrun, M. (2002). Interactive

geometry remeshing. ACM Trans. Graph., 21:347–

354.

Baqai, F. A., Lee, J.-H., Agar, A. U., and Allebach,

J. P. (2005). Digital color halftoning. IEEE Signal

Processing Magazine, 22:87–96.

Bourguignon, D., Chaine, R., Cani, M.-P., and Drettakis, G.

(2004). Relief: A Modeling by Drawing Tool. In

Eurographics Workshop on Sketch-Based Interfaces

and Modeling (SBM), pages 151–160, Grenoble,

France. Eurographics, Eurographics Association.

Chang, J., Alain, B., and Ostromoukhov, V. (2009).

Structure-aware error diffusion. ACM Trans. Graph.,

28:162:1–162:8.

Damera-Venkata, N. and Evans, B. L. (2001). Design

and analysis of vector color error diffusion halftoning

systems. Image Processing, IEEE Transactions on,

10(10):1552–1565.

Damera-Venkata, N., Evans, B. L., and Monga, V. (2003).

Color error-diffusion halftoning what differentiates

Multi-Class Error-Diffusion with Blue-noise Property

it from grayscale error diffusion? IEEE Signal

Processing Magazine, 20:51–58.

Floyd, R. W. and Steinberg, L. (1976). An Adaptive

Algorithm for Spatial Greyscale. Proceedings of the

Society for Information Display, 17(2):75–77.

Gonzalez, R. C. and Woods, R. E. (2001). Digital Image

Processing. Addison-Wesley Longman Publishing

Co., Inc., Boston, MA, USA, 2nd edition.

Haneishi, H., Suzuki, T., Shimoyama, N., and Miyake, Y.

(1996). Color digital halftoning taking colorimetric

color reproduction into account. J. Electronic

Imaging, 5(1):97–106.

Kang, H. R. (1999). Digital Color Halftoning. Society

of Photo-Optical Instrumentation Engineers (SPIE),

Bellingham, WA, USA, 1st edition.

Kim, S. Y., Maciejewski, R., Isenberg, T., Andrews, W. M.,

Chen, W., Sousa, M. C., and Ebert, D. S. (2009).

Stippling by example. In NPAR09, pages 41–50.

ACM.

Knox, K. T. and Eschbach, R. (1993). Threshold

modulation in error diffusion. J. Electronic Imaging,

2(3):185–192.

Li, P. and Allebach, J. P. (2001). Tone-dependent error

diffusion. In Society of Photo-Optical Instrumentation

Engineers (SPIE) Conference Series, volume 4663,

pages 310–321.

Ostromoukhov, V. (2001). A simple and efﬁcient error-

diffusion algorithm. In SIGGRAPH01, pages 567–

572. ACM.

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and

Flannery, B. P. (1992). Numerical Recipes in C: The

Art of Scientiﬁc Computing. Cambridge University

Press, New York, NY, USA, 2nd edition.

Rodrłguez, J. B., Arce, G. R., and Lau, D. L. (2008).

Blue-noise multitone dithering. IEEE Transactions on

Image Processing, 17(8):1368–1382.

Swaminarayan, S. and Prasad, L. (2006). Rapid automated

polygonal image decomposition. In Applied Imagery

and Pattern Recognition Workshop, 2006., pages 28–

28. IEEE.

Ulichney, R. A. (1988). Dithering with blue noise.

Proceedings of the IEEE, 76:56–79.

Wei, L.-Y. (2010). Multi-class blue noise sampling. ACM

Transactions on Graphics (TOG), 29(4):79.

Wei, L.-y. (2012). Private communication.

Weissbach, S. and Wyrowski, F. (1992). Error diffusion

procedure: theory and applications in optical signal

processing. Applied Optics, 31:2518–2534.

Zhou, B. and Fang, X. (2003). Improving mid-tone quality

of variable-coefﬁcient error diffusion using threshold

modulation. ACM Trans. Graph., 22(3):437–444.

APPENDIX: Pseudo Code of MCED

Alg.1 is the pseudo-code for the framework of

MCED, and the main functions are explained as

follows:

GetDisplacement() evaluates t

by accessing the

lookup table (Fig.6) we described in Section 4.2.

GetCoe f f icient() and GetStandardT hreshold()

are functions for ﬁnding appropriate diffusion coef-

ﬁcients and threshold for the standard ED.

Quantize() compares pixel value to the threshold

and returns 0 if below, 1 otherwise. (Eq.1)

HaveCon f lict() returns TRUE if more than one

sampling points from different classes situate at the

current position, and NoCon f lict() indicates only one

class sampled at the position.

FindMaxClass() ﬁnds the class whose sum of

densities at all the spatial positions is the maximum.

DistributeError() distributes the quantization er-

rors to neighboring pixels according to the error ﬁlter.

Algorithm 1: Multi-Class Error-Diffusion.

1: for each spatial position (x,y) do

2: p

(x,y) ←

∑

i=1

(x,y)

4: for each spatial position (x,y) do

5: // The first step Q

6: for each class i := 0 to n do

7: t

(x,y) ← GetDisplacement(p

(x,y), p

(x,y))

8: a

(i)

← GetCoe f f icient(p

(x,y))

9: u

(x,y) ← GetStandardT hreshold(p

(x,y))

10: u

(x,y) ← u

(x,y) + t

(x,y)

11: for each class i := 0 to n do

12: c

← Q(p

(x,y) + b

(x,y),u

(x,y)) // Eq.1

13:

14: // The second step E

15: if c

(x,y) = 1 then

16: if HaveCon f lict() then // i.e.:

∑

i6=0

> 1

17: c

(x,y) ← 1

18: e

(x,y) ← p

(x,y) − c

(x,y)

19: minclass ← FindMaxClass()

20: for each class i := 1 to n do

21: if i = minclass then // i.e.:s

= TRU E

22: c

(x,y) ← 1

23: else

24: c

(x,y) ← 0

25: e

(x,y) ← p

(x,y) − c

(x,y)

26: else if NoCon f lict() then // i.e.:

∑

i6=0

= 1

27: for each class i := 0 to n do

28: c

(x,y) ← c

29: e

(x,y) ← p

(x,y) − c

(x,y)

30: else // No class sampled:

∑

i6=0

= 0

31: for each class i := 0 to n do

32: c

(x,y) ← 0

33: e

(x,y) ← p

(x,y) − c

(x,y)

34: else // When c

= 0

35: for each class i := 0 to n do

36: c

(x,y) ← 0

37: e

(x,y) ← p

(x,y) − c

(x,y)

38:

39: for each class i := 0 to n do

40: DistributeError(i,x,y,e

(x,y),a

(i)

)

GRAPP 2016 - International Conference on Computer Graphics Theory and Applications