A Simple Algorithm for Topographic ICA

Ewaldo Santana

, Allan Kardec Barros

, Christian Jutten

, Eder Santana

and Luis Claudio Oliveira

Federal University of Maranhao, Dept. Electrical Engineering, Sao Luis, Maranhao, Brazil

GIPSA-lab, Department Images et Signal, Saint Martin d’Heres Cedex, France

Keywords:

Independent Component Analysis (ICA), Topographic ICA, Receptive Fields.

Abstract:

A number of algorithms have been proposed which ﬁnd structures that resembles that of the visual cortex.

However, most of the works require sophisticated computations and lack a rule for how the structure arises.

This work presents an unsupervised model for ﬁnding topographic organization with a very easy and local

learning algorithm. Using a simple rule in the algorithm, we can anticipate which kind of structure will result.

When applied to natural images, this model yields an efﬁcient code for natural images and the emergence

of simple-cell-like receptive ﬁelds. Moreover, we conclude that the local interactions in spatially distributed

systems and local optimization with norm L2 are sufﬁcient to create sparse basis, which normally requires

higher order statistics.

1 INTRODUCTION

Perhaps the most productive set of self-organizing

principles are information theoretic in nature. Shan-

non in his seminal work showed how to optimally de-

sign communication systems by manipulating the two

fundamental descriptors of information: entropy and

mutual information Shannon (1948). Inspired by this

achievement, Linsker proposed the “infomax" prin-

ciple, which shows that maximization of mutual in-

formation for Gaussian probability density functions

comes to correlation minimization Linsker (1992).

Using correlation as the basis of learning, some re-

searchers have developed several algorithms to mimic

the process of learning Oja (1989); Ray et al. (2013).

Bell and Sejnowski applied this same principle for

independent component analysis (ICA) with a very

clever local learning rule taking advantage of the sta-

tistical properties of the input data Bell and Sejnowski

(1995). Barlow hypothesized that the role of the vi-

sual system is exactly to minimize the redundancy in

real world scenes Barlow (1989).

Finding the maximum entropy distribution, one

of the principles of redundancy reduction when per-

formed with the constraint of a ﬁxed mean, provides

probability density functions with sharp peaks at the

mean and heavy tails, i.e. sparse distributions Si-

moncelli and Olshausen (2001). Thus, assuming that

the goal of the primary visual (V1) cortex of mam-

mals is to obtain a sparse representation of the natu-

ral scenes, Olshausen and Field derived a neural net-

work that self-organizes into oriented, localized and

bandpass ﬁlters reminiscent of receptive ﬁelds in V1

Olshausen and Field (1996). Exploiting V1, Vinje

and Gallant Vinje and Gallant (2000) experimentally

proved the sparse representations in natural vision. In

modeling natural scenes, Hyvarinen et al Hyvarinen

and Hoyer (2000) deﬁned an Independent Component

Analysis (ICA) generative model in which the com-

ponents are not completely independent but have a

dependency that is deﬁned in relation to some topog-

raphy. Components close to one another in this to-

pography have greater co-dependence than those that

are further away. Using a similar rationale, Osindero

et al Osindero (2006) presented a hierarchical energy-

based density model that is applicable to data-sets that

have a sparse structure, or that can be well character-

ized by constraints that are often well-satisﬁed, but

occasionally violated by a large amount. Moreover,

there have been a number of studies on sparse coding

and ICA that match rather well the receptive ﬁelds

of the visual cortex, and also a number of algorithms

which ﬁnds excellent organization that resembles that

of the visual cortex, i.e., Olshausen and Field (1996).

One of the difﬁculties faced by all these stud-

ies is the sophisticated computation required to ob-

tain sparse representations and the generative models

which are generally derived with several constraints

to conform with mathematical analysis. Analyzing

sensory coding in a supervised framework, Barros et

al Barros and Ohnishi (2002) proposed the minimiza-

tion of a nonlinear version of the local discrepancy

between the sensory input and a neuron internal ref-

erence signal which also yields wavelet like recep-

150

Santana, E., Barros, A., Jutten, C., Santana, E. and Oliveira, L.

A Simple Algorithm for Topographic ICA.

DOI: 10.5220/0005683501500155

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 4: BIOSIGNALS, pages 150-155

ISBN: 978-989-758-170-0

tive ﬁelds when applied to natural images. In this

work we propose an unsupervised model for ﬁnd-

ing topographic organization using convex nonlinear-

ities with a very easy and local learning algorithm.

Our development is based on the fact that most non-

linearities yield higher order statistical properties in

modeling. In our context, we model the neuron as

a system which performs non-linear stimuli ﬁltering

Barros and Ohnishi (2002), and use its output as in-

put signals from neighboring neurons. This arrange-

ment gives spatially coherent responses. This paper

is organized as follows: In Section 2, we present the

model and develop methods for obtaining the algo-

rithm. Section 3 shows simulations and results. Dis-

cussions and conclusions are proposed in section 4.

2 METHODS

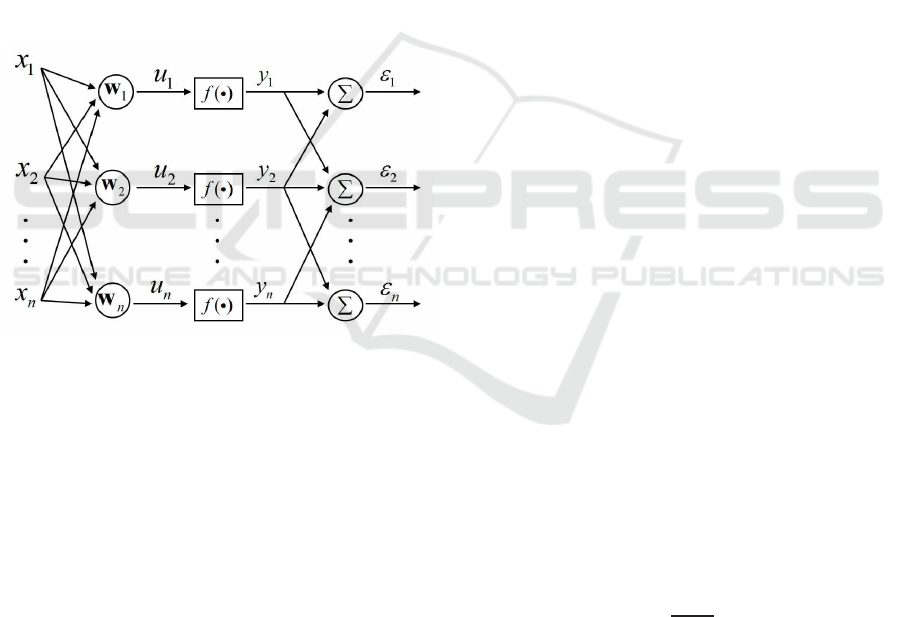
Figure 1: Proposed model, which works in parallel fashion.

First layer: input vector x; second layer: the input vector

are locally linearly combined by synaptic weights vector w

yielding the signal u; Third layer: the signal u pass through

a non-linearity, f(.) to get higher order characteristics of

input signal; Fourth layer: the local discrepancy.

Input signals, x

= [x

(k),...,x

(k)], are assumed gen-

erated by a linear combination of real world source

signals, s(k) = [s

(k),..., s

(k)]

, x = As, where A is

an unknown basis functions set.

In order to facilitate further development, we

also assume that the input signals are preprocessed

by whitening Hyvarinen and Hoyer (2000). In the

demixing model each signal, x

, at the input of

synapse j connected to neuron k will be multiplied

by the synaptic weight w

and summed to produce

the linear combined output signal of neuron k, which

is an estimation of s

∑

j=1

= f(u

), (1)

where f is an even symmetric non-linear function,

which is chosen to exploit the higher order statisti-

cal information from the input signal Hyvarinen and

Hoyer (2000). This signal, y

, interacts with neigh-

boring outputs, since in the nervous system the re-

sponse of a neuron tends to be correlated with the re-

sponse of its neighboring area Durbin and Mitchison

(2007). So, y

is used to generate a signal to adapt w

and make its output coherent with the response of its

neighbors.

We deﬁne the neighborhood of neuron k, all neu-

rons i that are close to neuron k in a matrix representa-

tion, and deﬁne the action of a neuron’s neighborhood

as a weighted sum of output signals from all neurons

in the neighborhood,

∑

f(u

), (2)

where i are the indices of the neighboring outputs k

and v

interacts with y

to generate a self reference

signal, ε

= y

+ αv

, where α determines the neigh-

borhood inﬂuence on neuron’s activation. This self

reference signal must be minimized in order to reduce

the local redundancy. Thus, we deﬁne the following

local cost,

= E[ε

] = E[(y

+ αv

)

], (3)

which should be minimized with respect to all

weights of neuron k. Taking the partial derivative of

Eq.(3) with respect to the parameters and equating it

to zero we obtain the following equation:



′

)(y

+ αv



= 0, (4)

where we used the fact that f

′

), with respect to

, is zero for i 6= k.

In order to avoid the trivial solution of zero

weight, we utilize the Lagrange multipliers to mini-

mize J

under constraint kw

k = 1 and observe that

the derivative of

∑

′

) with respect to w

is zero.

With this, we obtain the following two step algorithm,

= E



′

)ε



. (5)

This procedure is accomplished in parallel to ad-

just all weights for each neuron in the network,

where we include orthogonalization steps taken from

Foldiák (1990). In this way a matrix W is obtained.

Moreover, we can show that the proposed algo-

rithm converges as given in the theorem below.

Theorem: Assume that the observed stimuli fol-

low the ICA model and that the whitened version of

A Simple Algorithm for Topographic ICA

151

those signals are x=VAs, where A is an invertible ma-

trix and V is an orthogonal matrix, and s is the source

vector. Suppose that J(w

) = E{[ f(w

v)+α.v

]

} is

an appropriate smoothing even function. Moreover,

suppose that any source signal s

is statistically inde-

pendent from s

, for all i 6= j. This way, the local min-

imum of J(w

), under restriction k w

k = 1 describes

one line of the matrix (VA)

−1

and the correspondent

separated signal obeys

E[s

( f

′

))

+ s

f(s

) f

′′

) +

+ s

f(s

) f

′

) −s

f(s

) f

′

)] +

+E[( f

′

))

+ f(s

) f

′′

) −

− s

f(s

) f

′

)] < 0, ∀i ∈v

, (6)

We show the proof in the appendix.

3 SIMULATIONS AND RESULTS

We performed simulations with the closest eight neu-

rons neighbors, as deﬁned in Appendix A. We chose

the following even symmetric non-linearity: f(u

) =

.atan(0.5u

) −ln(1 + 0.25u

)). This function has

some advantages in terms of information transmission

between input and outputButko and Triesch (2007).

Moreover, this function will work on all statistics of

the signal, yielding therefore a better approximation

to the probability density function (pdf) of it Bell and

Sejnowski (1995). This can be intuitively understood

by expanding the sigmoidal function into a Taylor se-

ries, whereas one can easily notice that f(u

) can be

written as a linear combination of u

. That function

also satisﬁes the requirement of a unique minimum as

shown by Gersho Gersho (1969).

We applied the algorithm given by Equation (5)

to encode natural images, in a way similar to that

carried out in the literature Olshausen and Field

(1996). We take random samples of 16 x 16

pixel image patches from a set of 13 wild life pic-

tures,(http://www.naturalimagestatistics.net/) and put

each sample into a column vector of dimension

256x1. We used 200,000 whitened versions of those

samples as stimuli. For each set of 200,000 points the

algorithm runs over 20,000 times in order to obtain

a good estimation for matrix A. In this case we have

also 16 x 16 units in the network. We varied α from

0.005 to 1.0 to highlight the inﬂuence of the neigh-

borhood in the results.

In Fig.2, one can see the obtained basis vectors

(columns of matrix A) for α = 0.1 and 0.9, respec-

tively. The clustered topographical organization can

be easily seen taking one little square (receptive ﬁeld)

and considering its eight closest neighbors.

(a)

(b)

Figure 2: The topographic basis functions (columns of ma-

trix A) estimated from natural image data when f(u

) =

·atan(0.5u

) −Ln(1+ 0.25u

) was the non-linearity uti-

lized and neighborhood consisting of the 8 closest neigh-

bors.. (a) α = 0.005; (b) α = 0.9.

In these ﬁgures one can observe that basis vec-

tors which are similar in location, orientation and fre-

quency are close to each other. Moreover, we see the

importance of neighbours contribution on organiza-

tion: increasing α, the ﬁlters became more correlated.

In Figure 3 , one can see the α values and correspond-

ing mean of correlation coefﬁcients of all neurons in

neighborhood.

4 DISCUSSIONS AND

CONCLUSIONS

In this paper we have presented a model for unsuper-

vised neural network adaptation. In (5) we have a

very simple unsupervised rule to update the weights

in a neural network. In topographic organization lit-

erature, as far as we know, this is the simplest ever

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

152

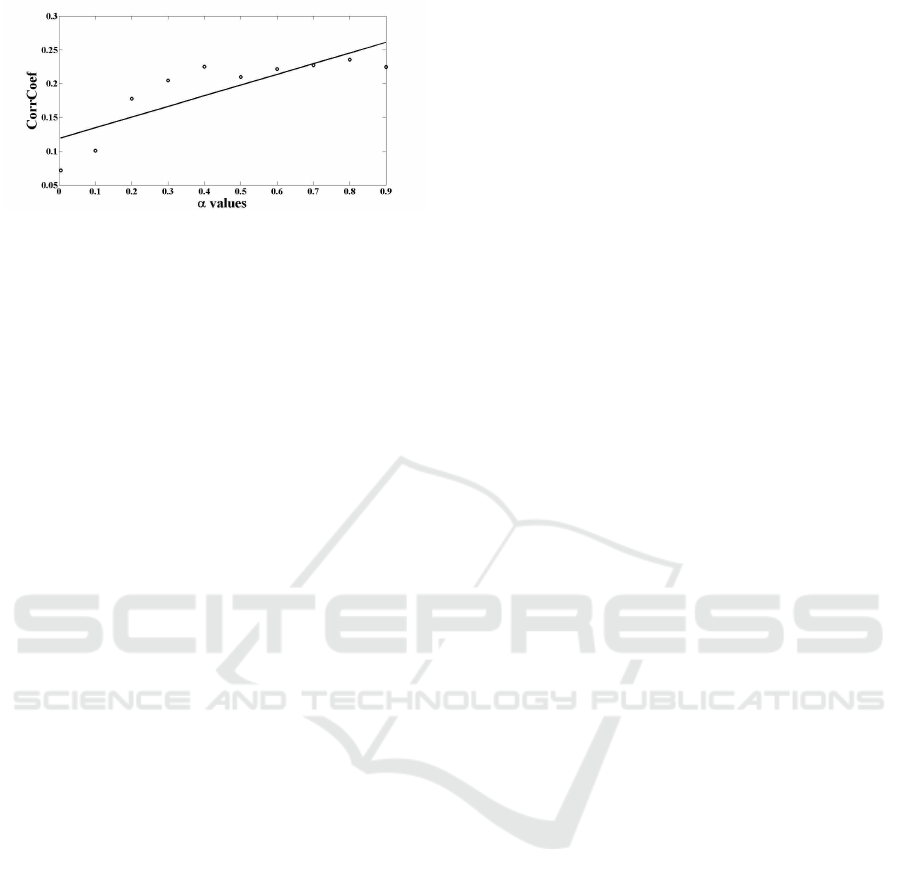
(a)

Figure 3: Mean of correlation coefﬁcient between pair of

basis functions as a function of α values.

suggested, when compared to others in the literature-

Hyvarinen et al. (2000); Hyvarinen and Hoyer (2000);

Osindero (2006). Besides, we have proven mathemat-

ically that the adaptation converges. One possible ap-

plication of this method is to image/signal recogni-

tion, as for each α in (3), we can adjust the character-

istics of the topological structure in order to ﬁt more

closely to the desired image.

There are at least two advantages in this model:

it organizes the resulting ﬁlters topographically and

it may be regarded as biologically plausible. Firstly,

we can see in Fig. 2 (a) that a small α results

in no organization at all, while in Fig. 2 (b), we

can see that an α = 0.9 causes the ﬁlters to ap-

pear organized. Moreover, we have found the cor-

relation in neighborhood ﬁlters. By using equation

Cov(a

)/(std(a

)std(a

)

), where a

and a

are two

basis functions in the neighborhoodof one neuron, we

can see that the correlation is directly proportional to

the value of α, as shown in Fig. 3. The correlation

between α and Cov(a

)/(std(a

)std(a

)

) was 0.88.

Secondly, it is well known that receptive ﬁelds in

the mammalian visual cortex resemble Gabor ﬁlters

Laughlin (1981), Linsker (1992). This way, the infor-

mation about the visual world would excite different

cells Laughlin (1981). In Figure 2 (a) and (b), we can

see that the estimation of matrix A is a bank of local-

ized, oriented and frequency selective Gabor-like ﬁl-

ters. Each little square, in the ﬁgures above, represent

one receptive ﬁeld. By visual inspection of Fig. 2 (b),

one can see that the orientation and location of each

visual ﬁeld mostly change smoothly as a function of

position on the topographic grid. Thus, the emergence

of organized Gabor-like receptive ﬁelds can be under-

stood as a biologically plausibility of our model.

This model can be regarded also as biologically

plausible as it works in an unsupervised fashion with

local adaptation rules Olshausen and Field (1996). To

do this, we had chosen some even symmetric non-

linearities which were applied upon a neuron inter-

nal signal.This signal interacts with similar ones from

neighborhoods neurons to generate its output. This

model mimics the V1 cells by an interaction between

neighborhood signals, which is possible due to the

fact that signals from neighborhood neurons are ref-

erence to the activation of one speciﬁc neuron Field

(1987). In addition, our method extracts oriented, lo-

calized and bandpass ﬁlters as basis functions of nat-

ural scenes without restricting the probability density

function of the network output to exponential ones,

as the IP algorithm of Butko et al Butko and Triesch

(2007). Moreover, Stork and WilsonStork and Wil-

son (1990) proposed an architecture very similar to

the one proposed here, which is largely based on neu-

ral architecture.

ACKNOWLEDGEMENTS

The authors would like to thank Brazilian Agency

FAPEMA for continued support.

REFERENCES

Barlow, H. B., Unsupervised learning, Neural Computa-

tion,v.01, pp. 295-311, 1989.

Barros, A. K. and Ohnishi, N., Wavelet like Receptive ﬁelds

emerge by non-linear minimization of neuron error,

International Journal of Neural Systems,v.13, n. 2, pp.

87-91, 2002.

Bell, Anthony J. and Sejnowski, Terrence J., An

Information-Maximixation Approach to Blind Sepa-

ration and Blind Deconvolution, Neural Computation,

n. 7, pp. 61-72, 1995.

Butko, N. J. and Triesch, J., Learning sensory representa-

tions with intrinsic plasticity, Neurocomputing, v. 70,

pp. 1130-1138, 2007.

Comon, Pierre. Independent component analysis, A new

concept?. Signal Processing, v.36,p 287-314, 1994.

Durbin, R and Mitchison, G., A dimension reduction frame-

work for understanding cortical maps, Nature, n.343,

pp. 644-647, 2007.

Field, David J., Relation between the statistics of natural

images and the response properties of cortical cells.

J. Optical Society of America, v. 04, n.12, pp. 2379 -

2394, 1987.

Foldiák, P., Some Aspects of Linear Estimation wiht Non-

Mean Squares error Criteria. Biological Cybernetics,

v. 64, pp. 165 - 170, 1990.

Gersho, A., Forming sparse representations by local anti-

Hebbian learning., Proc. Asilomar Ckts. and Systemas

Conf. (1969).

Hyvarinen, Aapo; Hoyer, Patrik O. and Inki, Mika., Topo-

graphic ICA as a Model of V1 Receptive Fields. Proc.

of International Joint Conference on Neural Networks,

v.03, pp 83-88, 2000.

A Simple Algorithm for Topographic ICA

153

Hyvarinen, Aapo and Hoyer, Patrik O., Topographic In-

dependent Component Analysis. Neural Computation,

v.13, pp 1527-1558. (2000).

Kohonen, T., Self-Organizing Maps. Springer, 2000.

Linsker, R., Local Synaptic Rules Sufﬁce to maximize Mu-

tual Information in a Linear Network. Neural Compu-

tation, v.04, pp 691-702, 1992.

Laughlin, Simon., A Simple Coding Procedure Enhances a

Neuron’s Information Capacity. Z. Naturforsch, v.36,

pp 910-912, 1981.

Oja, E., Neural Networks,Principal Components and Linear

Neural Networks. Neural Networks, v.05, pp 27-935,

1989.

Olshausen, B. A. and Field, D. J., Emergence of Simple-

Cell Receptive Field Properties by Learning a Sparse

Coding for natural Images. Nature, v.381, pp 607-609,

1996.

Osindero, Simon; Welling, Max and Hinton, Geoffrey

E., Topographic Products Models Applied to Natural

Scene Statistics. Neural Computation, v.18, pp 381-

414, 2006.

Ray, K. L., McKay, D. R., Fox, P. M., Riedel, M. C.,

Uecker, A. M., Beckmann, C. F., Smith, S. M., Fox,

P. T., Laird, A. ICA model order selection of task co-

activation networks. Front. Neurosci. 7:237; 2013

Simoncelli, E. P and Olshausen, B. A., Natural Image

Statistics and Neural representations. Annu. Rev. Neu-

roscience, n. 24, pp 1193-1216, 2001.

Shannon C. E., A Mathematical Theory of Communica-

tion. Bell Systems Technical Journal, v. 27, pp 379-

423, 1948.

Stork, D.G. and Wilson, H.R. Do Gabor functions pro-

vide appropriate descriptions of visual cortical recep-

tive ﬁelds? J Opt Soc Am A7, 1362-1373, 1990.

Vinje, W. E. and Gallant, J. L., Sparse Coding and Decorre-

lation in Primary Visual Cortex During natural Vision.

Vision Science, v. 287, pp 1273-1276, 2000.

APPENDIX

Take an indexed set of N neurons, as one can see in table 1,

and put them into a

√

N ×

√

N matrix (let’s suppose N=64,

Table 1: A set of N neurons.

1 2 3 4 5 6 7 8 ··· N

for example), as one can see in table 2

We deﬁne the neighborhood of neuron k, all neurons i

that are close to the neuron k in the matrix representation.

In other words, neurons i are neighbors of neuron k if the

coordinates of neuron i obeys the following relation

D(i,k) =

−a

)

+ (b

−b

)

6 T, (7)

where (a

) and (a

) are the coordinates of neuron

k and neuron i, respectively, in the matrix representa-

tion, T is a constant that deﬁnes the neighborhood size.

For example, for T = 1, the neighborhood of neuron 28

as highlighted in the table below. In this case v

{19,20,21,27,29, 35, 36,37}.

Table 2: One neighborhood of neuron 28.

1 2 3 4 5 6 7 8

9 10 11 12 13 14 15 16

17 18 19 20 21 22 23 24

25 26 27 28 29 30 31 32

33 34 35 36 37 38 39 40

41 42 43 44 45 46 47 48

49 50 51 52 53 54 55 56

57 58 59 60 61 62 63 64

With this deﬁnition of neighborhood, we are able to an-

alyze the algorithm stability in the following steps:

Assume that signal x can be modeled as x=As, where A

is an invertible matrix;

Let us make the following change in coordinates, p

, p

,··· , p

]

= A

, where V is the whitening ma-

trix to obtain the signals x;

In this new coordinates basis, we deﬁne the cost func-

tion as

J(p

) = E[ε

] = E{[ f (p

s) +α·v

]

}; (8)

One can analyze, without loss of generality, the stabil-

ity of J(p

) at point p

= [0,··· , p

,··· , 0]

= e

. In this

case, p

= 1 and than w

is one row of the inverse of VA.

For assumption, J(p

) is an even function and this analysis

applies for p

= −1;

Let d = [d

,··· , d

]

be a small perturbation on e

. Ex-

pressing J(e

+ d) into a Taylor series expansion about e

we obtain

J(e

+d) = J(e

)+d

∂J(e

)

∂p

∂

J(e

)

∂p

+o(kd

k).

(9)

∂J(p)

∂p

= s

′

s)[ f(p

s) +v

], (10)

∂J(p)

∂p

= s

′′

s)[ f(p

s) +v

] + s

′

s) f

′

(11)

and

∂J(p)

∂p

= s

′′

s)[ f(p

s) +v

] + s

′

s) f

′

(12)

Taking in account that signals out of neighborhood are

statistically independent, we have

∂(e

)

∂p

= 2{E



f(s

) f

′

)



+ α

∑

i∈v



f(s

) f

′

)



}, (13)

because in consequence of independency,

E[s

f(s

) f

′

)] = 0, if j /∈ v

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

154

In the same way, using the assumption of independence,

one can obtain

∂

J((e)

)

∂p

d =

= E

( f

′

))

+ s

f(s

) f

′′

)

+ α

∑

i∈v

( f

′

))

′′

)

+ E

( f

′

))

+ s

f(s

) f

′′

)

∑

i/∈v

( f

′

))

+ f(s

) f

′′

)

+ o(kdk

(14)

Supposing kwk = 1 and VA being orthogonal, we have

kpk = kA

wk = 1. Consequently, ke

+ dk = 1, which

implies d

1−

∑

∀l6=i

−1.

Remembering that

1−β = 1−

+o(β), one can dis-

card the terms which contains d

and d

in step 8 above,

because they are okd

k .

Now we can take the following approximation: d

≈

∑

∀l6=i

= −

∑

−

∑

Using the above approximation in step 11, and using

equation 13 and equation 14, in equation 9, one get

J(e

+ d) = J(e

)

+ α

∑

{E[s

( f

′

))

+ s

f(s

) f

′′

)

+ s

f(s

) f

′

) −s

f(s

) f

′

)]d

}

∑

E[( f

′

))

+ f(s

) f

′′

)

− s

f(s

) f

′

)]d

. (15)

Choosing properly a function f so that E[s

( f

′

))

f(s

) f

′′

) + s

f(s

) f

′

) − s

f(s

) f

′

)] +

E[( f

′

))

+ f(s

) f

′′

) − s

f(s

) f

′

)] < 0,∀i ∈ v

we obtain that J(e

+ d) will be always small that J(e

) in

equation 9.

A Simple Algorithm for Topographic ICA

155