
Modeling Uncertainty in Support Vector Surrogates of Distributed
Energy Resources
Enabling Robust Smart Grid Scheduling
J
¨
org Bremer
1
and Sebastian Lehnhoff
2
1
Department of Computing Science, University of Oldenburg, Uhlhornsweg, Oldenburg, Germany
2
R&D Division Energy, OFFIS – Institute for Information Technology, Escherweg, Oldenburg, Germany
Keywords:
Uncertainty, SVDD, Smart Grid, Distributed Generation.
Abstract:
Robust proactive planning of day-ahead real power provision must incorporate uncertainty in feasibility when
trading off different schedules against each other during the predictive planning phase. Imponderabilities like
weather, user interaction, projected heat demand, and many more have a major impact on feasibility – in the
sense of being technically operable by a specific energy unit. Deviations from the predicted initial operational
state of an energy unit may easily foil a planned schedule commitment and provoke the need for ancillary
services. In order to minimize control power and cost arising from deviations from agreed energy product
delivery, it is advantageous to a priori know about individual uncertainty. We extend an existing surrogate
model that has been successfully used in energy management for checking feasibility during constraint-based
optimization. The surrogate is extended to incorporate confidence scores based on expected feasibility under
changed operational conditions. We demonstrate the superiority of the new surrogate model by results from
several simulation studies.
1 INTRODUCTION
The current upheaval regarding control in the chang-
ing electricity grid leads to growing complexity and
a need for new control schemes (Nieße et al., 2012).
A steadily growing number of renewable energy re-
sources like photovoltaics (PV), wind energy con-
version (WEC) or co-generation of heat and power
(CHP) has to be integrated into the electricity grid.
This fact leads to a growing share of hardly pre-
dictable feed-in. The behavior of such units often
depends on uncertain prediction of projected weather
conditions, user interaction (e. g. hot water usage), or
similar. An algorithm for robust control would coor-
dinate distributed energy resources with a proactive
planning that already takes into account such uncer-
tainty issues for scheduling in order to minimize the
need for ancillary services in case of deviation from
planned electricity delivery. Without loss of gener-
ality, we will focus on algorithms for virtual power
plants (VPP) as an established control concept for
renewables’ integration (Nikonowicz and Milewski,
2012) for the rest of the paper. All concepts are nev-
ertheless applicable for different organizational struc-
tures, too.
Many balancing algorithms for a bunch of differ-
ent control schemes have already been proposed as a
solution to the problem of assigning a suitable, feasi-
ble schedule to each energy unit such that the sum of
all schedules resembles a desired load profile while
concurrently other objectives like minimal cost are
met, too. Among such solutions are centralized algo-
rithms as well as decentralized approaches for VPP as
organizational entity. A VPP can be seen as a cluster
of distributed energy resources (generators as well as
controllable consumers) that are connected by com-
munication means for control. From the outside, the
VPP cluster behaves like a larger, single power plant.
A VPP may offer services for real power provision
as well as for ancillary services (Nieße et al., 2012;
Lukovic et al., 2010; Braubach et al., 2009).
Traditionally, energy management is implemented
as centralized control. However, given the increasing
share of DER as well as flexible loads in the distribu-
tion grid today, the evolution of the classical, rather
static (from an architectural point of view) power sys-
tem to a dynamic, continuously reconfiguring system
of individual decision makers (e. g. as described in
(Ili
´
c, 2007; Nieße et al., 2014)), it is unlikely for such
centralized control schemes to be able to cope with
the rapidly growing problem size. Thus, the seminal
work of (Wu et al., 2005) identified the need for de-
42
Bremer, J. and Lehnhoff, S.
Modeling Uncertainty in Suppor t Vector Surrogates of Distributed Energy Resources - Enabling Robust Smart Grid Scheduling.
DOI: 10.5220/0005691600420050
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 2, pages 42-50
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

centralized control. Examples for VPP are given in
(Coll-Mayor et al., 2004; Nikonowicz and Milewski,
2012). An overview on existing control schemes and
a research agenda can e. g. be found in (McArthur
et al., 2007; Ramchurn et al., 2012).
In order to additionally address the integration of
the current market situation as well as volatile grid
states, (Nieße et al., 2014) introduces the concept of
a dynamic virtual power plant (DVPP) for an on de-
mand formation and situational composition of en-
ergy resources to a jointly operating VPP. In this ap-
proach VPPs gather dynamically together with re-
spect to concrete electricity products at an energy
market and will diverge right after delivery. Such dy-
namic organization even more relies on assumptions
and predictions about individual flexibilities of each
(possibly so far unknown) energy unit when going
into load planning.
Anyway, a general problem for all algorithms is
the presence of individual local constraints that re-
strict possible operations of all distributed energy re-
source (DER) within a virtual power plant. Each DER
first and foremost has to serve the purpose it has been
built for. But, usually this purpose may be achieved in
different alternative ways. For example, it is the (in-
tended) purpose of CHP to deliver enough heat for the
varying heat demand in a household at every moment
in time. Nevertheless, if heat usage can be decou-
pled from heat production by use of a thermal buffer
store, different production profiles may be used for
generating the heat. This leads, in turn, to different
respective electric load profiles that may be offered as
alternatives to a VPP controller. The set of all sched-
ules that a DER may operate without violating any
technical constraint (or soft constraint like comfort) is
the sub-search-space with respect to this specific DER
from which a scheduling algorithm may choose solu-
tion candidates. Geometrically seen, this set forms a
sub-space F ⊆ R
d
in the space of all possible sched-
ules.
In (Bremer et al., 2011) a model has been pro-
posed to derive a description for this sub-space of
feasible solutions that abstracts from any DER model
and its specific constraint formulations. These surro-
gate models for the search spaces of different DER
may be automatically combined to a dynamic opti-
mization model by serving as a means that guides an
arbitrary algorithm where to look for feasible solu-
tions. Due to the abstract formulations all DER may
be treated the same by the algorithm and thus the con-
trol mechanism can be developed independently of
any knowledge on the energy units that are controlled
afterwards.
Up to now, this approach takes into account
merely a hard margin that isolates feasible and infea-
sible schedules. A schedule is either feasible or not.
But, in real life problems this feasibility depends on
predictions about the initial operational state of the
unit from which the schedule is operated. If this initial
state deviates from the predicted, the schedule might
or might not still be operable. The uncertainty in pre-
dicting the initial state of the unit is reflected by an
uncertainty about the feasibility of any schedule. This
fact results in a need for a fuzzy definition of the fea-
sible region that contains all feasible schedules of a
unit.
In this contribution, we extend the model given
in (Bremer et al., 2011) to unsupervised fuzzy deci-
sion boundaries after (Liu et al., 2013) and demon-
strate the superior quality when deciding on feasibil-
ity of schedules under uncertain conditions. We start
with a discussion on related work and briefly recap the
used model technique before we define the extension
and propose a measure for the confidence of arbitrary
schedules. We conclude with several simulation re-
sults that support the extended approach.
2 RELATED WORK
2.1 Uncertainty in the Smart Grid
Several works scrutinize the problem of uncertainty
within the smart grid in general; mainly by using pre-
defined stochastic models (Alharbi and Raahemifar,
2015). Uncertainty in long term development exami-
nations like (Zio and Aven, 2011) are not in the scope
of this work. Lots of work has been done in the field
of wind (or photovoltaics) forecasting, e. g. (Zhang
et al., 2013; Sri et al., 2007), or on integration into
stochastic unit commitment approaches (Wang et al.,
2011), respectively. But, so far surprisingly low ef-
fort has been spent on integration into energy resource
modeling for the case of operability. In (Wildt, 2014)
uncertainty about demand response is integrated di-
rectly into a multi agent decision making process, but
in an unit specific and not in an abstract way. Integrat-
ing models of correlation in unit behaviour may be
handled by using factory approaches for the scenario
as has been demonstrated for the energy sector e. g. in
(Bremer et al., 2008). An example for modeling reli-
ability and assessment differentiated for different unit
types is given in (Blank and Lehnhoff, 2014).
On the other hand, a need for an abstract unit-
independent surrogate model of individual feasible re-
gions in distributed generation scenarios can for ex-
ample be derived from (Nieße et al., 2012; Hinrichs
et al., 2013a).
Modeling Uncertainty in Support Vector Surrogates of Distributed Energy Resources - Enabling Robust Smart Grid Scheduling
43

2.2 Surrogate Models for DER
Abstract surrogate models in the energy management
sector are usually built on a set of feasible schedules
that serve as a training set for deriving the surrogate
model. The procedure starts with initializing a unit
behavior model with a parametrization from the
physical unit or – in case of simulation – from its
simulation model. These parameters may be directly
read from the unit reflecting its current operation
state or may be further projected onto a future state
using the current operation schedule and predictions
on future operation conditions.
Whereas in the first case exact parameters are de-
rived, the latter case usually suffers from uncertainty
from different forecast sources. The initialization
defines the initial state of the unit at the starting
point from whence alternative schedules are to be
determined by sampling the behavior model which
simulates the future flexibilities of the energy unit. If
the initial operational state of the unit at the starting
point of the time frame over which the energy load
is balanced or optimized is fixed, a surrogate model
can be derived that abstracts from the specific unit at
hand and allows for an ad hoc integration at runtime
into the scheduling algorithm.
Such models based on support vector approaches
have been presented e. g. in (Bremer et al., 2011).
We will briefly recap this technique before extending
the ideas to uncertainty integration. The model is
based on support vector data description (SVDD) as
introduced by (Tax and Duin, 2004). The goal of
building such a model is to learn the feasible region
of the schedules of a DER by harnessing SVDD to
learn the enclosing boundary around the whole set of
operable schedules.
We will briefly introduce SVDD approach as for
instance described in (Ben-Hur et al., 2001; Bremer
et al., 2011). This task is achieved by determining a
mapping function Φ : X ⊂ R
d
→ H , with x 7→ Φ(x)
such that all data points from a given region X is
mapped to a minimal hypersphere in some high-
or indefinite-dimensional space H (actually, the
images go onto a manifold whose dimension is at
maximum the cardinality of the training set). The
minimal sphere with radius R and center a in H that
encloses {Φ(x
i
)}
N
can be derived from minimizing
kΦ(x
i
) − ak
2
≤ R
2
+ ξ
i
with k · k denoting the
Euclidean norm and with slack variables ξ
i
≥ 0 that
introduce soft constraints for sphere determination.
Introducing β and µ as the Lagrangian multipliers,
the minimization problem for finding the smallest
sphere becomes
L(ξ, µ, β) = R
2
−
∑
i
(R
2
+ ξ
i
− kΦ(x
i
) − a
2
)kβ
i
−
∑
i
ξ
i
µ
i
+C
∑
i
ξ
i
.
(1)
C
∑
i
ξ
i
is a penalty term and determines size and accu-
racy of the resulting sphere by determining the num-
ber of rejected outliers. Usually C reflects an a priori
fixed rejection rate.
After introducing Lagrangian multipliers and fur-
ther relaxing to the Wolfe dual form, the well known
Mercer’s theorem may be harnessed for calculating
dot products in H by means of a Mercer kernel in data
space: Φ(x
i
) · Φ(x
j
) = k(x
i
, x
j
); cf. (Sch
¨
olkopf et al.,
1999). In order to gain a more smooth adaption, it is
known (Ben-Hur et al., 2001) to be advantageous to
use a Gaussian kernel:
k
G
(x
i
, x
j
) = e
−
1
2σ
2
kx
i
−x
j
k
2
. (2)
Putting it all together, the equation that has to be max-
imized in order to determine the desired sphere is:
W (β) =
∑
i
k(x
i
, x
i
)β
i
−
∑
i, j
β
i
β
j
k(x
i
, x
j
). (3)
With k = k
G
we get two main results: the center a =
∑
i
β
i
Φ(x
i
) of the sphere in terms of an expansion into
H and a function R : R
d
→ R that allows to determine
the distance of the image of an arbitrary point from
a ∈ H , calculated in R
d
by:
R
2
(x) = 1 −2
∑
i
β
i
k
G
(x
i
, x) +
∑
i, j
β
i
β
j
k
G
(x
i
, x
j
). (4)
Because all support vectors are mapped right onto the
surface of the sphere, the radius R
S
of the sphere S can
be easily determined by the distance of an arbitrary
support vector. Thus the feasible region can now be
modeled as
F = {x ∈ R
d
|R(x) ≤ R
S
} ≈ X . (5)
Initially, such models have for example been used for
handwritten digit or face recognition, pattern denois-
ing, or anomaly detection (Chang et al., 2013; Park
et al., 2007; Rapp and Bremer, 2012). A relatively
new application is that of modeling feasible regions
and constraint abstraction for distributed optimization
problems especially in the field of energy manage-
ment, e. g. as used in (Hinrichs et al., 2013a).
Using SVDD as surrogate model within a VPP
control algorithm starts with generating a training set
of feasible schedules for a specific energy unit with
the help of a simulation model of this unit. Thus, a
schedule is a vector x ∈ R
d
consisting of d values
for mean active power to be operated during the re-
spective time inerval. In a first step, the simulation
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
44
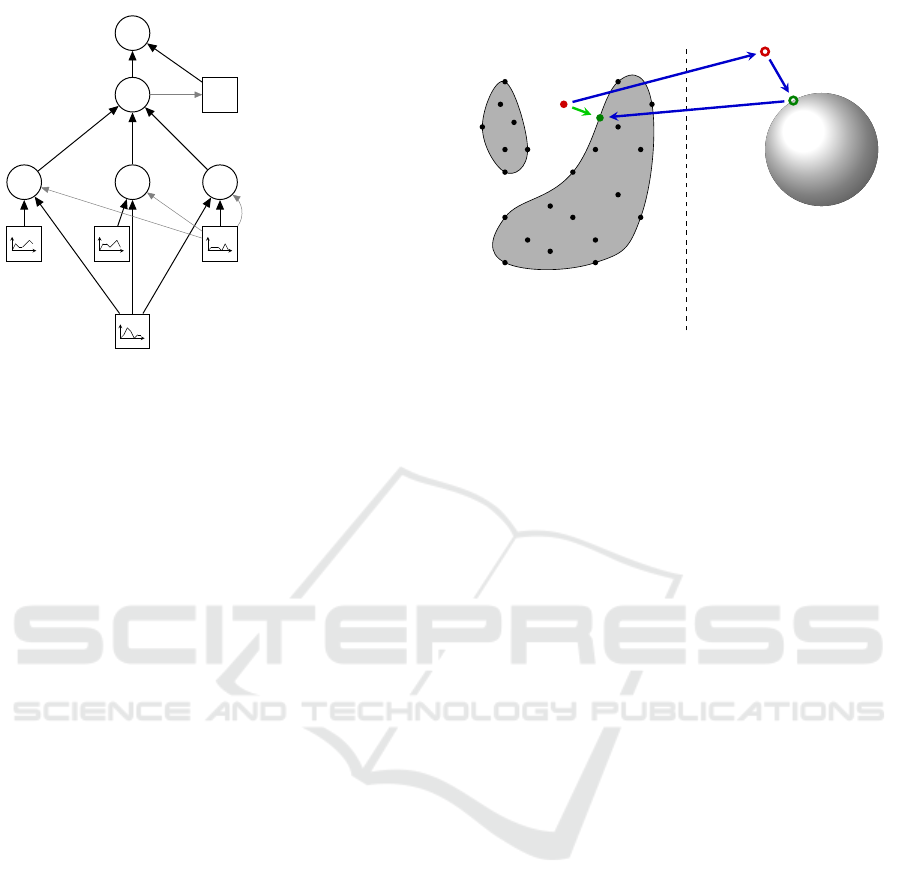
−
classification
R
R
S
schedule distance
k k k
comparison
support vectors
questionable
schedule
sgn( )
w
1
w
2
w
3
Figure 1: Scheme for using SVDD as surrogate model for
checking feasibility of operation schedules in distributed
energy management after (Sch
¨
olkopf, 1997).
model is parametrized with the estimated initial oper-
ation state of the unit (e. g. the temperature of a ther-
mal buffer store attached to a co-generation plant) at
the future point in time that marks the start of the time
frame for which a cluster schedule for the VPP is to be
found. A cluster schedule as result of an (distributed)
optimization process assigns a schedule to each en-
ergy unit within the VPP such that the sum of all
individual schedules resembles a given target sched-
ule (often an energy product to be sold at market) as
close as possible. This simple case is an instance of
the multiple choice constraint optimization problem
(Hinrichs et al., 2013b); for each unit a schedule has
to be chosen from the feasible region of that unit. Of-
ten, further objectives like cost are concurrently opti-
mized. Because the units are not necessarily known
at compile-time and in order to be able to implement
the control strategy independently, surrogates with a
well-defined interface are used for checking feasibil-
ity during optimization. In this way, a simulation
model for each unit is parametrized with a predicted
initial operation state and generates a training set of
feasible schedules for training the SVDD classifier
that in turn is used by the problem solver for check-
ing feasibility (Bremer et al., 2011). The process of
checking feasibility for the VPP case is depicted in
figure 1. A so far unaddressed problem is that of inte-
grating uncertainty issues in such models. Integrating
uncertainty into support vector data description has so
far led to only a few approaches. For instance, (Zheng
et al., 2006) introduced a fuzzy approach for the data
clustering use case. With the help of a fuzzy defi-
nition of membership that determines for each point
whether it belongs to the training set or not, they con-
trol the rate of hyper volume and outlier acceptance.
Another approach with fuzzy constraint treatment is
H
(k)
R
d
x
ˆ
Ψ
x
˜
Ψ
x
x
∗
Figure 2: Basic idea of an decoder for constraint-handling
based on SVDD (Bremer and Sonnenschein, 2014).
given by (GhasemiGol et al., 2010). A different ap-
proach is taken in (Liu et al., 2013). An individual
weighting is introduced allowing for a differentiated
consideration of accepted errors. Thus, data points
with a higher confidence have a larger impact on the
decision boundary. Equation (6) shows the respective
extension to (1) in the last term.
L(ξ, µ, β) = R
2
−
∑
i
(R
2
+ ξ
i
− kΦ(x
i
) − ak
2
)β
i
−
∑
i
ξ
i
µ
i
+C
∑
i
(κ[x
i
]ξ
i
).
(6)
A definition of a problem specific differentiated con-
fidence value for weighting has so far not been intro-
duced. Liu et al. used the SVDD distance of a first
training run as weighting for a second run. Here,
we may later harness some a priori information for
a more specific weighting.
In equation (6) the last term determines the trade-
off between accepted error and hypersphere volume
like the last term in equation (1). In contrast to the
standard version equation (1), each point x
i
is individ-
ually weighted according to its individual confidence
of membership to the positive class by κ[x
i
]. κ gives a
measure for the reasonability of x
i
.
We will later use this approach for modelling un-
certainty in the use case of energy management. Be-
forehand we briefly discuss a specialized application
for the SVDD model of feasible region: the ability to
be used as decoder.
Modeling Uncertainty in Support Vector Surrogates of Distributed Energy Resources - Enabling Robust Smart Grid Scheduling
45
2.3 Decoders for Scheduling
In order to be able to systematically generate feasi-
ble solutions directly from the search space model, a
decoder approach had been developed on top of the
support vector model instead of merely telling feasi-
ble and infeasible schedules apart. In (Bremer and
Sonnenschein, 2013) a so called support vector de-
coder has been introduced. Basically, a decoder is a
constraint handling technique that gives an algorithm
hints on where to look for feasible solutions. It im-
poses a relationship between a decoder solution and a
feasible solution and gives instructions on how to con-
struct a feasible solution (Coello Coello, 2002). For
example, (Koziel and Michalewicz, 1999) proposed
a homomorphous mapping between an n-dimensional
hyper cube and the feasible region in order to trans-
form the problem into a topological equivalent one
that is easier to handle. In order to be able to derive
such a decoder mapping automatically from any given
energy unit model, (Bremer and Sonnenschein, 2013)
developed an approach based on the mentioned sup-
port vector model (Bremer et al., 2011).
Provided the feasible region of an energy unit has
been encoded by SVDD, a decoder can be derived as
follows. The set of alternatively feasible schedules
after encoding by SVDD is represented as pre-image
of a high-dimensional sphere S. Figure 2 shows the
situation. This representation has some advantageous
properties. Although the pre-image might be some
arbitrary shaped non-continuous blob in R
d
, the high-
dimensional representation is a ball and geometrically
easier to handle with the following relations: If a
schedule is feasible, i.e. can be operated by the unit
without violating any technical constraint, it lies in-
side the feasible region (grey area on the left hand
side in figure 2). Thus, the schedule is inside the pre-
image (that represents the feasible region) of the ball
and thus its image in the high-dimensional represen-
tation lies inside the sphere. An infeasible schedule
(e. g. x in Fig. 2) lies outside the feasible region and
thus its image
ˆ
Ψ
x
lies outside the ball. But, some im-
portant relations are known: the center of the ball, the
distance of the image from the center and the radius
of the ball. One can now move the image of an infea-
sible schedule along the difference vector towards the
center until it touches the ball. Finally, the pre-image
of the moved image
˜
Ψ
x
is calculated to get a sched-
ule at the boundary of the feasible region: a repaired
schedule x
∗
that is now feasible. No mathematical
description of the original feasible region or of the
constraints are needed to do this. More sophisticated
variants of transformation are e. g. given in (Bremer
and Sonnenschein, 2013).
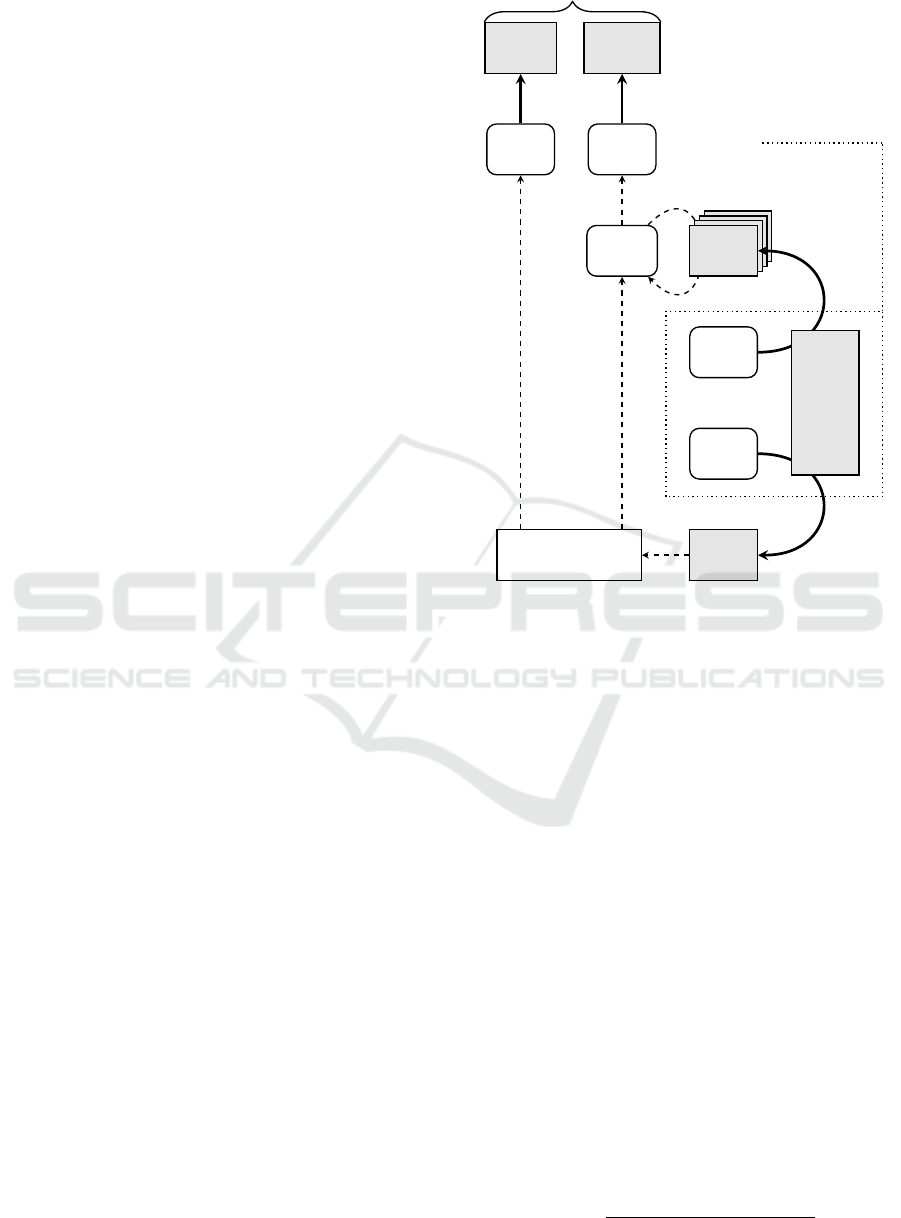
svdd
classifier
usw-svdd
classifier
train train
foreach
schedule
check feasibility
confidence score
model
model
model
model
vary
predict
model
training set X
generate
parametrize
& instantiate
parametrize
& instantiate
model class
scenario
compare
Figure 3: Integration of confidence scores and evaluation
scheme for comparing both classifiers.
3 MODELING CONFIDENCE
In order to model the uncertainty in a schedule’s op-
erability we define the confidence of a schedule as the
share of variations of the initial state that still allows
operating the schedule without any modification. Let
X be a set of d-dimensional schedules x
i
that is going
to serve as training set for building the SVDD model.
X has been generated by assuming operation of a unit
U starting from an initial operation state z
0
∈ Z
U
at a
certain future point in time with the set Z
U
of all pos-
sible operation states. This set is unit specific. To give
an example, Z
U
in the case of a co-generation plant
might be in the simplest version the set of assignments
for the state of charge (SOC) of an associated thermal
buffer store. Let Ω(z
0
) bet a set of variations of z
0
and
F [Ω(z
0
)] the set of schedules x
i
∈ X that are opera-
ble from any state in Ω(z
0
) without modification. We
now define the confidence of a schedule p ∈ X as the
ratio
κ[p] = P(p ∈ F [Ω(z
0
)]|p ∈ F [z
0
])
=
|{x|x ∈ F [z]∀z ∈ Ω(z
0
)}|
|Ω(z
0
)|
.
(7)
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
46
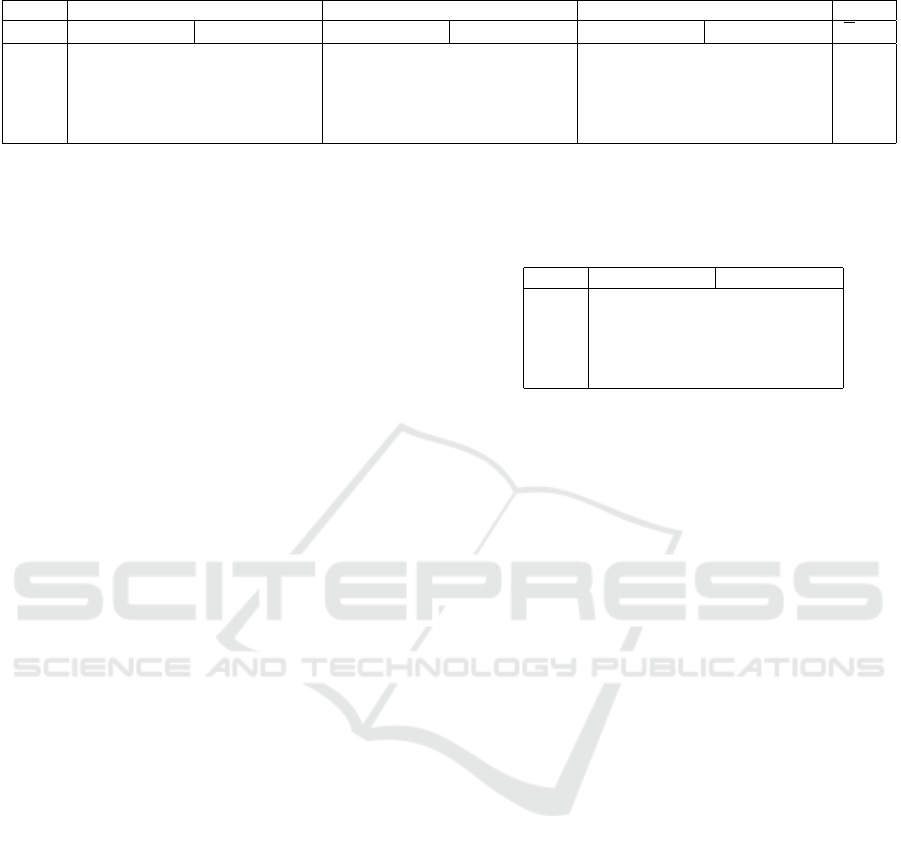
Table 1: Improved classification for a boiler with different water drawing profiles and different variations in usage prediction.
draught w
1
draught w
2
draught w
3
σ / kJ SVDD csw-SVDD SVDD csw-SVDD SVDD csw-SVDD ∆ / %
135 0.313 ± 0.341 0.513 ± 0.381 0.281 ± 0.324 0.501 ± 0.372 0.308 ± 0.339 0.505 ± 0.384 74,37
90 0.527 ± 0.341 0.674 ± 0.319 0.532 ± 0.340 0.699 ± 0.298 0.527 ± 0.341 0.674 ± 0.319 30.24
45 0.841 ± 0.190 0.904 ± 0.149 0.860 ± 0.187 0.918 ± 0.120 0.841 ± 0.190 0.904 ± 0.149 6.99
27 0.943 ± 0.085 0.965 ± 0.072 0.949 ± 0.081 0.969 ± 0.066 0.943 ± 0.085 0.965 ± 0.072 2.15
18 0.969 ± 0.053 0.981 ± 0.048 0.973 ± 0.047 0.984 ± 0.038 0.970 ± 0.053 0.981 ± 0.048 0.91
In this way, the confidence is the probability of still
being operable if a given variation is applied to the
initial operation state that had been taken as assump-
tion for generating the training set of feasible sched-
ules.
What remains open is the definition of variation
in initial states. The actual design of such variation
highly depends on the unit type at hand and on its
embedding into the actual operation site. For this rea-
son, this question cannot be answered in general here.
In this paper we define variation for our simulations
in a scenario specific way.
By using equation (6) instead of equation (1) in
the SVDD part of the surrogate model for the feasi-
ble regions of energy units (and for the derived de-
coder) and by using the expectation value of the fea-
sibility of a schedule under changed conditions for
the units operations as defined in (7) as a score for
the confidence of the schedule, we define the con-
fidence score weighted extension to the surrogate
model (csw-SVDD) used in (Bremer et al., 2011).
4 RESULTS
We tested the approach with a simulation study. For
this purpose we used appliances with a characteris-
tics that allows for a well defined simulated varia-
tion in initial operation state. We have chosen an
under-counter water boiler, a co-generation plant and
a fridge as example units for electricity generation as
well as demand. All models had already been used
in several studies and projects for evaluation (Bremer
et al., 2010; Bremer and Sonnenschein, 2013; Neuge-
bauer et al., 2015; Hinrichs et al., 2013a; Nieße and
Sonnenschein, 2013).
Fridge: A fridge allows for modelling different vari-
ations. We tested two variants: variations in
changing the thermal mass and variation of the ex-
pected start temperature.
Co-generation: For co-generation plants (CHP) we
modeled errors in expected weather conditions re-
sulting in differences for the usage of the con-
currently produced heat. Hence, we co-simulated
Table 2: Comparison of decoding errors as portion of cor-
rectly constructed schedules for different forecast devia-
tions using the example of a boiler with predicted hot water
demand.
σ / kJ SVDD csw-SVDD
9 0.074 ± 0.243 0.003 ± 0.056
18 0.350 ± 0.445 0.025 ± 0.152
27 0.524 ± 0.469 0.098 ± 0293
45 0.738 ± 0.411 0.594 ± 0.468
67.5 0.842 ± 0.355 0.804 ± 0.387
CHP together with the heat losses of a house
based on weather forecasts.
Water boiler: By keeping a water reservoir within a
certain temperature range by an electrical heating
device, electricity consumption can be scheduled
with rather few constraints. Assuming the tech-
nical insulation setting as fixed, losses are merely
dependent on the ambient temperature difference.
On the other hand, possible variations in schedul-
ing load depend on the predicted usage profile for
water drawing. Setting the ambient temperature
fixed, the initial state for scheduling is determined
by the temperature of the water in the tank and
the profile for predicted water drawing during the
scheduling horizon. For variations, we modeled
different prediction errors for the usage profile.
In order to evaluate the improvement of the mod-
ified model we trained two models with basically the
same training set of feasible schedules generated from
the simulation model of the unit which is also used for
evaluation of both surrogates. Figure 3 shows the set-
ting of the basic evaluation scenario.
Each scenario comprises a specific model class for
an energy unit and a prediction for an initial state
which serves as parametrization for instantiating a
model of the energy unit. From this model a training
set X of feasible schedules is generated. Each sched-
ule consists of a fixed number d of values for consec-
utive mean real power at which the unit can be op-
erated without violating any constraint. This training
set serves for training a classic SVDD classifier surro-
gate model for testing feasibility of a given schedule
without a need for the actual energy unit model. At
the same time each scenario contains a unit specific
Modeling Uncertainty in Support Vector Surrogates of Distributed Energy Resources - Enabling Robust Smart Grid Scheduling
47

definition of variation σ for the initial state. This vari-
ation is used to generate a set of models, each with
a random variation. Each schedule in the training set
is then checked for feasibility with each of these var-
ied models. The expectation value of feasibility un-
der a certain variety of initial operation states (given
the schedule x was feasible under the fixed, predicted
initial operation state) serves as confidence score κ[x]
for training a csw-SVDD. Finally, both classifiers can
be compared by using classical classifier evaluation
methods (Powers, 2008; Witten et al., 2011). To eval-
uate the classifier performance, we calculated the con-
fusion matrix by comparing classifier and the origi-
nal model that had been used for generating the train-
ing set and derived standard indicators for comparison
(Powers, 2011). Feasibility of a randomly (equally
distributed) generated schedule is tested for feasibil-
ity once with help of the classifier and once with the
help of the unit model. In each scenario, 10000 varia-
tions have been used to find the expectation value κ.
Table 1 shows some results for a water boiler.
In this scenario we estimated a given water profile
for hot water drawing as predicted usage. Hot water
usage strongly determines feasibility of a given
electrical profile. As variations we generated random
deviations from the given water profile of a given
size by adding normally distributed values with
given standard deviation σ (negative drawings were
corrected to zero for plausibility) ranging from 18
to 135 kJ per 15 minute time interval. We tested
scenarios with a duration of one hour with a 15
minute resolution and the following artificial draw-
ing profiles: w
1
= (180 kJ, 0 kJ, 0 kJ, 720 kJ),
w
2
= (0 kJ, 1440 kJ, 180 kJ, 540 kJ) and
w
3
= (180 kJ, 90 kJ, 90 kJ, 180 kJ).
The absolute performance (depicted is the recall
value) degrade fast with growing uncertainty in both
classifiers. This is as expected because of the growing
deviation from the expected initial state. Neverthe-
less, the csw-SVDD performs better in all cases and
the mean relative improvement and thus the advan-
tage grows with growing error in prediction. Table
2 shows the results (error rate of not correctly gener-
ated schedules) for a decoder built from the respective
classifier for profile 3 only. The results for the decoder
part are not as good as for the classifier model part but
nevertheless significant.
For evaluating the classifiers we primarily use the
Table 3: Comparison of classifier recall indicators (higher
values are better) for further scenarios.
scenario SVDD csw-SVDD
fridge 1 0.927 ± 0.045 0.994 ± 0.025
fridge 2 0.747 ± 0.028 0.829 ± 0.085
chp 0.838 ± 0.260 0.884 ± 0.226
Table 4: Comparison of classifier accuracy for a simulated
boiler with 24-dimensional schedules and deviations (σ) in
predicted water usage of different size in a different number
of time intervals.
σ, n SVDD csw-SVDD
60, 3 0.8431 ± 0.0939 0.9371 ± 0.0966
120, 1 0.8644 ± 0.1323 0.9507 ± 0.1051
120, 2 0.6802 ± 0.2196 0.9372 ± 0.1062
120, 3 0.5175 ± 0.2658 0.9027 ± 0.1291
recall indicator. The precision degrades in both cases
significantly. This is immediately apparent. The pre-
cision reflects the likelihood of a found schedule be-
ing feasible (Powers, 2011). Because feasibility here
is checked under changed preconditions and feasi-
bility is a property of the schedules, precision de-
grades in both classifiers at approximately the same
level. The new csw-SVDD classifier for energy re-
sources surrogate modeling shows but a higher recall
behavior, because the recall reflects the likelihood of
a schedule being feasible even under changed condi-
tions. But this is exactly what is needed for the use
case of checking feasibility of a schedule during en-
ergy management operations.
Table 3 shows some further results for a 2 hour
time frame. For fridge 1 an unpredictable user in-
teraction was simulated by adding a random thermal
mass (30 ± 5 kJ, equating to about 500 g of food with
room temperature) to the reefer cargo in the fridge.
For fridge 2 a variation of the predicted starting tem-
perature was introduced. In the CHP scenario the
thermal demand was varied to simulate a deviation
from the weather forecast.
Finally, table 4 shows some results for longer time
periods with 24-dimensional schedules. Again, these
are boilers with variations in a limited number of n
time periods. Due to a lack of real world data, a nor-
mal distribution of the variations has been assumed in
all simulations according to (Stadler, 2005). This as-
sumption is likely to become invalid in practice. An
advantage of the chosen approach for the csw-SVDD
surrogate is the ability to derive the decision boundary
unsupervised from the confidence scores of the indi-
vidual schedules in the training set regardless of the
underlying distributions. In this way, the approach
can be used unchanged for individual variations of
newly implemented and integrated energy resource
models; even if they are introduced later at run time.
5 CONCLUSION
Predictive energy management for balancing or plan-
ning electricity demand and production according to
operation schedules needs predictions of future opera-
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
48

tion alternatives and thus information about flexibili-
ties of all devices for the scheduler to choose from.
Such predictions on flexibility found meta-models
as representations of individually restricted search
spaces. Whether such a predicted operation schedule
is actually still operable when it comes to finally oper-
ating the assigned (optimal) ones depends on several
certain predictions that where made while construct-
ing the training set of probably feasible schedules.
A robust planning algorithm should take into ac-
count this uncertainty of operability already during
the phase planning. For the use case scrutinized in
this contribution, robustness of a schedule is defined
by the operability even under changed circumstances
and preconditions. This ability of a schedule is con-
densed into a confidence value that allows individ-
ual weighting during the training phase of the search
space meta-model.
To achieve this goal, we adapted an approach for
confidence integration in classification, added a con-
fidence model specific for electric flexibilities for op-
eration schedules, and demonstrated its applicability
with several use cases. The results are already promis-
ing for the model part and call for further extension
especially regarding concrete definitions of variety
and confidence for specific unit types.
Future work will have to target a better integra-
tion of uncertainty into decoders as well. If this
is achieved, a more robust scheduling within virtual
power plants will lead to a better support for the
integration of fluctuating renewable resources. For
the case of surrogate modelling this was already im-
proved with the approach proposed here.
balance
REFERENCES
Alharbi, W. and Raahemifar, K. (2015). Probabilistic coor-
dination of microgrid energy resources operation con-
sidering uncertainties. Electric Power Systems Re-
search, 128:1 – 10.
Ben-Hur, A., Siegelmann, H. T., Horn, D., and Vapnik, V.
(2001). Support vector clustering. Journal of Machine
Learning Research, 2:125–137.
Blank, M. and Lehnhoff, S. (2014). Correlations in re-
liability assessment of agent-based ancillary-service
coalitions. In Power Systems Computation Conference
(PSCC), 2014, pages 1–7.
Braubach, L., van der Hoek, W., Petta, P., and Pokahr,
A., editors (2009). Towards Reactive Scheduling for
Large-Scale Virtual Power Plants., volume 5774 of
Lecture Notes in Computer Science. Springer.
Bremer, J., Andreßen, S., Rapp, B., Sonnenschein, M., and
Stadler, M. (2008). A modelling tool for interac-
tion and correlation in demand-side market behaviour.
New methods for energy market modelling, pages 77–
92.
Bremer, J., Rapp, B., and Sonnenschein, M. (2010). Sup-
port vector based encoding of distributed energy re-
sources’ feasible load spaces. In IEEE PES Confer-
ence on Innovative Smart Grid Technologies Europe,
Chalmers Lindholmen, Gothenburg, Sweden.
Bremer, J., Rapp, B., and Sonnenschein, M. (2011). Encod-
ing distributed search spaces for virtual power plants.
In IEEE Symposium Series on Computational Intelli-
gence 2011 (SSCI 2011), Paris, France.
Bremer, J. and Sonnenschein, M. (2013). Constraint-
handling for optimization with support vector surro-
gate models – a novel decoder approach. In Filipe, J.
and Fred, A., editors, ICAART 2013 – Proceedings of
the 5th International Conference on Agents and Artifi-
cial Intelligence, volume 2, pages 91–105, Barcelona,
Spain. SciTePress.
Bremer, J. and Sonnenschein, M. (2014). Constraint-
handling with support vector decoders. In Filipe, J.
and Fred, A., editors, Agents and Artificial Intelli-
gence, volume 449 of Communications in Computer
and Information Science, pages 228–244. Springer
Berlin Heidelberg.
Chang, W.-C., Lee, C.-P., , and Lin, C.-J. (2013). A re-
visit to support vector data description (svdd). techni-
cal report, Department of Computer Science, National
Taiwan University, Taipei 10617, Taiwan.
Coello Coello, C. A. (2002). Theoretical and numerical
constraint-handling techniques used with evolutionary
algorithms: a survey of the state of the art. Com-
puter Methods in Applied Mechanics and Engineer-
ing, 191(11-12):1245–1287.
Coll-Mayor, D., Picos, R., and Garci
´
a-Moreno, E. (2004).
State of the art of the virtual utility: the smart dis-
tributed generation network. International Journal of
Energy Research, 28(1):65–80.
GhasemiGol, M., Sabzekar, M., Monsefi, R., Naghibzadeh,
M., and Yazdi, H. S. (2010). A new support vector
data description with fuzzy constraints. In Proceed-
ings of the 2010 International Conference on Intelli-
gent Systems, Modelling and Simulation, ISMS ’10,
pages 10–14, Washington, DC, USA. IEEE Computer
Society.
Hinrichs, C., Bremer, J., and Sonnenschein, M. (2013a).
Distributed Hybrid Constraint Handling in Large
Scale Virtual Power Plants. In IEEE PES Conference
on Innovative Smart Grid Technologies Europe (ISGT
Europe 2013). IEEE Power & Energy Society.
Hinrichs, C., Sonnenschein, M., and Lehnhoff, S. (2013b).
Evaluation of a Self-Organizing Heuristic for Inter-
dependent Distributed Search Spaces. In Filipe, J.
and Fred, A. L. N., editors, International Conference
on Agents and Artificial Intelligence (ICAART 2013),
volume Volume 1 – Agents, pages 25–34. SciTePress.
Ili
´
c, M. D. (2007). From hierarchical to open access electric
power systems. Proceedings of the IEEE, 95(5):1060–
1084.
Koziel, S. and Michalewicz, Z. (1999). Evolutionary al-
gorithms, homomorphous mappings, and constrained
parameter optimization. Evol. Comput., 7:19–44.
Modeling Uncertainty in Support Vector Surrogates of Distributed Energy Resources - Enabling Robust Smart Grid Scheduling
49

Liu, B., Xiao, Y., Cao, L., Hao, Z., and Deng, F.
(2013). Svdd-based outlier detection on uncer-
tain data. Knowledge and Information Systems,
34(3):597–618.
Lukovic, S., Kaitovic, I., Mura, M., and Bondi, U. (2010).
Virtual power plant as a bridge between distributed en-
ergy resources and smart grid. Hawaii International
Conference on System Sciences, 0:1–8.
McArthur, S., Davidson, E., Catterson, V., Dimeas, A.,
Hatziargyriou, N., Ponci, F., and Funabashi, T. (2007).
Multi-agent systems for power engineering applica-
tions – Part I: Concepts, approaches, and technical
challenges. IEEE Transactions on Power Systems,
22(4):1743–1752.
Neugebauer, J., Kramer, O., and Sonnenschein, M. (2015).
Classification cascades of overlapping feature ensem-
bles for energy time series data. In Proceedings of
the 3rd International Workshop on Data Analytics for
Renewable Energy Integration (DARE’15), ECML/
PKDD 2015. Springer.
Nieße, A., Beer, S., Bremer, J., Hinrichs, C., L
¨
unsdorf,
O., and Sonnenschein, M. (2014). Conjoint dynamic
aggrgation and scheduling for dynamic virtual power
plants. In Ganzha, M., Maciaszek, L. A., and Paprzy-
cki, M., editors, Federated Conference on Computer
Science and Information Systems - FedCSIS 2014,
Warsaw, Poland.
Nieße, A., Lehnhoff, S., Tr
¨
oschel, M., Uslar, M., Wiss-
ing, C., Appelrath, H.-J., and Sonnenschein, M.
(2012). Market-based self-organized provision of ac-
tive power and ancillary services: An agent-based ap-
proach for smart distribution grids. In COMPENG,
pages 1–5. IEEE.
Nieße, A. and Sonnenschein, M. (2013). Using grid related
cluster schedule resemblance for energy rescheduling
- goals and concepts for rescheduling of clusters in
decentralized energy systems. In Donnellan, B., Mar-
tins, J. F., Helfert, M., and Krempels, K.-H., editors,
SMARTGREENS, pages 22–31. SciTePress.
Nikonowicz, Ł. B. and Milewski, J. (2012). Virtual power
plants – general review: structure, application and op-
timization. Journal of Power Technologies, 92(3).
Park, J., Kang, D., Kim, J., Kwok, J. T., and Tsang, I. W.
(2007). Svdd-based pattern denoising. Neural Com-
puting, 19(7):1919–1938.
Powers, D. M. W. (2008). Evaluation evaluation. In Pro-
ceedings of the 2008 Conference on ECAI 2008: 18th
European Conference on Artificial Intelligence, pages
843–844, Amsterdam, The Netherlands, The Nether-
lands. IOS Press.
Powers, D. M. W. (2011). Evaluation: From precision, re-
call and f-measure to roc., informedness, markedness
& correlation. Journal of Machine Learning Tech-
nologies, 2(1):37–63.
Ramchurn, S. D., Vytelingum, P., Rogers, A., and Jennings,
N. R. (2012). Putting the ’smarts’ into the smart grid:
A grand challenge for artificial intelligence. Commun.
ACM, 55(4):86–97.
Rapp, B. and Bremer, J. (2012). Design of an event en-
gine for next generation cemis: A use case. In Hans-
Knud Arndt, Gerlinde Knetsch, W. P. E., editor, Envi-
roInfo 2012 – 26th International Conference on Infor-
matics for Environmental Protection, pages 753–760.
Shaker Verlag. ISBN 978-3-8440-1248-4.
Sch
¨
olkopf, B. (1997). Support Vector Learning. Disserta-
tion, Fachbereich 13 Informatik der Technischen Uni-
versit
¨
at Berlin, Oldenbourg Verlag, M
¨
unchen.
Sch
¨
olkopf, B., Mika, S., Burges, C., Knirsch, P., M
¨
uller, K.-
R., R
¨
atsch, G., and Smola, A. (1999). Input space vs.
feature space in kernel-based methods. IEEE Trans-
actions on Neural Networks, 10(5):1000–1017.
Sri, M., Huld, T., Dunlop, E. D., Albuisson, M., Lefevre,
M., and Wald, L. (2007). Uncertainties in photovoltaic
electricity yield prediction from fluctuation of solar
radiation. In 22nd European Photovoltaic Solar En-
ergy Conference.
Stadler, P. D.-I. I. (2005). Demand Response: Nichtelek-
trische Speicher fr Elektrizittsversorgungssysteme mit
hohem Anteil erneuerbarer Energien. Habilitation,
Fachbereich Elektrotechnik, Universitt Kassel.
Tax, D. M. J. and Duin, R. P. W. (2004). Support vector data
description. Mach. Learn., 54(1):45–66.
Wang, J., Botterud, A., Bessa, R., Keko, H., Carvalho,
L., Issicaba, D., Sumaili, J., and Miranda, V. (2011).
Wind power forecasting uncertainty and unit commit-
ment. Applied Energy, 88(11):4014 – 4023.
Wildt, T. (2014). Modelling uncertainty of household deci-
sion – making process in smart grid appliances adop-
tion. In Behave Energy Conference, Oxford, UK.
Witten, I. H., Frank, E., and Hall, M. A. (2011). Data
Mining: Practical Machine Learning Tools and Tech-
niques. Morgan Kaufmann, Amsterdam, 3 edition.
Wu, F., Moslehi, K., and Bose, A. (2005). Power system
control centers: Past, present, and future. Proceedings
of the IEEE, 93(11):1890–1908.
Zhang, J., Hodge, B.-M., Gomez-Lazaro, E., Lovholm, A.,
Berge, E., Miettinen, J., Holttinen, H., and Cutululis,
N. (2013). Analysis of Variability and Uncertainty in
Wind Power Forecasting: An International Compari-
son. Energynautics GmbH.
Zheng, E.-H., Yang, M., Li, P., and Song, Z.-H. (2006).
Fuzzy support vector clustering. In Wang, J., Yi, Z.,
Zurada, J. M., Lu, B.-L., and Yin, H., editors, ISNN
(1), volume 3971 of Lecture Notes in Computer Sci-
ence, pages 1050–1056. Springer.
Zio, E. and Aven, T. (2011). Uncertainties in smart grids
behavior and modeling: What are the risks and vul-
nerabilities? how to analyze them? Energy Policy,
39(10):6308 – 6320. Sustainability of biofuels.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
50
