
A Mass-flow based MILP Formulation for the Inventory Routing with
Explicit Energy Consumption
Yun He
1,2
, Cyril Briand
1,2
and Nicolas Jozefowiez
1,3
1
CNRS, LAAS, 7 Avenue du Colonel Roche, F-31400 Toulouse, France
2
Univ. de Toulouse, UPS, LAAS, F-31400 Toulouse, France
3
Univ. de Toulouse, INSA, LAAS, F-31400 Toulouse, France
Keywords:
Inventory Routing Problem, Energy Minimization, Mixed Integer Linear Programming.
Abstract:
In this paper, we present a new mass-flow based Mixed Integer Linear Programming (MILP) formulation for
the Inventory Routing Problem (IRP) with explicit energy consumption. The problem is based on a multi-
period single-vehicle IRP with one depot and several customers. Instead of minimizing the distance or inven-
tory cost, the problem takes energy minimization as an objective. In this formulation, flow variables describing
the transported mass serve as a link between the inventory control and the energy estimation. Based on phys-
ical laws of motion, a new energy estimation model is proposed using parameters like vehicle speed, average
acceleration rate and number of stops. The solution process contains two phases with different objectives: one
with inventory and transportation cost minimization as in traditional IRP, the other with energy minimization.
Using benchmark instances for inventory routing with parameters for energy estimation, experiments have
been conducted. Finally, the results of these two solution phases are compared to analyse the influence of
energy consumption to the inventory routing systems.
1 INTRODUCTION
Our purpose is to introduce an energy estimation
method and to propose a MILP optimization model
that incorporates energy consumption into the Inven-
tory Routing Problem (IRP) with mass flows. We start
from a general literature review of the IRPs and the
emerging Green Vehicle Routing Problems (GVRPs),
then we discuss the incorporation of these two prob-
lems to present our new formulation.
The Vendor Managed Inventory (VMI) is an in-
ventory management model where the supplier mon-
itors the inventory level of the whole system and
acts as a central decision maker for the long-term
replenishment policy of each retailer. With respect
to the traditional Retailer Managed Inventory (RMI),
the VMI results in a more efficient resource utiliza-
tion (Archetti et al., 2007). Under the context of
the VMI, the IRP combines the inventory manage-
ment, vehicle routing and scheduling. There are three
simultaneous decisions to make (Coelho et al., 2013):
1. when to serve a customer;
2. how much to deliver when serving a customer;
3. how to route the vehicle among the customers to
be served.
The IRP was first studied under the context of
the distribution of industrial gases (Bell et al., 1983).
After that, numbers of variants of the problem have
come out, but there exists no standard version. The
trade-offs between inventory costs and transportation
costs are studied and explicit formulas to evaluate
these trade-offs based on spatial density of customers
are obtained in (Burns et al., 1985). In (Dror and Ball,
1987), the authors proposed a method to reduce the
long-term version of the problem to a single-period
problem by defining single-period costs that reflects
long-term effects. In (Anily and Federgruen, 1990),
the authors tried to decide the long-run replenish-
ment strategies for a set of geographically dispersed
retailers and they proposed the first clustering algo-
rithm for the IRP. In (Savelsbergh and Song, 2007),
the authors studied the inventory routing with con-
tinuous moves with both pick-ups and deliveries and
developed a randomized greedy algorithm. The in-
ventory routing with backlogging is studied in (Ab-
delmaguid et al., 2009), where a heterogeneous fleet
is considered. In (Archetti et al., 2007), the authors
242
He, Y., Briand, C. and Jozefowiez, N.
A Mass-flow based MILP Formulation for the Inventory Routing with Explicit Energy Consumption.
DOI: 10.5220/0005698802420251
In Proceedings of 5th the International Conference on Operations Research and Enterprise Systems (ICORES 2016), pages 242-251
ISBN: 978-989-758-171-7
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

proposed a MILP formulation of the IRP and applied
a Branch-and-Cut algorithm to solve this problem.
Later in (Archetti et al., 2014), based on the formu-
lation in the previous paper, new formulations are de-
veloped and compared with existing formulations us-
ing a large set of benchmark instances.
Two important literature reviews are worth men-
tioning here. (Andersson et al., 2010) is a survey
of the industrial aspects of the problem, and (Coelho
et al., 2013) is a comprehensive review on the typolo-
gies of the problem as well as their solution methods.
Nowadays, the Supply Chain Management is
faced with a new challenge—the sustainability. As
one of the three bottom lines of Sustainable Sup-
ply Chain Management, environmental sustainability
is the most recognized dimension (Fish, 2015). As
shown in (Sahin et al., 2009), energy costs account
for about 60% of the total cost of a unit of cargo trans-
ported on road.
In the literature, there are a growing number of pa-
pers about the green logistics and sustainable supply
chain management. However, most of them treat the
inventory management and the vehicle routing sepa-
rately. The Energy Minimizing Vehicle Routing Prob-
lem (EMVRP) is studied in (Kara et al., 2007), where
the Capacitated Vehicle Routing Problem (CVRP) is
extended with a new cost function based on distance
and load of the vehicle. In (Xiao et al., 2012), a Fuel
Consumption Rate (FCR) considered CVRP is pro-
posed to minimize the fuel consumption. Focusing on
the pollution and CO
2
emission generated by the road
transport sector, the Pollution Routing Problem (PRP)
is proposed to explicitly control the Greenhouse Gas
(GHG) emission of the transportation (Bektas¸ and La-
porte, 2011). The only paper that incorporates envi-
ronmental aspects in the IRP is a case study from the
petrochemical industry and total CO
2
emissions are
considered as a cost in the objective function (Treitl
et al., 2014).
A detailed literature review of the GVRP can be
found in (Lin et al., 2014). In this review, the environ-
mental sensitive Vehicle Routing Problem is divided
into three groups: the Green-VRP for the optimiza-
tion of energy consumption; the PRP for the reduction
of pollution, especially GHG emissions; and the Ve-
hicle Routing in Reverse Logistics for the wastes and
end-of-life product collection. The authors point out
that incorporating inventory models with PRP models
can be promising.
This brief survey indicates that there lacks en-
ergy awareness in the inventory routing, or there lacks
a system wide view in the sustainable routing. As
the IRP integrates several decisions for the inventory
control of the whole system, it helps us to make strate-
gic decisions for energy optimization. First, under
the VMI policy, the customer demands are flexible
and can be distributed in different combinations. This
property allows us to determine an optimal set of de-
livery quantities that yields the most environmental
cost effectiveness while making sure that stock-out
never happens. Second, the order of visit and the ve-
hicle routes are to be determined. It is thus possible
to design a routing strategy that takes the roads with
the least energy costs. Third, the time of visit is also
adaptable. We can choose a delivery time that is both
convenient for the customers and that can also avoid
rush hours, as congestion is one of the causes of high
energy consumption and CO
2
emissions.
Our study focuses on the integration of the IRP
with explicit consideration on the energy consump-
tion in the transportation. The main contributions of
this paper are: (i) to propose an approach to estimate
the energy consumed in the transportation activities
of inventory routing; (ii) to reformulate the IRP to ex-
plicitly incorporate the energy consideration; (iii) to
analyse the possible energy savings and the trade-offs
between energy savings, travelled distances and in-
ventory costs.
The remainder of this paper is organized as fol-
lows: in Section 2, the problem is described in de-
tails. Then, the mathematical model is presented in
Section 3. After that, experimentation and results are
given in Section 4, followed by the conclusion in Sec-
tion 5.
2 PROBLEM STATEMENT
The problem in our study is based on a multi-period
single-vehicle deterministic inventory routing prob-
lem with one depot and several customers. The vehi-
cle can leave the depot only once per period. In each
period, it makes a tour around the customers that need
to be refilled and returns to the depot. Stock-out and
back-orders are not allowed in the model. Instead of
the distance and inventory minimization, we take en-
ergy minimization as objective. Both the Maximum
Level (ML) and the Order-up-to Level (OU) policy
are applied to see the influence of different replenish-
ment strategies to the energy consumption. A detailed
explanation of these policies is given in Section 3.
To facilitate the energy estimation, two units are
used to measure inventory components—the number
of components and the weight in kilograms (kg). The
number of components is used by the customers to
represent their inventory levels and to count the num-
ber of packages of delivered goods. The weight is
used by the transporters. It is the physical mass of the
A Mass-flow based MILP Formulation for the Inventory Routing with Explicit Energy Consumption
243

components transported by the vehicle.
The next parts present in details the parameters
and variables of the problem and the computation of
the energy estimation function. In particular, mass
flow variables are introduced to link energy estima-
tion and inventory management.
2.1 General Settings for Routing
The problem is constructed on a complete undirected
graph G = {V,E}. V = {0,.. .,n} is the vertex set. It
includes one depot denoted by 0 and the customers to
visit denoted by the set V
c
= {1, ...,n}. E = {(i, j) |
i, j ∈ V and i < j} is the set of undirected edges.
There are T replenishment planning periods. Each
period can be a day, a week or even a month accord-
ing to the real situation. In each period, only one tour
can be performed. If a tour is presented in a period,
the vehicle starts from the depot, travels through all
the customers who need to be served at this period
and returns back to the depot at the end of the period.
Three kinds of decision variables z
t
i
, x
t
i j
and y
t
i j
correspond to routing. For each i ∈ V
c
, t ∈ T , z
t
i
is a bi-
nary variable indicating whether customer i is served
at period t. It equals 1 if customer i is served and 0
otherwise. Particularly, z
t
0
indicates whether the tour
at period t is performed (equals 1) or not (0). For
each edge (i, j) ∈ E and each period t ∈ T , x
t
i j
is an
integer variable indicating the number of times that
edge (i, j) is used in the tour of period t. For each arc
(i, j) ∈ V ×V and each period t ∈ T , variable y
t
i j
is a
binary variable to indicate the direction of the vehicle
route. It equals 1 if the vehicle travels from node i to
j at period t and 0 otherwise.
The vehicle has a capacity Q expressed in num-
bers of components and a mass limit M. The empty
vehicle mass, or curb weight (kg) of the vehicle is W .
2.2 Inventory Characteristics
Inventory levels at customers and depot are monitored
during the whole planning time horizon. They are
summarised at the end of each replenishment period.
The customer demands are described as demand rates
per period. In each period, r
i
units of components are
demanded by customer i ∈ V
c
. In particular, r
0
is the
number of components made available at the depot
in each period. Each customer i ∈ V
c
has a stocking
capacity C
i
while the depot is supposed to have an un-
limited stocking capacity. h
i
is the inventory storage
cost per unit of component per period at customer i or
the depot. The weight of a component in kilograms at
customer i ∈ V
c
is denoted by m
i
.
Two variables are defined for the inventory man-
agement. The variable I
t
i
is the inventory level in num-
ber of components at the depot 0 or at the customer
i ∈ V
c
at the end of period t. The variable q
t
i
is the
number of components delivered to customer i ∈ V
c
during period t ∈ T .
2.3 Energy Estimation
There are many complicated models in the literature
that estimate the CO
2
emissions or the amount of pol-
lutants produced by a vehicle on road. (Demir et al.,
2014) is a review of vehicle emission models and
their inclusion into the existing optimization methods.
However, few models focus on the energy consumed
and most of them depend on vehicle type. This can
be partly explained by the fact that the main power
source of vehicles used today is petroleum. Neverthe-
less, with the emergence of electric and hybrid vehi-
cles, we find it more appropriate to estimate the en-
ergy consumption instead of fuel consumption. In
addition, for the generality of the problem, it is im-
portant that the model would apply for every type of
vehicles. According to (Samaras and Ntziachristos,
1998), travelling kinematic variation (accelerations,
idle duration, etc.) obviously affects engine load and
by turns the energy consumption. Thus, in this paper,
we propose a general simple model based on vehicle
dynamics. This model would be applicable to Euro-
pean suburban transportation network with short or
medium distances and potentially high traffic inten-
sity. It can give us a gross estimation of the energy re-
quired by a vehicle on a road segment with speed vari-
ation, independent of vehicle type or energy source.
In our model, the stop rate τ, i.e., the number of
stops per unit of distance is used to model the dy-
namics of the vehicle on a fixed segment of road.
This parameter can also represent the traffic condi-
tion on the road. More precisely, with a traffic near
free flow, τ takes a value near 0, which means that
the vehicle goes through the road fluently without any
stops; however, with congestion, this number is set
to a bigger value to indicate a frequent speed varia-
tion. Usually τ takes a value between 0 and 4 de-
pending on road types (Andr
´
e et al., 1998). Moreover,
there exists an interrelationship between the distance
travelled, the stop rate and the speed and acceleration
of the vehicle, which is generally explained in Sec-
tion 4.1 and is not the subject of our study.
Suppose a vehicle travelling from one location to
another. The path of the vehicle between two loca-
tions is supposed to be predefined with an average
stop rate τ, and the total distance travelled is s. So the
vehicle stops τ·s times during the trip. The coefficient
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
244
Target speed
acceleration
uniform
deceleration
time
velocity
stop
. . .
Figure 1: The speed variation of the vehicle with time.
of friction is a fixed parameter µ = 0.01. The gravita-
tional acceleration is g = 9.81m/s
2
. The environmen-
tal effects of the road (wind, temperature etc.) as well
as the viscosity of air are ignored. Road slopes are
also ignored for the moment but will be considered in
the future. As a result, the only forces exerted on the
vehicle are the rolling resistance and the traction.
Between every two stops, the vehicle speed is
supposed to follow a fixed pattern of variation—
acceleration, uniform speed movement and stop (Fig-
ure 1). Each time, the vehicle speeds up from 0 to
the target speed V with a fixed acceleration a
acc
. It
goes on at this speed for a while and then stops. The
stop is supposed to be instantaneous. This pattern is
repeated τ · s times supposing that the vehicle has no
speed at both the starting and the ending point. After
each stop, it speeds up again to the same target speed.
The next part explains how to estimate energy
consumption using this simple model.
The mathematical relationship between the physi-
cal quantities of energy (E), work (W ) and power (P)
are:
E =
Z
P(t)dt
P(t) = Fv(t)
E = W =
∑
Fs
with F a constant force, v(t) the speed at instant t and
s the distance travelled.
According to knowledge of physics and energy
conservation, under the hypothesis of speed variation
presented above, the total energy cost per unit of mass
when distance s is travelled with stop rate τ is then:
c = gµs + τsV
2
(1)
Figure 2 shows the power variation of the vehicle un-
der the previous speed variation. We can see that each
time the vehicle speeds up, there appears a ”peak” of
engine power which corresponds to a potentially high
energy consumption. This is also reflected by Equa-
tion 1—the more the vehicle stops on a road segment
(τ takes a bigger value), the higher the energy would
cost. See the Appendix for the detailed calculation.
In this way, we define c
i j
= gµs
i j
+ τ
i j
s
i j
V
2
i j
the
energy cost per unit of mass for each edge (i, j). It is
acceleration
uniform
deceleration
time
power
stop
. . .
Figure 2: The power variation with time.
related to the distance travelled s
i j
and the dynamics
of the vehicle on the road as expressed by the stop rate
τ
i j
and target speed V
i j
.
If m
i j
(kg) of mass is loaded on the vehicle when
traversing from i to j and the vehicle weighs W (kg),
the energy cost of the vehicle travelling from i to j is
thus:
c
i j
(m
i j
+W ) (2)
2.4 Commodity Mass Flow
As we can see from the energy estimation computa-
tion, the total energy cost is a linear function of mass.
Meanwhile, the mass or the quantity of products is
also an important element in the inventory manage-
ment. It is a measurement of the inventory levels. In
fact, there exists a mass flow inside the transportation
network and it can serve as a bridge linking the inven-
tory routing and the energy optimization.
In the traditional IRP formulations presented
in (Archetti et al., 2014), a flow formulation exists
to model the inventory flows inside the transportation
network. Our model takes advantage of this formula-
tion. Instead of considering the flow in terms of num-
ber of components, the mass of the shipped compo-
nents is considered. Once we decide the mass trans-
ported on each edge of the network at each period,
we can deduce the number of components left at each
customer vertex. Or inversely, if we know how many
units of components are delivered to each customer
at each period, we can decide the order of visits and
get a flow of mass in the transportation network that
minimizes the energy consumed.
In our model, variables m
t
i j
are defined as the mass
transported by the vehicle from i to j at period t. They
are linked with the vehicle flow variables y
t
i j
. If the
vehicle does not go from i to j at period t (y
t
i j
= 0),
m
t
i j
is equal to 0.
Figure 3 details the various flows traversing cus-
tomer i at period t. The inventory flow I
t
i
and the
demand r
i
, expressed in number of components, are
associated with the dotted arcs. They describe the
variation of the inventory level of i with time periods.
The solid arcs stand for the mass of the incoming and
A Mass-flow based MILP Formulation for the Inventory Routing with Explicit Energy Consumption
245

X
j∈V \{i}
m
t
ji
i, t
X
j∈V \{i}
m
t
ij
I
t−1
i
I
t
i
r
i
c
ji
c
ij
Figure 3: The flows passing through customer i at period t.
outgoing products (m
t
ji
and m
t
i j
respectively). They
are used to estimate the potential energy consumption,
with c
t
i j
the energy cost per unit of mass on edge (i, j).
The difference
1
m
i
(
∑
j∈V\{i}
m
t
ji
−
∑
j∈V\{i}
m
t
i j
) gives the
number of components q
t
i
delivered by the vehicle to
customer i during period t.
3 MATHEMATICAL MODEL
In this section, we present the mathematical model
using the mass flow.
3.1 Objectives
Two objectives are defined, one for inventory and dis-
tance optimization and the other for energy optimiza-
tion. The objective function (3) is the traditional one
as in (Archetti et al., 2014). It is the sum of the total
distance travelled plus the sum of the inventory stor-
age costs over all the periods.
min
∑
t∈T
∑
(i, j)∈V ×V
s
i j
y
t
i j
+
∑
t∈T
∑
i∈V
h
i
I
t
i
(3)
The objective function (4) is the sum of the total en-
ergy consumed in the inventory routing over all the
periods. Note that it contains two terms: one is a flex-
ible cost related to the transported mass of the vehicle
m
t
i j
, and the other is a fixed cost induced by the vehi-
cle curb weight W .
min
∑
t∈T
∑
(i, j)∈V ×V
c
i j
m
t
i j
+W
∑
t∈T
∑
(i, j)∈V ×V
c
i j
y
t
i j
(4)
3.2 Constraints
Here are the sets of constraints. Compared with the
basic flow formulation in (Archetti et al., 2014), mass
flow variables take place of commodity flow vari-
ables.
Inventory Management
Constraints (5) to (9) are for monitoring the inventory
levels of each location at each period.
I
t
0
= I
t−1
0
+ r
0
−
∑
i∈V
c
q
t
i
∀t ∈ T (5)
I
t
i
= I
t−1
i
− r
i
+ q
t
i
∀i ∈ V
c
,t ∈ T (6)
q
t
i
≥ C
i
z
t
i
− I
t−1
i
∀i ∈ V
c
,t ∈ T (7)
q
t
i
≤ C
i
− I
t−1
i
∀i ∈ V
c
,t ∈ T (8)
q
t
i
≤ C
i
z
t
i
∀i ∈ V
c
,t ∈ T (9)
Constraints (5) and (6) ensure that the inventory lev-
els of each station are coherent from one period to
another. The OU inventory policy is ensured by con-
straints (7) and (8)—after each delivery, the inventory
level of each visited customer is fulfilled to the max-
imum. If we delete Constraints (7), the model be-
comes one under the ML policy, where the replen-
ishment level is flexible but bounded by the stocking
capacity of each customer. Constraints (9) ensure that
if a customer i is not visited at a period t (z
t
i
= 0), the
delivered quantity q
t
i
equals 0 and if the customer is
visited, the delivered quantity never exceeds the ca-
pacity.
Commodity Mass Flow Management
Constraints (10) and (11) are the mass flow con-
straints.
∑
j∈V
c
m
t
0 j
=
∑
i∈V
c
q
t
i
m
i
∀t ∈ T (10)
∑
j∈V
m
t
ji
−
∑
j∈V
m
t
i j
= q
t
i
m
i
∀i ∈ V
c
,t ∈ T (11)
Constraints (10) ensure that at period t, the mass out
of the depot is equal to the total mass transported to all
the customers. Constraints (11) ensure that for each
customer i at each period t, the quantity received is
equal to the difference between the entering and the
leaving mass flow.
Vehicle Routing
Constraints (12) to Constraints (17) are typical
routing constraints.
Undirected Routing
∑
j∈V
c
x
t
0 j
= 2z
t
0
∀t ∈ T (12)
∑
j∈V
j<i
x
t
ji
+
∑
j∈V
c
j>i
x
t
i j
= 2z
t
i
∀i ∈ V
c
,t ∈ T (13)
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
246

Directed Vehicle Flow
∑
j∈V
c
y
t
0 j
= z
t
0
∀t ∈ T (14)
∑
j∈V
y
t
i j
= z
t
i
∀t ∈ T,i ∈ V
c
(15)
∑
j∈V
y
t
ji
= z
t
i
∀t ∈ T,i ∈ V
c
(16)
x
t
i j
= y
t
i j
+ y
t
ji
∀t ∈ T,(i, j) ∈ E (17)
Constraints (12) and (13) define the non-directed
route of the vehicle in each period. Constraints (14)–
(16) restrain the direction of the vehicle flow. They
link y and z variables to make sure that in each period
at most one tour is performed and that each customer
is visited at most once in each period. Constraints (17)
link variables y and x to ensure that each edge is used
at most once in each period.
Vehicle Capacity
Constraints (18) and (19) guarantee that the vehicle
capacity is never exceeded both in number of compo-
nents and in unit of mass.
∑
i∈V
c
q
t
i
≤ Qz
t
0
∀t ∈ T (18)
m
t
i j
≤ My
t
i j
∀t ∈ T,(i, j) ∈ V ×V (19)
Constraints (19) also link the mass flow and the vehi-
cle flow on the graph. They make sure that the direc-
tion of the vehicle flow is the same as that of the mass
flow.
Variable Domains
Constraints (20)–(26) are the variable domains.
0 ≤ I
t
i
≤ C
i
,I
t
i
∈ N ∀i ∈ V,t ∈ T (20)
0 ≤ q
t
i
≤ Q,q
t
i
∈ N ∀i ∈ V
c
,t ∈ T (21)
0 ≤ m
t
i j
≤ M, m
t
i j
∈ N ∀(i, j) ∈ V ×V,t ∈ T (22)
z
t
i
∈ {0,1} ∀i ∈ V,t ∈ T (23)
x
t
i j
∈ {0,1} ∀(i, j) ∈ E,i < j,t ∈ T (24)
x
t
0 j
∈ {0,1,2} ∀ j ∈ V
c
,t ∈ T (25)
y
t
i j
∈ {0,1} ∀(i, j) ∈ V ×V,t ∈ T (26)
All the variables take integer values. Note that for
variables x
t
0 j
, since direct routing is possible, they can
be assigned with value 2.
3.3 Solution Methodology
The solution process is divided into two phases. In the
first phase, the objective is to minimize the combined
cost of transportation and inventory as in objective
function (3). In the second phase, starting with the
solution of the first phase, the same model is solved to
minimize the total energy consumption as computed
in objective function (4).
The methodology allows us to quickly find a feasi-
ble solution for energy minimization in the first phase,
and then explore the energy minimization possibilities
in the second phase.
4 EXPERIMENTATION
This section explains the data generation method,
gives the system settings and provides an analysis of
the obtained results.
4.1 Data Generation
Based on existing IRP instances proposed in (Archetti
et al., 2007), new instances more adapted to energy
estimation are generated. Information on stop rates τ
and vehicle target speeds V relative to the distance
is added in the existing instances. The correlation
within these parameters is determined based on em-
pirical data of delivery trucks on real routes provided
by (Walkowicz et al., 2014). The following part ex-
plains how the data set is generated.
First, three types of road is considered—highway,
national route and urban road. For each edge between
two locations, the type of road is generated randomly.
Then, target speed and number of stops for different
types of roads are generated using different methods.
Details of these methods are given in the Appendix.
Finally, for all types of road, the average acceleration
is fixed at 1.01m/s
2
.
Then, a random number between 1 and 10 is gen-
erated for each customer i to represent the mass of a
package of components m
i
. Vehicle weight and mass
capacity are correlated according to vehicle informa-
tion provided in (EcoTransIT World Initiative (EWI),
2014).
In total, 256 cases are generated. Each case con-
tains 5 instances. The cases are categorized by the
number of periods (3 or 6 periods of replenishment
planning), the proportion of the inventory storage cost
in relation to the transportation cost (high or low), the
inventory replenishment policy (OU or ML), the pro-
portion of each type of road in the whole map and the
number of customers in the map.
4.2 System Settings
The model is realized in C++ with IBM
R
ILOG
R
CPLEX 12.6.1.0 and solved by the default Branch-
and-Bound algorithm with one thread. The operation
A Mass-flow based MILP Formulation for the Inventory Routing with Explicit Energy Consumption
247

system is Ubuntu 14.04 LTS with Intel
R
Core
R
i7-
4790 3.60GHz processor and 16 G memory.
A time limit of 1800 seconds is set for each of
the two phases. All the other settings of CPLEX are
as default. The results of both of the two phases are
compared in the next part.
4.3 Result Analysis
Performance
Eventually, within the time limit, nearly 70% of the
instances with distance and inventory optimization
can be solved to optimality by CPLEX, while only
one third of the instances can be solved to optimality
with energy minimization. Table 1 gives a summary
of the performance information.
The dimension of the instance is determined by
the number of periods (”T” column in the table) and
the number of customers (”n” column in the table).
The inventory policy (OU or ML) changes the con-
straint sets of the model. A combination of these three
parameters define a category of instances. Each cate-
gory contains 40 instances. In this table, computation
time of each solution phase (”time1” and ”time2”)
and the solution status within the time limit (”status1”
and ”status2”) are presented. The times are average
values over all the instances of the same category. If
all the instances of this category can be solved to opti-
mality by CPLEX, the status is noted ”Optimal”. Oth-
erwise, the average relative gap after 1800 seconds of
computation is reported.
As we can see from this table, energy minimiza-
tion is much more difficult to solve than inventory and
transportation cost minimization (time2 time1).
This may result from the large possible combination
of the values of the mass flows. It is normal to see that
the problem becomes more difficult as the dimension
of the instances increases. For both OU and ML poli-
cies, instances larger than 20 customers with 3 periods
or 15 customers with 6 periods become impossible
to solve for energy optimization (Phase 2) within the
time limit. And it seems that the influence of the in-
ventory policy to energy minimization is not as much
as in the traditional IRP. Figure 4 and 5 show the solv-
ing time increase with the number of customers for
different number of periods and inventory policies.
Energy Reduction
In general, 95 % of all the instances can expect an en-
ergy reduction. Of all the instances where energy is
reduced, the average reduction is 3.7%, and the max-
imum reduction can reach 19.4%. Meanwhile, the
distance and inventory cost remains nearly the same
Figure 4: Solution time of the first phase.
Figure 5: Solution time of the second phase.
(with an average augmentation rate of less than 1%).
In addition, the experiments show that nearly all of the
instances with 6 periods can be assigned an energy-
saving replenishment strategy and nearly 90% of the
instances with 3 periods can achieve a solution with
less energy consumption.
By inspecting the results in details, it is observed
that most of the energy reduction comes from the
transported mass, which correspond to the flexible
part of the energy minimizing objective function. The
energy reduction induced by the transported mass is
nearly 20% in average and it can reach as high as
66.3%. And by analysing the energy objective func-
tion, it is easy to see that minimizing the fixed part of
the energy cost or the part induced by the curb weight
is equivalent to a weighted minimization of the dis-
tance. Since the vehicle mass accounts for nearly half
of the total mass moving on the road, a great part of
the energy minimization is equivalent to distance min-
imization. This can explain the reason why finally the
total energy reduction is so small even though the en-
ergy consumed by transporting the products can be
highly reduced.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
248
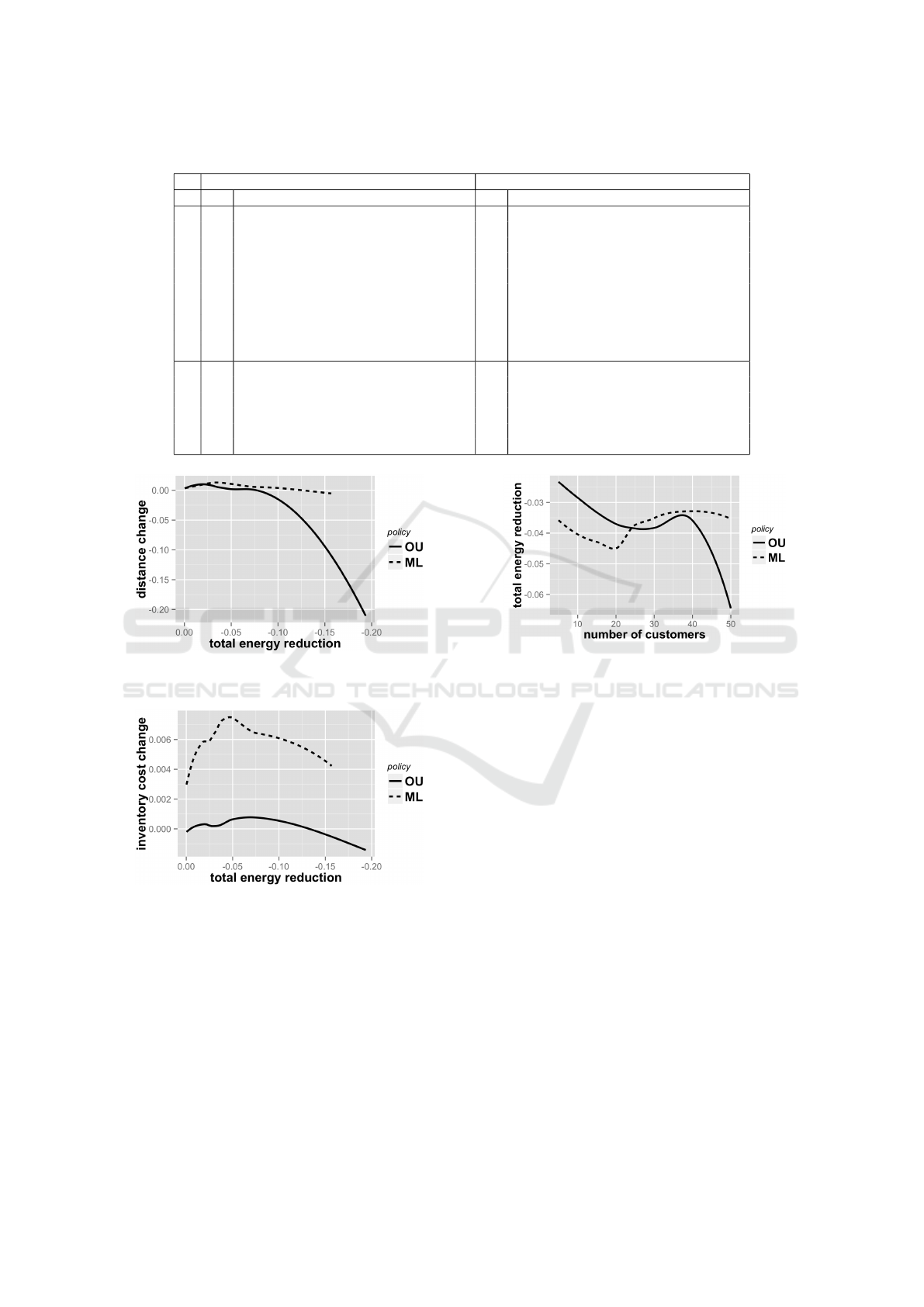
Table 1: Performance summary of all the instances.
OU policy ML Policy
T n time1 time2 status1 status2 n time1 time2 status1 status2
3
5 0.0665 0.108 Optimal Optimal 5 0.142 0.0759 Optimal Optimal
10 1.84 3.44 Optimal Optimal 10 2.37 2.47 Optimal Optimal
15 14.9 83.8 Optimal Optimal 15 10.0 23.6 Optimal Optimal
20 53.6 1235.4 Optimal 0.0228 20 138.8 1075.9 Optimal 0.0645
25 642.7 1799.1 0.0114 0.0594 25 71.33 1800.0 Optimal 0.1053
30 721.9 1800.0 0.0106 0.1028 30 307.1 1800.0 Optimal 0.1175
35 1079.4 1800.0 0.0196 0.132 35 112.6 1800.0 Optimal 0.1362
40 1624.6 1800.0 0.0336 0.1679 40 570.4 1800.0 0.0380 0.1564
45 1729.6 1800.0 0.0572 0.2185 45 1043.3 1800.0 0.0233 0.1873
50 1800.0 1799.6 0.0767 0.2260 50 1645.8 1800.0 0.0175 0.2108
6
5 0.694 1.194 Optimal Optimal 5 4.021 1.243 Optimal Optimal
10 26.94 234.7 Optimal Optimal 10 45.39 324.6 Optimal 0.0201
15 177.2 1769.9 Optimal 0.0342 15 262.1 1789.8 Optimal 0.0465
20 1307.7 1800.0 0.0372 0.1133 20 1545.3 1679.6 0.0180 0.1115
25 1449.7 1800.0 0.0298 0.1349 25 1563.9 1720.7 0.0304 0.1501
30 1800.0 1791.6 0.0453 0.1792 30 1800.0 1800.0 0.0416 0.1748
Figure 6: The relationship between distance and energy re-
duction.
Figure 7: The relationship between inventory and energy
reduction.
It should also be noted that the inventory policy
has an influence on the energy minimization poten-
tial. Figure 6 and 7 show the relationship between
distance (inventory) and energy reduction. The solid
curves represent average values of all the instances.
We can see that under the OU policy, most of the re-
duction is obtained by minimizing the distance trav-
elled. The more energy reduction there is, the less dis-
tance would be travelled. Under the ML policy, most
of the reduction is obtained by changing the inven-
Figure 8: The relationship between energy reduction and
number of customers under different inventory policy.
tory replenishment strategy. This could result from
the fact that the ML policy is more flexible than the
OU policy.
Figure 8 shows the energy reduction in relation
to the number of customers under different policies.
We can see that for small instances, ML policy tends
to produce a lower cost, but with the increase of the
dimension of instances, the model becomes more dif-
ficult to solve with ML policy than with OU policy,
so for the most difficult instances where non-optimal
solution is reached within the time limit, it is still OU
policy that gives a better result. These results imply
that inventory replenishment strategy is important for
energy minimization. Instead of always fill the inven-
tory to the maximum level as suggested by OU policy,
ML policy may give a better energy solution.
We could not observe much relationship between
road types and energy minimization. In fact, the in-
fluence of road types to the energy reduction becomes
noticeable only for instances with large number of
customers. This could result from a lack of realis-
tic data. So more tests should be done with more
realistic datasets. And the solution method should
be improved so that realistic-sized instances could be
A Mass-flow based MILP Formulation for the Inventory Routing with Explicit Energy Consumption
249

solved to optimality to show the energy saving poten-
tial of different road types.
5 CONCLUSIONS
Energy consumption is an important aspect in both
economical and ecological view. It becomes more
and more important with the sustainable requirement
of the inventory systems. However, few researchers
paid attention to the combination of inventory man-
agement, vehicle routing and energy minimization.
This new mass flow-based formulation of the IRP
with energy consumption addresses the problem ex-
plicitly. An energy estimation method is proposed
that combines vehicle dynamics and road character-
istics. This estimation gives us an energy cost func-
tion that is linear to the total mass. In this new IRP
formulation, the mass is added as a decision variable
and the energy cost function is considered as an objec-
tive. The relationship between the vehicle dynamics
in the transportation network, the inventory manage-
ment strategy and the energy consumption estimation
is examined. Our first experimentation shows that a
better energy cost can be achieved by adjusting the
inventory replenishment planning. Among all the in-
fluence factors, the inventory policy is an important
one.
Further works need to be done on the modelling
of traffic networks, so that different road types, espe-
cially road slops, traffic conditions as well as vehi-
cle speed levels could be considered in the decision
process. The estimation of the energy costs needs to
be more representative. More data are needed from
the real world to accomplish the work. The inventory
routing model needs to be improved to better control
the time and quantity of each delivery. Solution al-
gorithms and heuristics are to be explored to speed
up the computation, especially with realistic data that
would contain larger number of customers or longer
decision periods. The extension of the problem to a
multi-objective one is also a promising track of study.
ACKNOWLEDGEMENTS
This work was supported by the ECO-INNOVERA-
1rst call EASY (ANR-12-INOV-0002).
REFERENCES
Abdelmaguid, T. F., Dessouky, M. M., and nez, F. O.
(2009). Heuristic approaches for the inventory-routing
problem with backlogging. Computers and Industrial
Engineering, 56(4):1519–1534.
Andersson, H., Hoff, A., Christiansen, M., Hasle, G., and
Lø kketangen, A. (2010). Industrial aspects and
literature survey: Combined inventory management
and routing. Computers and Operations Research,
37(9):1515–1536.
Andr
´
e, M., Hassel, D., and Weber, F.-j. (1998). Devel-
opment of short driving cycles–Short driving cycles
for the inspection of in-use cars –Representative Eu-
ropean driving cycles for the assessment of the I/M
schemes. Technical Report May, INRETS - LEN,
Laboratoire
´
Energie Nuisances.
Anily, S. and Federgruen, A. (1990). One Warehouse Mul-
tiple Retailer Systems with Vehicle Routing Costs.
Management Science, 36(1):92–114.
Archetti, C., Bertazzi, L., Laporte, G., and Grazia Sper-
anza, M. (2007). A Branch-and-Cut Algorithm for a
Vendor-Managed Inventory-Routing Problem. Trans-
portation Science, 41(3):382–391.
Archetti, C., Bianchessi, N., Irnich, S., and Grazia Sper-
anza, M. (2014). Formulations for an inventory rout-
ing problem. International Transactions in Opera-
tional Research, 21:353–374.
Bektas¸, T. and Laporte, G. (2011). The pollution-routing
problem. 45:1232–1250.
Bell, W. J., Dalberton, L. M., Fisher, M. L., Greenfield,
A. J., Jaikumar, R., Kedia, P., Mack, R. G., and Prutz-
man, P. J. (1983). Improving the Distribution of Indus-
trial Gases with and On-Line Computerized Routing
and Scheduling Optimizer. Interfaces, 13(6):4–23.
Burns, L. D., Hall, R. W., Blumenfeld, D. E., and Daganzo,
C. F. (1985). Distribution Strategies that Minimize
Transportation and Inventory Costs.
Coelho, L. C., Cordeau, J.-F., and Laporte, G. (2013).
Thirty Years of Inventory Routing. Transportation
Science, 48(1):1–19.
Demir, E., Bektas¸, T., and Laporte, G. (2014). A review of
recent research on green road freight transportation.
European Journal of Operational Research, 237:775–
793.
Dror, M. and Ball, M. (1987). Inventory/routing: Reduc-
tion from an annual to a short-period problem. Naval
Research Logistics (NRL), 34:891–905.
EcoTransIT World Initiative (EWI) (2014). Ecological
Transport Information Tool for Worldwide Transports
Methodology and Data—Update .
Fish, L. A. (2015). Applications of Contemporary Manage-
ment Approaches in Supply Chains.
Kara, I., Kara, B. Y., and Yetis, M. K. (2007). Energy Min-
imizing Vehicle Routing Problem. Verlag Berlin Hei-
delberg, 1:62–71.
Lin, C., Choy, K. L., Ho, G. T. S., Chung, S. H., and Lam,
H. Y. (2014). Survey of Green Vehicle Routing Prob-
lem: Past and future trends. Expert Systems with Ap-
plications, 41:1118–1138.
Sahin, B., Yilmaz, H., Ust, Y., Guneri, A. F., and Gulsun,
B. (2009). An approach for analysing transportation
costs and a case study. European Journal of Opera-
tional Research, 193(1):1–11.
ICORES 2016 - 5th International Conference on Operations Research and Enterprise Systems
250

Samaras, Z. and Ntziachristos, L. (1998). Average hot emis-
sion factors for passenger cars and light duty trucks.
Technical Report LAT report No. 9811, Lab. of Ap-
plied Thermodynamics, Aristotle University of Thes-
saloniki.
Savelsbergh, M. and Song, J. H. (2007). Inventory routing
with continuous moves. Computers and Operations
Research, 34:1744–1763.
Treitl, S., Nolz, P. C., and Jammernegg, W. (2014). Incor-
porating environmental aspects in an inventory rout-
ing problem. A case study from the petrochemical in-
dustry. Flexible Services and Manufacturing Journal,
26:143–169.
Walkowicz, K., Duran, A., and Burton, E. (2014). Fleet dna
project data summary report. Technical report, NREL.
Xiao, Y., Zhao, Q., Kaku, I., and Xu, Y. (2012). Devel-
opment of a fuel consumption optimization model for
the capacitated vehicle routing problem. Computers
and Operations Research, 39(7):1419–1431.
APPENDIX
Energy Estimation
According to knowledge of physics and energy con-
servation, under the hypothesis of speed variation pre-
sented in Section 2.3, we have:
• In each acceleration phase, the speed of the ve-
hicle increases from 0 to the target speed V with
constant acceleration a
acc
. With F
acc
the traction
force of the engine, s
acc
the distance travelled,
E
acc
the energy consumed, and P
acc
(t) the engine
power:
v(t) = a
acc
t
s
acc
(t) =
1
2
a
acc
t
2
F
acc
− mgµ = ma
acc
P
acc
(t) = F
acc
v(t) = m(a
2
acc
+ gµ)a
acc
)t
E
acc
− mgµs
acc
=
1
2
mV
2
At the end of this phase, the engine power is
P
acc
= m(a
acc
+ gµ)V
the distance travelled is
s
acc
=
V
2
2a
acc
The total energy cost per unit of mass is
c
acc
= gµs
acc
+
1
2
V
2
• In the uniform-speed phase, the distance s
u
is
computed as the difference between the total dis-
tance s and the total distance travelled in acceler-
ation and deceleration. Since the deceleration is
considered to be instantaneous (s
dec
= 0), the total
distance travelled at uniform speed is calculated
as:
s
u
= s − τ s (s
acc
+ s
dec
) = s − τ s s
acc
with τ · s the total number of stops. The engine
power is also constant
P
u
(t) = F
u
V = mgµV
The total energy cost per unit of mass in the uni-
form phase is:
c
u
= gµ(s − τ s s
acc
).
• In each deceleration phase, since we consider an
instantaneous stop,
s
dec
= 0
P
dec
(t) = 0
E
dec
=
1
2
mV
2
and the energy cost per unit of mass is
c
dec
=
1
2
V
2
the total energy cost per unit of mass when distance s
is travelled with stop rate τ is then:
c = c
u
+ τ · s (c
acc
+ c
dec
).
Finally, we get:
c = gµs + τsV
2
Calculation of Parameters for Different
Road Types
On a highway, the maximum speed is fixed at
110km/h, and the number of stops is fixed at 2 stops
per edge independent of the road distance travelled.
On a national route, the vehicle speed is fixed at
80km/h and the number of stops is linearly depen-
dent on the distance with a random error. On an ur-
ban road, both the stop rate and the vehicle speed are
dependent on the distance travelled. The stop rate τ
is determined by a linear function of the distance as
in the case of national route. And the target speed V
is derived from the stop rate τ by an equation of the
form V = β + α
1
· τ + α
2
/τ.
A Mass-flow based MILP Formulation for the Inventory Routing with Explicit Energy Consumption
251
