Using Differential Evolution to Improve Pheromone-based

Coordination of Swarms of Drones for Collaborative Target

Detection

Mario G. C. A. Cimino, Alessandro Lazzeri and Gigliola Vaglini

Department of Information Engineering, Università di Pisa, Largo Lazzarino 1, Pisa, Italy

Keywords: Differential Evolution, Parametric Adaptation, Collaborative Target Detection, Marker-based Stigmergy,

Swarm Intelligence.

Abstract: In this paper we propose a novel algorithm for adaptive coordination of drones, which performs

collaborative target detection in unstructured environments. Coordination is based on digital pheromones

released by drones when detecting targets, and maintained in a virtual environment. Adaptation is based on

the Differential Evolution (DE) and involves the parametric behaviour of both drones and environment.

More precisely, attractive/repulsive pheromones allow indirect communication between drones in a flock,

concerning the availability/unavailability of recently found targets. The algorithm is effective if structural

parameters are properly tuned. For this purpose DE combines different parametric solutions to increase the

swarm performance. We focus first on the study of the principal parameters of the DE, i.e., the crossover

rate and the differential weight. Then, we compare the performance of our algorithm with three different

strategies on six simulated scenarios. Experimental results show the effectiveness of the approach.

1 INTRODUCTION AND

MOTIVATION

The Differential Evolution algorithm (DE) is a

stochastic population based algorithm, very suited

for numerical and multi-modal optimization

problems. Recently, DE has been applied in many

research and application areas. Compared with other

population-based algorithms, such as genetic

algorithm and particle swarm optimization, DE

exhibits excellent performance both in unimodal,

multimodal, separable, and non-separable problems.

Moreover, it is much simpler to use because it has

only three parameters (Das, 2011): the population N,

the differential weight F, and the crossover rate CR.

When managing the DE algorithm, the main effort is

to properly set the parameters in order to avoid

premature convergence towards a non-optimal

solution. As reported by literature, there is no

dominant setting, and for each problem a proper

study of the behaviour of DE is needed to find the

correct parameterization.

In this paper, we adopt DE algorithm to optimize

the behaviour of a swarm of aerial drones carrying

out collaborative target detection (Cimino, 2015b).

In our approach, stigmergy and flocking are

exploited to enable self-coordination in the

navigation of unstructured environments. Such

environments typically contain a number of

obstacles such as trees and buildings. Targets are

placed according to different patterns. More

specifically, stigmergy implies the use of an

attractive digital pheromone to locally coordinate

drones. When a drone detects a new piece of target,

it releases the attractive pheromone. Other drones in

the neighbourhood can sense and follow the

pheromone gradient to cooperate in detecting the

pattern of targets. With respect to (Cimino, 2015b)

in this study we sensibly improve the performance

of the algorithm, by adopting the parametric DE-

based adaptation, by introducing repulsive

pheromone and scattering mechanisms. Basically,

flocking implies a set of three behavioural rules,

named separate, align, and scatter. It maintains the

drones in groups enhancing the stigmergy when

occurring. In contrast, the repulsive pheromone

helps the drones to avoid multiple exploration of the

same zone. Indeed, the drone releases a repulsive

pheromone whereas it does not sense a target.

Finally, the scattering rule makes a drone to turn

Cimino, M., Lazzeri, A. and Vaglini, G.

Using Differential Evolution to Improve Pheromone-based Coordination of Swarms of Drones for Collaborative Target Detection.

DOI: 10.5220/0005732606050610

In Proceedings of the 5th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2016), pages 605-610

ISBN: 978-989-758-173-1

605

by an angle when it tails another drone.

In the literature there are two design methods to

develop collective behaviours in swarm systems:

behaviour-based design and automatic design

(Brambilla, 2013). The former implies the

developers to implement, study, and improve the

behaviour of each single individual until the desired

collective behaviour is achieved. This is the

approach adopted in (Cimino, 2015b). The latter is

usually used to reduce the effort of the developers.

Automatic design methods can be furtherly divided

in two categories: reinforcement learning and

evolutionary robotics (Brambilla, 2013). The first

implies a definition at the individual level of positive

and repulsive reinforce to give reward to the

individual. In general, it is usually hard for the

developer to decompose the collective output of the

swarm in individual rewards. Evolutionary robotics

implies evolutionary techniques inspired by the

Darwinian principle of selection and evolution.

Generally in these methods each swarm consists of

individuals with the same behaviour. A population

of swarms is then computed, where each population

member has a particular behaviour. A simulation is

made for each member and a fitness function is

computed. Then through a mutation and crossover

procedure a new generation is computed. This

process iteratively repeats improving the

performance of the swarm population.

2 RELATED WORK

DE has been used in several domains for

optimization and parameterization tasks (Das, 2011).

As an example, in (Nikolos, 2005) the authors used a

classical DE variant, namely DE/1/rand/bin, to

coordinate multiple drones navigating from a known

initial position to a predetermined target location.

Here, DE is set up with N=50, F=1.05 and CR=0.85.

The algorithm was defined to terminate in 200

generations, but it usually converges in 30 iterations.

Our problem sensibly differs, because the target

position is unknown, and our approach is

independent of the initial position.

In (Chakraborty, 2008) the authors confront DE

and Particle Swarm Optimization (PSO) for co-

operative distributed multi-robot path planning

problem. As for (Nikolos and Brintaki, 2005) initial

position of the robots and final position are known.

Here, both centralized and decentralized

formulations are proposed. In the centralized

approach, DE minimizes the distance for the next

step of each robot. In this case all information of the

position of each robot, the next position, and the

possible collision are provided to DE. In the

decentralized formulation, each robot runs DE for

itself considering the information of neighbour

robots. Authors conclude that the decentralized

approach needs less time in comparison to the

centralized one; moreover the performance is

comparable to PSO. In our approach, we consider to

use DE offline to find a proper and general purpose

parameter tuning for the swarms. Moreover, in our

formulation drones have a limited computing

capability, and then an online execution of DE is not

feasible.

In (Cruz-Alvarez, 2013) DE/1/rand/bin is used

with F=0.7, CR=1.0, N=120 for 250 generations, and

another variant called DE/1/best/bin is used with

F=0.8, CR=1.0, N=150 for 200 generations to tune

the behaviour of a robot in wall-following task. Here

it seems that DE/1/best/bin is able to find a slightly

better solution than DE/1/rand/bin. However,

authors used different parameters settings (F, N and

number of generations) for each variant, thus a

comparative analysis is difficult. In our approach we

focus on DE/1/rand/bin variant and evaluate several

combinations of CR and F.

3 SWARM BEHAVIORAL MODEL

In this section we improve the swarm algorithm of

(Cimino, 2015b). We refer to the time unit as a tick,

i.e., an update cycle of both the environment and the

drones. Each drone is equipped with: (a) wireless

communication device for sending and receiving

information from a ground station; (b) self-location

capability, e.g. based on global position system

(GPS); (c) a sensor to detect a target in proximity of

the drone; (d) processor with limited computing

capability; (e) a sensor to detect obstacles.

The environment and the pheromone dynamics

We consider a predefined area that contains a set

of targets to be identified. The environment is

modelled by a digital grid corresponding to the

physical area. The grid has C

cells, each identified

by (x, y) coordinates with x, y ∈ {1,…,C}. The

actual size of the area and the granulation of the grid

depend on the domain application. Figure 1 shows

Pheromone dynamics in an urban scenario. Here, the

intensity of the pheromone is represented as a dark

colour, and each target is represented by an “X”. A

darker gradation means higher pheromone intensity.

At the beginning, the pheromone is in one cell at its

maximum intensity, and then it diffuses to

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

606

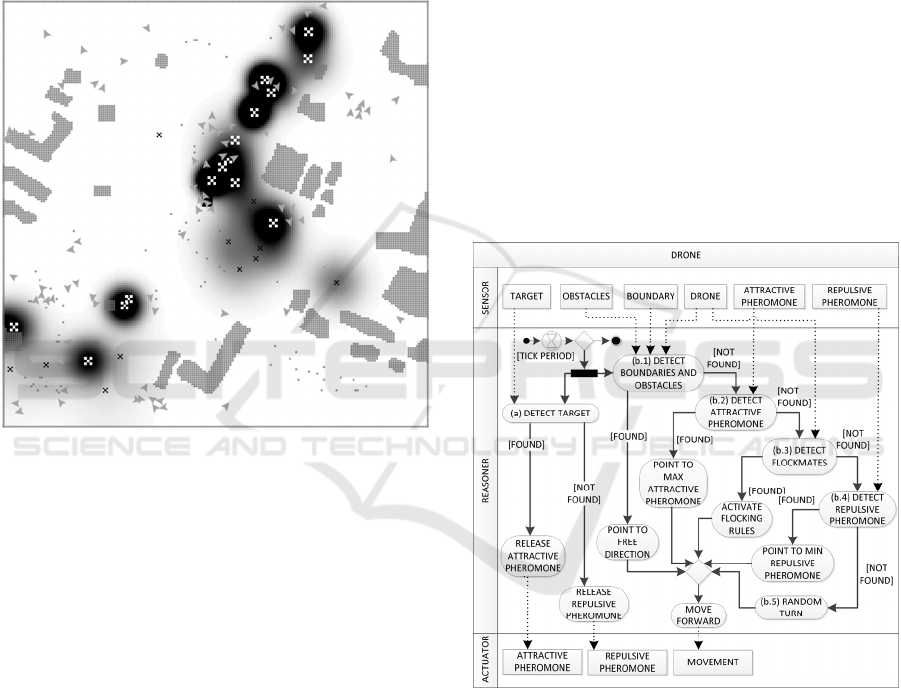
neighbouring cells. After a certain time the

pheromone evaporates, disappearing from the

environment. When a drone detects a piece of the

overall target, a pheromone of intensity I is released

in the cell corresponding to the drone location. Then,

at each tick the pheromone diffuses to the

neighbouring cells according to a diffusion rate

[0,1]

∈

. At the same time the pheromone

evaporates decreasing its intensity, by an

evaporation rate

[0,1]

∈

Figure 1: Pheromone dynamics in an urban scenario.

The drone behaviour

The drone behaviour is structured into five-layer

logic, where each layer has an increasing level of

priority. Starting from the lowest: the random fly

behaviour entails the exploration in absence of

stimuli/information; the repulsive pheromone-based

coordination reduces the redundancy of exploration;

the flocking behaviour assembles the flock enabling

local pheromone interactions; the positive

pheromone-based coordination exploits the digital

pheromone and directs the swarm toward potential

new targets; finally the highest priority level, the

objects/boundary avoidance, which prevents the

drone from exiting the area or colliding with

obstacles and other drones.

Fig. 2 shows a UML activity diagram of the

drone behaviour. Here, a rectangular box represents

sensors (left) and actuators (right), a rounded-corner

box represents an activity (a procedure), solid and

dashed arrows represent control and data flows,

respectively.

Every tick period, represented by the hourglass,

the drone performs two parallel processes: (a) the

target detection, which corresponds to the release of

the attractive pheromone on the digital grid or rather

of the repulsive pheromone; (b) the movement

procedure, which starts with the obstacle and

boundary detection. If a close obstacle (i.e., object or

drone) is detected (b.1), the drone points toward a

free direction. If a free direction is found, it moves

forward, otherwise it stays still. If there are no close

objects detected (b.2), the drone tries to sense

positive pheromone in its neighbouring cells and, if

detected, the drone points toward the maximum

intensity of it. Differently, if no pheromone is

detected (b.3), the drone tries to detect surrounding

drones in order to stay with the flock. Then, the

drone checks if a repulsive pheromone is in nearby

cells (b.4). If there is, the drone moves toward the

minimum intensity of it. Finally, if there are no

surrounding drones (b.5), it performs a random turn

and move forward.

Figure 2: Overall representation of the drone behaviour.

At the highest priority (b.1), the drone has to

avoid collision and to exit the search area. For this

purpose the drone is able to detect objects (i.e., other

drones or obstacle) at the object sensing distance (

)

on its trajectory. If a potential collision is detected

the drone chooses the minimum rotation angle to the

left or right to avoid the obstacle. If it finds a free

trajectory it moves forward, if there is no free

direction within 180 degree it stays still one tick.

The boundaries of the area are considered as a

“wall” of obstacles.

Using Differential Evolution to Improve Pheromone-based Coordination of Swarms of Drones for Collaborative Target Detection

607

The second priority is to follow the positive

pheromone gradient (b.2), provided by the ground

station. Given the drone position (i.e., the cell on the

grid), the cell with the maximum intensity of

positive pheromone and the minimum intensity of

the repulsive pheromone (b.4) in its 8 neighbouring

cells is returned to the drone. Then, the drone

follows the maximum pheromone intensity.

The flocking behaviour (b.3) consists in three

rules, represented by Fig.3. A drone considers as

flock mates all drones in a flock visibility radius (

The first rule is the separation: more specifically, if

the drone senses another drone closer than the flock

mobility distance (

), it turns away by a flock

separation angle (

). The second rule is the

alignment: the drone computes the average direction

of its flock mates and it adapts its direction by a

flock alignment angle (

). The third rule is the

scatter: the follower drone considers the closer

following drone in front of itself. If the follower is in

the tail sector of the following defined by angle flock

tail angle (

) the follower turns away the following

by a flock scatter angle (τ). These three rules

determine the structure of the swarm, permitting the

drones to navigate in coordinated group, exploring

the environment and, most important, sensing

pheromone released by flock mates.

The fourth priority (b.4) is to move against the

repulsive pheromone gradient. The drone received

the information of the lowest cell from the ground

station (b.2). Finally, if nothing is detected (b.5) then

the drone is in its basic behaviour (random fly). It

randomly turns by an angle smaller than the

maximum rand-fly turn angle (

(a) separation

(b) alignment (c) scattering

Figure 3: Flock visibility radius and other parameters in

flocking behaviour.

4 ADAPTATION WITH

DIFFERENTIAL EVOLUTION

The swarm algorithm presented in Section 3

involves a number of structural parameters to be

appropriately set for each given application scenario.

Determining such correct parameters is not a simple

task since different areas have different topology and

different targets distribution. In DE algorithm, a

population member is a real n-dimensional vector,

where n is the number of parameters to tune. DE

starts with a population of N members, injected or

randomly generated. In the literature, the population

size spreads from a minimum of 2n to a maximum

of 40n (Mallipeddi, 2011). A large population

increases the chance of finding an optimal solution

but it is very time consuming. To balance speed and

reliability we use N=20. At each iteration, and for

each population member (target), a mutant vector is

created by mutation of selected members and then a

trial vector is created by crossover of mutant and

target. Finally, the best fitting among trial and target

replaces the target.

In addition to DE, other classes of optimization

methods, such as Particle Swarm Optimization

(PSO) attracted attention in the last decade. The

interested reader is referred to (Cimino, 2015a) for

further details. Several DE strategies have been

designed, by combining different structure and

parameterization of mutation and crossover

operators (Mezura, 2006 and Zaharie, 2007). As

noted by (Das, 2011), practitioners mostly prefer to

use a classical DE variant like DE/1/rand/bin. The

differential weight F ϵ [0,2] mediates the generation

of the mutant vector. F is usually set in [0.4-1), and

a frequently used starting value is 0.8 (Mezura,

2006). There are different crossover methods in DE.

A competitive approach is the binomial crossover

(Zaharie, 2007). With binomial crossover, a

component of a vector is taken with probability CR

from the mutant vector and with probability 1-CR

from the target vector. A good value for CR is

between 0.3 and 0.9, and a frequently used starting

value is 0.7 (Mallipeddi, 2011).

The fitness measure to evaluate the effectiveness

of a solution is the average time (in ticks), over 5

runs, which the swarm of drones take to find 95% of

the targets of the scenario.

5 EXPERIMENTAL RESULTS

We implemented our algorithm using NetLogo, a

leading simulation platform for swarm intelligence

(ccl.northwestern.edu/netlogo), and MATLAB for the

adaptation algorithm (www.mathworks.com). We

evaluated our algorithm by comparing four different

strategies: the adaptive stigmergic and flocking

behaviour (S+F*) presented in Section 3; the

stigmergic and flocking behaviour (S+F) presented

in (Cimino, 2015b); the stigmergic behaviour (S), in

which the pheromone grid maintains only the

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

608

positive pheromone intensity information and the

drones do not perform flocking behaviour; finally,

the random fly behaviour (R), in which drones

randomly explore the area with no pheromone nor

flocking behaviour. We tested the swarm algorithm

on six different scenarios. For each scenario, each of

the three strategies has been specifically optimized

by the adaptation module. To compare the

approaches, 10 trials have been carried out for each

considered approach. We also determined that the

resulting performance indicator samples are well-

modelled by a normal distribution, using a graphical

normality test. Hence, we calculated the 95%

confidence intervals.

The total number of drones is 80; each drone is

represented as a black triangle, arranged in 4 swarms

placed in the corners of the map, except for Illegal

Dumps in which 3 swarms are placed in 3 corners

due to the topology. Characteristics of the topology

of targets and obstacles are summarised in Table 2.

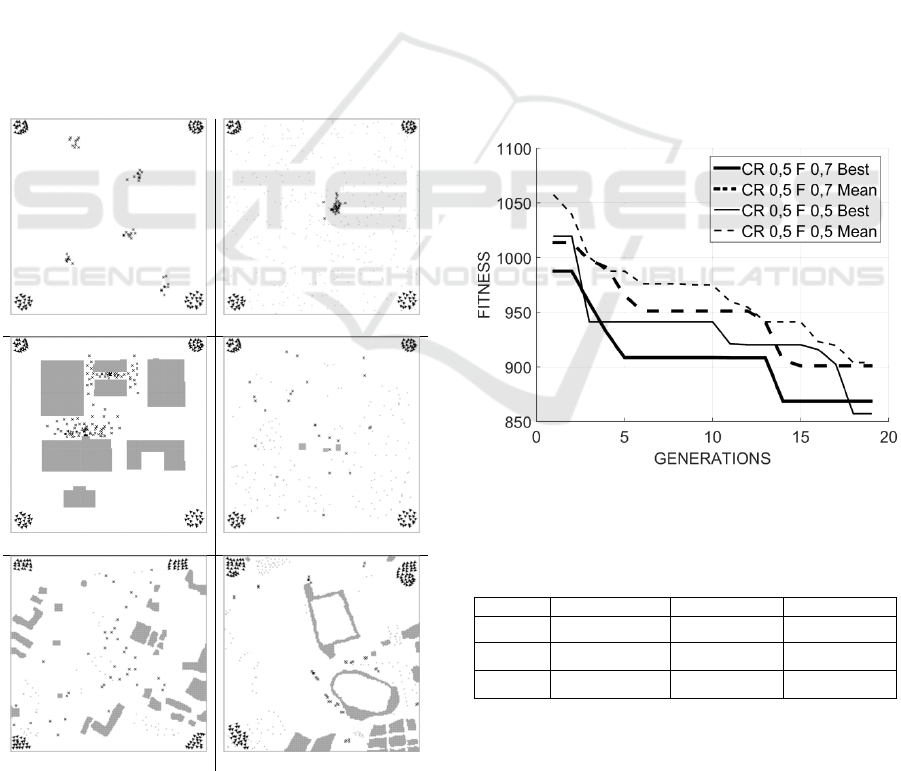
Figure 4 represents the initial configuration for

all scenarios. The three scenarios Field, Forest, and

Urban represent respectively an area of 40,000 m

(a) Field

(b) Forest

(e) Urban minefield (f) Illegal dumps

Figure 4: Maps of 3 synthetic and 3 real-world scenarios.

Figure 4 (a) does not contain obstacles at all, but

contains 5 clusters of 10 targets each. Figure 4 (b)

represents a timber with 1 cluster of 20 targets with

tree obstacles. Figure 4 (c) shows an industrial area

with 2 clusters of 55 targets, each representing a

pollutant lost. The two scenarios Rural minefield and

Urban minefield, represented in Figure 4 (d) and

Figure 4 (e), respectively, are two mined areas of

80,000 m

derived from real-world maps near

Sarajevo, in Bosnia-Herzegovina (www.see-

demining.org). The last scenario, Illegal Dump, is a

real-world example of illegal dumping taken from an

area of 80,000 m

near the town of Paternò, Italy

(www.trashout.me).

Figure 5 shows the evolutions of DE algorithm

against generations, with two different values of CR

and F. Here, the best and the mean solution (solid

and dashed line, respectively) have been calculated

over 5 runs. The optimization is characterized by a

very good improvement of the initial solution and by

a fast convergence: only 20 generations are needed

to reduce the average time by 20%. More precisely,

Table 1 shows that the final best performance is

achieved with CR=0.5 and F=0.7.

Figure 5: Evolution of the DE algorithm against

generations for different DE parameters.

Table 1: Final results of the evolution of Figure 5 in

numerical terms.

F\CR 0.3 0.5 0.7

0.5

933,67±14,16 903,85±29,77 950,80±16,36

0.7

966,60±15,53

900,65±19,06

907,15±12,96

0.9

951,40±15,67 930,60±22,36 933,73±54,14

Table 2 characterizes each scenario with the

results, in the form “mean ± confidence interval”. It

is worth noting that the proposed adaptive algorithm

“S+F*” outperforms the algorithms presented in

(Cimino, 2015b) in all scenarios. More specifically,

Using Differential Evolution to Improve Pheromone-based Coordination of Swarms of Drones for Collaborative Target Detection

609

in Field and Forest scenarios, the two algorithms

“S+F” and “S+F*” are comparable. This is due to

the simple layout of both scenarios, which does not

allow a good exploitation of the “S+F*” features.

Indeed, in the other scenarios, with a more complex

topology, the advantages of the “S+F*” strategy are

substantial.

Table 2: Features and numerical results of each scenario.

Scenario

N° of targets /

clusters

Type / n° of

obstacles

Completion time

(ticks)

Field 50 / 5

Trees: 0

Buildings: 0

R 1664±220

S 656±101

S+F 589±86

S+F*

582±121

Forest 20 / 1

Trees: 400

Buildings: 0

R 1862±356

S 615±67

S+F 602±124

S+F*

593±146

Urban 110 / 2

Trees: 0

Buildings: 7

R 2049±148

S 998±61

S+F 890±93

S+F*

666±100

Rural

Mines

28 / 28

Trees: 281

Buildings: 3

R 1588±216

S 1570±158

S+F

1530±225

S+F* 1123±116

Urban

Mines

40 / 40

Trees: 54

Buildings: 28

R 1844±140

S 1733±169

S+F

1704±225

S+F* 1025±76

Illegal

Dumps

42 / 11

Trees: 140

Buildings:19

R 1548±207

S 971±160

S+F 934±216

S+F*

757±112

6 CONCLUSIONS

In this paper, we have presented an algorithm to

adapt, via the DE algorithm, the coordination of a

swarm of drones performing target detection on the

basis of stigmergy and flocking. We first evaluated

several combinations of the structural parameters of

the DE. Results show that a crossover rate (CR) of

0.5 and a differential weight (F) of 0.7 produce

better solutions. Then, to test the effectiveness and

the reliability of the approach, we compared our

algorithm with three search strategies over real-

world and synthetic scenarios. As a result, our

approach resulted dominant in all scenarios. Future

work will (i) investigate our approach on additional

scenarios, (ii) use other optimization methods for the

adaptation, and (iii) include non-functional

requirements in the algorithm, such as computing

power and endurance of drones.

ACKNOWLEDGEMENTS

This work is partially supported by the Tuscany

Region, Italy, via the SCIADRO research project.

REFERENCES

Brambilla, M. Ferrante, E. Birattari & M. Dorigo, M.,

2013, ‘Swarm robotics: a review from the swarm

engineering perspective,’ Swarm Intelligence, vol. 7,

pp. 1-41.

Chakraborty, J., Konar, A., Chakraborty, U. K. & Jain, L.

C., 2008, ‘Distributed cooperative multi-robot path

planning using differential evolution’, in IEEE

Evolutionary Computation, World Congress on

Computational Intelligence, pp. 718-725.

Cimino, M.G.C.A., Lazzeri, A. & Vaglini, G., 2015a,

‘Improving the analysis of context-aware information

via marker-based stigmergy and differential

evolution’, Proceeding of the international

Conference on Artificial Intelligence and Soft

Computing (ICAISC 2015), in Springer LNAI,

Vol. 9120, Part II, pp. 1-12, 2015.

Cimino, M.G.C.A., Lazzeri, A. & Vaglini, G., 2015b,

‘Combining stigmergic and flocking behaviors to

coordinate swarms of drones performing target

search’, Proceedings of the 6

International

Conference on Information, Intelligence, Systems and

Application (IISA 2015), Springer, in press.

Cruz-Álvarez, V. R., Montes-Gonzalez, F., Mezura-

Montes, E. & Santos, J., 2013, ‘Robotic behavior

implementation using two different differential

evolution variants’, in Advances in Artificial

Intelligence, Springer Berlin Heidelberg, pp. 216-226.

Mallipeddi, R., Suganthan, P.N., Pan, Q.K. & Tasgetiren,

M.F., 2011, ‘Differential evolution algorithm with

ensemble of parameters and mutation strategies’, in

Applied Soft Computing, vol. 11, no. 2, pp.1679-1696.

Mezura-Montes, E., Velázquez-Reyes, J. & Coello, C.A.,

2006, ‘A comparative study of differential evolution

variants for global optimization,’ Proceedings of the

8th Annual Conference on Genetic and evolutionary

computation, ACM, pp.485-482.

Nikolos, I. K. & Brintaki, A. N., 2005, ‘Coordinated UAV

path planning using differential evolution’, in

Intelligent Control, in IEEE Proceedings of the 2005

International Symposium on Control and Automation,

pp. 549-556.

Das, S. and Suganthan, P. N., 2011, ‘Differential

evolution: a survey of the state-of-the-art’, in IEEE

Transactions on Evolutionary Computation, Vol. 15.1,

pp. 4-31.

Zaharie, D., 2007, ‘A comparative analysis of crossover

variants in differential evolution’, in Proceedings of

IMCSIT, 2nd International Symposium Advances in

Artificial Intelligence and Applications, pp. 171-181.

ICPRAM 2016 - International Conference on Pattern Recognition Applications and Methods

610