
Skyline Computation on Commercial Data
Michael Galli, Stefan Schn
¨
urle, Ruedi Arnold and Marc Pouly
Lucerne University of Applied Sciences and Arts, Horw, Switzerland
Keywords:
Preference-Based Optimization, Skyline Computation, Industrial Application.
Abstract:
Many different skyline algorithms for preference-based search have been proposed and compared in the lit-
erature, but most of these evaluations were based on synthetic data. In this paper, we present a case study of
skyline computation on commercial data that we consider representative for many e-commerce platforms. The
results of our measurements differ significantly from the results reported on synthetic data.
1 INTRODUCTION
In recent years, the importance of generating person-
alized customer experiences has grown significantly
for providers of e-commerce platforms. Using recom-
mender system technologies, individualized product
recommendations are being computed based on prod-
uct similarity, explicit user ratings and implicit pref-
erence data derived from shopping history, customer
profile information and demographic data. Because
recommender systems heavily rely on such long-term
data, they are known to cope badly with fast changing
customer preferences. Also, a considerable amount of
ratings must often be collected for new items before
they can be recommended for the first time, which
also penalizes products that are purchased less fre-
quently (Aldrich, 2011; Martin et al., 2011). These
are only some of the reasons why e-commerce plat-
form providers started to complement recommender
systems with other technologies that use more ex-
plicit user preferences instead of long-term data only.
For example, a classical filter-based catalog search
engine may be extended with preference information
that customers explicitly communicate to the system
in order to find products that do not only match all
filter constraints but additionally are optimal with re-
spect to current customer preferences. Likewise, cus-
tomers may design and personalize their own monthly
newsletters by enriching the usual account informa-
tion with individual preferences.
Both examples involve so-called skyline queries
(B
¨
orzs
¨
onyi et al., 2001) that generate the set of all
catalog items not dominated by any other item in the
set with respect to customer preferences. Following
the well-established notion of Pareto dominance, we
say that an item X dominates another item Y , if X is
better in at least one attribute and at least as good as
Y in all other attributes.
Various skyline algorithms have been proposed in
the literature. Since they usually require to process
all items at least once and, in the worst case, may be
forced to compare each item with every other, skyline
algorithms adopt a complexity somewhere between
linear and quadratic time in the number of items.
Pre-computation and caching strategies like in rec-
ommender systems are generally not possible due to
the many possible combinations of user preferences.
Thus, if intended for an online application like cat-
alog search, skyline computation may only be ap-
plicable for small to midsize product catalogs. For
offline applications like the newsletter system men-
tioned above, response time may be less critical. In
July 2013, the Amazon.com catalog reached 200M
items with an average growth of 175000 items per day
(Cole, 2013). These impressive figures are clearly ex-
ceptional. In contrast, a target market analysis from
our industry partner in Switzerland reported an av-
erage catalog size of less than 10K items including
a surprisingly large number of small shops with less
than 100 items (e.g. sports fan shops) and only a few
larger resellers with more than 100K items. Moreover,
preference-based optimization is often preceded by
filter operations in practice such that skyline queries
are rarely executed on the entire product database.
Our case study is based on a product catalog of
a Swiss car reselling platform with a total of 55208
items. We consider this catalog representative for the
broad e-commerce market not only in Switzerland.
It is also well-suited for applications like the search
or newsletter engine mentioned above because many
people find it easy to state preferences about cars. We
Galli, M., Schnürle, S., Arnold, R. and Pouly, M.
Skyline Computation on Commercial Data.
DOI: 10.5220/0005766604650471
In Proceedings of the 8th International Conference on Agents and Artificial Intelligence (ICAART 2016) - Volume 2, pages 465-471
ISBN: 978-989-758-172-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
465

will point out below that this data features the typical
statistical properties of an e-commerce catalog.
2 SKYLINE ALGORITHMS
The most relevant skyline algorithms proposed in the
literature classify as follows:
Block nested loop (BNL) algorithms keep a win-
dow of non-dominated items in main memory and
compare each new item X with the current window.
If X dominates one item in the window or vice versa,
eliminate the dominated item. Otherwise, add X to the
window and proceed with the next item (B
¨
orzs
¨
onyi
et al., 2001). Different window management strate-
gies were studied to stress early elimination of domi-
nated items (Chomicki et al., 2005). For data sets with
n items, time complexity of BNL algorithms varies
between O(n) in the best and O(n
2
) in the worst case.
Divide-and-Conquer (D&C) style algorithms re-
cursively partition the data set until each partition
contains only a few items, compute the skyline of
each partition individually and merge the results to
larger skylines (B
¨
orzs
¨
onyi et al., 2001). For data sets
with n items and d preferences, time complexity of
D&C algorithms is O(n · (log n)
d−2
) + O(n · log n) in
the best and worst case.
Lattice-based skyline algorithms such as BNL++
and the more recent Hexagon algorithm build a dedi-
cated lattice structure called better-than-graph (BTG)
and assign all items to the nodes of this graph in
such a way that items assigned to nodes on higher
levels in the graph dominate items assigned to lower
level nodes (Preisinger and Kissling, 2007; Preisinger
et al., 2006). The skyline is obtained by traversing
and pruning this graph. Hexagon shows linear time
complexity even in the worst case provided that the
number of BTG nodes is of the same order of mag-
nitude as the number of data items. This assumption
is necessary because BTGs grow exponentially with
the cardinality of the involved preferences. Hexagon
is therefore only applicable to categorical preferences
of rather small cardinality. For this reason, a new
algorithm called Scalagon was proposed that uses
Hexagon as a pre-filter on coarse preferences. In a
second step, Scalagon applies a BNL style algorithm
with the actual user preferences to the reduced data
set in order to produce the final skyline. In this way,
Scalagon promises to combined the advantages of
both worlds (Endres et al., 2015).
Other algorithms exist that gear into the query op-
timizer of the database system (Godfrey et al., 2005),
or that exploit database index structures and can there-
fore not be used in combination with joins and other
complex operations (Papadias et al., 2003; B
¨
orzs
¨
onyi
et al., 2001; Han et al., 2013). We omit these algo-
rithms in our case study as their constraints are too
limiting for generic application, and such deep access
to the database system is rarely tolerated in an indus-
trial environment. Finally, there are also heuristic ap-
proaches to skyline computation such as skyline sam-
pling (Balke et al., 2005) and other methods for ob-
taining only a representative subset of the entire sky-
line (Lofi and Balke, 2013).
Experiments on synthetic data show that BNL al-
gorithms perform well on data sets and preferences
inducing small skylines. In contrast to D&C, how-
ever, they are very sensitive to the number of prefer-
ences and correlations in the data set (B
¨
orzs
¨
onyi et al.,
2001). Due to the exponential growth in the underly-
ing lattice structure, Hexagon can only be used with
categorical preferences of low cardinality. However,
provided that this condition is met, the authors claim
superior runtime over BNL and D&C for any data
distribution and therefore call Hexagon an algorithm
for all practical seasons (Preisinger and Kissling,
2007). Again, this conclusion was derived from syn-
thetic data. Scalagon was designed to weaken the low-
cardinality constraints imposed on lattice-based sky-
line algorithms. (Endres et al., 2015) limit evaluation
to weakly anti-correlated data sets having small sky-
lines (less than 1% of the data set) and show predom-
inance of Scalagon over BNL on synthetic and real
data. Their paper is titled Scalagon: an efficient sky-
line algorithm for all seasons.
3 SKYLINES ON REAL DATA
In almost all cases, the conclusions with respect to the
mutual comparison of skyline algorithms were drawn
from experiments on synthetic data. More precisely,
synthetic data with sets of correlated, anti-correlated
and independent attributes were produced, since data
distribution is known to have a strong impact on sky-
line algorithms. Correlated data usually leads to small
skylines, whereas anti-correlated data usually induces
large skylines (Chaudhuri et al., 2006). Exemplary,
we refer to (Balke et al., 2005) where the synthetisa-
tion process is described in enough detail for us to re-
peat these experiments and confirm the corresponding
findings. In other cases, the authors confirmed the use
of synthetic data in e-mail communication. Scalagon
seems a notable exception in this regard as it has been
tested on two real data sets: a performance statistic
of NBA basketball players and a household data set
displaying the percentage of an American family’s
income spent on gas, electricity, water, etc. (Endres
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
466

et al., 2015; Tao et al., 2007). Both data sets were
obtained from crawled websites. We doubt, however,
that such statistical data shows properties similar to e-
commerce product catalogs. Also, the authors do not
specify the preferences used in their experiments.
In the course of an industry project that required
the evaluation of suitable skyline algorithms for spe-
cific commercial data sets and preferences, we ob-
served very different results from the ones derived
from synthetic (and real) data in the literature. In the
case study presented here, we use a database dump
of a Swiss car reselling platform with a total of 55208
items and 23 attributes (with keys ignored), which, af-
ter feature scaling and replacement of categorical val-
ues by identifiers, we make available to the commu-
nity (Galli et al., 2015). Despite the rather small size
of this data set, a target market analysis in Switzer-
land has shown that it is representative for the broad
e-commerce landscape. More importantly, however,
this data set shows the typical statistical properties
of a commercial product catalog. Some attributes are
strongly correlated, sometimes due to physical rea-
sons (e.g. cylinders and engine size have Pearson in-
dex 0.91) sometimes due to business specific rea-
sons (e.g. horsepower and price have Pearson in-
dex 0.71). Other attributes are strongly anti-correlated
(e.g. mileage and registration date have Pearson in-
dex −0.8), and other attributes are nearly indepen-
dent (e.g. mileage and horsepower have Pearson in-
dex −0.02). Correlation in data is known to have a
strong influence on the skyline size (Chaudhuri et al.,
2006). On the other hand, commercial product cata-
logs almost always contain strong outliers. For exam-
ple, price and mileage are anti-correlated with Pear-
son index −0.4, but in a database with more than 50K
cars there will always be at least one cheap car with
low mileage that e.g. the owner is forced into selling
for financial reasons. Such outliers dominate many
other items and therefore strongly countervail the ef-
fect of correlation. Finally, the attributes have very
different cardinalities. There are, for example, 5988
different prices but only 17 different colors and 2 pos-
sible values for the transmission. Thus, we find that
merely 6% of all items are assigned a unique value for
price, and 8% of all items a unique value for mileage.
We conducted experiments based on e-commerce
typical client-server infrastructures, but our findings
turned out to be similar to the ones obtained from lo-
cal installations. In order to abstract from network de-
lays and other disturbances, we only report the net
runtimes of skyline algorithms from a local instal-
lation. The system specifies as follows: Intel Core
i7-4700MQ CPU@2.40GHz x64, 4 cores, 8 threads,
RAM 8GB, solid state drive, Windows 8.1 Pro, Mi-
crosoft SQL Server Developer (64-bit) 11.0.5058.8.
All skyline algorithms were implemented in .NET C#
version 4.5.51650. The data set, experiments and all
implemented algorithms are made available as open-
source project (Galli et al., 2015).
Inspired by the industrial skyline application we
envisage and in close collaboration with our industry
partners, three sets of user preferences were defined:
1. Numeric Preferences: 10 numeric preferences ex-
press typical search queries for low prices, low
mileage, low consumption, high horsepower or
high registration day. Characteristically, these
preferences have, with an average of 1389 unique
values, rather high cardinality.
2. Categorical Preferences: 7 categorical preferences
express rather sophisticated preference queries for
color, car body, car maker, etc. To give a con-
crete example, the customer preference we chose
for color is: red blue green gold
black grey all others. Because we aim to
apply Hexagon, we here follow the weak order
preference semantics according to (Preisinger and
Kissling, 2007), i.e. all other colors are considered
equally preferred by the user.
3. Minimal Cardinality Preferences: 5 categorical
preferences with at most 6 unique values were
chosen in order to best possible meet the con-
straints imposed by the Hexagon algorithm. Mul-
tiplying the cardinalities gives 720, which is
only about 1.3% of the size of the data set.
Hexagon promises superior runtime in such cases
(Preisinger and Kissling, 2007). The preferences
chosen here concern fuel types, number of doors,
drive layouts, transmission types, etc.
In the following experiments we compare three
skyline algorithms: BNL with entropy-based window
management (Chomicki et al., 2003), D&C in its orig-
inal version (B
¨
orzs
¨
onyi et al., 2001) and Hexagon
(Preisinger and Kissling, 2007). Considerations on
Scalagon, that was published after completion of this
case study, can be found in Section 4. All runtime re-
sults are given in milliseconds, and we report the av-
erage, minimum and maximum runtime of each set
of experiments together with the standard deviation
and skyline size. All results are rounded to the near-
est integer. We further report minimum and maximum
Pearson correlation between any two attributes in the
corresponding preference set.
3.1 Results on Numeric Preferences
In the first set of experiments we executed all 120
combinations of 7 preferences out of the set of 10
Skyline Computation on Commercial Data
467
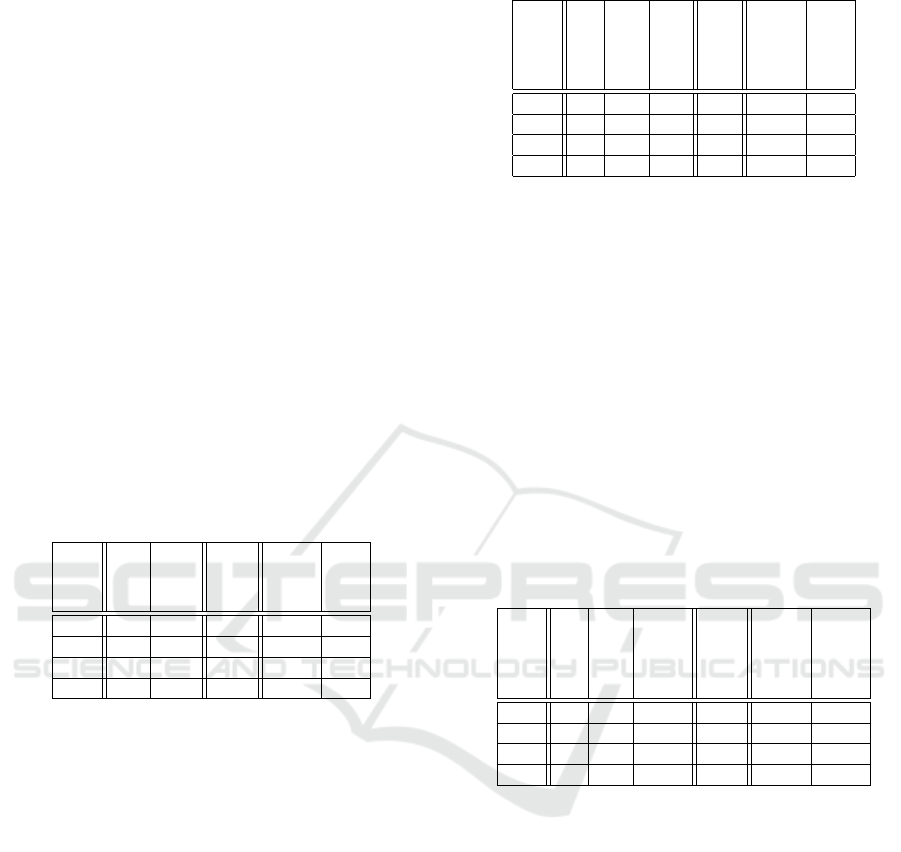
numeric preferences. Results are displayed in Table
1. Due to the large number of unique values in these
preferences, Hexagon could not calculate any of the
skylines. The product of preference cardinalities ex-
ceeds 10
17
in the average. The observation that BNL
performs best in this setting is consistent with the re-
sults derived from synthetic data in (B
¨
orzs
¨
onyi et al.,
2001). The largest skyline with 8251 items does not
exceed 15% of the overall data set, which confirms
that BNL is well-suited for rather small skylines.
D&C shows acceptable runtimes for practical use but
performs worse than BNL. On average, the minimum
and maximum correlation between any two attributes
in a preference set is −0.73 and 0.87, i.e. many pref-
erence sets contained at the same time strongly corre-
lated and anti-correlated attributes. This is one typ-
ical phenomenon that frequently occurs in practice
but that is often not sufficiently taken into account in
benchmark tests on synthetic data. Finally, we also
translated these queries into ANSI SQL according to
(B
¨
orzs
¨
onyi et al., 2001) and obtained an average run-
time of 33237 ms. This shows the practical benefit of
a dedicated skyline algorithm quite impressively.
Table 1: Performance results on numeric preference sets.
BNL [ms]
D&C [ms]
Skyline
Min Corr.
Max Corr.
Avg 124 452 2353 −0.73 0.87
Min 6 198 82 −0.81 0.63
Max 626 1789 8251 −0.24 0.92
Std 130 307 2067 0.13 0.07
3.2 Results on Categorical Preferences
In the second set of experiments we executed all 21
combinations of 5 preferences out of the set of 7 cate-
gorical preferences, see Table 2. Due to the low pref-
erence cardinalities, Hexagon was able to compute
all skylines in this setting. However, BNL still per-
forms best among all three skyline algorithms on av-
erage, best and worst case, which again confirms its
leading position for small skylines. Executing these
queries in ANSI SQL takes 25830 ms on average.
We also observe that, compared to the numeric pref-
erences above, there is much less correlation and anti-
correlation in this data.
3.3 Results on Mixed Preferences
In reality, users will most probably communicate a
mixed set of numeric and categorical preferences to
the system, e.g. they may search for a family car
rather than a cabriolet, have a budget of around 5K,
Table 2: Performance results on categorical preference sets.
BNL [ms]
D&C [ms]
Hexagon [ms]
Skyline
Min Corr.
Max Corr.
Avg 14 103 273 62 −0.13 0.25
Min 3 75 245 9 −0.21 0.06
Max 34 132 314 313 −0.01 0.36
Std 10 15 19 81 0.08 0.12
prefer red cars over blue cars with mileage as low as
possible. In the third set of experiments, we take such
scenarios into account by taking 100 random draws
from the total set of 17 numeric and categorical pref-
erences. Each draw contained a random number of
between 3 and 7 preferences with 5.13 preferences
per run on average, see Table 3. More than 50% of
these runs could not be executed by the Hexagon al-
gorithm due to large preference cardinalities. The run-
time results we report on Hexagon are therefore in-
complete. In this most realistic setting, BNL outper-
forms Hexagon by a factor of 360 on average. D&C
performs slightly worse than BNL but still sufficient
for online applications in practice. Again, skylines are
rather small and preference sets simultaneously con-
tain attributes with different correlations.
Table 3: Performance results on mixed preference sets.
BNL [ms]
D&C [ms]
Hexagon [ms]
Skyline
Min Corr.
Max Corr.
Avg 7 196 2550 166 −0.40 0.48
Min 2 45 146 1 −0.81 −0.01
Max 96 467 35137 2763 0.01 0.92
Std 11 69 5451 331 0.22 0.28
3.4 Results on Minimal Cardinality
Finally, we executed all 10 combinations of 3 prefer-
ences out of the set of 5 categorical preferences with
minimal cardinality, see Table 4. This set of prefer-
ences has been tailored specifically to the needs of
Hexagon and, indeed, Hexagon shows superior run-
time over BNL. However, to our surprise, D&C per-
forms even better than Hexagon for such preferences
with very low cardinalities.
4 DISCUSSION
The experiments we conducted are based on commer-
cial data, featuring typical statistical properties of e-
commerce product catalogs, and different sets of real-
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
468

Table 4: Performance on minimum cardinality preferences.
BNL [ms]
D&C [ms]
Hexagon [ms]
Skyline
Min Corr.
Max Corr.
Avg 816 69 156 8169 −0.06 0.21
Min 6 41 129 1 −0.19 0.00
Max 2578 84 179 18435 0.00 0.36
Std 1040 15 17 6213 0.09 0.15
world user preferences specified in close collabora-
tion with our industry partner. In almost all cases,
BNL turned out to be the best choice for a practical
skyline algorithm. Based on a study with synthetic
data sets, the authors of the Hexagon algorithm claim
superior results over BNL for any data distribution,
provided that the size of the better-than-graph is of
the same order of magnitude as the number of catalog
items. This assumption is considered realistic for e-
commerce applications by the authors, and Hexagon
is called an algorithm for all practical seasons in
(Preisinger and Kissling, 2007). We disagree in both
of these points: In e-commerce applications we will
almost always have preferences with high cardinal-
ity, e.g. among similar products, customers prefer the
one with a lower price, or they search for products
with a price around a certain budget. In such cases,
Hexagon can hardly be applied for skyline compu-
tation. In our experiments, only very few configura-
tions met this constraint and could actually be com-
puted using Hexagon. Among these runs, Hexagon
has never succeeded to outperform BNL and D&C –
not even on the preference sets that we specifically
tailored to the strengths of Hexagon. One could of
course suspect our implementation of Hexagon to be
the source for these unexpected findings. We therefore
contacted the authors of the Hexagon algorithm, but
regrettably, they refused to provide their own imple-
mentation of the algorithm. Furthermore, the D&C al-
gorithm, that consistently showed only slightly worse
runtime compared to BNL, has great potential for par-
allelization on modern microprocessor architectures.
Our current implementation is not parallelized and
still beats Hexagon in all cases. Finally, we did not in-
vestigate very large skylines in this case study as they
are practically not manageable by the user. In such
cases we would rather fall back to skyline sampling
and approximation schemes.
After completion of this case study, a new algo-
rithm named Scalagon was published (Endres et al.,
2015) that promises applicability to high cardinal-
ity preferences by combining the relative strengths
of Hexagon and BNL. We were given access to an
implementation of Scalagon in the R programming
language (Rooks, 2014) and repeated the experi-
Table 5: Scalagon performance on mixed preference sets.
BNL [ms]
Scalagon [ms]
Hexagon [ms]
Avg 7 175 2550
Min 2 10 146
Max 96 6060 35137
Std 11 628 5451
ments on mixed preferences from Section 3.3 with
exactly the same preferences, see Table 5. In con-
trast to Hexagon, Scalagon could successfully execute
all skyline queries and therefore keeps its promise to
overcome the cardinality constraint. The runtime fig-
ures displayed here are to be interpreted with great
care since for Scalagon we used the implementation
in the R programming language issued by the authors,
whereas BNL is implemented and executed in the
.NET setting specified above. However, in the worst
case, the two implementations differ by a factor of
63, which, as we think, cannot be explained away by
the use of different programming languages. A closer
inspection of the individual runtimes reveals that the
larger the skyline the larger the difference in runtime
between BNL and Scalagon.
5 CONCLUSION
Most existing evaluations and comparisons of skyline
algorithms are based on synthetic data. We presented
a case study of skyline computation on commercial
data and real-world user preferences that we consider
representative for many e-commerce businesses. The
results of our measurements differ significantly from
the results reported on synthetic data in the litera-
ture. BNL and D&C style algorithms outperformed
lattice-based algorithms in all our experiments – very
much to our surprise even on preference sets that we
specifically tailored to the strengths of the latter. Be-
cause the details of the exact synthetisation process
are often omitted in the literature, we can only conjec-
ture on the statistical properties that may lead to these
very different conclusions. The asymptotic complex-
ity of skyline algorithms is generally determined with
respect to the number of items and preferences. In
addition, statistical correlation and skyline size are
considered an important influence factor (B
¨
orzs
¨
onyi
et al., 2001). Hexagon imposes an additional con-
straint on preference cardinality. In this context, we
suspect one potentially big difference between syn-
thetic and catalog data. If we sample synthetic data
tuples from a potentially large space (e.g. for prod-
Skyline Computation on Commercial Data
469

uct prices) we obtain many different values. In con-
trast, merely 6% of the items in our product catalog
contain a unique value for price, and this is certainly
not untypical for e-commerce. Likewise, preference
queries in practice usually include pairs of indepen-
dent, correlated and anti-correlated attributes at the
same time, yet almost all experiments in the litera-
ture investigate only pure settings. We could also ob-
serve a strong influence of outliers in the data set on
the performance of skyline algorithms. Again, in con-
trast to synthetic data, commercial catalogs will al-
most always contain strong outliers. Interestingly, the
Scalagon algorithm includes a heuristic for detecting
outliers in the pre-filter phase (Endres et al., 2015),
but to our best knowledge there are no detailed studies
on outliers in skyline computation. An important ad-
vantage of synthetic data is that it avoids bias (Balke
et al., 2007). Our experiments were based on a sin-
gle yet typical e-commerce product catalog such that
they clearly do not allow for a universally valid in-
terpretation. Still, when preference queries are to be
computed in concrete commercial applications and on
data sets, whose statistical properties have been ana-
lyzed, the rich skyline literature with all its investiga-
tions on synthetic data still does not provide helpful
indications on which skyline algorithm to apply.
ACKNOWLEDGEMENTS
We gratefully acknowledge the close and inspiring
collaboration with our industry partner Arcmedia AG
(www.arcmedia.ch) as well as Roland Christen and
Daniel Pf
¨
affli for integration and testing of skyline al-
gorithms in a professional e-commerce environment
and the valuable feedback they provided.
REFERENCES
Aldrich, S. E. (2011). Recommender systems in commer-
cial use. AI Magazine, 32(3):28–34.
Balke, W.-T., G
¨
untzer, U., and Siberski, W. (2007). Re-
stricting skyline sizes using weak pareto dominance.
Inform., Forsch. Entwickl., 21(3-4):165–178.
Balke, W.-T., Zheng, J. X., and G
¨
untzer, U. (2005). Ap-
proaching the efficient frontier: cooperative database
retrieval using high-dimensional skylines. In Hutchi-
son, D., Kanade, T., Kittler, J., Kleinberg, J. M., Mat-
tern, F., Mitchell, J. C., Naor, M., Nierstrasz, O.,
Pandu Rangan, C., Steffen, B., Sudan, M., Terzopou-
los, D., Tygar, D., Vardi, M. Y., Weikum, G., Zhou, L.,
Ooi, B. C., and Meng, X., editors, Database Systems
for Advanced Applications, volume 3453 of Lecture
Notes in Computer Science, pages 410–421. Springer
Berlin Heidelberg, Berlin, Heidelberg.
B
¨
orzs
¨
onyi, S., Kossmann, D., and Stocker, K. (2001). The
skyline operator. In Proceedings of the 17th Inter-
national Conference on Data Engineering, April 2-6,
2001, Heidelberg, Germany, pages 421–430.
Chaudhuri, S., Dalvi, N., and Kaushik, R. (2006). Robust
cardinality and cost estimation for skyline operator.
In ICDE. Institute of Electrical and Electronics En-
gineers, Inc.
Chomicki, J., Godfrey, P., Gryz, J., and Liang, D. (2003).
Skyline with presorting. In Dayal, U., Ramamritham,
K., and Vijayaraman, T., editors, ICDE, pages 717–
719. IEEE Computer Society.
Chomicki, J., Godfrey, P., Gryz, J., and Liang, D. (2005).
Skyline with presorting: theory and optimizations. In
Klopotek, M. A., Wierzchon, S. T., and Trojanowski,
K., editors, Intelligent Information Systems, Advances
in Soft Computing, pages 595–604. Springer.
Cole, P. (2013). Amazon.com catalog blows past 200m
items. https://sellerengine.com/amazon-com-catalog-
blows-past-200m-items, last visited: 2015-10-10.
Endres, M., Roocks, R., and Kissling, W. (2015). Scalagon:
An efficient skyline algorithm for all seasons. In DAS-
FAA: 20th Int. Conference of Database Systems for
Advanced Applications, pages 292–308.
Galli, M., Schn
¨
urle, S., Arnold, R., and Pouly, M.
(2015). prefsql code repository and experimental set-
ting. https://github.com/migaman/prefSQL, last vis-
ited: 2015-10-10.
Godfrey, P., Shipley, R., and Gryz, J. (2005). Maximal
vector computation in large data sets. In B
¨
ohm, K.,
Jensen, C. S., Haas, L. M., Kersten, M. L., Larson, P.,
and Ooi, B. C., editors, VLDB, pages 229–240. ACM.
Han, X., Li, J., Yang, D., and Wang, J. (2013). Efficient sky-
line computation on big data. IEEE Trans. on Knowl.
and Data Eng., 25(11):2521–2535.
Lofi, C. and Balke, W.-T. (2013). On skyline queries and
how to choose from pareto sets. In Catania, B. and
Jain, L. C., editors, Advanced Query Processing (1),
volume 36 of Intelligent Systems Reference Library,
pages 15–36. Springer.
Martin, F. J., Donaldson, J., Ashenfelter, A., Torrens, M.,
and Hangartner, R. (2011). The big promise of rec-
ommender systems. AI Magazine, 32(3):19–27.
Papadias, D., Tao, Y., Fu, G., and Seegerr, B. (2003). An op-
timal and progressive algorithm for skyline queries. In
Proc. of the 2003 ACM SIGMOD International Con-
ference on Management of Data, SIGMOD ’03, pages
467–478, New York, NY, USA. ACM.
Preisinger, T. and Kissling, W. (2007). The hexagon algo-
rithm for pareto preference queries. In Proc. of the
3rd Multidisciplinary Workshop on Advances in Pref-
erence Handling.
Preisinger, T., Kissling, W., and Endres, M. (2006).
The bnl++ algorithm for evaluating pareto preference
queries. In In Proc. of the Multidisciplinary Workshop
on Advances in Preference Handling.
Rooks, P. (2014). The rpref package the rpref package:
database preferences and skyline computation in r.
http://www.p-roocks.de/rpref/, last visited: 2015-10-
21.
ICAART 2016 - 8th International Conference on Agents and Artificial Intelligence
470

Tao, Y., Xiao, X., and Pei, J. (2007). Efficient skyline and
top-k retrieval in subspaces. IEEE Trans. Knowl. Data
Eng., 19(8):1072–1088.
Skyline Computation on Commercial Data
471
