Towards Statistical Comparison and Analysis of Models

Onder Babur

, Loek Cleophas

1,2

, Tom Verhoeff

and Mark van den Brand

Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands

Stellenbosch University, ZA-7602 Matieland, South Africa

Keywords:

Model-Driven Engineering, Model Comparison, Statistical Analysis, R, Vector Space Model, Clustering.

Abstract:

Model comparison is an important challenge in model-driven engineering, with many application areas such

as model versioning and domain model recovery. There are numerous techniques that address this challenge in

the literature, ranging from graph-based to linguistic ones. Most of these involve pairwise comparison, which

might work, e.g. for model versioning with a small number of models to consider. However, they mostly ignore

the case where there is a large number of models to compare, such as in common domain model/metamodel

recovery from multiple models. In this paper we present a generic approach for model comparison and analysis

as an exploratory ﬁrst step for model recovery. We propose representing models in vector space model, and

applying clustering techniques to compare and analyse a large set of models. We demonstrate our approach

on a synthetic dataset of models generated via genetic algorithms.

1 INTRODUCTION

Models are considered as central parts in Model-

Driven Engineering (MDE), potentially orchestrating

the whole software development process. As MDE

gains popularity and widespread use, the complex-

ity and variety of models increase. To cope with

this problem, many approaches have been proposed:

model comparison, matching, merging, etc. These

approaches ﬁnd many application areas in MDE,

e.g. merging different model versions or detecting

model clones. While the comparison techniques

range from graph-based to linguistic ones, most in-

volve pairwise or three-way (for model versioning

from a common ancestor) comparison.

Domain model recovery, on the other hand, tack-

les the problem of extracting the common domain

model out of various individual models; obtained ei-

ther directly or indirectly by reverse engineering. Two

examples of this can be drawn directly from our on-

going project for a ﬂexible multiphysics engineer-

ing simulation framework: constructing (1) a stan-

dardized metadata schema that can support a number

of input formats/schemas, and (2) a common meta-

model/ontology to orchestrate the interoperability of a

heterogeneous set of tools. The study in (Babur et al.,

2015a) indicates the overwhelming number of tools in

The research leading to these results has been funded

by EU programme FP7-NMP-2013-SMALL-7 under grant

agreement number 604279 (MMP).

the domain, which makes it really difﬁcult to extend

manual model extraction efforts such as in (Babur

et al., 2015b) to cover the whole domain.

As formulated above, domain model recovery

qualiﬁes as another potential application area for

model comparison, but with a multiplicity of mod-

els to consider. This dimension has been diagnosed

in (Klint et al., 2013) as an interesting aspect to ex-

plore. (Rubin and Chechik, 2013) further discusses

the inadequacy of pairwise comparison techniques for

multiple models and proposes an N-way model merg-

ing algorithm. To the best knowledge of the authors

the statistical dimension of the generic model com-

parison problem has been largely overlooked.

In this paper, we present an initial attempt at

model comparison and analysis for large datasets us-

ing Information Retrieval (IR) techniques and statis-

tical analysis, as an exploratory ﬁrst step in model re-

covery. In IR, a vector space model (VSM) is used to

represent text documents, with vector elements cor-

responding to word occurrence (incidence) or fre-

quency. We borrow this concept to represent mod-

els as vectors of the bigram combinations of related

model elements. This model, in turn, is supplied with

inverse document frequency and type-based weight-

ing scheme to compute distances of models in the

vector space. We then use the R statistical software

(Maechler et al., 2013) to cluster, analyse and visu-

alise the dataset. As an initial feasibility test of our

approach, we use synthetically generated model pop-

Babur, Ö., Cleophas, L., Verhoeff, T. and Brand, M.

Towards Statistical Comparison and Analysis of Models.

DOI: 10.5220/0005799103610367

In Proceedings of the 4th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2016), pages 361-367

ISBN: 978-989-758-168-7

361

ulations obtained using the metamodel-driven model

mutation framework in (van den Brand et al., 2011).

Positioning Model Comparison as a First Step for

Model Recovery. Model comparison (Stephan and

Cordy, 2013) is found in the literature as a com-

mon operation in a wide range of application areas,

such as model versioning (Altmanninger et al., 2009),

model clone detection (Deissenboeck et al., 2010),

model merging (Brunet et al., 2006), model match-

ing (Kolovos et al., 2009) and model recovery (Klint

et al., 2013). It is typically deﬁned as a binary opera-

tor (sometimes ternary in model versioning), mapping

two model elements to a similarity measure. It can be

categorized according to the output: boolean (exact

matchers), similarity category (e.g. near-miss clones

for model clone detection), or similarity degree (e.g. a

real number in the range [0.0, 1.0]).

Model recovery can be considered as an umbrella

term that encapsulates different approaches named

domain model recovery (Klint et al., 2013), meta-

model recovery (Javed et al., 2008), automated do-

main modeling (Reinhartz-Berger, 2010), etc. We can

regard model recovery as reverse engineering a com-

mon model out of several entities, either directly from

variant models, or from other sources such as design

documents and source code - adding another layer of

reverse engineering. For this paper, we choose to ig-

nore this second layer; instead we lift the problem

completely to the model level. So the starting point

for our consideration is a set of homogeneous mod-

els, representing a common domain. A concrete ex-

ample would be the class diagrams of similar soft-

ware packages. While these models share similarities

of the domain, no individual model is an instantiation

of a metamodel or a conﬁguration of a feature model.

We would rather like to use model comparison in the

sense of analysing the similarities among models, try-

ing to ﬁnd clusters and obtaining an overview of the

whole dataset. The analysis information can be re-

garded as a ﬁrst exploratory step in domain model re-

covery from multiple models.

Information Retrieval and Clustering. Informa-

tion Retrieval (Manning et al., 2008) has a long his-

tory of developments in dealing with effectively in-

dexing, analyzing and searching various forms of con-

tent including natural language text documents. As

a ﬁrst step for document retrieval in general, docu-

ments are collected and indexed via some unit of rep-

resentation. Index construction can be implemented

using models ranging from boolean indices to com-

plex neural networks. One such model is the vector

space model (VSM) with the following major steps:

• A vector representation of occurrence of the vo-

cabulary in a document (binary), named term in-

cidence;

• Optionally zones (e.g. ’author’ or ’title’ zones sep-

arate from the text bodies);

• Optionally weighting schemes to be used as mul-

tipliers such as:

– inverse document frequency (see Section 2) to

increase the discriminative effect of rare words;

– zone weights, e.g. higher for important zones.

Once the VSM is constructed, the similarity of

documents can be deﬁned as the distance between

these vectors. There exist several distance/similarity

measures, such as Euclidian, Cosine or Manhattan.

VSM with a selected distance measure is the prerequi-

site for identiﬁng common groups of documents in the

vector space. Among many different clustering meth-

ods (Jain and Dubes, 1988), K-means is a simple but

effective one. It aims to identify cluster centers and

minimises the residual sum of (squares of) distances

of the points assigned in each cluster. Hierarchical

clustering techniques assume an unknown number of

clusters and rather build a nested tree structure (den-

drogram) of the data points, representing proximities

and potential clusters.

Objectives. The purpose of this study is to answer

the following questions:

• RQ1. How can we represent models for N-way

comparison and analysis?

• RQ2. How can we analyse and compare a large

set of models?

2 METHOD FOR COMPARING A

LARGE SET OF MODELS

In this section, we elaborate our approach on a small

example. We describe the main steps as:

1. Obtaining a set of homogeneous models (of same

type, e.g. UML class diagram) to be analyzed.

2. Generating the bigram vocabulary from the input

models and the bigram types from the metamodel

(that is, the generic metamodel e.g. UML meta-

model, rather than lower level domain-speciﬁc

metamodels); types being similar to zones in IR.

3. Calculating the term incidence matrix with an idf

and type-based weighting scheme.

4. Analyse the dataset via simple K-means and/or hi-

erarchical clustering with Manhattan distance.

A Small Exemplary Dataset. First we deﬁne a

simple metamodel with basic building blocks, based

on the Ecore kernel at (Budinsky, 2004), to base our

MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development

362

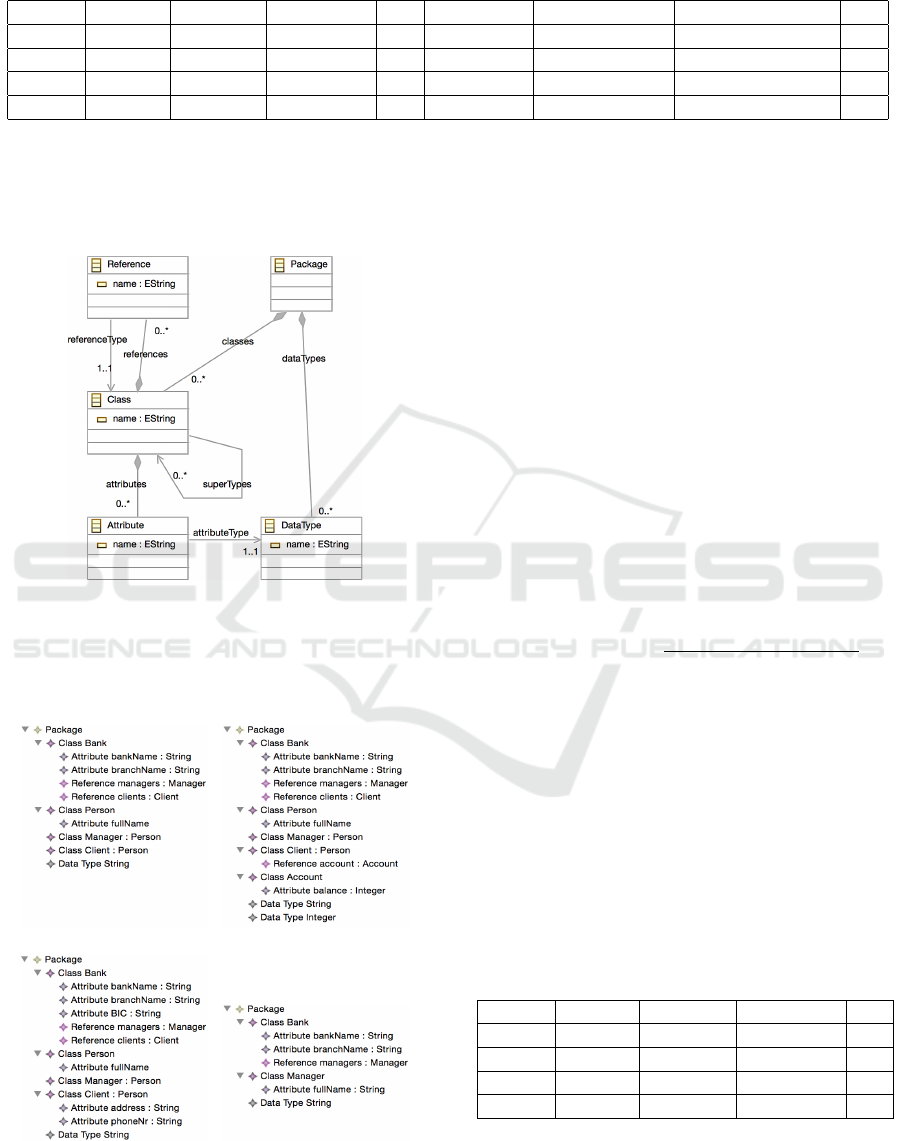
Table 1: Term incidence matrix of the input models. Note that some of the terms have been abbreviated due to space

constraints, e.g. rootPackage-Bank as r-Bank and Bank-managers as Bank-mrs.

Model r-Bank r-Person r-Account . . . Bank-mrs mrs-Manager Manager-Person . . .

M1 1 1 0 . . . 1 1 1 . . .

M2 1 1 1 . . . 1 1 1 . . .

M3 1 1 0 . . . 1 1 1 . . .

M4 1 0 0 . . . 1 1 0 . . .

experiments on; since real metamodels such as Ecore

are too large and complex for the purpose of this

study. Figure 1 demonstrates the metamodel to drive

the examples.

Figure 1: Simple metamodel for experiments.

Based on this metamodel, we construct four mod-

els with a few differences such as addition of new

classes or removal of attributes, depicted in Figure 2.

(a) Model 1 (b) Model 2

Figure 2: A small set of models.

Generating the Bigram Vocabulary. From the in-

put models and metamodel, we construct a typed

bigram vocabulary. The type information comes

from the metamodel: From Figure 1, we get the set

{classes, attributes, references, supertypes, refer-

enceType, attributeType dataTypes}. Next, we tra-

verse all the models to extract the union of bigrams as

our vocabulary: the examples in Figure 2 would yield

Model 1 = { rootPackage-Bank, rootPackage-

Person, . . . , Bank-bankName, . . . , bankName-

String, . . . } The choice of bigrams vs. unigrams cap-

tures relational information between model elements.

Calculating Term Incidence Matrix. The bigram

sets for each model allow us construct the term in-

cidence matrix as in Table 1. We propose to apply

a weighting scheme on the term incidence matrix,

which includes two multipliers: an inverse document

frequency (idf) and a type (zone) weight. The idf of

a term t is used to assign greater weight to rare terms

across models, and is deﬁned as:

id f (t) = log



1 +

# total models

# models with the term t



Furthermore, a type weight is given to the bigrams

representing their semantic importance. We claim, for

instance, that classes are semantically more impor-

tant than attributes, thus deserve a greater weight. We

have used this experimental scheme for this paper:

zoneWeight(t, w) : {classes → 1.0, attributes → 0.5,

dataTypes→ 0.5, references→ 0.5, supertypes→ 0.2,

referenceType → 0.2, attributeType → 0.2}

The resulting matrix where term incidences are

multiplied by idf and weights is given in Table 2.

Table 2: Idf and type weighted matrix.

Model r-Bank r-Person r-Account . . .

M1 0,30 0,37 0 . . .

M2 0,30 0,37 0,70 . . .

M3 0,30 0,37 0 . . .

M4 0,30 0 0 . . .

K-means Clustering. As the next step of our ap-

proach, we reduce the model similarity problem into

a distance measurement of the corresponding vector

Towards Statistical Comparison and Analysis of Models

363

representations of models. Among various measures,

Manhattan distance seems to be suitable since it cor-

responds to the edit distance of two models. p and

q being two vectors of n dimensions, Manhattan dis-

tance is deﬁned as:

manhattan(p, q) =

∑

i=1

− q

While clustering makes little sense for our small

example dataset we can still compute the center of just

one cluster and the distances of models to the center.

The center can be considered as a rough average of

that cluster. Similarly, the model closest to the center

can be considered as a representative of that cluster.

The models’ distances to center are given in Figure 3.

●

M1 M2 M3 M4

123

Distances

Models

Figure 3: Distances of models to the cluster center.

3 A DATASET FOR MODEL

COMPARISON

Model Mutation Framework. We use the model

mutation framework in (van den Brand et al., 2011)

to synthetically generate populations of models to

be used for comparison. The framework is capa-

ble of generating mutations on a model based on its

metamodel, i.e. the mutated instances will still be

metamodel-compliant. It can be conﬁgured to gener-

ate random distribution of different types of mutations

such as addition, removal or modiﬁcation of model el-

ements. For more information on the features and op-

eration, please refer to (van den Brand et al., 2011).

Synthetic Generation of Model Populations. Us-

ing the mutation framework, we have generated a sim-

ple setting for creating model populations based on

the metamodel in Figure 1 and a slightly modiﬁed

version of the bank model example in Figure 2. The

goal is to emulate a model population evolved from

a common model (e.g. a hypothetical domain model).

The genetic algorithm starts with the initial generation

consisting of only M

, i.e. the root model. At every it-

eration, the set of models at that level (called a gener-

ation) is mutated with one atomic addition (with 70%

probability) or removal (with 30% probability) oper-

ator. The number of offsprings generated at each iter-

ation is set by a branching factor b, and the total num-

ber of iterations is set by a generation count n. For

our experiments, we did not consider any ﬁtness func-

tion (i.e. every generated model survives) or crossover

operations. One further simpliﬁcation is that modiﬁ-

cation of model elements (e.g. renaming) is also not

included as a mutation operator.

The algorithm basically creates tree structures rep-

resenting model generations with atomic mutations at

each branch. Following this setting, we have gener-

ated one dataset to test our approach: with b = 2 and

n = 5, where we keep the older generations and thus

have the whole population tree.

4 EXPERIMENTS & DISCUSSION

Experiment on the Whole Tree. The ﬁrst analysis

on the dataset was determining the number of clusters,

k. A simple method for this is running the clustering

for a range of 1 to a suitably large N and visualis-

ing the total sum of squares within clusters. Figure 5

shows these numbers for N = 15. A visual heuris-

tic was used for locating ’elbows’ in the plot, poten-

tially good candidates for k. Inspecting the ﬁgure, we

picked k = 7 by its signiﬁcant drop after k = 6, and

the relative saturation after k > 7.

We in turn cluster the dataset with Manhattan dis-

tance and k = 7. The tree-like structure of model pop-

ulation, with each node as one model, branch as a mu-

tation, and depth as a generation, allows a good visu-

alisation of the clustering algorithm. The clustering

was done with the Kmeans function of amap package

and the result is depicted in Figure 4. Each cluster was

coded with a unique colour/pattern. The visualisation

agrees with the initial intention; populations evolve in

different directions and start to form clusters.

Experiment on the Leaves. We would also like to

analyse the set of models, ﬁnding representative mod-

els and outliers among them. To emulate this sce-

nario, we used only the youngest generation (i.e. the

leaves of the tree) to cluster. First we clustered the set

with just k = 1 to ﬁnd a center and plot the distances

of each model to the center, depicted in Figure 6. Two

implications are that there are no representative mod-

els close enough to the center, and no visible outliers

within the single cluster. This is expected as mod-

els have accumulated mutations over generations and

form separate clusters (Figure 4).

This scenario is suitable for applying hierarchical

clustering just on the leaves, and try to reconstruct a

hierarchical similarity scheme resembling the one in

Figure 4. Indeed, we obtained a dendrogram of the

models using the hclust function in stats package with

Manhattan distance, given in Figure 7. The nodes on

MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development

364

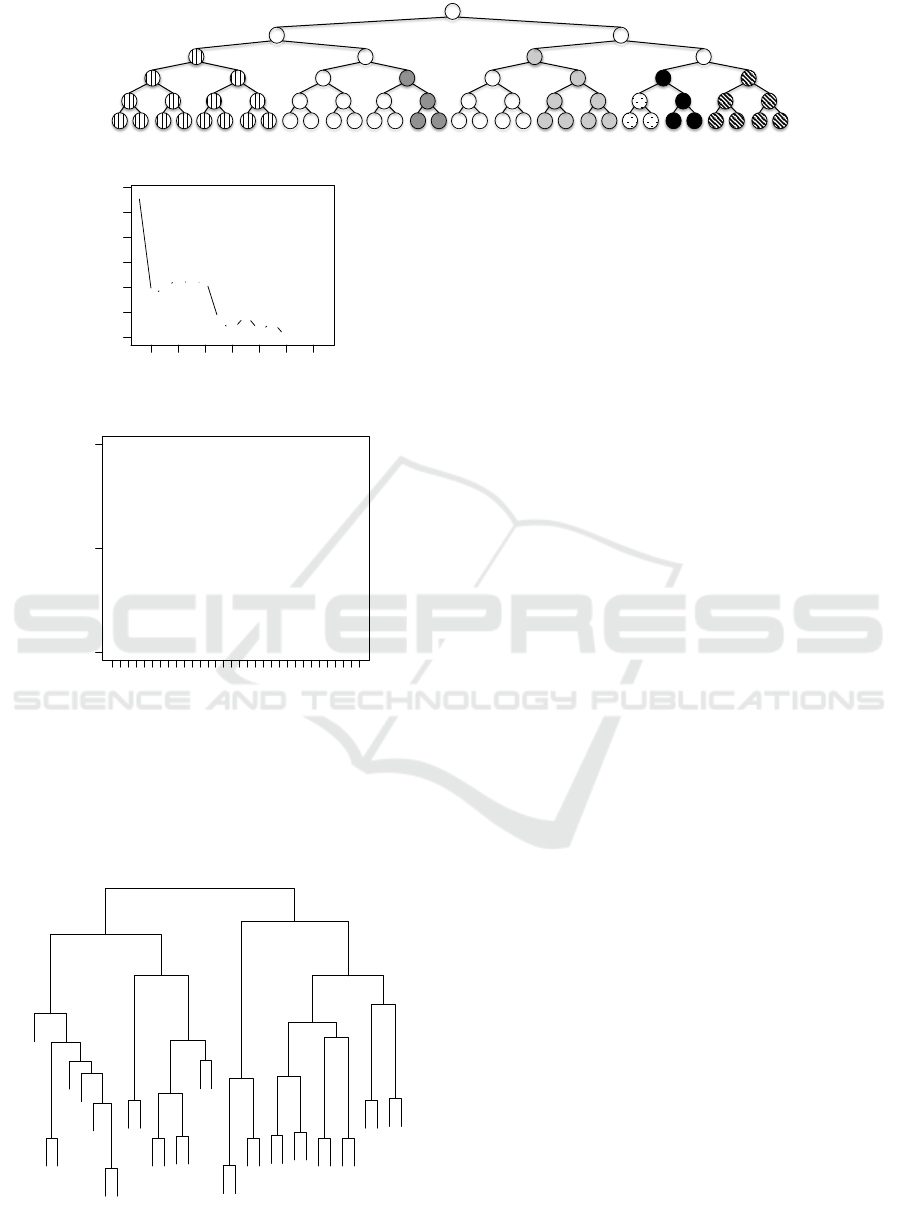
Figure 4: Population tree with 7 clusters.

●

2 4 6 8 10 12 14

50 60 70 80 90 110

Number of Clusters

Within groups sum of squares

Figure 5: Total sum of squares within clusters vs # clusters.

●

●●

●

●●

●

●●

●

●●

●

●●

●

1 4 7 10 13 16 19 22 25 28 31

6 7 8

Manhattan distances to center

Models

Figure 6: Distances of the leaf models to the center.

the dendrogram are labelled 1 to 32 and correspond

to the consecutive leaves from left to right in Fig-

ure 4. There is an obvious resemblance between the

two structures; the dendrogram can be interpreted as

an approximate reconstruction of the population tree.

0 2 4 6 8 10

Cluster Dendrogram

hclust (*, "complete")

Height

Figure 7: Hierarchical clustering - dendrogram.

An Initial Assessment of our Approach. Based on

our experiments, a statistical perspective on the com-

parison and analysis of large datasets seems promis-

ing. While the dataset was synthetic and relatively

small, we were able to obtain intuitive results. Using

VSM allows a uniform representation of models for

statistical analysis, while the accompanying idf and

type-based weighting scheme yields a suitable scal-

ing in the vector space (RQ1). Using a distance mea-

sure and clustering over VSM, many characteristics

and relations among the models, such as representa-

tives, clusters and outliers, can be analysed (RQ2).

An advantage of our approach is the scalability

and tool support. The algorithm complexity range

from linear (e.g. VSM construction) to polynomial

(e.g. K-means as observed complexity and hierarchi-

cal clustering) with respect to the number and size

of models. Moreover, R provides a plethora of ef-

ﬁcient and ﬂexible statistical libraries for analysis.

Metamodel-based construction of the bigram vocab-

ulary provides a good amount of reduction in vector

space, improving over basic IR indexing.

Threats to Validity. While our initial experiments

indicate the potential of our approach for large-scale

model comparison and analysis, there are a number

of threats to validity. The biggest one is that we have

used a synthetic, simpliﬁed and homogeneous dataset.

The variations in the synthetic dataset are simpler than

in a real world scenario where larger, more complex

and possibly heterogeneous models are reverse engi-

neered from different tools. For instance, we currently

handle neither Natural Language Processing (NLP)

issues such as synonyms/renamings, nor semantical

equivalence of model elements. Furthermore, while

the general architecture of our approach seems plausi-

ble, we have not evaluated other options for individual

steps; but chosen them intuitively as a ﬁrst attempt.

5 RELATED WORK

Only a few model comparison techniques consider

the multiplicity of input models without doing pair-

wise comparisons, such as N-way merging based on

weighted set packing in (Rubin and Chechik, 2013).

Feature model extraction (She et al., 2011) and con-

Towards Statistical Comparison and Analysis of Models

365

cept mining (Abebe and Tonella, 2010) use NLP to

cluster features/concepts. (Ratiu et al., 2008) builds

domain ontologies as the intersection of graphs of

APIs, but does not focus on the statistical dimension

of problem. Metamodel recovery (Javed et al., 2008)

is another approach which assumes a once existing

(but somehow lost) metamodel, and does not hold for

our scenario. (Dijkman et al., 2011) applies a tech-

nique similar to ours, speciﬁcally for business pro-

cess models using process footprints and thus lacks

the genericness of our approach. Note that a thor-

ough literature study beyond the technological space

of MDE, for instance regarding data schema match-

ing and ontology matching/alignment, is out of scope

for this paper and is therefore omitted.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we have presented a new perspective

on the N-way comparison and analysis of models as

a ﬁrst step in model recovery. We have proposed a

generic approach using the IR techniques VSM and

tf-idf to uniformly represent multiple models, and ap-

ply statistical analysis with K-means and hierarchi-

cal clustering. Using a model mutation framework,

we have synthetically generated a dataset to apply our

method and demonstrate its potential uses. The re-

sults indicate that our approach is a promising ﬁrst

step for analysing large datasets, being generic and

scalable/efﬁcient using R.

As future work, the most important goal is to work

with real datasets of possibly heterogeneous models,

rather than the synthetic one. A real dataset (e.g. class

diagrams of multiple domain tools) can be acquired

through reverse engineering, which we have omitted

for this paper. The NLP or semantic issues pose the

next set of challenges to tackle. A careful assessment

of different and more advanced options for model rep-

resentation, distance measures, and clustering tech-

niques needs to be done in order to increase the accu-

racy and efﬁciency of our approach. Although this is

presented as an exploratory step, it can also be inves-

tigated how VSM and clustering information can be

used for model merging and domain model recovery.

REFERENCES

Abebe, S. L. and Tonella, P. (2010). Natural language pars-

ing of program element names for concept extraction.

In Program Comprehension (ICPC), 2010 IEEE 18th

International Conference on, pages 156–159. IEEE.

Altmanninger, K., Seidl, M., and Wimmer, M. (2009). A

survey on model versioning approaches. International

Journal of Web Information Systems, 5(3):271–304.

Babur,

O., Smilauer, V., Verhoeff, T., and van den Brand, M.

(2015a). Multiphysics and multiscale software frame-

works: An annotated bibliography. Technical Report

15-01, Dept. of Mathematics and Computer Science,

Technische Universiteit Eindhoven, Eindhoven.

Babur,

O., Smilauer, V., Verhoeff, T., and van den Brand,

M. (2015b). A survey of open source multiphysics

frameworks in engineering. Procedia Computer Sci-

ence, 51:1088–1097.

Brunet, G., Chechik, M., Easterbrook, S., Nejati, S., Niu,

N., and Sabetzadeh, M. (2006). A manifesto for model

merging. In Proc. of the 2006 Int. Workshop on Global

Integrated Model Management, pages 5–12. ACM.

Budinsky, F. (2004). Eclipse modeling framework: a devel-

oper’s guide. Addison-Wesley Professional.

Deissenboeck, F., Hummel, B., Juergens, E., Pfaehler, M.,

and Schaetz, B. (2010). Model clone detection in prac-

tice. In Proc. of the 4th Int. Workshop on Software

Clones, pages 57–64. ACM.

Dijkman, R., Dumas, M., Van Dongen, B., K

arik, R.,

and Mendling, J. (2011). Similarity of business pro-

cess models: Metrics and evaluation. Inf. Systems,

36(2):498–516.

Jain, A. K. and Dubes, R. C. (1988). Algorithms for clus-

tering data. Prentice-Hall, Inc.

Javed, F., Mernik, M., Gray, J., and Bryant, B. R. (2008).

Mars: A metamodel recovery system using grammar

inference. Inf. and Software Tech., 50(9):948–968.

Klint, P., Landman, D., and Vinju, J. (2013). Exploring the

limits of domain model recovery. In Software Mainte-

nance (ICSM), 2013 29th IEEE International Confer-

ence on, pages 120–129. IEEE.

Kolovos, D. S., Ruscio, D. D., Pierantonio, A., and Paige,

R. F. (2009). Different models for model matching:

An analysis of approaches to support model differenc-

ing. In Comparison and Versioning of Software Mod-

els, 2009. ICSE Workshop on, pages 1–6. IEEE.

Maechler, M., Rousseeuw, P., Struyf, A., Hubert, M., and

Hornik, K. (2013). cluster: Cluster Analysis Basics

and Extensions. R package version 1.14.4.

Manning, C. D., Raghavan, P., Sch

utze, H., et al. (2008).

Introduction to information retrieval, volume 1. Cam-

bridge university press Cambridge.

Ratiu, D., Feilkas, M., and J

urjens, J. (2008). Extracting

domain ontologies from domain speciﬁc apis. In Soft-

ware Maintenance and Reengineering, 2008. CSMR

2008. 12th European Conf. on, pages 203–212. IEEE.

Reinhartz-Berger, I. (2010). Towards automatization of

domain modeling. Data & Knowledge Engineering,

69(5):491–515.

Rubin, J. and Chechik, M. (2013). N-way model merging.

In Proc. of the 2013 9th Joint Meeting on Foundations

of Software Engineering, pages 301–311. ACM.

She, S., Lotufo, R., Berger, T., Wøsowski, A., and Czar-

necki, K. (2011). Reverse engineering feature models.

In Software Engineering (ICSE), 2011 33rd Interna-

tional Conference on, pages 461–470. IEEE.

MODELSWARD 2016 - 4th International Conference on Model-Driven Engineering and Software Development

366

Stephan, M. and Cordy, J. R. (2013). A survey of model

comparison approaches and applications. In Model-

sward, pages 265–277.

van den Brand, M., Hofkamp, A., Verhoeff, T., and Proti

Z. (2011). Assessing the quality of model-comparison

tools: a method and a benchmark data set. In Proc. of

the 2nd Int. Workshop on Model Comparison in Prac-

tice, pages 2–11. ACM.

Towards Statistical Comparison and Analysis of Models

367