e-Learning Platform Ranking Method using a Symbolic Approach based
on Preference Relations
Soraya Chachoua, Nouredine Tamani, Jamal Malki and Pascal Estraillier
L3i Laboratory, University of La Rochelle, Avenue Michel Cr
´
epeau, La Rochelle, France
Keywords:
e-Learning Platforms, Qualitative Weight and Sum (QWS), Aggregation and Ranking.
Abstract:
e-Learning platforms are of a great help in teaching and learning fields given their ability to improve training
activity quality. Subsequently, several e-Learning systems have been developed in many domains. The diver-
sity of such platforms in a single field makes it arduous to select the optimal platform in terms of tools and
services that meet users’ requirements. Therefore, we propose in this paper a ranking approach of e-Learning
platforms relying on symbolic values, borrowed from the Qualitative Weight and Sum method (QWS) (Stuffle-
beam, 1994), preference relations and aggregating operators providing a total order among the considered
e-Learning platforms.
1 INTRODUCTION AND
MOTIVATION
The past decade has seen tremendous changes in ed-
ucational and industrial training methods along with
the increasing of the number of users having diverse
needs and objectives. Indeed, there are a huge num-
ber of free and commercial e-Learning systems which
have been developed in different areas such as ed-
ucation (Venkataraman and Sivakumar, 2015), lan-
guage learning (Ba
˜
nados, 2013), business training
(Colace et al., 2006; Ubell, 2000), medicine (Schnei-
der et al., 2015; Hannan, 2013) and public administra-
tions (Stoffregena et al., 2015), etc. which provide on-
line and remote training making user learning tasks
more flexible and easier. The multitude of e-learning
platforms developed for a single domain (such as in
language learning, for instance, we can distinguish
tens of e-learning applications and on-line platforms
like babel, busuu, duolingo, ef, tell me more, Pim-
sleur, etc.) makes it difficult to pick the more suitable
one according to one’s needs and objectives.
The choice of a suitable system in compliance
with user’s needs and goals based on some cri-
teria is important. Some criteria are mandatory
to choose platform but they are insufficient, such
as the compatibility of the e-Learning system on
hand to certain norms and standards like SCORM
1
,
1
SCORM: Sharable Content Object Reference Model,
http://scorm.com
QTI
2
, IMS
3
, etc. These standards ensure a struc-
tured learning object creation and e-Learning qual-
ity through properties, such as adaptability, sustain-
ability, interoperability and reusability. We refer the
reader to (Garc
´
ıa and Jorge, 2006) for an e-Learning
platform evaluation based on the SCORM specifica-
tion.
Besides, many other evaluation approaches have
been proposed such as (Britain and Liber, 2004), in
which the framework considers two models. The for-
mer addresses the different ways to produce learning
processes in an e-Learning system, which has been
reused in (Laurillard, 2013), and the latter character-
izes the different evaluation criteria of learning mod-
els as introduced in (Liber et al., 2000).
Qualitative methods have also been considered for
e-Learning systems evaluation; the most commonly
used one is Qualitative Weight and Sum, denoted
by QWS (Stufflebeam, 1994). It relies on a list of
weighted criteria (Graf and List, 2005; Hamtini and
Fakhouri, 2012) for the evaluation of e-Learning sys-
tems. In practice, it is based on qualitative weight
symbols expressing six levels of importance, namely:
E for essential, ∗ for extremely valuable, # for very
valuable, + for valuable, | for marginally valuable,
and 0 for not valuable. Hence, e-Learning system’s
2
QTI: Question and Test Interoperability, http://www.ims
global.org
3
IMS: Instructional Management Systems, http://www.ims
global.org
114
Chachoua, S., Tamani, N., Malki, J. and Estraillier, P.
e-Learning Platform Ranking Method using a Symbolic Approach based on Preference Relations.
In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 1, pages 114-122
ISBN: 978-989-758-179-3
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

performance is measured by symbolic weights at-
tached to some criteria as described in (Graf and List,
2005), such that low-weighted criteria cannot over-
power high-weighted ones. For instance, if a crite-
rion weighted #, the platform can only be judged #
or lesser (+, | or 0) but not ∗ or higher. To obtain
a global evaluation for a platform, QWS approach
aggregates the symbols attached to criteria through
a simple counting, which is finally used to rank the
considered e-learning systems. Because of the naive
aggregation function used by the approach, the result
may be counterintuitive and not clear to explain and
justify. For example, let us suppose three e-Learning
systems, denoted by e
1
, e
2
, e
3
respectively, for which
the aggregation function delivers the results as sum-
marized in Table 1. It is easy to conclude that e
1
is
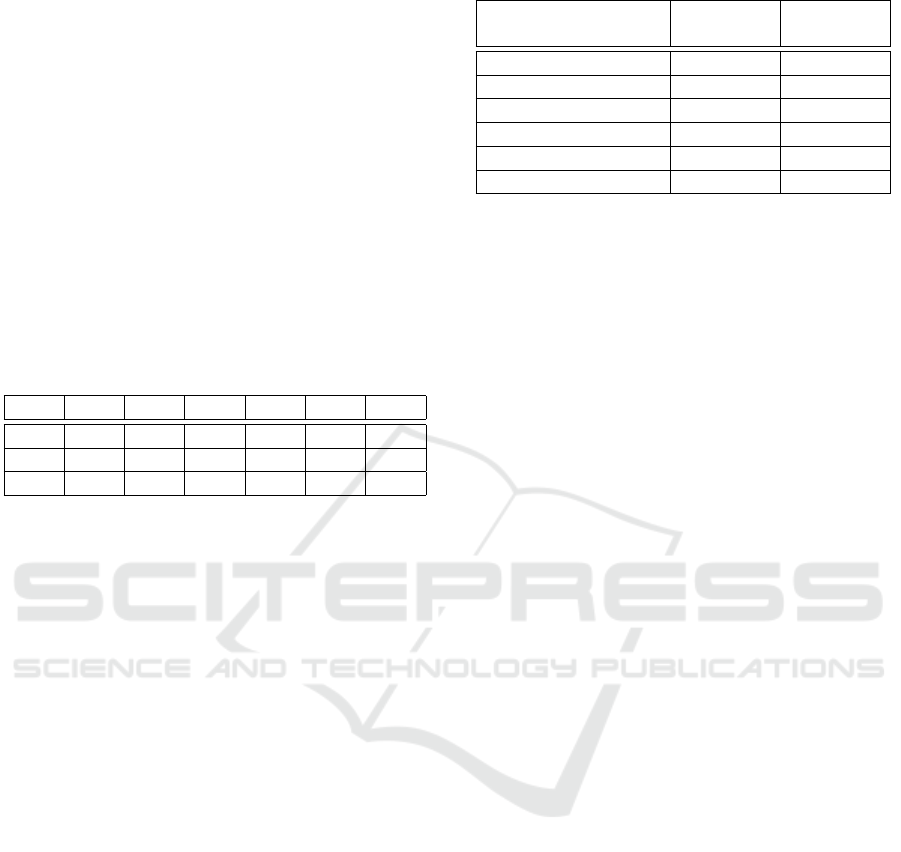
Table 1: Example of e-Learning system aggregation results.
E ∗ # + | 0
e
1
- 3 4 - 2 -
e
2
- 2 4 - 2 -
e
3
- 2 8 1 2 -
better than e
2
, since e
1
is better than e
2
on symbol ∗
and both tied the score for the other symbols. But, it is
not that easy to say whether e
1
is better than e
3
or not,
because even though e
1
performs well on symbol ∗, e
3
is much more better than e1 on symbols # and +. In
the latter case, further analysis has to be conducted to
conclude. As some e-learning systems are not compa-
rable, then the approach delivers a pre-order over the
evaluated platforms.
To deal with this issue, one can consider the Ana-
lytic Hierarchy Process (AHP) method (Hamtini and
Fakhouri, 2012). AHP is used to deal with complex
decision-making processes. It translates the symbols
defined in QWS into values as detailed in Table 2, bor-
rowed from (Stufflebeam, 1994). Thus, AHP captures
both subjective and objective values, checks their con-
sistency and reduces bias decision making in testing
and evaluating e-Learning systems (Maruthur et al.,
2015). The criteria are gathered up by category and
sub-category. The results of the feature’s category or
subcategory evaluation computed by the weight cal-
culation functions are percentages of the form of a
real number as described in (Hamtini and Fakhouri,
2012). For example, let us say that the percentage
returned for the feature Chat is 14%. Then, accord-
ing to Table 2, the judgment of this result is between
“marginally valuable” and “valuable”, but which is it?
The percentages returned can be difficult to interpret
for comparing e-learning platforms when several at-
tributes have to be dealt with.
As these methods return numerical values or av-
Table 2: QWS symbols translated into AHP weights.
QWS Weight in
AHP
Essential E 5
Extremely valuable ∗ 4
Very valuable # 3
Valuable + 2
Marginally valuable | 1
Not valuable 0 0
erages (Graf and List, 2005), which can be less ex-
pressive and non-intuitive enough from a user stand-
point for system quality assessment and ranking, then
we propose in this paper a hybrid approach for sys-
tem assessment and ranking combining QWS values,
symbolic preference relations and formal comparison
operators, which have been proved to be total orders
allowing the distinction of optimal e-Learning plat-
forms from the user standpoint.
The remainder of the paper is structured as fol-
lows. Section 2 details our symbolic-based approach
for e-Learning systems evaluation. Section 3 presents
an illustrative example of our approach to evaluate
and to rank a set of open-source e-Learning systems.
Finally, section 4 concludes the paper and introduces
some future work.
2 HYBRID E-LEARNING
SYSTEM EVALUATION
APPROACH
In this section, we detail our approach for e-Learning
platform evaluation and ranking relying on symbols
borrowed from QWS method and qualitative prefer-
ence relation and comparison operators. In Subsec-
tion 2.1, we introduce our evaluation approach and in
Subsection 2.2, we show the use of our approach for
e-learning platform ranking.
2.1 Symbolic Approach for e-Learning
Platforms Evaluation
We define the evaluation symbols as follows.
Definition 1 (Evaluation Symbols). The evaluation
symbols as defined in QWS approach are:
E = essential, * = extremely valuable, # = very valu-
able, + = valuable, | = marginally valuable and 0 =
not valuable. We denote by S = {E, ∗, #, +, |, 0} an
ordered set of evaluation symbols.
We define a preference relations more preferred
than or equal to, denoted by , and less preferred
e-Learning Platform Ranking Method using a Symbolic Approach based on Preference Relations
115

than or equal to, denoted by , over the evaluation
symbol set S as follows.
Definition 2 (Preference relations  and ). Let
S = {E, ∗, #, +, |, 0} be an ordered set of evaluation
symbols such that:
• Position 1 is for symbol E, denoted by pos
S
(E)
• Position 2 is for symbol ∗, denoted by pos
S
(∗)
• Position 3 is for symbol #, denoted by pos
S
(#)
• Position 4 is for symbol +, denoted by pos
S
(+)
• Position 5 is for symbol |, denoted by pos
S
(|)
• Position 6 is for symbol 0, denoted by pos
S
(0)
We define the preference relation more preferred
than or equal to  over S as follows.
∀(a, b) ∈ S
2
: a  b iff pos
S
(a) ≤ pos
S
(b) (1)
The preference relation less preferred than or
equal to, denoted , is defined as follows.
∀(a, b) ∈ S
2
: a  b iff pos
S
(a) ≥ pos
S
(b) (2)
We can easily prove that the preference relation 
is a total order.
Property 1. (Total order properties). The preference
relations  and  are a total order.
Proof. The proof of property 1 is detailed in Ap-
pendix A.
Based on the above defined preference relations,
we define two comparison operators named pre f Min
and pre f Max, so that it will be possible to compare
systems on each criterion describing them. These op-
erators will serve as means to aggregate the evalua-
tions obtained for system criteria.
Definition 3. (pre f Max and pre f Min comparison
operators). pre f Max and pre f Min operators are de-
fined by formulas (3) and (4) respectively.
The function pre f Max is defined by the following
formula (3).
S × S → S
(a, b) 7→ max(a, b) =
(
a i f (a  b)
b otherwise.
(3)
The function pre f Min is defined by the following
formula (4).
S × S → S
(a, b) 7→ min(a, b) =
(
a i f (a  b)
b otherwise.
(4)
When we apply the comparison operators
pre f Max and pre f Min over our symbolic set S , we
obtain Table 3.
Property 2. (pre f Max properties). pre f Max is as-
sociative, commutative, idempotent, it has E as ab-
sorbent element and 0 as neutral element.
Proof. Proofs of pre f Max properties are detailed in
Appendix B.
Property 3. (pre f Min properties). pre f Min is as-
sociative, commutative, idempotent, it has 0 as ab-
sorbent element and E as neutral element.
Proof. Proofs of pre f Min properties are detailed in
Appendix C.
2.2 Using our Comparison Operators to
Rank e-Learning Systems
The evaluation of e-Learning platforms is based on
categories, each of which defines some criteria as de-
fined in (Atthirawong and MacCarthy, 2002), for ex-
ample the category Communication tools, and their
criterion such as Chat. Categories and their criteria
are summarized in Table 4. The five categories con-
sidered in platform evaluation are the following:
• Communication tools
• Software and installation
• Administrative tools and security
• Hardware presentation tools
• Management features
To evaluate each category, we use the comparison op-
erators pre f Max and pre f Min. But to evaluate a
considered e-Learning system, we need the evalua-
tion of the five categories. For that purpose, we de-
fine two aggregation operators, called pre f MinMax
and pre f MaxMin, which are based on our compari-
son operators.
Definition 4. (pre f MinMax). Let A be a matrix of n
lines and m columns of evaluation symbols of S . We
define the minimum guaranteed satisfaction value as
follows.
We denote a matrix from A as:
A = (a
i j
)
1≤i≤m
1≤ j≤n
and a
i j
∈ S
We define pre f MinMax of A as:
S
m×n
→ S
A 7→ pre f MinMax(A) =
pre f Min
1≤i≤m
(pre f Max
1≤ j≤n
(a
i j
))
(5)
CSEDU 2016 - 8th International Conference on Computer Supported Education
116

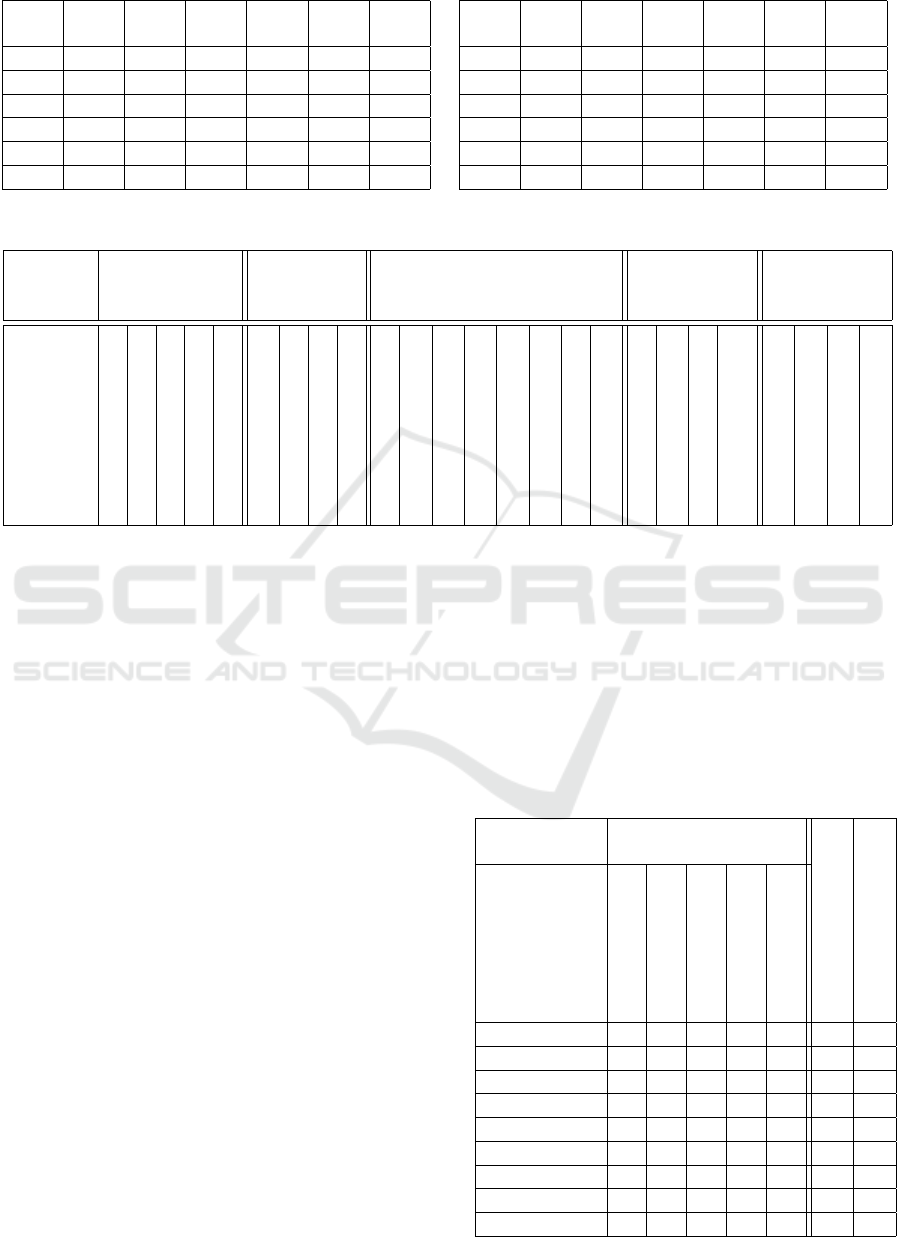
Table 3: The operators pre f Max and pre f Min table.
pre f −
Max
E ∗ # + | 0
E E E E E E E
∗ E ∗ ∗ ∗ ∗ ∗
# E ∗ # # # #
+ E ∗ # + + +
| E ∗ # + | |
0 E ∗ # + | 0
pre f −
Min
E ∗ # + | 0
E E ∗ # + | 0
∗ ∗ ∗ # + | 0
# # # # + | 0
+ + + + + | 0
| | | | | | 0
0 0 0 0 0 0 0
Table 4: Overview of the evaluation hierarchy categories and their criteria.
Category Communication
tools
Software &
Installation
Administrative
tools and Security
Hardware
Presentation
tools
Management
features
Criterion Chat Forum Mail Video conference Calendar Downloading Installation Assistance Documentation Courses administration Tracking progress Online registration Learning path creation Report Learning path organisation Test evaluation Security Announcements Learning Objects Exercices Content import Multi course management Multi user management Evaluation management User Group
Definition 5. (pre f MaxMin). We define the
maximum possible satisfaction value of S
m×n
as
pre f MaxMin:
S
m×n
→ S
A 7→ pre f MaxMin(A) =
pre f Max
1≤i≤m
(pre f Min
1≤ j≤n
(a
i j
))
(6)
The pre f MinMax operator computes the least
optimistic value amongst the criteria, whereas
pre f MaxMin operator computes the greatest pes-
simistic value amongst the criteria.
3 ILLUSTRATIVE EXAMPLE
We apply our e-Learning systems evaluation approach
to a set of nine open-source e-Learning enumerated
below, and which have been tested and compared their
(Lebrun et al., 2008),(Reiter et al., 2006) (Dogbe Se-
manou et al., 2007) (Laforcade and Oubahssi, 2014).
1. Claroline: version 1.9.2, http://www.claroline.net
2. Dokeos: version 2.1.1, http://www.dokeos.com/fr
3. eFront: version 3.6.11,
http://www.efrontlearning.net
4. ILIAS: version 4.1.3, http://www.ilias.de
5. Open ELMS: version 7, http://www.openelms.org
6. Ganesha: version 4.5, http://www.ganesha.fr
7. Olat: version 7.2.1, http://www.olat.org
8. AnaXagora: version 3.5,
http://www.anaxagora.tudor.lu
9. Sakai: version 10.4, https://sakaiproject.org
Table 5: pre f Min and pre f Max results for Communication
Tools category.
Category Communication
tools
pre f Min
pre f Max
Criterion chat Forum Mail Conference Video Calendar
Claroline # # + # + + #
Dokeos ∗ + + ∗ ∗ + ∗
eFront | # # + + | #
ILIAS # + + 0 + 0 #
Open ELMS 0 0 ∗ 0 0 0 ∗
Ganesha # # + 0 0 0 #
Olat ∗ ∗ ∗ 0 ∗ 0 ∗
AnaXagora # # # 0 + 0 #
Sakai ∗ # ∗ ∗ # # ∗
e-Learning Platform Ranking Method using a Symbolic Approach based on Preference Relations
117

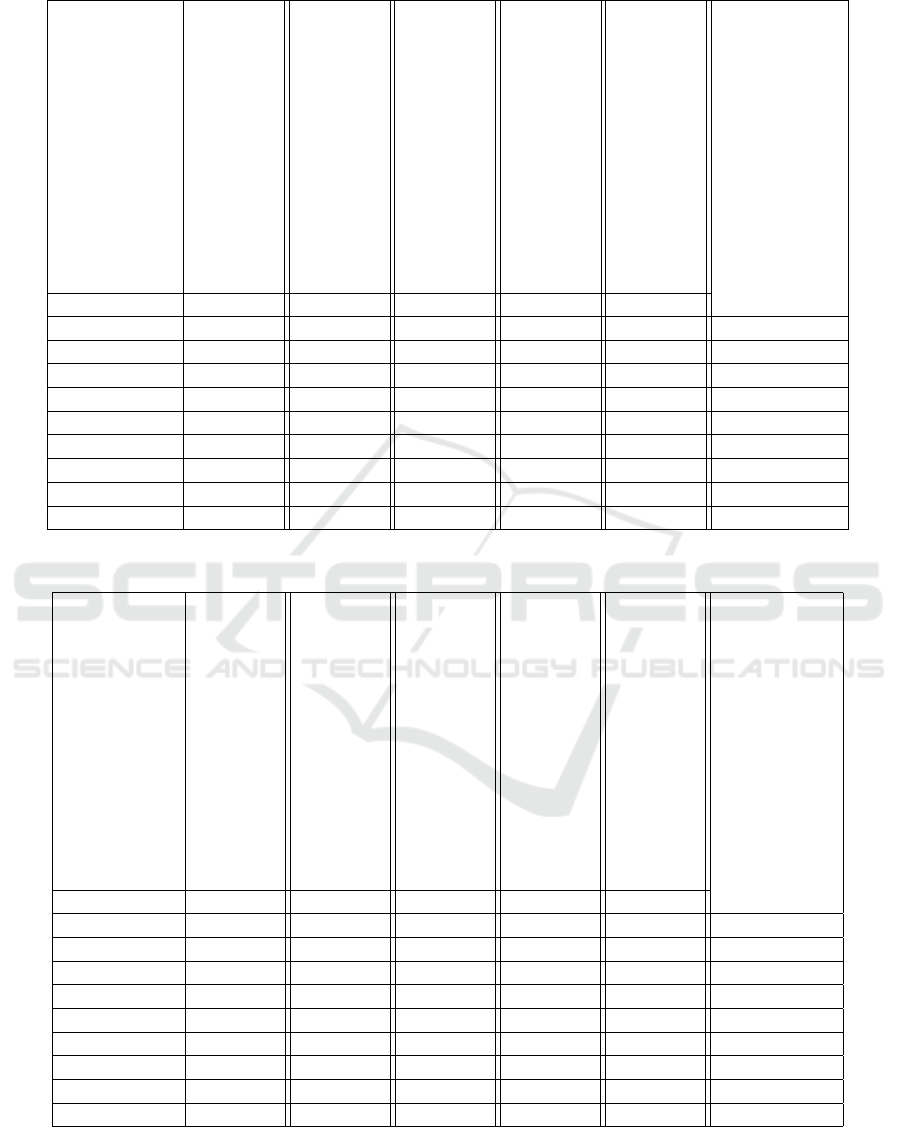
Table 6: Results of pre f MaxMin computation over the set of e-learning platform.
Category Communication tools Software & Installation Administrative tools and Security Hardware presentation tools Management features
pre f MaxMin
Platform pre f Min pre f Min pre f Min pre f Min pre f Min
Claroline + + + # + #
Dokeos + | | # + #
eFront | # | | | #
ILIAS 0 | | 0 | |
Open ELMS 0 | | 0 0 |
Ganesha 0 | + 0 # #
Olat 0 | | 0 | |
AnaXagora 0 | | 0 | |
Sakai # | | 0 | #
Table 7: Results of pre f MinMax computation over the set of e-learning platform.
Category Communication tools Software & Installation Administrative tools and Security Hardware presentation tools Management features
pre f MinMax
Platforms pre f Max pre f Max pre f Max pre f Max pre f Max
Claroline # ∗ ∗ ∗ # #
Dokeos ∗ # E ∗ E #
eFront # ∗ ∗ + + +
ILIAS # + # # + +
Open ELMS ∗ + ∗ ∗ # +
Ganesha # + E # # +
Olat ∗ # ∗ ∗ ∗ #
AnaXagora # + ∗ # ∗ +
Sakai ∗ ∗ E ∗ E ∗
Each criterion takes a symbolic value from the set S
based on users opinions community. To obtain the
evaluation of each criterion, we have carried out sur-
veys in our university involving under-graduated stu-
dents (small group of 10 students), who have tested
each e-learning platform during a training session (2
CSEDU 2016 - 8th International Conference on Computer Supported Education
118

Table 8: E-Learning platform’s features evaluation.
Category Communication
tools
Software &
Installation
Administrative
tools and Security
Hardware
presentation
tools
Management
features
Criterion
chat
Forum
Mail
Video conference
Calendar
Downloading
Installation
Assistance
Documentation
Courses administration
Tracking progress
Online registration
Learning path creation
Report
Learning path organisation
Test evaluation
Security
Announcements
Learning Objects
Exercises
Content import
Multi course management
Multi user management
Evaluation management
User group
Claroline # # + # + ∗ + # ∗ # # + + ∗ + # # ∗ ∗ # ∗ + + + # Dokeos ∗ + + ∗ ∗ # | + + + E + | E | # # ∗ ∗ # ∗ + + E + eFront | # # + + ∗ # # # | ∗ + # ∗ # # # | + + + + | + | ILIAS # + + 0 + + | | | | + # | | | | # 0 # + 0 + | + | Open ELMS 0 0 ∗ 0 0 + | + + | # + + # | ∗ | 0 ∗ 0 # 0 0 # # Ganesha # # + 0 0 + | + + # E | + E # # + 0 # 0 # # # # # Olat ∗ ∗ ∗ 0 ∗ + | | # # ∗ | + # | # # 0 ∗ ∗ ∗ | + ∗ ∗ AnaXagora # # # 0 + + | + | # ∗ | ∗ + # # + 0 + # | | # # ∗ Sakai ∗ # ∗ ∗ # ∗ | ∗ | E ∗ | E ∗ ∗ ∗ | ∗ # 0 # | # E ∗
e-Learning Platform Ranking Method using a Symbolic Approach based on Preference Relations
119

hours). We are aware that the process is subjective
and a different panel of students or users can express
different opinions about the e-Learning platforms. We
recall that this data collection aims at illustrating the
use of our approach. The values obtained for each cri-
terion in its category are summarized in Table 8. The
application of our approach on the set of considered
systems is performed as follows.
1. for each category in Table 4 we calculate values
of pre f Min and pre f Max for all functionalities
based on Definition 3. In Table 5, we display the
results obtained by applying our approach on the
category “Communication Tools” for our consid-
ered set of e-learning platforms.
2. for all categories in Table 8 we calculate values of
pre f MaxMin and pre f MinMax. Results of both
calculus are displayed in Table 6 and 7 respec-
tively.
According to Table 6, we obtain the following ranking
over the set of e-learning system considered.
1. Claroline, Dokeos, eFront, Ganesha and Sakai.
2. Ilias, Open ELMS, Olat and AnaXagora.
According to Table 7, we obtain the following
ranking over the set of e-learning system considered.
1. Sakai
2. Claroline, Dokeos and Olat
3. eFront, ILIAS, Open ELMS, Ganesha and
AnaXagora
Finally, users can make a choice based on either
pre f MaxMin or pre f MinMax operators or can com-
bine the result returned by both. For instance, in
our illustrative example, Claroline, Dokeos, eFront,
Ganesha and Sakai are all optimal platforms accord-
ing to pre f MaxMin operator, whereas Sakai is the op-
timal one according to pre f MinMax operator. But,
we can notice that Sakai performs better since it is
optimal according to both operators.
4 CONCLUSION AND FUTURE
WORK
In this paper, we have presented an e-Learning sys-
tems evaluation approach based on a symbolic set of
value, a total order preference relation and compar-
ison operators. To describe e-Learning system, we
have used categories, each of which defines some cri-
terion of well-known properties of these systems. We
apply our approach on a set of open source e-Learning
systems for which you have gathered through small
surveys their evaluation on the considered criteria.
The proposed approach assesses the quality of an e-
Learning system amongst a set of e-Learning plat-
forms by considering a maximum possible satisfac-
tion and/or a minimum guaranteed satisfaction. Once
this value is obtained, it becomes easy to rank the set
of e-learning systems considered from the most to the
least satisfactory, and to deliver to the user the one or
several optimal systems.
Our approach brings a solution to the problem of
choosing a system according to well-defined criteria.
It is still to perform a larger survey to obtain values as
accurate as possible for the criteria. It is also worthy
to consider user profiles when performing surveys in
such a way that we obtain different values for different
profiles. A profile can be defined over a population of
users based on their interests and training objectives.
REFERENCES
Atthirawong, W. and MacCarthy, B. (2002). An applica-
tion of the analytical hierarchy process to international
location decision-making. In Gregory, Mike, Proceed-
ings of The 7th Annual Cambridge International Man-
ufacturing Symposium: Restructuring Global Manu-
facturing, Cambridge, England: University of Cam-
bridge, pages 1–18.
Ba
˜
nados, E. (2013). A blended-learning pedagogical model
for teaching and learning efl successfully through an
online interactive multimedia environment. Calico
Journal, 23(3):533–550.
Britain, S. and Liber, O. (2004). A framework for pedagog-
ical evaluation of virtual learning environments.
Colace, F., Santo, M. D., and Pietrosanto, A. (2006). Eval-
uation models for e-learning platform: an ahp ap-
proach.
Dogbe Semanou, D. A. K., Durand, A., Leproust, M.,
and Vanderstichel, H. (2007). Etude comparative de
plates-formes de formation
`
a distance. le cadre du
Projet@ 2L Octobre.
Garc
´
ıa, F. B. and Jorge, A. H. (2006). Evaluating e-learning
platforms through scorm specifications. In IADIS Vir-
tual Multi Conference on Computer Science and In-
formation Systems (MCCSIS 2006), IADIS.
Graf, S. and List, B. (2005). An evaluation of open source e-
learning platforms stressing adaptation issues. In Pro-
ceedings of the 5th IEEE International Conference on
Advanced Learning Technologies, ICALT’05, pages
163–165. IEEE Computer press.
Hamtini, T. M. and Fakhouri, H. N. (2012). Evalu-
ation of open-source e-learning platforms based
on the qualitative weight and sum approach
and analytic hierarchy process. Technical re-
port, Retrieved 2013/05/21 from http://www. iiis.
org/CDs2012/CD2012SCI/IMSCI 2012/PapersPdf/E
A418WG. pdf.
CSEDU 2016 - 8th International Conference on Computer Supported Education
120

Hannan, T. M. (2013). Politique-en-pratique pour la pol-
yarthrite rhumatoide:
´
etude randomis
´
ee d’essai et la
cohorte control
´
ee de e-learning visant une meilleure
gestion de la physioth
´
erapie.
Laforcade, C. P. and Oubahssi, L. (2014).
´
Etude compara-
tive de plates- tude comparative de plates- formes de
formation
`
a distance.
Laurillard, D. (2013). Rethinking university teaching:
A conversational framework for the effective use of
learning technologies. Routledge.
Lebrun, M., Docq, F., Smidts, D., et al. (2008). Claro-
line, une plate-forme denseignement et dapprentissage
pour stimuler le d
´
eveloppement p
´
edagogique des en-
seignants et la qualit
´
e des enseignements: premi
`
eres
approches. In Colloque de lAIPU, Montpellier.
Liber, O., Olivier, B., and Britain, S. (2000). The toomol
project: supporting a personalised and conversa-
tional approach to learning. Computers & Education,
34(3):327–333.
Maruthur, N. M., Joy, S. M., Dolan, J. G., Shihab, H. M.,
and Singh, S. (2015). Use of the analytic hierarchy
process for medication decision-making in type 2 dia-
betes. PloS one, 10(5).
Reiter, S., Kohlbecker, J., and Watrinet, M.-L. (2006).
Anaxagora: a step forward in e-learning. In
ECEL2006-5th European Conference on elearning:
ECEL2006, page 291. Academic Conferences Lim-
ited.
Schneider, A., Albers, P., and Mattheis, V. M. (2015).
E-Learning en urologie: Mise en oeuvre de
l’apprentissage et l’enseignement Platform CASUS -
Avez patients virtuels conduire a une am
´
elioration
des r
´
esultats d’apprentissage d’une
´
etude randomis
´
ee
chez les
´
etudiants, volume Volume 94. Karger AG ,
Basel.
Stoffregena, J., Pawlowski, J. M., and Pirkkalainen, H.
(2015). A barrier framework for open e-learning in
public administrations.
Stufflebeam, D. L. (1994). Empowerment evaluation, ob-
jectivist evaluation, and evaluation standards: Where
the future of evaluation should not go and where it
needs to go. Evaluation practice, 15(3):321–338.
Ubell, R. (2000). Engineers turn to E-Learning, volume
Volume 37. IEEE Spectrum.
Venkataraman, S. and Sivakumar, S. (2015). Engaging stu-
dents in group based learning through e-learning tech-
niques in higher education system. International Jour-
nal of Emerging Trends in Science and Technology,
2(01).
Appendix
A Proof of Property 1 Total Order
We only prove hereinafter the property for the
preference relation . The proof of the property
for the preference relation  is similar to the one of .
Proof 1. ( is total order) The preference relation 
is a total order iff:
1.  is reflexive
2.  is antisymmetric
3.  is transitive
1. Relation  is reflexive iff ∀a ∈ S : a  a. There-
fore, a  a iff pos
S
(a) ≤ pos
S
(a) which is verified
for the comparison operator ≤ since ≤ is reflex-
ive. Then  is reflexive.
2. Relation  is antisymmetric iff ∀a, b ∈ S : a = b.
Then:
a  b ∧ b  a iff pos
S
(a) ≤ pos
S
(b) ∧ pos
S
(b) ≤
pos
S
(a) which is verified for ≤ since ≤ is anti-
symmetric.
Then  is antisymmetric.
3.  is transitive iff ∀a, b, c ∈ S : a  b ∧ b  c ⇒
a  c. As a  b ∧ b  c then pos
S
(a) ≤ pos
S
(b)
∧ pos
S
(b) ≤ pos
S
(c). Therefore, pos
S
(a) ≤
pos
S
(c) since ≤ is transitive. That means that
a  c and  is transitive.
B Proof of pre f Max Properties
Proof 2. (pre f Max properties).
1. pre f Max is associative on S:
∀a, b, c ∈ S , then: pre f Max(pre f Max(a, b), c) =
pre f Max(a, pre f Max(b, c)). We denote by I the
left term Pre f Max(Pre f Max(a, b), c) and by II
the right term Pre f Max(a, Pre f Max(b, c)).
Table 9 shows results of evaluation of the left and
the right terms, which are identical. Therefore
pre f Max is associative.
Table 9: The formula results.
I II
a  b ∧ a  c a ⇒a  pre f Max(b, c) ⇒ II = a
a  b ∧ c  a c ⇒ c  b (transivity)
pre f Max(b, c) = c ⇒ II = c
since c  a
b  a ∧ b  c b pre f Max(b, c) = b ⇒ II = b
since b  a
b  a ∧ c  b c pre f Max(b, c) = c ∧ c  a
(transitivity) ⇒ II = c
2. pre f Max is commutative iff ∀a, b ∈ S :
pre f Max(a, b) = pre f Max(b, a).
From table 3, the pre f Max matrix is symmetric
so pre f Max is commutative.
e-Learning Platform Ranking Method using a Symbolic Approach based on Preference Relations
121

3. pre f Max is idempotent iff ∀a ∈ S :
pre f Max(a, a) = a.
From the main diagonal of table 3, we conclude
that pre f Max is idempotent.
4. pre f Max has 0 as neutral element iff ∀a ∈ S :
pre f Max(a, 0) = a.
Table 3 shows that pre f Max has 0 as neutral ele-
ment.
5. pre f Max has E as absorbent element iff ∀a ∈ S :
pre f Max(a, E) = E.
Table 3 also shows that pre f Max has E as ab-
sorbent element.
C Proof of pre f Min Properties
Proof 3. (pre f Min properties)
1. pre f Min is associative on S :
∀a, b, c ∈ S : pre f Min(pre f Min(a, b), c) =
pre f Min(a, pre f Min(b, c)). We denote by I the
left term Pre f Min(Pre f Min(a, b), c) and by II
the right term Pre f Min(a, Pre f Min(b, c)).
Table 10 shows results of evaluation of the
left and the right terms, which are identical.
Therefore pre f Min is associative.
Table 10: The formula results.
I II
a  b ∧ b  c c ⇒ a  pre f Min(b, c) ⇒ II = c
since a  c
a  b ∧ c  b b ⇒a  pre f Min(b, c) ⇒ II = b
since a  b
b  a ∧ a  c c ⇒ b  c (transivity)
pre f Min(b, c) = c ⇒ II = c
since a  c
b  a ∧ c  a a a is the smallest symbol
between a, b and c, so II = a
2. pre f Min is commutative iff ∀a, b ∈ S :
pre f Min(a, b) = pre f Min(b, a).
From table 3, the pre f Max matrix is symmetric
so pre f Min is commutative.
3. pre f Min is idempotent iff ∀a ∈ S :
pre f Min(a, a) = a.
From the main diagonal of table 3, we conclude
that pre f Min is idempotent.
4. pre f Min has E as neutral element iff ∀a ∈ S :
pre f Min(a, 0) = a.
Table 3 shows that pre f Min has E as neutral ele-
ment.
5. pre f Min has 0 as absorbent element iff ∀a ∈ S :
pre f Min(a, E) = E.
Table 3 also shows that pre f Min has 0 as ab-
sorbent element.
CSEDU 2016 - 8th International Conference on Computer Supported Education
122