
Computer Supported Evolution Inside Van Hiele Levels 1 and 2
Borislav Lazarov
1
and Rumyana Papancheva
2
1
Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, Sofia, Bulgaria
2
Faculty of Social Sciences, University ”Prof. Dr Asen Zlatarov”, Burgas, Bulgaria
Keywords:
Pre-deductive Phase, Van Hiele Levels, Communicative Abilities.
Abstract:
The goal of the study is to clarify the communicative abilities of 5th grade students related to the computer
supported geometry education. Theoretical frame is the Van Hieles’ model. The experimental teaching gives
an idea of how the language characteristics of Level 1 and 2 could be improved by a short-term game-like math
education. Some coding-decoding activities make students to be more accurate in written communications.
1 A MODERN VECTOR IN MATH
EDUCATION
In the last 30 years ICT enhanced math education be-
came routine practice in secondary school. It was
based mainly on the development of computer al-
gebra systems (CAS) and dynamic geometry soft-
ware (DGS). Key role in this trend plays the so-called
inquiry-based approach (Rocard et al., 2007) which
is a kind of a modern Socratic style (Lazarov, 2014).
But in 2007 there appeared a paper where the role of
the mathematics education in secondary school was
reconsidered (Haapasalo, 2007). It is a matter of fact
that the advanced usage of ICT refers to some specific
communication skills and applications of mathemat-
ics methods. No other school subject than mathemat-
ics can face better these demands of life, so the vector
of the secondary school math education should con-
tain components that meet the ICT needs of a modern
individual.
Our recent research shows that high school stu-
dents who use dynamic geometry software (DGS) in
studying mathematics developed intuitively specific
communication skills (Lazarov, 2015). Their writ-
ten math slang includes synthetic symbols and icons
(like dynamic pictures and graphs) parallel to the tra-
ditional formulas and shorthands. This slang evolves
along with the educational process and reflects the
level of student’s geometrical reasoning. Our practice
clearly shows that the constructing of DGS applets re-
quires a student to have reached at least Van Hiele
Level 3
1
. In fact any dynamically stable construction
1
We are going to make a lot of references to the first
(i.e. such that preserves the geometrical properties of
the objects after some transformations) is made fol-
lowing an algorithm reflecting the properties of the
figures. The design of such algorithm requires student
to apply at least short deductive chains using the DGS
syntax. Our experience confirms that the proper us-
age of DGS syntax needs a long training ’within the
following categories concerning what modern tech-
nology can maintain and promote:
(1) Links between conceptual and procedural knowl-
edge,
(2) Metacognitions and problem-solving skills,
(3) Sustainable components of mathematics making,
(4) Interplay between systematic approaches and min-
imalist instruction,
(5) Learning by design’ (Haapasalo, 2007).
But following the Van Hieles’ theory, in order to be
at Level 3 a student should pass consecutively Lev-
els 1 and 2. So the question is what kind of math
activities will contribute to the development of ICT
skills in pre-deductive phase. We started exploring
the mathematics and informatics curriculum to find
the most adequate starting point for introducing inte-
grated mathematics and IT approaches.
2 THE STATUS QUO IN
BULGARIA
The change in the teaching style that happens on
the borderline between primary and secondary school
three Van Hiele levels so we give a brief description of them
in an Appendix.
186
Lazarov, B. and Papancheva, R.
Computer Supported Evolution Inside Van Hiele Levels 1 and 2.
In Proceedings of the 8th International Conference on Computer Supported Education (CSEDU 2016) - Volume 2, pages 186-192
ISBN: 978-989-758-179-3
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

in Bulgaria (4th-5th grade) has several dimensions.
First of all, it considers the subject-oriented approach
which comes to substitute the (more or less) topic-
oriented mode of teaching in primary school. A sec-
ond important moment is the change of the teachers
who are engaged with a particular class. The related
subjects like mathematics and information technol-
ogy are already separate disciplines in the school plan,
sometimes covered by one teacher, but more often by
different persons. The math and IT syllabus are made
by different commissions at the Ministry of Education
which yields to relatively poor interrelated connec-
tions. The Bulgarian math syllabus up to 2015/2016
scholastic year does not provide additional space for
activities of mixed (conventional and IT based) type
in which the necessary skills for inquiry-based educa-
tion to be built. Such status quo makes it hard to take
advantages of IT in traditional math education and
vice versa. So the teachers and educators are search-
ing their own way to achieve integration of IT in math
education in the mode they think is most appropriate
for a particular target group.
Our way started with the target group of high abil-
ity senior secondary school students (Lazarov, 2014).
At this stage all students have reached the Van Hiele
Level 3, and some of them proceeded on Level 4. Stu-
dents’ knowledge, skills and attitude (KSA) are trans-
ferable from the conventional context of math educa-
tion to the DGS environment, therefore we can speak
about students’ competence of synthetic type (syn-
thetic competence). Further, we tried to apply similar
approach to intermediate secondary school students
with average abilities, i.e. incomplete Van Hiele Level
3. The results were far from satisfactory (Shabanova
& Lazarov, 2014). Only a small fraction of the target
group managed to transfer the math KSA into a new
context of DGS exploration. It became clear that the
foundation of the transferability should be established
somewhere in the early secondary school.
3 APPLICATION OF A
CLASSICAL MODEL
The Van Hiele model of learning geometry provides
a convenient base for interpreting and analyzing the
students’ levels of understanding. In parallel, this
model clarifies the way they form geometrical rea-
soning. Special role in the model plays the develop-
ment of the language in which students express their
knowledge, as far as each level has its own linguis-
tic symbols and own network of relationships con-
necting those symbols (Usiskin, 1982). For instance,
student’s progress from Level 1 to Level 2 yields a
significant structuring of relationships and a refine-
ment of concepts. Teacher should feel how such tran-
sition occurs and should tune his/her language for ad-
equate verbalization of the intuitive knowledge, be-
cause the verbalization goes together with a restruc-
turing of concepts. As we mentioned above, the nec-
essary level for meaningful use of DGS is Level 3,
so the concept restructuring must first occur at Level
2 before students can start exploring the logical rela-
tionships needed for creating DGS applets.
The geometry education in Bulgarian 5th grade
is characterized with a significant intensification. As
evidence we point that the number of new geometri-
cal concepts in 5th grade is about 4 times bigger than
all geometrical concepts introduced in the previous 4
years. Moreover, many problems require a construc-
tion to be done and a solution to be written which
needs more developed language for communications
in both directions - understanding the statements and
composing statements. For instance, let us consider
the following problem:
Draw ∠POQ = 30
◦
and a point A on the ray OQ such
that OA = 10 cm. Find the distance from A to the ray
OP. (Lozanov et al., 2011)
Here students are expected to turn a description
into a picture before starting the solution. They
should draw an arbitrary ray, then measure the an-
gle (using protractor), then find a specific point and
erect a perpendicular from it to a line (to do this, stu-
dents should know that the distance equals the length
of the perpendicular). The solution of the problem
is based on both conceptual and procedural knowl-
edge and skills. This two knowledge types seem to
be developed iteratively (Rittle-Johnson & Koedinger,
2004). In our opinion such activities are accessible for
Level 2 and up and could be built by integrating IT in
math education.
What follows refers to our research in lower sec-
ondary school (Bulgarian 5th grade), which supposes
the Van Hiele Level 2 (sometimes incomplete) has
been reached. We tried to manipulate students’ at-
titude towards elaborating more precise and reliable
communication style in learning mathematics by ap-
plying IT. We hope this approach will guarantee the
foundation of KSA which is necessary for the next
steps in building synthetic competence.
4 FRAMEWORK OF THE STUDY
The goal of our study was to clarify the communica-
tive abilities of 5th grade students related to the com-
puter supported geometry education. Designing our
experimental teaching we took into account the fol-
Computer Supported Evolution Inside Van Hiele Levels 1 and 2
187

lowing two requirements (Kadijevich, 2006):
(1) when utilize mathematics, don’t forget available
tool(s); when make use of tool, don’t forget the un-
derlying mathematics;
(2) to solve the assigned task, use, whenever possi-
ble, a process approach as well as an object approach,
working with different representations .
According to the above requirements, we chose the
MS Paint application with Basic shapes for the IT ac-
tivities. This application provides relevant resources
for Levels 1 and 2: ready-made shapes as isosceles
triangle, right-angled triangle, as well as three types
of transformations: rotation, stretching, dragging.
Another moment in the research design was the
choice of the topic. We recognize the unavoidable
usage of familiar everyday concepts on the first two
levels, so we expected students’ descriptions to be in
the form of a meta-language (mixture of geometrical
and everyday life language, expanded with pictures
and shorthands). Students were assigned to sketch a
monster using some geometrical shapes. Among the
other educational reasons, this topic was selected be-
cause of the anthropomorphic and zoomorphic terms
that potentially could help the composite figures to be
properly depicted. Let us point the anthropomorphic
origin of some concepts in geometry like legs of a tri-
angle and trapezium in Bulgarian math language. The
idea of the topic came from a creative writing project,
proposed by Linda Yollis in her blog (Yollis, 2014).
The accent in her project work was on developing cre-
ative thinking and writing skills.
5 PARAMETERS OF THE STUDY
The target group was composed of 5th grade students
(no indication for additional interest in mathematics
among them). The experimental teaching lasted 6
academic hours distributed in the following manner:
– Diagnostic test.
– Math class. Revision of geometrical students’
knowledge.
– ICT class. Students created on computer their mon-
sters, constructed by different geometrical figures, us-
ing a simple computer graphic program - MS Paint.
– Language class. Writing a description of a picture.
Each student wrote a short description of his/her own
monster.
– ICT class. Students exchanged their descriptions
and based on the written texts they created a copy of
the original monsters on computer.
– Control test.
Students worked individually but grouped by pairs on
the next assignments:
(A1) A monster to be drawn using the following basic
shapes: rectangle (including square), triangle (isosce-
les, right), and circle.
(A2) The own monster to be described by words and
to be sent to a classmate for depicting.
(A3) The descriptions to be interchanged in the class-
mate pair, the other monster to be depicted following
only the description and to be compared with the orig-
inal.
During the lessons some comments and remarks on
the assignment were done. Students were pointed out
that the figure type is invariant when applying any of
the three transformations.
6 INDICATORS AND DATA
COLLECTION
We observed several indicators but some of them were
covered by all students (like classifying the general
type of a polygon or reconstructing an abstract figure
following a verbal description), so we took them away
from the analysis. The following indicators were used
to determine the initial Van Hiele level including the
degree of completeness inside the level:
(i1) recognizing the square and the rectangle no mat-
ter how it is oriented;
(i2) the square is considered as rectangle;
(i3) recognizing the type of a triangle (isosceles,
right);
(i4) combining two properties of triangle (isosceles
and right);
(i5) usage of geometrical properties of the figure in
description;
(i6) usage of elements of the figure like side and ver-
tex in depiction;
(i7) applying elements of the figure like side and ver-
tex in reconstruction;
(i8) reconstruction of abstract figure following verbal
description.
Indicators for determining the individual Van Hiele
level are based on the Burger-Shaughnessy opera-
tionalization (Burger & Shaughnessy, 1986), given in
the Appendix. Most of them refer to Level 2, but some
indicate Level 1, like (i1). Burger-Shaughnessy fea-
tures suppose a direct communications with students
to analyze the geometrical reasoning. Our approach
is oriented mostly to analyze the features of the stu-
dent’s written language at Levels 1 and 2. So we col-
lected data from the tests, students’ computer pictures
and written descriptions of their pictures. There were
22 pairs of students who took part in the experimental
teaching. Below we are going to present the details
CSEDU 2016 - 8th International Conference on Computer Supported Education
188
about 4 pairs that are representative for the most typ-
ical cases. The observed students are coded as PgA,
PpA, RsA, RkA, KoG, KrG, RaG, SaG.
7 STATISTICS
Table 1 shows the coverage of the indicators: 0 means
that an indicator is not covered and 1 stands for a cov-
ered indicator. Some indicators were partially cov-
ered, e.g. the corresponding test item is correct but in
the written material there were mistakes or gaps – we
scored these cases with 1.
Table 1: Coverage of the indicators.
i1 i2 i3 i4 i5 i6 i7 i8 Σ
PgA 1 1 1 1 1 0 0 1 6
PpA 1 1 1 0 0 0 0 0 3
RsA 1 1 1 1 1 1 1 1 8
RkA 1 0 1 1 1 0 0 0 4
KoG 1 0 1 1 1 0 0 1 5
KrG 0 0 1 0 0 0 0 0 1
RaG 0 0 0 0 0 0 0 0 0
SaG 1 0 1 1 1 0 0 1 5
We consider a total score Σ ≥ 4 as reaching Level
2, and Σ ≤ 3 as reaching Level 1. Initially, we in-
troduced more indicators, but these indicators were
either covered by all students or there was no student
who covered them. For instance:
usage of non geometrical concepts in description –
all;
application of elements of the figure like side and ver-
tex in description – none.
8 EXAMPLES AND COMMENTS
In this section we are going to consider some particu-
lar cases which are emblematic for the different stages
of language forming inside Levels 1 and 2. Let us
highlight that we did not register any usage of pure
geometrical concepts. All students’ descriptions of
their monsters were based on anthropomorphic fea-
tures; all geometrical shapes were colored and usually
the color stands before the shape in description.
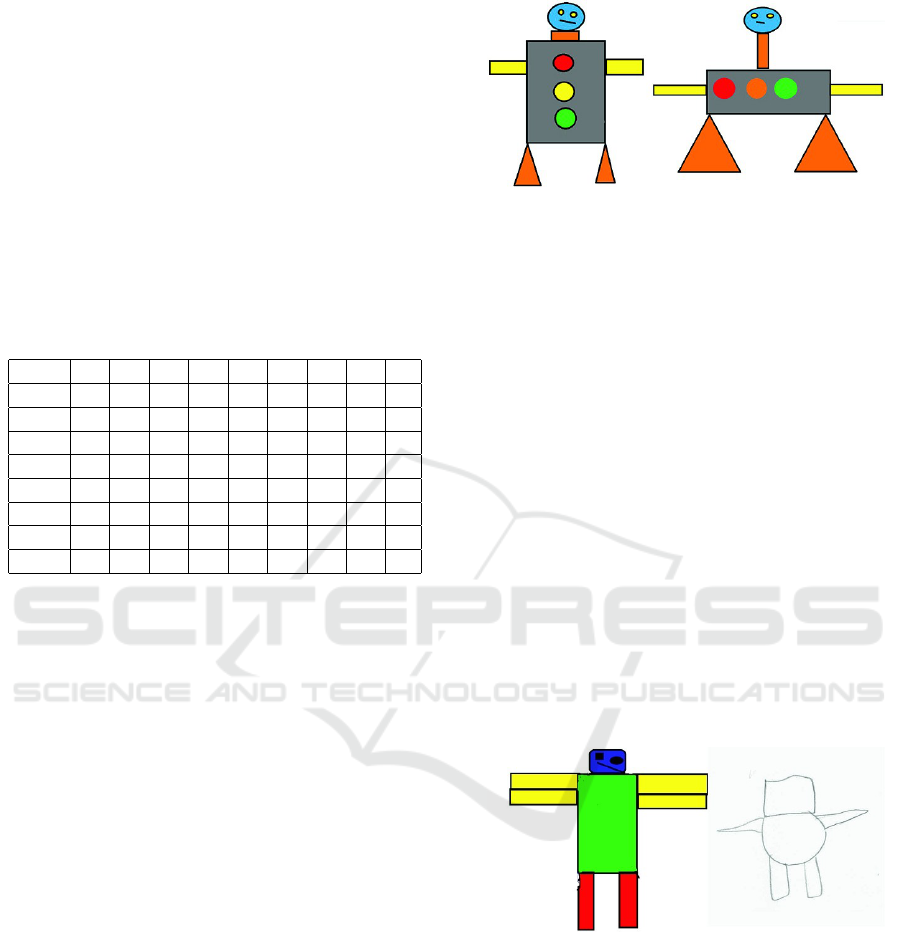
Case 1
The monster created by PgA and its replica recon-
structed by KrG are shown in Figure 1.
PgA (Level 2, Σ = 6) uses simple sentences to de-
scribe his monster, e.g. My body is a gray rectangle
Figure 1: Monster created by PgA and its decoded replica
by KrG.
as a traffic light. My neck is an orange rectangle.
There is no detailed information about sizes, direc-
tions, triangle types and so on. Just shapes, colors
and relations over and bellow.
Nevertheless, even with this simple and insuffi-
cient information, the replica created by KrG (Level
1, Σ = 1) and based on the text description, is quite
accurate. We could explain the poor description with
limited students’ knowledge of geometry at this level.
But this limited geometrical resource was sufficient
enough for the students to communicate with each
other.
Case 2
The monster created by PpA (Level 1, Σ = 3) is shown
in Figure 2 (left). The monster created by PpA is
shown in Figure 2. The student, from the position
of his monster, wrote: My head is a blue square with
rounded edges.
Figure 2: Monster created by PpA and a picture from his
test.
From mathematical point of view, this description
is completely wrong, because a polygon cannot have
rounded edges. But in computer graphic software ap-
plications (including MS Paint) we could see an icon
called rounded rectangle. Some students expand their
language including icon-labels on an equal level with
geometrical concepts. The teacher could use such
contradictions to clarify the terms and to upgrade stu-
dents’ knowledge.
The right image on Figure 2 is taken from the
PpA’s control test. The test task was to draw a figure
Computer Supported Evolution Inside Van Hiele Levels 1 and 2
189

where the arms are triangles and legs are rectangles;
the arms and the legs should be connected with the
circle body at only one vertex. PpA follows mainly
the anthropomorphic context, without paying enough
attention to geometrical details.
Case 3
The monster created by KoG (Level 2, Σ = 5) and its
replica reconstructed by PpA are shown in Figure 3.
Figure 3: Monster created by KoG and its replica decoded
by PpA.
KoG’s description is the richest one in geometrical
concepts. He described the arms as two orange equi-
lateral triangles, the horns as right triangles. But no
details about the position of these triangles was given.
So the reconstructor PpA has put the arms connected
to the body by side, not by vertex. Such problem solv-
ing examples, connected with coding and decoding
processes, could be used to develop students’ criti-
cal thinking. Here one can see how anthropomorphic
context dominates over geometrical knowledge.
Case 4
The monster, created by KrG and its replica by PgA
(Level 2, Σ = 6) are shown in Figure 4.
Figure 4: Monster created by KrG and the reconstruction
by PgA.
In her description KrG wrote that the arms are
formed by four rectangles: the straight are green and
the down are yellow. Such multimodality of the spo-
ken language (Ginsberg, 2015) applied to geometri-
cal purposes is an evidence for incomplete Level 2 of
formation of mathematical concepts and terminology.
However, KrG showed significant progress during the
experimental teaching. Her starting point was recog-
nized as Level 1, but further in her description lan-
guage appeared properly used geometrical concepts
as right triangle and rhombus. KrG covered (i6) and
(i7) and approached Level 2.
9 CONCLUSIONS
Ginsberg (ibid., pp 4-5) gives very interesting ex-
ample of misunderstanding in communication be-
tween teacher and students. Similar misunderstand-
ing appears every time when the teacher’s expecta-
tions about the geometry reasoning of the students are
not coherent with their actual Van Hiele level. There
were also quite different standing points between the
authors of this article before the analysis of the exper-
imental data was done. One of us was quite sure that
students operate at least at Level 2, but the other was
more skeptic. Our experimental teaching was held in
the beginning of 5th grade before the new geometry
topics from the school plan started. Based on the out-
comes of our study, we recommend Bulgarian teach-
ers to be very careful when using professional math
slang in their instructions.
Indeed, our observed students used mainly every-
day life expressions and images instead of geometri-
cal concepts. Some of them recognized the impor-
tance of clarity in communications after getting some
coding-decoding experience during the experimental
teaching. However, we consider problems like the one
quoted in section 3 to be still beyond the average 5th
graders’ zone of proximal development.
De Villiars stated the following open question:
could hierarchical thinking be developed earlier at
Van Hiele Levels 1 and 2 through various strategies
and using tools such as dynamic geometry software?
(De Villiers, 2010). We claim that the ability to use
DGS is equally related to mathematics and ICT, but
also it needs specific communication skills to express
the KSA. Evolution along the Van Hiele levels causes
development of a meta-language that reflects the de-
gree of geometrical reasoning but also accelerates the
evolution itself. However, DGS is not a relevant ed-
ucational tool for construction activities at Levels 1
and 2 – there is not enough mathematical KSA accu-
mulated for proper use of DGS. Even the basic under-
standing of a DGS interface requires significant math
knowledge (compare with the Level 3 features in Ap-
pendix). Thus some preparatory training should be
done for some connections between elements of the
CSEDU 2016 - 8th International Conference on Computer Supported Education
190

figures at Level 1 and 2. Short deductive chains ap-
pear naturally during such training and computer ap-
plications of lower class than DGS allow to achieve
clarity and precision of the expression of these chains.
ACKNOWLEDGEMENTS
The authors thank to the reviewers for the suggestions
which are taken into account in the final version of
this paper. The authors are very thankful to Albena
Vassileva for the improvement of the text.
REFERENCES
Burger, W. F. & Shaughnessy, J. M. (1986). Characteriz-
ing the Van Hiele levels of development in geome-
try. Journal for Research in Mathematics Education,
17(1), pp 31-48.
De Villiers, M. (2010) Some Reflections on the Van Hiele
theory. Invited plenary presented at the 4th Congress
of teachers of mathematics of the Croatian Mathemat-
ical Society, Zagreb, 30 June – 2 July 2010.
Ginsberg, D. (2015) Multimodal semiotics of mathematics
teaching and learning. Dissertation, Georgetown Uni-
versity. Washington, DC, 2015, pp 9-10
Haapasalo, Lenni (2007) Adapting Mathematics Education
to the Needs of ICT. eJMT, Vol. 1, No 1.
Kadijevich, Dj. (2006). Coordinating the Process and object
features of mathematical knowledge by CAS. Confer-
ence Proceedings of DES-TIME-2006.
Lazarov, B. (2014) Socratic Style Support for Transferabil-
ity of Math Knowledge and Skills. The Korean So-
ciety of Mathematical Education. Proceedings of the
2014 Int’l Conference on Mathematical Education,
Cheongju National University of Education, October
17-18, 2014, pp 75-85.
Lazarov, B. (2015) Project-oriented Education as a Platform
for Transfer of Math KSA. Proceedings of the 7th In-
ternational Conference on Computer Supported Edu-
cation Volume 2, Lisbon, Portugal, 23-25 May, 2015,
pp 325-330
Lozanov, C., Vitanov, T. & Kalcheva, A. (2011) Mathemat-
ics for 5th grade. Sofia, Anubis, p 77, problem 8 (in
Bulgarian)
Rittle-Johnson, B. & Koedinger, K. (2004). Comparing in-
structional strategies for integrating conceptual and
procedural knowledge. In D. Mewborn, P. Sztajn, D.
White, H. Hiegel, R. Bryant and K. Nooney (Eds.),
Proceedings of the Twenty-fourth Annual Meeting of
the North American Chapters of the International
Group for the Psychology of Mathematics Education.
ERIC Clearinghouse for Science, Mathematics, and
Environmental Education. OH: Columbus, pp. 969-
978.
Rocard, M. et al. (2007) Science Education Now: A Re-
newed pedagogy for the Future of Europe. High Level
Group on Science Education. EUROPEAN COMMIS-
SION, Directorate-General for Research.
Shabanova, M. & Lazarov, B. (2014) Detecting Math-and-
ICT Competence. Proceedings of the 6th Interna-
tional Conference on Computer Supported Education,
Volume 2, Barcelona, Spain, 1 - 3 April, 2014, pp 153-
158
Van Hiele, P. M. (1984) A child’s thought and geometry.
In D.Fuys, D.Geddes and R.Tischler (Eds), English
translation of selected writings of Dina van Hiele-
Geldof and P.M. van Hiele, pp. 237-241. Brooklyn
College, N.Y. 1984.
Usiskin, Z. (1982) Van Hiele levels and Achievement
in Secondary School Geometry. Final report of the
CDASSG Project. Chicago: Univ. of Chicago.
Yollis, L. (2014) http://yollisclassblog.blogspot.bg/2014/10/
monstrous-fun.html (active in Dec 2015)
APPENDIX
Operationalization of Van Hiele Levels 1-3
Burger & Shaughnessy characterized pupils’ geomet-
rical reasoning at the first three Van Hiele levels as
follows:
Level 1 (Recognition)
(1) Often use irrelevant visual properties to identify
figures, to compare, to classify and to describe.
(2) Usually refer to visual prototypes of figures, and
is easily misled by the orientation of figures.
(3) An inability to think of an infinite variation of a
particular type of figure (e,g. in terms of orientation
and shape).
(4) Inconsistent classifications of figures; for exam-
ple, using non-common or irrelevant properties to sort
figures.
(5) Incomplete descriptions (definitions) of figures by
viewing necessary (often visual) conditions as suffi-
cient conditions.
Level 2 (Analysis)
(1) An explicit comparison of figures in terms of their
underlying properties.
(2) Avoidance of class inclusions between different
classes of figures, eg. squares and rectangles are con-
sidered to be disjoint.
(3) Sorting of figures only in terms of one property,
for example, properties of sides,
while other properties like symmetries, angles and di-
agonals are ignored.
(4) Exhibit an uneconomical use of the properties of
figures to describe (define) them, instead of just using
sufficient properties.
(5) An explicit rejection of definitions supplied by
other people, e.g. a teacher or textbook, in favour of
their own personal definitions.
Computer Supported Evolution Inside Van Hiele Levels 1 and 2
191

(6) An empirical approach to the establishment of the
truth of a statement; e.g. the use of observation and
measurement on the basis of several sketches.
Level 3 (Ordering)
(1) The formulation of economically, correct defini-
tions for figures.
(2) An ability to transform incomplete definitions into
complete definitions and a more spontaneous accep-
tance and use of definitions for new concepts.
(3) The acceptance of different equivalent definitions
for the same concept.
(4) The hierarchical classification of figures, e.g.
quadrilaterals.
(5) The explicit use of the logical form ”if ... then’ in
the formulation and handling of conjectures, as well
as the implicit use of logical rules such as modus po-
nens.
(6) An uncertainty and lack of clarity regarding the
respective functions of axioms, definitions and proof.
CSEDU 2016 - 8th International Conference on Computer Supported Education
192
