Verification of BPMN Model Functional Completeness by using the

Topological Functioning Model

Erika Nazaruka, Viktoria Ovchinnikova, Gundars Alksnis and Uldis Sukovskis

Department of Applied Computer Science, Riga Technical University, Sētas iela 1, Riga, Latvia

Keywords: BPMN, Model Verification, Completeness, Topological Functioning Model.

Abstract: BPMN (Business Process Model and Notation) models are used to specify business knowledge in the

language that is familiar for business people. They consist of multiple process diagrams that highlight

different aspects of interaction among participants. Verification of BPMN models is important since

graphical fragmentary presentation could be a source of errors such as incompleteness, deadlocks, livelocks,

incorrect terminations etc. We consider verification of model completeness. The model is transformed to the

topological functioning model (TFM) in order to check completeness of inputs, outputs and functioning

cycles of the entire specified system. The proposed approach is dedicated to the verification of the model at

the beginning of analysis, and it could be supplemented by other methods at the design stage. This approach

is more dedicated to analysis of the whole system, than to the verification of the concrete fragment work.

1 INTRODUCTION

Business Process Model and Notation (BPMN) is a

standard of a business process graphical notation

that allows presenting business process steps from

the start to the end (Object Management Group,

2015). This has its advantages, namely, a business

analyst can depict all steps of a business process,

showing manual and automated steps, dependencies

among them, data flows, step flows by business

units etc. However, each process is only a fragment

of the entire business that may have dozens of such

processes. The question is how to check the

correctness of each of them, correctness of

dependencies among them, and completeness of

them.

The verification of business process

specifications usually uses informal techniques, such

as workshops, where stakeholders can determine and

show possible issues in the defined processes

(Falcioni et al., 2012). However, in some cases

specifications may be simulated and formally

verified. Formal verification allows discovering of

unwanted behavior and situations, however, this

requires derivation of formal model from informal

business process specifications (Falcioni et al.,

2012).

In this research we consider a formal

mathematical model, the Topological Functioning

Model (TFM), based on principles of the system

theory and algebraic topology. It specifies the

system in a holistic manner, showing its interaction

with the external systems and inner functionality at

the high level of abstraction.

The research objective is to understand

advantages and limitations of TFM application for

verification of completeness of BPMN processes. In

other words, the obtained results should clear what

aspects the TFM can help to verify unlike other

formal models such as Petri Nets, YAWL, or

temporal logic. As other author work showed,

analysis of the completeness of BPMN models, i.e.

whether they specify the domain under the discourse

completely, is not solved enough.

In order to achieve the research goal, we have

defined mappings from BPMN model elements to

the TFM elements and discussed the verification of

BPMN model completeness, illustrating the process

on the example.

The paper is organized as follows. Section 2

describes related work on BPMN process

verification. Section 3 describes elements of BPMN

models and the TFM as well as mappings between

them in brief. Section 4 illustrates application of the

TFM for BPMN process verification and states main

results. Conclusion summarizes advantages and

limitations of the TFM application based on the

research results.

Nazaruka, E., Ovchinnikova, V., Alksnis, G. and Sukovskis, U.

Veriﬁcation of BPMN Model Functional Completeness by using the Topological Functioning Model.

In Proceedings of the 11th International Conference on Evaluation of Novel Software Approaches to Software Engineering (ENASE 2016), pages 349-358

ISBN: 978-989-758-189-2

349

2 RELATED WORK

Although verification of BPMN models is not a new

topic, it is still actual. BPMN model verification is

based on mappings into other, more formal,

languages, e.g. into programming languages such as

Java and Prolog, formal languages such as

PROMELA, Petri Nets, CSP (Communicating

Sequential Processes), timed and process automata,

and into mathematical languages such as temporal

logic.

In (Falcioni et al., 2012), authors indicated that a

usage of formal languages (e.g., Petri Nets or

Process Algebra) as a target language in mappings

from BPMN specifications may lead to the loss of

some concepts and verification from those aspects

may be impossible. Another side effect of using

formal languages as a target may be verification of

unnecessary aspects that are native for those

languages. In order to deal with such issues, the

authors suggested using a Java model and an

unfolding technique based verification approach for

business processes depicted in the BPMN 2.0

collaboration diagrams. This approach is

implemented as an Eclipse plug-in and applied for

several real scenarios. The authors noted that their

approach reduces problems of state explosion and

implementation/respect of synchronization policies

of the target language. The interesting “side-effect”

is discovering of the collaboration “anti-patterns”.

Another interesting approach is a use of Prolog

language (Ligeza et al., 2012) in order to check the

correctness of data flows by using declarative

specification of the BPMN model.

In (Solaiman et al., 2015) the authors suggested

automated transformation into PROMELA, the input

language of the SPIN model checker, in addition

applying also Linear Temporal Logic for verification

of correctness properties (in other words, logical

sequence). PROMELA is also a choice of authors in

(Yamasathien and Vatanawood, 2014), where

BPMN models are verified via workflow pattern

transformations. The SPIN tool is mature enough to

be used for verification of multi-threaded software

applications (SPIN, 2015). As the authors noted,

SPIN can verify safety and liveness properties of

abstract models. The main issue that the authors

meant is identification of semantically independent

common correctness requirements for their

verification by default, i.e. such principles as

connectedness, well-threadedness, and coherence.

Another formal model that is widely used is a

Petri net. Petri nets (Universität Hamburg, 2015) is a

formal language for modeling parallel and

concurrent execution of the system. They can be

used for verification of compensations and

transactions in BPMN models (Takemura, 2008),

time properties when the execution time of web

services is not known (Huai et al., 2010) and others.

Authors in (Flavio et al., 2010) proposed

transforming BPMN models to CSP formal language

in order to use benefits of CSP verification via

model checking. In contrast to the previous work,

they omitted “few constructs dealing with

transactions, such as compensation events and

cancel events, or time”. Their main goal is

measuring quality of services in order to verify the

efficiency of specified business processes.

Another formal languages that can be used for

BPMN model verification are Timed Automata (TA)

and Process Automata (PA). The author in (Morales,

2013) suggests transformation to TA-networks in

order to verify controllability of BPMN models, i.e.

“correctness against requirements expressed in

temporal logic”. The author also (as we do) suggests

grouping all partial behaviors in order to get the

complete participant’s view. After that, the author

checks the completeness of those views. This differs

from our approach since we merge all participant

behaviors into one model. In their turn, authors in

(Tantitharanukul et al., 2010) verify deadlocks and

multiple terminations in BPMN using PA.

In order to check deadlocks and soundness of

BPMN models, they could be transformed to YAWL

(Ye et al., 2008), that is a workflow language with

formal semantics.

BPMN models can be transformed into formal

specifications based on linear temporal logic (LTL)

and computation tree logic (CTL) that allows

checking such properties as safety, liveness, fairness,

invariant properties, and response properties (El

Hichami et al., 2014), deadlocks, livelocks and

multiple terminations (Kherbouche et al., 2012).

Summarizing, most of proposed formal

techniques are used for verification of such

important model properties as deadlocks, thread

correctness, data flows, correct termination etc. The

completeness of the model in system-theoretical

viewpoint is attempted to be solved only in

(Morales, 2013). The difference is that we consider

the completeness of inputs, outputs and functioning

cycles instead of completeness form a concrete user

perspective.

MDI4SE 2016 - Special Session on Model-Driven Innovations for Software Engineering

350

3 VERIFICATION OF THE TFM

TRANSFORMED FROM THE

BPMN MODEL

3.1 The TFM in Brief

The TFM is a formal mathematical model that has

been proposed at Riga Technical University (RTU),

Latvia, by Janis Osis in 1969. At that time this

model has been dedicated for mathematical

specification of functionality of complex mechanical

systems (Osis and Asnina, 2011).

The TFM represents system functionality in a

holistic manner from a computation independent

viewpoint (Asnina and Osis, 2011c). It describes the

functional and structural aspects of the software

system in the form of a directed graph. The digraph

vertices depict functional characteristics of the

system named in human understandable language,

while edges depict causal relations between them.

Such specification is more perceived, precise and

clear then the large textual descriptions.

A TFM is a topological space (X, Q), where X is

a set of functional features and Q is a set of

relationships between elements in X (Osis and

Asnina, 2011b). The composition of the TFM is

presented in (Osis and Asnina, 2011).

A functional feature represents some system’s

functional characteristic, e.g., a business process, a

task, an action, or an activity (Osis and Asnina,

2011a). It can be specified by a unique tuple <A, R,

O, PrCond, PostCond, Pr, Ex>, where (Osis and

Asnina, 2011b):

 A is object’s action,

 R is a set of results of the object’s action (it is

an optional element),

 O is an object that gets the result of the action

or a set of objects that are used in this action,

 PrCond is a set of preconditions or atomic

business rules,

 PostCond is a set of post-conditions or atomic

business rules,

 Pr is a set of feature’ providers, i.e. entities

(systems or sub-systems) which provide or

suggest an action with a set of certain objects,

 Ex is a set of executors (direct performers) of

the functional feature, i.e. a set of entities

(systems or sub-systems) which enact a

concrete action.

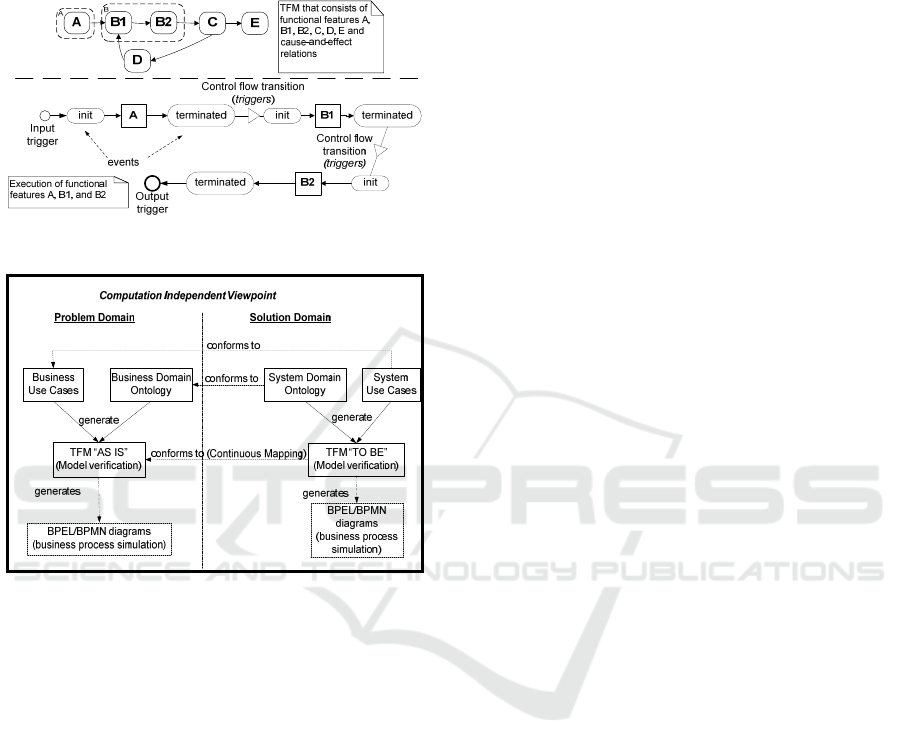
The cause-and-effect relations between

functional features define the cause from which the

triggering of the effect depends (Figure 1).

The formal definition of the cause-and-effect

relations and their combinations are given in (Asnina

and Ovčiņņikova, 2015) and are as follows:

1) Formal definition of a cause-and-effect

relation: A cause-and-effect relation T

is a binary

relationship that relates exactly two functional

features X

and X

. Both X

and X

may be the same

functional feature in case of recursion. Each cause-

and-effect relation is a unique 5-tuple (1).

= <ID, X

, X

N, S>, where (1)

 ID is a unique identifier of a relation;

 X

is a cause functional feature;

 X

is an effect functional feature;

 N is a Boolean value of the necessity of X

for

generating X

(default value is true);

 S is a Boolean value of the sufficiency of X

for generating X

(default value is true).

2) Formal definition of a logical relation: A

logical relation L

specifies the logical operator

conjunction (AND), disjunction (OR), or exclusive

disjunction (XOR) between two or more cause-and-

effect relations T

The logical relation denotes

system execution behavior (e.g., decision making,

parallel or sequential actions). Each logical relation

is a unique 3-tuple (2).

= <ID, T, R

>, where (2)

 ID is a unique identifier of a relation;

 T is a set of cause-and-effect relations

, ..., T

}

that participate in this logical

relation;

 R

is a logical operator AND, OR, or XOR

over T; the default values is operator OR.

The execution of the functional feature instance

is illustrated in Figure 1. After triggering the

instance is initiated, then executed and terminated.

In case of successful execution its termination leads

to triggering the initiation of the next (effect)

functional feature instances. In case of failure, the

triggering will not occur.

The TFM is characterized by the topological and

functioning properties (Osis and Asnina, 2011a).

The topological properties are connectedness,

neighborhood, closure and continuous mapping. The

functioning properties are cause-and-effect relations,

cycle structure, inputs and outputs.

Rules of composition and derivation processes of

the TFM from the system description is provided by

examples and described in detailed in (Asnina,

2006), (Osis et al., 2007), (Osis et al., 2008) and

(Osis et al., 2008). Construction of the TFM with

attention put on continuous mappings between

problem and solution domain is provided in (Asnina

and Osis, 2010). The TFM can also be generated

Veriﬁcation of BPMN Model Functional Completeness by using the Topological Functioning Model

351

automatically from the business use case

descriptions, which can be specified in the IDM

toolset (Osis and Slihte, 2010), (Slihte et al., 2011),

(Slihte and Osis, 2014). It also can be manually

created in the TFM Editor from the IDM toolset.

Figure 1: The execution of the functional feature instance.

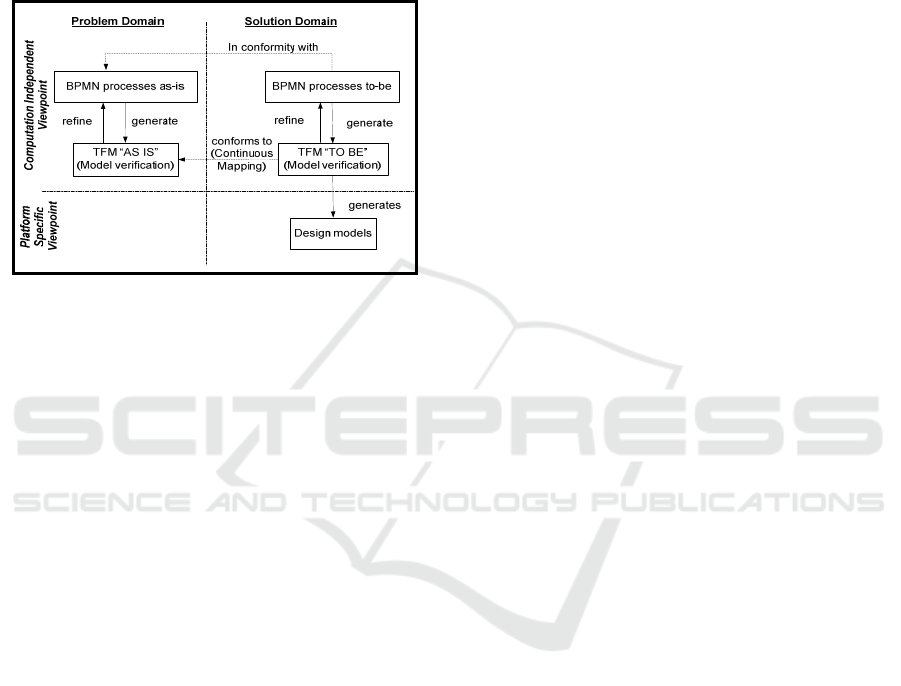
Figure 2: System analysis with the TFM as a start point.

The UML use case diagram can be obtained from

the TFM, according to (Osis and Asnina, 2011d),

(Donins, 2012). According to (Osis and Donins,

2010), (Donins et al., 2011) the TFM can be

manually (but according to the precise rules)

transformed into most used UML diagram types,

including UML Activity Diagrams and State Chart

Diagrams.

The TFM can be used as a formal blueprint of

the system functioning at the beginning of analysis

and then transformed to BPMN processes (Asnina,

2009). Such forward modeling and analysis allows

formal determination of system boundaries, system

completeness and causal dependencies between parts

of functioning (Figure 2). Depending on the analysis

context, business or system goals are criteria used

for model decomposition into BPMN processes.

3.2 BPMN Models in Brief

Let us look at communications between participants

defined according to the BPMN 2.0 standard (Object

Management Group, 2011) as well as at other

BPMN elements in brief.

There are three basic types of sub-models within

a complete BPMN model. The first type is Processes

(Orchestration) that includes the following sub-

types, namely, private non-executable and private

executable internal Business Processes as well as

public Processes. The second type is called

Choreography. And the third one is Collaborations.

The last type may include Processes and/or

Choreographies.

If we look at them from the viewpoint of defined

communications between participants, then we can

conclude the following. Communications within

BPMN sub-models exist in case of public Processes,

Choreographies, Collaborations and Conversations.

They are depicted as message flows (Message Flow)

or a set of message exchanges (Choreography)

between Participants (Pools). In case of

Conversation diagrams, message exchanges are

shown as Conversations (nodes and links). In other

words, flow elements are modeled as processes, but

the interaction between processes is modelled in

terms of Collaboration and Choreography.

As mentioned in (Object Management Group,

2011, pp. 127-128), a Message Flow depicts the

flow of communications (messages) between two

Participants. Messages can be sent and received.

The message can be depicted as a Choreography

Task in a Choreography. In a particular case of a

Collaboration diagram, namely, a Conversation

diagram, a Conversation may be shown as a set of

Message Flows.

Summarizing BPMN elements, they are business

or system actors represented by swim-lines (pools

and lanes); system activities that define business

system’ functionality represented by processes, sub-

processes, and tasks; decomposition of system

processes where processes can be divided to sub-

processes to tasks; system events that initiate

execution of functionality represented by start,

intermediate, and end events; connecting elements (a

sequence flow, message flow, and association) that

connect to each other such constructs as activities,

events and gateways; and, finally, gateways that

determine different decisions (forking, merging, and

joining of paths).

3.3 Mappings from BPMN to TFM

If BPMN models are used as a source of knowledge

instead of textual descriptions of business/system

use cases (Figure 3) than verification of the artifacts

MDI4SE 2016 - Special Session on Model-Driven Innovations for Software Engineering

352

become harder. Main issues in using BPMN

diagrams are their fragmentary nature and a large

number of modelling constructs in comparison with

simple graphical or structural textual scenarios. The

TFM as a formal start helps in avoiding these issues

due to TFM formalism, a minimal number of

modelling constructs and a holistic representation of

the domain under discussion (Asnina, 2009).

Figure 3: System Analysis with the BPMN model as a

start point.

Constructs of business process models and TFM

constructs are intended to describe behavior of the

system at the business process level, and, therefore,

these constructs can be mapped, if they have the

equal or similar semantics in the field of business

process modeling.

Table 1 illustrates mappings between BPMN and

TFM elements. In short, tasks, events and data

objects form TFM functional features. In their turn,

sequence and message flows (as well as

conversation and sub-conversation nodes) form

TFM cause-and-effect relations. And, the last,

gateways set logical operators on the combination of

outgoing or incoming cause-and-effect relations.

Such elements as Text Annotation, Category,

Message (decoration), ParticipantMultiplicity,

ParticipantAssociation, Conversation Link, Task

markers (loop, multi-instance, and compensation),

Compensation and Data Store have not any

corresponding notion in the TFM. We should note

that information of the multi-instance mode, looping

or canceling of BPMN processes or activities will be

lost in the result of such transformation.

Another aspect is that in the TFM information

about participants is held in the description of

functional features. Besides that participants may be

as providers as executors of the functional features.

By default it is assumed that participants are the

same as executors, since the other case is rare even

in BPMN models.

Such TFM element as a functioning cycle does

not have direct correspondence with any BPMN

elements. However, the cycle should be determined

after gluing all transformed BPMN diagrams.

The only BPMN diagram which transformation

may lead to the natural appearance of the

functioning cycles is the Conversation Diagram.

Transformation of other diagrams requires

understanding of the sequence and dependency

between each pair of them.

Summarizing, transformation from the BPMN to

the TFM raises the level of abstraction and allows

specifying processes holistically, thus, allowing

verification of completeness of process descriptions

from the functional point of view (that will be

discussed in the next sub-section).

3.4 Verification of the Obtained TFM

The verification of the obtained TFM consists of two

parts. The first one is structural verification, and the

second one is functional verification.

As mentioned in Section 3.1, the structurally

valid TFM must satisfy four topological and four

functioning properties, i.e. it is structurally valid if:

 Has no isolated vertices,

 Preserves continuous mapping among different

levels of abstraction,

 Has functioning cycles,

 Has inputs and outputs,

 Has mathematically proved boarders, i.e.

contains only system’s functional features for

inner functioning and interaction with the

external systems.

The TFM is functionally valid if:

 All cause-and-effect relations or their

combinations are necessary and sufficient in

order to trigger subsequent functional features.

 Functioning cycles contain all the necessary

functional aspects in the order that is required

by the domain logic.

 Both sets of inputs and outputs are complete.

Any incompliance with the mentioned

characteristics means that the BPMN model is not

complete or specifies the functional business logic

incorrectly. The incorrectness could be expressed as

absence of inputs or outputs as well as incorrect

cycles and paths in the obtained digraph.

Veriﬁcation of BPMN Model Functional Completeness by using the Topological Functioning Model

353

Table 1: Mappings between BPMN and TFM elements.

BPMN element TFM element

Association A fact that Flow Object belongs to the artifact

Group (visualization) A group (visualization)

Text Annotation none

Category none

Message (decoration) none

Sequence Flow A cause-effect relation between functional features with the same executor

Collaboration,

Conversation (diagram)

A part of the topological space where executors of functional features are

different

Pool (Participant), PartnerEntity,

PartnerRole

An executor (or a provider) of the functional feature

ParticipantMultiplicity none

ParticipantAssociation none

Message Flow,

Conversation (node),

Sub-conversation (node)

A cause-and-effect relation between functional features with different

executors; conversation nodes must be expanded

Conversation Link none

Process (within pools), Sub-Process A part of the topological space where the same executor is set for all

functional features; process resources are functional features executors.

Lane (sub-partition within a Process) A part of the topological space where functional features are logically joined

in some set according to some purpose

Choreographies (between pools) A part of the topological space; however, information of the sender and

recipient is split among functional features

Activity (atomic) or Task An action with the object/result of the functional feature; a resource of the

activity is an executor of the functional feature (or a provider)

Task marker (loop, multi-instance,

compensation)

none

Service Task, User Task, Manual Task,

Business Rule Task, Script Task

An action with the object/result of the functional feature

Send Task A cause functional feature in the cause-effect relation where functional

features with different executors take part

Receive Task An effect functional feature in the cause-effect relation where functional

features with different executors take part

Activity (non-atomic) A set of functional features

Performer An executor of the functional feature

Start Event An indicator of initialization of the input/cause functional feature; timer,

conditional and signal start events contain preconditions for triggering the

functional feature

End Event An indicator of finishing the output/effect functional feature; the end event

may contain the post-condition of the functional feature

Middle Event An indicator of triggering the functional feature; in case of catching events it

may indicate the input functional feature or the precondition of the triggered

functional feature; link events indicate the cause (source) and the effect

(target) functional features in the cause-effect relations

Gateway;

Event-Based Gateway

A decision node that is expressed as logical operators in combination of

cause-and-effect relations; exclusive gateways are equal to operator XOR;

inclusive gateways are equal to OR; parallel gateways are equal to AND;

complex gateways are equal to decision tables assigned to the combination of

outgoing cause-effect relations.

Compensation none

Data Object,

Data Object Reference

An object or a result of the functional feature; however, the collection may be

expressed using only the plural form of the noun

Data Store none

Data Association An indicator to which functional feature the object belongs

MDI4SE 2016 - Special Session on Model-Driven Innovations for Software Engineering

354

4 THE EXAMPLE

4.1 Domain Description

Let us take as an example a system for sport event

organization. Let us call it “Registration at the sport

event”. A short version of the systems description is

as follows: “The visitor may visit and leave the sport

event website after doing some tasks in the website.

He/she may request sport event data and after that

the website returns the requested data to the visitor.

The visitor may request the list of participants and

see all participants in the list or may request a

registration form, register to the sport event and fill

participant data. When participant’s data is added it

needs to be checked. If participant’s data is correct

and all mandatory fields are filled, then the price of

participation needs to be automatically determined

and provided, according to the distance, count of

participants and the date of registration. After that

the visitor needs to pay for participation. When the

sport event website receives the payment, the visitor

becomes a participant. The participants are added to

the participants list, unique identifiers and existing

groups are assigned for each participant.

Registration confirmation is send by the e-mail.

After that the visitor receives the registration

confirmation”.

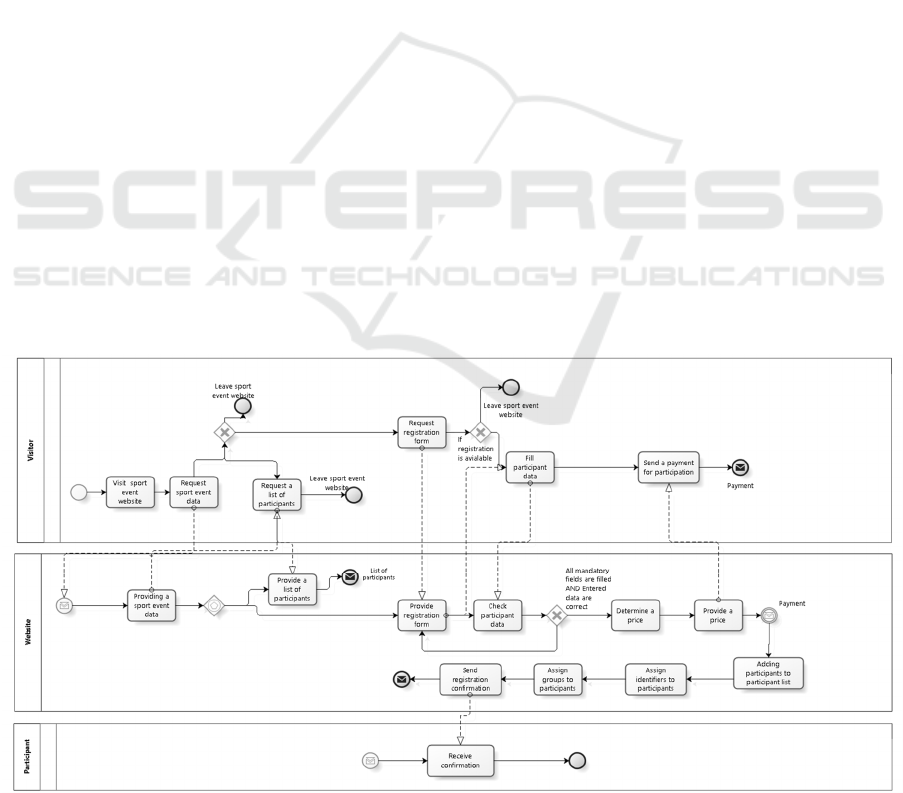
The created specification in BPMN is illustrated

in Figure 4. There are three participants: Visitor,

Participant and Website (the system itself).

4.2 Results of Transformation

According to the mappings (Table 1), the created

BPMN model is transformed to the TFM (Figure 5).

End events “Leave sport event website” are

transformed to functional feature “4 Leaving sport

event website”. Intermediate event “Receive

payment” to functional feature “14 Receiving

payment”. Other elements are specified as functional

feature tuples <ID, A, R, O, Ex, Pr, PreCond,

PostCond> (Table 2) modified for better readability

and cause-effect relations in the model.

If the BPMN model contains more than one task

between start and end event, than the last task is a

cause for the first task triggering, since the TFM

specifies cyclic creation of process instances

(certainly, taking into account all the necessary and

sufficient causes).

The obtained TFM may contain functional

features that belong to the external systems. Thus,

this aspect, system boarders, also must be verified.

4.3 Verification Results

First, let us verify structural validity of the TFM. It

has no isolated vertices, has cycles, inputs and

outputs. In order to verify system’s boarders let us

closure the set N of system inner properties, i.e.

those where both the provider and executor is Sport

Event Website. N = {3, 6, 8, 10, 11, 12, 14, 15, 16,

17, 18}. The set of Sport Event Website functional

features called X = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,

13, 14, 15, 16, 17, 18, 19}.

Figure 4: The BPMN model of “Registration at the sport event”.

Veriﬁcation of BPMN Model Functional Completeness by using the Topological Functioning Model

355

Figure 5: The topological space of “Registration at the sport event” based on transformation of BPMN diagrams.

Table 2: TFM functional features, where V denotes Visitor, SEW – the Sport Event Website, and P - Participant. A set of

post-conditions is empty, and therefore is not presented in the table.

Id Action (A) Result (R) Object (O) Executer

(Ex)

Provider (Pr) Preconditions

1 Visiting sport event

website

V SEW

2 Requesting data [of] sport event V SEW

3 Providing data [of] sport event SEW SEW

4 Leaving sport event

website

V SEW

5 Requesting list [of] participants V SEW

6 Providing list [of] participants SEW SEW

7 Requesting form [of] registration V SEW

8 Providing form [of] registration SEW SEW

9 Filling data [of] participants V SEW (If registration is

available)

10 Checking [validity of data

of]

participants SEW SEW

11 Determining price SEW SEW (All mandatory fields are

filled) AND (Entered data

are correct)

12 Providing price SEW SEW

13 Sending payment [for] participation

[registration]

V External system

14 Receiving payment SEW SEW

15 Adding participants [to] list [of

participants]

SEW SEW (If payment is received)

16 Assigning identifiers [to] participants SEW SEW

17 Assigning groups [to] participants SEW SEW

18 Sending confirmation [of] registration SEW SEW

19 Receiving confirmation [of] registration P External system

MDI4SE 2016 - Special Session on Model-Driven Innovations for Software Engineering

356

Functional features 2, 4, 5, 7, 9, and 13 shows

system’s input signals from Visitor to the website,

while 19 – website’s output signal to Participant.

Next, let us examine functioning cycles. The

TFM has three cycles: checking participant data (9 –

10 - 9), requesting sport event website information

(2 – 3 – 5 – 6 – 2 and 2 – 3 – 7 – 8 - 2), and the main

cycle of the registration process (3 – 7 – 8 – 9 – 10 –

11 – 12 – 14 – 15 – 16 – 17 - 3). The cycles contain

all necessary functional features.

The last is verification of cause and effect

combinations. Verification of single incoming

cause-and-effect relations showed that they all are

necessary and sufficient. Table 3 shows verification

of combinations of incoming combinations of cause-

and-effect relations.

Table 3: Necessity and sufficiency of incoming cause-and-

effect relations in the TFM.

Combination of Cause-and-

Effect Relations

Necess-

ary

Suffi-

cient

XOR {(6-2), (8-2)} True True

XOR {(2-3), (17-3)} True True

XOR {(8-9), (10-9)} True True

XOR {(6-4), (3-4), (8-4), (12-4)} True True

AND {(13-14), (12-14)} True True

Output combinations of cause-and-effect

relations are XOR {(3-5), (3-4)}, XOR {(6-2), (6-

4)}, XOR {(10-11), (10-9)), OR ((17-18), (17-3)},

XOR {(8-2), (8-4), (8-9)}. These also represent

complete sets of effects of functional feature

execution.

Therefore, the constructed BPMN model is

complete (from the functional viewpoint), but

contains one task that is out of system boarders, i.e.

“Visit sport event website”.

5 CONCLUSIONS

The presented approach aims to verification of

completeness of problem domain specification in

BPMN models. It does not solve such problems as

determination of deadlocks, multiple terminations,

transactions, compensations and so on.

The defined mappings between BPMN and TFM

elements allow transformation of a set of BPMN

diagrams to the TFM. Verification of topological

and functioning properties of the TFM helps in

checking completeness of sets of inputs, outputs and

inner functional characteristics as well as

connectedness and causal dependencies of functional

characteristics of the system.

However, to a greater extent the presented

verification approach is manual. Verification of the

logic still requires expert knowledge, and it is a

significant limitation of the approach. The hardest

task is to identify all functioning cycles, since they

are not evident when use output and input events.

However, check of input and output sets of

functional characteristics allows determination of

missed or incorrectly specified triggering conditions.

The future work is dedicated to definition of

patterns for model transformations and a way for

automation of speculations, e.g., using domain

ontologies as a set of valid facts about the domain.

REFERENCES

Asnina, E., 2006. The Computation Independent

Viewpoint: a Formal Method of Topological

Functioning Model Constructing. Applied computer

systems, Volume 26, pp. 21-32.

Asnina, E., 2009. A Formal Holistic Outline for Domain

Modeling. Riga, RTU, pp. 400-407.

Asnina, E. and Osis, J., 2010. Computation Independent

Models: Bridging Problem and Solution Domains. In:

Proceedings of the 2nd InternationalWorkshop on

Model-Driven Architecture and Modeling Theory-

Driven Development (MDA & MTDD 2010), in

conjunction with ENASE 2010. Lisbon: SciTePress,

pp. 23-32.

Asnina, E. and Osis, J., 2011c. Topological Functioning

Model as a CIM-Business Model. In: Model-Driven

Domain Analysis and Software Development:

Architectures and Functions. Hershey - New York:

IGI Global, pp. 40 - 64.

Asnina, E. and Ovčiņņikova, V., 2015. Specification of

Decision-making and Control Flow Branching in

Topological Functioning Models of Systems. In: J.

Filipe and L. Maciaszek, eds. ENASE 2015 :

Proceedings of the 10th International Conference on

Evaluation of Novel Approaches to Software

Engineering, Spain, Barcelona, 29-30 April, 2015.

s.l.:SciTePress, pp. 364-373.

Donins, U., 2012. Topological Unified Modeling

Language: Development and Application, Riga: RTU.

Donins, U. et al., 2011. Towards the Refinement of

Topological Class Diagram as a Platform Independent

Model. In: Proceedings of the 3rd International

Workshop on Model-Driven Architecture and

Modeling-Driven Software Development (MDA &

MDSD 2011). Lisbon: SciTePress, pp. 79-88.

El Hichami, O. et al., 2014. Towards formal verification of

business process using a graphical specification. In:

Information Science and Technology (CIST), 2014

Third IEEE International Colloquium in. s.l.:IEEE,

pp. 12-17.

Falcioni, D., Polini, A., Polzonetti, A. and Re, B., 2012.

Direct Verification of BPMN Processes through an

Veriﬁcation of BPMN Model Functional Completeness by using the Topological Functioning Model

357

Optimized Unfolding Technique. In: 12th

International Conference on Quality Software (QSIC),

27-29 Aug. 2012. s.l.:IEEE, pp. 179-188.

Flavio, C., Alberto, P., Barbara, R. and Damiano, F., 2010.

An ECLIPSE Plug-In for Formal Verification of

BPMN Processes. In: Communication Theory,

Reliability, and Quality of Service (CTRQ), 2010

Third International Conference on. s.l.:IEEE, pp. 144-

149.

Huai, W., Liu, X. and Sun, H., 2010. Towards

Trustworthy Composite Service Through Business

Process Model Verification. In: Ubiquitous

Intelligence & Computing and 7th International

Conference on Autonomic & Trusted Computing

(UIC/ATC), 2010 7th International Conference on.

s.l.:IEEE, pp. 422-427.

Yamasathien, S. and Vatanawood, W., 2014. An approach

to construct formal model of business process model

from BPMN workflow patterns. In: Digital

Information and Communication Technology and it's

Applications (DICTAP), 2014 Fourth International

Conference on. s.l.:IEEE, pp. 211-215.

Ye, J., Sun, S., Wen, L. and Song, W., 2008.

Transformation of BPMN to YAWL. In: Computer

Science and Software Engineering, 2008 International

Conference on. s.l.:IEEE, pp. 354-359.

Kherbouche, O., Ahmad, A. and Basson, H., 2012.

Detecting structural errors in BPMN process models.

In: Multitopic Conference (INMIC), 2012 15th

International. s.l.:IEEE, pp. 425-431.

Ligeza, A., Kluza, K. and Potempa, T., 2012. AI approach

to formal analysis of BPMN models. Towards a

logical model for BPMN diagrams. In: Computer

Science and Information Systems (FedCSIS), 2012

Federated Conference on. s.l.:IEEE, pp. 931-934.

Morales, L., 2013. Business process verification using a

Formal Compositional Approach and Timed

Automata. In: Computing Conference (CLEI), 2013

XXXIX Latin American. s.l.:IEEE, pp. 1-10.

Object Management Group, 2011. Documents Associated

With Business Process Model And Notation™

(BPMN™) Version 2.0. [Online] Available at:

http://www.omg.org/spec/BPMN/2.0/ [Accessed 10

January 2015].

Object Management Group, 2015. Business Process

Model and Notation. [Online] Available at:

http://www.bpmn.org/ [Accessed 11 January 2015].

Osis, J. and Asnina, E., 2011a. Is Modeling a Treatment

for the Weakness of Software Engineering?. In:

Model-Driven Domain Analysis and Software

Development: Architectures and Functions. Hershey -

New York: IGI Global, pp. 1-14.

Osis, J. and Asnina, E., 2011b. Topological Modeling for

Model-Driven Domain Analysis and Software

Development: Functions and Architectures. In: Model-

Driven Domain Analysis and Software Development:

Architectures and Functions. Hershey - New York:

IGI Global, pp. 15-39.

Osis, J. and Asnina, E., 2011d. Derivation of Use Cases

from the Topological Computation Independent

Business Model. In: Model-Driven Domain Analysis

and Software Development: Architectures and

Functions. Hershey - New York: IGI Global, pp. 65 -

89.

Osis, J. and Asnina, E., 2011. Model-Driven Domain

Analysis and Software Development: Architectures

and Functions. Hershey - New York: IGI Global.

Osis, J., Asnina, E. and Grave, A., 2007. MDA Oriented

Computation Independent Modeling of the Problem

Domain. In: Proceedings of the 2nd International

Conference on Evaluation of Novel Approaches to

Software Engineering (ENASE 2007). Barselona:

INSTICC Press, pp. 66-71.

Osis, J., Asnina, E. and Grave, A., 2008. Computation

Independent Representation of the Problem Domain in

MDA. e-Informatica Software Engineering Journal,

2(1), pp. 29-46.

Osis, J., Asnina, E. and Grave, A., 2008. Formal Problem

Domain Modeling within MDA. In: Software and

Data Technologies, Communications in Computer and

Information Science. Berlin: Springer-Verlag Berlin

Heidelberg, pp. 387-398.

Osis, J. and Donins, U., 2010. Formalization of the UML

Class Diagrams. Berlin, Springer-Verlag, pp. 180-192.

Osis, J. and Slihte, A., 2010. Transforming Textual Use

Cases to a Computation Independent Model. Lisbon,

SciTePress, pp. 33-42.

Slihte, A. and Osis, J., 2014. The Integrated Domain

Modeling: A Case Study. In: Databases and

Information Systems: Proceedings of the 11th

International Baltic Conference (DB&IS 2014),

Estonia, Tallinn, 8-11 June, 2014. Tallinn: Tallinn

University of Technology Press, pp. 465-470.

Slihte, A., Osis, J. and Donins, U., 2011. Knowledge

Integration for Domain Modeling. Lisbon, SciTePress,

pp. 46-56.

Solaiman, E., Sun, W. and Molina-Jimenez, C., 2015. A

Tool for the Automatic Verification of BPMN

Choreographies. New York, NY, IEEE, pp. 728-735.

SPIN, 2015. Verifying Multi-threaded Software with

SPIN. [Online] Available at: http://spinroot.com

/spin/whatispin.html. [Accessed January 2016].

Takemura, T., 2008. Formal Semantics and Verification of

BPMN Transaction and Compensation. In: Asia-

Pacific Services Computing Conference, 2008. APSCC

'08. s.l.:IEEE, pp. 284-290.

Tantitharanukul, N., Sugunnasil, P. and Jumpamule, W.,

2010. Detecting deadlock and multiple termination in

BPMN model using process automata. In: Electrical

Engineering/Electronics Computer

Telecommunications and Information Technology

(ECTI-CON), 2010 International Conference on.

s.l.:IEEE, pp. 478-482.

Universität Hamburg, 2015. Petri Nets World. [Online]

Available at: http://www.informatik.uni-

hamburg.de/TGI/PetriNets/ [Accessed January 2015].

MDI4SE 2016 - Special Session on Model-Driven Innovations for Software Engineering

358