Channel Allocation in Cognitive Radio Networks using Evolutionary

Technique

Vinesh Kumar

, Sanjay K. Dhurandher

, Bhagyashri Tushir

and Mohammad S. Obaidat

School of Computer and Systems Sciences, Jawaharlal Nehru University, Delhi, India

CAITFS, Division of Information Technology, NSIT, University of Delhi, Delhi, India

Department of Computer Science & Information Science, Fordham University, Bronx, New York, U.S.A.

Keywords:

Signal to Interference Plus Noise Ratio, Channel, Probability, Markov Chain, Non-dominated Set of Solutions.

Abstract:

Cognitive radio technology provides a platform at which licensed and unlicensed user share the spectrum. In

spectrum sharing, interference plays an important role. Therefore, in this work, interference is considered as

a parameter for spectrum sharing between licensed and unlicensed users. The authors in this work proposed

a novel channel allocation technique using Non-dominated set of solutions according to following objectives:

maximum SINR, probability for maximum SINR and maximum free time of channels. The Non-dominated

set of solutions has been calculated using Naive and Slow method. The simulation analysis further shows that

the proposed technique outperforms the existing technique in terms of throughput and utilization by 65.47%

and 47.31% respectively.

1 INTRODUCTION

Cognitive radio being an emerging technology, is

used for efﬁcient utilization of the spectrum, by intro-

ducing cognitive users to search the data transmission

opportunities in the absence of primary or licensed

users. The architecture of cognitive radio was intro-

duced by J. Mitola in (Mitola, 2000). In addition to

this, the signal processing aspects of Cognitive ra-

dio was given by Simon Haykin in (Haykin, 2005).

Cognitive radio based on the concept of cognitive cy-

cle, has four main functions namely spectrum sens-

ing, spectrum sharing, spectrum decision and spec-

trum adaptation. In this cycle each function plays an

important role.

In spectrum sharing, both licensed and unlicensed

users share the spectrum. The coexistence of licensed

and unlicensed users is an important issue in spec-

trum sharing. In (Haykin, 2005; Akyildiz et al., 2006;

?; Masonta et al., 2013; Tragos et al., 2013; Dhu-

randher et al., 2009; Ahmed et al., 2014; Dhurand-

her et al., 2015), the researchers found that interfer-

ence and bandwidth play an important role in spec-

trum sharing in cognitive radio networks. In (Haykin,

2005), the author provides the fundamentals of cog-

nitive radio networks and also analyse the impact of

interference when primary and secondary users share

the spectrum. (Akyildiz et al., 2006) presented a de-

tailed survey of cognitive radio networks and also dis-

cussed the issues related to spectrum sharing in detail.

(Wang and Liu, 2011) discussed an overview of cog-

nitive radio networks and also studied spectrum sens-

ing and sharing in detail. They discussed various open

issues related to spectrum sharing in cognitive radio

networks and found that interference is an important

parameter in spectrum sharing. (Masonta et al., 2013)

focus on various aspects of channel and issues re-

lated to spectrum sharing in cognitive radio networks.

This paper provides a complete survey of spectrum

decisions. (Tragos et al., 2013) reviewed the various

techniques related to spectrum assignment in cogni-

tive radio networks. During this study, they described

the role of interference in spectrum assignment and

found that interference plays a central role in chan-

nel allocation in cognitive radio networks in (Tragos

et al., 2013). From the works of (Haykin, 2005; Aky-

ildiz et al., 2006; Wang and Liu, 2011; Masonta et al.,

2013; Tragos et al., 2013), it is clear that interference

plays a key role, when primary and secondary users

share the spectrum in any network. Keeping this in

mind, the proposed work focuses on minimizing the

interference.

The rest of the paper is organized as follows. In

Section-II, the related work and motivation towards

designing the proposed scheme has been discussed.

In Section-III, the system model has been discussed.

106

Kumar, V., Dhurandher, S., Tushir, B. and Obaidat, M.

Channel Allocation in Cognitive Radio Networks using Evolutionar y Technique.

DOI: 10.5220/0005939801060112

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 6: WINSYS, pages 106-112

ISBN: 978-989-758-196-0

Section-IV presents the simulations and analysis of

the result. Finally Section V concludes this work.

2 RELATED WORK AND

BACKGROUND

(Jiang et al., 2013) presented a scheme for chan-

nel allocation and reallocation in cognitive radio net-

works. They used a multidimensional Markov chain

and a multi antenna interface which was connected

with only one channel, that was also used for chan-

nel allocation. In this paper, the channel alloca-

tion behavior in server and non server based system

was studied and analysed. The researchers presented

an analytic model and deﬁned the performance met-

rics namely blocking probability, dropping probabil-

ity and throughput for secondary users. From the

simulation analysis, it was found that the proposed

scheme improved the performance of cognitive radio

system. They considered multiple antennas with one

channel only.

(Bayhan and Alag

oz, 2014) presented a scheme

for best ﬁt channel selection in cognitive radio net-

works. For this, a Markov model based scheme was

developed and used for theoretical analysis of best

ﬁt channel selection. Also, the concept of spectrum

fragmentation was introduced. The performance of

proposed scheme over longest ideal time based chan-

nel selection scheme is crucial in terms of spectrum

utilization. From the simulation analysis, it was ob-

served that the proposed scheme preformed well and

provided signiﬁcant results in practical situations. In

this work, only discrete state space is considered.

(Jalali et al., 2015) presented a dynamic chan-

nel access strategy for underlay cognitive radio net-

works using markov model. The researchers intro-

duced a partial channel occupancy (PCO) mode. The

PCO mode provides a partial occupied bandwidth to

secondary users, when secondary users co-exist with

primary users. They developed a continuous time

markov chain based model, that was used to evalu-

ate the performance of licensed and unlicensed net-

works. Furthermore, a cost against gain analysis were

presented and used to check the applicability of the

proposed technique for a given trafﬁc scenario. The

proposed scheme was well supported by simulation

analysis.

(Gelabert et al., 2010) presented a discrete time

Markov chain model for spectrum sharing between

primary and secondary users with imperfect sens-

ing. The researchers introduced the concept of spec-

trum awareness implementation approach. Using this

approach, the miss-detection and false alarm proba-

bilities were deﬁned and discussed. With the help

of these probabilities, a discrete time markov chain

model was presented and derived. Based on the

Markov model, a scheme was presented and simu-

lated using a system level simulator. Through the

simulation analysis, the error in spectrum sensing was

analyzed and it was found that the spectrum sensing

could be improved by setting the value of interfer-

ence. The proposed scheme works only for central-

ized manner not distributed manner.

(Bedeer et al., 2014) presented an approach based

on multi objective optimization, that was used to in-

vestigate the optimal link adaptation of OFDM based

cognitive radio system. The researchers in this work

presented an algorithm in such a way that the through-

put of the system was maximized and the transmit

power was minimized with respect to licensed and un-

licensed users. The proposed algorithm was analysed

and simulated. From the simulation analysis, it was

found that the performance of the proposed algorithm

tends to an exhaustive search for the discrete optimal

allocations with a reduced computational effort. In

this work, an imperfect sensing was considered but

in imperfect sensing, the interference constraints may

get violated. The interference violation has not been

considered in this work.

(Qin et al., 2009) presented the multi objective op-

timization model using genetic algorithm. To imple-

ment the genetic algorithm, the chromosome is used

to identify the inﬂuence of evolving a radio. Using

this chromosome, Multi Objective Cognitive Radio

(MOCR) algorithm was proposed. The performance

of the algorithm was analyzed and simulated. The re-

sult shows that the proposed algorithm provides bet-

ter results. In this work, only routing constraints were

used to design the chromosome. Some other parame-

ters can be used to design chromosome.

(Suliman et al., 2009) presented the analysis of

cognitive radio networks with imperfect sensing. The

researchers developed two dimensional Markov chain

model with the help of false alarm probabilities and

missed detection probabilities. Using this model, the

behaviour of the network was analysed. In addition,

the balance equation from the Markov chain and pri-

mary user termination probabilities were also deﬁned

and evaluated. From the simulation analysis, it was

observed that as per the changes in the arrival rate of

primary users, the probability of successful commu-

nication for secondary users decreased. In this work,

the state equation is deﬁned only for few cases, which

may be extended for some other cases as well.

(Wen et al., 2012) presented a Max overall perfor-

mance algorithm using the concept of genetic algo-

rithm. They deﬁned the Max Sum Bandwidth (MSB)

Channel Allocation in Cognitive Radio Networks using Evolutionary Technique

107

rule, Max Access Fair (MAF) rule and Max Overall

Performance (MOP) rule and using these rules and

Genetic algorithm, the ﬁtness function was deﬁned.

Applying these, an algorithm was proposed by the au-

thors. From the simulation analysis, it was found that

the proposed MOP algorithm gave a good overall per-

formance. The researchers considered bandwidth and

fairness as the metric and no other metric was consid-

ered.

(Wang et al., 2009) proposed a primary prioritized

markov approach for dynamic spectrum allocation.

They used continuous time markov chain to model

the interactions between primary and secondary users.

The researchers classiﬁed the proposed model into

two parts namely primary prioritized CTMC with-

out queue and primary prioritized CTMC with queue.

Each of them was further divided into two parts as sin-

gle user and multi user cases. Each prioritized based

model for dynamic spectrum access has been derived

and discussed in this work. Through simulation anal-

ysis, it was found that the proposed model provided

95% performance gain over a CSMA based random

access approach and also attained an optimal tradeoff

between spectrum utilization and fairness. The au-

thors did not consider the overhead of the network in

the proposed scheme.

(Mahdi et al., 2012) presented an adaptive dis-

crete PSO (ADPSO) algorithm using G.A and PSO.

They deﬁned the transmission parameter adaptation

in cognitive radio networks and high data rate, less

power consumption were consider as the main objec-

tives. To design ADPSO algorithm, the researchers

focused on: 1) To reduce the time taken for con-

vergence when optimal set of parameters found. 2)

Overcoming the problem of local optimum in PSO

and G.A. The ADPSO algorithm was proposed and

for evaluating the proposed al-gorithm the multi car-

rier system was used. From simulation results, it was

found that the proposed algorithm performed well in

terms of convergence time and the algorithms was

also found to overcome the problem of local opti-

mum.

From the aforementioned study, it is observed

that the SINR/interference of a channel is one of

the important parameters toward channel allocation in

CRNs. For better communication, the channel uti-

lization and SINR are to be maximized according

to (Xiao et al., 2012; Kumar and Minz, 2015). To

overcome the limitations of the schemes discussed

earlier in (Jiang et al., 2013; Bayhan and Alag

oz,

2014; Jalali et al., 2015; Gelabert et al., 2010; Be-

deer et al., 2014; Qin et al., 2009; Suliman et al.,

2009; Wen et al., 2012; Wang et al., 2009; Mahdi

et al., 2012) and for better utilization of channels, the

authors of the work proposed in this paper were moti-

vated to design a Multi Objective based channel allo-

cation scheme in cognitive radio networks.

The proposed work in this paper is along the line

of previous research on channel allocation in cogni-

tive radio networks using Markov model by (Teotia

et al., 2015) and Multi Objective optimization Tech-

niques by (Kumar, 2015). Here, we presented Non-

dominated set of solutions based channel allocation

using multi objectives.

3 PROPOSED SYSTEM MODEL

Let there be n channels or sub-bands in a frequency

band where each channel has n states and there ex-

ists SINR for each state at a time instant. Let the

states be denoted by C

, C

, . . . C

n−1

at time in-

stants T

, T

, . . . T

n−1

Let the state C

at time instance T

have SINR S

with probability P

. Let the primary user change the

state with probability P

(Teotia et al., 2015) presented a Markov model

based approach for channel allocation with the use of

a Markov chain to calculate the probability of SINR

at each state.

Using the concept of Markov chain in (?), the

three parameters namely time, SINR and probability

were calculated. These three parameters are shown in

Table 1.

Table 1: Parameter for Channel Allocation.

States Probability SINR Time

. . . .

n−1

In (Kumar, 2015), using the parameters in Table 1,

a multi-objective function f (P, S, T ) is deﬁned as:

f (P, S, T ) = W

(1)

where f

represents the function of probability, f

de-

notes the function of SINR and f

denotes the func-

tion of time and W

, W

denotes the corresponding

weights.

A multi-objective optimization problem using

Equation 1 has been deﬁned in Equation 2 as:

Min f (K) = W

(k) +W

(k) (2)

subject to

1 ≤ K ≤ n

WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems

108

∑

i=1

= 1

Where f

(k) = 1−P, f

(k) = 1−SINR, f

(k) = 1−T

and n denotes the number of times.

In equation 2, f

, f

are the three objectives ac-

cording to which channels are allocated to secondary

users. There exists a solution space for these objec-

tives which consists of the set of solutions. This set

of solutions contains a Non-dominated set of solu-

tions. There exist various techniques to ﬁnd the Non-

dominated set of solutions in this solution set namely

Naive and Slow, Kung et. al. approach etc in (Deb,

2001). To calculate Non-dominated set of solutions

in this work the authors have used Naive and Slow al-

gorithm in (Deb, 2001; Kumar, 2015; ?). Using this

Non-dominated set of solutions, an algorithm for op-

timal allocation of channels to secondary users has

been proposed.

Algorithm 1: Channel allocation in cognitive radio

networks.

Input: States S = S

, S

. . . S

n−1

;

Probability of the states

P = P

, P

. . . P

n−1

;

SINR of channels SINR =

SINR

, SINR

. . . SINR

n−1

;

Time T = T

, T

. . . T

−1

Output: Channel allocation K

∗

1 Obtain the SINR of each state.

2 for each State S

∈ S, i = 1, 2, 3 . . . n do

3 Calculate the Probability of SINR with the

help of markov chain.

4 Obtain the time of each state

5 Obtain the solution set(K) that optimize

f (K) = W

(K) +W

(K)

6 k

= k

7 while |K| ≥ 1 do

8 Apply Naive and Slow algorithm to obtain

the non dominating set(K

∗

)

9 k

= k − (K

∗

)

10 Assign channel that exist in K

∗

to secondary

users.

11 return C.A

Proposed Algorithm: The procedure of the pro-

posed technique is described in algorithm 1.

Let there exist M = {M

, M

, . . . , M

} chan-

nels, P = {P

, P

, . . . , P

} primary users and s =

, s

, . . . , s

} secondary users in a cognitive radio

network. Suppose at a given time instant t, N chan-

nels are used by primary users. Hence remaining

M − N channels are free at that time t. The sec-

ondary users may use these free channels. There are s

secondary users competing for these channels. Now,

the secondary user base station initially senses the

channels according to the cognitive cycle and then

use these channels according to the non-dominated

set of solutions. Suppose the secondary user s

∈ s

wishes to use the channel M

∈ M , then the sec-

ondary user base station ﬁrst considers SINR, proba-

bility and time at that channel. Using the SINR, prob-

ability and time, a multi-objective function is formu-

lated in such a way that SINR should be maximum

with maximum probability and maximum free time

of channels. A solution set has been obtained from

the multi-objective function, and Non-dominated set

of solutions has been calculated from this solution set

using Naive and Slow approach. Now the secondary

user base station assigns to be channel M

for com-

munication to be secondary users

based on the non-

dominated set of solutions. The channels that have

higher SINR and maximum free time is allocated to

secondary users. When the free channels are allocated

according to Non-dominated set of solutions, remove

the Non-dominated set of solutions from the solution

set. Now, again calculate the Non-dominated set of

solution from the remaining solution set and allocate

the free channels according to it. Apply the same pro-

cedure on the remaining solution set until the cardi-

nality of solution set is one. This procedure is carried

out for all secondary users. Thus, it is observed that

the channels that are allocated according to the pro-

posed scheme have less interference and better com-

munication. Hence, the proposed scheme provides an

optimal utilization of channels in cognitive radio net-

works.

4 SIMULATION RESULTS AND

ANALYSIS

The performance of existing and proposed algorithm

is measured by comprehensive simulation study us-

ing OMNeT++ network simulator proposed by (Varga

and Hornig, 2008). The Cognitive radio network de-

veloped for simulation operates in a centralized man-

ner. In the network, base station is the central en-

tity which performs most of the actions and the sec-

ondary user base station makes decisions on assigning

the channels to the secondary users.

Each primary user is connected to its base station

via a channel. All the secondary users are connected

to one base station, and each primary user base

station is connected to secondary user base station.

Primary and secondary user communicate with each

other through base station. In the network at a given

Channel Allocation in Cognitive Radio Networks using Evolutionary Technique

109

time, PU can be in generating, receiving or in idle

state. At each iteration state of primary user, channel,

source and destination user are selected randomly.

Simulation Parameters: The performance of

both the algorithms is analysed in terms of packet

delivery ratio (PDR),throughput, end to end delay

(EED), packet ﬂow (PF) and channel utilization by

altering the simulation time and number of channels

in the network. The PDR represents the ratio of the

number of delivered data packets received by the des-

tinations to the number of data packets generated by

the sources. The throughput of the network is calcu-

lated as average rate of data packets delivered over the

network and it is measured in bytes/second. The EED

is measured as the time taken in seconds by a data

packet to reach the destination. PF is the total number

of packets generated in the network per simulation.

Channel utilization when plotted against number of

channels is measured as average time in seconds for

which primary and secondary users uses the channels.

Channel utilization when plotted against simulation

time is calculated as percentage time in seconds for

which channels are used by primary and secondary

user per simulation time.

For the simulation of algorithms different topolo-

gies have been considered. Number of primary users,

secondary users and channels varies between 10 to 50,

20 to 100 and 10 to 50 respectively.

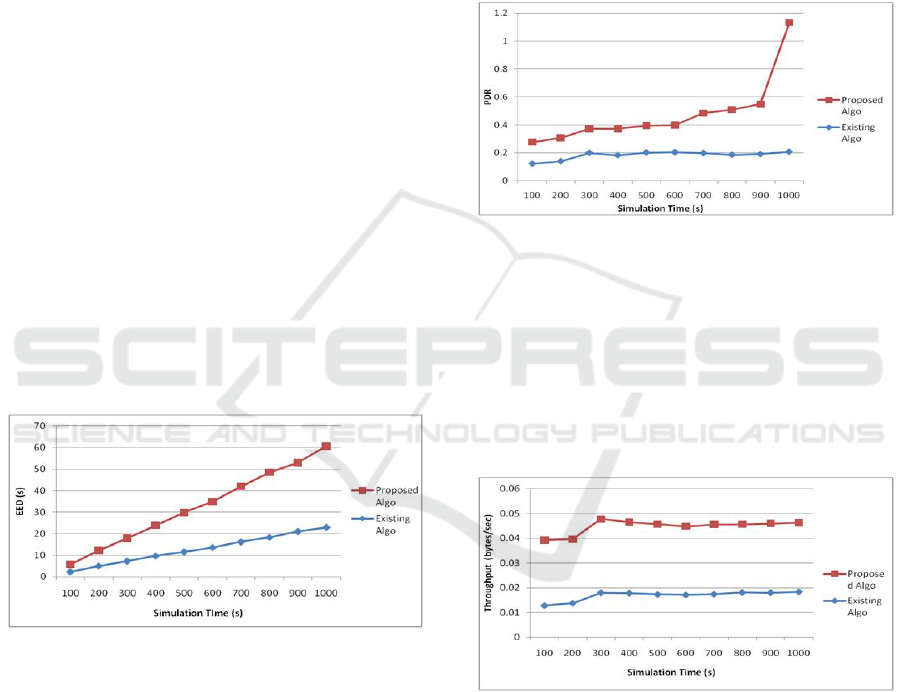
Figure 1: EED vs Simulation Time.

The variation of the existing and proposed algo-

rithm in terms of EED in shown in Figure 1. For

both the algorithms the EED increases with increase

in simulation time. As the simulation time of the net-

work increases, the packet ﬂow in the network in-

creases. This in turn increases the processing time

for each packet hence increasing the EED. Also more

number of channels are allocated using proposed algo

hence its EED is more than existing algo. By chang-

ing the simulation time, the mean EED for existing

algo is observed to be 12.85s while for proposed algo

it is 20.01s. Thus the percentage increase in EED

when channel allocation is performed using proposed

algorithm is 56.32%.

From Figure 2 it is observed that PDR for both

the algorithms show non uniform behavior with in-

crease in simulation time. There is sharp increase in

the PDR of proposed algorithm when simulation time

is 1000s. This point represents the minimum inter-

ference and conﬂict experienced by destination nodes

which results in delivery of maximum packets. For

the existing algorithm mean PDR is 0.182 while for

proposed algorithm the mean PDR is 0.297. So dur-

ing channel allocation using proposed algo the PDR

is increased by 63.18%.

Figure 2: PDR vs Simulation Time.

Figure 3 depicts the variation of throughput

(bytes/sec) of both the algorithms with the simula-

tion time. Throughput for the algorithms increases

with increase in simulation time. In case of the

existing algorithm mean throughput is found to be

0.0168 bytes/sec and for proposed algorithm 0.0278

bytes/sec. Hence when channels are allocated us-

ing proposed algorithm, the improved throughput is

65.47%.

Figure 3: Throughput vs Simulation Time.

Figure 4 and ﬁgure 5 shows the relation between

channel utilization and number of channels and sim-

ulation time respectively. From the graphs it is seen

that the channel utilization of the existing and pro-

posed algorithm shows non uniform behaviour with

increases in number of channels and simulation time

respectively. With respect to number of channels and

compared to existing algo the mean utilization is im-

proved by 57.48s for proposed algo. Whereas with

respect to simulation time the mean utilization is im-

proved by 0.075s for proposed algo.

WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems

110

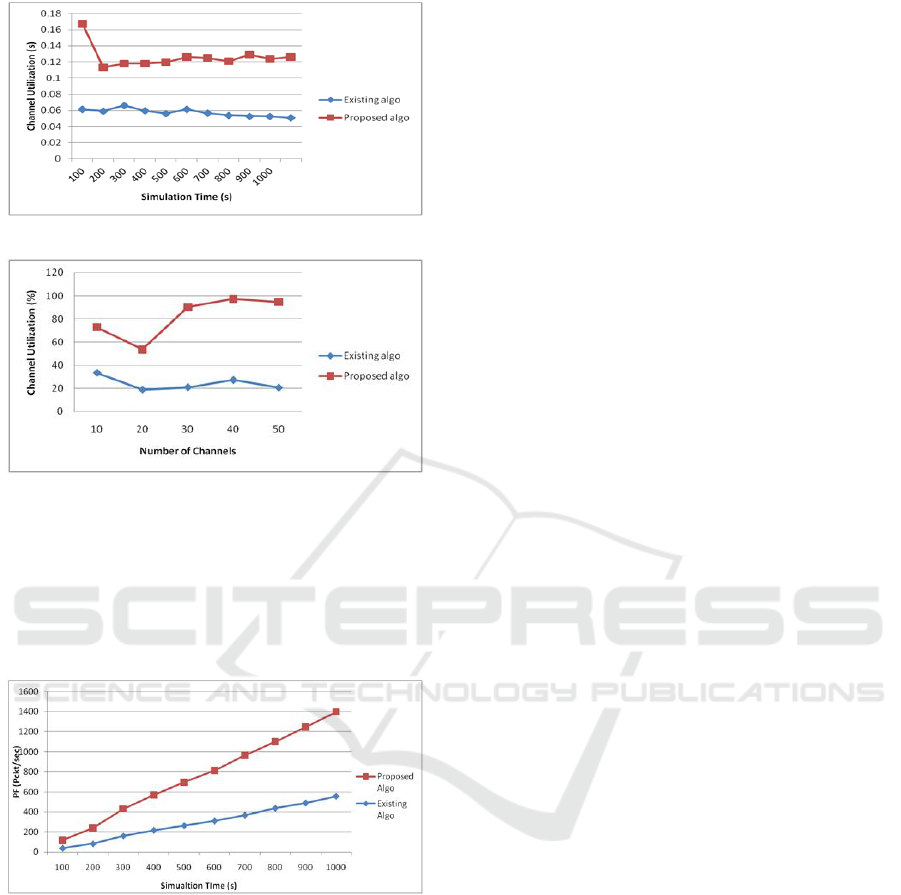
Figure 4: Channel Utilization vs Simulation Time.

Figure 5: Channel Utilization vs Number of Channels.

Figure 6 shows the variation of PF with simula-

tion time. For both the algorithms with increase in

simulation time the number of packets in the network

increases linearly. With increase in simulation time,

more time is available for users to generate and re-

ceive packets thus increasing the packet ﬂow.

Figure 6: Packet Flow vs Simulation Time.

5 CONCLUSION AND FUTURE

WORK

In this paper, a novel technique for channel as-

signment in cognitive radio network is designed in

accordance with the objectives: maximum SINR,

probability for maximum SINR and maximum free

time of channels. The objectives are achieved using

Non-dominated set of solutions. To calculate Non-

dominated set of solution Naive and Slow method is

used. It is observed that the proposed algorithm sur-

passes the existing algorithm in terms of channel uti-

lization and throughput.

In Future, other approaches can be used to opti-

mize the multi objective optimization problem. Also,

any other heuristic approach based algorithm for

channel allocation may be developed.

REFERENCES

Ahmed, E., Gani, A., Abolfazli, S., Yao, L., and Khan,

S. (2014). Channel assignment algorithms in cog-

nitive radio networks: Taxonomy, open issues, and

challenges. Communications Surveys Tutorials, IEEE,

PP(99):1–1.

Akyildiz, I. F., Lee, W.-Y., Vuran, M. C., and Mohanty,

S. (2006). Next generation/dynamic spectrum ac-

cess/cognitive radio wireless networks: a survey.

Computer Networks, 50(13):2127–2159.

Bayhan, S. and Alag

oz, F. (2014). A markovian approach

for best-ﬁt channel selection in cognitive radio net-

works. Ad Hoc Networks, 12:165–177.

Bedeer, E., Dobre, O., Ahmed, M. H., Baddour, K. E., et al.

(2014). A multiobjective optimization approach for

optimal link adaptation of ofdm-based cognitive radio

systems with imperfect spectrum sensing. Wireless

Communications, IEEE Transactions on, 13(4):2339–

2351.

Coello, C. C., Lamont, G. B., and Van Veldhuizen, D. A.

(2007). Evolutionary algorithms for solving multi-

objective problems. Springer Science & Business Me-

dia.

Deb, K. (2001). Multi-objective optimization using evolu-

tionary algorithms. John Wiley & Sons.

Dhurandher, S. K., Misra, S., Ahlawat, S., Gupta, N.,

and Gupta, N. (2009). E2-scan: an extended credit

strategy-based energy-efﬁcient security scheme for

wireless ad hoc networks. IET communications,

3(5):808–819.

Dhurandher, S. K., Woungang, I., Obaidat, M., Kumar, K.,

Joshi, M., and Verma, M. (2015). A distributed adap-

tive admission control scheme for multimedia wireless

mesh networks. Systems Journal, IEEE, 9(2):595–

604.

Gelabert, X., Sallent, O., P

erez-Romero, J., and Agust

ı,

R. (2010). Spectrum sharing in cognitive radio

networks with imperfect sensing: A discrete-time

markov model. Computer Networks, 54(14):2519–

2536.

Haykin, S. (2005). Cognitive radio: brain-empowered wire-

less communications. Selected Areas in Communica-

tions, IEEE Journal on, 23(2):201–220.

Jalali, E., Balapuwaduge, I. A. M., Li, F. Y., and Pla, V.

(2015). A dynamic channel access strategy for under-

lay cognitive radio networks: Markov modelling and

performance evaluation. Transactions on Emerging

Telecommunications Technologies.

Jiang, T., Wang, H., and Leng, S. (2013). Channel

allocation and reallocation for cognitive radio net-

Channel Allocation in Cognitive Radio Networks using Evolutionary Technique

111

works. Wireless Communications and Mobile Com-

puting, 13(12):1073–1081.

Kumar, V. (2015). Channel Allocation in Cognitive Radio

Networks. PhD thesis, Jawaharlal Nehru University,

New Delhi.

Kumar, V. and Minz, S. (2015). Ccra: channel criticality

based resource allocation in cognitive radio networks.

International Journal of Communication Systems.

Mahdi, A. H., Mohanan, J., Kalil, M., Mitschele-Thiel, A.,

et al. (2012). Adaptive discrete particle swarm op-

timization for cognitive radios. In Communications

(ICC), 2012 IEEE International Conference on, pages

6550–6554.

Masonta, M. T., Mzyece, M., and Ntlatlapa, N. (2013).

Spectrum decision in cognitive radio networks: A sur-

vey. Communications Surveys & Tutorials, IEEE,

15(3):1088–1107.

Mitola, J. (2000). Cognitive Radio—An Integrated Agent

Architecture for Software Deﬁned Radio. PhD thesis,

Royal Institute of Technology (KTH).

Qin, H., Su, J., and Du, Y. (2009). Multiobjective evo-

lutionary optimization algorithm for cognitive radio

networks. In Information Engineering and Electronic

Commerce, 2009. IEEC’09. International Symposium

on, pages 164–168. IEEE.

Suliman, I., Lehtom

aki, J., Br

aysy, T., and Umebayashi, K.

(2009). Analysis of cognitive radio networks with im-

perfect sensing. In Personal, Indoor and Mobile Radio

Communications, 2009 IEEE 20th International Sym-

posium on, pages 1616–1620. IEEE.

Teotia, V., Dhurandher, S. K., Woungang, I., and Obaidat,

M. S. (2015). Markovian model based channel allo-

cation in cognitive radio networks. In IEEE Interna-

tional Conference on Data Science and Data Intensive

Systems. IEEE.

Tragos, E. Z., Zeadally, S., Fragkiadakis, A. G., and Siris,

V. A. (2013). Spectrum assignment in cognitive radio

networks: A comprehensive survey. Communications

Surveys and Tutorials, IEEE, 15(3):1108–1135.

Varga, A. and Hornig, R. (2008). An overview of the om-

net++ simulation environment. In Proceedings of the

1st International Conference on Simulation Tools and

Techniques for Communications, Networks and Sys-

tems & Workshops, Simutools ’08, pages 60:1–60:10,

ICST, Brussels, Belgium, Belgium. ICST (Institute for

Computer Sciences, Social-Informatics and Telecom-

munications Engineering).

Wang, B., Ji, Z., Liu, K., and Clancy, T. C. (2009). Primary-

prioritized markov approach for dynamic spectrum al-

location. Wireless Communications, IEEE Transac-

tions on, 8(4):1854–1865.

Wang, B. and Liu, K. R. (2011). Advances in cognitive

radio networks: A survey. Selected Topics in Signal

Processing, IEEE Journal of, 5(1):5–23.

Wen, K., Fu, L., and Li, X. (2012). Genetic algorithm based

spectrum allocation for cognitive radio networks. In

Advances in Computer, Communication, Control and

Automation, pages 693–700. Springer.

Xiao, X., Liu, S., Lu, K., and Wang, J. (2012). Max-

div: an optimal randomized spectrum access with

maximum diversity scheme for cognitive radio net-

works. International Journal of Communication Sys-

tems, 25(7):832–848.

WINSYS 2016 - International Conference on Wireless Networks and Mobile Systems

112