FPGA Implementation of F

-Linear Pseudorandom Number Generators

based on Zynq MPSoC: A Chaotic Iterations Post Processing Case Study

Mohammed Bakiri

1,2

, Jean-Franc¸ois Couchot

and Christophe Guyeux

FEMTO-ST Institute, University of Franche-Comt

e, Rue du Mar

echal Juin, Belfort, France

Centre de D

eveloppement des Technologies Avanc

ees, ASM-IPLS Team, Baba Hassen, Algeria

Keywords:

Random Number Generators, System on Chip, FPGA, High Level Synthesis, RTL, Chaotic Iterations,

Statistical Tests, Security.

Abstract:

Pseudorandom number generation (PRNG) is a key element in hardware security platforms like ﬁeld-

programmable gate array FPGA circuits. In this article, 18 PRNGs belonging in 4 families (xorshift, LFSR,

TGFSR, and LCG) are physically implemented in a FPGA and compared in terms of area, throughput, and

statistical tests. Two ﬂows of conception are used for Register Transfer Level (RTL) and High-level Synthe-

sis (HLS). Additionally, the relations between linear complexity, seeds, and arithmetic operations on the one

hand, and the resources deployed in FPGA on the other hand, are deeply investigated. In order to do that, a

SoC based on Zynq EPP with ARM Cortex-A9 MPSoC is developed to accelerate the implementation and the

tests of various PRNGs on FPGA hardware. A case study is ﬁnally proposed using chaotic iterations as a post

processing for FPGA. The latter has improved the statistical proﬁle of a combination of PRNGs that, without

it, failed in the so-called TestU01 statistical battery of tests.

1 INTRODUCTION

Producing randomness is a common need in many ap-

plications such as simulation (Gentle, 2013), numer-

ical analysis (Zepernick and Finger, 2013), computer

programing, cryptography (Luby, 1996). Such gen-

erators are usually divided in two categories: “pseu-

dorandom” (PRNGs), which use algorithms to deter-

ministically produce numbers that look like random

(they pass statistical tests with success), and “true”

random number generators (TRNGs) that use a phys-

ical source of entropy to produce randomness.

Deterministic algorithms of pseudorandom gener-

ation can be developed by targeting a speciﬁc hard-

ware system, like a Field Programmable Gate Ar-

ray (FPGA), before automatically deploying it on the

hardware architecture by using ad hoc frameworks.

Modern FPGAs allow rapid prototyping to explore

various hardware solutions and accelerate Time to

Market. The design methodology on FPGA relies on

the use of two high levels of implementation, namely

the Register Transfer Level (RTL) ﬂow and the High

Level Synthesis (HLS) (Cong et al., 2011) one. The

HLS ﬂow enables an automatic synthesis to FPGA

support in a high programing level. It also acceler-

ates the IP creation by enabling C, C++, and Sys-

temC speciﬁcations to generate the RTL level for FP-

GAs implementation. Conversely, traditional RTL

ﬂow summarizes the Hardware Description Language

(HDL) using verilog/VHDL languages. In fact, many

recent papers use HLS ﬂow to accelerate some re-

search study in many applications like in cryptogra-

phy (Homsirikamol and Gaj, 2015).

A way to solve at least partially such secu-

rity issues is to rigorously and directly implement

PRNGs on FPGAs. To do so, we studied the main

functionalities and complexity that distinguish one

PRNG for another, which are: LFSR (LFSR113,

LFSR258, and LUT-SR), LCG (PCG32, MWC256,

CMWC4096, and MRG32k3a), TGFRS (Mersenne

Twister, Well512, and TT800), xorshift (xorshift64,

xorshift128, xorshift

∗

, and xorshift+), and Cellular

Automata generators (cf., Section 2). Then, Section 3

presents a deep analysis to identify characteristics and

main proprieties that contribute to the hardware per-

formance of each PRNG. To do so, we use a Zynq

device (Rajagopalan et al., 2011) and the two ﬂows

(HLS & RTL) as support to develop a complete Sys-

tem on Chip physical support for hardware PRNG,

which is detailed in Section 4. Due to well known

limitations of these linear generators in cryptographic

applications (e.g., linear complexity as described in

302

Mohammed, B., Couchot, J-F. and Guyeux, C.

FPGA Implementation of F

-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case Study.

DOI: 10.5220/0005967903020309

In Proceedings of the 13th International Joint Conference on e-Business and Telecommunications (ICETE 2016) - Volume 4: SECRYPT, pages 302-309

ISBN: 978-989-758-196-0

Section 3), chaotic iterations are ﬁnally introduced

in Section 5 as a possible post processing for hard-

ware PRNGs. The latter improves the statistical pro-

ﬁle of the generated numbers as veriﬁed by the so-

called TestU01 battery of tests (L’Ecuyer and Simard,

2007).

2 F

-LINEAR GENERATORS

Let F

be the ﬁnite ﬁeld of cardinality 2. Let us

ﬁrstly recall that a common way to deﬁne a pseu-

dorandom number generator is to consider two func-

tions, namely f : F

→ F

and g : F

→ F

, where

usually N > M and g is one way, such that internally

n+1

= f (x

) is computed, while externally y

n+1

g(x

n+1

) is produced (x

being a seed provided by the

user). A linear PRNG of r bits are a special case of

linear recurrence modulo 2, which can be deﬁned by

the following equations:

= A × x

i−1

(a) y

= B × x

(b)

r =

∑

`=l

{i,`−1}

−`

= y

{i,0}

{i,1}

{i,2}

...(c)

(1)

Indeed the ﬁrst equation (a) deﬁnes the function f ,

where x

= (x

i,0

,...,x

i,k−1

) ∈ F

is the k-bit vector

at step i and A is a k × k transition matrix with k-bit

-vector. The other equations (b) and (c) deﬁne the

function g, where y

= (y

i,0

,...,y

i,w−1

) ∈ F

is the w-

bit output vector at step i, while B is a w × k output

transformation matrix with elements in F

. The latter

produces the output bits that correspond to the inter-

nal RNG state, which is rewritten as r ∈ [0,1]: the

output at step i. We focus on implementing four fam-

ilies of generators in one or both ﬂows, which are:

Linear Feedback Shift Register. It uses a se-

quence of shift registers to generate one bit per it-

eration. In such a PRNG, the matrix A represents

the LFSR coefﬁcients. Accordingly, if any of these

coefﬁcients exists, it deploys a XOR operand on

some designed registers to build a feeadback input

to the ﬁrst register. LFSR113, LFSR258 (L’Ecuyer,

1999b), and Taus88 (L’Ecuyer, 1996) are examples

of LFSR. Additionally, Look-up Table Shift Register

(LUT-SR) (Thomas and Luk, 2013)) is another LFSR

generator, which uses LUT as a k-bit shift-register to

allow the cascading for any required size.

Linear Congruential Generators. They

are based on linear recurrence equations having

the form: x

i+1

= (ax

+ c) mod 2

. Multiply-

With-Carry MWC256 and Complementary MWC

CMWC4096 (Couture and L’Ecuyer, 1997) are

two implementations of LCG, where in MWC

the increment c = b(ax

i−r

+ c

i−1

)/2

c is an initial

carry, and the CMWC takes the complement of

− 1) − x

(MWC) to form a new output. Another

example is a new improvement of LCG named

PCG32 (O’Neill, 1988), which uses a permutation

function (dropping bits using ﬁxed and random

rotations). We can also evoke the MRG32K3a

generator (L’Ecuyer, 1999a), which is a combined

Multiple Recursive Generator computed as follows:

= x

Twisted Generalized Feedback Shift Register.

It is based on matrix linear recurrence of n sequence

words, each containing w-bits. For each recurrence

operation k, k = 0,1,...,m, the TGFSR operates with

three sequence words: the ﬁrst two sequence words

and x

k+1

being computed with bitmask vectors

MSB

LSB

) with the middle sequence word x

k+m

0 6 m 6 n, as follows:

k+n

= x

k+m

⊕ (((x

& S

MSB

) | (x

k+1

& S

LSB

)) × A).

(2)

At iteration i = k + n, TGFSR uses a tamper-

ing module (bitwise/shift computation) to reduce

the dimensionality n of equidistribution. Mersenne

Twister (MT) (Matsumoto and Nishimura, 1998),

Well512 (Panneton et al., 2006), and TT800 (Mat-

sumoto and Kurita, 1994) are examples of TGFSR.

XORshift Generators. They are very fast

PRNGs, in which the internal state is repeatedly

changed by applying a series of shift and exclusive-

or (XOR ⊗) operations. XORshift

∗

generators (Vi-

gna, 2014a), XORshift64 (Marsaglia et al., 2003), and

XORshift+ (Vigna, 2014b) are instances of such gen-

erators.

Cellular Automata Generator. This is a dis-

crete generator proposed as formal models of self-

reproducing robots. It includes at least 3 cells with

an internal state machine that can be a Boolean func-

tion rule. Therefore, the CA structure can hold and

update the internal state for each cell, depending on

the local rules registered by the Wolfram code (Gleick,

1997) (2

possibilities) and the states of their neigh-

borhoods.

3 HARDWARE

IMPLEMENTATION

In this section, we start a deep analysis of the PRNG

implementations on FPGA using Register Trans-

fer Level (RTL) and/or High Level Synthesis (HLS)

ﬂows. Results are studied according to: (1) the space,

timing, and computational complexity, (2) the seed

and period, and (3) the arithmetic operators and dy-

namic range FPGA resources. Table 1 and Table 2

FPGA Implementation of F

-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case

Study

303

(a) LCG Familly

(b) TGFSR Familly

(d) LFSR Familly

Figure 1: Computational Complexity Analysis with

Berlekamp-Massey Algorithm.

show obtained results when implementing 18 PRNGs.

Figure 1 presents, for its part, the computation com-

plexity and its impact on performance. Each PRNG is

implemented either in just one or both (HLS & RTL)

ﬂows. Concerning the software platform, we used Vi-

vado HLS tool for HLS ﬂow and Vivado synthesis for

RTL ﬂow of Xilinx.

3.1 Space, Timing, and Computational

Complexities

The space represents the allocated cost of most ob-

jects used in the algorithm (tables, indexes, loops,

etc.). Regarding FPGAs, the latter can be translated

in memories, registers, and LUT resources, etc. The

question raised in this section is thus: how much

space states are needed to provide pseudorandom

numbers with a good statistics proﬁle? We won-

der too whether there is any relation between the

space (mean resources) used in FPGA and a suc-

cess in passing stringent statistical Linear Complexity

Test (Blackburn et al., 1994) of test. To answer this

question, we ﬁrst deﬁne what is a linear complexity.

Most PRNGs mentioned in this article are linearly

recursive. If we take a ﬁnite binary sequence (x

) =

i,0

,...,x

i,k−1

) ∈ F

, its linear complexity L

) is

the length of the shortest characteristic polynomial

(see Equation (1)) of the LFSR generating the same

sequence (for a sequence equal to x

= x

= ··· =

k−2

= 0 and x

k−1

= 1, the linear complexity is k

and L

k+1

> L

). Non randomness is claimed when

the length is short. This is conﬁrmed by the fact that

almost all generators (with the exception of PCG32,

xorshift

∗

, and MRG32k3a) presented in this article

fail in statistical Linear Complexity Test of Test.

A ﬁrst way to compute this complexity is to con-

sider the NIST tests battery (Barker and Roginsky,

2010). But the improved Test battery additionally in-

corporates some “jump” aspects in this test, leading

to the fact that most generators succeeding in NIST

linear complexity test ﬁnally fail to pass the one of

Test. Indeed, the latter calculates the jumps that occur

in the linear complexity for each local subsequence,

that is, the k’s that satisfy L(k) − L(k − 1) > 0. This

number of jumps represents how much bits have to be

added to the sequence to increase its linear complex-

ity. Ideal PRNGs have to perform jumps symmetric

to the k/2-line (Rueppel, 1985), as in a perfect linear

complexity, maximum jump heights of k/4 and close

to b(k + 1)/2c for k-sequences are required.

Regarding FPGAs, these jumps determine how

much resources are required in order to have a perfect

complexity proﬁle. For illustration purposes, some

of these PRNG jumps have been computed, see Fig-

ure 2. Concerning 32 bit sequences, the number of

perfect successive jumps (< 2) is large for all PRNGs

(XOR64, for instance, has a total of 6 jumps, 4 of

them being perfect). However, in the 64 bit case, two

kind of results have been obtained. On the one hand,

we found PCG32 and MRG that can pass Test have

low successive jumps compared to xorshift

∗

. This is

due to the multiplication space used for these gen-

erators. This is conﬁrmed in Figure 1, that summa-

rizes the linear complexity for each family of PRNGs,

which is close to k/2 = 32.

Let us now consider xorshift

∗

generators, which

also use 64-bit multiplications. Their linear complex-

ity is closely perfect, as can be seen in Figure 1. The

key difference here is the permutation function used

for multiplication. In LCG family, this is the main

function applied to perform an uniform scrambling

operation. On the opposite, they are deployed to inject

bias in randomness in xorshift

∗

. The PCG32 deploys

SECRYPT 2016 - International Conference on Security and Cryptography

304

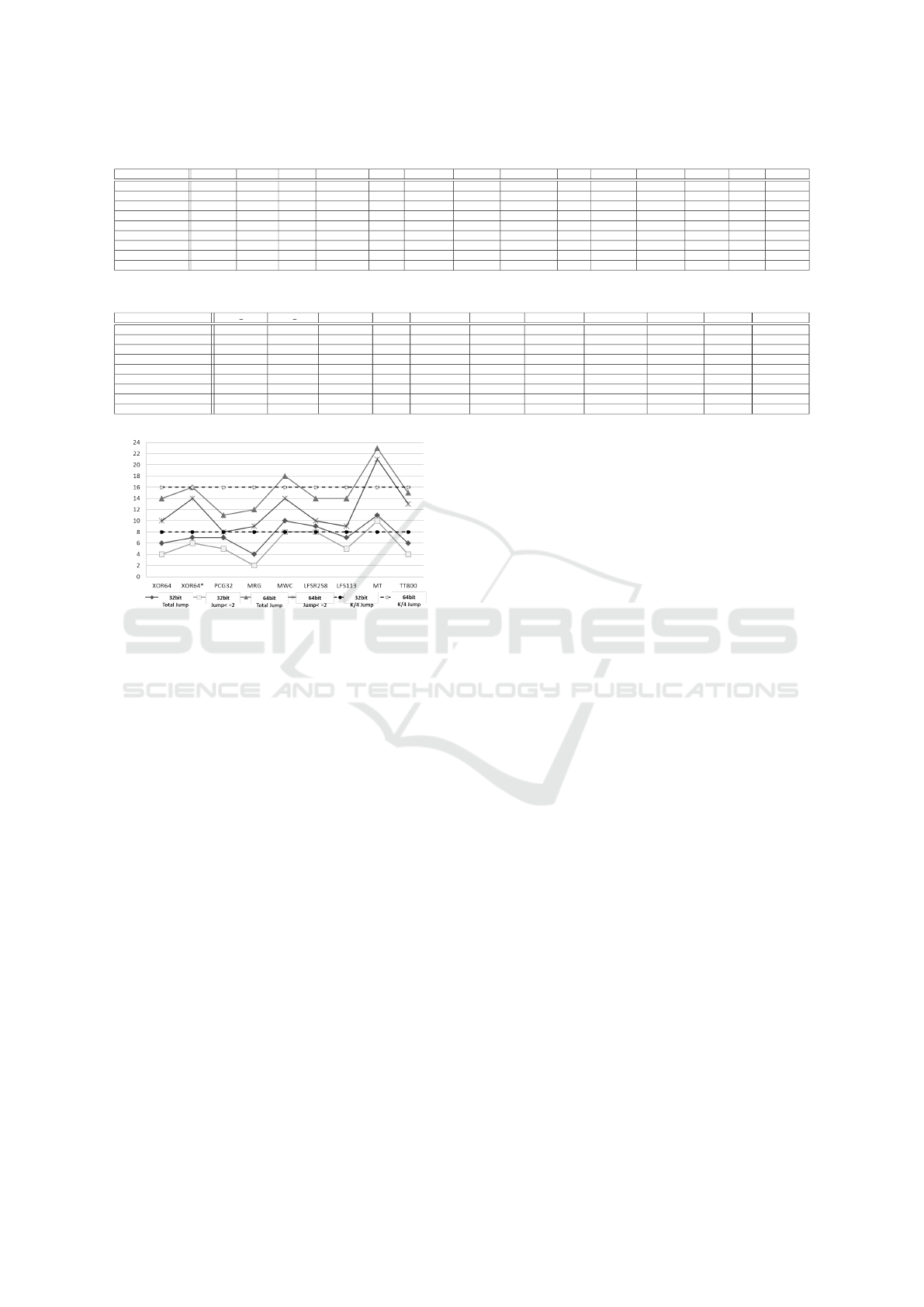
Table 1: HLS Implementation.

PRNG LFSR113 TAUS88 PCG32 MRG32k3a TT800 WELL512 MWC256 CMWC4096 XOR

∗

LFSR258 XORP128 XORP64 XOR+ KISS124

Output Range 32 32 32 32 32 32 32 32 64 64 64 64 64 64

Period 2ˆ 113 88 32 191 800 512 8222 131086 1024 258 128 64 128 124

LUT 66 56 371 214 173 90 219 285 303 132 49 64 136 271

FF 113 88 367 522 549 147 399 471 394 258 64 65 133 746

RAM 0 0 0 0 2 2 1 8 4 0 0 0 4 0

DSP 0 0 10 8 6 0 4 2 10 0 0 0 0 7

Frequences Mhz 769 555 333 160 160 214 153 148 224 617 510 894.45 225 149

Area 1432 1152 5904 5888 5776 1896 4944 6048 5576 3120 904 1032 2152 8136

Throughput Gbps 24.6 17.76 10.6 5.12 5.12 6.8 4.9 4.7 14.33 39.5 156.32 57.24 14.40 4.7

Table 2: RTL Implementation on FPGA.

PRNG MT WS MT NS LUT-SR CA LFSR113 TAUS88 LFSR258 XORP128 XORP64 XOR+ KISS124

Output Rang 32 32 32 32 32 32 64 64 64 64 64

Period 2ˆ 19937 19937 1024 32 113 88 258 128 64 128 124

LUT 523 184 64 98 95 96 207 53 65 147 742

FF 120 179 64 40 128 77 320 128 64 196 256

RAM 2 2 0 0 0 0 0 0 0 0 0

DSP 3 0 0 0 0 0 0 0 0 0 6

Frequences Mhz 118 462 609 598 595 667 556 531 588 403 78.1

Area 5144 3272 576 1104 1784 1384 4216 1448 1032 2744 7984

Throughput Gbps 3.8 13.2 19.5 19.1 19 21.3 35.5 17 37.6 25.7 5

Figure 2: Jump Computation for 32/64 bit of random.

64-bit multiplications (128-bit state), but it uses only

36-bit of state while always dropping the MSB parts

(the states space used are constant for any operation).

This fact means a loss of information that can create

a new jump in complexity, even if we use more com-

plected seeds (i.e., pcglong). In other words, it needs

some time to be perfectly linear (see Figure 1(a) start-

ing from 41-bit). In hardware level, doing the same

operation leads to unnecessary area and power con-

suming.

The second point to investigate is the size and

number of jumps in complexity proﬁle. If we consider

multiplications for instance, each PRNGs embedding

them needs 2 ∗ n outputs of multipliers (DSP or LUT

blocs in FPGA) for each n-bit input multiplication:

for each jump, an additional input multiplier is used.

In other words and compared to stable complexity, a

ﬁxed jump during time does not use the full capacity

of the multiplier (see Section 3.3).

3.2 Seed and Period

Most generator implementations require a seed to ini-

tiate the internal states. It is also a space determinis-

tic parameter for the PRNG. Regardless of the space

size, the consumption can be quite large if the seed is

large. This seed can be: single or multiple value(s) in

table(s), a constant or a value generated from a given

algorithm, or it can even be extracted from a physical

source (TRNG). Additionally, the seed can also con-

tribute to the period of the PRNG. A period of a power

of two is recommended to have an uniform output,

due to the following reason: if it is not the case, some

hardware resources cannot be used (e.g., MRG32k3

has an output of 2

− 209 and 209 values are never

used).

In our implementations (RTL and HLS), we

choose to seed TGFSR and MWC generators with

an array using one of Knuth’s generators (see (Knuth,

1997, p. 106) for multiplier). Depending on the seed

period and using MT as an example, we can store each

value of the seed in one memory at a time and for each

clock cycle. The RAM memory, conﬁgured in the

read-before-write mode, operates like a feedback shift

ory at an appropriate write address, while the previ-

ous data are transferred to the output ports. The latter,

coming from RAM, are then processed following the

Equation (2). Therefore, different address controllers

are used for each process (seed and generation). For

the other PRNGs, the seed can be a constant or gen-

erated by another algorithm.

Let us illustrate the performance impact using

Mersenne Twister (MT) with (WS) and without (NS)

the seed algorithm in RTL level. When including the

seed in implementation, we need to store 624 values

in two memories for each clock cycle, which are used

later in random transformation and tempering. There-

fore, the total area and time resources is increased.

Otherwise, in the case of the absence of the seed, the

latter is generated and stored separately in memories,

before the deployment of the PRNG. During our com-

parisons of the two approaches on MT generator, we

have remarked that, with seed, frequency is reduced

FPGA Implementation of F

-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case

Study

305

to less than 200MHz compared to the case without

it. Therefore, to increase performances, most PRNGs

do not include the seed internally (software is used).

The LUT-SR PRNG is an exception, which consumes

less space but needs to wait 1,024 clock cycles for the

seed generation.

3.3 Arithmetic Operators and Dynamic

Range

The arithmetic operators area is a key issue at hard-

ware level, which can be considered as a major factor

of the quality of the ﬁnal implementation. These oper-

ators can be a single basic operation (like addition or

subtraction, multiplication of variables or constants),

algebraic functions (division, modulo, etc.), or any

other elementary function. However, in hardware

level, these arithmetic operations (specially the mul-

tiplication) are hard coded by the tools (Xilinx) us-

ing optimized algorithms for that (Canonical Signed

Digit (CSD), Booth recoding, etc.).

In the binary ﬁeld F

, most PRNGs use only pos-

itive integer values and ﬁxed point representations

in hardware level, while if we take for instance the

computing of the partial products, the latter can use

only glue logic (i.e., AND gates or a series of ad-

ditions). These partial products are deﬁned as Dis-

tributed Arithmetic (DA (Meyer-Baese and Meyer-

Baese, 2007)), they perform a multiply-and-add op-

eration at the same time using most basic logic ele-

ments (LUTs). Their size and performance depend on

both the word length (addressing the LUT increases

the table exponentially) and their binary representa-

tions, regarding dynamic range and precision. This

word length represents the ratio between the largest

and the smallest nonzero and positive number that can

be represented (integer), which is expressed as follow:

fxpt

= r

− 1 where r is in binary format (Radix-2)

and n is the number of digits in ﬁxed-point precision.

Modern FPGAs use Digital Signal Processing

(DSP48E1) slices to obtain the optimal implementa-

tion of these operators and avoid overﬂows and un-

derﬂows for complex operations. It supports many in-

dependent functions including multiply, MAC, mag-

nitude comparator, bit-wise logic functions, etc. Be-

cause multiplications are widely used in PRNGs, they

can be implemented with DSP used as a 25x18-bit

multiplier, and which can be pipe-lined. In Figure 1,

we can see the obvious impact of DR on computation

complexity, which means that larger DR are translated

to logic space, operator, and timing. Let us take for

instance the LFSR258 of DR= 2

, which applies ex-

act logic operators as shift, logic AND, and xorshift.

Its complexity is linear with the “DA” used when

1 < DR < 16 bits, otherwise it jumps higher with the

use of more complicated logic to operate multiplica-

tions (DSP) and store values.

4 SOC SYSTEM BASED ON ZYNQ

PLATFORM FOR PRNG

4.1 Hardware and Firmware Design

Xilinx Zynq-7000 Extensible Processing Platform

(EPP) (Rajagopalan et al., 2011) is a silicon system

on chip (SoC) for FPGAs, which has been proposed

by Xilinx. The latter is deﬁned as Peripheral Sys-

tem (PS), which is a sub-system with ARM. The full

FPGA, for its part, is the Programmable Logic (PL)

that is connected with PS through an AXI bus inter-

face. Therefore, and for pseudorandom number gen-

eration, we have developed a complete SoC infras-

tructure divided in two parts: hardware and ﬁrmware.

The hardware architecture of our system used to

integrate and test PRNGs is illstrated in Figure 3.

It contains, respectively: the ARM Cortex-A9 dual

cores MPSoC, the high performance DDR3 512Mb,

an UART, and ﬁnally the PRNGs (RTL or HLS imple-

mentation). Additionally, to read the random output

on the CPU, we have used both an AXI-PRNG inter-

connect and an AXI Direct Memory Access controller

engine (DMA). The ﬁrmware for it parts, is used to

initialize the system, for transaction synchronization,

and for the interface with an external peripheral.

Meanwhile, the CPU initialises and reads/writes

data of an IP in PL (i.e., PRNG) over the AXI mas-

ter using general-purpose GP ports. On the other

hand, the AXI slave is used for PL master IP over

High Performance (HP) ports. Each of these inter-

faces can handle up to 16 bytes of data. The inter-

face protocol, for its part, can be conﬁgured either as

Stream for high-speed streaming data, or as Lite/Full

for high-performance memory-mapped requirements

(data transactions over an address).

This interconnect component is re-conﬁgurable

using the ﬁrmware, which deploys two GPIO IPs for

that task. GPIO-0 is used to select one PRNG at a

time, and GPIO-1 is used for the data burst size of

the PRNG. For instance, all PRNGs implemented in

HLS or RTL including the AXI-PRNG interconnect

are AXI Stream Interface, while the CPU is Memory-

Mapped Interface. Additionally to CPU, the AXI

DMA engines, which oversees the data transaction

between the slave and master IPs, deploys the receiver

channel Slave to Memory Map (S2MM) connected to

a salve port and the transmitter channel Memory-Map

SECRYPT 2016 - International Conference on Security and Cryptography

306

Figure 3: PRNG Platform Based on Zynq.

to Slave (MM2S) connected with the master.

4.2 Comparison

Table 1 and Table 2 give some performance results of

PRNG implementation in terms of area (space) and

throughput (speed). The Xilinx tool calculates all re-

sources used in FPGA as logic gates, LUT, Flip-Flop

(register), additionally to DSP and memory blocks.

Hence, for our area comparison, we only calculated

LUT and FF as (LUT + FF) × 8, since DSPs and

RAM memories are hard blocs that can mostly affect

time performances. The throughput performance is

calculated as Frequency× Output range. It depends

on two parameters, namely the logic critical path used

and the output range (32 or 64 bits).

We obtained that the lowest area resources are

for LUT-SR, Taus88, and xorshift64, while combined

PRNGs like KISS and MRG32k3a have a large area

consumption too. Additionally, the throughput of

Taus88 and LUT-SR with LFSR113 of 32 bit genera-

tors, have the highest throughput performance, while

the best are xorshift64 and LFSR258 in the 64 bit

case. On the other hand, the LCG and TGFSR fam-

ilies are expected to have the lowest throughput per-

formance, as they operate large arithmetic operations

like 64 bit multiplications using DSP (it will be worse

when using LUT). Besides that, using memories for

TGFSR will drop the PRNG frequency automatically

to the half without counting other logic. Once again,

the combined generators have the weakest throughput

performances. To conclude the FPGA resource per-

formance aspects of this comparison, LFSR and xor-

shift PRNGs are more recommended to limit space

and for better speed performances in hardware appli-

cations (mobile phone, smart cards, and so on).

Hardware PRNGs presented here must be evalu-

ated too regarding their randomness, which can be

done using statistical tests. The TestU01 battery is

currently the most complete and stringent battery of

tests for RNGs, which groups more than 516 tests in-

side 7 big sub-batteries. Among them, the Big Crush

is the most difﬁcult one.

After applying our experiments illustrated in

Figure 4, we have obtained that only PCG32,

MRG32K3a, and xorshift

∗

generators can pass the

Big-Crush of TestU01, which is coherent with the lit-

erature. Obtained test results have shown that a par-

ticular and common test called the linearity complex-

ity test is very frequently failed. In details, TestU01

uses the Berlekamp-Massey algorithm with the jump

statistic to calculate the expected values compared to

a chi-square test (the expected value). Such a fail-

ure is related to what has been detailed in Section 3.1

about the linear complexity computation. Indeed all

PRNGs are linear, but this does not lead to the linear

complexity of a long random sequence.

Figure 4: Linear Complexity Test failing for TestU01.

To put it in a nutshell, if we take the ratio of

area/throughput as main criterion, we are balancing

between high performance (xorshift64 and LFSR113)

and the ability to pass statistical tests (PCG32 and

xorshift

∗

), which is not surprising. Another result

is that combining PRNGs leads to a performance

decrease in hardware level. Next section studies a

family of speciﬁc combinations which are based on

Chaotic Iteration.

5 CHAOTIC ITERATION POST

PROCESSING

In this section, a recent pseudorandom number post

treatment based on Chaotic Iterations (CIs (Bahi

et al., 2009; Fang et al., 2014; Bahi et al., 2013))

is recalled. It is based on Devaney (Devaney, 2003)

theory of chaos. This theory focuses on recurrent se-

quences of the form x

∈ R: x

i+1

= f (x

), and stud-

ies for which function f such sequences presents el-

ements of complexity and disorder. In particular, it

is wondered when effects of an alteration of the ini-

FPGA Implementation of F

-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case

Study

307

tial term x

can be predicted. Such chaotic sequences

are candidate to provide pseudorandomness, leading

to the ﬁeld of chaotic pseudorandom number genera-

tors (CPRNGs).

Let us now recall the mathematical deﬁnition of

chaotic iterations CIs (Bahi et al., 2009). They are a

particular kind of vectorial discrete dynamical system

in which at i-th iteration, only a subset of components

of the iteration vector are updated.

Deﬁnition 5.1. Let f : {0; 1}

−→ {0;1}

and S ∈

P (J1, NK)

a sequence of subsets of the integer inter-

val J1, NK called a “chaotic strategy”, where P (X) is

the set of all subsets of X and N is the set of natural

numbers. General chaotic iterations ( f ,(x

,S)) are

deﬁned for any n ∈ N

∗

and i ∈ J1; N K by:











∈ B

, N > 2

(

n−1

if i /∈ S

f (x

n−1

)

if i ∈ S

For our PRNG applications, CIs have been im-

plemented by the following process. The iteration

function f is the negation function ( f ((x

,...,x

)) =

,...,x

)). In this case, the CI based pseudoran-

dom number generator is denoted by XOR-CIPRNG,

which can be rewritten as x

i+1

= x

⊗ S

(Bahi et al.,

2015). In the modiﬁed version we implemented, two

inputted PRNGs denoted by x

and y

are used for

deﬁning the chaotic strategy S, as described in Algo-

rithm 1. Furthermore, we added a third inputted set

generator z

for more complexity. This generator will

pick randomly a subset of the inputs at each iteration.

Only the log(log(n)) least signiﬁcant bits (in this case,

3 bits) are ﬁnally taken for pseudorandomness.

Algorithm 1: Xorshift based Chaotic Iteration.

Input: s (a 32-bit word)

Output: r (a 32-bit word)

← PRNG1, y

← PRNG2, z

← PRNG3

if (z

& 1) 6= 0 then

s ← s ⊗ (x

& 0x0 f f f f f f f f )

end

if (z

& 2) 6= 0 then

s ← s ⊗ (x

 32)

end

if (z

& 4) 6= 0 then

s ← s ⊗ (y

& 0x0 f f f f f f f f )

end

r ← s ⊗ (y

 32)

We tested more than 275 combinations using CI

post processing, a few of them being summarized

in Table 3. In the ﬁrst row of this table, triplets

[i, j, k] represent the combination of PRNG1, PRNG2,

and PRNG3 successively, where for i and j, 0 is for

xorshift64, 1 means xorshift

, while the third compo-

nent k is respectively set to 1,2,3,4, and 5, correspond-

ing to LFSR113, Taus88, TT800, WELLRNG512,

and Mersenne Twister.

If we compare with the combined generators KISS

and MRG32k3a previously evaluated, we can no-

tice the same characteristic in terms of area and

throughput. Let us remark that some combinations

need huge area resources, due to internal space re-

quired for some PRNGs like the Mersenne Twister

or CMWC4096. But objective of this article is

to show that PRNGs which previously failed some

statistical tests can pass them after the CI post

treatment: indeed, all the combinations of Table 3

achieve to pass the most stringent Big-Crush bat-

tery of Testu01. Furthermore, if we consider the

combinations of [xorshift64, xorshift

, LFSR113]

or [xorshift

, xorshift

, Taus88], the obtained CI-

PRNGs are more performing than MRG32k3a (which

also pass the TestU01) without using any DSP&RAM

blocs. To sum up, chaotic iterations post processing

can contribute to increase the statistical performance

of PRNGs.

Table 3: Chaotic Iterations Post Processing Implementa-

tion.

PRNG 011 012 013 014 015 112

LUT 283 430 362 499 367 356

FF 540 975 557 854 607 519

DSP 0 6 0 3 2 0

RAM 0 2 2 2 8 0

Area/10

6.58 11.2 7.3 10.8 7.79 7.0

T(Gbps) 6.9 5.5 6.5 5 5.5 5.9

6 CONCLUSION

A novel implementation of various PRNGs in FPGA

is detailed in this paper, in which two ﬂows of con-

ception (RTL and HLS) demonstrate the performance

level of each PRNG in terms of area throughout and

statistical tests. Our study has shown that these per-

formances are related to linear complexity, seed size,

and arithmetic operations. In order to investigate

these parameters, a SoC based on Zynq EPP platform

(hardware and ﬁrmware) has been developed to accel-

erate the implementation and tests of various PRNGs

on FPGA. On this platform, xorshift64 and LFSR113

have outperformed the other candidates when con-

sidering hardware performance, while PCG32 and

xorshift

∗

are the best when studying statistical ones

(they succeeded to pass the whole TestU01 batteries).

Finally, a hardware post processing treatment based

SECRYPT 2016 - International Conference on Security and Cryptography

308

on chaotic iterations has been proposed, which has

achieved to improve the statistical proﬁle of ﬂawed

generators. We plan to investigate which combina-

tions and parameters of chaotic iterations can be cho-

sen to reach an ideal PRNG (fast, small, and secure).

ACKNOWLEDGEMENTS

This work is partially funded by the Labex ACTION

program (contract ANR-11-LABX-01-01).

REFERENCES

Bahi, J., Couturier, R., Guyeux, C., and H

eam, P.-C. (2015).

Efﬁcient and cryptographically secure generation of

chaotic pseudorandom numbers on gpu. The journal

of Supercomputing, 71(10):3877–3903.

Bahi, J., Guyeux, C., and Wang, Q. (2009). A novel pseudo-

random generator based on discrete chaotic iterations.

In INTERNET’09, 1-st Int. Conf. on Evolving Internet,

pages 71–76, Cannes, France.

Bahi, J. M., Fang, X., Guyeux, C., and Larger, L. (2013).

Fpga design for pseudorandom number generator

based on chaotic iteration used in information hiding

application. Appl. Math, 7(6):2175–2188.

Barker, E. and Roginsky, A. (2010). Draft NIST special

publication 800-131 recommendation for the transi-

tioning of cryptographic algorithms and key sizes.

Blackburn, S., Carter, G., Gollmann, D., Murphy, S., Pa-

terson, K., Piper, F., and Wild, P. (1994). Aspects of

linear complexity. In Communications and Cryptog-

raphy, pages 35–42. Springer.

Cong, J., Liu, B., Neuendorffer, S., Noguera, J., Vissers,

K., and Zhang, Z. (2011). High-level synthesis for

fpgas: From prototyping to deployment. Computer-

Aided Design of Integrated Circuits and Systems,

IEEE Transactions on, 30(4):473–491.

Couture, R. and L’Ecuyer, P. (1997). Distribution proper-

ties of multiply-with-c arry random number genera-

tors. Mathematics of Computation of the American

Mathematical Society, 66(218):591–607.

Devaney, R. L. (2003). An Introduction to Chaotic Dynam-

ical Systems, 2nd Edition. Westview Pr.

Fang, X., Wang, Q., Guyeux, C., and Bahi, J. M. (2014).

Fpga acceleration of a pseudorandom number genera-

tor based on chaotic iterations. Journal of Information

Security and Applications, 19(1):78–87.

Gentle, J. E. (2013). Random number generation and Monte

Carlo methods. Springer Science & Business Media.

Gleick, J. (1997). Chaos: Making a new science. Random

House.

Homsirikamol, E. and Gaj, K. (2015). Hardware bench-

marking of cryptographic algorithms using high-level

synthesis tools: The sha-3 contest case study. In

Applied Reconﬁgurable Computing, pages 217–228.

Springer.

Knuth, D. E. (1997). The Art of Computer Program-

ming, Volume 2 (3rd Ed.): Seminumerical Algo-

rithms. Addison-Wesley Longman Publishing Co.,

Inc., Boston, MA, USA.

L’Ecuyer, P. (1996). Maximally equidistributed combined

tausworthe generators. Mathematics of Computation

of the American Mathematical Society, 65(213):203–

213.

L’Ecuyer, P. (1999a). Good parameters and implementa-

tions for combined multiple recursive random number

generators. Operations Research, 47(1):159–164.

L’Ecuyer, P. (1999b). Tables of maximally equidis-

tributed combined lfsr generators. Mathematics of

Computation of the American Mathematical Society,

68(225):261–269.

L’Ecuyer, P. and Simard, R. (2007). Testu01: Ac li-

brary for empirical testing of random number gener-

ators. ACM Transactions on Mathematical Software

(TOMS), 33(4):22.

Luby, M. G. (1996). Pseudorandomness and cryptographic

applications. Princeton University Press.

Marsaglia, G. et al. (2003). Xorshift rngs. Journal of Sta-

tistical Software, 8(14):1–6.

Matsumoto, M. and Kurita, Y. (1994). Twisted gfsr genera-

tors ii. ACM Transactions on Modeling and Computer

Simulation (TOMACS), 4(3):254–266.

Matsumoto, M. and Nishimura, T. (1998). Mersenne

twister: a 623-dimensionally equidistributed uniform

pseudo-random number generator. ACM Transactions

on Modeling and Computer Simulation (TOMACS),

8(1):3–30.

Meyer-Baese, U. and Meyer-Baese, U. (2007). Digital sig-

nal processing with ﬁeld programmable gate arrays,

volume 65. Springer.

O’Neill, M. E. (1988). PCG: A family of simple fast

space-efﬁcient statistically good algorithms for ran-

dom number generation.

Panneton, F., L’Ecuyer, P., and Matsumoto, M. (2006). Im-

proved long-period generators based on linear recur-

rences modulo 2. ACM Transactions on Mathematical

Software (TOMS), 32(1):1–16.

Rajagopalan, V., Boppana, V., Dutta, S., Taylor, B., and

Wittig, R. (2011). Xilinx zynq-7000 epp–an exten-

sible processing platform family. In 23rd Hot Chips

Symposium, pages 1352–1357.

Rueppel, R. A. (1985). Linear complexity and random se-

quences. In Advances in CryptologyEUROCRYPT85,

pages 167–188. Springer.

Thomas, D. B. and Luk, W. (2013). The lut-sr family of

uniform random number generators for fpga architec-

tures. Very Large Scale Integration (VLSI) Systems,

IEEE Transactions on, 21(4):761–770.

Vigna, S. (2014a). An experimental exploration of

marsaglia’s xorshift generators, scrambled. arXiv

preprint arXiv:1402.6246.

Vigna, S. (2014b). Further scramblings of marsaglia’s xor-

shift generators. arXiv preprint arXiv:1404.0390.

Zepernick, H.-J. and Finger, A. (2013). Pseudo random

signal processing: theory and application. John Wiley

& Sons.

FPGA Implementation of F

-Linear Pseudorandom Number Generators based on Zynq MPSoC: A Chaotic Iterations Post Processing Case

Study

309