
On Nonlinearity Measuring Aspects of Stochastic Integration Filter
Jind
ˇ
rich Havl
´
ık, Ond
ˇ
rej Straka, Jind
ˇ
rich Dun
´
ık and Ji
ˇ
r
´
ı Ajgl
European Centre of Excellence - New Technologies for Information Society,
Department of Cybernetics, University of West Bohemia, Technick
´
a 8, Pilsen, Czech Republic
Keywords:
State Estimation, Bayesian Approach, Stochastic Integration, Measures of Nonlinearity, Measures of
Non-Gaussianity.
Abstract:
The paper deals with Bayesian state estimation of nonlinear stochastic dynamic systems. The focus is aimed at
the stochastic integration filter, which is based on a stochastic integration rule. It is shown that the covariance
matrix of the integration error calculated as a byproduct of the rule can be used as a measure of nonlinearity.
The measure informs the user about validity of the assumptions of Gaussianity, which is adopted by the
stochastic integration filter. It is also demonstrated how to use this information for a prediction of the number
of remaining iterations of the rule. The paper also focuses on utilization of the integration error covariance
matrix for improving estimates of the mean square error of the estimates, which is produced by the filter.
1 INTRODUCTION
Nonlinear state estimation of discrete-time stochas-
tic dynamic systems is an important field of study,
which has undergone a rapid development in the last
two decades. The importance of this field stems from
its crucial role in many areas such as signal process-
ing, target tracking, satellite navigation, fault detec-
tion, and adaptive and optimal control problems. It is
an essential part of any decision-making process.
The system state completely characterizes the sys-
tem at a given time and usually is not directly measur-
able. The system behavior is described by a stochastic
dynamic discrete-time model consisting of a stochas-
tic difference equation characterizing dynamics of the
state and by a stochastic algebraic equation represent-
ing a relation between the state and the measurement.
The solution to the state estimation problem usually
follows the Bayesian approach or the optimization ap-
proach.
The Bayesian approach is built up on the Bayesian
recursive relations (BRRs) (Sorenson, 1974), which
provide the state estimate in the form of a conditional
probability density function (PDF) of the state condi-
tioned by the measurement. However, the exact solu-
tion to the BRRs can be found only for a few special
cases, such as a linear system with Gaussian distur-
bances. For a nonlinear or non-Gaussian system the
conditional PDF has a complex shape and the solu-
tion usually cannot be found in a closed form. Hence,
some approximations must be employed.
A group of approximate methods providing ap-
proximate conditional PDF capturing the complexity
of the conditional PDF with a great fidelity are called
global methods. They are represented namely by the
Gaussian sum method (Ristic et al., 2004), the point-
mass method (Kramer and Sorenson, 1988), and the
particle filter (Doucet et al., 2001). The practical use
of the global methods is limited especially due to their
extensive computational complexity.
Another group of methods is formed by assum-
ing Gaussian approximation of the conditional PDF
provided by the BRRs. Such methods are denoted as
Gaussian filters (GFs) (Ito and Xiong, 2000) or local
Bayesian methods (Arasaratnam and Haykin, 2009).
The GFs are represented namely by the quadrature
Kalman filter (Arasaratnam et al., 2007), the cuba-
ture Kalman filter (Arasaratnam and Haykin, 2009),
and the stochastic integration filter (SIF) (Dun
´
ık et al.,
2013b), which utilizes the iterative stochastic integra-
tion rule (SIR) (Genz and Monahan, 1998).
Contrary to the Bayesian approach, the optimiza-
tion approach assumes minimization of a certain de-
sign criterion, usually the mean square error (MSE),
leading to filters such as the extended Kalman filter,
the divided difference filter (Nørgaard et al., 2000),
or the unscented Kalman filter (Julier and Uhlmann,
2004). The optimization is usually feasible by enforc-
ing a linear structure of the filter.
Even though optimization methods and local
Bayesian methods were derived by different ap-
proaches, finally they provide formally same solution
Havlík, J., Straka, O., Duník, J. and Ajgl, J.
On Nonlinearity Measuring Aspects of Stochastic Integration Filter.
DOI: 10.5220/0005983903530361
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 353-361
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
353

to the state estimation problem, which is computa-
tionally reasonable and therefore often used in prac-
tice.
The GFs perform well only for mildly nonlinear
functions, for which the Gaussianity assumption is
approximately valid. For strong nonlinearities the
assumption is only a rough approximation. During
the last decade several methods quantifying nonlin-
earity or non-Gaussianity, which have been applied
in monitoring the GF assumption validity, have ap-
peared (Mallick, 2004), (Li, 2012) and (Dun
´
ık et al.,
2013a). Such methods are usually based on eval-
uating effects of nonlinearities in neighborhoods of
conditional means or testing unimodal or non-heavy-
tailed properties of the conditioned PDFs.
The goal of the paper is to show that the SIF based
on SIRs possesses nonlinearity measuring capabilities
itself. The information can be used to give the user
an idea how strong nonlinear behavior the system ex-
hibits or how much the Gaussian assumption is vio-
lated and how much the estimates should be trusted.
Further, it will be shown that the information can be
utilized to predict computational requirements of the
SIRs employed by the filter to achieve a desired ac-
curacy. And above all, the information will be used
to make the estimate of the MSE provided by the SIF
more precise.
The rest of the paper is organized as follows: Sec-
tion 2 is devoted to a brief introduction to the nonlin-
ear state estimation, its solution by the GFs, and mea-
sures of nonlinearity and non-Gaussianity. The SIR is
briefly presented in Section 3. Section 4 presents the
revealed capability of the SIF to measure nonlinearity
and its application. Next, in Section 5 the utilization
of this information to provide an improved estimate
of the MSE is outlined and the paper is concluded by
Section 6.
2 STATE ESTIMATION AND
GAUSSIAN FILTERS
The aim of this section is to formulate the nonlin-
ear state estimation problem, to present its general
solution by means of the BRR, to describe the GFs,
and to present two measures of nonlinearity and non-
Gaussianity proposed in literature.
2.1 Formulation of the Nonlinear State
Estimation Problem
Let a discrete-time nonlinear stochastic system be
considered in the following state-space form
x
k+1
= f
k
(x
k
) + w
k
, k = 0, 1,2,. . ., (1)
z
k
= h
k
(x
k
) + v
k
, k = 0, 1,2,. . ., (2)
where the vectors x
k
∈ R
n
x
, and z
k
∈ R
n
z
repre-
sent the state of the system, and the measurement at
time instant k, respectively, f
k
: R
n
x
→ R
n
x
and h
k
:
R
n
x
→ R
n
z
are known vector functions, and w
k
∈ R
n
x
,
v
k
∈ R
n
z
are mutually independent state and mea-
surement white noises. The PDFs of the noises are
Gaussian with zero means and known covariance ma-
trices (CMs) Σ
w
k
and Σ
v
k
, respectively, i.e., p(w
k
) =
N {w
k
;0
n
x
×1
,Σ
w
k
}
1
and p(v
k
) = N {v
k
;0
n
z
×1
,Σ
v
k
}, re-
spectively, where 0
a×b
denotes an a × b matrix of
zeros. The PDF of the initial state is Gaussian and
known as well, i.e., p(x
0
) = N {x
0
;
¯
x
0
,P
0
}. The ini-
tial state is independent of the noises.
State estimation aims at searching the state x
k
based on measurements up to the time instant `, which
will be denoted as z
`
4
= [z
T
0
,z
T
1
,. . ., z
T
`
]
T
. Due to the
stochastic nature of the system, the state estimate is
described by the conditional PDF p(x
k
|z
`
). In this
paper, the filtering (k = `) and the one-step prediction
(k = ` + 1) problems will be considered only.
To find the filtering estimate p(x
k
|z
k
) the Bayesian
approach is used, and the following BRRs provide the
solution (Sorenson, 1974):
p(x
k
|z
k
) =
p(x
k
|z
k−1
)p(z
k
|x
k
)
R
p(x
k
|z
k−1
)p(z
k
|x
k
)dx
k
, (3)
where the one-step prediction PDF is
p(x
k
|z
k−1
) =
Z
p(x
k−1
|z
k−1
)p(x
k
|x
k−1
)dx
k−1
, (4)
and p(x
k
|x
k−1
) = p
w
k−1
(x
k
− f
k−1
(x
k−1
)) and
p(z
k
|x
k
) = p
v
k
(z
k
− h
k
(x
k
)).
An analytical solution to (3) and (4) is an intri-
cate functional-domain problem. It can be analyti-
cally computed for a few cases only. Such a case
is given by linear functions and Gaussian PDFs in
the system equations (1) and (2). So, for a nonlin-
ear or a non-Gaussian system, approximate solutions
are mostly necessary.
2.2 Gaussian Filters
The GFs suppose that the joint prediction PDF
p(z
k
,x
k
|z
k−1
) is at each time instant Gaussian
(Arasaratnam and Haykin, 2009)
p(z
k
,x
k
|z
k−1
) = N
z
k
x
k
;
h
¯
z
k|k−1
¯
x
k|k−1
i
,
P
zz
k|k−1
P
xz
T
k|k−1
P
xz
k|k−1
P
xx
k|k−1
.
(5)
1
For the sake of simplicity all PDFs will be given by their
argument, if not stated otherwise, i.e., p(w
k
) = p
w
k
(w
k
).
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
354

Then the filtering PDF p(x
k
|z
k
) and the one-step pre-
dictive PDF p(x
k
|z
k−1
) are also Gaussian
p(x
k
|z
k
) = N {x
k
;
¯
x
k|k
,P
xx
k|k
}, (6)
p(x
k
|z
k−1
) = N {x
k
;
¯
x
k|k−1
,P
xx
k|k−1
}. (7)
The GFs compute the first two moments of (6) and
(7), i.e., the conditional means
¯
x
k|k
= E[x
k
|z
k
] and
¯
x
k|k−1
= E[x
k
|z
k−1
] and the conditional CMs P
xx
k|k
=
cov[x
k
|z
k
] and P
xx
k|k−1
= cov[x
k
|z
k−1
].
The GF algorithm can be written in the following
form:
Algorithm 1: Gaussian Filter.
Step 1: (initialization) Set the time instant k = 0 and
define a priori initial condition by its first two moments
¯
x
0|−1
, E[x
0
] =
¯
x
0
, (8)
P
xx
0|−1
, E[(x
0
−
¯
x
0|−1
)(x
0
−
¯
x
0|−1
)
T
] = P
0
. (9)
Step 2: (filtering, measurement update) The filtering
mean
¯
x
k|k
and CM P
xx
k|k
are computed by the means of
¯
x
k|k
=
¯
x
k|k−1
+ K
k
(z
k
−
¯
z
k|k−1
), (10)
P
xx
k|k
= P
xx
k|k−1
− K
k
P
zz
k|k−1
K
T
k
, (11)
where
K
k
= P
xz
k|k−1
(P
zz
k|k−1
)
−1
(12)
is the filter gain and the measurement prediction
¯
z
k|k−1
is given by
¯
z
k|k−1
= E[z
k
|z
k−1
]. (13)
The predictive CMs P
xz
k|k−1
and P
zz
k|k−1
are computed as
P
zz
k|k−1
= E[(z
k
−
¯
z
k|k−1
)(z
k
−
¯
z
k|k−1
)
T
|z
k−1
]
= E[(h
k
(x
k
) −
¯
z
k|k−1
)
× (h
k
(x
k
) −
¯
z
k|k−1
)
T
|z
k−1
] + Σ
v
k
, (14)
P
xz
k|k−1
= E[(x
k
−
¯
x
k|k−1
)(z
k
−
¯
z
k|k−1
)
T
|z
k−1
]. (15)
Step 3: (prediction, time update) The predictive mean
¯
x
k+1|k
and CM P
xx
k+1|k
are given by
¯
x
k+1|k
= E[x
k+1
|z
k
] = E[f
k
(x
k
)|z
k
], (16)
P
xx
k+1|k
= E[(x
k+1|k
−
¯
x
k+1|k
)(x
k+1|k
−
¯
x
k+1|k
)
T
|z
k
]
= E[(f
k
(x
k
) −
¯
x
k+1|k
)(f
k
(x
k
) −
¯
x
k+1|k
)
T
|z
k
]
+ Σ
w
k
. (17)
Let k = k + 1.
The algorithm then continues by Step 2.
The particular GFs vary in the way they compute
the integrals determining the predictive characteristics
of the measurement (13-15) and the predictive char-
acteristics of the state (16, 17). Mostly, the integrals
cannot be calculated analytically. For example, the in-
tegrals can be approximated by the SIR, which leads
to the SIF.
2.3 Measures of Nonlinearity and
Non-Gaussianity
The GFs are designed under the Gaussianity assump-
tion (5), which will become invalid due to the non-
linearities present in the system. This may conse-
quently severely degrade the performance of the fil-
ter, disrupt its accuracy or credibility. Hence, it is
convenient to monitor working conditions of the fil-
ter, which affect validity of the assumption. For this
purpose the measures of nonlinearity (MoNL) or non-
Gaussianity (MoNG) render an applicable tool. The
MoNL and MoNG may be used for sequential moni-
toring of the GF assumption and an impact of approx-
imations along a trajectory of the GF.
Two examples of MoNL, which will be later used
for a comparison, are described below. The described
MoNL evaluate the nonlinearity of a function y =
g(x), where x is a random variable with a mean
¯
x and
a CM P
xx
defining a region, where the nonlinearity
will be analyzed. The MoNL can be used in the fil-
tering or the predictive step of the GF (Algorithm 1).
In the filtering step the function g(x) is equal to is
h
k
(x
k
), i.e., g(x) = h
k
(x
k
), and in the predictive step
g(x) = f
k
(x
k
).
Differential Geometry Measure based MoNL
The MoNL based on a differential geometry mea-
sure (DGM) was originally proposed in (Bates and
Watts, 1988) for the nonlinear parameter estimation
and later it was extended for the nonlinear state esti-
mation (Mallick, 2004). The MoNL directly assesses
the curvature
2
of the nonlinear function at a given
point. The state-independent version of the measure
is defined as
MoNL
DGM
i
=
kX
T
i
¨
GX
i
k
k
˙
GX
i
k
, (18)
where X
i
∈ R
n
x
, {X
i
}
q
i=1
is a set of q user-defined
points somehow respecting the probabilistic descrip-
tion of x ,
˙
G =
∂g(x)
∂x
|
x=
¯
x
is the Jacobian of g(x), and
¨
G =
∂
2
g(x)
∂x∂x
|
x=
¯
x
is the Hessian of g(x).
Therefore, the measure assesses the contribution
of the Taylor series expansion (TSE) second order
2
Amount by which a curve deviates from a tangent
(hyper-)plane.
On Nonlinearity Measuring Aspects of Stochastic Integration Filter
355

term
3
relative to the TSE first order term which de-
fines the tangential (linear) approximation of the func-
tion. The measure (18) can be evaluated at multiple
points X
i
and, its maximum can be selected for as-
sessing nonlinearity of g(x), i.e.,
MoNL
DGM
= max
i∈{1,2,...,q}
MoNL
DGM
i
. (19)
Least-Squares based MoNL
In (Dun
´
ık et al., 2013a) the weighted least-squares
(WLS) based MoNL was proposed assessing the
WLS residue, i.e., the difference between the nonlin-
ear function and its linear (least-squares) approxima-
tion defined by parameters
θ
∗
= argmin
θ
(Y − Xθ)
T
W(Y − Xθ), (20)
where X =
[X
0
,..., X
q
]
1,. . ., 1
T
, Y = [Y
0
,..., Y
q
]
T
, Y
i
=
g(X
i
),∀i, X
i
∈ R
n
x
, Y
i
∈ R
n
y
, {X
i
}
q
i=1
is a set of user-
defined points, and W is a diagonal weighting ma-
trix respecting placement of the points X
i
. Then, the
MoNL is given by
MoNL
WLS
= Y
T
[W − WX(X
T
WX)
−1
X
T
W]Y.
(21)
The points {X
i
}
q
i=1
are suitably selected (user-
defined) weighted points to represent the probabilistic
description of x. The largest element can be selected
for assessing of nonlinearity g(x).
3 STOCHASTIC INTEGRATION
FILTER
The SIF (Dun
´
ık et al., 2013b) utilizes the SIR (Genz
and Monahan, 1998) for calculating the integrals aris-
ing in the GF algorithm (13)-(17). The main advan-
tage of the SIR is that it provides faster rate of con-
vergence than the simple Monte Carlo (MC) integra-
tion rule (Genz and Monahan, 1998). The SIF takes
this advantage from the SIR and guarantees asymp-
totically exact or in some cases (linear or polynomial
functions f
k
and h
k
, depending on the SIR degree) ex-
act calculation of the integrals. The integrals are cal-
culated utilizing approximate description of a random
variable representing a state estimate by a set of points
and the corresponding weights.
3
The Hessian can be further decomposed into the compo-
nent in the tangential plane and the perpendicular compo-
nent (Mallick, 2004).
The SIF is given by the algorithm of the GF
(Algorithm 1), where the integrals (13)-(17) are ap-
proximately computed using SIR. Algorithm 2 illus-
trates the degree-3 SIR for computing an approximate
value of the integral
I(γ) = E[γ] =
Z
γ(x)N (x;
¯
x,P
xx
)dx. (22)
for a given function y = γ(x),γ : R
n
x
→ R
n
γ
, a mean
value
¯
x and a covariance matrix P
xx
of x.
Algorithm 2: Degree-3 Stochastic Integration Rule.
Step 1: Select a maximum number of iterations N
max
or an error tolerance ε.
Step 2: Set the current iteration number N = 0, initial
value of the integral
ˆ
I
0
(γ) = 0
n
γ
×1
, initial square error
of the integral V
0
= 0
n
γ
×n
γ
, and set ζ
0
=
¯
x.
Step 3: Repeat (until N = N
max
or maxV
N
< ε
2
)
a) Set N = N + 1.
b) Generate a uniformly random orthogonal matrix
Q
N
of dimension n
x
× n
x
and generate a random
number ρ
N
from the Chi distribution with (n
x
+ 2)
degrees of freedom, i.e., ρ
N
∼ Chi(n
x
+ 2).
c) Compute a set of points {ζ
i
}
2n
x
i=0
and appropriate
weights {ω
i
}
2n
x
i=0
according to
ζ
i
=
¯
x − ρ
N
S
xx
Q
N
e
i
, (23)
ζ
n
x
+i
=
¯
x + ρ
N
S
xx
Q
N
e
i
, (24)
ω
0
= 1 −
n
x
ρ
2
N
, ω
i
= ω
n
x
+i
=
1
2ρ
2
N
, (25)
where i = 1, 2, . .., n
x
, e
i
is the i-th column of the
n
x
× n
x
identity matrix, and S
xx
is a decomposition
of matrix P
xx
so that P
xx
= S
xx
[S
xx
]
T
.
d) Compute the following relations for the approxima-
tion of the integral value at current iteration SR
(3)
(spherical-radial degree-3 SIR), the updated integral
value
ˆ
I
N
(γ), and the corresponding mean square er-
ror estimate V
N
, i.e.,
SR
(3)
(Q
N
,ρ
N
) =
2n
x
∑
i=0
ω
i
γ(ζ
i
), (26)
D =
SR
(3)
(Q
N
,ρ
N
) −
ˆ
I
N−1
(γ)
N
, (27)
ˆ
I
N
(γ) =
ˆ
I
N−1
(γ) + D, (28)
V
N
=
N − 2
N
V
N−1
+ DD
T
. (29)
Step 4: Once the stopping conditions are fulfilled, the
approximate value of the integral I(γ) is
ˆ
I
N
(γ).
Note that the maximum in the stopping condition
maxV
N
< ε
2
denotes the maximum over all elements
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
356

of V
N
and that the points ζ
i
and weights ω
i
are speci-
fied to satisfy
2n
x
∑
i=0
ω
i
ζ
i
=
¯
x, (30)
2n
x
∑
i=0
ω
i
(ζ
i
−
¯
x)(ζ
i
−
¯
x)
T
= P
xx
. (31)
The SIF of higher and lower degrees can be found in
(Genz and Monahan, 1998).
Algorithm 2 is used for approximative calcula-
tions of (13)-(17) using the SIR, i.e., it produces esti-
mates of
¯
z
k|k−1
, P
zz
k|k−1
, P
xz
k|k−1
,
¯
x
k|k−1
and P
xx
k|k−1
. The
SIR estimates will be further denoted as the original
quantity with an extra hat over them, i.e., for example
ˆ
¯
z
k|k−1
is an estimate of
¯
z
k|k−1
produced by the SIR
of arbitrary degree and stopping condition. Analo-
gously,
ˆ
P
xz
k|k−1
is an estimate of P
xz
k|k−1
. The differ-
ences between the SIR estimates and original quanti-
ties will be denoted as the quantity with tilde, i.e.,
˜
z
k|k−1
4
=
¯
z
k|k−1
−
ˆ
¯
z
k|k−1
or analogously
˜
P
xz
k|k−1
4
= P
xz
k|k−1
−
ˆ
P
xz
k|k−1
. In the fol-
lowing sections an arbitrary degree SIR with an arbi-
trary stopping condition is assumed. For this reason,
the notation SR(Q
N
,ρ
N
) will be used without the su-
perscript indicating the rule degree.
4 MEASURING NONLINEARITY
BY SIR
This section will analyze the byproduct of the SIR cal-
culation - the square error V
N
of the integral approx-
imate value
ˆ
I
N
(γ), which has been overlooked in SIF
design so far. First, certain aspects of Algorithm 2
will be clarified.
4.1 Square Error of Integral Value
The GFs require computation of the integral values
in the form of (22). The SIR of arbitrary degree (for
example Algorithm 2 for degree-3) approximates this
integral by a sample mean of spherical-radial rules
ˆ
I
N
(γ) =
1
N
N
∑
j=1
SR(Q
j
,ρ
j
), (32)
which are given as a sum of n
p
weighted semi-random
points
4
SR(Q
j
,ρ
j
) =
n
p
∑
i=1
ω
i
γ(ζ
i
(Q
j
,ρ
j
)), (33)
where the notation ζ
i
(Q
j
,ρ
j
) was used to explicitly
denote dependence of ζ
i
on Q
j
and ρ
j
. The random-
ization is handled using
i) the random orthogonal matrix Q
j
, which governs
rotation in the state space,
ii) the scaling parameters, i.e., ρ
j
∼ Chi(n
x
+ 2) for
the degree-3 rule, which govern spread of the
points ζ
i
.
The SIR also computes an estimate V
N
of the MSE of
the integral value approximation
ˆ
I
N
(γ). The error of
ˆ
I
N
(γ) denoted as
˜
I
N
(γ) = I
N
−
ˆ
I
N
has zero mean and
its MSE is
E
˜
I
N
(γ)
˜
I
N
(γ)
T
= var[
˜
I
N
] = var
ˆ
I
N
=
1
N
var (SR(Q,ρ)). (34)
Its estimate by the SIR is
V
N
=
1
N
ˆvar (SR(Q,ρ)), (35)
where ˆvar(SR(Q, ρ)) is calculated as the sample vari-
ance of SR(Q,ρ) as
V
N
=
1
N
1
N − 1
N
∑
i=1
SR(Q
i
,ρ
i
) −
ˆ
I
N
(γ)
·
T
.
(36)
The notation (α)(·)
T
stands for (α)(α)
T
.
Theorem. For a linear function γ(x) = Γ · x, where
Γ ∈ R
n
γ
×n
x
, arbitrary mean value
¯
x, a CM P
xx
and
∀N > 1, it holds that var(SR(Q,ρ)) = 0.
Proof. For arbitrary rotation matrix Q
j
and scaling
parameter ρ
j
, the arbitrary degree spherical-radial
SIR is
SR(Q
j
,ρ
j
) =
∑
i
ω
i
γ(ζ
i
(Q
j
,ρ
j
))
=
∑
i
ω
i
Γζ
i
(Q
j
,ρ
j
)
= Γ
∑
i
ω
i
ζ
i
(Q
j
,ρ
j
)
= Γ
¯
x, (37)
where the relation (30) was used. As SR(Q
j
,ρ
j
)
given by (37) does not depend on Q
j
and ρ
j
for a
linear function γ, it holds that var(SR(Q, ρ)) = 0.
4
Number of points is governed by the degree of the SIR.
For example, n
p
= 2n
x
+ 1 for the degree-3 rule.
On Nonlinearity Measuring Aspects of Stochastic Integration Filter
357
P
xx
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
MoNL
10
-4
10
-3
10
-2
10
-1
10
0
10
1
10
2
10
3
SIR
DGM
WLS
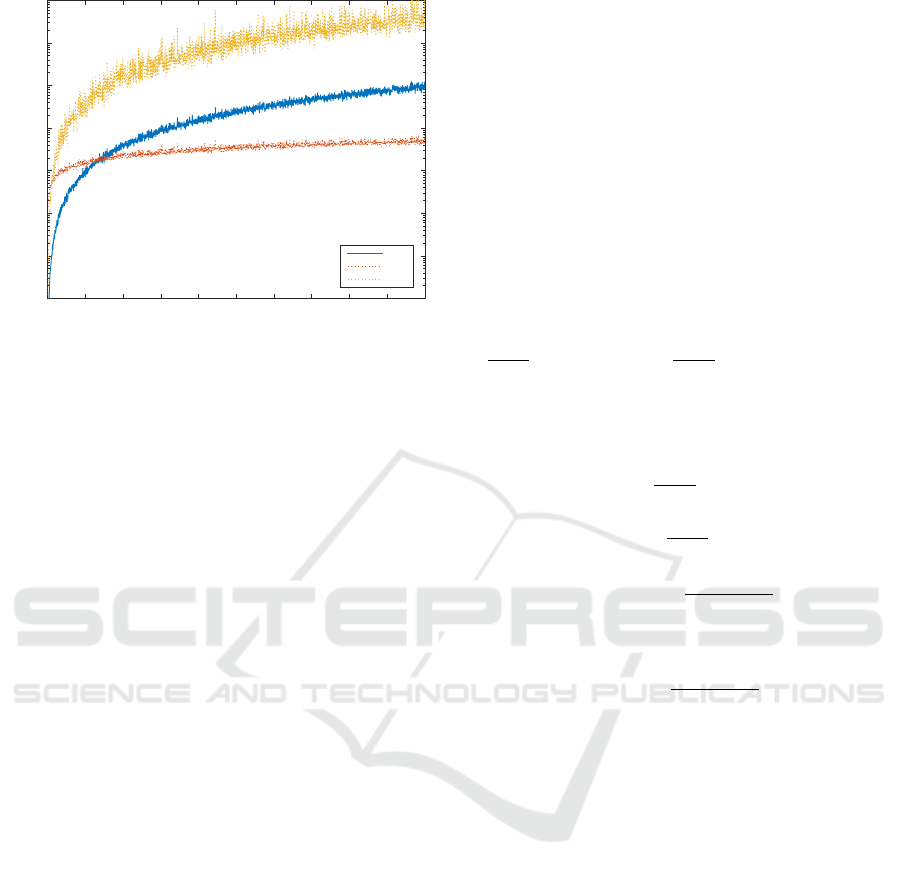
Figure 1: Dependency of MoNLs on growing variance P
xx
for γ(x).
As a consequence of (35) the SIR algorithm pro-
vides a quantity for an estimation of the variance of
calculated SRs
var(SR(Q,ρ)) ≈ N · V
N
. (38)
4.2 Relation of Square Error of
Estimated Integral with MoNL
The variance of the calculated SRs, var(SR(Q,ρ))
approximately given by N · V
N
, can be viewed as a
measure of nonlinearity, because it is zero for a lin-
ear function and there is a reason to believe that for
a growing strength of nonlinearity of γ, the variance
grows as well. The quantity N · V
N
will be denoted
as MoNL
SIR
. An illustration follows to support this
belief.
To facilitate analyzing of behavior of MoNL
SIR
for different nonlinearities, the following approach
will be adopted: Instead of changing the function γ
for a fixed
¯
x and P
xx
, the nonlinear function γ will be
fixed and the variance P
xx
will change. The variance
P
xx
governs the region over which the nonlinearity is
analyzed and hence for growing P
xx
, i.e., enlarging
the region, the nonlinearity should become stronger.
The following static example has been chosen:
Assume the function of interest y = γ(x) = x
2
, the ran-
dom variable x is given by mean value ¯x = 0.1 and
variance P
xx
∈ (0, 2). The SIR was used to calcu-
late MoNL
SIR
with the parameter N
max
= 100. The
MoNL
DGM
and MoNL
WLS
used the same ζ-points to
calculate the value of the measure. In case of the
MoNL
WLS
, the weighting matrix was chosen as the
eye matrix. The Figure 1 depicts the results of the ex-
periment. All three measures inform the user of rising
influence of nonlinearity for growing variance P
xx
.
4.3 Prediction of Number of Iterations
in SIR
In some cases, the user may specify the stopping con-
dition in Algorithm 2 by the error tolerance ε only,
i.e., without specification of the maximum number of
iterations N
max
. Throughout the iterations, it is possi-
ble to predict the number of steps required to achieve
all elements of V
N
to be lower than ε
2
. The proce-
dure is as follows: At each iteration N the variance
var(SR(Q,ρ)) can be estimated by N · V
N
. Consider
N
TOT
being a number of iterations such that after N
TOT
steps the variance V
N
TOT
of
ˆ
I
N
TOT
error will be approx-
imately
1
N
TOT
var(SR(Q,ρ)) ≈
1
N
TOT
· N · V
N
4
=
ˆ
V
N
TOT
(39)
and the maximum element of
ˆ
V
N
TOT
will be smaller
than ε
2
, i.e., max(
ˆ
V
N
TOT
) < ε
2
. Hence
max
ˆ
V
N
TOT
= max
1
N
TOT
· N · V
N
< ε
2
N
N
TOT
maxV
N
< ε
2
ε
2
N · max V
N
< N
TOT
. (40)
Thus the total number of steps can be estimated by
N
TOT
=
ε
2
N · max V
N
, (41)
where d·e is the ceil function rounding to the nearest
larger integer.
The total number of steps N
TOT
gives the user the
information about how long it will take to obtain the
integral value
ˆ
I
N
with the desired accuracy ε.
5 MSE ESTIMATED BY SIF
In this section the SIF will be analyzed in the terms of
the MSE and based on the findings from the previous
section and calculation of the MSE estimate will be
proposed.
5.1 Theoretical values of MSE
The GFs compute the CM P
xx
k|k
, which can be seen as
an estimate of the MSE, i.e.,
P
xx
k|k
≈ MSE = E
(x
k
−
¯
x
k|k
)(·)
T
. (42)
Now, the true MSE will be calculated and compared
with the CM
ˆ
P
xx
k|k
calculated by the SIF.
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
358

For convenience, consider the estimate
¯
x
k|k
(10) as
an affine function of z
k
, i.e.,
¯
x
k|k
= Az
k
+ b, (43)
where
A =
ˆ
P
xz
(
ˆ
P
zz
)
−1
, (44)
b =
¯
x − A
ˆ
¯
z. (45)
Note that for clarity purposes the subscript k|k −1 will
be omitted for the predictive moments.
Substituting (43) into (42) yields
E
(x
k
−
¯
x
k|k
)(·)
T
= E[(x
k
− Az
k
− b)(·)
T
]
|
{z }
E[αα
T
]
=
= E
(x
k
−
¯
x − A(z
k
−
¯
z))(·)
T
| {z }
E[(α−
¯
α)(α−
¯
α)
T
]
+[
¯
x − A
¯
z − b][·]
T
| {z }
¯
α
¯
α
T
.
(46)
After applying the expectation operator the MSE is
E
(x
k
−
¯
x
k|k
)(·)
T
= P
xx
−P
xz
A
T
| {z }
A
−AP
zx
| {z }
B
+ AP
zz
A
T
| {z }
C
+[
¯
x − A
¯
z − b][·]
T
| {z }
D
, (47)
where the estimator-related expressions were labeled
as A,B,C, and D. In the following paragraphs these
expressions will be analyzed separately by substitut-
ing (44) and (45) into the terms:
A = −P
xz
A
T
= −P
xz
(
ˆ
P
zz
)
−1
ˆ
P
zx
= −(
˜
P
xz
+
ˆ
P
xz
)(
ˆ
P
zz
)
−1
ˆ
P
zx
= −
˜
P
xz
(
ˆ
P
zz
)
−1
(P
zx
−
˜
P
zx
) −
ˆ
P
xz
(
ˆ
P
zz
)
−1
ˆ
P
zx
=
˜
P
xz
(
ˆ
P
zz
)
−1
˜
P
zx
−
˜
P
xz
(
ˆ
P
zz
)
−1
P
zx
−
ˆ
P
xz
(
ˆ
P
zz
)
−1
ˆ
P
zx
,
(48)
B = A
T
(49)
C = AP
zz
A
T
=
ˆ
P
xz
(
ˆ
P
zz
)
−1
(
˜
P
zz
+
ˆ
P
zz
)(
ˆ
P
zz
)
−1
ˆ
P
zx
=
ˆ
P
xz
(
ˆ
P
zz
)
−1
˜
P
zz
(
ˆ
P
zz
)
−1
ˆ
P
zx
+
ˆ
P
xz
(
ˆ
P
zz
)
−1
ˆ
P
zx
,
(50)
D = (
¯
x − A
¯
z − b)(·)
T
= (A
ˆ
¯
z − A
¯
z)(A
ˆ
¯
z − A
¯
z)
T
=
ˆ
P
xz
(
ˆ
P
zz
)
−1
˜
z
˜
z
T
(
ˆ
P
zz
)
−1
ˆ
P
zx
. (51)
Hence, (47) can be rewritten as
E
(x
k
−
¯
x
k|k
)(·)
T
= P
xx
+ A + B + C + D
= P
xx
−
ˆ
P
xz
(
ˆ
P
zz
)
−1
ˆ
P
zx
| {z }
ˆ
P
xx
k|k
+2
˜
P
xz
(
ˆ
P
zz
)
−1
˜
P
zx
| {z }
E
−
˜
P
xz
(
ˆ
P
zz
)
−1
P
zx
− P
xz
(
ˆ
P
zz
)
−1
˜
P
zx
| {z }
F
+
ˆ
P
xz
(
ˆ
P
zz
)
−1
˜
z
˜
z
T
(
ˆ
P
zz
)
−1
ˆ
P
zx
| {z }
G
+
ˆ
P
xz
(
ˆ
P
zz
)
−1
˜
P
zz
(
ˆ
P
zz
)
−1
ˆ
P
zx
| {z }
H
=
ˆ
P
xx
k|k
+ 2E + F +G + H
| {z }
MSE
err
k|k
, (52)
which can be understood as the sum of the SIF esti-
mate
ˆ
P
xx
k|k
of P
xx
k|k
and a sum of numerical integration
caused error terms 2E, F , G and H (denoted as the
MSE
err
k|k
), which provides the error in approximation
of the MSE. By using the estimate V
N
of the integral
mean squared error related to calculation of
ˆ
¯
z,
ˆ
P
xz
,
and
ˆ
P
zz
, which will be denoted as V
ˆ
¯
z
N
, V
ˆ
P
xz
N
and V
ˆ
P
zz
N
,
respectively, the terms E, F , G and H of MSE
err
k|k
can
be estimated as:
The term E can be calculated during computation of
V
P
xz
N
using (36) as
˜
P
xz
(
ˆ
P
zz
)
−1
˜
P
zx
≈
≈
1
N
1
N − 1
N
∑
i=1
SR(Q
i
,ρ
i
) −
ˆ
P
xz
(
ˆ
P
zz
)
−1
SR(Q
i
,ρ
i
) −
ˆ
P
xz
T
, (53)
where the SR approximate P
xz
at i-th iteration.
The term F depends on the true CM P
xz
. Thus the
expectation of F w.r.t. the Q and ρ used for
ˆ
P
xz
computation is zero, i.e.,
E[F ] = E
−
˜
P
xz
(
ˆ
P
zz
)
−1
P
zx
−P
xz
(
ˆ
P
zz
)
−1
˜
P
zx
=0.
(54)
The term G can be approximated after applying the
expectation operator due to mutual independence
of
ˆ
P
xz
,
ˆ
P
zz
and
˜
z. Then, E[
˜
z
˜
z
T
] is the variance of
¯
z, which can be approximated by V
ˆ
¯
z
N
, i.e.,
G ≈
ˆ
P
xz
(
ˆ
P
zz
)
−1
V
ˆ
¯
z
N
(
ˆ
P
zz
)
−1
ˆ
P
zx
. (55)
The term H cannot be replaced by its estimate as
ˆ
P
zz
and
˜
P
zz
are clearly dependent. Here, the ap-
proach replacing
˜
P
zz
by its interval estimate will
On Nonlinearity Measuring Aspects of Stochastic Integration Filter
359
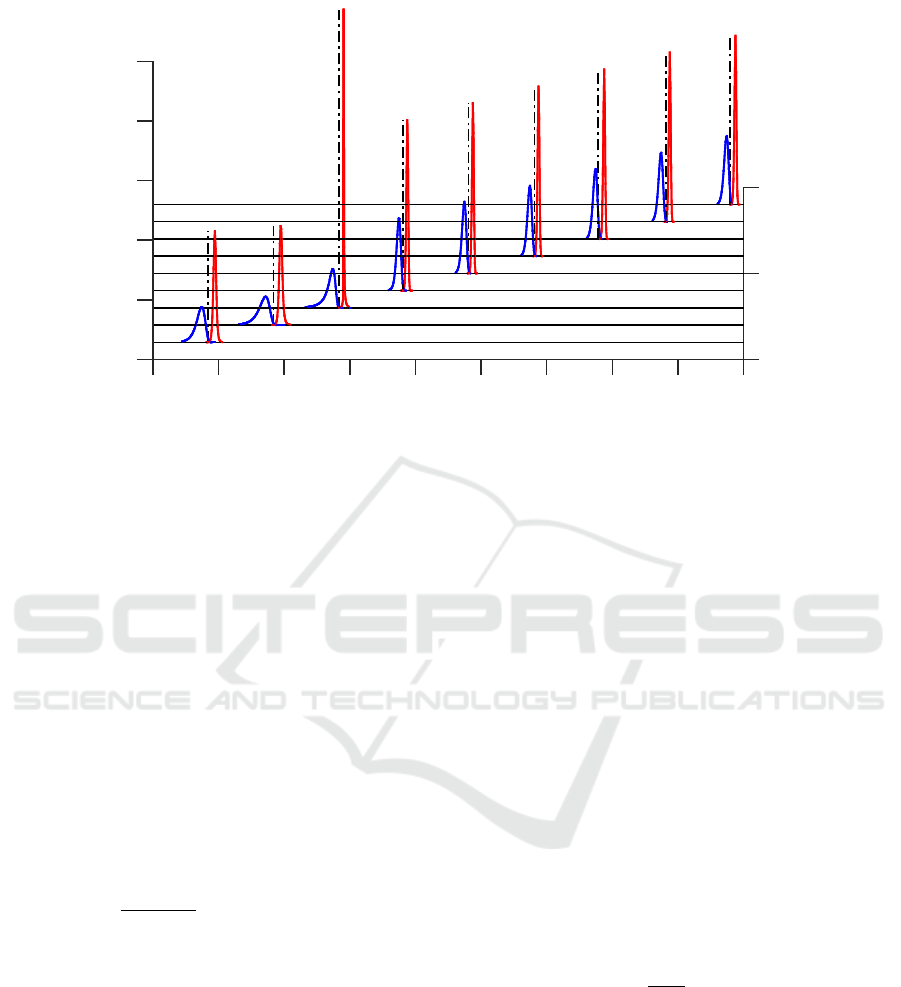
P
0
0.5
0
1
0.90.80.7
MSE
0.60.50.40.30.20.10
0.4
0.3
0.1
0.2
0.5
0
histogram of 3-σ bounds
Figure 2: MSE interval estimates (blue solid line - low limit histogram, red solid line - high limit histogram) and true MSE
(black vertical dashed line) for several values of covariance P
0
.
be adopted. As
˜
P
zz
has multivariate Gaussian dis-
tribution with zero mean and matrix of variances
given by V
ˆ
P
zz
N
,
˜
P
zz
in H can be replaced by a ma-
trix where its each element is a 3-σ interval es-
timate of the corresponding element of
˜
P
zz
. This
matrix of 3-σ interval estimates will be denoted as
˜
P
zz
. Then the term H can be approximated as
H ≈
ˆ
P
xz
(
ˆ
P
zz
)
−1
˜
P
zz
(
ˆ
P
zz
)
−1
ˆ
P
zx
. (56)
Hence, the true MSE can be estimated by a 3-σ inter-
val estimate taking into account all errors of numeri-
cal integration being neglected so far. This interval is
given by substituting estimates (53) - (56) into (52),
i.e.,
E
(x
k
−
¯
x
k|k
)(·)
T
=
ˆ
P
xx
k|k
+ MSE
err
k|k
≈
ˆ
P
xx
k|k
+
2
N(N − 1)
N
∑
i=1
SR(Q
i
,ρ
i
) −
ˆ
I
N
(γ)
× (
ˆ
P
zz
)
−1
SR(Q
i
,ρ
i
) −
ˆ
I
N
(γ)
T
+
ˆ
P
xz
(
ˆ
P
zz
)
−1
V
ˆ
¯
z
N
(
ˆ
P
zz
)
−1
ˆ
P
zx
+
ˆ
P
xz
(
ˆ
P
zz
)
−1
˜
P
zz
(
ˆ
P
zz
)
−1
ˆ
P
zx
. (57)
The relation (57) represents the improved estimate of
the MSE provided by the SIF. This improvement is
facilitated by the SIR, which in addition to the ap-
proximate integration also calculates the MSE of the
calculation error V
N
. This quantity is not provided by
any other GF.
5.2 Example
In the following example MSE
err
k|k
from the previous
section is illustrated. Again the same static scalar ex-
ample as in Section 4.2 has been chosen, i.e.,
z
0
= x
2
0
+ v
0
, (58)
where v
0
∼ N (0, R) is the measurement noise with
zero mean Gaussian distribution and its variance is
R = 10
−4
, the random variable x
0
is Gaussian with
x
0
∼ N (x
0
;0.1, P
0
), where P
0
had been tested for
values 0.1,0.2, . .. , 0.9. The test scenario was per-
formed in the scope of N
MC
= 10
6
independent Monte
Carlo simulations of state x
0
estimation. The filter-
ing estimate ¯x
0|0
and most importantly the filtering
CM P
xx
0|0
were obtained using the SIF with parame-
ters N
max
= 100 and ε = 10
−4
. The relatively high
simulation count secured high precision computation
of the true MSE value denoted as
MSE
true
=
1
N
MC
N
MC
∑
i=1
( ¯x
i
0|0
− x
i
0
)
2
, (59)
where superscript i denotes i-th Monte Carlo simula-
tion, x
i
0
is the true state at the i-th simulation and ¯x
i
0|0
is its filtering estimate. The MSE
true
was compared to
the MSE estimate (57) calculated by the SIF.
The results are depicted in Figure 2, where his-
tograms of low (blue) and high (red) limits of the 3-σ
intervals are plotted. The true values of the MSE are
depicted as dashed vertical lines. The results confirm
for several values of P
0
, that the SIF is capable to pro-
vide quality interval estimate of the MSE. The SIF is
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
360

thus very versatile estimator capable of high quality
self-assessment
6 CONCLUSIONS
The paper dealt with the Bayesian state estimation of
nonlinear stochastic dynamic systems and specifically
with the stochastic integration filter, which is based
on a stochastic integration rule. Within the iterative
algorithm of the SIF an instrument for measuring the
nonlinearity was discovered. The instrument uses a
quantity, which is a byproduct of the SIR, which has
been used in the stopping condition so far. Such in-
formation provides an information of how much the
nonlinearity in the system violates the Gaussian as-
sumption of the SIF. The paper also provided a re-
lation that can be used to predict the number of SIR
iterations required to achieve the accuracy requested
by the user.
Further, in the paper a method to calculate im-
proved estimates of the MSE was developed. It was
shown that the MSE contains additional terms besides
the conditional variance matrix provided by the stan-
dard GFs. By utilizing the SIR byproducts the addi-
tional terms can be estimated by interval estimate. By
including the additional term estimates the SIF is able
to provide more accurate information about its state
estimates. Both the new nonlinearity measure and the
improved MSE were illustrated using simple numeri-
cal examples.
The interesting part of the discoveries made in this
paper is that it opens wide area for a future work. The
SIF can be further improved in terms of saving com-
putational demands, when the measurement function
is almost linear, or when the function is strongly non-
linear an execution of the algorithm can be paused and
for example Gaussian sum approach can be adopted
to improve estimate quality.
ACKNOWLEDGEMENTS
This work was supported by the Czech Science Foun-
dation, project no. GA 16-19999J.
REFERENCES
Arasaratnam, I. and Haykin, S. (2009). Cubature Kalman
filters. IEEE Transactions on Automatic Control,
54(6):1254–1269.
Arasaratnam, I., Haykin, S., and Elliott, R. J. (2007).
Discrete-time nonlinear filtering algorithms using
Gauss–Hermite quadrature. Proceedings of the IEEE,
95(5):953–977.
Bates, D. M. and Watts, D. G. (1988). Nonlinear Regression
Analysis and Its Applications. John Wiley & Sons.
Doucet, A., De Freitas, N., and Gordon, N. (2001). Se-
quential Monte Carlo Methods in Practice, chapter
An Introduction to Sequential Monte Carlo Methods.
Springer. (Ed. Doucet A., de Freitas N., and Gordon
N.).
Dun
´
ık, J., Straka, O., and
ˇ
Simandl, M. (2013a). Nonlinear-
ity and non-Gaussianity measures for stochastic dy-
namic systems. In Proceedings of the 16th Interna-
tional Conference on Information Fusion, Istanbul.
Dun
´
ık, J., Straka, O., and
ˇ
Simandl, M. (2013b). Stochas-
tic integration filter. IEEE Transactions on Automatic
Control, 58(6):1561–1566.
Genz, A. and Monahan, J. (1998). Stochastic integration
rules for infinite regions. SIAM Journal on Scientific
Computing, 19(2):426–439.
Ito, K. and Xiong, K. (2000). Gaussian filters for nonlinear
filtering problems. IEEE Transactions on Automatic
Control, 45(5):910–927.
Julier, S. J. and Uhlmann, J. K. (2004). Unscented filtering
and nonlinear estimation. IEEE Review, 92(3):401–
421.
Kramer, S. C. and Sorenson, H. W. (1988). Recursive
Bayesian estimation using piece-wise constant ap-
proximations. Automatica, 24(6):789–801.
Li, X. R. (2012). Measure of nonlinearity for stochastic sys-
tems. In Proceedings of the 15th International Con-
ference on Information Fusion, Singapore.
Mallick, M. (2004). Differential geometry measures of non-
linearity with applications to ground target tracking.
In Proceedings of the 7th International Conference on
Information Fusion, Stockholm, Sweden.
Nørgaard, M., Poulsen, N. K., and Ravn, O. (2000). New
developments in state estimation for nonlinear sys-
tems. Automatica, 36(11):1627–1638.
Ristic, B., Arulampalam, S., and Gordon, N. (2004). Be-
yond the Kalman Filter: Particle Filters for Tracking
Applications. Artech House.
Sorenson, H. W. (1974). On the development of practical
nonlinear filters. Information Sciences, 7:230–270.
On Nonlinearity Measuring Aspects of Stochastic Integration Filter
361
