
A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System
Mounir Hammouche
1
, Samir Sakhi
1
, Mahmoud Belhocine
2
, Abdelhafid Elourdi
3
and Samir Bouaziz
3
1
Laboratoire Systèmes Numériques, Ecole Militaire Polytechnique, BP 17, Bordj El Bahri, Algiers, Algeria
2
Centre for Development of Advanced Technologies, Algiers, Algeria
3
Laboratoire SATIE - CNRS UMR 8029, Université Paris Saclay, F-91405 Orsay, France
Keywords: GPS, INS, Reduced Inertial Sensor System (RISS), Kalman Filter, Fuzzy Controller.
Abstract: Navigation technology has an important role in designing intelligent vehicles and advanced robots. To have
a continuous navigation solution that does not suffer from interruption, GPS (Global Positioning System)
data is merged with relative positioning techniques such as inertial navigation system (INS) or odometry
(Odm). To accomplish the reliability and integrity desired, it is therefore necessary to take into account
physical capabilities and limitations of each sensor during navigation. A fuzzy switcher controller (FSC) is
well suited for this task. FSC is an Expert rule-based method for choosing the best fusion from multiple
redundant integration methodologies (GPS/INS, GPS/Odometry, Odometry/INS or GPS/INS/Odometry)
based on navigation conditions and accuracy of the navigation systems.
1 INTRODUCTION
Road navigation systems are one of the main field of
interest in the intelligent transport domain such as
advanced driver assistance, route guidance or
traveller information which require a Road Side
Equipment (RSE) able to provide an accurate
position at low price (Boysen,2004). The commonly
used sensors in these applications may be divided
into two categories, external sensors and Dead
Reckoning Sensors (DRS) such as Inertial
Navigation System (INS) and Odometry.
The common external sensors for land vehicle
positioning are satellite navigation systems such as
Global Positioning Systems (GPS). However, in
GPS-denied environments (tunnels, canyons urban)
the GPS satellite signal is not often available. Hence
the positioning information provided is not accurate.
To achieve continuous navigation solution even
during GPS outages, the GPS is augmented with
dead reckoning sensors.
Inertial Navigation Systems and Odometry have
always been presented as valuable sensors in many
applications. Their advantages are well known: high
update rates; position and heading accuracy in short
time. However, Combining odometry with INS
which is called in the literature “Reduced Inertial
Sensor System –RISS- (North, 2012)” can enhance
the positioning accuracy compared to INS or
odometry alone. Indeed, odometry and INS have, to
some degree, complementary characteristics: INS can
provide the heading/attitude information (Xiaochuan,
2009), while odometry can remarkably limit the
position error accumulation of INS with respect to
time. To design more precise systems, external
sensors are usually integrated with dead reckoning
sensors taken on many forms, such as GPS/INS
integration, GPS/Odm integration or integrating the
three sensors together (GPS/RISS) (North, 2012).
This latter gives the best solution when the three
sensors are used in best conditions. In the case of
failure of one of them the position accuracy
decreases (North, 2012).
To accomplish the best reliability and integrity
desired, it is therefore necessary to choose which
sensors integration gives the best result. A Fuzzy
Logic based on expert rules derived from careful
observations of the physical functioning of each
sensor is certainly required to process the available
data. The algorithms must provide fault detection and
data fusion capabilities to make the best use of the
available information (Xiaochuan, 2009), (Singhala,
2014).
390
Hammouche, M., Sakhi, S., Belhocine, M., Elourdi, A. and Bouaziz, S.
A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System.
DOI: 10.5220/0005984103900397
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 390-397
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
To fuse information coming from sensors
different approaches can be found in the literature.
Many of them rely on the implementation of an
Extended Kalman Filter (EKF) (Boysen, 2004),
(Boucher, 2004), (Hay, 2005), (Sukkarieh, 2000).
The performance of the EKF is reliable in many
practical situations, but the non-linear state equations
may lead to instability problems. Other filtering
methods can be found in the literature, such as the
Unscented Kalman Filter (St-Pierre, 2004) and
particle based solution (Boucher, 2004).
This paper aims to develop an experimental
approach of GPS/INS/Odometry data fusion that uses
fuzzy rule-based system. It is divided into four (4)
main sections. Section 2 presents different integration
methodologies (GPS/INS, GPS/Odometry,
GPS/INS/Odometry and Odometry/ INS integration)
and a brief description of Fuzzy Switcher. Finally
section 3 presents the results and discussion with a
hardware implementation. A conclusion is given in
Section 4.
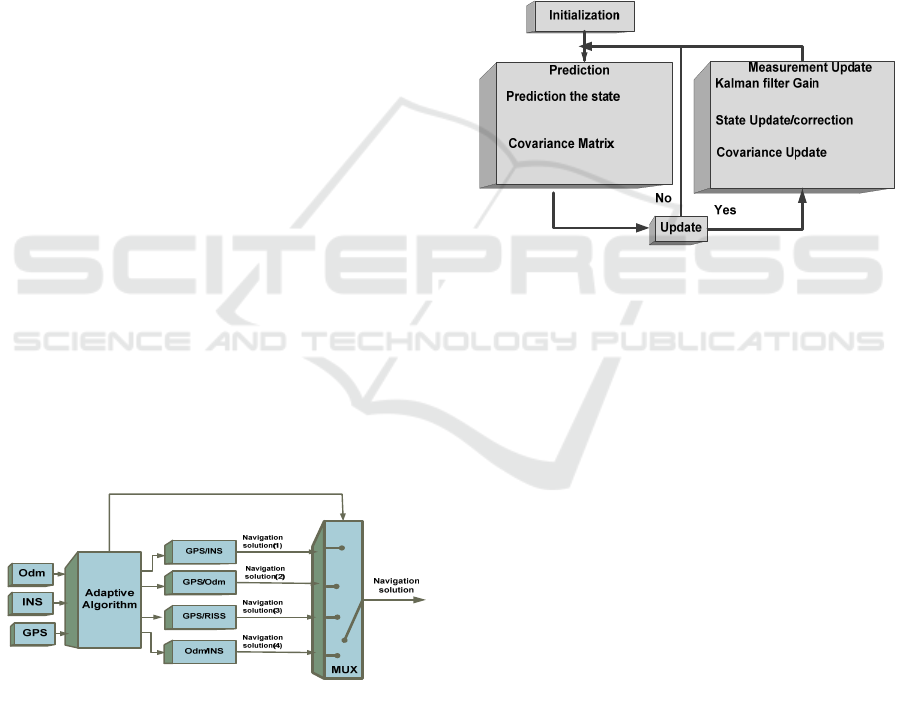
2 INTEGRATION ALGORITHMS
The concept of integrating GPS and dead reckoning
sensors (INS or Odometry) has been well discussed
in the research community. Different integration
strategies have been developed and tested with
different grades of INS. Typically; three main
strategies are used, namely loose integration, tight
integration and ultra-tight (or deep) integration. We
have chosen the loose coupling integration scheme
with close-loop. This schema lets control the
navigation accuracy and reduce the cost of design
(Sakhi, 2014).
Figure 1: Architecture of proposed integrated
GPS/INS/Odm system.
The implemented algorithms consist of four (4)
filters. The first filter fuses the INS and GPS
measures, the second filter fuses the odometry and
GPS measures, and the third filter fuses odometry
and inertial data, while the fourth filter fuses the three
sensors data together. Then, an adaptive algorithm,
based on signal degradation conditions of the
different navigation systems, is used to choose the
best combination that gives the best navigation
solution. These algorithms are summarized in the
following diagram (Figure 1).
Kalman filter is a suitable filter used to integrate
sensors information. The prediction step, of the used
filter, is based on a kinematics model of motion.
Because of the non-linearity of the process model, we
have used an EKF filter.
The Extended Kalman filter (EKF) proceeds by
linearizing the model about the latest estimate to
meet the Kalman Filter assumptions (Boucher, 2004).
EKF is summarized by the flow chart showed in
Figure 2.
Figure 2: Kalman Filter Algorithm.
x
k
: state vector of the process at epoch t
k
,
z
k+1
: actual observation,
Φ
k+1/k
: state transition matrix from time t
k
to t
k+1,
R
k
,Q
k
: measurement and process covariance matrix,
P
k
: error covariance matrix,
K
k+1
: Kalman gain matrix,
z
k+1
:
observation matrices,
Where , represent a prior and a posterior
estimated state vector.
The implemented algorithms consist of an
Extended Kalman filter of 5-states including position,
velocity, and angular velocity in two (2) dimensions
for GPS/INS integration. However, for both
INS/Odm and GPS/RISS integration we have used a
Kalman filter of 3-state. The three integrated
algorithms are summarized in the following.
2.1 INS/GPS Integration Algorithm
Several techniques are proposed in the literature for
inertial and GPS fusion (Xiaochuan, 2009),
(Quinchia, 2011), (North, 2009). We have chosen the
loose coupling integration scheme with close-loop, as
shown in Figure 3, in order to reduce inertial unit
1
1111111
()
TT
kkkkkkk
KPHHPHR
−−−
+++++++
=+
11/
ˆˆ
K
kkk
x
x
−+
++
=Φ
1111
()
kkkk
P
Ik H P
+−
++++
=−
11 1
111
()
ˆˆ ˆ
kk k
kkk
x
xK
z
Hx
+−
++ +
−
+++
=+ −
11/ 1/
T
kkkkkkk
P
P
Q
−+
++ +
=Φ Φ +
ˆ
k
x
+
ˆ
k
x
−
A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System
391
errors. This has implications for inertial units of low
and medium precision (Sakhi, 2014).
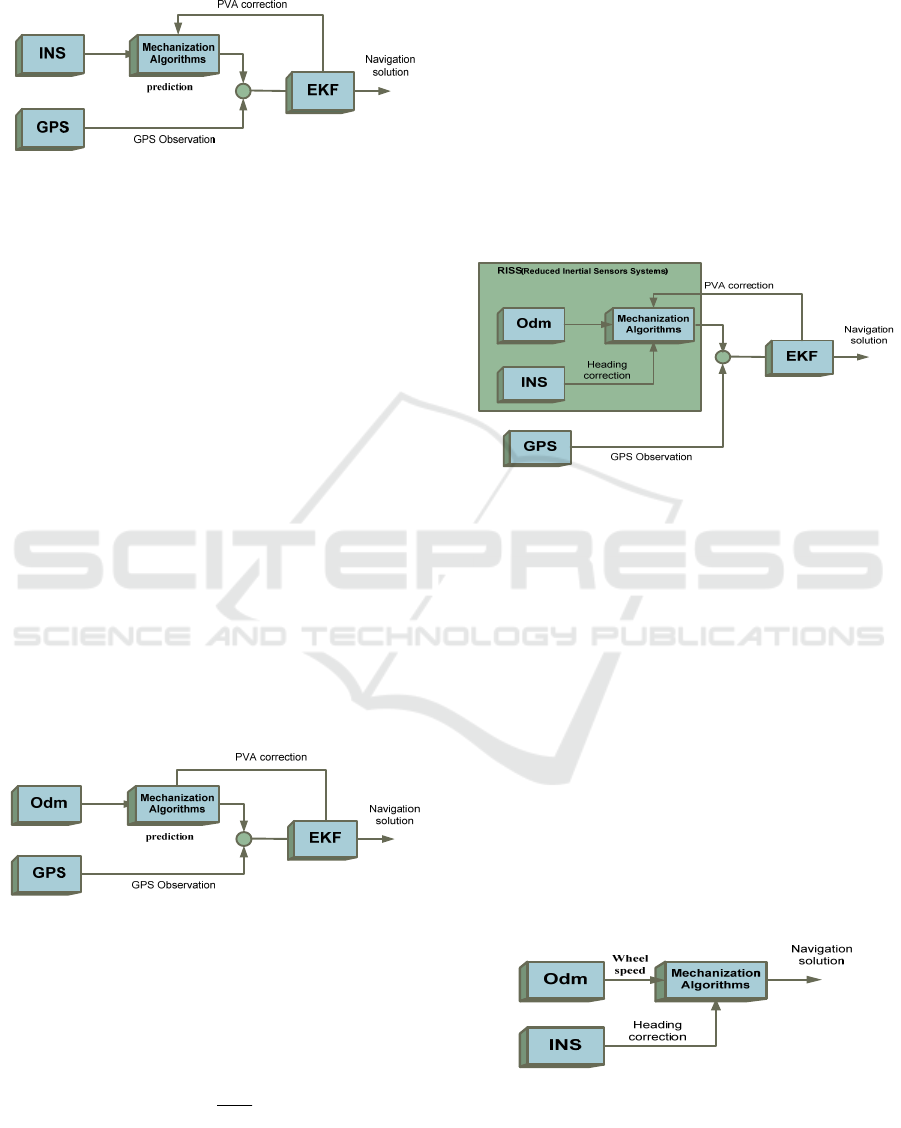
Figure 3: Loose coupling integration scheme (INS/GPS).
We have used the kinematics model which is
defined by the following equations (Kubrak, 2007)
instead of using dynamics model of a robot in order
to reduce the complexity of calculations.
(1)
2.2 Odometry/GPS Integration
Algorithm
Many techniques are proposed for integrating
Odometry with GPS (Lamon, 2004). We have
chosen a loose coupling integration scheme with
close-loop, where the state feedback PVA (Position,
Velocity and Attitude) correction to the Odometry
system, as shown in Figure 4 in order to reduce scale
factor errors.
Figure 4: Loose coupling integration scheme (GPS/Odm).
The motion model equations that transform
odometer measures in the navigation frame are
equations expressing the predicted function:
(2)
Where this state is defined by the coordinates of
its center M and the angle relative to , the
velocity of the center based on the average wheel
speeds and the steering angle of wheels .
2.3 RISS/GPS Integration Algorithm
The concept of RISS (Reduced Inertial Sensor
System ) was used in vehicle navigation in order
to further higher the accuracy of the positioning
solution. The RISS used in (North, 2009) involves a
single-axis gyroscope and the vehicle odometer
model to provide 2-D navigation solution , with
the assumption that the vehicle mostly stays in
the horizontal plane.
Figure 5: Schematic diagram of the RISS/GPS Integration.
The discrete form of Mechanization equations is:
(1) () ()cos(())
(1) () ()sin(())
(1) ()
e
e
e
x
kxkTVk k
yk yk TV k k
kkTWz
θ
θ
θθ
+= +
+= +
+= +
(3)
Where Wz is the gyroscope measurement (rate of
turns) in radium/second.
2.4 Odometry/INS Integration
Algorithm
Different configurations are proposed in the
literature (North, 2012), (Rogers, 2012) for
integrating Odometers and INS. In (North, 2012), N.
Eric used an IMU and the information delivered by
odometry as measurement update of the Kalman
filter .
Figure 6: Schematic diagram of the Odm/INS Integration.
In our work, after testing several methods we
have chosen the RISS configuration which gives a
+
−
•
2
.
••
.
•
2
.
••
.
•
(1) () ()0.5 ()
(1) () ()
(1) () ()0.5 ()
(1) () ()
(1) () ()
m
mme exm
mm
exm
mme eym
m
eym
mm
m
mme
x
kxkTxkTak
xk xk Ta k
yk yk Tyk Ta k
yk yk Ta k
kkTk
θθθ
+= + +
+= +
+= + +
+= +
+= +
+
−
(1) () ()cos(())
(1) () ()sin(())
()
( 1) () tan(())
e
e
e
x
kxkTVk k
yk yk TV k k
Vk
kkT k
L
θ
θ
θθ φ
+= +
+= +
+= +
θ
x
V
φ
+
−
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
392
good positioning accuracy with simple integration
strategies without the need of filter. The system
model based on inertial and Odometry data is
depicted in (Figure 6).
2.5 Fuzzy Switcher Controller (FSC)
When designing a fusion system, we must take into
consideration the multi-rate sensor data collection,
and implement the integration algorithm
appropriately. Here, the term “fusion” refers
generally to the process of combining three sets of
measures to produce a consistent solution. That is,
we need to fuse odometry, inertial and GPS data
when all sensors perform well, but in the case of a
sensor failure, which may lead to degradation of
overall system performance, we have to eliminate its
use.
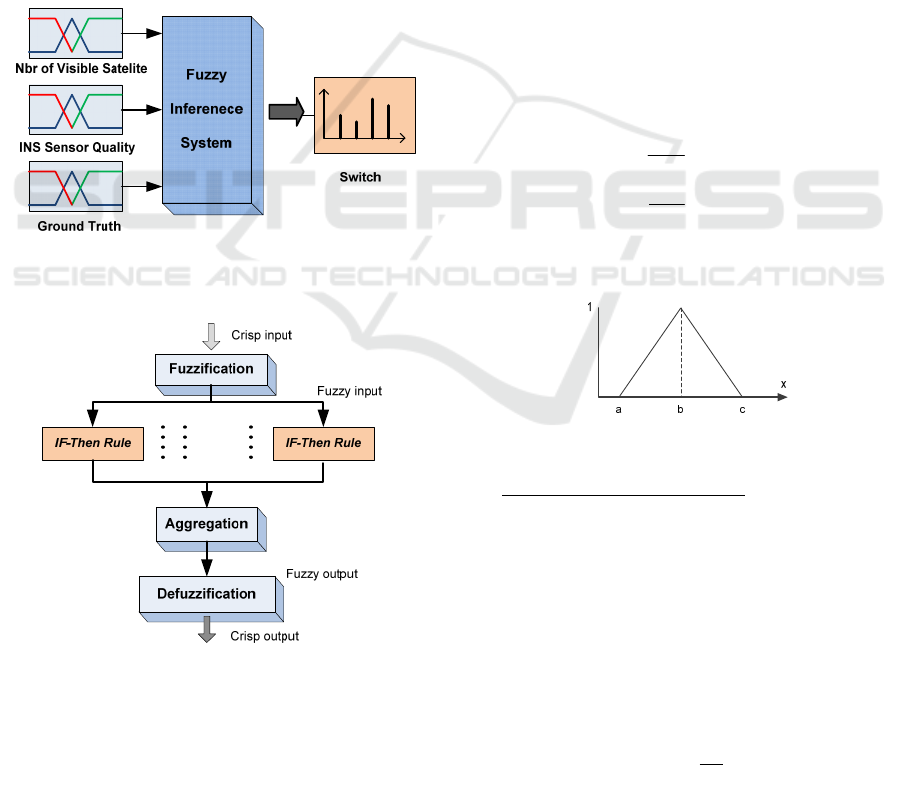
Figure 7: Architecture of the fuzzy logic data classification
system.
Figure 8: Block diagram of the fuzzy inference system
(Wang, 2006).
A fusion algorithm that takes into accounts the
physical capabilities and limitations of each sensor is
therefore necessary. A Fuzzy Logic is well suited for
this task. The down-mentioned expert rule-based
method for choosing best fusion result from multiple
redundant algorithms can help in selecting the most
accurate fusion algorithm. Our fuzzy algorithm uses
three fuzzy membership function inputs and one
output, as shown in Figure 7.
In a typical fuzzy system (Figure 8) the crisp
inputs are first converted to the input fuzzy sets
using the membership functions. Then, the input
fuzzy sets are mapped into a consequent fuzzy set
based on the adopted fuzzy logic operators, if-then
rules and aggregation strategy. Finally, the
consequent fuzzy set is converted into a scalar
quantity as the system output using a defuzzification
method.
2.5.1 Fuzzification Interface
It transforms crisp data (GPS data, Ground Truth,
and sensor’s data quality) into fuzzy sets. The
assignment of membership values to fuzzy variables
are based on experimental testing and logical
operations. For a computational simplicity, the
triangle membership function (equation 4) , shown
in Figure 9, is used.
,
() ,
0,
xa
axb
ba
cx
f
xbxc
cb
otherwise
−
⎧
<≤
⎪
−
⎪
−
⎪
=<≤
⎨
−
⎪
⎪
⎪
⎩
(4)
Figure 9: Trapezoidal fuzzy membership function.
Path Condition Fuzzification: It is beneficial to
know if a robot (or vehicle) is crossing sandy
surfaces in order to eliminate the use of odometers
and reduce positioning errors. For the detection of
sandy surfaces, the robot literally bounces on the
ground when the rear bogie wheels go through rough
terrain. Shocks occurring during the experiment are
easily identified when looking at the roll angel
variation. The equations used to calculate roll from
accelerometers are based on the idea presented in
(Kubrak, 2007).
1
tan
z
y
a
a
φ
−
⎛⎞
⎜⎟
⎜⎟
⎝⎠
=
(5)
: , are the accelerometer readings.
yz
where a a
()
x
μ
A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System
393
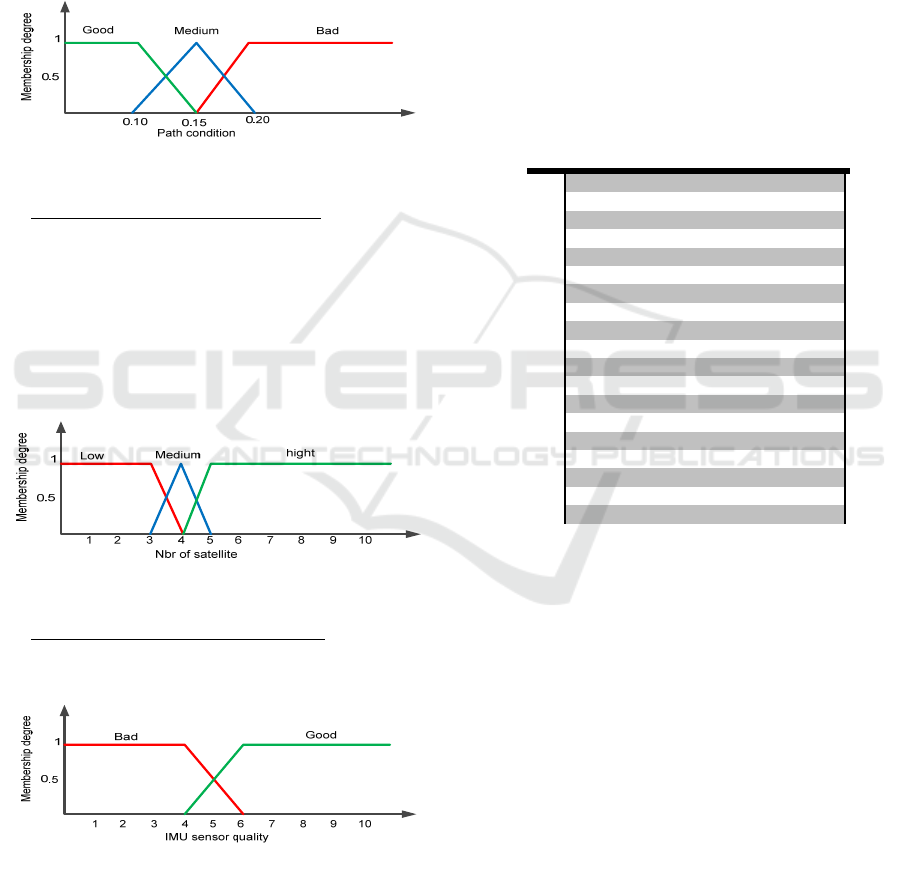
An effective method for estimating the ground
truth is to calculate the current roll angle of the land
vehicle displacements. The Variation of this angle is
beings used to select the appropriate fuzzy decision
to the navigated terrain.
In our case the roll angle is the mean computed
for a period of 1 second (which corresponding to 40
samples of odometer’s data). After experiments test
we have assigned our membership function of path
condition as shown in Figure 10.
Figure 10 : The first input variable (Path Condition).
Number of Satellite Fuzzification: The second
input (Figure 11) represents the number of satellites.
As we have seen in experiments, RISS outperforms
all the other compared solutions when the number of
visible satellites is less than tree (3). Furthermore,
the RISS solution provides very good results,
compared to IMU or Odometer alone. So it is very
important to detect degradations of GPS signal to
use RISS for position estimation.
Figure 11: The second input variable (number of satilites).
IMU‘s Data Quality Fuzzification: Our fusion
algorithm takes into account the physical capabilities
and limitations of each sensor.
Figure 12: The third input variable (number of satellites).
Therefore, it is necessary to determine the quality
of IMU data during experiments. Since we are
looking to produce a simple and flexible algorithm
suitable for any IMU quality, we took into account
this point by giving users the possibility to predefine
the quality of the IMU before starting experiments.
Users can a score from 0 (very bad) to 10 (good), as
shown in Figure 12, based on the bias and scale
factor of the used inertial navigation sensor.
2.5.2 Inference System
To describe the relationship between the input and
the output, a set of rules is applied as shown in Table
1. The fuzzy rules are derived directly from the three
basic rules defined at the beginning of this section
and they cover all possible combinations of input
variables.
Table 1: If-then rules used in the fuzzy inference system
for data classification.
Inputs Output
N.
NVS PAC SQ SW
1 Low Low Bad
INS/Odm
2 Low Low Good
INS/Odm
3 Low Med Bad
INS/Odm
4 Low Med Good
INS/Odm
5 Low High Bad
INS/Odm
6 Low High Good
INS/Odm
7 Med Low Bad
GPS/INS
8 Med Low Good
GPS/INS
9 Med Med Bad
GPS/INS
10 Med Med Good
GPS/INS
11 Med High Bad
GPS/Odm
12 Med High Good
RISS
13 Med Low Bad
GPS/INS
14 High Low Good
GPS/INS
15 High Med Bad
GPS/Odm
16 High Med Good
GPS/INS
17 High High Bad
GPS/Odm
18 High High Good
RISS
NVS: Nbr of visible satellites, PAC: path condition
SQ: sensor quality, SW: Switch data fusions.
2.5.3 Defuzzification Interface
Several popular methods exist for defuzzification
such as max-membership principle, centroid method,
weighted average method, centre of sums (Singhala,
2014). In our algorithm, the result of the
defuzzification has to be a single value that
determines which sensors integration is used to give
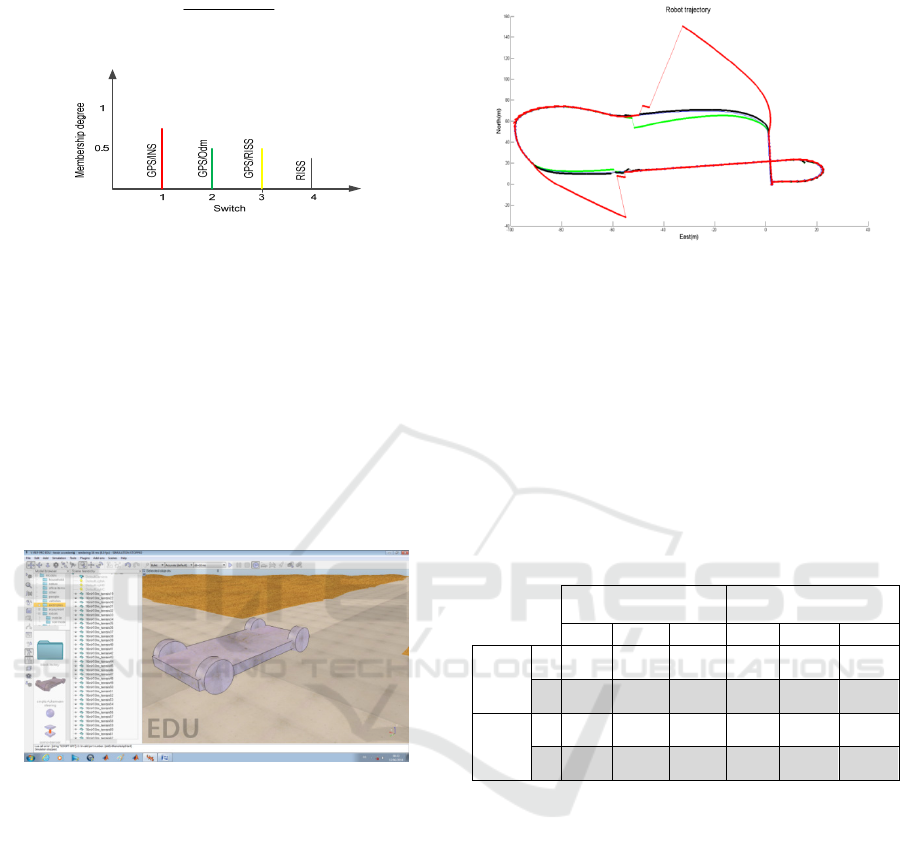
the best results, as shown in Figure 13.
In our case, outputs of the fuzzy fusion system,
SW (switch) are dimensionless weighting factors that
emphasize either the 1
st
(GPS/INS), 2
nd
(GPS/Odm),
3
nd
(GPS/RISS) or 4
th
(RISS) solution is the best in
terms of accuracy. The weighted average
defuzzification technique is the most prevalent and
widely adopted defuzzification method. The centroid
method is given by the following algebraic
expression:
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
394
(6)
Figure 13: The output variable (Switch).
3 RESULTS AND DISCUSSION
In order to evaluate the FSC performances, several
driving were performed using data of a driving
simulator framework called Virtual Robot
Experimentation Platform (V-REP). The V-REP is a
very versatile and ideal for multi-robot applications.
This software is an open source for use in research
or academic environments which can model
dynamics of several robots (Tharin, 2012).
Figure 14: Screen shot of V-REP’s application main
window.
We have used a Simple Ackermann steering
mobile robot. It has four-wheel drive and a steered
locomotion system. The sensor part includes two
encoders measuring rear wheels rotation at 20Hz.
The system provide also GPS (1HZ) data and
inertial (acceleration and gyroscope) at 40Hz.
3.1 Evaluation of Algorithms during
GPS Outages
This section aims to evaluate the "standalone"
performances of the different integrations by
simulating a long GPS outage in sensor’s data
acquisition. During a period without GPS signal, no
updates are performed. The resulting trajectory is
built using only the prediction. Therefore, difference
in terms of positions is well highlighted.
Figure 15: Estimated and reference trajectories: bleu for
reference, Red for GPS/INS, Green for GPS/Odm, black
for the GPS/RISS integration.
Table 2 presents difference in terms of position,
resulting from a comparison of trajectories computed
with the various GPS outages. These divergences are
expressed using Root Mean Square (RMS). The
maximum differences is also listed. Note that these
different integrations are computed using only the
trajectory differences during the outages.
Table 2: Comparison of trajectories computed with GPS
outages of various duration. ( 5 s and 10 s).
First GPS outage
for 10s
Second GPS outage
for 5s
GPS/INS GPS/Odm GPS/RISS GPS/INS GPS/Odm GPS/RISS
East
errors
(m)
Max
16.25 1.21 3.42 4.11 1.50 2.11
R
M
S
10.85 0.64 3.64 1.12 0.16 0.85
North
errors
(m)
Max
70.23 11.26 2.05 43.29 2.41 1.55
R
M
S
24.28 6.04 1.32 11.72 1.48 0.69
Outages of short duration (5 seconds) are well
bridged by the Odometry navigation system. Indeed,
the maximum position deference ranges from 1.5 m
to 11 m. But the range of errors proportionally
increases with the GPS outages duration due to
accumulation of errors which appears clearly in the
first case when the outages is 10s. Moreover, the
position accuracy of a GPS/RISS trajectory ranges
from 1 m to 3 m. These results show that the
reduced inertial navigation system (RISS) is able to
bridge GPS outages of long duration or short
duration with best position accuracy.
3.2 Evaluation of Fuzzy Switcher
Controller
Several experiments with GPS outages and rough
terrain condition, using good and bad quality of
[] []
[]
18
1
18
1
i
i
Pi W i
Defuz
Wi
=
=
×
=
∑
∑
A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System
395
IMU, were processed to evaluate FSC performances.
We did a comprehensive set of tests in V-REP using
different speeds varying between 5-25 m/s. The
deferent characteristics, i.e. the RMS, and the max
are well presented.
The trajectory used for this evaluation is similar
to the applied in section A. Here, we introduced a
variation in the number of satellites (on view) to see
the functionality of the FSC during GPS signal
degradation. However, we have simulated four GPS
outages as shown in Figure 17.
The potential parameter used to detect the
surface condition is computed from the variance of
the roll angle using 40 last samples of the
acceleration corresponding to 1s which is the
frequency of GPS, as mentioned before. The rough
terrain is easily detected as show in the Figure 16.
In the down-mentioned simulation results we
have presented only the case of a medium Quality of
inertial navigation system. However, we have given
a mark of “6”. Figure 18 shows the output of Fuzzy
switcher controller. Hence we are using an IMU
with a good quality, the FSC switches to GPS/RISS
during good surface and good GPS signal, but when
the vehicle go by a rough surface the FSC
eliminates the use of odometers measures by
switching to GPS/INS. The same case is produced
during GPS signals degradation. The FSC eliminate
the use of GPS by switching to RISS.
Figure 16: Variance of the roll angle during trajectory.
Figure 17: Variation of number of satellites.
Figure 18: Outputs of the FSC during trajecory.
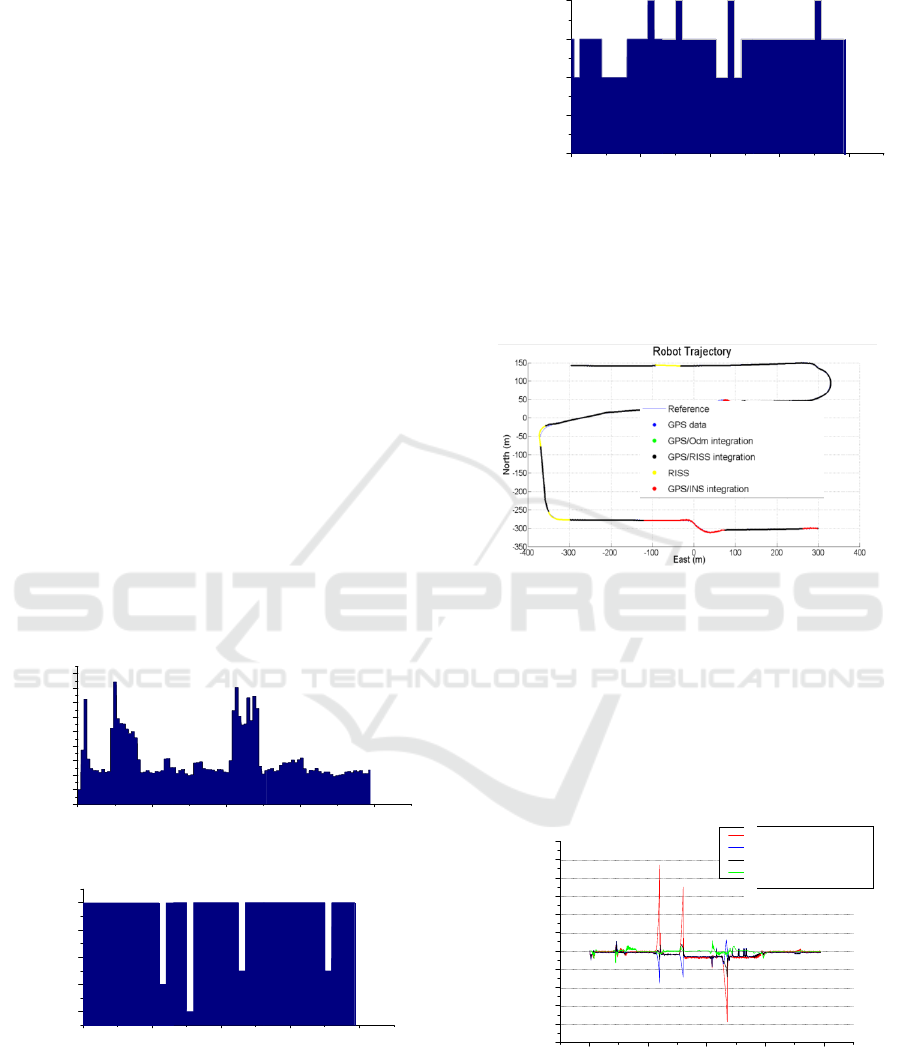
Figure 19 shows the estimated trajectory of the
robot and the ground truth during the simulation.
The trajectory is portion-colored to easily see the
different integrations used during the trajectory.
Figure 19: Trajectory plot using FSC.
Simulation results (Figure 20 and Figure 21 )
clearly show the advantage of FSC over GPS/RISS,
GPS/Odm and GPS/IMU. However there is a big
difference in 2-D positional errors when we compare
GPS/INS and GPS/Odometry with results of FSC
integration during GPS outages. This later has an
average of the maximum positional error off 3m as
shown in Table 4.
Figure 20: East position Error computed by different
integrations.
0 2000 4000 6000 8000
-0,05
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
The Var i anc e( r ad)
Samples
0 2000 4000 6000 8000
0
2
4
6
8
Nbr of vi si ble satel l ite
Samples
0 2000 4000 6000 8000
0
1
2
3
4
(RISS)
(
GPS/RISS)
(GPS/INS)
Samples
Fuzzy Output(Switch)
(
GPS/Odm)
0 2000 4000 6000 8000
-25
-20
-15
-10
-5
0
5
10
15
20
25
30
Error in East(m)
Samples
GPS/INS errors
GPS/Odm errors
GPS/RISS errors
AFSA errors
GPS/INS errors
GPS/Odom errors
GPS/RISS errors
FSC errors
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
396
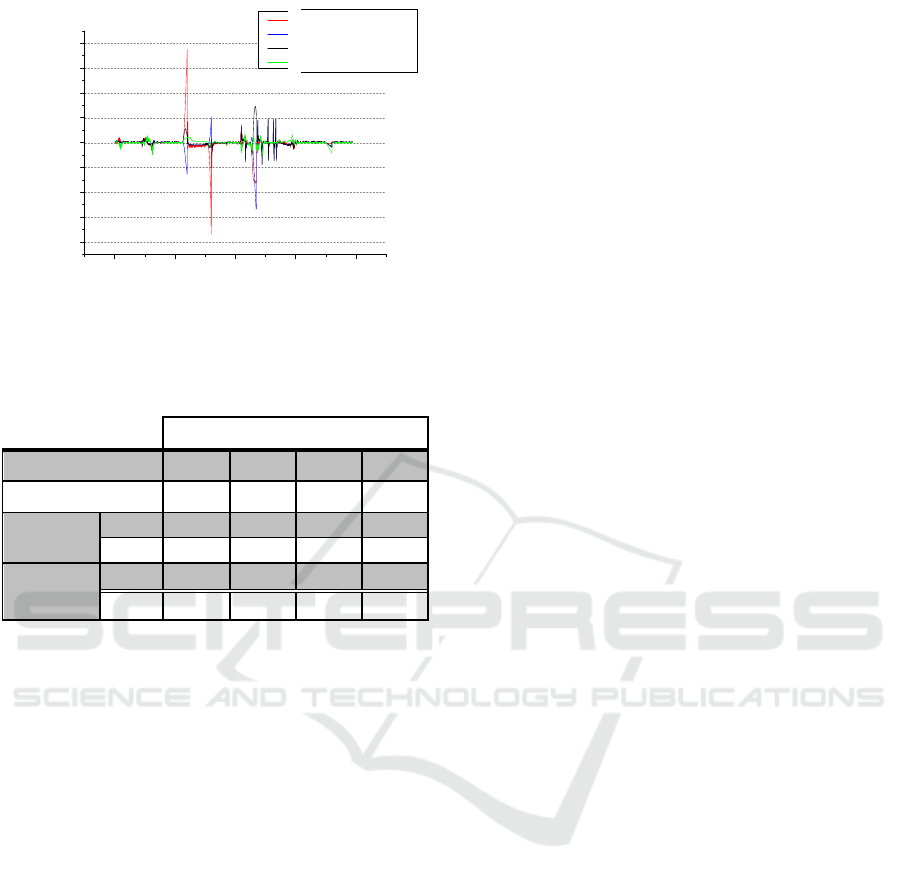
Figure 21: North position error computed by different
integrations.
Table 3: Simulation measurements.
Errors during GPS outages
Outage .N° 1 2 3 4
Duration (s) 10 10 10 10
East
errors (m)
Max
2.709 2.801 4.617 1.565
RMS
1.969 1.778 2.042 0.547
North
errors (m)
Max
3.070 3.299 3.188 1.011
RMS
2.159 1.188 1.588 0.996
4 CONCLUSIONS
In this paper we introduced a Fuzzy Switcher
Controller (FSC) for navigation systems. Several
methodologies of integrating inertial sensors,
Odometry and GPS data using a loosely coupled
integration techniques are also presented. Results
show that the Fuzzy switcher controller has a
powerful adaptability to physical capabilities and
limitations of navigation systems which improves
the navigation positioning accuracy. Compared to
others integration methods, the new position errors
are controlled within ± 3m even during a GPS
outages or a rough terrain condition.
REFERENCES
Boysen, P.A. and Zunker, H. ,2004. Low Cost Sensor
Hybridisation and Accuracy Estimation for Road
Applications. ESA Conference Navitec 2004.
Noordwijk, The Netherlands. .
North, E., et al., 2012. Improved Inertial/Odometry/GPS
Positioning of Wheeled Robots Even in GPS-Denied
Environments," InTech Europe.
Xiaochuan, Z. et al., 2009. A Novel Information Fusion
Algorithm for GPS/INS Navigation System. In
Proceedings of the IEEE International Conference on
Information and Automation, Zhuhai/Macau, China,
pp. 818-823.
Singhala, P. et al., 2014. Temperature Control using Fuzzy
Logic International Journal of Instrumentation and
Control Systems (IJICS) vol. 4.
Boysen, P. A. and Zunker, H., 2004. Low Cost Sensor
Hybridisation and Accuracy Estimation for Road
Applications. In ESA Conference Navitec, Noordwijk,
The Netherlands.
Boucher, C., et al., 2004. Non-linear filtering for land
vehicle navigation with GPS outage. in IEEE
International Conference on Systems, pp. 1321 -1325.
Hay, C., et al., 2005. Wheel-Speed Dead Reckoning for
Vehicle Navigation. In GPS World, p. 37 42.
Sukkarieh, 2000. Low Cost, High Integrity, Aided Inertial
Navigation Systems for Autonomous Land Vehicles.
PhD. Thesis, Sydney. Sydney, Australia.
St-Pierre, M. and Ing, D. G. D., 2004. Comparison
between the unscented Kalman filter and the extended
Kalman filter for the position estimation module of an
integrated navigation information system," in IEEE
Intelligent Vehicles Symposium Parma, Italy, 2004.
Sakhi, S., 2014. Centrale d'acquisition pour le trace
d'engins mobiles Thèse doctorat, Ecole Militaire
Polytechnique d'Alger, Algérie.
Quinchia, A. G. and Ferrer, C., 2011. A Low-Cost
GPS&INS Integrated System Based on a FPGA
Platform. In International Conference on Localization
and GNSS, ICL-GNSS, Tempere, Finland.
North, E. et al., 2009. Enhanced Mobile Robot Outdoor
Localization Using INS/GPS Integration. In
International Conference on Computer Engineering &
Systems ( ICCES), Cairo, Egypt.
Lamon, P. and Siegwart, R., 2004. Inertial and 3D-
odometry fbsion in rough terrain-Towards real 3D
navigation. In International Conference On intelligent
Robots and Systems (IEEE/RSJ), Sendai, Japan.
Rogers-Marcovitz, F., et al., 2012. Aiding Off-Road
Inertial Navigation with High Performance Models of
Wheel Slip. In International Conference on Intelligent
Robots and Systems (IEEE/RSJ), Vilamoura, Algarve,
Portugal.
Wang, J.-H., 2006. Intelligent MEMS INS/GPS
Integration For Land Vehicle Navigation. PHD,
Department of Geomatics Engineering Calgary,
Alberta. Canada.
Kubrak, D., 2007. Etude de l’hybridation d’un récepteur
GPS avec des capteurs bas coûts pour la navigation
personnelle en milieu urbain. Thèse de Doctorat,
l’École Nationale Supérieure des Télécommunications
Paris, France.
Tharin, J., et al., 2012. V-REP User manual . Switzerland,
4 edition.
0 2000 4000 6000 8000
-20
-15
-10
-5
0
5
10
15
20
Error in North(m)
Samples
GPS/INS errors
GPS/Odm errors
GPS/RISS errors
AFSA errors
GPS/INS errors
GPS/Odom errors
GPS/RISS errors
FSC errors
A Fuzzy Controller for GPS/INS/Odm Integrated Navigation System
397
