Output Tracking Control for Networked Control Systems

Tiago G. de Oliveira

, Reinaldo M. Palhares

and V

ıctor C. S. Campos

Graduate Program of Electrical Engineering, Federal University of Minas Gerais, Belo Horizonte, Minas Gerais, Brazil

Department of Electronics Engineering, Federal University of Minas Gerais, Belo Horizonte, Minas Gerais, Brazil

Department of Electrical Engineering, Federal University of Ouro Preto, Jo

ao Monlevade, Minas Gerais, Brazil

Keywords:

Networked Control Systems, Time Delay, Lyapunov Functional, Integral Inequalities, Takagi-Sugeno Fuzzy

Models.

Abstract:

This paper aims to compare alternative time delay relaxations for a class of nonlinear systems controlled

via network and described by Takagi-Sugeno fuzzy models. In this regard, three alternatives were proposed

and compared with a very recent relaxation proposed in the literature. Basically, the changes are made at

two strategic points. The ﬁrst point is the Lyapunov functional proposed and the second one is related to

the introduction of different integral inequalities conditions. A numerical example of a network-based fuzzy

tracking control systems is presented to highligth the advantages of the alternatives relaxations.

1 INTRODUCTION

The usual communication network architecture for

control systems established during the past decades

is point to point communication, ie, connection be-

tween the plant, sensors and actuators is made via a

physical medium, for example, a cable. However, the

increasing complexity of control systems is leading

this architecture to reach its limits. Because of this,

more and more communication architectures are be-

ing replaced by one in which all communication is

done through a common communication medium for

all equipments.

The introduction of this type of architecture can

increase the efﬁciency, ﬂexibility and reliability of

these systems and reduce installation and mainte-

nance costs. Networked Control Systems are cur-

rently in evidence, as they provide the control sys-

tem with features such as cost reduction, easy main-

tainable and increases ﬂexibility and agility (with

regard to possible adaptations and modiﬁcations).

These characteristics become more important when

the complexity of control systems increases.

A classic control structure (point to point) con-

siders that the means of communication between the

components are ideal, i.e. there is no loss or delay in

the transmitted information. A networked control sys-

tem should take into account the characteristics of the

physical environment in which the information circu-

lates, because it will inﬂuence the system dynamics.

The following characteristics of the physical environ-

ment can be listed:

• Bandwidth: the network may have a limitation in

data transmission capacity, limiting the informa-

tion that travels over the network;

• Packet Loss: the network has information loss,

ie, the information sent may not reach their des-

tiny;

• Delay: the information takes time to reach your

destiny, therefore, a network delay should be con-

sidered.

At the beginning, the NCSs operated using a pe-

riodic triggered control method (also called time-

triggered control). In this triggering method, a ﬁxed

sample interval should be selected to guarantee a de-

sired performance under worst case conditions such

as external disturbances, uncertainties, time-delays

and so on. Therefore, this kind of triggering leads

to sending many “unnecessary” sampling signals

through the network, which incur in high utilization

of the communication bandwidth Yue et al. (2013).

In order to eliminate this problem, it was recently re-

placed by the event-triggered control method. This

method provides a useful way of determining when

the sampling action is carried out, which guarantees

that only “necessary” state signals will be send out

to the controller Yue et al. (2013), which reduces

the utilization of the communication bandwidth. Al-

bert (2004) presents a comparison between event-

Oliveira, T., Palhares, R. and Campos, V.

Output Tracking Control for Networked Control Systems.

DOI: 10.5220/0006003602550260

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 1, pages 255-260

ISBN: 978-989-758-198-4

255

triggered and time-triggered concepts from the con-

trol theory point of view. Hu et al. (2012); Yue et al.

(2013) an H

∞

tracking controller for NCS with event-

triggering sampling method. Zhang et al. (2015); Jia

et al. (2009); Tseng et al. (2001) design a H

∞

con-

troller for output tracking for a T-S fuzzy system us-

ing the event-triggered method.

In the last years, more and more efforts have been

done to derive new powerful convex stability condi-

tions including alternative integral inequalities as, for

example, the Wirtinger based integral inequality that

has been proven to encompass the standard Jensen in-

tegral inequality Seuret and Gouaisbaut (2013). In

Feng and Zheng (2016) the stability analysis problem

of Takagi-Sugeno fuzzy systems with time-varying

delay is investigated, utilizing the Wirtinger inequal-

ity and the reciprocally convex combination tech-

nique. Souza et al. (2014) presents new less conser-

vative stability conditions analysis for Takagi-Sugeno

fuzzy systems subject to interval time-varying and

based on an appropriate Lyapunov functional selec-

tion combined with an integral inequality choice.

Park et al. (2015a) introduced a Wirtinger based dou-

ble integral inequality and new stability conditions

have been obtained. In Sun et al. (2009) a new delay-

dependent stability is obtained in terms of LMI by

constructing a Lyapunov functional and using integral

inequalities without introducing any free-weighting

matrices.

The main objective of this paper is to derive less

conservative conditions for stability and stabilization

gathering those new relaxations based on integral in-

equalities and modiﬁcations to the Lyapunov func-

tional. The idea is to present a state-of-the-art of re-

cent conditions to the problem of output tracking con-

trol for networked Takagi-Sugeno fuzzy models with

event-triggered control. In order to do this, the Lya-

punov functional has been modiﬁed to include a triple

integral term as proposed in Zhang et al. (2015) and

its effect has been analysed. The analysis also in-

cludes the new class of integral inequaliteis proposed

in Park et al. (2015) and the so-called auxiliary func-

tions.

Notation: The notation considered in this paper is

standard. sym{X } denotes X + X

. “⊗” represents

the Kronecker product for matrices. The term “∗” in-

dicates a term induced by symmetry in a matrix.

2 PROBLEM FORMULATION

This paper deals with nonlinear systems described by

T-S fuzzy models. Consider the system described as

follows:

Plant Rule R

: if θ

(t) is M

and θ

(t) is M

and

... and θ

(t) is M

, then:

(

˙x(t) = A

x(t) + B

u(t) + E

w(t)

y(t) = C

x(t)

(1)

where i = 1,2,. .., r, and r denotes the number

of if-then rules; x(t) ∈ R

is the vector of state

variables; u(t) ∈ R

is the vector of control in-

put, w(t) ∈ R

is the vector of exogenous in-

puts and y(t) ∈ R

is the vector of controlled vari-

ables. θ

( j = 1, 2,... ,g) are the premise variables,

θ(t) = [θ

(t),θ

(t),. ..,θ

(t)] ∈ R

is a vector com-

posed by stacking the premise variables. M

i j

(i =

1,2, ...,r)( j = 1,2, .. .,g) are the fuzzy sets. A

and E

are the system matrices with appropriate di-

mensions.

By making use of a center-average defuzziﬁer,

product fuzzy inference and singleton fuzziﬁer, the T-

S fuzzy model is inferred as:











˙x(t) =

∑

i=1

x(t) + B

u(t) + E

w(t)]

y(t) =

∑

i=1

x(t)]

(2)

This membership functions satisfy the following

properties:

∈ [0,1],

∑

i=1

= 1,

∑

i=1

˙µ

= 0.

(3)

We also consider the following reference model

(

˙x

(t) = A

(t) + B

r(t)

y(t) = C

(t)

(4)

An event-triggered (ET) scheme is introduced to

decide wheter or not the sample-data should be trans-

mitted. Figure 1 shows the conﬁguration of the

network-based fuzzy tracking control system.

Figure 1: Conﬁguration of the system (Zhang et al., 2015).

The initial triggering instant is deﬁned as 0, i.e.

h = 0, when k = 0. t

∈ N is the triggering instant

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

256

and h is the samplig period. The next triggering in-

stant is deﬁned by the following:

k+1

= t

h + inf

i∈N





[ξ(t

h + ih) − ξ(t

h)]



−ε



ξ(t



> 0

, ∀k ∈ N (5)

where ξ(t) will be deﬁned in 8.

The parameters ε (0 < ε < 1) and matrix W (W >

0) determinate how frequently and how much sample-

data should be transmitted. In Yue et al. (2013); Peng

et al. (2013); Hu et al. (2012) the parameter W and

controller parameters are determined by some LMI-

based criteria for a given ε.

Clearly the fuzzy system and the fuzzy controller

operate asynchronously due to the event-triggering

process and the network-induced delays in data trans-

mission.

The control rule of the state feedback controller is

deﬁned as follows:

If θ

h) is M

and θ

h) is M

and . . . and

h) is M

, then:

u(t) = F

x(t

h) + F

h) (6)

Then, the fuzzy controller is deﬁned as:

u(t) =

∑

i=1

(θ(t

h))[F

x(t

h) + F

h)],

t ∈ [t

h + τ

k+1

h + τ

tk+1

, ) (7)

where τ

= τ

+τ

. τ

is the delay corresponding to

the time that the information takes to travel between

the system and the controller. τ

is the delay cor-

responding to the time that the information takes to

travel between the controller and the actuator. Other

delays such as the time the computer takes to calcu-

late the controller gains are ignored.

Let e(t) = y(t) − y

(t) and ε

(t − τ(t)) = ξ(t −

τ(t)) − ξ(t

h). Using the system model and the ref-

erence model, an augmented system can be obtained

as follows:











ξ(t) =

∑

i=1

∑

j=1

[

ξ(t) +

ξ(t − τ(t))

−

(t − τ(t)) +

ω(t)]

e(t) =

∑

i=1

[

ξ(t)]

(8)

with ξ(t − τ(t)), the augmented state, and ε

(t − τ(t))

satisfying:



(t − τ(t))



≤ σ



(t − τ(t)) − ε

(t − τ(t)



(9)

where σ is a positive scalar and



0 A









0 B





−C







= µ

(θ(t)), µ

(k)

= µ

(θ(t

h)) ≥ 0,

i = 1, 2,. ..,r,

∑

i=1

(k)

∑

i=1

= 1, ∀k ∈ N

ω(t) =



(t) r

(t)



(10)

where F

and F

are the fuzzy control gains.

Zhang et al. (2015) designs a network-based fuzzy

tracking controller such that the output of the fuzzy

system follows the output of the reference model as

close as possible by taking into consideration the de-

viation bounds of asynchronous normalized member-

ship functions, which are described by:

(θ(t)) − µ

(θ(t

h))

≤ δ

, i = 1,2, .. .,r, ∀k ∈ N

(11)

where δ

are given positive constants. In order to ob-

tain the δ

bounds, the Lemmas available in: Zhang

et al. (2015); Peng et al. (2013); Zhang and QL.Han

(2013) are introduced. In this scenario, three different

alternatives are proposed in our paper to be analyzed

and compared with the solution proposed by Zhang

et al. (2015). The alternatives are listed below:

• Alternative 1: Change the Lyapunov functional

in Zhang et al. (2015), by adding a tripple integral

term and use Lemmas 1, 2, 3 and 4;

• Alternative 2: Maintain the Lyapunov functional

in Zhang et al. (2015) and use (Park et al., 2015b,

Lemma 5.1) to modify the integral inequalities;

• Alternative 3: Change the Lyapunov functional

in Zhang et al. (2015) by adding a tripple integral

term to the funcional and use the integral inequal-

ities proposed by (Park et al., 2015b, Lemma 5.1).

For that, we consider the following Lyapunov

functional:

V (t,ξ

) =

∑

i=0

(t,ξ

) (12)

(t,ξ

) =



ξ(t)

t−τ

ξ(s)ds





ξ(t)

t−τ

ξ(s)ds



(t,ξ

) =

t−τ

(s)Q

ξ(s)ds

(t,ξ

) =

t−τ

(s)Q

ξ(s)ds

Output Tracking Control for Networked Control Systems

257

(t,ξ

) = τ

−τ

t+s

(θ)R

ξ(θ)dθds

(t,ξ

) =

−τ

t+s

(θ)R

ξ(θ)dθds

(t,ξ

) = (τ

− τ(t))

t−

τ(t)

(θ)R

ξ(θ)dθ

(t,ξ

) = (τ

− τ(t))



(ξ(t) − ξ(t −

τ(t)))

(ξ(t) − ξ(t −

τ(t))]

(t,ξ

) =

−τ

t+s

t−λ

(θ)G

ξ(θ)

−τ

t+s

t−λ

dsdθdλ

where ξ

= ξ(t + θ), ∀θ ∈ [−τ

,0], P =





with P

= P

, Q

= Q

,(i = 1, 2), R

= R

,(i =

1,2, 3,4), G

= G

,(i = 1,2).

The main difference between this functional and

the one proposed in Zhang et al. (2015) is the intro-

duction of the triple integral term in V

. Notice that

alternative 02 makes use of the same Lyapunov func-

tional as Zhang et al. (2015). Given all of this, we are

now able to present the conditions in the result below.

Theorem 1: Given positive scalars

γ,τ

,τ

,ε, δ

(i = 1,2, .. .,r), σ and a weighting ma-

trix U > 0, under the event-triggered communication

scheme, the system 8 is asymptotically stable with

the L

-gain tracking performance, if there exist sym-

metric matrices W > 0,P

> 0,Q

> 0,R

> 0,G

> 0

and matrices P

,X, S,Z,M

(i = 1,2, .. .,r),T

i j

(i, j = 1,2, .. ., 2r) such that the following LMIs

hold:



∗ P



> 0, (13)



∗ R



> 0, (14)







(1)

i j

τZ

∗ −γ

I 0 0

∗ ∗ −τR

∗ ∗ ∗ −U

−1







≤ 0, (15)





(2)

i j

∗ −γ

I 0

∗ ∗ −U

−1





≤ 0, (16)







1,1

1,2

.. . T

1,2r

2,1

2,2

.. . T

2,2r

2r,1

2r,2

.. . T

2r,2r







< 0, (17)

i j

+ T

− 2M

≤ 0, (18)

−2N

− T

( j+r),(i+r)

− T

(i+r),( j+r)

≤ 0. (19)

where e

= I(i,:) ⊗ I (i = 1, 2,...,9) are the p × 9p

matrices, I denotes a matrix identity of order p, I(i,:)

denotes the i-th row of an 9 × 9 identify matrix, p is

the dimension of ξ(t),

(1)

i j

=Ω

(0)

i j

+ e

εWe

+ sym



εWe



− (1 − ε)We

− κ

ϒκ

(2)

i j

=Ω

(0)

i j

+ τΩ

(1)

i j

+ e

εWe

+ sym



εWe



− (1 − ε)We

− κ

ϒκ

Ω

(0)

i j

X + X

+ Q

+ P

− 9R

−

+ e

(τ

+ τ

− σX + σX

+ S − 2R

− e

− Q

− 9R

− R

+ e

+ R

− e

180R

− e

720R

+ sym





σX

−X + P

+ e

− e



+ sym



− e

(2R

+ P

(τ

+ 6R



sym



σB

− e

σB

+ e



+ sym



− S

+ e

− S)e



+ sym



(6R

− τ

− e

)



Ω

(1)

i j

=sym



− e



+ e

σE

i j

+ T ji + T

(i+r),( j+r)

+ T

( j+r),(i+r)

+ T

i,( j+r)

+ T

( j+r),i

−

∑

k=1



+ T

+ N

( j+r),(k+r)

+ T

(k+r),( j+r)



The fuzzy control gains and the matrix in the

event-triggered communication scheme are given by

= Y

−1

( j = 1,2, .. .,r) and W = X

−T

W X

−1

Proof. The proof is similar to that of Proposition 1

in (Zhang et al., 2015, Appendix A and B) with the ex-

ception of using Lemmas (Park et al., 2015b, Lemma

5.1) instead of (Zhang et al., 2015, Lemma 2), and

thus is omitted.

Remark: The other proofs are also similar. Alter-

native 1 uses the Lyapunov functional 12 and (Zhang

et al., 2015, Lemmas 1, 2, 3 and 4) to the integral

terms. Alternative 2 uses the same Lyapunov func-

tional of Zhang et al. (2015) and the (Park et al.,

2015b, Lemma 5.1) instead of (Zhang et al., 2015,

Lemma 2).

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

258

3 EXAMPLE

We consider the example in (Zhang et al., 2015,

Section 5, p. 38). The purpose is to compare the

maximum allowable upper bounds that guarantee the

asymptotic stability of each system. We consider an

initial state x(0) = [1 0]

and x

(0) = −2, distur-

bance input ω(t) = 12cos(t)e

−t

and reference input

r(t) = 6 sin(1.2t)e

−0.11t

. Consider the following T-S

fuzzy system.





0 1 0

0 −0.1 0

0 0 −1









0 1 0

25 −0.1 0

0 0 −1







0 1 0

0 0 1





0 1 0





1 0 −1



D =

{

x(t) : |x

(t)| ≤ 5, |x

(t)| ≤ 4

}

(θ(t)) = 1 − x

(t)/25, µ

(θ(t)) = x

(t)/25,

θ(t) = x

(t).

This system is described in the augmented form

as in (8). Table 1 presents the maximum allowable

upper bound to the time-varying delay, τ

, achieved

for a given lower bound, τ

Table 1: System.

Method τ

= 0 τ

= 0.5 τ

= 1.0

Zhang et al. (2015) 0.12 0.72 1.41

Alternative 1 1.45 2.23 2.69

Alternative 2 2.13 2.73 3.27

Alternative 3 2.47 2.79 3.58

The results obtained show that the alternatives

proposed can provide higher upper bounds than ex-

isting results. For comparision purpose, the max-

imum time-varying delay is set to 1.0 s. The

gains of the state feedback controller were obtained

through Alternative 3, which was the best alterna-

tive among the alternatives proposed, that is:

[−5.9879 − 7.2412 22.7661] and

= [−3.2195 −

0.93731 11.763]. Figure 2 depicts the output tracking

errors. In a tracking problem, it is expected that the

tracking error tends to zero as time increases. Notice

that the error obtained by Alternative 3 is smaller than

the error obtained in Zhang et al. (2015).

Generally, considering small values of delay, the

result obtained by Zhang et al. (2015) is very similar

to the results obtained through the alternatives pro-

posed in this article. The great advantage of the meth-

ods proposed in this article is that they maintain a bet-

0 5 10 15 20 25 30

−10

−5

e(t)

Alternative 3

0 5 10 15 20 25 30

−10

−5

Time (s)

e(t)

Zhang et al. (2015)

Figure 2: Output Tracking Error.

ter output tracking dynamic for a greater range of de-

lay values.

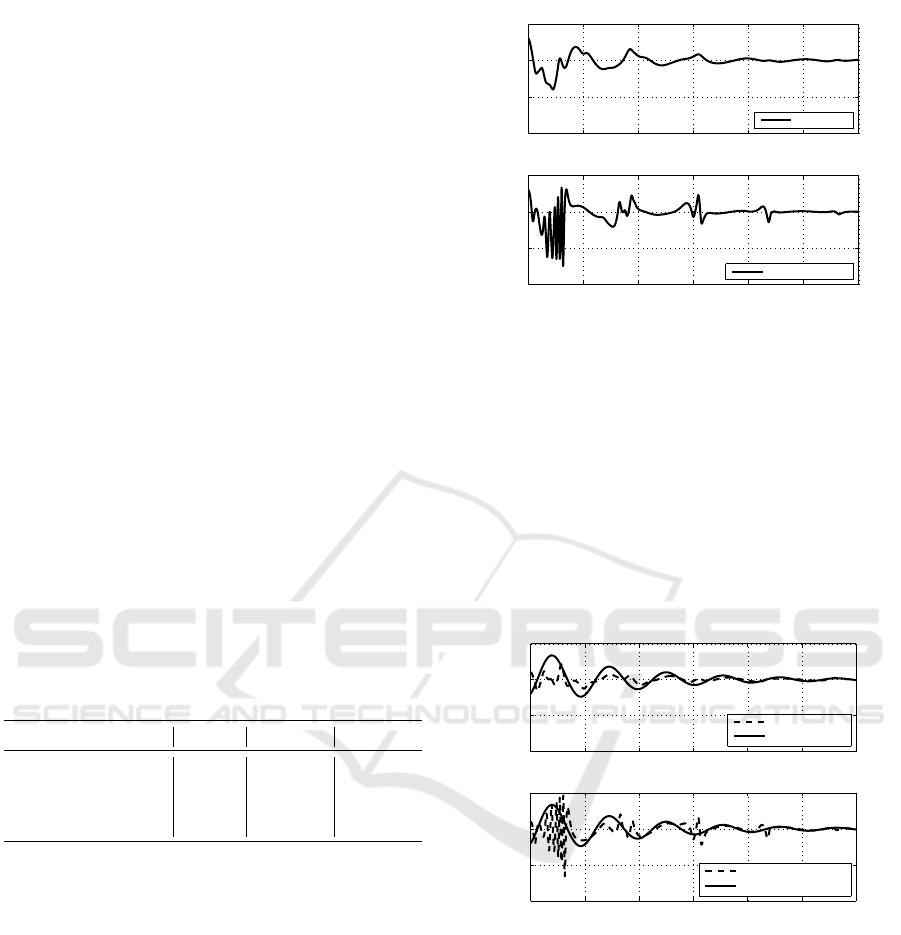
Figure 3 presents the output tracking responses.

Applying an input signal with limited energy, it is ex-

pected that the output signal of the system has lim-

ited energy. As can be seen, for the maximum de-

lay value equal to 1.0 s, both systems present output

signal with limited energy. According to the ﬁgure,

the controller designed through Alternative 3 presents

a better disturbance rejection in relation to the con-

troller designed by Zhang et al. (2015).

0 5 10 15 20 25 30

−10

−5

y(t) − Alternative 3

(t)

0 5 10 15 20 25 30

−10

−5

Time (s)

y(t) − Zhang et al. (2015)

(t)

Figure 3: Output Tracking Responses.

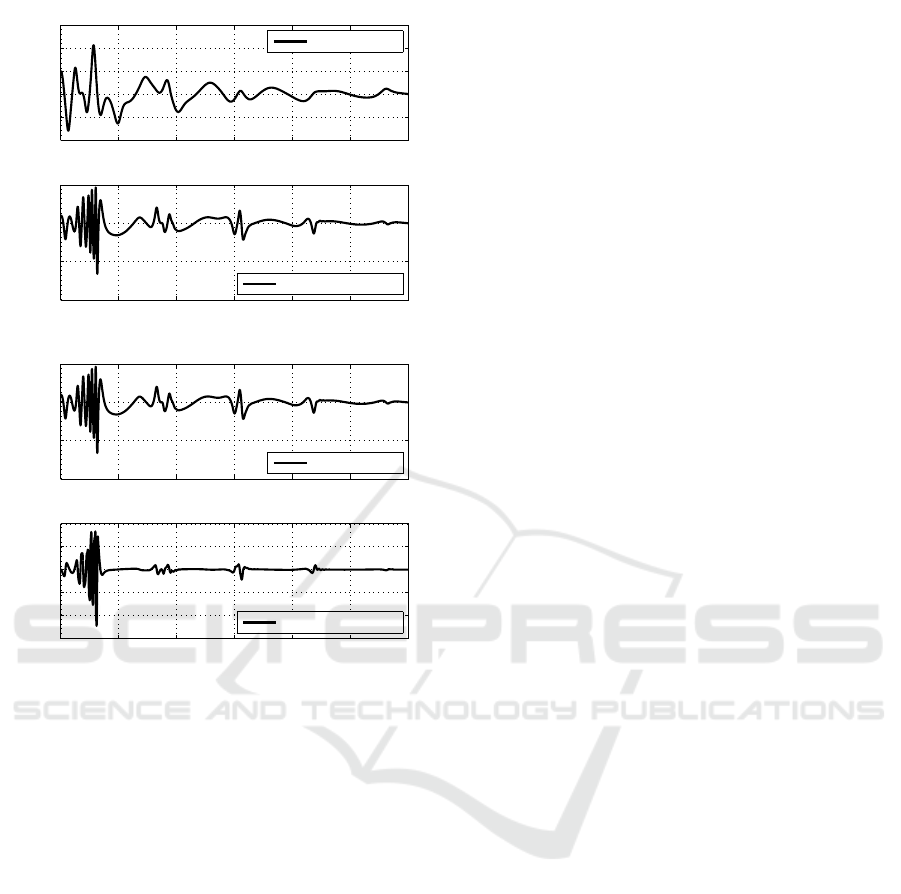
Figure 4 depicts the performance of the system

states. What is expected in this problem is to mini-

mize the effect of disturbances in the ﬁrst state vari-

able, acting only in the second state variable of the

model as denoted by the input matrices B

. As we can

note, the controller obtained using Alternative 3 re-

jects the disturbance in the second state variable bet-

ter than the controller designed by Zhang et al. (2015).

Note that the axes of this ﬁgure have different ampli-

tudes, in order to obtain the best resolution possible.

Output Tracking Control for Networked Control Systems

259

0 5 10 15 20 25 30

−2

−1

(t) − Alternative 3

0 5 10 15 20 25 30

−10

−5

(t) − Zhang et al. (2015)

0 5 10 15 20 25 30

−10

−5

(t) − Alternative 3

0 5 10 15 20 25 30

−150

−100

−50

100

Time (s)

(t) − Zhang et al. (2015)

Figure 4: States of the Systems.

4 CONCLUSION

In this paper the output tracking problem for net-

worked control has been handled considering differ-

ent choices for integral inequalities relaxations as well

as proper selection of Lyapunov functionals. In gen-

eral, the results obtained suggest that less conserva-

tive conditions can be obtained just considering slight

alterations in very recent results.

ACKNOWLEDGMENT

The authors acknowledge the ﬁnancial support of the

Brazilian agencies CNPq and CAPES.

REFERENCES

Albert, A. (2004). Comparison of event–triggered and

time–triggered concepts with regard to distributed

control systems. Embedded World, 2004:235–252.

Feng, Z. and Zheng, W. X. (2016). Improved stability con-

dition for Takagi–Sugeno fuzzy systems with time–

varying delay. IEEE Transactions on Cybernetics.

Hu, S., Zhang, Y., and Du, Z. (2012). Network–

based H

∞

tracking control with event–triggering sam-

pling scheme. IET Control Theory & Applications,

6(4):533–544.

Jia, X., Zhang, D., Hao, X., and Zheng, N. (2009). Fuzzy

tracking control for nonlinear networked control sys-

tems in Takagi–Sugeno fuzzy model. IEEE Transac-

tions on Cybernetics, 39(4):1073–1079.

Park, M., Kwon, O., Park, J. H., Lee, S., and Cha,

E. (2015a). Stability of time-delay systems via

Wirtinger–based double integral inequality. Automat-

ica, 55:204–208.

Park, P., Lee, W. I., and Lee, S. Y. (2015b). Auxil-

iary function–based integral inequalities for quadratic

functions and their applications to time-delay systems.

Journal of the Franklin Institute, 352(4):1378–1396.

Peng, C., Han, Q., and Yue, D. (2013). To transmit or not

to transmit: a discrete event–triggered communication

scheme for networked Takagi–Sugeno fuzzy systems.

IEEE Transactions on Fuzzy Systems, 21(1):164–170.

Seuret, A. and Gouaisbaut, F. (2013). Wirtinger–based in-

tegral inequality: application to time–delay systems.

Automatica, 49(9):2860–2866.

Souza, F. O., Campos, V. C. S., and Palhares, R. M. (2014).

On delay–dependent stability conditions for Takagi–

Sugeno fuzzy systems. Journal of the Franklin Insti-

tute, 351(7):3707–3718.

Sun, J., Liu, G., and Chen, J. (2009). Delay–dependent sta-

bility and stabilization of neutral time–delay systems.

International Journal of Robust and Nonlinear Con-

trol, 19(12):1364–1375.

Tseng, C., Chen, B., and Uang, H. (2001). Fuzzy track-

ing control design for nonlinear dynamic systems via

Takagi–Sugeno fuzzy model. IEEE Transactions on

Fuzzy Systems, 9(3):381–392.

Yue, D., Tian, E., and Han, Q. (2013). A delay system

method for designing event–triggered controllers of

networked control systems. IEEE Transactions on Au-

tomatic Control, 58(2):475–481.

Zhang, D., Han, Q., and Jia, X. (2015). Network–based

output tracking control for Takagi–Sugeno fuzzy sys-

tems using an event-triggered communication scheme.

Fuzzy Sets and Systems, 273:26–48.

Zhang, X. and QL.Han (2013). Novel delay–derivative–

dependent stability criteria using new bounding tech-

niques. International Journal of Robust and Nonlin-

ear Control, 23(13):1419–1432.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

260