
Evaluation of Local 3-D Point Cloud Descriptors in Terms of Suitability
for Object Classification
Jens Garstka and Gabriele Peters
Human-Computer Interaction, Faculty of Mathematics and Computer Science,
University of Hagen, D-58084 Hagen, Germany
Keywords:
Local 3-D Feature Descriptors, Performance Evaluation, Object Classification.
Abstract:
This paper investigates existing methods for local 3-D feature description with special regards to their suitabil-
ity for object classification based on 3-D point cloud data. We choose five approved descriptors, namely Spin
Images, Point Feature Histogram, Fast Point Feature Histogram, Signature of Histograms of Orientations, and
Unique Shape Context and evaluate them with a commonly used classification pipeline on a large scale 3-D
object dataset comprising more than 200000 different point clouds. Of particular interest are the details of the
choice of all parameters associated with the classification pipeline. The point clouds are classified by using
support vector machines. Fast Point Feature Histogram proves to be the best descriptor for the method of
object classification used in this evaluation.
1 INTRODUCTION
Latest advances in image based object recognition,
e. g., deep convolutional neural networks may sug-
gest that the problem of object classification is solved.
However, it is still possible to list many situations in
which deep learning approaches based on image data
fail. This happens mainly if the objects are translucent
or if they have no or an arbitrary texture, respectively.
This is often the case for non-natural human-made ob-
jects. Figure 1 illustrates one of these cases.
Figure 1: This patchwork sofa illustrates one of the situa-
tions where an image based object recognition or classifica-
tion is difficult due to arbitrary textures — image by Dolores
Develde, 2012, Creative Commons Attribution 3.0 License.
To address these problems, it is helpful to re-
gard the 3rd dimension for object classification. It
allows to reduce the mentioned problems at least in
some cases. The sofa shown in Figure 1, for ex-
ample, could certainly be recognized using a three-
dimensional representation.
A description of 3-D objects can be divided into
two broad categories: global and local. Global de-
scriptors define a representation of an object which
effectively and concisely describes the entire 3-D ob-
ject. In most cases, these methods require an a priori
segmentation of the scene into object an background
and are not suitable for partially visible objects from
cluttered scenes. Furthermore, it has to be consid-
ered that objects might have different poses or might
be deformed. Local descriptors allow robust and ef-
ficient recognition approaches that can operate under
partial occlusion and are invariant to different poses
and deformation.
Beginning with the introduction of Microsoft Ki-
nect in 2010, even research groups with a small bud-
get were enabled to easily generate 3-D data on their
own. As a consequence a lot of research regarding lo-
cal 3-D feature descriptors was done in recent years.
This paper investigates five approved local 3-D fea-
ture descriptors of 3-D point clouds with a focus on
their suitability for object classification. The text is
structured as follows. In Section 2, existing evalua-
tions and the evaluated local 3-D feature descriptors
are presented. In Section 3 the used classification
pipeline is introduced in detail. In Section 4 the five
local 3-D feature descriptors are applied and evalu-
ated in context of the classification pipeline. Finally,
Section 5 and Section 6 discuss the results and give a
short conclusion.
540
Garstka, J. and Peters, G.
Evaluation of Local 3-D Point Cloud Descriptors in Terms of Suitability for Object Classification.
DOI: 10.5220/0006011505400547
In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 540-547
ISBN: 978-989-758-198-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 RELATED WORK
Subsequently, already published evaluations of local
3-D feature descriptors and the local 3-D feature de-
scriptions considered in this paper are introduced.
2.1 Existing Evaluations
There is a number of publications that deal with evalu-
ations of 3-D feature descriptors in the last five years.
A survey and evaluation of local shape descriptors
(Heider et al., 2011) divides existing local descriptors
into three classes. Focus of the evaluation are 3-D
meshes and only local shape descriptors for meshes
are examined.
The evaluation of local shape descriptors for 3-D
shape retrieval (Tang and Godil, 2012) is similar to
the work of (Heider et al., 2011), with the difference
that they perform the tests of 6 simple mesh descrip-
tors on the SHREC 2011 Shape Retrieval Contest of
Non-rigid 3D Watertight Meshes dataset (Lian et al.,
2011).
An evaluation from Alexandre with focus on local
3-D descriptors for object and category recognition
(Alexandre, 2012) is the publication that is themati-
cally most similar to our work. The tested algorithms
are the same ones as those examined in this paper.
However, the pipeline proposed by Alexandre is un-
suitable for a larger amount of data.
The evaluation of local 3-D feature descriptors for
a classification of surface geometries in point clouds
(Arbeiter et al., 2012) investigates how local 3-D fea-
ture descriptions can be used to classify primitive lo-
cal surfaces such as cylinders, edges, or corners in
point clouds. Arbeiter et al. compare a small selec-
tion of three local 3-D feature descriptors.
The goal of the evaluation of 3-D feature descrip-
tors in the work of (Kim and Hilton, 2013) is a multi-
modal registration of 3-D point clouds, meshes, and
images. Although the descriptors used in this work
are the same as in this paper, conclusions regarding
a classification of 3-D point clouds can hardly be de-
rived from their results.
Finally, a survey on 3-D object recognition in clut-
tered scenes with local surface features (Guo et al.,
2014) provides a good overview of the available de-
scriptors and divides them with a taxonomy into dif-
ferent descriptor types. In addition, there is an infor-
mal comparison of the performance of each descrip-
tor, which, however, is based on the statements given
in each individual publication and not on an own eval-
uation.
2.2 Local 3-D Feature Descriptors
The goal of local 3-D feature descriptors is the de-
scription of particularly “interesting” local areas of a
3-D object. The advantages of local representations
consist in their robustness with respect to noise, and
their variability concerning object shape and partial
occlusions. A wide variety of methods exists (Guo
et al., 2014), but not all are suitable for 3-D point
clouds, but rather meshes or depth images. The fol-
lowing five local 3-D feature descriptors are suitable
for the local description of 3-D point clouds and are
evaluated in this paper.
The Spin Image (SI) descriptor (Johnson and
Hebert, 1998; Johnson and Hebert, 1999) is arguably
the most cited and approved local 3-D descriptor. It
is a histogram based method that requires a normal
vector as a rotation axis. In a nutshell, all 3-D points
of the local environment are collected while the 2-D
histogram is rotated around the normal vector.
The Point Feature Histogram (PFH) (Rusu et al.,
2008a) is a histogram based approach as well. Rusu
et al. compute Darboux frames (Rusu et al., 2008a)
for each 3-D point of a local spherical environment.
The three angles of each Darboux frame are subdi-
vided into 5 intervals and filled in a histogram with
125 bins.
Since the computational complexity for the deter-
mination of Darboux frames at each point within a
k-neighborhood is O(k
2
), the computation of PFH is
relatively slow. For this reason, Rusu et al. proposed
a simplified version of PFH named Fast Point Fea-
ture Histogram (FPFH) (Rusu et al., 2009). They pre-
served the basic characteristics of the descriptor, but
replaced the computation of the Darboux frame with
an approximation of it.
Tombari et al. propose a descriptor called Signa-
tures of Histograms of Orientations (SHOT) (Tombari
et al., 2010b; Salti et al., 2014). A spherical neigh-
borhood is divided into several segments. For each
segment a histogram is filled with the cosine values
of the angles between the z-axis of the local reference
frame and the normal vectors of all points that are part
of the currently considered segment.
Another local 3-D feature descriptor introduced
by Tombari et al. is Unique Shape Context (USC)
(Tombari et al., 2010a). It is an extension of the 3-D
Shape Context (3DSC) (Frome et al., 2004), which
essentially consists of a spherical histogram divided
into radial, elevation, and azimuth divisions. Tombari
et al. determine a unique local reference frame to en-
sure that the histogram has unique orientation.
Evaluation of Local 3-D Point Cloud Descriptors in Terms of Suitability for Object Classification
541

Keypoint
Selection
Feature
Description
Point Cloud Bag of Words Classification
Figure 2: The classification pipeline used for the evaluation of local 3-D feature descriptors. It consists of four main steps:
keypoint selection, feature descriptions, a bag-of-words model, and the classification.
3 CLASSIFICATION PIPELINE
At a conceptual level, a 3-D classification pipeline is
based on four main steps. These are the keypoint se-
lection (Salti et al., 2011; Dutagaci et al., 2012; Filipe
and Alexandre, 2013), the extraction of local feature
descriptions (Alexandre, 2012; Guo et al., 2014), a
bag-of-words model (Wu and Lin, 2011; Cholewa and
Sporysz, 2014), and a machine learning method for
the classification task for which support vector ma-
chines (Toldo et al., 2010) are widely used. Figure 2
depicts these steps with a conceptual illustration of
such a pipeline. The individual steps and their param-
eters are discussed in detail in the next subsections.
3.1 Point Clouds
The dataset used in the context of this work is the
RGB-D Object Dataset (Lai et al., 2011). The dataset
contains 51 object classes, e. g., banana, calculator,
glue stick, or sponge. Each object class comprises
several different objects of the same object class. The
object class coffee mug, for example, contains 8 dif-
ferent types of coffee cups. In summary, the datasets
contains 300 different objects where each object was
captured in different poses. This results in 207841
distinct point clouds. The mean point cloud resolu-
tion (pcr) of these point clouds is ≈ 0.001295.
As not only the complete set of object classes, but
also a part of it will be used in context of this evalua-
tion, a subset is specified in the following. It consists
of 10 randomly selected object classes, namely cap,
coffee mug, food bag, greens, hand towel, keyboard,
kleenex, notebook, pitcher, and shampoo. These 10
object classes contain approx. 36500 3-D point clouds
from 53 distinct objects (cf. Figure 3).
Figure 3: A picture of one object from each of the 10 se-
lected object classes, which are left to right, top to bottom:
cap, coffee mug, food bag, greens, hand towel, keyboard,
kleenex, notebook, pitcher, and shampoo.
3.2 Keypoint Selection
Keypoints, also referred to as interest points, are
points in images or 3-D point clouds that distinctively
describe an interesting region. They are supposed to
be stable under varying conditions. To ensure that our
evaluation results are independent of the choice of a
keypoint selection algorithm, two different keypoint
selection algorithms are used throughout this paper.
The first method is the keypoint algorithm in-
troduced in context of the Intrinsic Shape Signature
(ISS) (Zhong, 2009). According to (Salti et al., 2011)
and (Filipe and Alexandre, 2013) the ISS keypoint al-
gorithm yields the best scores in terms of repeatability
and is the fastest of the tested algorithms. All rele-
vant parameter values for the Intrinsic Shape Signa-
ture keypoint algorithm have been determined in the
evaluation of (Salti et al., 2011). Based on their re-
sults we use a radius of 6 · pcr for our evaluation.
Considering the fact that there are still many cur-
rent pipelines that rely on sparse sampling (Guo et al.,
2014), sparse sampling is used as a second option.
The distance of points using sparse sampling varies
significantly depending on the approach (Johnson and
Hebert, 1998; Frome et al., 2004; Drost et al., 2010;
Aldoma et al., 2012b). Thus, we use a radius of 6 · pcr
for sparse sampling, as well.
3.3 Feature Description
In this subsection we discuss the individual parame-
ters of the five local 3-D feature descriptors (cf. Sub-
section 2.2) we compare in our evaluation.
3.3.1 Spin Image
There are three main parameters to configure Spin Im-
age (SI): the height, the width, and the radius used for
the determination of the normal vector. The height
and the width of SI histograms described in (John-
son and Hebert, 1998) is 20 × 10. In a later work
they propose a size of 15 × 15 (Johnson and Hebert,
1999), while (Aldoma et al., 2012a) prefer a size of
17 × 9. In contrast to Johnson and Hebert, who use
meshes in their experiments, Aldoma et al. use point
clouds. Furthermore, they use an uneven number of
square bins with an edge length equal to the point
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
542

cloud resolution to take account of the sparse distri-
bution of point clouds. Therefore, we decided to fol-
low Aldoma et al. and use spin images with a size of
17×9 = 153 bins for our evaluation. The normal vec-
tor will be calculated based on the same radius used
to compute the histogram: 9 · pcr.
3.3.2 Point Feature Histogram
PFH requires two radii, the spherical support area and
a radius to approximate the normal vectors of the Dar-
boux frames. The size of the spherical support ar-
eas, i. e., the k-neighborhoods, are given by (Rusu
et al., 2008a) in meters and centimeters within an in-
terval of [2.0cm, 3.5 cm] for an indoor kitchen scene
and [50 cm, 150 cm] for an outdoor urban scene. Our
test data mainly includes household objects with a
size of at most 30 cm. Thus, we can assume that lo-
cal features can be limited to a size of 5cm or a k-
neighborhood with a radius of 2.5 cm, which fits to
the radii that are used by Rusu et al. for the kitchen
scene and is approximately equivalent to 19.3 · pcr.
An indication of the size of the area used for
the approximation of the normal vectors is given by
(Alexandre, 2012). He proposes a radius of 1cm
which is ≈ 7.7 · pcr in our dataset. Therefore, we use
a radius of 20 · pcr for the spherical support area, and
a radius of 8 · pcr to approximate the normal vector.
3.3.3 Fast Point Feature Histogram
As the Fast Point Feature Histogram (Rusu et al.,
2009) is based on the Point Feature Histogram and
follows the same mechanism, we use the same radii
as for the Point Feature Histogram.
3.3.4 Signatures of Histograms of Orientations
(Tombari et al., 2010b) recommend histograms with
11 bins and a segmentation of the spherical environ-
ment with 8 azimuth divisions, 2 elevation divisions,
and 2 radial divisions. Additionally, Tombari et al.
specify the size of the support area with 15 · pcr. We
will use all these parameter values for our evaluation,
too.
3.3.5 Unique Shape Context
All required parameter values for USC are given by
(Tombari et al., 2010a): 10 radial divisions, 14 az-
imuth divisions, and 14 elevation divisions. The outer
radius of the spherical histogram is 20 · pcr, the inner
radius of the spherical histogram is 2 · pcr, the radius
to approximate the normal vector is 20 · pcr, and the
density radius is 2 · pcr. We use these values in our
evaluations as well.
3.4 Bag-of-words
A bag-of-words model is used to count the occur-
rences of words of a text in a histogram. In the same
way a bag-of-words model can be used to count the
occurrences of local feature descriptions. In this con-
text it is often called a bag-of-features.
The only parameter required in advance is the
number of bins of the histogram. For each bin, a rep-
resentative local 3-D feature description is required.
These descriptions are taken from the centers of each
cluster determined by k-means clustering on precom-
puted local 3-D feature descriptions. The initial cen-
ters of the clusters are chosen at random by using a
k-means variant named k-means++ (Arthur and Vas-
silvitskii, 2007). The distance measure used is the
Euclidean distance.
Depending on the referred source, the selected
number of clusters k differs by orders of magnitude.
Toldo et al. use values of k between 20 and 80 (Toldo
et al., 2009) and values from 50 to 150 (Toldo et al.,
2010), Knopp et al. use 10% of all feature descriptions
extracted from a training set as a value of k (Knopp
et al., 2010). Madry et al. use between 7 and 300
clusters (Madry et al., 2012; Madry et al., 2013) and
Yi et al. use 20% of the average number of features
they extracted for each patch of all objects in their
training set (Yi et al., 2014). For this reason, 7 dif-
ferent histogram sizes, i. e., 10, 20, 50, 100, 200, 500,
and 1000 will be compared in this evaluation.
3.5 Classification
Most of the classification approaches in (Toldo et al.,
2009; Toldo et al., 2010; Knopp et al., 2010; Madry
et al., 2012; Madry et al., 2013; Seib et al., 2013; Yi
et al., 2014) use support vector machines as underly-
ing technique. Only the approach proposed by Yi is
based on a different concept using a language model.
Rusu et al. state, that support vector machines
have already been used for a classification based on
a bag-of-features model for color images with great
success (Rusu et al., 2008b; Rusu, 2010). In the refer-
enced works, Rusu et al. test support vector machines,
k-nearest neighbor searches, and k-means clustering
in different configurations against each other. The
best results are achieved using an SVM with a ra-
dial basis function (RBF) as kernel. There are some
other approaches, e. g., the work presented by (Lai
et al., 2011), where in some cases an alternative ma-
chine learning approach leads to slightly better re-
sults. However, since SVMs are the most widely
used classification method in this problem domain,
the evaluation presented here will also use SVMs as
Evaluation of Local 3-D Point Cloud Descriptors in Terms of Suitability for Object Classification
543
binary classifier for each object class. Accordingly, a
Gaussian radial basis function is used as kernel.
3.6 Summary
In summary, for a given 3-D point cloud we ex-
tract a set of keypoints with ISS and sparse sam-
pling. For each keypoint we compute a local 3-D fea-
ture description based on one of the five selected al-
gorithms and determine the nearest representative to
count the feature description in the corresponding bin
of the bag-of-features histogram. Finally, the bag-of-
features histogram is used as input vector for the SVM
of each object class and the best matching object class
is selected based on the SVM responses.
4 EVALUATION
In this section the evaluation of local 3-D feature de-
scriptors is presented in detail. Initially, the most ap-
propriate keypoint algorithm, the optimal size of a
bag-of-features histogram, and the best SVM training
parameters are determined. This is done in Subsec-
tion 4.1, 4.2, and 4.3. In these subsections, all pipeline
parameters are optimized to maximize the correct as-
signment of an object corresponding to object class C
to C. Subsequently, Subsection 4.4 merges these opti-
mizations to an overall classification. Subsection 4.5
examines the computation times required to classify
3-D point clouds this way.
4.1 SVM-parameters
A Gaussian radial basis function
K(x
i
, x
j
) = e
−γkx
i
−x
j
k
2
, γ > 0
requires the specification of a single parameter γ
which has to be determined depending on the data
which is used to train the support vector machine. Ad-
ditionally, the support vector machine requires a pa-
rameter C > 0, which is the penalty parameter of the
error term, i. e., a multiplier of the distance of mis-
classified samples to their region.
A Note on SVM Training Histograms:
The following subsections contain small SVM train-
ing histograms with the size of 4 × 4 bins. All these
histograms have the same axes and labels. To retain
readability, the axes and labels are not included for
each histogram. Instead, the labels and axes of all
histograms are shown only once in Figure 4. The val-
ues of C increase from left to right, while the values
of γ increase from top to bottom.
Figure 4: Axes and labels of all SVM training histograms
in this paper. C is the penalty parameter for misclassified
samples, γ is the parameter of the radial basis function.
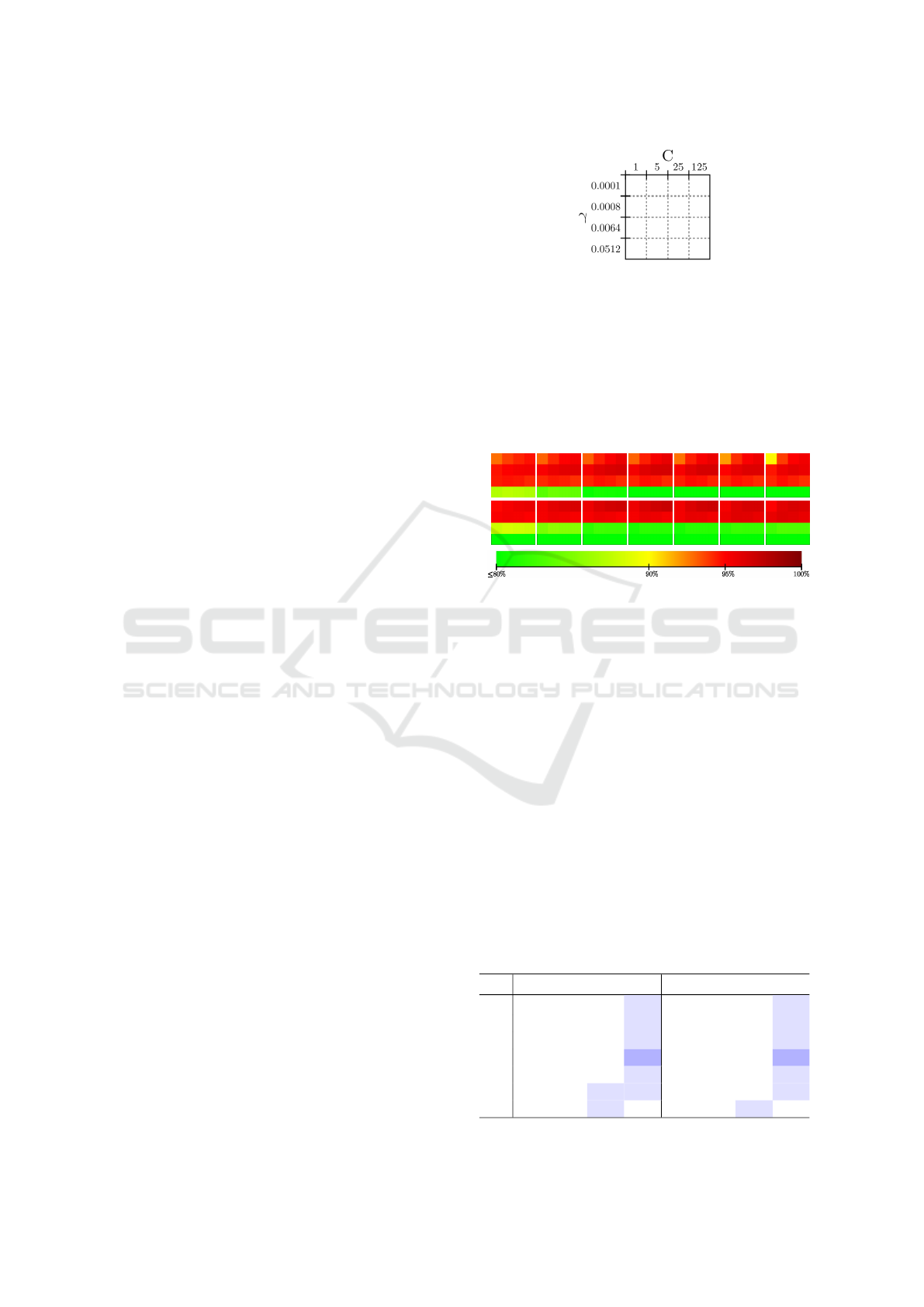
4.2 Sparse Sampling vs. ISS
To select the more appropriate keypoint algorithm, the
achieved classification rates for both methods, sparse
sampling and ISS, are compared.
10 20 50 100 200 500 1000
ISS keyp.sparse sam.
Figure 5: Mean binary classification rates of FPFH – com-
parison of ISS keypoints and sparse sampling (labels shown
in Figure 4). The color scale below the histograms indicates
the mean binary classification rates.
Figure 5 illustrates the mean binary classification
rates in excerpts for FPFH. Each column represents a
bag-of-features size. The upper row illustrates results
that can be achieved with keypoints determined by the
ISS algorithm, while the lower row contains the re-
sults based on sparse sampling. The mean binary clas-
sification rates for both methods have nearly the same
values shifted by one γ-step. In order to complement
the visual interpretation, Table 1 contains the values
for ISS with gamma = 0.008 (second row of each ISS
histogram) and sparse sampling with gamma = 0.001
(first row of each sparse sampling histogram).
Table 1: Binary classification results for FPFH that can be
achieved with ISS keypoints for γ = 0.0008 and sparse sam-
pling for γ = 0.0001. (Blue cells: max. value).
ISS keypoints sparse sampling
BoF C : 1 5 25 125 C : 1 5 25 125
10 94.66 95.09 95.34 95.47 94.88 95.38 95.68 95.84
20 95.22 95.75 96.04 96.15 95.51 96.06 96.37 96.56
50 95.45 96.12 96.48 96.58 95.67 96.33 96.74 96.90
100 95.46 96.18 96.57 96.65 95.65 96.44 96.92 97.14
200 95.29 96.11 96.56 96.62 95.54 96.33 96.82 97.04
500 94.97 95.91 96.30 96.30 95.32 96.21 96.56 96.66
1000 94.63 95.69 96.02 95.79 95.04 96.13 96.48 96.32
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
544
The differences in classification rates between ISS
and sparse sampling are always less than 0.5%. This
cannot be denoted as significant. For this reason, the
number of keypoints should be considered with re-
spect to the computation time. The average number
of approx. 355 keypoints per point cloud identified
by sparse sampling is more than two and a half times
higher, than the average number of approx. 132 key-
points determined by ISS. Accordingly, sparse sam-
pling will not be used due to the larger number of fea-
tures to be calculated.
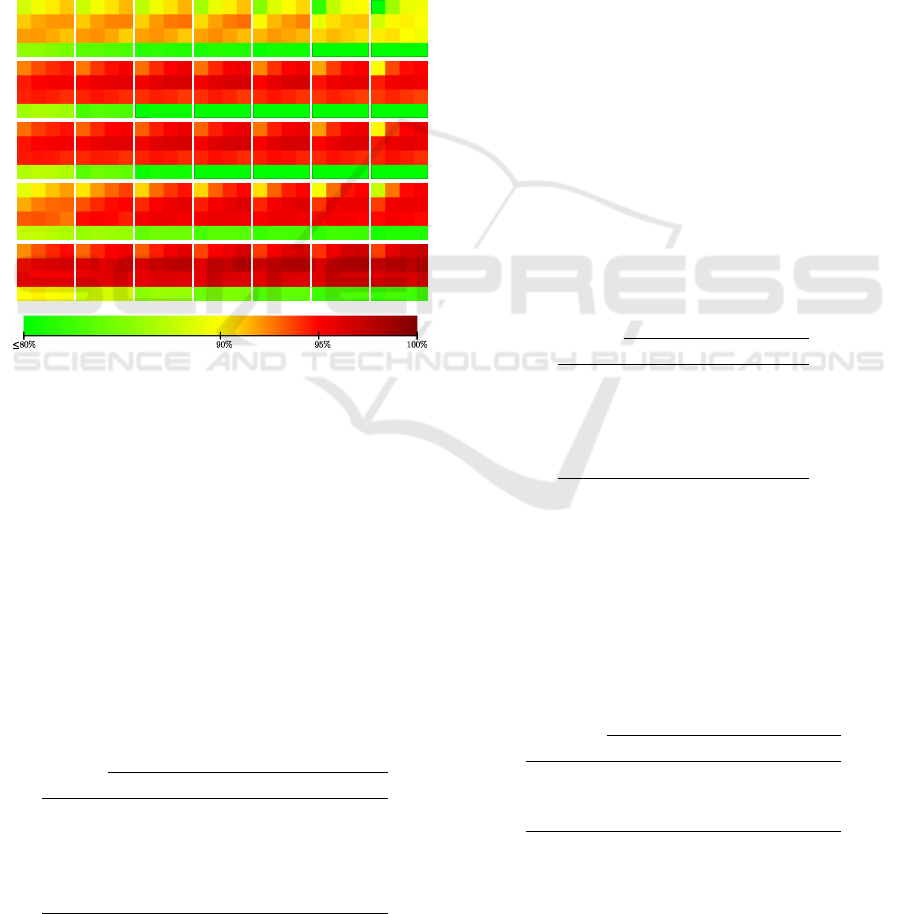
4.3 Local 3-D Feature Descriptors
10 20 50 100 200 500 1000
SI
PFHFPFH
SHOTUSC
Figure 6: Mean binary classification rates of all evaluated
local 3-D feature descriptors (labels shown in Figure 4).
The color scale below the histograms indicates the mean
binary classification rates.
Figure 6 illustrates the binary classification results
for different local 3-D feature descriptors. The low
classification results of SI are immediately apparent.
Additionally, the darkest shade of red indicating the
best classification results can be found for C = 125
(right column) and γ = 0.0008 (second row) of each
histogram. Table 2 summarizes the best configura-
tion of parameters for each of the evaluated local 3-D
feature descriptors, as well as the corresponding clas-
sification rates.
Table 2: Classification rate of the considered descriptors
with final set of pipeline parameters. (KP: keypoint algo-
rithm, BoF: size of bag-of-features).
KP BoF C γ rate
SI ISS 50 125 0.008 92.80%
PFH ISS 100 125 0.008 96.56%
FPFH ISS 100 125 0.008 96.65%
SHOT ISS 100 125 0.008 96.27%
USC ISS 200 125 0.008 97.62%
4.4 Overall Classification Results
The mean binary classification rates shown so far,
consider only how well an object corresponding to
object class C is correctly assigned to C. In prac-
tice, however, it is decisive how often an object cor-
responding to object class C is incorrectly assigned to
another objects class C
0
. This value is relatively high
due to the fact that the shapes of many objects are very
similar. Thus, the overall classification rate is by far
lagging behind the mean binary classification rate of
approx. 96%. In fact, an exact assignment (a point
cloud is only assigned to the correct object class and
all other SVMs reject the point cloud) can neither be
achieved considered all 51 object classes, nor while
using the subset of 10 object classes (see Section 3.1).
However, when choosing only that object class
where the corresponding SVM returns the highest
distance between the input vector (i. e., the bag-of-
features histogram) with respect to the separating hy-
perplane, the classification rates shown in Table 3 can
be achieved. Above that, the classification rates that
can be achieved for 10 object classes are only slightly
lower than those that were achieved by (Alexandre,
2012).
Table 3: Overall classification rates that can be achieved
considering the highest distance between the input vector
and the separating hyperplane for each SVM.
51 classes 10 classes
SI 7.4% 23.8%
PFH 6.0% 62.9%
FPFH 9.4% 65.0%
SHOT 3.6% 22.8%
USC 8.5% 59.7%
4.5 Computation Times
The computation times of the five local 3-D feature
descriptors may be of particular interest to select one
of these algorithms depending on the requirements.
Table 4 gives a brief overview of the system used for
all computations.
Table 4: System used for evaluation.
Configuration
CPU Intel Xeon E5630 @2.53GHz
Memory 12GB DDR3 @1066MHz
OS Debian 8.0 GNU/Linux 64bit
The average computation times to classify a 3-D
point cloud with one of the five local 3-D feature de-
scriptors are shown in Table 5. The values reflect the
Evaluation of Local 3-D Point Cloud Descriptors in Terms of Suitability for Object Classification
545

computation times that are required for classification.
The computation of keypoints, local 3-D feature vec-
tors, and bag-of-feature are not taken into account.
Table 5: Average classification times. The values indicate
the time to classify the bag-of-features histogram within
each SVM.
10 classes all 51 classes
SI ≈ 2.13ms ≈ 10.9ms
PFH ≈ 7.40ms ≈ 37.8ms
FPFH ≈ 2.29ms ≈ 11.7ms
SHOT ≈ 5.85ms ≈ 29.8ms
USC ≈ 3.40ms ≈ 17.3ms
Table 6 shows the mean computation times of a
single local 3-D feature description and a factor that
enables a quick comparison of the computation times
with respect to the fastest algorithm SI.
Table 6: Computation times of 3-D feature description al-
gorithms used within the experiments in ascending order.
The last column shows the factor with respect to the fastest
algorithm SI.
Time Factor
SI ≈ 0.045ms 1
SHOT ≈ 0.28ms ≈ 6
FPFH ≈ 6.69ms ≈ 150
USC ≈ 9.95ms ≈ 220
PFH ≈ 64.51ms ≈ 1430
5 DISCUSSION
Our evaluation of five local 3-D feature descriptors
with a focus on 3-D object classification shows, that
it is possible to achieve approx. 60% to 65% correct
class assignments with PFH, FPFH, and USC (cf. Ta-
ble 3). The two other algorithms, SI and the SHOT
achieve classification rates of only 22% and 23%.
In case of SI the mean binary classification rate of
92.80% is considerably lower compared to the other
algorithms. The reason for the bad results of SHOT
remains unclear. Considering the algorithms with re-
spect to the computation and classification times, SI
and SHOT are by far the fastest methods (cf. Table 5
and 6). However, the classification rates of these two
algorithms are so low that the two algorithms should
not be used in this context. Of the remaining three al-
gorithms FPFH is the fastest and best method, i. e., the
method with the highest classification rate at the same
time. However, considering the classification results
of all local 3-D feature descriptors in context of the
full test dataset using all 51 object classes (cf. Table 3)
it turns out that a classification of 3-D objects, that are
almost indistinguishable in terms of shape, is in fact
not possible. For this reason, the use of local 3-D
features can only be seen as a complement to color-
based object classification. This is in particular the
case when ambiguous textures or bad lighting condi-
tions complicate a color image based method.
6 CONCLUSION
Summarizing, the Fast Point Feature Histogram pro-
vides the best results in terms of computation time and
classification rate. However, it has to be taken into ac-
count that an object classification on the sole basis of
3-D representations only works when the classes are
sufficiently different.
REFERENCES
Aldoma, A., Marton, Z.-C., Tombari, F., Wohlkinger, W.,
Potthast, C., Zeisl, B., Rusu, R., Gedikli, S., and
Vincze, M. (2012a). Tutorial: Point cloud library:
Three-dimensional object recognition and 6 dof pose
estimation. Robotics Automation Magazine, IEEE,
19(3):80–91.
Aldoma, A., Tombari, F., Rusu, R. B., and Vincze, M.
(2012b). Our-cvfh–oriented, unique and repeat-
able clustered viewpoint feature histogram for ob-
ject recognition and 6dof pose estimation. In Pattern
Recognition, pages 113–122. Springer.
Alexandre, L. A. (2012). 3d descriptors for object and cate-
gory recognition: a comparative evaluation. In Work-
shop on Color-Depth Camera Fusion in Robotics at
the IEEE/RSJ International Conference on Intelligent
Robots and Systems (IROS), Vilamoura, Portugal.
Arbeiter, G., Fuchs, S., Bormann, R., Fischer, J., and Verl,
A. (2012). Evaluation of 3d feature descriptors for
classification of surface geometries in point clouds.
In 2012 IEEE/RSJ International Conference on In-
telligent Robots and Systems, IROS 2012, Vilamoura,
Algarve, Portugal, October 7-12, 2012, pages 1644–
1650.
Arthur, D. and Vassilvitskii, S. (2007). k-means++: The
advantages of careful seeding. In Proceedings of the
eighteenth annual ACM-SIAM symposium on Discrete
algorithms, pages 1027–1035. Society for Industrial
and Applied Mathematics.
Cholewa, M. and Sporysz, P. (2014). Classification of dy-
namic sequences of 3d point clouds. In Artificial Intel-
ligence and Soft Computing, pages 672–683. Springer.
Drost, B., Ulrich, M., Navab, N., and Ilic, S. (2010). Model
globally, match locally: Efficient and robust 3d object
recognition. In Computer Vision and Pattern Recogni-
tion (CVPR), 2010 IEEE Conference on, pages 998–
1005. IEEE.
Dutagaci, H., Cheung, C. P., and Godil, A. (2012). Eval-
uation of 3d interest point detection techniques via
ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics
546

human-generated ground truth. The Visual Computer,
28(9):901–917.
Filipe, S. and Alexandre, L. A. (2013). A comparative eval-
uation of 3d keypoint detectors. In 9th Conference on
Telecommunications, Conftele 2013, pages 145–148,
Castelo Branco, Portugal.
Frome, A., Huber, D., Kolluri, R., Bulow, T., and Malik,
J. (2004). Recognizing objects in range data using
regional point descriptors. In Proceedings of the Eu-
ropean Conference on Computer Vision (ECCV).
Guo, Y., Bennamoun, M., Sohel, F., Lu, M., and Wan,
J. (2014). 3d object recognition in cluttered scenes
with local surface features: A survey. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
36(11):2270–2287.
Heider, P., Pierre-Pierre, A., Li, R., and Grimm, C. (2011).
Local shape descriptors, a survey and evaluation. In
Proceedings of the 4th Eurographics conference on
3D Object Retrieval, pages 49–56. Eurographics As-
sociation.
Johnson, A. and Hebert, M. (1999). Using spin images for
efficient object recognition in cluttered 3d scenes. Pat-
tern Analysis and Machine Intelligence, IEEE Trans-
actions on, 21(5):433–449.
Johnson, A. E. and Hebert, M. (1998). Surface matching
for object recognition in complex three-dimensional
scenes. Image and Vision Computing, 16(9):635–651.
Kim, H. and Hilton, A. (2013). Evaluation of 3d feature de-
scriptors for multi-modal data registration. In 2013 In-
ternational Conference on 3D Vision, 3DV 2013, Seat-
tle, Washington, USA, June 29 - July 1, 2013, pages
119–126.
Knopp, J., Prasad, M., Willems, G., Timofte, R., and
Van Gool, L. (2010). Hough transform and 3d surf for
robust three dimensional classification. In Computer
Vision–ECCV 2010, pages 589–602. Springer.
Lai, K., Bo, L., Ren, X., and Fox, D. (2011). A large-
scale hierarchical multi-view rgb-d object dataset. In
Robotics and Automation (ICRA), 2011 IEEE Interna-
tional Conference on, pages 1817–1824. IEEE.
Lian, Z., Godil, A., Bustos, B., Daoudi, M., Hermans, J.,
Kawamura, S., Kurita, Y., Lavou
´
e, G., Van Nguyen,
H., Ohbuchi, R., et al. (2011). Shrec’11 track: Shape
retrieval on non-rigid 3d watertight meshes. 3DOR,
11:79–88.
Madry, M., Afkham, H. M., Ek, C. H., Carlsson, S., and
Kragic, D. (2013). Extracting essential local object
characteristics for 3d object categorization. In Intelli-
gent Robots and Systems (IROS), 2013 IEEE/RSJ In-
ternational Conference on, pages 2240–2247. IEEE.
Madry, M., Ek, C. H., Detry, R., Hang, K., and Kragic, D.
(2012). Improving generalization for 3d object cate-
gorization with global structure histograms. In Intelli-
gent Robots and Systems (IROS), 2012 IEEE/RSJ In-
ternational Conference on, pages 1379–1386. IEEE.
Rusu, R., Blodow, N., and Beetz, M. (2009). Fast point fea-
ture histograms (fpfh) for 3d registration. In Robotics
and Automation, 2009. ICRA ’09. IEEE International
Conference on, pages 3212–3217.
Rusu, R. B. (2010). Semantic 3d object maps for every-
day manipulation in human living environments. KI-
K
¨
unstliche Intelligenz, 24(4):345–348.
Rusu, R. B., Blodow, N., Marton, Z. C., and Beetz, M.
(2008a). Aligning point cloud views using persistent
feature histograms. In Intelligent Robots and Systems,
2008. IROS 2008. IEEE/RSJ International Conference
on, pages 3384–3391. IEEE.
Rusu, R. B., Marton, Z. C., Blodow, N., and Beetz, M.
(2008b). Learning informative point classes for the
acquisition of object model maps. In Control, Automa-
tion, Robotics and Vision, 2008. ICARCV 2008. 10th
International Conference on, pages 643–650. IEEE.
Salti, S., Tombari, F., and Stefano, L. D. (2011). A per-
formance evaluation of 3d keypoint detectors. In
3D Imaging, Modeling, Processing, Visualization and
Transmission (3DIMPVT), 2011 International Con-
ference on, pages 236–243. IEEE.
Salti, S., Tombari, F., and Stefano, L. D. (2014). Shot:
Unique signatures of histograms for surface and tex-
ture description. Computer Vision and Image Under-
standing, 125(0):251 – 264.
Seib, V., Christ-Friedmann, S., Thierfelder, S., and Paulus,
D. (2013). Object class and instance recognition on
rgb-d data. In Sixth International Conference on Ma-
chine Vision (ICMV 13), pages 90670J–90670J. Inter-
national Society for Optics and Photonics.
Tang, S. and Godil, A. (2012). An evaluation of lo-
cal shape descriptors for 3d shape retrieval. CoRR,
abs/1202.2368.
Toldo, R., Castellani, U., and Fusiello, A. (2009). A bag of
words approach for 3d object categorization. In Com-
puter Vision/Computer Graphics CollaborationTech-
niques, pages 116–127. Springer.
Toldo, R., Castellani, U., and Fusiello, A. (2010). The bag
of words approach for retrieval and categorization of
3d objects. The Visual Computer, 26(10):1257–1268.
Tombari, F., Salti, S., and Di Stefano, L. (2010a). Unique
shape context for 3d data description. In Proceedings
of the ACM workshop on 3D object retrieval, pages
57–62. ACM.
Tombari, F., Salti, S., and Di Stefano, L. (2010b). Unique
signatures of histograms for local surface descrip-
tion. In Computer Vision–ECCV 2010, pages 356–
369. Springer.
Wu, C.-C. and Lin, S.-F. (2011). Efficient model detection
in point cloud data based on bag of words classifica-
tion. Journal of Computational Information Systems,
7(12):4170–4177.
Yi, Y., Guang, Y., Hao, Z., Meng-Yin, F., and Mei-ling,
W. (2014). Object segmentation and recognition in 3d
point cloud with language model. In Multisensor Fu-
sion and Information Integration for Intelligent Sys-
tems (MFI), 2014 International Conference on, pages
1–6. IEEE.
Zhong, Y. (2009). Intrinsic shape signatures: A shape de-
scriptor for 3d object recognition. In Computer Vision
Workshops (ICCV Workshops), 2009 IEEE 12th Inter-
national Conference on, pages 689–696. IEEE.
Evaluation of Local 3-D Point Cloud Descriptors in Terms of Suitability for Object Classification
547
