
A Convex Approach for Non-rigid Structure from Motion Via Sparse
Representation
Junjie Hu
1
and Terumasa Aoki
1,2
1
Graduate School of Information Sciences (GSIS), Tohoku University, Aramaki Aza Aoba 6-3-9, Aoba-ku, Sendai, Japan
2
New Industry Creation Hatchery Center (NICHe), Tohoku University, Aramaki Aza Aoba 6-6-10, Aoba-ku, Sendai, Japan
Keywords:
Non-rigid Structure From Motion, Sparse Representation, l1-norm Minimization.
Abstract:
This paper presents a convex solution for simultaneously recovering 3D non-rigid structures and camera mo-
tions from 2D image sequences based on sparse representation. Most existing methods rely on low rank as-
sumption. However, it will lead to poor reconstruction for objects with strong local deformation. Also, when
camera motion is unknown, there is no convex solution for non-rigid structure from motion (NRSfM). In order
to solve this problem, we estimate non-rigid structures by sparse representation. In this paper, we estimate
camera motions through a sparse spectral-norm minimization approach, and then a fast l1-norm minimization
algorithm is introduced to reconstruct 3D structures. Both of them are convex, therefore, our method gives
a global optimum. Our method can handle objects with strong local deformation and also doesn’t need low
rank prior. Experimental results show that our method achieves state-of-the-art reconstruction performance on
CMU benchmark dataset.
1 INTRODUCTION
Structure from Motion (SfM) is a well-known tech-
nology to simultaneously recover 3D structures and
camera motions of a rigid object from 2D correspond-
ing points. Although there are still some open prob-
lems such as real-time reconstruction, point match-
ing, large scale and dense reconstructions, the theory
has been well established over the past two decades
(Carlo and Kanade, 1992). Non-rigid Structure from
Motion (NRSfM) is an extension of SfM for non-rigid
objects. It’s also a fundamental problem in computer
vision. During the past decade, it has attracted lots of
researches and many different algorithms have been
proposed. However, there are still some problems to
be unsolved. The difficulty is mainly caused by the
inherently high number of degrees of freedom. For
rigid objects, the rigidity prior is enough to make the
problem well posed because well-known multi-view
relations are valid. However, this prior is not valid
for non-rigid deformable objects. For time-varying
observed 2D points, to obtain the corresponding 3D
points becomes ill posed.
Most existing methods have been attempted to
solve NRSfM by using additional constraints. For
instance, some approaches assume that the 3D non-
rigid structures can be modeled as a linear combi-
nation of several predefined bases of shapes (Bre-
gler et al., 2000; Torresani et al., 2008; Xiao et al.,
2004). Also, other approaches attempt to represent a
3D point trajectory by using a fixed set of discrete co-
sine transform (DCT) trajectory bases (Akhter et al.,
2008; Gotardo and Martinez, 2011; Park et al., 2010).
It also has been shown that it is a dual representation
to shape representation (Akhter et al., 2011). Gatardo
et al. combined these two concepts and proposed
an efficient method that recover the trajectory using
DCT bases in a linear shape space (Gotardo and Mar-
tinez, 2011). Besides, Dai et al. proposed a well-
known rank minimization approach which minimizes
the rank of 3D structures based on nuclear minimiza-
tion algorithm and achieves one of the most remark-
able performance (Dai et al., 2014). The nuclear min-
imization based approaches then were also used to re-
construct 3D structures from realistic videos (Fragki-
adaki et al., 2014; Garg et al., 2013). These linear
representation based methods can achieve better re-
construction performance for some objects with small
deformation, but it is unable to handle strong defor-
mations such as complex human motions. Another
problem of these methods is that the number of bases
must be predefined accurately, because the improper
number of bases will largely degrade the algorithm’s
performance. Unfortunately, the simple way to find
Hu J. and Aoki T.
A Convex Approach for Non-rigid Structure from Motion Via Sparse Representation.
DOI: 10.5220/0006078603330339
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 333-339
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
333

Figure 1: Illustration of the basic idea studied in this paper. The non-rigid 3D shape is represented as a linear combination of
some predefined shape bases via sparse representation. We try to find out a convex solution to estimate the sparse coefficients
of the shape bases.
the optimal number of bases has not been discovered,
so we have to repeat numerous experiments to esti-
mate it.
The above limitations of existing methods
prompted us to think in another way. We thought
that the objects with complex deformation need to
be modeled by using more better bases of shapes or
trajectory. In order to avoid the problem of the esti-
mation of basis number, in this paper, we formulate
NRSfM as a sparse l1-norm minimization problem.
The 3D non-rigid structure is represented as a linear
combination of shape bases in the dictionary. One
benefit of using shape basis is it allows to recover 3D
object in a sequential way which has recently been
paid many attentions (Agudo et al., 2014; Agudo and
Moreno-Noguer, 2015; Paladini et al., 2010). Due
to the fact that camera motion is unknown, the tradi-
tional sparse l1-norm minimization approach is non-
convex. Recently, Zhou et al. proposed a convex
approach to estimate camera motion based on sparse
spectral-norm minimization (Zhou et al., 2015) which
encourages us to solve sparse l1-norm minimization
problem in a convex way. As the fact that we learn
the better shape bases through dictionary learning
technique, our method can handle the objects with
complex deformation. Comparing to Zhu’s trajectory
learning method (Zhu and Lucey, 2015), our method
gives a convex solution to camera motion and also al-
lows to recover 3D structures in a sequential way. Ex-
periments demonstrate that our method could achieve
much more accurate reconstruction performance than
several existing well-known algorithms.
2 PREVIOUS WORKS
2.1 Batch Approaches
Batch approaches need to leverage the information of
all frames. After tracking 2D points over all frames,
these methods recover camera motions and 3D shapes
from 2D measurements. It can be represented as:
W = RS
s.t. R
f
R
T
f
= I
(1)
where R ∈ R
2F×3F
is the orthographic camera mo-
tion, and R
f
denotes the camera motion of f -th frame.
S ∈ R
3F×P
is the 3D non-rigid shapes matrix. W
∈ R
2F×P
, is the projections of S in a set of 2D images.
Due to the inherently high number of degrees of free-
dom, additional constraint is required to recover S,
such as modeling the 3D shapes as a linear combina-
tion of several predefined bases of shapes:
W = RCB (2)
where B and C denote the predefined shape bases
and the weight of these bases, respectively. Instead
of using predefined shape bases or trajectory bases,
Dai et al. (Dai et al., 2014) formulate the following
rank minimization problem based on the assumption
of representing 3D shapes in a low rank space which
is convex and can be solved efficiently by minimizing
the nuclear-norm which is its convex approximation:
min rank(S)
s.t. W = RS
(3)
By such additional constraint, the non-rigid shape
can be recovered exactly. Apparently, it is necessary
to recover camera motions firstly. It has been proved
that the camera motion can be recovered uniquely and
accurately in a batch way only by using orthonormal-
ity constraints(Akhter et al., 2008; Dai et al., 2014).
But the camera motion can not be recovered for com-
plex deformable objects because the small deforma-
tion condition is essential for the recovery of camera
motion according to (Yezzi and Soatto, 2003; Zhang
and Hung, 2015).
2.2 Sequential Approaches
Sequential approaches recover 3D shape and camera
motion per frame. It can be represented as:
F
∑
f =1
W
f
= R
f
S
f
s.t. R
f
R
T
f
= I
(4)
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
334

where F denotes the total number of frames. S
f
,
W
f
are 3D shape and its 2D projection points for
f -th frame respectively. In order to solve the above
ill-posed problem, usually, camera motion and shape
deformation are considered to be smooth. Besides,
many additional conditions are also put to constrain
the deformation (Agudo et al., 2014; Agudo and
Moreno-Noguer, 2015; Paladini et al., 2010). The 3D
shape and camera motion can be solved by minimiz-
ing the following energy function:
min
R
f
,S
f
F
∑
f =1
||W
f
− R
f
S
f
||
2
F
+ λ||R
f
− R
f −1
||
2
F
+µ||S
f
− S
f −1
||
2
F
(5)
where ||.||
F
denotes the Frobenius norm of matrix.
This optimization function is nonconvex and usually
it is solved by an alternating scheme (algorithm 1).
To date, in spite of all the efforts, the reconstruction
performance of sequential approaches is still not good
comparing with batch methods.
Algorithm 1: Sequential non-rigid structure from motion.
Input:
2D observations per frame W
f
Output:
camera motion R
f
and 3D non-rigid shape S
f
for each
frame
1: Initialize R
f
and S
f
;
2: while not converged do
3: update S
f
;
4: update R
f
;
5: end while
3 PROPOSED METHOD
Although small deformations can be modeled accu-
rately by a set of predefined shape bases or trajectory
bases, more sufficient bases should be prepared for
handling complex or strong deformations. It has been
shown that complex deformation can be modeled in
a nonlinear shape manifold (Tao and Matuszewski,
2013). Such nonlinear shape manifold can be approx-
imated well by sparse representation. Thus, in this
paper, we model the 3D non-rigid shape using a over-
complete dictionary. Such dictionary represents lots
of shape bases that learned from training data. As the
choice of bases is extremely important for NRSfM,
good basis should be assigned large weight; on the
other hand, bad basis should be abandoned. Thus, a
sparse solution is promising. Our method can be for-
mulated as the following optimization problem:
min
C
1
2
||W
f
− R
f
K
∑
i=1
C
i
B
i
||
2
F
+ λ||C||
1
(6)
where K is the total number of shape basis. B
i
,C
i
rep-
resent the i-th shape basis in dictionary and its weight,
respectively. C is a vector contains the weight of each
shape basis C
i
. ||.||
1
denotes the l1-norm of vector
which is a convex relaxation of l0-norm minimiza-
tion. However, when R is unknown, the above mini-
mization problem is nonconvex. A common strategy
to solve Eq. (6) is to use the alternating scheme as de-
scribed in algorithm 1. However, the algorithm is not
convex, thus it may get stuck at local minimum. In
this paper, we aim at solving the above optimization
problem in a convex way; the steps of our algorithm
are summarized in algorithm 2.
3.1 Camera Motion Estimation
The first task in our method is to estimate camera mo-
tion R accurately. Although Dai et al. introduced a
convex approach to recover R by semi-definite pro-
gramming (SDP). Their method recovers R in a batch
way and still need to be predefined the number of
rank, so it can’t be employed to solve sequential
NRSfM. Therefore, we have to find an efficient solu-
tion to recover camera motion sequentially. As proved
in (Zhou et al., 2015), for each M
i
= R
f
C
i
, because
of the orthonormality of R:
M
i
M
T
i
= C
2
i
I (7)
such that:
||M
i
||
2
≤ |C
i
| (8)
where M
i
is a 2 × 3 matrix which contains camera
motion R
f
with weight of i-th shape basis. It’s a con-
vex relaxation to the constraint in Eq. (7), where ||.||
2
denotes the spectral-norm of matrix. Instead of solv-
ing Eq. (6), [16] introduced to solve the following
spectral-norm minimization problem:
min
M
i
1
2
||W
f
−
K
∑
i=1
M
i
B
i
||
2
F
+ λ||M||
2
(9)
Minimizing the above optimization function gives a
convex solution to M
i
and it can be solved efficiently
based on the algorithm of (Zhou et al., 2015). Next,
we solve the following bilinear factorization problem
to get R by the factorization algorithm of (Del Bue
et al., 2012).
min
R,C
i
||M − R
f
C||
2
F
s.t. R
f
R
T
f
= I
(10)
3.2 3D Shape Estimation
After recovering camera motion R, we will estimate
3D shape. The above spectral-norm minimization ap-
proach Eq. (9) and bilinear factorization algorithm
A Convex Approach for Non-rigid Structure from Motion Via Sparse Representation
335

Figure 2: Visualization of global optimum for l1-norm min-
imization.
Eq. (10) have already given a solution to camera mo-
tion R as well as the weights of shape bases C, it is
expected that if we can solve the original convex prob-
lem Eq. (6) we can achieve more accurate reconstruc-
tion performance. As seen in Figure 2, solving l1-
norm convex relaxation problem (spectral minimiza-
tion) can give a convex solution for camera motion R,
and when R is known, we solve the original sparse l1-
norm minimization problem Eq. (6) and find a global
optimum for NRSfM by using a fast l1-norm mini-
mization algorithm (Lee et al., 2006). The final de-
formable 3D shape is represented as:
S
f
=
K
∑
i=1
C
i
B
i
(11)
3.3 Shape Bases Learning
There are lots of dictionary learning algorithms. A
common strategy is to solve the following minimiza-
tion function:
min
B,L
1
2
F
∑
f =1
||S
f
−
K
∑
i=1
L
i
B
i
||
2
F
+ β||L||
1
s.t. ||B
i
||
F
≤ 1
(12)
where S
f
, B
i
, L
i
denote the f -th shape of training data,
a shape basis in the dictionary and its weight respec-
tively. The learned shape bases need to concisely rep-
resent the variability of training data. We use the al-
gorithm used in (Zhou et al., 2015) to learn our dic-
tionary.
Algorithm 2 : Convex sparse l1-norm minimization algo-
rithm for NRSfM.
Input:
2D observations per frame W
f
and shape bases dictio-
nary B
Output:
camera motion R
f
and 3D non-rigid shape S
f
for each
frame
1: Calculate M
f
by Eq. (9);
2: Recover camera motion R
f
by Eq. (10);
3: Estimate the weight C
i
of each shape basis in dictionary
by Eq. (11);
4: return S
f
=
∑
K
i=1
C
i
B
i
4 EXPERIMENTAL RESULTS
In this section, we compare our method against the
trajectory basis method (PTA) (Akhter et al., 2008),
Dai’s rank minimization method (BMM) (Dai et al.,
2014), and Zhou’s sparse spectral-norm minimization
method (Zhou et al., 2015) on the CMU motion cap-
ture database (Carnegie mellon university, ). This
database provides 41 landmark positions correspond-
ing to human motions. We selected five human mo-
tions with strong local deformations (Walking, Run-
ning, Jumping, Pickup, Marching) from this database.
For each motion, we selected three sequences as train-
ing data and one sequence for testing from the same
motion subject. For each testing data, we generated
2D projections of the 3D markers with the synthe-
sized orthographic camera around the subject for 360
degrees with the angle speed 5 per frame.
The size of the dictionary is set as 300. Since
PTA and BMM rely on low rank assumption, we set
the number of their low rank parameter from 3 to 13
and reported the best result. To compare the perfor-
mances, we measured the average 3D reconstruction
error using the same error metric as PTA and BMM
as follows:
e
3D
=
1
σFn
F
∑
f =1
N
∑
n=1
e
f n
, σ =
1
3F
F
∑
f =1
(σ
f
x + σ
f
y + σ
f
z)
(13)
Figure 3: From first row to last row: 3D shape of Walking,
Jumping, Marching and Pickup in 3 views recovered by the
proposed method, respectively. Recovered shapes are blue
circles and ground truth is dark dots.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
336

Table 1: Average 3D reconstruction error of PTA, BMM, Zhou’s method and proposed method. (K) denotes the rank number
which gave the smallest 3D error.
Dataset PTA(K) BMM(K) Zhou’s method Proposed method
Walking 0.1197(8) 0.1001(4) 0.0666 0.0394
Running 0.4212(3) 0.1638(5) 0.1093 0.0706
Jumping 0.2086(13) 0.1395(12) 0.1111 0.0728
Marching 0.1414(12) 0.1323(9) 0.1385 0.0731
Pickup 0.1211(13) 0.1412(12) 0.1163 0.0706
Figure 4: From first row to last row: One view of 3D shapes of Running recovered by PTA, BMM, zhou’s method and the
proposed method, respectively. Recovered shapes are blue circles and ground truth is dark dots.
where σ
f
x, σ
f
y and σ
f
z are the standard deviations
of the X, Y and Z coordinates of the original shape in
frame f.
Table 1 shows the average 3D reconstruction er-
ror of different methods. It is seen that the pro-
posed method achieved the best performance on each
data. Figure 3 shows the 3 views of the reconstructed
shapes of Walking, Jumping, Marching, Pickup by
the proposed method. It is clear that our sparse l1-
norm minimization approach achived very accurate
reconstruction performance. Figure 4 shows the vi-
sual comparison between our method and other ap-
proaches on Running. Our method reconstructed the
legs (which is strongly deformed part of Running)
precisely than others. Also, Figure 5 (a) shows the
impact of the low rank to PTA and BMM while vary-
ing K on Running, this result proved that the per-
formance of low rank based methods largely rely on
the proper number of K. Figure 5 (b) shows the re-
sults of the proposed method with different size of
dictionary on Running. It can be observed that the
3D error decreases when the size of the dictionary in-
creases. In conclusion, experimental results show that
our method can handle non-rigid objects with strong
local deformation much better than several current
low rank based methods and Zhou’s sparse spectral-
norm minimization method. Since we don’t use the
time smoothness constraint, one more benefit of the
proposed method is that it can be easily paralleled.
5 CONCLUSION
In this paper, we presented a convex solution for
NRSfM based on sparse representation. It does not
rely on low rank assumption and can reconstruct 3D
A Convex Approach for Non-rigid Structure from Motion Via Sparse Representation
337
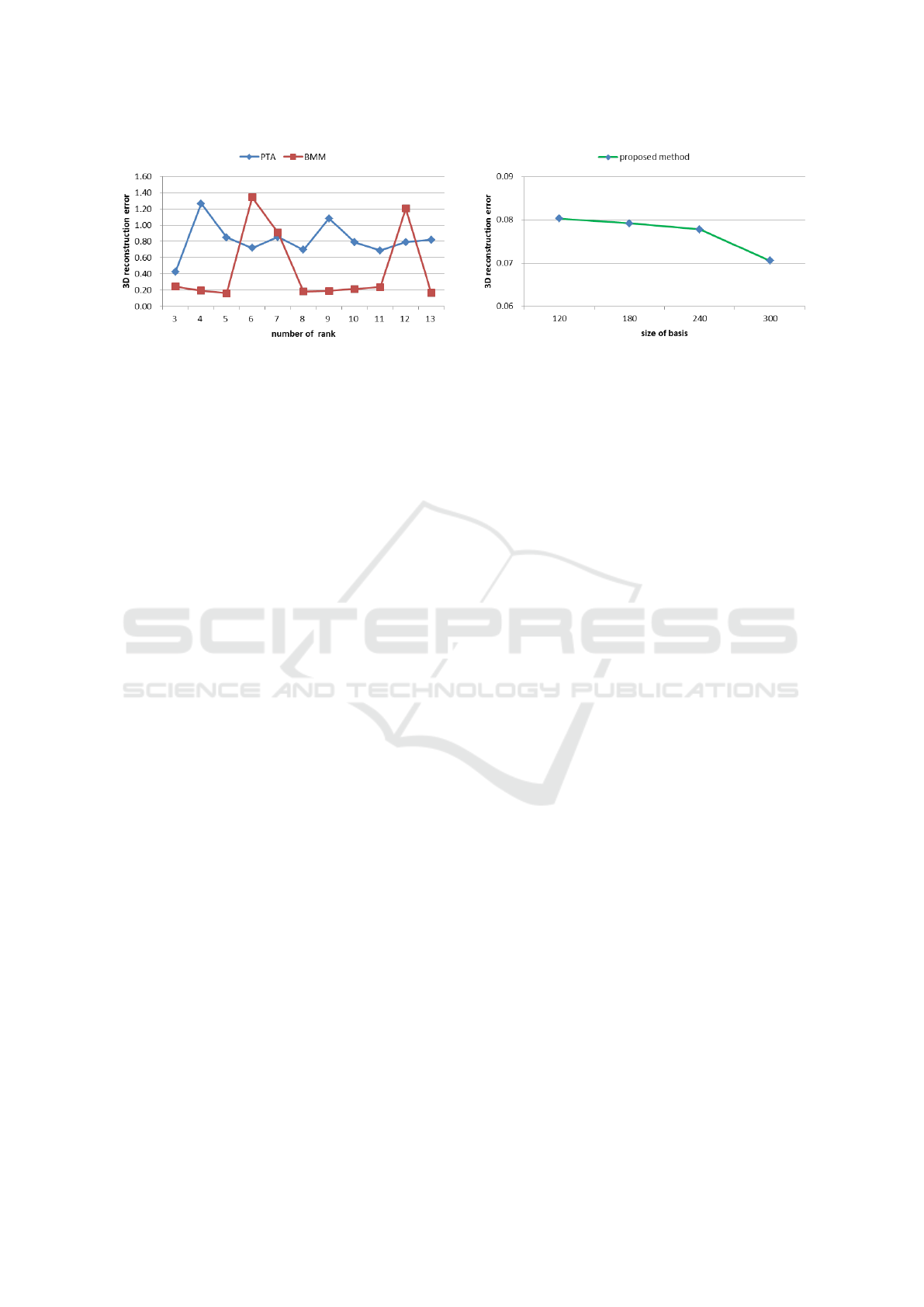
(a) (b)
Figure 5: The comparison of 3D reconstruction error between low rank based methods PTA , BMM with different rank and
our method with different dictionary size on Running.
shapes in a sequential way. As a result, we showed
that our method achieved the best reconstruction per-
formance on CMU database against several existing
methods. Unlike the low rank based methods such as
BMM and PTA, increasing the number of bases will
reduce reconstruction error for our method. We be-
lieve that our method is a reasonable choice for solv-
ing NRSfM when training data is available.
REFERENCES
Agudo, A., Agapito, L., Calvo, B., and Montiel, J. (2014).
Good vibrations: A modal analysis approach for se-
quential non-rigid structure from motion. In Proceed-
ings of the IEEE Conference on Computer Vision and
Pattern Recognition, pages 1558–1565.
Agudo, A. and Moreno-Noguer, F. (2015). Simultaneous
pose and non-rigid shape with particle dynamics. In
Proceedings of the IEEE Conference on Computer Vi-
sion and Pattern Recognition, pages 2179–2187.
Akhter, I., Sheikh, Y., Khan, S., and Kanade, T. (2008).
Nonrigid structure from motion in trajectory space. In
Advances in neural information processing systems,
pages 41–48.
Akhter, I., Sheikh, Y., Khan, S., and Kanade, T. (2011).
Trajectory space: A dual representation for nonrigid
structure from motion. Pattern Analysis and Machine
Intelligence, IEEE Transactions on, 33(7):1442–
1456.
Bregler, C., Hertzmann, A., and Biermann, H. (2000). Re-
covering non-rigid 3d shape from image streams. In
Computer Vision and Pattern Recognition, 2000. Pro-
ceedings. IEEE Conference on, volume 2, pages 690–
696. IEEE.
Carlo, T. and Kanade, T. (1992). Shape and motion from
image streams under orthography: a factorization
method. International Journal of Computer Vision,
9(2):137–154.
Carnegie mellon university, . Cmu graphics lab motion cap-
ture database. http://mocap.cs.cmu.edu/.
Dai, Y., Li, H., and He, M. (2014). A simple prior-
free method for non-rigid structure-from-motion fac-
torization. International Journal of Computer Vision,
107(2):101–122.
Del Bue, A., Xavier, J., Agapito, L., and Paladini, M.
(2012). Bilinear modeling via augmented lagrange
multipliers (balm). Pattern Analysis and Machine In-
telligence, IEEE Transactions on, 34(8):1496–1508.
Fragkiadaki, K., Salas, M., Arbelaez, P., and Malik, J.
(2014). Grouping-based low-rank trajectory comple-
tion and 3d reconstruction. In Advances in Neural In-
formation Processing Systems, pages 55–63.
Garg, R., Roussos, A., and Agapito, L. (2013). Dense
variational reconstruction of non-rigid surfaces from
monocular video. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 1272–1279.
Gotardo, P. F. and Martinez, A. M. (2011). Non-rigid struc-
ture from motion with complementary rank-3 spaces.
In Computer Vision and Pattern Recognition (CVPR),
2011 IEEE Conference on, pages 3065–3072.
Lee, H., Battle, A., Raina, R., and Ng, A. Y. (2006). Effi-
cient sparse coding algorithms. In Advances in neural
information processing systems, pages 801–808.
Paladini, M., Bartoli, A., and Agapito, L. (2010). Sequential
non-rigid structure-from-motion with the 3d-implicit
low-rank shape model. In Computer Vision–ECCV
2010, pages 15–28. Springer.
Park, H. S., Shiratori, T., Matthews, I., and Sheikh, Y.
(2010). 3d reconstruction of a moving point from a
series of 2d projections. In ECCV, pages 158–171.
Tao, L. and Matuszewski, B. (2013). Non-rigid structure
from motion with diffusion maps prior. In Proceed-
ings of the IEEE Conference on Computer Vision and
Pattern Recognition, pages 1530–1537.
Torresani, L., Hertzmann, A., and Bregler, C. (2008).
Nonrigid structure-from-motion: Estimating shape
and motion with hierarchical priors. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
30(5):878–892.
Xiao, J., Chai, J., and Kanade, T. (2004). A closed-form
solution to non-rigid shape and motion recovery. In
ECCV, pages 573–587.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
338

Yezzi, A. J. and Soatto, S. (2003). Deformotion: Deforming
motion, shape average and the joint registration and
approximation of structures in images. International
Journal of Computer Vision, 53(2):153–167.
Zhang, P. B. and Hung, Y. S. (2015). Non-rigid struc-
ture from motion through estimation of blend shapes.
In Digital Image Computing: Techniques and Appli-
cations (DICTA), 2015 International Conference on,
pages 1–7. IEEE.
Zhou, X., Leonardos, S., Hu, X., and Daniilidis, K. (2015).
3d shape estimation from 2d landmarks: A convex re-
laxation approach. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 4447–4455.
Zhu, Y. and Lucey, S. (2015). Convolutional sparse cod-
ing for trajectory reconstruction. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
37(3):529–540.
A Convex Approach for Non-rigid Structure from Motion Via Sparse Representation
339
