
Paraconsistent Logic with Multiple Fuzzy Linguistic Truth-values
Manren Wang
1
and Xudong Luo
2,
*
1
Department of Philosophy (Zhuhai), Sun Yat-sen University, Zhuhai, China
2
Institute of Logic and Cognition, Department of Philosophy, Sun Yat-sen University, Guangzhou, China
Keywords:
Knowledge Presentation and Reasoning, Uncertainty in AI, Soft Computing, Paraconsistent Logic, Fuzzy
Logic, Multi-valued Logic, Linguistic Truth-value.
Abstract:
This paper extends the two-valued paraconsistent logic into an one in which a proposition takes a truth-value
from a set of multiple fuzzy linguistic terms. More specifically, we propose the corresponding inference
rule and semantics, and finally prove the soundness of our new fuzzy logical system and its completeness.
Moreover, we use an example to illustrate the applicability of our logic system in real life.
1 INTRODUCTION
Paraconsistent logic is a branch of non-classical
logic in which the inconsistency can be accepted
but the contradiction cannot imply any proposition
(Da Costa, 1958; Da Costa et al., 1995; Akama and
Da Costa, 2016) (while in a classic logic system, the
contradiction can imply any proposition). Paraconsis-
tent logic is very useful (Priest et al., 1989; Tanaka
et al., 2012; Abe, 2016). In fact, its basic idea can be
applied to other kinds of logic system like paraconsis-
tent relevant logic (Kamide, 2013, 2016) and paracon-
sistent deontic logic (Costa and Carnielli, 1986). Also
it is very useful in artificial intelligence. For exam-
ple, when an expert system cannot deal with contrary
options of different experts, the way in which para-
consistent logic cope with inconsistence will be so
helpful to cope with the issue. Because of the trait of
holding contradictions, paraconsistent logic will push
forward the development of artificial intelligence to a
new stage and inject energy constantly.
As paraconsistent logic, fuzzy logic (Zadeh, 1965,
1983, 1996) is widely applied as well (Yager and
Zadeh, 1992; Zhan et al., 2014). The main idea be-
hind fuzzy logic is using fuzzy sets and fuzzy in-
ference rules to simulate the synthetic reasoning of
human mind. It is so accordant with human mind’s
customary vague thinking that it has been applied to
many aspects of our life, such as the control systems
of air conditioning, washing machine, robot, and so
on.
*
The corresponding author
Lots of studies about fuzzy temporal logic
(Mukherjee and Dasgupta, 2013; Poli, 2015) and
fuzzy modal logic (Vidal et al., 2015; Jing et al., 2014)
have already done, but not many are on fuzzy para-
consistent logic. Turunen et al. (2010) firstly link
paraconsistent logic and fuzzy logic together by in-
troducing the paraconsistent semantics for Pavelka
style fuzzy sentential logic. They emphasise that they
do not introduce a new non-classical logic but intro-
duce paraconsistent semantics of Pavelka style fuzzy
sentential logic based on Balnap’s four valued para-
consistent logic and Lukasiewicz Pavelka’s logic sys-
tem. Rodrguez et al. (2014) went further to intro-
duce another paraconsistent algebraic semantics for
Lukasiewicz-Pavelka logic and remove some limita-
tions of their work in 2010. Although their work is
very significant, they only dealt with the theoretical
aspect, but did not show the practical value of their
theory. In addition, they just unidirectionally con-
struct a paraconsistent semantic for fuzzy logic. In
the opposite direction of their research (i.e., constuct-
ing a fuzzy semantic for paraconsistent logic), they
did not get involved. Arnon (2014) introduced proof
systems and semantics for two paraconsistent exten-
sions of the system T of Anderson et al. (1978), and
prove strong soundness, completeness, and decidabil-
ity for both in his article. The semantics of both sys-
tems is based on excluding just one element from the
set of designated values.
The basic idea behind fuzzy logic can be applied
in other kinds of logic, so a new fuzzy semantic can
be born. In fact, based on the classical intuitionistic
logic, Turunen (1992) developed a kind of fuzzy in-
Wang M. and Luo X.
Paraconsistent Logic with Multiple Fuzzy Linguistic Truth-values.
DOI: 10.5220/0006117200530062
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 53-62
ISBN: 978-989-758-220-2
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
53

tuitionistic logic. Though he did not use the term of
Zadeh’s fuzzy set, he used exactly the same thought
as Zadeh. He also believed that the truth-value of a
proposition should be in a finite set rather than a bi-
nary set with 0 and 1. Thiele and Kalenka (1993)
introduced fuzzy temporal logic based on the clas-
sical two-valued temporal logic. Moon et al. (2004)
introduced fuzzy branching temporal logic. In recent
years, many applications of fuzzy temporal logic have
been proposed, such as the control of the robot be-
haviour (Ijsselmuiden et al., 2014), the prediction of
railway custom flow (Dou et al., 2014), and so on. Al-
though the idea of fuzzy logic has been used to extend
intuitionistic logic, modal logic, and temporal logic
early, few researchers have proposed the complete
fuzzy paraconsistent logic and concerned its practi-
cability.
Fuzzy logic and paraconsistent logic both have ex-
tinct characteristics. Paraconsistent logics are spe-
cially tailored to deal with inconsistency, while fuzzy
logics are primarily used to deal with graded truth and
vagueness (Ertola et al., 2013). Both of them are de-
veloping rapidly and independently in their own area.
If we can apply the idea of fuzzy logic to paracon-
sistent logic, it will help both to develop together. In
fact, this is possible and necessary. In paraconsistent
logics, the truth value of a proposition is only 0 or 1,
which is not always the case in real life. People often
cannot decide absolutely true or false, right or wrong,
good or bad, but people are accustomed to some inex-
act fuzzy concepts, such as little true, very right, very
good, relatively large, and so on. In this case, two-
valued logic fails to meet the needs, so it is necessary
to take some fuzzy elements into account and turn the
original two-valued one into multi-valued one, so that
it can be applied to wider spread areas in real life and
artificial intelligence.
The rest of this paper is organised as follows. Sec-
tion 2 recaps some basic concepts and notations in
fuzzy set theory. Section 3 constructs a new seman-
tic with fuzzy linguistic truth-value for paraconsistent
logic. Section 4 presents the axiom system of our
logic. Section 5 proves its soundness and complete-
ness. Section 6 gives an example to show how the
fuzzy paraconsistent logic can be used to solve a real
problem. Finally, Section 7 concludes the paper with
future work.
2 PRELIMINARIES
This section will recap basic concepts and notations
of fuzzy set (Zadeh, 1965), which we will use to build
up our fuzzy paraconsistent logic.
Definition 1 (Fuzzy Set). Let U be a crisp set, a fuzzy
set F on U is defined by a membership function:
µ
F
: U → [0, 1].
Specifically, µ
F
(u) ∈ [0, 1] represents the membership
degree of u in F.
Definition 2 (Linguistic Truth-value). The linguistic
truth-value set is defined as follows:
LTS = {absolute-true, very-true,
moderate-true, slightly-true,
slightly- f alse, moderate- f alse,
very- f alse, absolute- f alse}. (1)
For convenience, we denote
LTTS = {absolute-true, very-true,
moderate-true, slightly-true}, (2)
LTFS = {absolute-false, very-false,
moderate-false, slightly-false}. (3)
In this paper, we let τ ∈ LT S represent a comple-
ment to τ. Pairs of the linguistic truth-values that are
complement to each other include: absolute-true and
absolute-false, very-true and very-false, moderate-
true and moderate-false, slightly-true and slightly-
false.
Definition 3 (Membership Function of Linguistic
Truth-value). For any x ∈ [0, 1],
µ
absolute- f alse
(x) =
1 if x = 0,
0 otherwise;
(4)
µ
very- f alse
(x) = e
−80x
2
; (5)
µ
moderate- f alse
(x) = e
−140(x−0.25)
2
; (6)
µ
slightly- f alse
(x) = e
−200(x−0.45)
2
; (7)
µ
slightly-true
(x) = µ
slightly- f alse
(1 − x); (8)
µ
moderate-true
(x)=µ
moderate- f alse
(1 − x); (9)
µ
very-true
(x)=µ
very- f alse
(1 − x); (10)
µ
absolute-true
(x) =
1 if x = 1,
0 otherwise.
(11)
The curves of membership functions of the above
linguistic truth-value is shown in Fig. 1.
Definition 4 (Operators on Linguistic Truth-value).
µ
A∧B
(x, y) = min{µ
A
(x), µ
B
(y)}, (12)
µ
A∨B
(x, y) = max{µ
A
(x), µ
B
(y)}, (13)
µ
A→B
(x, y) = max{1 − µ
A
(x), µ
B
(y)}, (14)
µ
¬A
(x) = 1 − µ
A
(x). (15)
Definition 5 (Fuzzy Modus Ponens Rule). Suppose A
and A
0
are fuzzy sets on domain X, and B and B
0
are
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
54

0 0.1 0.2 0.3 0.4
0.5 0.6
0.7 0.8 0.9 1
0
0.5
1
very-false
moderate-false
slightly-false
very-true
moderate ture
slightly-true
x
µ
(
x)
Figure 1: Membership function of linguistic truth-value.
the fuzzy sets on domain Y. If we know A → B and A
0
,
then we can get B
0
, which is defined as follows:
µ
B
0
(y) = sup{min{µ
A
0
(x), µ
A→B
(x, y)} | x ∈ X}. (16)
Definition 6 (Linguistic Approximation). τ ∈ LT T S
is called the linguistic approximation of τ
∗
(denoted
as τ = τ
∗
) when ∀τ
1
∈ LTT S,
ED(τ, τ
∗
) ≤ ED(τ
1
, τ
∗
),
where ED is the Euclidean Distance, which is defined
as follows: for two fuzzy sets A and B,
ED(A, B)=
q
Σ{(µ
A
(x) − µ
B
(x))
2
| x ∈ [0, 1]}.
3 LOGIC SYSTEM
This section will present the syntax and semantics
of our logic system. Basically, the syntax of our
fuzzy paraconsistent logic (denoted as F
n
(1 ≤ n ≤ ω))
is the same as that of paraconsistent logic systems
C
n
(1 ≤ n ≤ ω) (Costa et al., 2005), but our semantics
are different. However, for the sake of completely un-
derstanding our whole logic system, we still present
its syntax here.
3.1 Syntax
Just like C
n
, F
n
is a series of logic system F
1
, F
2
, . . .,
F
n
, . . ., F
ω
. Each logic system is strictly stronger than
those which follow it. In particular, F
ω
is the weakest
logic system.
Definition 7 (Language). The language of F
n
is de-
noted as L
0
, which consists of the following three
kinds of initial symbol:
1. proposition symbol: p
0
, p
1
, . . . , p
k
, . . .;
2. connection symbol: ¬, ∧, ∨, →; and
3. punctuation: left parenthesis ( and right paren-
thesis ).
Definition 8 (Formula). The initial symbols in L
0
can
be combined arbitrarily. A finite sequence of a com-
bination of initial symbols in L
0
is called a formula
in L
0
iff it can be generated by limited applications of
the following rules:
1. an atomic proposition is a formula;
2. if A is a formula, then ¬A is also a formula;
3. if A and B are formulas, then (A∧ B), (A ∨ B) and
(A → B) are also formulas.
In this paper, we use capital letters A, B,C . . . to
represent a formula. The set consisting of all the for-
mulas in L
0
is denoted as Form(L
0
).
And there are some special notations in F
n
:
1. A
0
=
d f
¬(A ∧ ¬A), which means that proposition
A should comply with the law of contradiction.
2. A
n+1
= (A
n
)
0
=¬(A
n
∧ ¬A
n
) and A
1
= A
0
.
3. A
(n)
=A
1
∧ A
2
∧ . . . ∧ A
n
, which intuitively means
that A acts in full accordance with the way in
which it acts in classical logic.
4. ¬
(n)
A=¬A ∧ A
(n)
3.2 Semantics
Definition 9 (Valuation). A value V is a mapping V :
Form(L
0
) → LT S such that:
1. if V (A) = τ ∈ LT FS, then V (¬A) = τ;
2. if V (¬¬A) = τ ∈ LT S, then V (A) = τ;
3. if V (B
(n)
) ∈ LTT S, V (A → B) ∈ LTT S, V (A →
¬B) ∈ LT T S, then
µ
V (A)
(x) = max{sup
y∈Y
{min{µ
V (B
(n)
)
(x),
µ
¬B→¬A
(y, x)}},
sup
y∈Y
{min{µ
V (B
(n)
)
(x),
µ
B→¬A
(y, x)}};
4. if V (A) = τ, then
V (A → B) = (min(τ,V (B)));
Paraconsistent Logic with Multiple Fuzzy Linguistic Truth-values
55

5. V (A ∧ B) = (min(V (A),V (B));
6. V (A ∨ B) = (max(V (A),V (B)); and
7. if V (A
(n)
) ∈ LT T S, V (B
(n)
) ∈ LT T S, then V ((A ∧
B)
(n)
) ∈ LTT S, V ((A ∨ B)
(n)
) ∈ LTT S, V ((A →
B)
(n)
) ∈ LT T S.
In the above definition, V (A) = τ ∈ LT S means
that the truth-value of A is τ, V (A) ∈ LT T S means the
credibility of A is high, and V (A) ∈ LT FS means the
credibility of A is low. So, in the above definition:
• The first property means when the credibility of A
is low, the truth-value of ¬A is the complement of
A. Instead, when the credibility of A is high, the
truth-value of ¬A cannot simply be the comple-
ment of A. It intuitively means A and ¬A cannot
own low credibility at the same time, instead they
can have high credibility simultaneously.
• The second property means that the truth-value of
¬¬A implies that of A, but not vice versa.
• The third property means that if the credibility of
the proposition “B satisfies the contradictory law”
is high, then the law of reduction to absurdity is
established.
• The fourth, fifth, sixth properties redefine the se-
mantic of implication, conjunction and disjunc-
tion.
• The last property means that if the credibility of
the proposition “A and B satisfy the contradictory
law” is high, then the credibility of the compound
proposition of A and B is high.
By the above definition, given V (A) and V (B), we
can obtain the valuation of A ∧ B is showed in Table
1, the valuation of A∨ B is showed in Table 2, and the
valuation of A → B is showed in Table 3.
The following definition extends the concept of
model in paraconsistent logic into our fuzzy paracon-
sistent logic.
Definition 10 (Model). A value V is called a model of
formula set Γ iff for any formula A ∈ Γ, V (A) ∈ LTT S.
Definition 11 (Semantic Consequence). A formula A
is called the semantic consequence of Γ, denoted as
Γ |= A, iff for any model V of Γ, V (A) ∈ LT T S. When
Γ is empty, we denote |= A and say A is of commonly
high credibility.
4 AXIOM SYSTEM
This section will present the axiom system of our
logic.
4.1 Axioms
The axioms of F
n
(1 ≤ n ≤ ω) is the same as the ax-
ioms of C
n
(1 ≤ n ≤ ω). That is, they are formulas
that have one of the following forms:
1. A → (B → A)
2. (A → B) → ((A → (B → C)) → (A → B))
3. A → (B → (A ∧ B))
4. (A ∧ B) → A
5. (A ∧ B) → B
6. (A → C) → ((B → C) → (A ∨ B → C))
7. A → (A ∨ B)
8. B → (A ∨ B)
9. A ∨ ¬A
10. ¬¬A → A
11. B
(n)
→ ((A → B) → ((A → ¬B) → ¬A))
12. (A
(n)
∧ B
(n)
) → ((A ∧ B)
(n)
∧ (A ∨ B)
(n)
∧ (A →
B)
(n)
)
A
(n)
intuitively means that A acts in full accor-
dance with the way in which it acts in classical logic.
So it can be seen what axioms 11 and 12 intuitively
mean. Also, we can see that connection symbol
∧, ∨, → and ¬
(n)
in our logic respectively have the
properties of the conjunctive, disjunction, implication
and negation in the classical logic.
Furthermore, it can be proved that all the axioms
are commonly of high credibility by the three opera-
tors as showed in Tables 1, 2 and 3.
4.2 Inference Rules
The inference rule of F
n
has only one and it is Modus
Ponens.
Definition 12 (Modus Ponens rule). If we know that
(V (A) = τ
1
) implies V (B) = τ
2
and know V (A) = τ
0
1
,
then we can get V (B) = τ
0
2
, which is defined as fol-
lows:
τ
0
2
= (τ
0
), (17)
where τ
0
is defined as:
µ
τ
0
(y)=sup
x∈X
{µ
τ
0
2
(x)∧max{1−µ
τ
1
(x), µ
τ
2
(y)}}.
(18)
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
56
Table 1: The linguistic truth true table
of the conjunctive operator in our fuzzy
paraconsisitent logic.
V(A)
V(B)
absolute-true very-true moderate-true slightly-true slightly-false moderate-false very-false absolute-false
absolute-true absolute-true very-true moderate-true slightly-true slightly-false moderate-false very-false absolute-false
very-true very-true very-true moderate-true slightly-true slightly-false false very-false absolute-false
moderate-true moderate-true moderate-true moderate-true slightly-true slightly-false false very-false absolute-false
slightly-true slightly-true slightly-true slightly-true slightly-true slightly-false moderate-false very-false absolute-false
slightly-false slightly-false slightly-false slightly-false slightly-false slightly-false moderate-false slightly-false absolute-false
moderate-false moderate-false moderate-false moderate-false moderate-false moderate-false moderate-false very-false absolute-false
very-false very-false very-false very-false very-false very-false very-false very-false absolute-false
absolute-false absolute-false absolute-false absolute-false absolute-false absolute-false absolute-false absolute-false absolute-false
Table 2: The linguistic true truth table
of the disjunctive operator in our fuzzy
paraconsisitent logic.
V(A)
V(B)
absolute-true very-true moderate-true slightly-true slightly-false moderate-false very-false absolute-false
absolute-true absolute-true absolute-true absolute-true absolute-true absolute-true absolute-true absolute-true absolute-true
very-true absolute-true very-true very-true very-true very-true very-true absolute-true absolute-true
moderate-true absolute-true very-true moderate-true moderate-true moderate-true moderate-true moderate-true moderate-true
slightly-true absolute-true very-true moderate-true slightly-true slightly-true slightly-true moderate-true moderate-true
slightly-false absolute-true very-true moderate-true slightly-true slightly-false moderate-false very-false absolute-false
moderate-false absolute-true very-true moderate-true slightly-true moderate-false moderate-false very-false absolute-false
very-false absolute-true very-true moderate-true slightly-true very-false very-false very-false absolute-false
absolute-false absolute-true very-true moderate-true slightly-true absolute-false absolute-false absolute-false absolute-false
Table 3: The linguistic truth value table
of the complement operator in our fuzzy
paraconsisitent logic.
V (A) absolute-true very-true moderate-true slightly-true slightly-false moderate-false very-false absolute-false
V (¬A) absolute-false very-false moderate-false slightly-false slightly-true moderate-true very-true absolute-true
Paraconsistent Logic with Multiple Fuzzy Linguistic Truth-values
57

4.3 Proof
Definition 13 (Proof). We say there is a proof from
formula set Γ to formula A, if there is a finite sequence
of formulas A
1
, A
2
, . . . , A
m
, such that A
m
is A and for
every j (1 ≤ j ≤ m), A
j
satisfies one of the following
conditions:
1. A
j
is an axiom of F
n
;
2. A
j
is a formula in Γ; and
3. there are i and k (i, k < j) such that A
j
is obtained
by A
i
and A
k
with Modus Ponens.
Definition 14. If we have a proof from formula set Γ
to formula A, we call A is Γ deductible in F
n
, denoted
as Γ ` A. When Γ is empty, we denote it as ` A and
say A is a theorem of F
n
.
Theorem 1. All the axioms and rules in classical
proposition logic are set up in F
n
(1 ≤ n ≤ ω). In par-
ticular, Deduction Theorem is set up in F
n
(1 ≤ n ≤ ω).
Theorem 2. In F
n
(1 ≤ n ≤ ω), we have:
` (A → ¬A) → A,
` A
(n)
→ (¬A)
(n)
,
` A
(n)
,
B
(n)
, A → B ` ¬B → ¬A.
Theorem 3. In F
n
(1 ≤ n ≤ ω), the following formulas
which hold in classic propositional logic do not hold:
A ∧ ¬A → B,
A → ¬¬A,
(¬A ∧ (A ∨ B)) → B,
(A → B) → (¬B → ¬A),
¬(A ∧ ¬A).
For the sake of page limit, we cannot give out the
detailed proof of the above theorem here, but we will
do in the extended version of this paper.
5 SOUNDNESS AND
COMPLETENESS
This section will prove the soundness and complete-
ness of our logic.
5.1 Soundness
Intuitively, we say a logic system is sound, meaning
that for a formula of a logic, if it is correct in the sense
of syntax, then it is correct in the sense of semantics.
Formally, we have:
Theorem 4. F
n
is sound, i.e., Γ ` A ⇒ Γ |= A.
Proof. Since Γ ` A, we have a sequence A
1
, A
2
, . . .,
A
m
, such that A
m
is A, and for every j (1 ≤ j ≤ m), A
j
satisfies one of the following conditions:
1. A
j
is an axiom of F
n
;
2. A
j
is a formula in Γ; and
3. there are i and k(i, k < j) such that A
j
is obtained
by A
i
and A
k
with Modus Ponens.
When j = 1, A
1
is an axiom of F
n
or a formula in
Γ, and then obviously we have Γ |= A
1
. When j > 1,
suppose Γ |= A
j
is suitable for every positive integer
that is less than j. If A
j
is an axiom of F
n
or a formula
in Γ, and then obviously we have Γ |= A
j
. If A
j
is
obtained by using Modus Ponens rule, then ∃ i and k
(i, k < j), such that A
k
is A
i
→ A
j
. Accordingly, we
have Γ |= A
i
and Γ |= A
i
→ A
j
. So we have V (A
i
) ∈
LTT S, V (A
i
→ A
j
) ∈ LT T S for any model V . Let
V (A
i
) = τ, then we have τ ∈ LTFS and further we
have max{τ,V (A
j
)} ∈ LT T S. Therefore, we can get
max{τ,V (A
j
)} = V (A
j
) ∈ LT T S. Thus, we have Γ |=
A
j
.
By the method of induction, we know that for all
j, Γ |= A
j
, so Γ |= A
m
, i.e., Γ |= A.
5.2 Completeness
Intuitively, we say a logic system is completeness,
meaning that for a logic formula, if it is correct in
the sense of semantics, then it is correct in the sense
of syntax.
Definition 15. Γ is a set of formulas, Γ ⊆ Form(L
0
).
Let Γ denote the set of all formulas A such that Γ ` A.
1. We say that a set Γ of formulas is trivial iff Γ =
Form(L
0
); otherwise, it is non-trival.
2. Γ is inconsistent iff there is at least one formula A
such that both A and ¬A belong to Γ; otherwise,
Γ is consistent.
Non-trival is an important concept in paraconsis-
tent logic. If a formula set Γ can deduce all the formu-
las, then it does not need to be studied. That is why
we say that it is trivial. Classical logic allows contra-
dictories to imply everything, so inconsistent logic is
trivial. Nonetheless, paraconsistent logic admits the
existence of inconsistent but is not a trivial theory.
So, a nontrivial and inconsistent theory is just what
paraconsistent logic is studying, but any trivial and
inconsistent theory needs not to be studied.
Definition 16. Γ is maximal non-trivial iff it is non-
trivial and, for any formula A, if A 6∈ Γ, then Γ ∪ {A}
is trivial.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
58

Theorem 5. Every non-trivial set of formulas is con-
tained in a maximal non-trivial set.
Proof. The proof is the same as that in classical logic,
so for the sake of space it is omitted .
Theorem 6. Every maximal non-trivial set of formu-
las has a model.
Proof. Define a mapping
V : Form(L
0
) → LT S
satisfying that for a formula A, if A ∈ Γ then V (A) ∈
LTT S; otherwise, V (A) ∈ LT FS. It is then easy to see
that V satisfies all the conditions in the definition of a
valuation (i.e., Definition 9).
Intuitively, the following theorem of completeness
means that all the formulas with high credibility in Γ
can be deduced from F
n
.
Theorem 7. F
n
(1 ≤ n ≤ ω) is complete, i.e., Γ |= A ⇒
Γ ` A.
Proof.
Γ |= A ⇔for all the model of Γ,V (A) ∈ LT T S
⇔ 6 ∃V such that V is the model of Γ
and V (A) ∈ LT FS
⇔ 6 ∃V such that V is the model of Γ
and V (¬A) ∈ LT T S
⇒Γ ∪ {¬A} has no model
⇒Γ ∪ {¬A} is trivial
⇒Γ ∪ {¬A} = the set of all the formulas
⇒Γ ∪ {¬A} can deduce all the formulas
⇒Γ ∪ {¬A} ` ¬¬A
⇒Γ ∪ {¬A ∨ A} ` ¬¬A
⇒Γ ` ¬¬A
⇒Γ ` A.
6 ILLUSTRATION
The technology of expert system is one of the most
successful applications of artificial intelligence. An
expert system is to collect as more expert knowledge
as possible and typically translate them into a series
of rules in the form of “if . . . then . . .”. According to
these rules, the computer will be able to solve a prob-
lem like an expert. Many traditional expert systems
are built upon the basis of classical logic, which has
some significant limitations. For example, different
experts in the same field may have different opinions
for some deep problems, and thus it may lead to some
inconsistency in the knowledge base. However, even
if there are some inconsistent knowledge, we should
not give up the whole knowledge base because there
are some useful and consistent knowledge. So, re-
quired is a certain degree tolerance of contradictions.
This is exactly the practical value of fuzzy paracon-
sistent logic.
Let us examine an example of a medical expert
system (Yang, 2005). Suppose that for the disease
d
1
and d
2
, doctors 1 and 2 have their own diagnos-
tic rules as follows:
• The rules of doctor 1:
1. if a patient gets symptom s
1
and s
2
, then the
patient suffers from disease d
1
;
2. if a patient gets symptom s
1
and s
3
, then the
patient suffers from disease d
2
;
3. if a patient has disease d
1
, then the patient does
not suffer from disease d
2
; and
4. if a patient has disease d
2
, then the patient does
not suffer from disease d
1
.
• The rules of doctor 2:
1. if a patient gets symptom s
1
and s
4
, then the
patient suffers from disease d
1
; and
2. if a patient gets symptom s
3
and does not get
symptom s
1
, then the patient suffers from dis-
ease d
2
.
Now suppose we get two patients. Patient a gets
symptom s
1
, s
3
, and s
4
but does not get symptom s
2
;
and patient b gets symptom s
2
, s
3
, and s
4
but does not
get symptom s
1
. According to doctor 1, patient a has
disease d
2
but does not have disease d
1
. Rather, ac-
cording to doctor 2, patient a has disease d
1
. That is,
there is a contradiction about the diagnosis of patient
a. Nonetheless, this contradiction does not influence
upon the diagnosis of patient b. Patient b has disease
d
2
according to doctor 2 and does not have disease
d
1
according to doctor 1. Although the knowledge
base contains contrary knowledge about patient a, it
can still be used to diagnose b. So, the knowledge
base with contradictions is still useful and should not
be abandoned. Fuzzy paraconsistent logic has greater
practical value just because it can solve such problems
that paraconsistent logic cannot solve.
Sometimes it is insufficient that a symptom is
merely confirmed the presence or absence, we need
to determine how serious the symptom is. If we de-
sign an objective indicator to measure the severity of
certain symptoms, such as body temperature can be
an indicator of the severity of fever, the concentration
of a substance can be an indicator of the severely of
virus infection, the diagnose will be more accurate.
Paraconsistent Logic with Multiple Fuzzy Linguistic Truth-values
59
0 0.1 0.2 0.3 0.4
0.5 0.6
0.7 0.8 0.9 1
0
0.5
1
very-low
low little-low
little-high high very-high
x
µ
(
x)
Figure 2: Membership functions of d
1
and d
2
.
Suppose symptom s
1
is fever. Normally, the oral
temperature of an adult is 37 degree centigrade. Thus,
it is reasonable to use the difference between body
temperature and 37 as the indicator of the sever-
ity of fever. Specifically, we assume there are six
grades for the severity: very-slight, moderate-slight,
a little-slight, a little-severe, moderate-severe, and
very-serious. For the proposition of “someone being
a high fever”, we can say very-false, moderate-false,
slightly-false, slightly-true, moderate-true, and very-
true. The six kinds of linguistic truth-value can cor-
respond to the six grades of severity of fever. Hence,
we can draw the membership function of six linguistic
truth-values of s
1
as shown in Figure 1.
In our new medical expert system, we still lack the
figures of membership functions of other three symp-
toms.Without losing generality, we can set them as
shown in Figure 1.
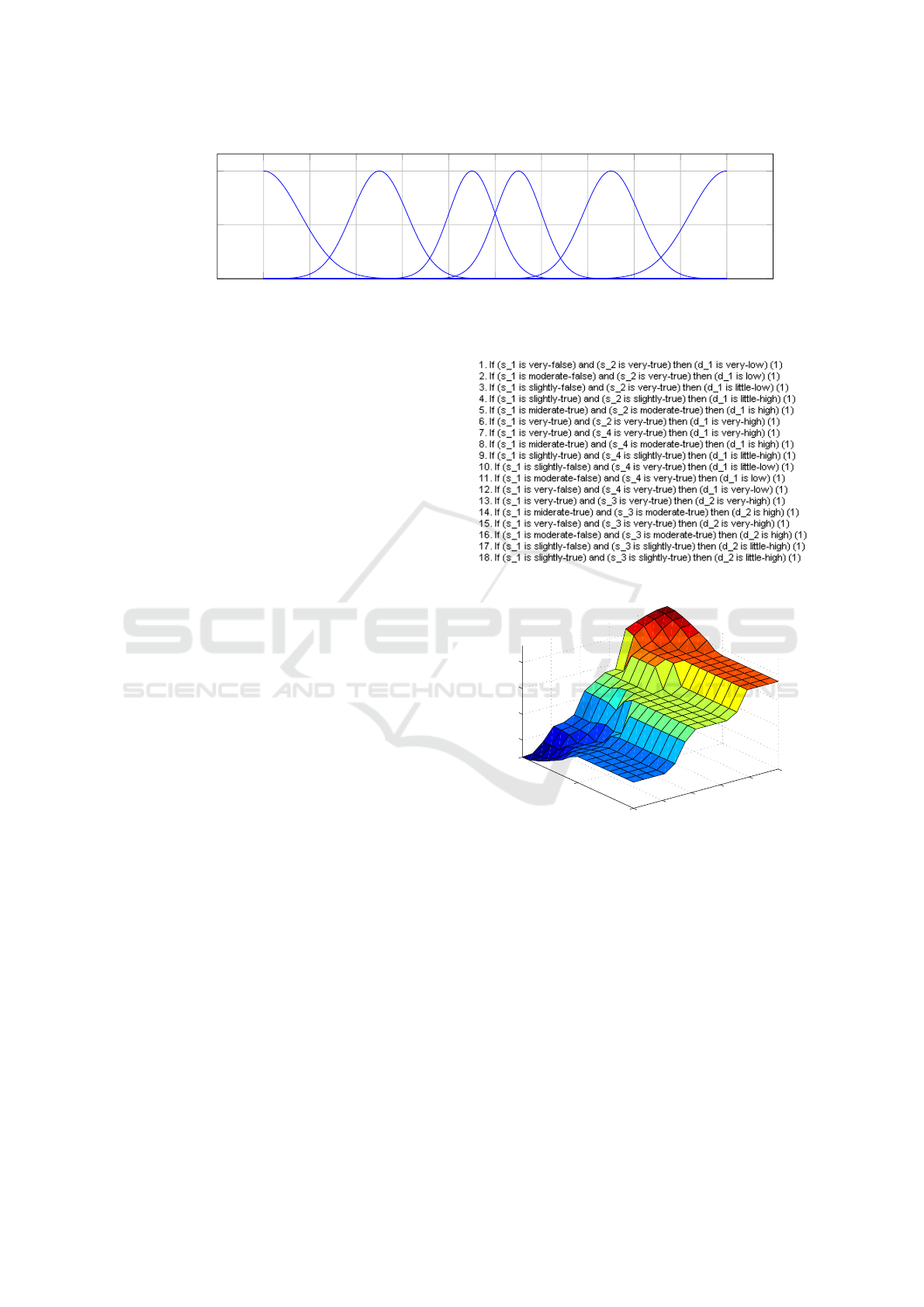
After we get the exact data of four symptoms, the
next step is to define the fuzzy rules. The diagnosed
rules of doctors 1 and 2 can be simply written as fol-
lows:
1. s
1
∧ s
2
→ d
1
,
2. s
1
∧ s
4
→ d
1
,
3. s
1
∧ s
3
→ d
2
,
4. ¬s
1
∧ s
3
→ d
2
.
According to the above four rules, we can set the cor-
responding fuzzy rules as shown in Figure 3.
We divide the possibility of having a disease into
six grades: very-low, low, little-low, little-high, high,
and very-high. Then we can define the membership
functions of d
1
and d
2
as follows:
µ
very-low
(x) = e
−80x
2
, (19)
µ
low
(x) = e
−140(x−0.25)
2
, (20)
µ
little-low
(x) = e
−200(x−0.45)
2
, (21)
µ
little-high
(x) = µ
little-low
(1 − x), (22)
µ
high
(x) = µ
low
(1 − x), (23)
µ
very-high
(x) = µ
very-low
(1 − x), (24)
Figure 3: Fuzzy rules.
0
0.2
0.4
0.6
0.8
1
0
0.5
1
0.2
0.4
0.6
0.8
s
1
s
2
d
1
Figure 4: The possibility of d
1
changes with those of s
1
and
s
2
.
where x ∈ [0, 1]. The curves of the above membership
functions is shown in Figure 2.
According to the situation of symptoms, this infer-
ence fuzzy system can output the possibility of having
a disease. With the help of the rule viewer of Matlab,
we can see the whole output situation of the fuzzy rea-
soning system, as shown in Figure 4. There each co-
ordinate has a corresponding meaning. For example,
point (0.8, 0.5, 0.581) represents that when the input
value of s
1
is 0.8 and that of s
2
is 0.5, the possibility
of having disease d
2
is of 0.581.
From the above example, we can see our fuzzy
paraconsistent logic has greater practical value than
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
60

Figure 5: When s
1
and s
3
are serious and s
4
is slight, more
likely the patient suffers from d
2
.
Figure 6: When s
1
and s
4
are serious and s
3
is slight, more
likely the patient suffers from d
1
.
paraconsistent logic. In fact, in the medical expert
system above, there is a contradiction about the di-
agnosis of patients a with symptom s
1
, s
3
and s
4
, so
that according to the two-valued paraconsistent logic
we cannot decide whether a is suffering from disease
d
1
or d
2
. However, in the medical expert system with
ours of multiple linguistic truth-values, we can cal-
culate the possibilities of suffering from diseases d
1
and d
2
. So, we can base on the more accurate data to
decide what kind of treatment should be taken.
Figures 5 and 6 show how the possibility of a dis-
ease varies with the severity degree of symptoms. The
data of Figure 5 is {0.9, 0, 0.9, 0.2, 0.597, 0.915},
meaning that if s
1
is severe, s
3
is severe and s
4
is
slight, then the possibility of d
2
is very large, and so it
is better to use drugs that can properly treat disease d
2
.
The data of Figure 6 is {0.9, 0, 0.2, 0.9, 0.915, 0.597},
meaning that if s
1
is severe, s
4
is severe and s
3
is
slight, then the possibility of d
1
is very large, and so
it is better to use drugs that can properly treat disease
d
1
.
Paraconsistent logic advocates that contradictions
should be tolerated, but have to be limited in a certain
range, which is correct. However, from another view-
point, it actually equals to leave the contradictions to
fend for themselves, which seems a little irresponsi-
ble. So the way in which paraconsistent logic deals
with contradictions somehow is improper. Rather, we
can see from the above example that our fuzzy para-
consistent logic can make up for this shortcoming.
Actually, it can provide the weights of the both sides
of a contradiction, so that people can make better de-
cisions when facing a contradiction.
7 CONCLUSION
Paraconsistent logic is the unique logic that can deal
with an inconsistent theory, so it has a wide applica-
tion in many areas, especially in artificial intelligence.
However, it is still a semantically two-valued logic.
Obviously, absolutely true or false is not enough in
real life because people tend to use the vague phrases
like very-true, slightly-true, slightly-false, very-false,
and so on. Therefore, this paper enables a proposition
in paraconsistent logic to take its truth value from a set
of multiple linguistic terms, so that it can be applied
to a wider scope in real life. Moreover, we also prove
the soundness and completeness of this kind of para-
consistent logic with multiple linguistic truth-values.
In addition, this paper illustrates the practical value of
our fuzzy paraconsistent logic by a real life example,
but its significance is far more than that. Actually,
the potential applications of our fuzzy paraconsistent
logic are not limited to expert systems, other more
areas such as legal, political and economic areas are
applicable, too. Inconsistence and fuzzification are
ubiquitous, so our fuzzy paraconsistent logic has great
potential waiting to be explored.
ACKNOWLEDGEMENTS
This work was partially supported by the Bairen Plan
of Sun Yat-sen University.
REFERENCES
Abe, J. M. (2016). Paraconsistent logics and applications.
In New Approaches in Intelligent Control, volume 107
Paraconsistent Logic with Multiple Fuzzy Linguistic Truth-values
61

of Intelligent Systems Reference Library, pages 273–
300. Springer.
Akama, S. and Da Costa, N. C. (2016). Why paraconsis-
tent logics? In Towards Paraconsistent Engineering,
volume 110 of Intelligent Systems Reference Library,
pages 7–24. Springer.
Anderson, A. R., Belnap, N. D., and Dunn, J. M. (1978).
Entailment: The logic of relevance and necessity.
Philosophical Books, 19(2):75–77.
Arnon, A. (2014). Paraconsistent fuzzy logic preserving
non-falsity. Fuzzy Sets and Systems, 292:75–84.
Costa, N. D. and Carnielli, W. (1986). On paraconsistent
deontic logic. Philosophia, 16(3-4):293–305.
Costa, N. D., D.Krause, and O.Bueno (2005). Paraconsis-
tent logics and paraconsistency. Philosophy of Logic,
4:791–911.
Da Costa, N. C., B
´
eziau, J.-Y., Bueno, O. A., et al. (1995).
Aspects of paraconsistent logic. Logic Journal of the
IGPL, 3(4):597–614.
Da Costa, N. C. A. (1958). On the theory of inconsistent
formal systems. Bulletin De La Socit De Chimie Bi-
ologique, 40(7-8):1179–1187.
Dou, F., Jia, L., Wang, L., Xu, J., and Huang, Y. (2014).
Fuzzy temporal logic based railway passenger flow
forecast model. Computational Intelligence and Neu-
roscience, 2014:Article No. 42.
Ertola, R., Esteva, F., Flaminio, T., Godo, L., and Noguera,
C. (2013). Exploring paraconsistency in degree-
preserving fuzzy logics. In Proceedings of the 8th
Conference of the European Society for Fuzzy Logic
and Technology, pages 117–124.
Ijsselmuiden, J., Nch, D., Grosselfinger, A. K., Arens, M.,
and Stiefelhagen, R. (2014). Automatic understanding
of group behavior using fuzzy temporal logic. Jour-
nal of Ambient Intelligence and Smart Environments,
6(6):623–649.
Jing, X., Luo, X., and Zhang, Y. (2014). A fuzzy dynamic
belief logic system. International Journal of Intelli-
gent Systems, 29(7):687–711.
Kamide, N. (2013). Formalizing inconsistency-tolerant rel-
evant human reasoning: A decidable paraconsistent
relevant logic with constructible falsity. In Proceed-
ings of 2013 IEEE International Conference on Sys-
tems, Man, and Cybernetics, pages 1865–1870.
Kamide, N. (2016). A decidable paraconsistent relevant
logic: Gentzen system and routley-meyer semantics.
Mathematical Logic Quarterly, 62(3):177–189.
Moon, S., Lee, K., and Lee, D. (2004). Fuzzy branching
temporal logic. IEEE Transactions on Systems Man
and Cybernetics: Part B Cybernetics, 34(2):1045–
1055.
Mukherjee, S. and Dasgupta, P. (2013). A fuzzy real-time
temporal logic. International Journal of Approximate
Reasoning, 54(9):1452–1470.
Poli, V. S. R. (2015). Fuzzy temporal predicate logic for
incomplete information. In Proceedings of 2015 In-
ternational Conference on Fuzzy Theory and Its Ap-
plications, pages 86–90.
Priest, G., Tanaka, K., and Weber, Z. (1989). Paraconsistent
Logic. M
¨
unchen.
Rodrguez, J., Turunen, E., Da, R., and Montero, J.
(2014). Another paraconsistent algebraic semantics
for lukasiewiczpavelka logic. Fuzzy Sets and Systems,
242(242):132–147.
Tanaka, K., Berto, F., Mares, E., and Paoli, F. (2012).
Paraconsistency: Logic and applications, volume 26.
Springer.
Thiele, H. and Kalenka, S. (1993). On fuzzy temporal logic.
In Proceeding of the 2nd IEEE International Confer-
ence on Fuzzy Systems, pages 1027–1032.
Turunen, E. (1992). On fuzzy intuitionistic logic. Kyber-
netika, 28(7):72–77.
Turunen, E.,
¨
Ozt
¨
urk, M., and Tsoukis, A. (2010). Para-
consistent semantics for pavelka style fuzzy sentential
logic. Fuzzy Sets and Systems, 161(14):1926–1940.
Vidal, A., Esteva, F., and Godo, L. (2015). On modal ex-
tensions of product fuzzy logic. Journal of Logic and
Computation, page exv046.
Yager, R. R. and Zadeh, L. A. (1992). An Introduction to
Fuzzy Logic Applications in Intelligent systems, vol-
ume 165 of The International Series in Engineering
and Computer Science. Springer.
Yang, W. (2005). Theoretical significance and practical
value of paraconsistent logic. Journal of Renmin Uni-
versity of China, (2):63–69.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control,
8(65):338–353.
Zadeh, L. A. (1983). The role of fuzzy logic in the manage-
ment of uncertainty in expert systems. Fuzzy sets and
systems, 11(1):199–227.
Zadeh, L. A. (1996). Fuzzy logic=computing with words.
IEEE transactions on fuzzy systems, 4(2):103–111.
Zhan, J., Luo, X., Feng, C., and Ma, W. (2014). A fuzzy
logic based bargaining model in discrete domains:
Axiom, elicitation and property. In Proceedings of
2014 IEEE International Conference on Fuzzy Sys-
tems, pages 424–431.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
62
