Protein Disorder Prediction using Information Theory Measures on the

Distribution of the Dihedral Torsion Angles from Ramachandran Plots

Jonny A. Uribe

, Juli

an D. Arias-Londo

and Alexandre Perera-Lluna

Department of Systems Engineering and Computer Science, Universidad de Antioquia,

Calle 67 No. 53 - 108, 050010, Medell

ın, Colombia

Research Center for Biomedical Engineering, ESAII, Universitat Polit

ecnica de Catalunya,

Pau Gargallo 5, 08028, Barcelona, Spain

Keywords:

Intrinsically Disordered Proteins, Intrinsically Disordered Regions, Entropy Measures, Kullback-Leibler

Divergence, Dihedral Torsion Angles, Ramachandran Plot, Conditional Random Fields.

Abstract:

This paper addresses the problem of order/disorder prediction in protein sequences from alignment free meth-

ods. The proposed approach is based on a set of 11 information theory measures estimated from the distribu-

tion of the dihedral torsion angles in the amino acid chain. The aim is to characterize the energetically allowed

regions for amino acids in the protein structures, as a way of measuring the rigidity/ﬂexibility of every amino

acid in the chain, and the effect of such rigidity on the disorder propensity. The features are estimated from

empirical Ramachandran Plots obtained using the Protein Geometry Database. The proposed features are used

in conjunction with well-established features in the state of the art for disorder prediction. The classiﬁcation

is performed using two different strategies: one based on conventional supervised methods and the other one

based on structural learning. The performance is evaluated in terms of AUC (Area Under the ROC Curve), and

three suitable performance metrics for unbalanced classiﬁcation problems. The results show that the proposed

scheme using conventional supervised methods is able to achieve results similar than well-known alignment

free methods for disorder prediction. Moreover, the scheme based on structural learning outperforms the

results obtained for all the methods evaluated, including three alignment-based methods.

1 INTRODUCTION

Disordered proteins are proteins which do not adopt

a ﬁxed 3D structure in their native state. There are

two possible dispositions: the complete protein re-

mains without a ﬁxed tertiary structure or some of its

parts fail to fold and persist in a ﬂexible conﬁgura-

tion. These two kind of arrangements are known as

Intrinsically Disordered Proteins (IDP) and Intrinsi-

cally Disordered Regions (IDR) respectively (Dunker

et al., 2008). In the last years, discovery and charac-

terization of disordered proteins has become one of

the fastest growing areas in protein science (He et al.,

2009), mainly because many IDPs were found to be

associated with human diseases including cancer, dia-

betes, cardiovascular affection, amyloidoses and neu-

rodegenerative diseases (Uversky et al., 2008). Nev-

ertheless, the experimental determination of IDP and

IDR is costly and require both, a lot of time and an

extensive expertise (He et al., 2009). Taking into ac-

count the large amount of proteins sequences avail-

able, there is a need for alternative methods able to

offer a reliable and fast way to detect disorder in

proteome-wide analysis. In this scenario, as in many

other bioinformatics subﬁelds, computational meth-

ods have become valuable candidates to provide al-

ternative solutions (Peng et al., 2015)(Varadi et al.,

2015).

One of the main distinguishing characteristics of

the current computational methods for detecting dis-

order, lies in the use of Multiple Sequence Align-

ment (MSA) algorithms. In particular PSI-BLAST

(Altschul et al., 1997) is recurrently used for several

disorder predictors as a preliminary phase for identi-

fying proteins homologues, and tune Position Score

Matrices (PSSM). PSSM can capture the statistical

variations of every amino acid on targeted proteins.

These matrices are used later as inputs for the dis-

order predictors, improving in this way the perfor-

mance in comparison with the use of only the raw

protein sequences. The power of sequence alignment

in bioinformatics methods is undeniable but imposes

a set of issues. One of them is the computational cost

that can become relevant when the method is used

Uribe J., Arias-LondoÃ

so J. and Perera-Lluna A.

Protein Disorder Prediction using Information Theory Measures on the Distribution of the Dihedral Torsion Angles from Ramachandran Plots.

DOI: 10.5220/0006140500430051

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 43-51

ISBN: 978-989-758-214-1

on large scale proteome analysis (thousands to mil-

lions of proteins). A second and more relevant draw-

back is the implicit assumption that the proteins un-

der evaluation have a pool of homologous proteins

into the known databases, from which annotations

can be transferred. In the disorder identiﬁcation do-

main, some of the methods that take advantage of the

MSA algorithms include PONDR (Xue et al., 2010),

DISOPRED (Jones and Cozzetto, 2014) and SPINE-

D (Zhang et al., 2012).

On the other hand, methods that avoid sequence

alignment can reach more modest classiﬁcation re-

sults on known datasets, but can be applied compara-

tively faster on huge databases of unlabeled proteins

(DeForte and Uversky, 2016), and more importantly,

they do not make assumptions about the existence of

homologues proteins.

Among the most used alignment-free methods

for protein disorder prediction are IUPRED and Es-

pritz (Dosztnyi et al., 2005), (Walsh et al., 2012).

IUPRED uses the amino acid pair interaction en-

ergy estimated using only the amino acid composi-

tions, to create matrices of potentials between amino

acids. The authors concluded that when a sequence

contains few hydrophobic residues, the composition-

based mutual interaction energy will be small, indi-

cating the lack of potential for folding. In IUPRED

the scoring matrices were adjusted using a Support

Vector Machine (SVM)(Vapnik, 1998) and indepen-

dent models were created for short and long disorder

regions. IUPRED is computationally fast and have

been used in proteome-wide analyses (Oates et al.,

2013) (Potenza et al., 2015). The systems that use

predictors ensembles (metapredictors) recurrently in-

cluded IUPRED as a component (Bulashevska and

Eils, 2008) (Lieutaud et al., 2008), and in many works

where new predictors are proposed, IUPRED is used

as a baseline for comparison purposes (He et al.,

2009)(Deng et al., 2012).

On the other hand, Espritz is based on a Bidirec-

tional Recursive Neural Network whose inputs are 5

scales obtained from the clustering of AAindex prop-

erties (Kawashima and Kanehisa, 2000), and a one-

hot enconding vector of length 20, which identify the

amino acid being modeled/evaluated at a time. It

means that given an amino acid, this property vector

will have a value 1 for only one position, and 0s for

the 19 other positions. Espritz is also a fast predictor

used in similar scenarios than IUPRED and therefore

well suitable for performance comparison.

One strategy for improving the current protein dis-

order prediction levels, is to ﬁnd novel characteristics

that can carry information related to the folded or un-

folded state of amino acids groups. Moreover, one of

the main challenges of the characterization methods

used by disorder predictors, is be able to codify infor-

mation about critical components responsible of pro-

teins stability and/or related to the energetics of pro-

teins folding. In this context, the dihedral torsion an-

gles of the amino acid chain can play a relevant role,

since they are commonly used to deﬁne the degrees of

freedom of the residues, i.e. these angles contain in-

formation about restrictions, allowed values and ten-

dencies associated to the secondary structure of the

proteins (Hollingsworth and Karplus, 2010). Due to

this fact, in (Baruah et al., 2015), the dihedral angles

were used with the aim of estimating the conforma-

tional entropy of IDP, IDR, and completely ordered

proteins. The proposed metric was found to be a po-

tential measure for the discrimination of complete dis-

ordered vs complete ordered proteins.

The information about the set of torsion angles

that one amino acid is able to access, can be found on

graphical representations called Ramachandran plots

(RP). RPs are empirical distributions of the torsion

angles estimated from thousands of proteins with

known structure. Therefore, RPs can be used to

quantify the statistical preference that known proteins

obey, and furthermore by using the RPs of adjacent

amino acids in a protein, estimate the conditional re-

lationships into an amino acid neighborhood.

Bearing this in mind, in this work a set of 11 infor-

mation theory metrics estimated on empirical RPs, are

used for the creation of sequence based features that

allow the quantiﬁcation of disorder tendency along a

protein. The proposed features are based on entropy

measures and divergences on RPs coming from in-

dividual, duples and triads of amino acids, and link-

ing amino acid context for capturing disorder propen-

sity. The measures between amino acids, are based

on the estimation of conditional distributions between

adjacent residues, and on the quantiﬁcation of diver-

gences among the marginal distributions of neighbor

amino acids. Additionally, well-known characteris-

tics for the detection of disorder are evaluated in con-

junction with the proposed features. The classiﬁca-

tion of order/disorder is carried out using two dif-

ferent strategies: a conventional supervised learning

method based on SVM and Random Forest, and a

structural learning scheme based on Conditional Ran-

dom Fields (CRFs) (Lafferty et al., 2001). CRFs are

discriminative non-parametric models able to capture

the correlation amongst neighboring labels in a se-

quence, therefore they are suitable for the annotation

of amino acids as ordered/disordered considering the

dependence into segments of the whole protein se-

quence.

The rest of the papers is organized as follows: sec-

BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms

tion 2 presents the set of variables proposed and the

learning strategies. It also describes the dataset and

the validation methodology. Section 3 presents the

results obtained and ﬁnally section 4 includes some

conclusions extracted from the work.

2 MATERIAL AND METHODS

2.1 Characterization

The RPs used in this work were obtained from the

Protein Geometry Database (Berkholz et al., 2009),

using a resolution of 5 degrees per bin. In this way

φ and ψ coordinates took each 72 values, giving then

5184 discrete bins per amino acid. Intensities in every

bin quantify the preference for a particular φ and ψ

conﬁguration.

The 20 amino acids have different preference in

the φ and ψ space. This occurs because differences in

the three-dimensional structure of the residues confer

different ranges of ﬂexibility. A plot showing some

RPs for representative amino acids is shown in Figure

1. It is easy to note that the space explored by amino

acid Proline is quite limited in comparison with other

amino acids as, for example, Glycine. The backbone

covalent link in Proline imposes strong rigidity on the

molecule, reducing the possible φ and ψ valid angles.

By contrast, the residue in Glycine is just a single

atom of hydrogen giving the molecule ample ﬂexi-

bility and also the possibility of exploring a bigger

φ and ψ space. This kind of differences suggest that

RPs can be used to quantify the ﬂexibility tendency of

amino acids and, consequently, create measures that

contribute to identify the disordered regions.

2.1.1 Metrics Estimated on Individual Amino

Acids

Let us consider the RP of an aminoacid as a bivari-

ate probability distribution, assuming the set of back-

bone dihedral angles Φ and Ψ as random variables.

As more “ﬂexible” an amino acid is, more pairs of

angles would be able to visit. A way to measure the

rigidity/ﬂexibility of one amino acid is by using the

Shannon Entropy of the torsion angle distributions.

Let P

(Φ = φ,Ψ = ψ) = P

(φ,ψ) be the probability

of taking the disposition given by the couple angles φ

and ψ, in the a-th amino acid; the Shannon entropy of

the whole map can be expressed as

= −

∑

∀φ

∑

∀ψ

(φ,ψ)log(P

(φ,ψ)) (1)

A low value of H indicates a “rigid” amino acid, i.e.

an amino acid able to visit a less number of regions

Figure 1: Ramachandran Plots of some amino acids, Pro-

line, Aspartic Acid, Tyrosine and Glycine. φ is along x-axis

and ψ is along y-axis.

in the RP. Considering that relevant information can

be diffused on map regions with low probability in-

tensity, Renyi entropies were also used. The Renyi

estimator of the individual RP entropy can be deﬁned

1 −α

log

∑

∀φ

∑

∀ψ

(φ,ψ)

. (2)

where the order parameter α has the function of

weighting probabilities values, in order to make low

represented regions comparable to high populated

ones. Another way to characterize the energetically

allowed regions for amino acids in the protein struc-

tures, is by comparing the RP of individual amino

acids with respect to a consensus RP. The consensus

RP essentially contains all possible regions explored

for any amino acid in the dataset. Relative variations

of a given individual amino acid RPs, with respect to

the consensus RP, offer a mechanism for capturing lo-

cal preferences. Let R(φ, ψ) denote the reference RP

distribution, the difference between R and the RP dis-

tribution of the a-th amino acid can be estimated using

the Kullback-Leibler (KL) divergence given by:

(R||P

) =

∑

∀φ

∑

∀ψ

R(φ,ψ)log

R(φ,ψ)

(φ,ψ)

. (3)

2.1.2 Metrics Estimated on Pairs of Amino

Acids

Although considering individual amino acids is a

good method for capturing information related to dis-

order, more powerful descriptors can be obtained if

Protein Disorder Prediction using Information Theory Measures on the Distribution of the Dihedral Torsion Angles from Ramachandran

Plots

sets of amino acids along the chain are studied. Using

consecutive pairs of amino acids is a natural exten-

sion for investigating local interacting residues. Once

again the KL divergence can be used for measur-

ing the dissimilarities between all possible pairs of

residues’s RPs. The divergence between two amino

acids a and b can be expressed as

||P

) =

∑

∀φ

∑

∀ψ

(φ,ψ)log

(φ,ψ)

(4)

Since KL divergence is not a symmetric measure,

a commonly used symmetric version of KL is given

by Ds

+ D

). This correspond to travers-

ing the protein from N-terminus to C-terminus and

vice-versa, and then averaging their contributions.

Nevertheless, in previous experiments the values of

(·,·) between the RPs P

and P

were almost equal

to the symmetric version, so the one direction coding

was ﬁnally employed.

The comparison carried out by D

(·,·) evaluates

the dissimilarity between the energetically allowed

regions for the a-th and b-th amino acids. How-

ever, by considering that consecutive amino acids in

a protein share a dipetide plane, the dissimilarity be-

tween neighbors amino acids can be estimated us-

ing the distribution of the torsion angles ψ

of the

i-th amino acid, and the distribution of φ

i+1

of the

next one. In order to quantify such a dissimilarity,

the comparison between adjacent amino acids can

be estimated evaluating the KL divergence between

the marginal distributions P

(ψ) =

∑

∀φ

(φ,ψ), and

i+1

(φ) =

∑

∀ψ

i+1

(φ,ψ). As in the former case, this

measure can also be estimated by traversing the pro-

tein from N-terminus to C-terminus.

2.1.3 Metrics Estimated on Triads of Amino

Acids

Local interaction between amino acids can be ex-

plored beyond, for example using triplets, quatruples

or quintuples. In this work a method for quantify-

ing the local interaction between consecutive amino

acids is proposed. The intuition behind the proposed

method is to use the marginal distributions of torsion

angles estimated from neighbors amino acids, to eval-

uate how one amino acid modify the regions in the RP

that the torsion angles of the next one can visit. This

analysis can be extended to chains of amino acids of

arbitrary length. In this work this idea is explored for

triads of amino acids.

Let us consider a triad of consecutive amino acids

A, B, an C, as shown in Fig. 2. By assuming that

the random variable Ψ

(which denote the torsion an-

gles ψ in the A-th amino acid), is independent from

the random variable Φ

, the joint distribution between

(ψ) and P

(φ), denoted by P

(φ) can be estimated

as the product between the two marginal distributions,

when both random variables take the same value, i.e.

(φ) = P

(Ψ = φ)P

(Φ = φ). Taking into account

that the set of torsion angles Ψ

is limited directly

by Φ

due to structural conformation restrictions, the

conditional distribution P

(ψ|φ) can be expressed as

Figure 2: Schematic of a triads of amino acids A, B, and C,

whose dependence can be represented using the conditional

marginal distribution along the triads.

(ψ|φ) =

(ψ,φ)

(φ)

(5)

Assuming that Φ

is in turn limited by the set Ψ

of the previous amino acid, the marginal distribution

(ψ) can be estimated conditioning it with respect

the aminoacid A, by replacing P

(φ) with the joint

distribution P

(φ). The marginal distribution P

(ψ)

can be expressed as

(ψ) =

∑

∀φ

(ψ|φ)P

(φ) (6)

The procedure can be extended to the next amino

acid in a similar way, by using the former P

(ψ) to

estimate the joint distribution P

(φ). The entropy of

the last “conditional” marginal distribution estimated

in this way, can be considered as a metric of the vari-

ability in the energetically allowed regions of the last

amino acid conditioned on the previous ones.

The ﬁnal set of the proposed metrics included

a simple dot product between marginal probabili-

ties from consecutive RPs, the Shanon entropies esti-

mated on the logarithm of the RPs, and two different

Renyi entropies using the parameter al pha equal to

0.1 and 0.3.

Additionally characteristics with known rele-

vance in the identiﬁcation of disorder were used.

This included secondary structure predictions from

PSIPRED (McGufﬁn et al., 2000), selected physical-

chemical properties from AAIndex (Kawashima and

Kanehisa, 2000), pseudo amino acid compositions

(Chou, 2001), pattern of asymmetric charge variation

(Das et al., 2015), sequence complexity and a simple

indicator of amino acid positions in the protein chain.

Overall 85 properties are used, from these 11 are the

BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms

ones proposed in this work and are summarized in Ta-

ble 1. Details about complementary features can be

found in the Appendix.

2.2 Classiﬁcation Methods

Three different classiﬁcation models were used in this

work for identifying disordered and ordered amino

acids. In ﬁrst place Random Forest (RF) was used

with 500 trees grown. The number of variables ran-

domly sampled at each split was selected in cross vali-

dation on training data. The predictor based on the set

of proposed measures and a Random Forest classiﬁer,

was named RF InfoThor.

On the other hand Support Vector Machines

(SVM) were trained using a Gaussian RBF kernel.

The regularization parameter C and the kernel band-

width σ, were found through a grid search using train-

ing data. The predictor based on the set of pro-

posed measures and a SVM classiﬁer, was named

SVM InfoThor.

The classiﬁcation using RF and SVM, assumes

that the label of each amino acid is independent from

each other into the protein sequence. On the contrary,

structural learning methods are able to model differ-

ent statistical dependences among elements on a se-

quence. This is the case of the probabilistic models

known as Conditional Random Fields (CRFs), which

are able to segment and label sequence data (Laf-

ferty et al., 2001). The CRFs have several advan-

tages in comparison to more classical models for se-

quence classiﬁcation such as hidden Markov mod-

els. To name just a few, CRFs belong to the class

of discriminative models, so the try to model directly

the conditional distribution of the labels given the in-

put variables, which is more suitable for classiﬁca-

tion purposes. Besides, CRFs are not restricted to

strong independence assumptions made in those mod-

els, and the loss function used for training is convex,

guaranteeing convergence to the global optimum. In

this work a Chain-structured CRF is used to model

correlation amongst neighboring labels. The predic-

tor based on the set of proposed measures and a CRF

classiﬁer, was named CRF InfoThor.

2.3 Experimental Setup

The proposed characterization methods were evalu-

ated on the target data set and their result were com-

pared with sequence based predictors: IUPRED and

Espritz and also with MSA based methods, SPINE-D,

DISOPRED and PONDR.

2.3.1 Data Sets

High quality and extensive disorder proteins

databases are still a missing resource in the ﬁeld.

The most referenced and commonly used database

is DisProt (Sickmeier et al., 2007) which contains

manually curated annotations supported on scientiﬁc

publications. Version 6.02 created in 2013 contains

694 proteins. Unfortunately DisProt is not free of

problems, in particular the ordered residues are not

labeled and many disordered regions have more than

one annotation.

The SL benchmark data set (Sirota et al., 2010) is

a subset of Disprot that mitigates some of these issues.

For the sake of comparison with other predictions

methods, the performance of the proposed measures

was evaluated on the SL329 Data set, which was pre-

pared in (Zhang et al., 2012). The referenced authors

created the database selecting proteins with sequence

homology less than (25%) from the SL benchmark

data set. SL329 contains 329 proteins with 51292 or-

dered residues and 39544 disordered residues.

2.3.2 Model Validation

All the experiments were carried out using a 10-

fold cross-validation strategy. In general data sets

can include some level of imbalance between ordered

and disordered proteins, then some metrics able to

quantify the performance in such scenarios were in-

cluded. The set of metrics used includes: AUC, Sen-

sitivity, Speciﬁcity, B

ACC

, MCC and P

Excess

. AUC

refers to the area under the ROC curve, being dis-

order the positive class. MCC is the Matthews cor-

relation coefﬁcient, which according to (Baldi et al.,

2000) is an appropriate measure of performance for

unbalanced data sets. MCC can be estimated as

MCC =

T P·T N−FP·F N

√

(T P+F P)·(T P+FN)·(T N+F P)·(T N+F N)

, where

TP denotes True Positive, TN stands for True Neg-

ative, FP is False Positive and FN is False Negative.

On the other hand, B

ACC

is the balanced accuracy

which can be expressed as

ACC

Sensi + Speci

(7)

where Sensi = T P/(T P + FN), and Speci =

T N/(T N +FP) are the sensitivity and the speciﬁcity

respectively. Finally, P

Excess

called the probability of

excess, depends also on the sensitivity and speciﬁcity

and can be expressed as P

Excess

= Sensi + Speci −1.

Protein Disorder Prediction using Information Theory Measures on the Distribution of the Dihedral Torsion Angles from Ramachandran

Plots

Table 1: Summary of Ramachandran Plot Based Metrics.

Descriptor name Description

Hs a Shanon entropy on the vectorized RPs of every single amino acid

Hs density(a) Shanon entropy on the kernel density estimates of the vectorized RPs

Hs density(log(a)) Shanon entropy on the estimated densities of the logarithm of the counts from the Rps

(0.1)Hr

(0.31) Renyi Entropy using alpha parameter 0.1 and 0.31 on the RPs matrices

KL individual RP Kullback-Leibler Divergence of individual amino acid RP and reference RP

KL consecutive RPs Kullback-Leibler Divergence between every amino acid RP vs the next

amino acid RP in the protein chain

KL Marg. Angles (eps) Kullback-Leibler Divergence on the marginals angles φ and ψ of

neighborhood amino acids, adding a epsilon value on the distributions

KL Marg. Angles (freqs) Kullback-Leibler Divergence on the marginals angles φ and ψ of

neighborhood amino acids, using densities estimates on marginal distributions

Dot Product Marg. Angles Dot product between the marginals angles φ and ψ

Marginal on Triads Marginal on cumulative φ angle triads

3 RESULTS

3.1 Results on SL329 Data Set

Table 2 shows evaluation results on benchmark SL329

data set. It is possible to observe that the methods us-

ing sequence alignment (SPINE-D and DISOPRED)

obtained better performance on this data set than

IUPRED, as expected. On other hand, Espritz showed

a good performance compared with MSA-based

methods. The conventional proposed approaches,

SVM InfoThor and RF InfoThor, got competitive

results in MCC and balanced accuracy metrics

when compared with IUPRED. However, it was the

proposed structural learning scheme CRF InfoThor,

which obtained the best performance among all the

methods evaluated, and according to all the metrics.

In terms of MCC and AUC, CRF InfoThor outper-

forms IUPRED in about 13% and 6% respectively,

considering relative differences. CRF InfoThor also

outperforms the state-of-art MSA-based methods,

sometimes with a considerably margin, for example

MCC metric of CRF InfoThor is 14% higher that

the same value in PONDR-FIT. The performance of

CRF InfoThor is better, although pretty close, to the

one obtained by SPINE-D. This result could be ex-

plained due to the fact that SPINE-D corresponds

to an adaptation of a secondary structure predictor,

which was based on the prediction of torsion angles

from sequence proﬁles (Faraggi et al., 2009) (Faraggi

et al., 2012). CRF InfoThor can use information of

torsion angles by applying a more simple strategy

based only in the protein sequence, and without the

need of using MSA algorithms.

Figure 3 shows in a simpler way the performance

of the evaluated models. From it, is easier to observe

how CRF InforThor metrics are comparable and even

better with respect to the performance of the state-of-

Table 2: Performance comparison among Disorder Identiﬁ-

cation Methods on SL329 data set.

Method AUC MCC B

ACC

Excess

CRF InfoThor 0.8876 0.6393 0.8172 0.6343

SVM InfoThor 0.8027 0.4789 0.7362 0.4724

RF InfoThor 0.8206 0.5092 0.7450 0.4899

SPINE-D 0.8860 0.6300 0.8150 0.6300

DISOPRED2 0.8580 0.5900 0.7950 0.5900

PONDR-FIT 0.8430 0.5500 0.7600 0.5200

IUPRED 0.8392 0.5536 0.7575 0.5151

Espritz 0.8632 0.6058 0.7981 0.5963

Figure 3: Performance comparison of methods evaluated on

the SL329 data set.

art methods.

In order to evaluate the importance of the vari-

ables for the order/disorder prediction, the statisti-

cally most relevant variables were found using the

SVM InfoThor model, following this scheme: The

SVM was repeatedly trained using only one variable

at a time, and AUC metric on test samples was used

for ranking the features. This process was carried out

in a 10-fold cross-validation test. The relative impor-

tance was later adjusted to a 0 to 100 scale, where

100 was indicative of the most important feature. Al-

though this analysis ignores the contribution that co-

variated features provide to the classiﬁcation perfor-

mance, it is able to offer a ﬁrst indication of the im-

BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms

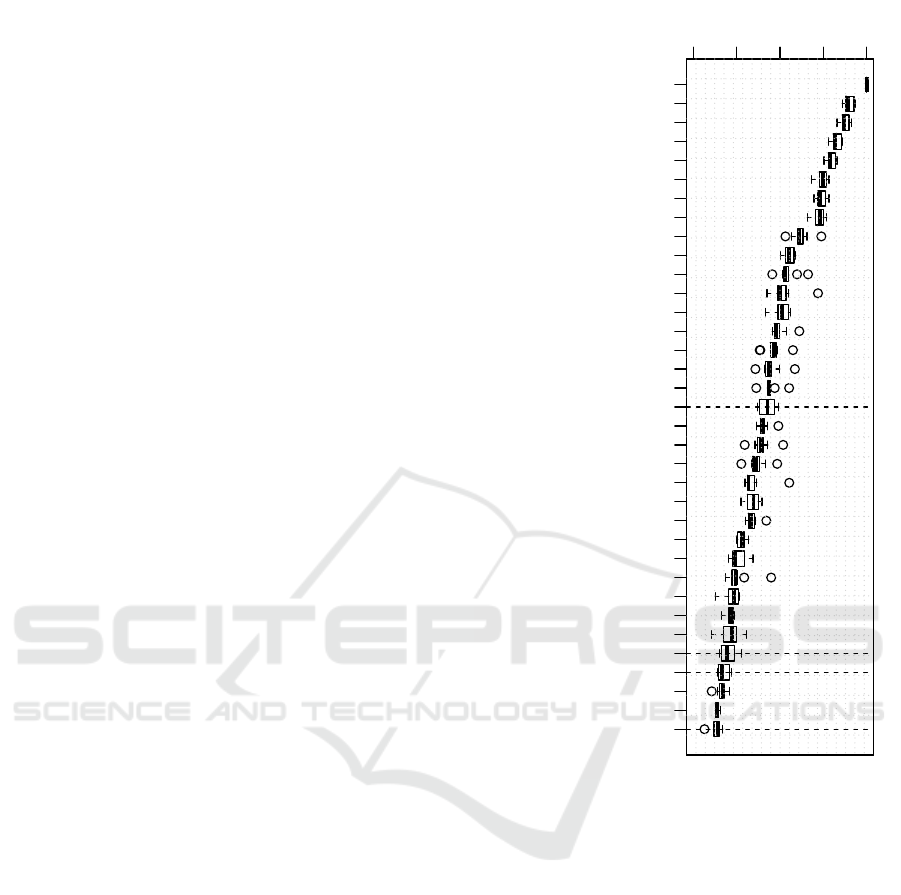
pact that proposed characteristics have in the model.

According to this analysis, the 35 most important

features are shown on Figure 4. RP based character-

istics are signaled with horizontal dotted lines.

The complexity on the raw sequence is consis-

tently the most valuable feature for discrimination. It

is followed in relevance by the tuned scale IDPHy-

dropathy and other already well known descriptors. It

is notorious that the simple dot product metric, quan-

tifying difference between marginal probabilities of

φ and ψ consecutive amino acids, scored high in rel-

evance. Some of the proposed characteristics were

ranked also in this elite set, concretely: KL Marginal

Angles (eps), KL Marginal Angles (freqs) and KL Di-

vergence on RP. From this data, can be stated that the

Kullback-Leibler divergence metrics on the marginals

of RP distributions were key to reach the discrimina-

tive power of the model.

4 DISCUSSION AND

CONCLUSIONS

Ramachandran Plot’s importance in the determination

of secondary and tertiary structure have been clearly

recognized for many decades. Torsion angles between

amino acids determine unequivocally the structural

folding of proteins and thus RPs have been used as

complementary tool for predicting and evaluating ex-

perimental found conﬁgurations of thousands of pro-

teins. In this sense, RPs can be interpreted as proba-

bility distributions that allow to quantify the statistical

preference that known proteins obey in relation with

their torsion angles and secondary structure state.

In the case of disordered proteins, the challenge is

immense because torsion angles between these amino

acids explore continually many conﬁguration states

without converging to any particular point. The pro-

posed features in this work, which are based on in-

formation theory metrics on the RPs, explore the

discrimination capability of the information obtained

from torsion angles of the chain. According to the

results, the proposed metrics contain relevant infor-

mation that can be used in combination with conven-

tional features in the state-of-art, in order to improve

the accuracy in the identiﬁcation of disorder. Taking

into account that the proposed features are estimated

from RPs, they can be considered fast and easy to

compute. Therefore, their use in proteome-wide anal-

ysis can be introduced easily.

Structural limitations permit to assume that amino

acids in disorder, are also conﬁned to the allowed re-

gions in the RPs, but the dynamical rules governing

torsion angle variation remain unknown. For some

Complexity

IDPHydropathy

BASU050102

NISK860101

WERD780101

topIDPScale

AAIndex PCA 1

VINM940101

Pseudo Amino Acid 1

RADA880108

Pseudo Amino Acid 6

Pseudo Amino Acid 2

GUYH850101

Pseudo Amino Acid 8

Amino Acid I

Pseudo Amino Acid 5

Pseudo Amino Acid 7

Dot Product Marg. Angles

GEIM800108

Pseudo Amino Acid 10

Pseudo Amino Acid 9

Pseudo Amino Acid 4

Amino Acid F

Amino Acid L

ss_coil

Amino Acid P

Pseudo Amino Acid 3

KYTJ820101

CHAM820102

Amino Acid Y

KL Marginal Angles (eps)

KL Marg. Angles (freqs)

NAKH920105

BLAM930101

KL Divergence on RP

60 70 80 90 100

Figure 4: Boxplots of Feature Relevance for the 35 most

important features on the 10 CV SVM model, trained on

SL329 Dataset. Importance is measured in a 0-100 scale,

being 100 the value of the most important feature. Horizon-

tal lines signal the proposed RP derived features.

IDR their propensities to shape into an speciﬁc sec-

ondary structure after binding, show that assuming

completely randomness on the torsion angles of dis-

ordered amino acids is almost surely not appropriate

(Uversky, 2013). In the context of IDPs, empirical

known RPs can be considered as statistical cumula-

tive values from a related process focused in folding

the protein; process that is intentionally and subtly

avoided by the disordered amino acids. Accordingly,

the empirical RPs give indirect indications of the dis-

order in proteins and can be used as source of infor-

mation for training disorder predictors. The combina-

tion of the proposed features and CRF reached better

performance than state-of-art predictors on the evalu-

ated data set, without the need of include a previous

MSA stage. This encourages future work in the im-

Protein Disorder Prediction using Information Theory Measures on the Distribution of the Dihedral Torsion Angles from Ramachandran

Plots

provement of the characterization phase based on the

RPs and the evaluation of other classiﬁcation strate-

gies, that can take even more advantage of the new

features. It is clear also that the proposed method-

ology must be evaluated on large data sets as those

resources become available.

REFERENCES

Altschul, S. F., Madden, T. L., Sch

affer, A. A., Zhang,

J., Zhang, Z., Miller, W., and Lipman, D. J. (1997).

Gapped blast and psi-blast: a new generation of pro-

tein database search programs. Nucleic acids re-

search, 25(17):3389–3402.

Baldi, P., Brunak, S., Chauvin, Y., Andersen, C. A., and

Nielsen, H. (2000). Assessing the accuracy of predic-

tion algorithms for classiﬁcation: an overview. Bioin-

formatics, 16(5):412–424.

Baruah, A., Rani, P., and Biswas, P. (2015). Conforma-

tional entropy of intrinsically disordered proteins from

amino acid triads. Scientiﬁc reports, 5.

Berkholz, D. S., Krenesky, P. B., Davidson, J. R., and

Karplus, P. A. (2009). Protein Geometry Database:

a ﬂexible engine to explore backbone conformations

and their relationships to covalent geometry. Nucleic

acids research, page gkp1013.

Bulashevska, A. and Eils, R. (2008). Using Bayesian multi-

nomial classiﬁer to predict whether a given protein se-

quence is intrinsically disordered. Journal of theoret-

ical biology, 254(4):799–803.

Campen, A., Williams, R. M., Brown, C. J., Meng, J.,

Uversky, V. N., and Dunker, A. K. (2008). TOP-

IDP-scale: a new amino acid scale measuring propen-

sity for intrinsic disorder. Protein and peptide letters,

15(9):956.

Chou, K.-C. (2001). Prediction of protein cellular attributes

using pseudo-amino acid composition. Proteins:

Structure, Function, and Bioinformatics, 43(3):246–

255.

Das, R. K., Ruff, K. M., and Pappu, R. V. (2015). Relating

sequence encoded information to form and function

of intrinsically disordered proteins. Current opinion

in structural biology, 32:102–112.

DeForte, S. and Uversky, V. N. (2016). Order, disorder, and

everything in between. Molecules, 21(8):1090.

Deng, X., Eickholt, J., and Cheng, J. (2012). A compre-

hensive overview of computational protein disorder

prediction methods. Molecular BioSystems, 8(1):114–

121.

Dosztnyi, Z., Csizmok, V., Tompa, P., and Simon, I. (2005).

IUPred: web server for the prediction of intrinsically

unstructured regions of proteins based on estimated

energy content. Bioinformatics, 21(16):3433–3434.

Dunker, A. K., Oldﬁeld, C. J., Meng, J., Romero, P., Yang,

J. Y., Chen, J. W., Vacic, V., Obradovic, Z., and Uver-

sky, V. N. (2008). The unfoldomics decade: an update

on intrinsically disordered proteins. BMC genomics,

9(Suppl 2):S1.

Faraggi, E., Yang, Y., Zhang, S., and Zhou, Y. (2009). Pre-

dicting continuous local structure and the effect of its

substitution for secondary structure in fragment-free

protein structure prediction. Structure, 17(11):1515–

1527.

Faraggi, E., Zhang, T., Yang, Y., Kurgan, L., and Zhou, Y.

(2012). SPINE X: improving protein secondary struc-

ture prediction by multistep learning coupled with

prediction of solvent accessible surface area and back-

bone torsion angles. Journal of computational chem-

istry, 33(3):259–267.

He, B., Wang, K., Liu, Y., Xue, B., Uversky, V. N., and

Dunker, A. K. (2009). Predicting intrinsic disorder in

proteins: an overview. Cell research, 19(8):929–949.

Hollingsworth, S. A. and Karplus, P. A. (2010). A fresh look

at the Ramachandran plot and the occurrence of stan-

dard structures in proteins. Biomolecular concepts,

1(3-4):271–283.

Huang, F., Oldﬁeld, C. J., Xue, B., Hsu, W.-L., Meng,

J., Liu, X., Shen, L., Romero, P., Uversky, V. N.,

and Dunker, A. K. (2014). Improving protein order-

disorder classiﬁcation using charge-hydropathy plots.

BMC bioinformatics, 15(Suppl 17):S4.

Jones, D. T. and Cozzetto, D. (2014). DISOPRED3: precise

disordered region predictions with annotated protein-

binding activity. Bioinformatics, page btu744.

Kawashima, S. and Kanehisa, M. (2000). AAindex:

amino acid index database. Nucleic acids research,

28(1):374–374.

Lafferty, J., McCallum, A., and Pereira, F. (2001). Con-

ditional random ﬁelds: Probabilistic models for seg-

menting and labeling sequence data. In Proceedings of

the 18h International Conference on Machine Learn-

ing - ICML 2001, pages 282–289.

Lieutaud, P., Canard, B., and Longhi, S. (2008). MeDor: a

metaserver for predicting protein disorder. BMC ge-

nomics, 9(Suppl 2):S25.

McGufﬁn, L. J., Bryson, K., and Jones, D. T. (2000). The

PSIPRED protein structure prediction server. Bioin-

formatics, 16(4):404–405.

Oates, M. E., Romero, P., Ishida, T., Ghalwash, M.,

Mizianty, M. J., Xue, B., Dosztnyi, Z., Uversky, V. N.,

Obradovic, Z., Kurgan, L., and others (2013). D2p2:

database of disordered protein predictions. Nucleic

acids research, 41(D1):D508–D516.

Peng, Z., Yan, J., Fan, X., Mizianty, M. J., Xue, B., Wang,

K., Hu, G., Uversky, V. N., and Kurgan, L. (2015).

Exceptionally abundant exceptions: comprehensive

characterization of intrinsic disorder in all domains of

life. Cellular and Molecular Life Sciences, 72(1):137–

151.

Potenza, E., Di Domenico, T., Walsh, I., and Tosatto, S. C.

(2015). MobiDB 2.0: an improved database of intrin-

sically disordered and mobile proteins. Nucleic acids

research, 43(D1):D315–D320.

Sickmeier, M., Hamilton, J. A., LeGall, T., Vacic, V.,

Cortese, M. S., Tantos, A., Szabo, B., Tompa, P.,

Chen, J., Uversky, V. N., and others (2007). DisProt:

the database of disordered proteins. Nucleic acids re-

search, 35(suppl 1):D786–D793.

BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms

Sirota, F. L., Ooi, H.-S., Gattermayer, T., Schneider, G.,

Eisenhaber, F., and Maurer-Stroh, S. (2010). Parame-

terization of disorder predictors for large-scale appli-

cations requiring high speciﬁcity by using an extended

benchmark dataset. BMC genomics, 11(Suppl 1):S15.

Uversky, V. N. (2013). Unusual biophysics of intrinsically

disordered proteins. Biochimica et Biophysica Acta

(BBA)-Proteins and Proteomics, 1834(5):932–951.

Uversky, V. N., Oldﬁeld, C. J., and Dunker, A. K. (2008).

Intrinsically disordered proteins in human diseases:

introducing the D2 concept. Annu. Rev. Biophys.,

37:215–246.

Vapnik, V. N. (1998). Statistical Learning Theory. Wiley-

Interscience.

Varadi, M., Vranken, W., Guharoy, M., and Tompa, P.

(2015). Computational approaches for inferring the

functions of intrinsically disordered proteins. Fron-

tiers in molecular biosciences, 2.

Venkatarajan, M. S. and Braun, W. (2001). New quantitative

descriptors of amino acids based on multidimensional

scaling of a large number of physicalchemical proper-

ties. Molecular modeling annual, 7(12):445–453.

Walsh, I., Martin, A. J., Di Domenico, T., and Tosatto, S. C.

(2012). ESpritz: accurate and fast prediction of pro-

tein disorder. Bioinformatics, 28(4):503–509.

Xue, B., Dunbrack, R. L., Williams, R. W., Dunker,

A. K., and Uversky, V. N. (2010). PONDR-FIT: a

meta-predictor of intrinsically disordered amino acids.

Biochimica et Biophysica Acta (BBA)-Proteins and

Proteomics, 1804(4):996–1010.

Zhang, T., Faraggi, E., Xue, B., Dunker, A. K., Uversky,

V. N., and Zhou, Y. (2012). SPINE-D: accurate predic-

tion of short and long disordered regions by a single

neural-network based method. Journal of Biomolecu-

lar Structure and Dynamics, 29(4):799–813.

APPENDIX

Physic-chemical Properties

Several sets of physic-chemical properties were ex-

tracted from AAindex (Kawashima and Kanehisa,

2000), by applying hierarchical and k-means cluster-

ing for identifying relevant partitions. From every

subset, a representative indice was picked up. These

features are listed in Table 3. Additionally, the proper-

ties proposed in (Venkatarajan and Braun, 2001) were

also used. They were named as AAIndex PCA 1-

5. Fine tuned hydrophobicity scales from (Campen

et al., 2008) and (Huang et al., 2014) were also added.

These features are named in this work as topIDPScale

and IDPHydropathy.

Table 3: Physic-chemical properties used from AAIndex 1.

AAindex Code Description

KYTJ820101 Hydropathy index

ZIMJ680104 Isoelectric point

WERD780101 Propensity to be buried inside

VINM940101 Normalized ﬂexibility parameters

CHAM820101 Polarizability parameter

CHAM820102 Free energy of solution in water

CHOC760101 Residue accessible surface area

COHE430101 Partial speciﬁc volume

JOND920102 Relative mutability

FAUJ880104 Length of the side chain

CRAJ730103 Normalized frequency of turn

BURA740102 Normalized frequency structure

ROSM880103 Loss of Side chain hydropathy

GEIM800108 Aperiodic indices

RICJ880109 Relative preference value at Mid

ANDN920101 alpha-CH chemical shifts

BEGF750103 Conformational parameter of beta-turn

BUNA790103 Spin-spin coupling constants

ZIMJ680102 Bulkiness

OOBM770105 Short range non-bonded energy

YUTK870103 Unfolding Activation Gibbs energy

GUYH850101 Partition energy

BLAM930101 Alpha helix propensity

RADA880108 Mean polarity

TSAJ990102 Volumes not including cryst. waters

NAKH920105 AA composition of MEM

CEDJ970104 AA composition intracellular proteins

NISK860101 14 A contact number

BASU050102 Interactivity scale

Pseudo Amino Acid Composition Set

Amino acid composition in windows of size 15 in

the protein, enriched with pseudo amino acid counts

were used (Chou, 2001). These features were named

Amino Acids A, C, D, E, F, G, H, I, K, L, M, N, P,

Q, R, S, T, V, W, Y, and Pseudo Amino Acids 1 to 10

respectively.

Secondary Structure Features

Secondary structure prediction have a strong rela-

tion with the prediction of disorder. In fact, sev-

eral methods created initially for detecting secondary

shapes were adapted for ﬁnding IDPs. In this work

the probability output of secondary structure predic-

tor PSIPRED (McGufﬁn et al., 2000) was used. Al-

though the predictions from PSIPRED can be im-

proved if the input includes a multiple sequence align-

ment, such procedure was not made for avoiding any

intensive computation delay. Features from PSIPRED

were called ss helix, ss beta and ss coil.

Protein Disorder Prediction using Information Theory Measures on the Distribution of the Dihedral Torsion Angles from Ramachandran

Plots