Comparison of Network Topologies by Simulation of Advertising

Imre Varga

Department of Informatics Systems and Networks, University of Debrecen,

Kassai str. 26, H-4028 Debrecen, Hungary

Keywords:

Network Topology, Information Spreading, Clustered Systems, Effectiveness of Advertising.

Abstract:

Information spreading processes and advertising strategies are often studied by different epidemic models on a

given topology. The goal ofthis paper isto discover and summarize the effect of underlying network topologies

on a general spreading process. A complex set of different networks is studied by computer simulations from

regular networks through random networks to different scale-free network topologies. The speed of spreading

and the micro-scale features of these systems highlight the differences caused by different network topologies.

This may help to plan for example advertising strategies on different social networks.

1 INTRODUCTION

In the last years, the intensively growing network

science showed that our natural, technical and so-

cial environment is full of different kind of networks

(Newman, 2010). One can observe and study a

large amount of spreading processes over these net-

works such as disease spreading (Shirley and Rush-

ton, 2005; Eames, 2007), rumor and gossip spreading

(Domenico et al., 2013; Lind et al., 2013), diffusion

of innovations (Rogers, 2003; Kun et al., 2007) or

spreading on technological networks (Pastor-Satorras

and Vespignani, 2001; Karsai et al., 2011; Buzna

et al., 2006). All of them are important from eco-

nomic, social and scientiﬁc point of view. However,

this ﬁeld is intensively studied nowadays new scien-

tiﬁc results unfold new questions.

The goal of this paper is to perform an overall

study of the effect of the network topology on a gen-

eral information spreading process. In the literature,

one can ﬁnd studies of topology comparison related

to technological or biological processes. They mainly

based on either SIS or SIR or SIRS spreading mod-

els (Wang et al., 2003; Ganesh et al., 2005; Pastor-

Satorras et al., 2015) and various sets of network

structures from regular to complex ones. However,

the clustered scale-free networks, which are very re-

alistic from the social point of view, are still undis-

covered. Moreover, the most of the published works

can handle only one information channel. Our ap-

plied model can describe state change either purely

driven by an outer ﬁeld (as in the case of percolation)

or spreading based on only personal contacts (such

as disease spreading) or spreading where the previous

two channels compete (advertising and human com-

munication) similar to (Kocsis and Kun, 2011). In the

latter case, new nuclei of spreading appear continu-

ously in time and then start to growmaking the system

more complex. The analyzed networks are selected

from different network classes. The far aim is to be

able to predict somehow effectiveness of advertising

based on the information spreading results. Whether

it is worth to spend more money on advertising or the

interpersonal communication is enough to speed up

the awareness about a product? If the advertising ef-

fort is constant, can a service be well known soon by

a clustered society? Does the degree distribution of

the society have an effect to the number of informed

people during a time-limited campaign? If the contact

pattern in the public is given, what can we expectfrom

our advertising strategy? When the news reached the

half of the society, are the informed and uninformed

individuals forming large segregated clusters or the

society becomes a steady mixture of them? It is very

difﬁcult to answer these questions. Thus ﬁrst we have

to know the details of simple spreading processes.

In Sec. 2 a detailed description of the different

studied static network topologies is presented. It is

followed by the introduction of the applied spreading

model and the simulation technique in Sec. 3. The

particular results can be found in Sec. 4. Based on

these ones can understand how the topology changes

the features of the spreading process. Then the work

is closed by conclusions and consequences in Sec. 5.

Varga, I.

Comparison of Network Topologies by Simulation of Advertising.

DOI: 10.5220/0006142100170022

In Proceedings of the 2nd International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2017), pages 17-22

ISBN: 978-989-758-244-8

2 UNDERLYING NETWORK

TOPOLOGIES

During the information spreading simulations, several

different undirected network topologies were studied

from different classes of networks from regular lat-

tices to scale-free networks. All the networks contain

N = 10

nodes, the average number of neighbors is

hki = 6, so the densities of the networks are the same

keeping them comparable. Nevertheless, the micro-

scale topologies differ completely. The following net-

works are studied.

• Network A: regular 2D triangular network.

Nodes are on a plain according to the vertices

of a triangular/hexagonal lattice periodically, so

there are no borders of the lattice. In this way

all vertices are connected by the same amount of

edges. The degree distribution can be described

by a Kronecker-delta (P(k) = δ

). The average

shortest path length hLi covers hundreds of con-

nections (large network diameter) and the average

clustering coefﬁcient hCi is high in this regular

structure. (Exact values for this and for the up-

coming networks can be found in Table 1.)

• Network B: regular spatial (3D) primitive cubic

network. The unit cell of the structure is a cube.

In order to ensure the equality of all nodes, the

system is periodic avoiding the side effects of the

ﬁnite size. The degree distribution can be given

in the same way as in the previous case, but due

to the 3D structure the characteristic path length

is smaller than in network A. In this lattice none

of the neighbors of any node are connected to

other neighbors, so the clustering coefﬁcients of

all nodes are exactly 0.

• Network C: random network. N nodes are

connected by 3N links choosing the connected

nodes randomly, avoiding self-loops and dupli-

cated links. If the ﬁnal system contains discon-

nected nodes or small separate clusters only the

giant component is studied ensuring contiguous

system. These networks have small-world prop-

erty so their characteristic path length is tiny com-

pared to the system size. The connection trian-

gles are very rare in these random graphs so the

clustering coefﬁcient is almost zero. (Erd˝os and

R´enyi, 1959; Watts and Strogatz, 1998)

• Network D: rewired ’small-world’ network.

Starting from a regular ring lattice, where each

node is connected to its 6 nearest neighbors. We

apply a rewiring process. Links are chosen by

β probability to be rewired, so a chosen link is

removed and two new nodes are connected by a

new link chosen by equal probability (avoiding

self-loops and duplicated links). In the studied

rewired network β = 0.1 is used to ensure small-

world property with high clustering. (Watts and

Strogatz, 1998)

• Network E: scale-free network of the Barab´asi-

Albert model. Using preferential attachment in

the linking method the result is a network with de-

gree distribution obeying power-law function with

exponent γ = 3. In the case of our system size, the

distances between nodes and the clustering coef-

ﬁcient are both quite small. (Barab´asi and Albert,

1999; Albert and Barab´asi, 2002)

• Network F: Clustered scale-free network. While

scale-free networks are so frequent in our envi-

ronment simple BA networks cannot capture the

clustered structure of for example the human in-

teractions. The ‘friend of my friend is my friend’

effect can be captured by the method published

in (Varga, 2015). Here the linking method of a

growing network consists not just the preferential

attachment but triplet formation steps as well. The

result is a scale-free network (with the same de-

gree distribution exponent as BA networks) with

high clustering in the case of large systems.

Table 1: Summery of the average shortest path length hLi

and the average clustering coefﬁcient hCi of the studied net-

work topologies in case of N = 10

and hki = 6.

hLi hCi

network A 397.0 0.400000

network B 74.4 0.000000

network C 7.9 0.000007

network D 13.1 0.448380

network E 5.9 0.000011

network F 7.9 0.617884

The chosen networks belong to different network

classes summarizing as follows. Network A and net-

work B are regular networks, while others have small-

world property. Only network E and network F are

scale-free networks. Network A, network D and net-

work F are clustered systems, only they have high

clustering coefﬁcient. (See Table 1.)

3 INFORMATION SPREADING

SIMULATIONS

Discrete-time agent-based simulations are carried out

on the underlying networks described in Sec. 2. Here

nodes represent the agents, while links mean personal

connections between them. Each agent has 2 distinct

states denoted by A

(t):

COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk

• A

= 0: uninformed state, no awareness, no opin-

ion

• A

= 1: informed state, agent has awareness of

something or has (positive or negative) opinion

During the simulated time evolution of the system

two information channels have inﬂuenceon the agents

(Kocsis and Kun, 2011):

• Vertical channel: mass media, advertisement

• Horizontal channel: word-of-mouth, interper-

sonal communication

The dynamics of the system are described by an SI

(Susceptible-Infected)epidemic model, where in each

time step each agent can remain in its previousstate or

an uninformed agent can became informed. There is

no way of an informed agent to forgetinformation and

get back to the uninformed state. The state-change

probability of uninformed agent i to become informed

state can be given as

(p, q) = 1−exp



−q



∑

+ (1− p)(1− A

)



(1)

where p and q are the parameters of the model, j

runs over the neighbors of agent i and N

is the num-

ber of neighboring agents of agent i. The value of

p gives the probability of spreading P

(interpersonal

communication), while the probability of nucleation

is P

= 1− p (the effect of the advertisement, the birth

of pioneers). This parameter has two special values.

If p = 0, we can get pure percolation without spread-

ing. By p = 1 we can exclude the inﬂuence of mass

media. Parameter q is just a strength factor, so larger q

leads to faster time evolution (less time to reach satu-

ration). The term p

∑

describes the spreading.

It expresses that one can have higher chance to hear a

given information about an advertised product or ser-

vice from his/her friends if most of them are already

informed. In this way not the number of informed

friends are important, but the ratio of them in con-

trast to the model of (Kocsis and Kun, 2011). This is

a very important difference, but not the only one. In

our model only one parameter (p) is enough to handle

both channels, because it was found that the ratio of

the sensitivity of the two channels is relevant.

Our system can be also applied to model spreading

of innovations, where the beneﬁt of changing a device

to a higher level one is signiﬁcant, if it is compatible

with most of the friends’ devices. This term can de-

scribe a kind of opinion formation method as well.

One can judge something or form an opinion about

something if he/she knows more points of view (in-

dependently of the nature of friends’ opinions). Our

opinion, which can be imagined as a special kind of

information, can also be based on outer information

sources (advertising, mass-media). Its probability is

described by the term (1− p)(1− A

) in Eq. 1. In in-

novation spreading context this is the motivation of

individuals to be a pioneer user or an early buyer.

The exponential function is necessary just to get a

monotonicfunction between 0 and 1 (Kocsis and Kun,

2011). At the initial state all agents are in the un-

informed state, then we can follow the time evolution

of the system {A

(t)}

i=1,...,N

by computer simulations.

Spreading is in the focus of the recent research, so

p > 0.1 cases are analyzed. The runs were stopped

when saturation was reached. In the following anal-

ysis, tens of independent runs were averaged. Due to

this and the large size of the networks (N = 10

) ran-

dom effects and statistical noise are eliminated. The

simulation software is developed by the author.

4 SIMULATION RESULTS

4.1 Macro-scale Behavior

After the initial state due to the nucleation a few

agents become informed continuously. Then commu-

nication become more and more dominant as infor-

mation spreads from neighbor to neighbor. While the

state change is irreversible sooner or later every agent

will be informed. This process can be characterized

by the average number of informed agents

hAi(t) =

∑

i=1

(t)

. (2)

The time evolution of the system can be described

by hAi(t) which shows saturation following the func-

tional form

hAi(t) = (1− e

−qt

)

1+ e

−α(t−t

)

, (3)

where the ﬁrst factor illustrates percolation due to nu-

cleation, while the second factor is a logistic function

representing spreading. In Eq. 3 t

indicates the loca-

tion of the inﬂection point of logistic function and α

is the slope of tangential of the curve at the inﬂection

point. These values characterize the spreading pro-

cess. The shape of hAi(t) curve is always the same.

When spreading is dominant the ﬁrst factor is negli-

gible in Eq. 3, so independently of the network topol-

ogy and the given values of the parameters p and q

one can get logistic function form. Rescaling time

axis by t

′

= α(t − t

) all the curves fall to the same

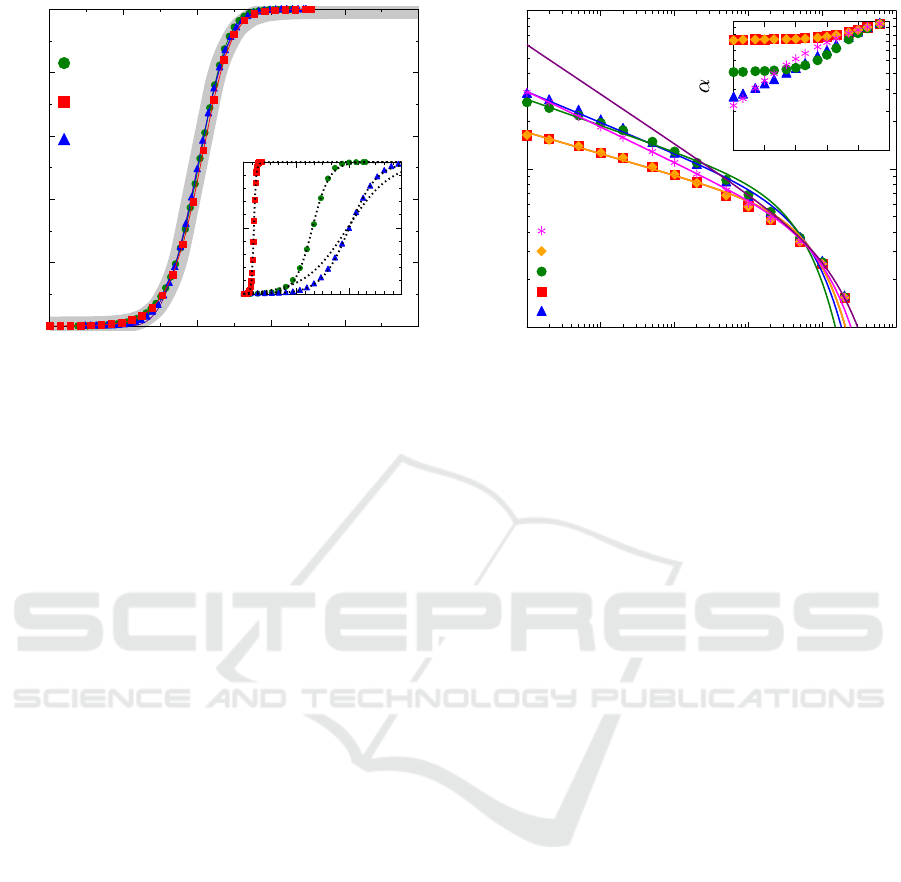
curve getting data collapse. It is illustrated in Fig. 1.

The speed of the spreading is measured by

the change of average number of informed agents

Comparison of Network Topologies by Simulation of Advertising

0.0

0.2

0.4

0.6

0.8

1.0

-10 -5 0 5 10 15

♣

network A

1-p=10

-4

, q=0.1

network D

1-p=10

-4

, q=0.1

network E

1-p=10

-4

, q=0.3

network F

1-p=10

-5

, q=0.1

0.0

0.5

1.0

0 150 300 450

♣

hAi

′

= α(t − t

)

hAi

Figure 1: (Color online.) The time evolution of four sys-

tems with different underlying network topology and dif-

ferent values of parameters p and q. The average level of

informed agent as a function of time hAi(t) is shown in the

inset (dashed curves are ﬁtted by logistic form). Rescaled

time leads to data collapse as demonstrated on the main

panel. The gray track indicate the general logistic function.

∆hAi (t) = α/4, which is the derivative of hAi(t) with

a maximum at the inﬂection point t

. In this way, α

and t

determine the spreading process. It is impor-

tant to know how these values depend on the network

topology and on the parameters p and q. Large num-

ber of simulations have been carried out in a board pa-

rameter range to discover the parameter space. While

q is just a kind of strength factor, its role proved to

be simple. The location of the inﬂection point is in-

versely proportional to q, while the top speed of the

spreading is directly proportional to this parameter, so

∝ q

−1

and α ∝ q independently of the topology.

The effect of parameter p is not so simple. Sim-

ulation results show that the place of the inﬂection

point as a function of parameter p can be ﬁtted by a

power-law function with exponential cut-off follow-

ing the form

= ax

−b

exp(−x/c), (4)

where coefﬁcients a, b and c depend on the network

topology, but the function form is independent. (See

the main panel of Fig. 2.) The top speed of spreading

characterized by α behaves in different way tuning

the dominance of vertical information channel so the

advertising effort. In case of differentnetwork topolo-

gies the shape of α(p) is completely different. If the

topology of human interaction is similar to a simple

random network (topology C) or rewired WS topol-

ogy (network D) or scale-free BA network (topology

E) then there is a range where advertising does not

increase the slope of hAi(t) resulting in constant α.

Meanwhile in the case of regular (network topology A

110

-1

-2

-3

-4

-5

1-p

♣

network A

network B

network C

network D

network E

network F

-2

-1

110

-1

-2

-3

-4

-5

1-p

♣

Figure 2: The maximum of spreading speed appears ear-

lier (smaller t

), if mass-media is deﬁnitely present (large

p) not just the personal interactions. The simulation results

are ﬁtted by Eq. 4. Inset: The maximal slope of the logistic

function of average number of informed agent hAi in the in-

fection point is monotonically increasing by increasing the

weight of advertising, but the underlying network topology

has a very strong inﬂuence to the shape of the curves as one

can see.

and B) and clustered scale-free networks (topology F)

stronger mass-media results in more informed agents

within a given time interval. (See the inset of Fig. 2.)

4.2 Micro-scale Behavior

The average number of informed agents is a macro-

scopic feature of the system, but does not tell any-

thing about the spreading process in a micro-scale. In

this model the vertical information channel creates in-

formed agent as a kind of nucleus, while the horizon-

tal channel leads to the growing of this small clus-

ter of informed agent(s). So at the beginning of the

time evolution more and more small clusters appear

step-by-step, then the neighboring uninformed agents

get a chance to become informed due to the spreading

process, so the separate clusters start to grow. In this

phase the number of clusters N

is equal to the number

of nuclei which is determined by parameters p and q,

but does not inﬂuenced by the network topology be-

cause initial time evolution is similar to percolation.

Thus the number of informed clusters N

as a func-

tion of time increases linearly with a slope depending

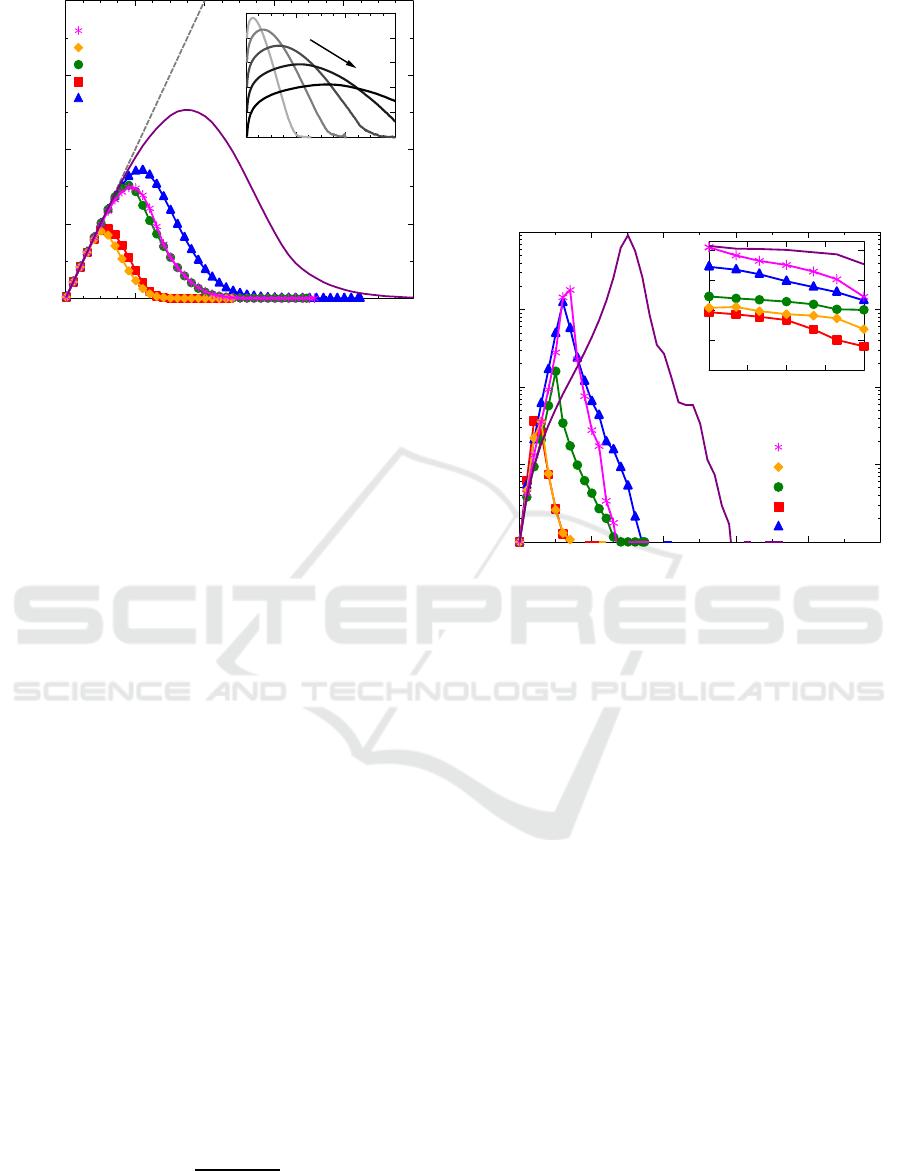
only on the parameters p and q. It is shown in the

main panel of Fig. 3, where the N

(t) curves start with

the same linear section indicated by the gray dashed

line.

Meanwhile newer nuclei appear again and the

small clusters grow continuously the distance of clus-

COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk

500

1000

1500

2000

0 100 200 300 400 500

♣

network A

network B

network C

network D

network E

network F

0 100 200 300

Figure 3: The number of clusters N

built from informed

agents as a function of time. First all networks behave in the

same way illustrated by the gray dashed line (its slope de-

pends on parameter q), then the system reaches a topology

dependent maximum of the number of clusters. Here the

decreasing curves show merging of growing clusters. Inset:

(t) curves at different value of parameter p. Increasing

the dominance of horizontal information channel (increas-

ing p is marked by arrow) the maximum number of clusters

is decreasing and the clusters start to merge later.

ters starts to decrease. Sooner or later (depending on

the topology) clusters merge together forming larger

clusters. Due to this merging, the number of clus-

ters N

(t) reaches its maximum and then starts to de-

crease. Finally all the informed agents belong to the

same cluster called giant component. The time t

max

needed to reach the maximum of N

(t) and the max-

imum number of clusters N

max

) at given values of

p and q depends on the topology as one can see in

Fig. 3. Not just the average shortest path length hLi,

but the average clustering coefﬁcient hCi as well is

important from this point of view. For example, the

characteristic path length of network B is almost 10

times larger than in case of network F, so one can

think that the average distance between clusters are

larger so clusters in network B can merge together

later than in network F. The results disprove this as-

sumption, N

(t) reaches maximum earlier in the case

of network B, than in network F due to high hCi.

The size of the clusters of informed agents is con-

tinuously increasing due to the spreading of informa-

tion and the merging of clusters. Average cluster size

hSi(t) is usually deﬁned by the second moment of the

cluster size distribution excluding the giant compo-

nent. It is given in form

hSi =

∑

(t)

∑

(t)

, (5)

where n

(t) is the dynamic cluster size distribution or

the number of clusters involving S informed agents.

First hSi(t) is increasing exponentially then it reaches

a sharp peak and then decreases exponentially. The

reason of the presence of this peak is the fact that the

giant component is excluded. Thus in the growing

phase, the sizes of clusters are increasing rapidly, then

one of the clusters become dominant and it annexes

other clusters. In this way as time passes just smaller

and smaller clusters remain unconnected/isolated re-

sulting in decreasing average cluster size. See Fig. 4.

0 200 400 600 800 1000

♣

network A

network B

network C

network D

network E

network F

-1

-2

-3

-4

-5

♣

♣♣

hSi

max

1 − p

Figure 4: Average cluster size hSi (deﬁned by Eq. 5) as a

function of time has sharp peak which strongly depends on

the topology. Inset: The maximum of the average cluster

size weakly depends on parameter p. As one can see net-

work topology results in larger differences than any change

in the spreading model parameter.

The time where the peak appears means when the

society continuously tends to be informed not just a

set of informed groups. If the peak is low it means

that giant component is very dominant, while high

peaks indicate clustered society with quasi-equivalent

domains of informed agents. Real social networks are

often modeled by scale-free networks, but by compar-

ing network E and F one can see large differences. In

BA networks small number of clusters are present and

their average size is also small due to the huge giant

component. In contrary in clustered scale-free topol-

ogy (network F) there can be double amount of clus-

ters with more than 10 times larger size so not just the

underlying network is clustered but also the informed

agent system over the topology. It can inﬂuence the

effectiveness of advertising as well. The large differ-

ences of the average cluster size peak hSi

max

in case of

different topologies are present independently of the

strength of vertical information channel (advertising)

determined by 1− p. See the inset of Fig. 4. To get an

appropriate advertising strategy not only the spread-

ing model but also the underlying network topology

is important.

Comparison of Network Topologies by Simulation of Advertising

5 CONCLUSIONS

Recent simulation results have shown out that al-

though the underlying networks have the same size

and density the topologies of networks have a huge

inﬂuence on spreading processes. In this work the ap-

plied networks were chosen from different classes of

topologies to ﬁgure out that the characteristic proper-

ties of the spreading process depend on both the aver-

age path length and the average clustering coefﬁcient.

Although Barab´asi-Albert network and its clustered

variant are quite similar scale-free networks in the for-

mer one the speed of information spreading is much

faster. Naturally, the long distances of the planar tri-

angular lattice are the reason of the slow spreading

compared to the also regular spatial cubic network.

Usually longer paths and clustered communities lead

to slower spreading. It was also found that the de-

gree distribution of the network has only a small ef-

fect on the spreading. The random network and the

BA network behave in a similar way qualitatively and

quantitatively from several points of view, however

their degree distributions are completely different. As

it was mentioned both scale-free networks have the

same degree distribution exponent, but spreading on

them vary a lot.

Sometimes the network topology is much more

important than the parameters of the given spreading

model of competing channels, as it was demonstrated

by the analysis of size distribution of islands of in-

formed agents. It must be taken into account, when

we study real complex systems, where spreading is

important. From the application point of view micro-

scopic and macroscopic topological network proper-

ties must be considered in the planning stage. For ex-

ample to create an effective advertising strategy ﬁrst

the topological features of the underlying (online) so-

cial network must be studied. As several kinds of so-

cial research have highlighted the interaction network

of individuals can be described by clustered scale-free

network. Thus the application of regular structures

or simple preferential attachment without clustering

can result in a false prediction about the success of

the advertising campaign. Results of the recent study

point out some advantages and disadvantages of the

structural properties of several network topologies in

spreading processes.

REFERENCES

Albert, R. and Barab´asi, A.-L. (2002). Statistical mechanics

of complex networks. Reviews of Modern Physics,

74:47–97.

Barab´asi, A.-L. and Albert, R. (1999). Emergence of scal-

ing in random networks. Science, 286(5439):509–

512.

Buzna, L., Peters, K., and Helbing, D. (2006). Modelling

the dynamics of disaster spreading in networks. Phys-

ica A, 363(1):132–140.

Domenico, M. D., Lima, A., Mougel, P., and Musolesi, M.

(2013). The anatomy of a scientiﬁc rumor. Scientiﬁc

Reports, 3:2980.

Eames, K. T. (2007). Modelling disease spread through

random and regular contacts in clustered populations.

Theoretical Population Biology, 73:104–111.

Erd˝os, P. and R´enyi, A. (1959). On random graphs. i. Pub-

licationes Mathematicae, 6:290–297.

Ganesh, A., Massouli, L., and Towsley, D. (2005). The

effect of network topology on the spread of epidemics.

In Proceedings of IEEE INFOCOM, volume 2, pages

1455–1466.

Karsai, M., Kivel¨a, M., Pan, R. K., Kaski, K., Kert´esz, J.,

Barab´asi, A.-L., and Saram¨aki, J. (2011). Small but

slow world: How network topology and burstiness

slow down spreading. Physical Review E, 83:025102.

Kocsis, G. and Kun, F. (2011). Competition of information

channels in the spreading of innovations. Physical Re-

view E, 84:026111.

Kun, F., Kocsis, G., and Farkas, J. (2007). Cellular automata

for the spreading of technologies in socio-economic

systems. Physica A, 383(2):660–670.

Lind, P. G., da Silva, L. R., Andrade, J. S., and Herrmann,

H. J. (2013). Spreading gossip in social networks.

Physical Review E, 76:036117.

Newman, M. E. J. (2010). Networks - An Introduction. Ox-

ford University Press. 17-99.

Pastor-Satorras, R., Castellano, C., Mieghem, P. V., and

Vespignani, A. (2015). Epidemic processes in com-

plex networks. Reviews of Modern Physics, 87:925.

Pastor-Satorras, R. and Vespignani, A. (2001). Epidemic

spreading in scale-free networks. Physical Review

Letters, 86:3200.

Rogers, E. M. (2003). Diffusion of innovations. Free Press,

5th edition.

Shirley, M. D. F. and Rushton, S. P. (2005). The impact

of network topology on disease spread. Ecological

complexity, 2(3):287–299.

Varga, I. (2015). Scale-free network topologies with cluster-

ing similar to online social. In Proceedings of the In-

ternational Conference on Social Modeling and Sim-

ulation & Econophysics Colloquium, Proceedings in

Complexity, pages 323–333, Kobe, Japan. Springer.

Wang, Y., Chakrabarti, D., Wang, C., and Faloutsos, C.

(2003). Epidemic spreading in real networks: an

eigenvalue viewpoint. In IEEE Proceedings of 22nd

International Symposium on Reliable Distributed Sys-

tems, pages 25–34.

Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics

of ’small-world’ networks. Nature, 393(6684):440–

442.

COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk