Modiﬁed Krill Herd Optimization Algorithm using Focus Group Idea

Mahdi Bidar

, Edris Fattahi

, Malek Mouhoub

and Hamidreza Rashidy Kanan

Department of Computer Science, University of Regina, Regina, Canada

Department of Computer and Information Technology Engineering, Islamic Azad University, Marivan, Iran

Department of Computer Engineering, Shahid Rajaee Teacher Training University, Tehran, Iran

Keywords:

Metaheuristics, Evolutionary Computation, Krill Herd Algorithm, Exploration, Exploitation.

Abstract:

Krill Herd algorithm is one of most recently developed nature-inspired optimization algorithms which is in-

spired by herding behavior of krill individuals. In order to improve the performance of this algorithm to deal

more effectively with high dimensional numerical functions, we propose a new method, called Focus Group

idea to modify the solutions found by searching agents in group cooperation. In order to evaluate the effect of

the proposed method on the performance of the Krill Herd algorithm, we conducted experiments on a set stan-

dard benchmark functions. The obtained results demonstrate the ability of the proposed method to improve

the performance of the Krill Herd optimization algorithm.

1 INTRODUCTION

Recently the world has been grappling with high di-

mensional and complex real world optimization prob-

lems. The urgency for solving these challenging prob-

lems has caused heated discussion among scientist

in different areas (Yang and Press, 2010). It has

been proven that due to the high dimension of these

problems, the logical and classical methods cannot

come in useful, as using them is so time consum-

ing and in some cases inapplicable. Due to men-

tioned reasons, the meta-heuristic means which are

inspired by physical or biological processes would

be among the appropriate options. These evolution-

ary techniques have earned much popularity due to

their success in dealing with hard to solve problems

(Yang and Press, 2010). Although they do not guar-

antee ﬁnding the optimal solution, they have shown

impressive performance in accessing acceptable so-

lutions in very efﬁcient time. Two main compo-

nents of each meta-heuristic algorithm are explo-

ration and exploitation. Each meta-heuristic algo-

rithm uses a combination of these two components

which is the main reason why the related searches

are so powerful. Evolutionary techniques include Ge-

netic algorithms (GAs) which was developed based

on Darwinian theory (Goldberg and Holland, 1988;

Mitchell, 1998), Ant Colony Optimization (ACO), in-

spired by collective foraging behavior of ants (Dorigo

et al., 1996), PSO, inspired by bird ﬂocking and ﬁsh

schooling (Kennedy, 2011), vector-based evolution-

ary algorithm proposed by Storn (Storn and Price,

1995), Artiﬁcial Bee Colony (ABC), a further devel-

opment of ACO, proposed by Karaboga (Karaboga,

2005), Fireﬂy Algorithm (FA), inspired by ﬁreﬂies’

behavior in emitting light in order to attract other ﬁre-

ﬂies (Yang, 2010a), Gravitational Search Algorithm

(GSA), introduced based on the law of gravity and

mass interactions (Yang, 2010a), Bat-Inspired algo-

rithm (Rashedi et al., 2009) and Cuckoo Optimization

Algorithm (COA), inspired by eggs laying and breed-

ing characteristics of cuckoos (Yang, 2010b). Due to

their ability to deal with hard optimization problems,

these solving methods have been widely applied to

different areas including pattern recognition, control

objectives, image processing and ﬁlter modeling.

Krill Herd (KH) is a nature-inspired optimization

algorithm which was developed based on herding be-

havior of krill in the nature (Bhandari et al., 2014).

The minimum distances from the food and the high-

est density of the krill herds are considered as objec-

tives of the KH algorithm. Although meta-heuristic

algorithms are able to deal with different optimiza-

tion problems, enhancing and improving their perfor-

mance to deal with wider range of problems or be-

come able to deal with speciﬁc applications is an open

issue. Various ideas and methods such as chaotic

sequences or fuzzy methods have been applied and

combined with meta-heuristic algorithms to do so. In

this regard, we introduce a new method called Focus

Bidar M., Fattahi E., Mouhoub M. and Rashidy Kanan H.

Modiﬁed Krill Herd Optimization Algorithm using Focus Group Idea.

DOI: 10.5220/0006187904650472

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 465-472

ISBN: 978-989-758-220-2

465

Group to enhance the performance of the Krill Herd

algorithm when solving high dimensional numerical

functions. Focus Group is a method which tries to

modify the solutions found by group’s members in

a group discussion. Despite the other evolutionary

algorithms which concentrate on the use of the best

solutions, this method enables algorithms to consider

all the solutions found to reach the optimal one. To

evaluate the effect of this new method in improving

the performance of Krill Herd optimization algorithm,

we applied it to a set of standard benchmark func-

tions. The obtained results demonstrate the ability of

the proposed method in enhancing the performance of

Krill Herd algorithm.

2 KRILL HERD ALGORITHM

Krill Herd (KH) is a recently proposed meta-heuristic

optimization algorithm which was inspired by Krill’s

herding behavior to solve global optimization prob-

lems (Gandomi and Alavi, 2012). The ﬁtness func-

tion of each krill individual is deﬁned as its distances

from food and highest density of the swarm. The

time-dependent position of an individual krill is inﬂu-

enced by the following three main factors: the move-

ment induced by other krill individuals, the foraging

activities and the random diffusion. When hunters at-

tack krill, they remove krill individuals and this lead

to diminish their density. Formation of the krill herd

depends on many parameters. Increasing krill den-

sity and reaching food are considered as two main ob-

jectives of herding behavior after reducing krill den-

sity which these two lead the krill individuals to herd

around the global optima. In this process, an individ-

ual krill moves toward the ﬁttest individual that has

found the best solution when it searches for the high-

est density and food. So the closer the distance to the

high density and food, the better value is produced

by the objective function. Predators hunt individuals

and cause reduction of the average krill density, and

distances the krill swarm from the food location. In

the Krill Herd algorithm presented in Figure 1, the

ﬁtness of each individual is evaluated considering the

distance of that individual from the food and from the

highest density of the krill swarm.

For n dimensional decision space, the Krill Herd

algorithm conforms to the following Lagrangian

model:

= N

+ F

+ D

(1)

where N

is the motion induced by other krill individ-

uals in the herd, F

is the foraging motion and D

the physical diffusion of the ith krill individuals. The

Krill Herd Optimization Algorithm

begin

Initial parameter setting

Pre-calculation

Initial krill positions

For each iteration

Population evaluation

For each krill

Calculation of Best krill effect

Calculation of Neighbors Krill effect

Movement Induced

Calculation of food attraction

Calculation of best position attraction

Foraging motion

Physical diffusion

Motion process

Crossover and mutation

Update krill’s position

end

Update the current best

end

Figure 1: The pseudo-code of Krill Herd optimization algo-

rithm (Gandomi and Alavi, 2012).

movement of i-th krill can be considered as shown in

(2) in motion induced by other krill individuals.

new

= N

max

+ w

old

(2)

where

= α

local

+ α

t arget

(3)

where N

max

is the maximum induced speed, w

the inertia weight of the motion induced, N

old

is the

last motion induced and α is direction of movement.

local

is the local effect caused by neighbors and

target

is target direction effect caused by the best in-

dividual. The effect of the neighbors can be assumed

as an attractive/repulsive tendency between the indi-

viduals for a local search which is formulated as fol-

low:

local

∑

j=1

i, j

(4)

where

i j

−X



− X

+ ε

(5)

And also

t arg et

= C

best

i,best

(6)

where C

best

is the effective coefﬁcient of the krill in-

dividual with the best ﬁtness to the i-th krill individual

and deﬁned as follow:

best

= 2



rand +

max



(7)

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

466

where rand is a random values between 0 and 1 and

it is for enhancing exploration, I is the actual itera-

tion number and Imax is the maximum number of it-

erations. The foraging motion is proportional to two

main parameters, food location and previous experi-

ence about food location. This motion can be formu-

lated as follow:

= V

+ ω

old

(8)

where

= β

f ood

+ β

best

(9)

is the foraging speed, ω

is the inertia weight of

the foraging motion, F

old

is the last foraging motion

and β

f ood

is food attractive and β

best

is the effect of the

best ﬁtness of the i-th krill so far. Physical diffusion

of krill can be considered as (10):

= D

max

(1 −

max

)δ (10)

where D

max

is the maximum diffusion speed, δ is the

random directional vector, I and I

max

are i-th and max-

imum iteration number. The location vector of krill

during the interval t to t+1 is given by (11):

(t + ∆t) = X

(t) + ∆t

(11)

where ∆t is an important constant that should be care-

fully set based on the optimization problem. After

Motion calculation, to improve the performance of

KH algorithm, crossover and mutation operators are

added to algorithm.

3 FOCUS GROUP

The Focus Group (FG) idea is inspired by the behav-

ior of the members of a group in sharing, correct-

ing and improving their ideas on a speciﬁc topic until

reaching the best one. More precisely, FG consists

of some people discussing a given subject and shar-

ing ideas in order to reach the best solution to a given

problem. The main characteristic of the FG is its abil-

ity of producing and improving ideas or data based

on cooperation of its members. This approach could

be considered as an optimization operator, used for

optimization purposes. In a FG, each member’s idea

will be taken into consideration by all members and

will affect their idea. After repetitions of this proce-

dure, the best and the most conceivable choice will be

reached. It is worth mentioning that another charac-

teristic of a FG is that, at each time just one member is

allowed to talk and this is mainly due to importance of

hearing all ideas with care in order to take them into

account. While different, all these ideas should be

valued. Better ideas possess higher values and have

greater impact on the other members’ ideas.

Referring to KH optimization algorithm proposed

by Gandomi (Gandomi and Alavi, 2012), when preda-

tors such as seabirds, penguins and seals attack krill,

they remove krill individuals which results in reduc-

tion in the krill density and distancing them from

food. So reformation of the krill’s herd after reduc-

tion of krill density depends on many factors. This

process (herding of the krill individuals) is a multi-

objective process which follows two main goals: in-

creasing krill density and reaching food. To achieve

the ﬁrst goal, krill individuals make their ultimate ef-

fort and try to increase and maintain the herd density

and move due to their mutual effects. The movement

direction of each krill individual, α

, is inﬂuenced

by local swarm density as local effect, target swarm

density as target effect and repulsive swarm density

known as repulsive effect. This movement is as fol-

low:

new

= N

max

+ w

old

(12)

where

= α

local

+ α

t arg et

(13)

where α

local

is the effect caused by individual neigh-

bors and α

target

is the effect caused by the best krill

individual. This means that the movement direction

of krill individuals is inﬂuenced by their neighbors

and the best individual. According to the focus group

idea in a group, all members have their own impact

on the other members’ ideas in a way that the best

krill individual has greatest impact and the worst krill

has the least impact on the other members’ ideas. So

contrary to the Gandomi’s idea in the Krill Herd op-

timization algorithm about the movement of the krill

individuals, the focus group idea points to the fact that

the movement of each krill individual should be inﬂu-

enced by all krill individuals. However, individuals

with higher ﬁtness have higher effects and individu-

als with lower ﬁtness have lower effects. So, ﬁtting

the focus group description, equation (13) should be

reformulated as follow:

∑

j=1

i, jbest

) (14)

where

i, jbest

= (

j,ibest

−X



j,ibest

−X



+ ε

) (15)

and

i, jbest

−K

j,ibest

worst

−K

best

(16)

where N is the population size, X

is the current lo-

cation of i-th individual, X

j,ibest

is the best location

Modiﬁed Krill Herd Optimization Algorithm using Focus Group Idea

467

visited by j-th individual in all iterations and C

the coefﬁcient effect of i-th krill individual which is

the exponentially distributed random number. The

larger random numbers are allocated to individuals

with higher ﬁtness and the smaller ones are allo-

cated to the individuals with lower ﬁtness. Also K

j,ibest

equals to best ﬁtness of j-th individual in all it-

erations and K

equals to ﬁtness of i-th individual, K

best

and K

worst

are the best and worst ﬁtness achieved

by all krill individuals.

4 EXPERIMENTATION

In order to evaluate the performance of the proposed

algorithms, we applied it to a set of standard bench-

mark functions listed in Table 1. These benchmarks

include high dimensional functions which are difﬁ-

cult to solve due their dimension (Fister et al., 2013)

and are being used most frequently by the researchers

to examine the performance of the different optimiza-

tion algorithms. If we exclude Sphere and DixonPrice

which are unimodal functions, the rest are multimodal

functions. In spite of unimodal functions which have

one local optimum, multimodal functions have many

local minimum points with a risk of being trapped in

them. In Table 1, n is the dimension of the functions,

Search Space is the problem space which is a subset

of R

. The Global Minimum is the minimum value

of the functions which are zero for all functions ex-

cept for Michalewicz function (Its minimum point is

-9.66). The dimension for F1 to F9 functions is con-

sidered 20 and for F10 is considered 10. Below is the

description of the benchmark functions we have used

in our experiments. More details can be found in (Ali

et al., 2005).

F1. Ackley function: This is a popular test problem

for evaluating the performance of the optimization

methods. Its many local optimum solutions chal-

lenge the performance of the optimization meth-

ods by posing a risk on them, to be trapped in one

of local optimum solutions and this is specially

the case for the hill climbing methods. Ackley

is continuous, differentiable, non-separable, scal-

able and multimodal. The global minimum of the

function is f (x

) = 0 with corresponding solution

= (0,...,0). The test domain is 32.768 ≤ x

≤

32.768.

F2. Griewank function: This function has many local

optimum solutions that are regularly distributed in

the problem space. This is also a non-separable,

scalable and a differentiable function. Its global

optimum solution is f (x

) = 0 with correspond-

ing solution x

= (0, . . . , 0). The domain of test is

600 ≤ x

≤ 600.

F3. Levy function: Levy is a continuous optimiza-

tion problem with several local optimum solution

distributed in the problem space. It has global op-

timum solution f (x

) = 0 which is located at x

(1,...,1). This problem is subject to 10 ≤x

≤10.

F4. Rastrigin function: Rastrigin is a continuous

multimodal function with many local optimum

solution distributed in the search space. It is a

difﬁcult problem to solve due to its large search

space and large number of local optimum solu-

tions. Its global optimum solution is f (x

) = 0

with corresponding zero vector x

= (0, . . . , 0).

The test domain is 5.12 ≤ x

≤ 5.12.

F5. Schwefel function: Schwefel belongs to contin-

uous multimodal class of test functions. It is also

differ-entiable, separable and scalable functions.

Its many local optimum solutions make it gener-

ally difﬁcult solution to solve. Its global minimum

is f (x

) = 0 which is located at x

= (0, . . . , 0).

The problem constraint is 500 ≤ x

≤ 500.

F6. Dixon Price function: This function is continu-

ous, differentiable, non-separable and unimodal

function. It has global minimum f (x

) = 0 which

is located at x

= (2(

−2

)) for i = 1 ...n, where n

is the dimension of the problem. The test domain

is 10 ≤ x

≤ 10.

F7. Rosenbrock function: Rosenbrock is a popu-

lar function for gradient-based optimization al-

gorithms. It is continuous, differentiable, non-

separable and unimodal function. It has global

minimum f (x

) = 0 which is located in nar-

row valley. The corresponding solution is x

(1,...,1) and the problem constraint is 5 ≤ x

≤

10.

F8. Sphere function: Sphere is a poplar test function

which is used most frequently by the researchers

for examining the performance of the optimiza-

tion methods. This function is continuous, differ-

entiable, separable and unimodal test function. Its

global optimum solution is f (x

) = 0 with corre-

sponding solution x

= (0,...,0), where 5.12 ≤

≤ 5.12.

F9. Powell function: Powell function is continuous,

differentiable, separable and unimodal function.

It has global optimum f (x

) = 0 which located

at x

= (3, 1, 0, 1 . . . , 3, 1, 0, 1) where 4 ≤ x

≤ 5.

F10. Michalewicz function: This function is contin-

uous multimodal function. It has global minimum

f (x

) = 9.66 for 10 dimension version (n = 10).

This problem is subject to 0 ≤ x

≤ π.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

468

Table 1: The standard benchmark functions used in our experiments.

ID Name Function Domain Global

Mini-

mum

F1 Ackley

f (x) = −20 exp



−0.2

−1

∑

i=1



−

exp



−1

∑

i=1

cos(2πx

)



+ 20 + e

∈ [−32.768, 32.768] 0

F2 Griewank f (x) = 1 +

4000

∑

i=1

−

∏

i=1

cos



√



∈ [−600, 600] 0

F3 Levy

f (x) = sin

(πω

) +

n−1

∑

i=1

(ω

−1)

∗



1 + 10sin

(πω

+ 1)



+(ω

−1)



1 + sin

(2πω

)



where ω

= 1 +

−1

, f or all i = 1,.. .,n

∈ [−10, 10] 0

F4 Rastrigin f (x) = 10n +

∑

i=1

−10 cos(2πx

)) x

∈ [−5.12, 5.12] 0

F5 Schwefel

f (x) = 418.9829n−

∑

i=1

sin





∈ [−500, 500] 0

F6 Dixon Price f (x) = (x

−1)

∑

i=2



−x

i−1



∈ [−10, 10] 0

F7 Rosenbrock f (x) =

n−1

∑

i=1



100



i+1

−x



+ (x

−1)



∈ [−5, 10] 0

F8 Sphere f (x) =

∑

i=1

∈ [−5.12, 5.12] 0

F9 Powell f (x) =

n/4

∑

i=1







4i−3

+ 10x

4i−2

)

5(x

4i−1

−x

)

+(x

4i−3

+ 2x

4i−1

)

+ 10(x

4i−3

−x

)







∈ [−4, 5] 0

F10 Michalewicz f (x) = −

∑

i=1

sin(x

)sin





∈ [0,π] -9.66

F11. Colville function: Colville function is continu-

ous, differentiable, non-separable and multimodal

function. It has several local minimum solutions

which make it tricky and hard to ﬁnd global min-

imum. Its global minimum is f (x

∗

) = 0 which is

located at x

∗

= (1,...,1). The problem domain is

−10 ≤ x

≤ 10.

F12. Shubert function: Shubert function is

continuous, differentiable, separable and

multimodal function. It has 18 global

minimum some of which are located at

(−1.4251,−7.0835), (−7.0835, −7.7083),

(5.4828,4.8580). Its global minimum

is f (x

∗

) = −186.73. The test domain is

−10 ≤ x

≤ 10.

F13. Six-hump camel function: This function is con-

tinuous, differentiable, non-separable and mul-

timodal function. It has two global opti-

mum f (x

∗

) = −1.0316 which are located at

(−0.0898, 0.7126), (0.0898,−0.7126). This

function is subject to −10 ≤ x

≤ 10.

F14. Bohachevsky1 function: This function is con-

tinuous, differentiable, separable and multimodal.

Its global optimum is f (x

∗

) = 0 is located at

(0, 0). The test domain is−100 ≤x

≤ 100.

F15. De Jong N.5 function: This function is contin-

uous multimodal function with many sharp drops

on an almost ﬂat surface. The global minimum

of the function is f (x

∗

) = 0.99 where −65.536 ≤

≤ 65.536.

F16. Easom function: Easom function is two-

dimensional function in domain −100 ≤ x

≤

100. This function belongs to continuous, dif-

ferentiable, separable and multimodal function

class. Its global minimum is f (x

∗

) = −1, located

at(π, π).

F17. Matyas function: Matyas function is continu-

ous, differentiable, non-separable unimodal func-

tion. Its global minimum is f (x

∗

) = 0 located at

(0, 0). The test domain is −10 ≤ x

≤ 10.

F18. Beale function: This is continuous, differen-

Modiﬁed Krill Herd Optimization Algorithm using Focus Group Idea

469

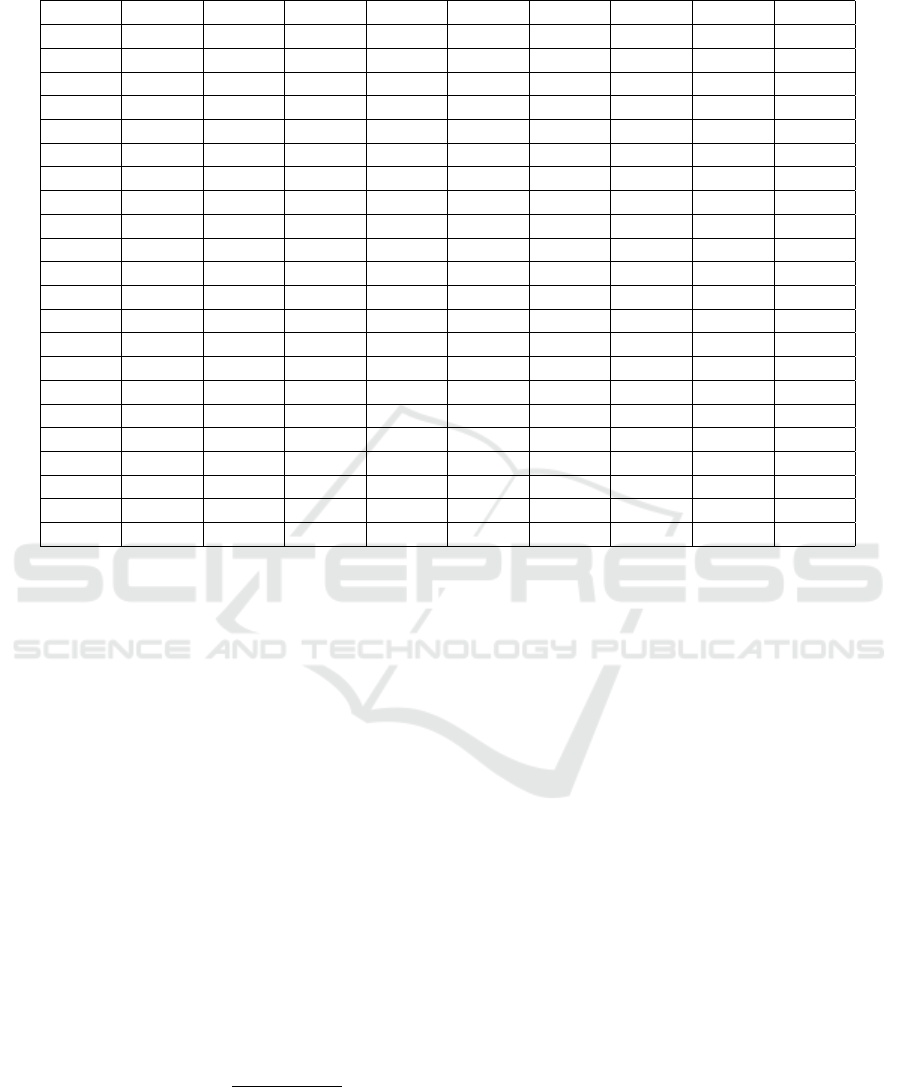
Table 2: The average of the normalized results of the proposed KHFG optimization algorithms and several famous meta-

heuristic optimization algorithms in 50 trials for the benchmark functions.

ID KHFG KH PSO GA ES CS ACO ABC TLBO

F1 0.97 0.94 0.89 1 0.77 0 0.99 1 1

F2 0.99 0.99 1 0.99 0 0.98 0.98 0.99 0.99

F3 0.98 0.36 0.68 0.36 1 0 0.44 0.86 0.37

F4 1 0.99 0.97 0.99 0 0.93 0.97 0.97 0.98

F5 0.21 0.3 0 1 0.99 0.33 0.99 0.24 0.25

F6 1 0.87 0.21 0.01 0 0.46 0 0.99 0.99

F7 0.72 0.58 0.9 1 0.29 0 0.99 0.99 1

F8 1 1 0.99 0.99 0 0.99 1 1 1

F9 1 0.92 0.24 0.06 0 0.9 0 0.99 1

F10 0.96 0.8 0.69 0 1 1 0.13 0.36 0.36

F11 0.99 0.98 0.99 0.97 0 1 0.98 0.99 0.99

F12 0.99 0.99 0.66 0 0.49 1 0 0.99 0.99

F13 1 1 1 0.77 0 1 0.93 0.99 0.99

F14 0.99 0.99 0 0.99 0.99 1 0.92 0.85 0.85

F15 0.99 1 0.97 0 0.99 0.62 0.01 0.75 0.75

F16 1 0.99 0.5 0.5 0 1 0.99 0.99 0.99

F17 1 0.99 0.54 0.53 0 0.99 0.96 1 1

F18 1 1 0 0.99 0.99 0.84 0.99 1 1

F19 0.57 1 1 0 1 0.99 1 1 1

F20 1 1 0.99 0.76 0 1 0.07 1 1

SUM 18.4 17.76 13.47 12.21 15.11 8.8 13.41 18.04 17.57

Rank 1 3 6 8 5 9 7 2 4

tiable, non-separable and unimodal test function.

The global minimum of the function is f (x

∗

) = 0

located at (3, 0.5)t. This function is subject to

−4.5 ≤ x

≤ 4.5.

F19. Goldstein Price function: Goldstein Price

is continuous, differentiable, non-separable and

multimodal function. Its global optimum is

f (x

∗

) = 3 which is located at (−1, 0) where

−2 ≤ x

≤ 2.

F20. Forrester’s function: This function is one-

dimensional, continuous and multimodal func-

tion. It has a global optimum f (x

∗

) = −6.0207

at (0.7572). The test domain is 0 ≤ x

≤ 1.

Several experiments with have been be carried out

to obtain the real performance of an algorithm. The

results are obtained on 50 trials with different initial-

ization conditions. In all the experiments, the number

of iterations and the number of krill individuals are set

to 200 and 25 respectively. The results are normalized

using (5).

i,normalized

= 1 −

−X

min

)

max

−X

min

)

(17)

where, X

i,normalized

is the normalized value of solution

i, X i is the ﬁtness value of solution i, X

min

and X

max

are the minimum and the maximum ﬁtness value of

the found solutions respectively.

KHFG is compared with the following eight well-

known meta-heuristic optimization algorithms: Ge-

netic Algorithm (GA), Particle Swarm Optimization

(PSO), Evolution Strategy (ES), Cuckoo Search (CS),

Krill Herd (KH), Ant Colony Optimization (ACO),

Artiﬁcial Bee Colony (ABC) and Teaching-Learning

Based Optimization (TLBO). The obtained results

of the proposed FG optimization algorithms together

with the results of the mentioned meta-heuristic opti-

mization algorithms are listed in Table 2. It should be

mentioned that these obtained results are the average

of the normalized results on 50 trials.

In order to make a fair comparison of the proposed

KHFG and the mentioned optimization algorithms,

the normalized results are summed and ranked. As

we can easily see, KHFG optimization algorithm out-

performs the other methods in 10 out of 20 functions.

In order to compare the performance of differ-

ent algorithms different methods such as Chess Rat-

ing System and Wilcoxon Rank Sum Tests can be

used. In this experiment Nonparametric Wilcoxon

Rank Sum Tests is used. We conduct this experi-

ments on the results achieved by the proposed algo-

rithm and other mentioned meta-heuristic algorithms

on presented benchmark functions and the results of

this experiments is presented in Table 1. The results

of this experiment are presented with P-value and h

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

470

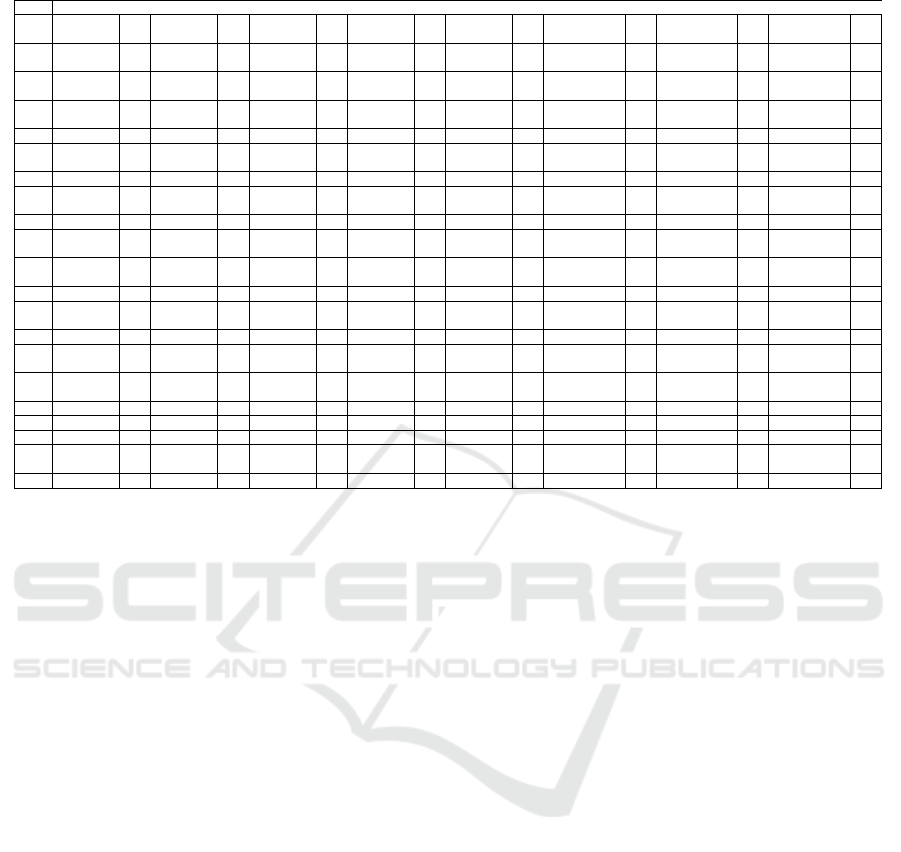
Table 3: Statistical Comparison between KHFG and the other ﬁve algorithms.

ID KH PSO GA ES CS ACO ABC TLBO

value value value value value value value value

F1 4.85E-18 1+ 3.68E-18 1+ 5.12E-12 1- 3.68E-18 1+ 4.59E-16 1+ 1.14E-02 1- 2.14 E-02 1- 2.14 E-02 1-

F2 2.21E-14 1- 2.81E-15 1- 3.68E-18 1+ 3.68E-18 1+ 4.14E-11 1+ 1.23E-02 1+ 6.8 E-03 1- 5.8 E-03 1-

F3 1.92E-12 1+ 4.19E-12 1+ 3.68E-18 1+ 2.51E-16 1- 3.68E-18 1+ 5.44E-01 1+ 1.215 E-01 1+ 6.098 E-01 1+

F4 2.11E-04 1+ 3.51E-05 1+ 3.68E-18 1+ 2.11E-19 1+ 3.68E-18 1+ 3E-0.2 1+ 2.41 E-01 1+ 1.11 E-02 1+

F5 4.73E-18 1- 3.68E-18 1+ 2.48E-21 1- 5.26E-21 1- 8.27E-21 1- 7.77E-01 1- 3.28 E-01 1- 3.92 E-02 1-

F6 1.12E-06 1+ 3.68E-18 1+ 4.64E-08 1+ 6.22E-14 1+ 4.14E-06 1+ 1 1+ 4.00E-04 1+ 4 E-04 1+

F7 2.87E-03 1+ 4.58E-04 1- 6.98E-09 1- 8.40E-06 1+ 1.32E-06 1+ 2.73E-01 1- 2.82 E-01 1- 2.827 E-01 1-

F8 6.71E-01 0 1.41E-01 0 8.14E-12 1+ 3.68E-18 1+ 8.67E-02 1+ 0 0 0 0 0 0

F9 2.37E-01 1+ 4.46E-01 1+ 3.68E-18 1+ 3.68E-18 1+ 3.68E-18 1+ 9.946 E-01 1+ 6 E-04 1+ 5.4 E-03 1-

F10 7.96E-15 1+ 3.26E-17 1+ 3.68E-18 1+ 2.21E-21 1- 3.51E-05 1- 8.309 E-01 1+ 5.99 E-01 1+ 5.995 E-02 1+

F11 9.26E-01 1+ 7.68E-03 0 1.52E-05 1+ 3.68E-18 1+ 3.16E-01 0 1.65 E-02 1+ 1.8 E-03 1+ 1.8 E-03 1+

F12 1.45E-02 1- 1.29E-02 1+ 1.38E-04 1+ 1.64E-03 1+ 3.62E-02 1- 9.999 E-01 1+ 9 E-04 1+ 8 E-04 1+

F13 8.47E-05 0 9.34E-04 0 2.32E-08 1+ 3.23E-09 1+ 5.12E-01 0 7.00E-02 1+ 0 1+ 0 1+

F14 2.60E-17 1+ 3.68E-18 1+ 3.68E-18 1+ 1.12E-01 0 4.85E-21 1- 8.00E-02 1+ 1.453 E-01 1+ 1.404 E-01 1+

F15 5.97E-01 1- 3.68E-18 1+ 4.31E-15 1+ 1.18E-01 0 3.07E-21 1+ 9.798 E-01 1+ 2.333 E-01 1+ 2.374 E-01 1+

F16 4.14E-04 1+ 3.68E-18 1+ 4.14E-04 1+ 5.22E-11 1+ 9.85E-01 0 1 E-02 1+ 5 E-04 1+ 5.5 E-03 1+

F17 1.51E-02 1+ 3.68E-18 1+ 3.68E-18 1+ 3.68E-18 1+ 8.18E-15 1+ 4 E-02 1+ 0 0 0 0

F18 2.07E-01 0 4.08E-02 1+ 8.46E-03 1+ 3.68E-18 1+ 6.24E-10 1+ 1 E-02 1+ 0 0 0 0

F19 2.18E-02 1- 5.45E-01 1- 7.31E-03 1- 3.43E-19 1- 6.14E-19 1- 4.247 E-01 1- 4.247 E-02 1- 4.247 E-01 1-

F20 6.70E-01 0 3.68E-18 1+ 3.68E-18 1+ 3.68E-18 1+ 1.45E-01 0 9.3 E-01 1+ 0 0 0 0

which help us to ﬁnd out whether there is signiﬁ-

cant difference between the performances of two al-

gorithms. In this experiment h can get three differ-

ent values, 1

, 0 and 1

−

and each value indicates

different fact. h=1 indicates that the performances

of two compared algorithm is signiﬁcantly different

with 95% conﬁdence. 1

shows that an algorithm has

higher performance compared with another algorithm

in the comparison and 1

−

vice versa. And 0 indicates

that there is no statistical difference.

Table 3 shows the results of Null Hypothesis Sig-

niﬁcance Testing which has been done by Nonpara-

metric Wilcoxon Rank Sum Tests on the proposed al-

gorithm and other mentioned algorithms in MATLAB

2010. It also indicates that in most of the experiments

the results achieved by KHFG are comparable with

the results achieved by the other methods. Follow-

ing are some discussion about the results presented in

Table 3.

1. F1 is ackley function. The KHFG algorithm

achieved the third best mean value compared

with those of other algorithms and ranked sec-

ond. There is statistically signiﬁcant difference

between KHFG algorithm and KH, PSO, CS and

ES. GA, ABC, TLBO have signiﬁcant perfor-

mance over the KHFG algorithm.

2. F3 is Levy function. The KHFG algorithm

achieved the second best mean value compared

with those of other algorithms and ranked sec-

ond. There is statistically signiﬁcant difference

between KHFG algorithm and KH, PSO, CS, GA,

ACO, ABC and TLBO. ES has signiﬁcant perfor-

mance over the KHFG algorithm

3. F8 is Sphere function. The KHFG algorithm

achieved the best mean value compared with

those of other algorithms. There is no statisti-

cally signiﬁcant difference between KHFG algo-

rithm and KH, PSO, ABC, ACO and TLBO algo-

rithms. There is statistically signiﬁcant difference

between KHFG algorithm and GA, CS and ES al-

gorithms.

4. F12 is Shubert function. The proposed method

achieved the second best mean value in this ex-

periment. The statistical results show that the

proposed FGKH has signiﬁcant importance over

PSO, GA, ES, ACO, ABC and TLBO. There is

no signiﬁcant importance between the proposed

method and KH algorithm. There is only CS al-

gorithm that has signiﬁcant importance over the

FGKH algorithm.

5. F16 is Easiom test function. The FGKH algorithm

achieved the best results in this experiment among

the mentioned evolutionary techniques. The pro-

posed method has signiﬁcant importance over al-

most all algorithms except ES algorithm. There is

no signiﬁcant importance between FGKH and ES

algorithm.

6. F20 is Forrester’s function. The proposed al-

gorithm ranked ﬁrst in this experiment. It has

Modiﬁed Krill Herd Optimization Algorithm using Focus Group Idea

471

also signiﬁcant importance over PSO, GA, ES

and ACO algorithm. There is no signiﬁcant im-

portance between FGKH and KH, CS, ABC and

TLBO algorithms.

5 CONCLUSION

This paper introduces a new method called Focus

Group Idea to improve the ﬁtness of the KH algo-

rithm by modifying the solutions found by the search-

ing agents. This idea put the emphasis on utilizing

all members’ solutions with the focus on their ﬁtness.

According to the deﬁnition of the Focus Group Idea,

each member can affect the other members’ ideas

considering the quality of its solution. In other words,

the more quality solution it has the more impact it

has on the other members’ ideas (solutions). In order

to evaluate the performance of the proposed method

we experimentally compared KHFG to other well

known evolutionary techniques for solving a set of

standard benchmark functions. The results achieved

by KHFG in comparison with those of the other meth-

ods, demonstrate the ability of proposed method in

improving the performance of the KH algorithm.

REFERENCES

Ali, M. M., Khompatraporn, C., and Zabinsky, Z. B.

(2005). A numerical evaluation of several stochas-

tic algorithms on selected continuous global optimiza-

tion test problems. Journal of Global Optimization,

31(4):635–672.

Bhandari, A. K., Singh, V. K., Kumar, A., and Singh, G. K.

(2014). Cuckoo search algorithm and wind driven op-

timization based study of satellite image segmentation

for multilevel thresholding using kapurs entropy. Ex-

pert Systems with Applications, 41(7):3538–3560.

Dorigo, M., Maniezzo, V., and Colorni, A. (1996). Ant sys-

tem: optimization by a colony of cooperating agents.

IEEE Transactions on Systems, Man, and Cybernet-

ics, Part B (Cybernetics), 26(1):29–41.

Fister, I., Yang, X.-S., and Brest, J. (2013). Modiﬁed ﬁre-

ﬂy algorithm using quaternion representation. Expert

Systems with Applications, 40(18):7220–7230.

Gandomi, A. H. and Alavi, A. H. (2012). Krill herd: a

new bio-inspired optimization algorithm. Communi-

cations in Nonlinear Science and Numerical Simula-

tion, 17(12):4831–4845.

Goldberg, D. E. and Holland, J. H. (1988). Genetic al-

gorithms and machine learning. Machine learning,

3(2):95–99.

Karaboga, D. (2005). An idea based on honey bee swarm

for numerical optimization, technical report-tr06, er-

ciyes university, engineering faculty, computer engi-

neering department. Technical report.

Kennedy, J. (2011). Particle swarm optimization. In

Encyclopedia of machine learning, pages 760–766.

Springer.

Mitchell, M. (1998). An introduction to genetic algorithms.

Rashedi, E., Nezamabadi-Pour, H., and Saryazdi, S. (2009).

Gsa: a gravitational search algorithm. Information

sciences, 179(13):2232–2248.

Storn, R. and Price, K. (1995). Differential evolution-a sim-

ple and efﬁcient adaptive scheme for global optimiza-

tion over continuous spaces, volume 3.

Yang, X.-S. (2010a). Fireﬂy algorithm, levy ﬂights and

global optimization. In Research and development in

intelligent systems XXVI, pages 209–218. Springer.

Yang, X.-S. (2010b). A new metaheuristic bat-inspired al-

gorithm. In Nature inspired cooperative strategies for

optimization (NICSO 2010), pages 65–74. Springer.

Yang, X.-S. and Press, L. (2010). Nature-inspired meta-

heuristic algorithms, second edition.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

472