
Optimization of Integrated Batch Mixing and Continuous Flow in
Glass Tube & Fluorescent Lamp
Mina Faragallah
1
and A. A. Elimam
2
1
Continuous Improvement Engineer, Mondeléz Egypt, 10
th
Ramadan, Egypt
2
Mechanical Engineering Department, The American University in Cairo, New Cairo, Egypt
Keywords: Production Planning, Continuous Production, Batch Mixing, Linear Programming.
Abstract: This paper deals with production planning of in-series continuous flow, and discrete production plants. The
work is applied to glass and fluorescent lamp industry, where raw materials are mixed in batches, charged to
a continuous furnace to produce glass tubes, and then assembled into discrete lamps. A non-linear
programming model was formulated from the raw material mixing stage till the production of fluorescent
lamps. Using the model, the amount of each raw material can be obtained at minimum cost, while satisfying
the desired properties of the produced glass. The model also provides the optimum lamp production
amounts, inventory levels, and the glass pull rate from the furnace, which determines the production
amounts of glass tubes. An important factor in the continuous flow process is the amount of broken glass
(cullet) added in the furnace, which has an impact of raw material cost and natural gas consumption. In
order to solve the model, separable programming methods and linear approximations were used to transform
the non-linear terms. Results are validated versus actual production data from local Glass & Lamp factories,
and the model proved to be an efficient tool of integrating the whole process at minimum cost.
1 INTRODUCTION
The sequence of manufacturing a fluorescent lamp
starts with the production of light bulb. Glass tube
production is considered a continuous process and it
is followed by a discrete assembling process. The
production of glass bulb starts with mixing of glass
basic material. Silica sand, dolomite, limestone,
potash feldspar, soda ash, borax, carbon, sodium
sulphate, magnesium, and alumina are the major raw
materials used to form the glass batch. The batch is
then charged to the furnace at 1475
o
C. In order to
shape glass into tubes, the molten glass flow over a
rotating hollow cylinder to take the shape and a flow
of air is blown inside the hollow cylinder. Then, the
formed tubes are pulled using conveyors, cooled
down at room temperature, and cut according to the
desired length. The edges are modified to facilitate
the assembly process. The tubes are then coated with
the phosphorous coating, and the tungsten filament
are assembled to the coated bulb. After that the bulb
goes through exhausting, in which the tubes are
vacuumed, the inert gas and the mercury drop are
inserted inside the bulb and then, the bulb is sealed.
End-Caps are then added to the edges of the sealed
bulb and finally the lamp is tested before packaging.
2 PROBLEM DEFINITION
In such an industry, the production processes are
dependent to one another. Any stoppages at one of
the processes due to breakdowns or material
shortages will affect the whole operation. For
example, when the assembly process stops, the
production of glass tubes should stop as well.
However, glass production is a continuous flow
operation where the production line runs 24 hours a
day over 7 days of the week. The furnace is the
crucial component at the whole production line
where any change in the production quantity for
example should be introduced gradually because of
the considerable setup cost. Therefore, furnace
shutdown can cause significant loss to the factory. In
case of low demand and in order to avoid shutting-
down the furnace, the production quantity is reduced
to the minimum, leading to lower utilization. In
addition, the unit cost of the glass tube increases due
Faragallah M. and A. Elimam A.
Optimization of Integrated Batch Mixing and Continuous Flow in Glass Tube Fluorescent Lamp.
DOI: 10.5220/0006192401190127
In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 119-127
ISBN: 978-989-758-218-9
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
119

to the reduction in production quantities. Therefore,
decisions should be taken with the objective to
minimize the total variable cost of the integrated
operations. The variable costs are raw material,
energy, inventory, and crushing cost. Several factors
should be considered in order to achieve such an
objective. The variables, representing these factors,
are the amount of each raw material inside the glass
batch, the Glass Pull Rate (P), the percentage of
glass culets added to the batch (MG), the thickness
of the glass tube, the inventory level in various
stages (straight tube, shaped tube, and fluorescent
lamp), and the scheduled scrap quantity. Given these
variables, the following variety of actions could be
pursued in order to minimize waste
• Given the chemical composition and the
cost of each raw material, the factory has to
decide upon the weight percentage of each
raw material inside the batch to minimize
the raw material cost without affecting the
basic characteristics of the final product,
such as the glass density, and the thermal
expansion coefficient.
• Increasing the glass cullet percentage in the
batch reduces the raw material, so the raw
material cost is reduced. On the other side,
the amount of glass cullet required
increases, so the amount of glass tubes
crushed increases.
• Also, reduction in P cause reduction in the
production quantity. However, this will
increase the residence time inside the
furnace causing changes in the chemical
composition of glass inside the furnace.
Therefore, change in P should be
minimized.
• The factory has to make a decision on the
inventory level and on the amount at each
stage, straight tube, end-formed tube,
fluorescent lamp based on the inventory
cost at each level and the storage limits.
• Moreover, the factory might decide upon
crashing some of the glass tubes if the
inventory level increases.
3 LITERATURE REVIEW
The problem mentioned above have been discussed
in the literature under two major research areas,
namely: raw material mixing to form the final
product and production planning.
Several scholars tackled the raw material glass
mixing to reach an efficient batch calculation.
Khaimovich and Subbotin (2005) have developed an
automated program for this batch calculation. The
aim of the program is to decide upon the amount of
each raw material to achieve a specified weight
percentage of each oxide by developing a system of
linear equations. In a follow up paper, Khaimovich
(2005) improved on the program to account for the
cullet composition.
Changchit and Terrell (1990) developed a linear
model to decide upon the amount of each raw
material in ceramic batch calculation. The model
objective function minimizes the batch cost. Linear
constraints were included to ensure satisfying the
desired ceramic properties.
Another two models were formulated to model
the mixing problem in two different industries. The
first is developed by Hayta, Mehmet, and Ünsal
Çakmakli (2001) to find the optimum mix of wheat
to produce break making flour. The other model,
which was developed by Steuer, Ralph E. (1984),
modeled the mixing process to form sausage.
In addition to raw material mixing contributions,
several articles discussed the production planning of
discrete processes. Díaz-Madroñero, Peidro, and
Mula (2015) presented a review of mathematical
models developed to tackle both production and
transportation routing problem. The paper have
presented how different models tackled various
aspects including production, inventory, and routing.
Although many papers tackled the production
planning problem in discrete production, small
attention is given to the production planning of
continuous processes.
Fabian, Tibor (1958) developed an integrated
production planning model for the continuous
process of iron and steel production. The model was
divided into three sections that were integrated at the
end of the paper. The first part dealt with the
production of iron. The second part of the model
was formulated to represent the steel production
operation. The final part dealt with the rolling
operations. Assumptions were made to facilitate the
solution and to guarantee linearity, such as constant
batch size and constant size of the output.
In another two scholars, Dutta, Sinha, and Roy
developed integrated production steel plant model.
In the first (1990), the aim was to optimize the
product mix taken into consideration allocation of
plant capacities to different products, capacity
expansion decisions, and the optimum route of a
product across available machines. The second paper
(1994) dealt with the allocation of energy in case of
shortage. The model developed with the objective of
maximizing profit, while considering energy as a
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
120
limiting constraint.
Almada-Lobo, Oliveira, and Carravilla (2008)
also tackled the production planning and scheduling
of continuous process problem in coloured glass
containers manufacturing. As a result of changing
the product colour, setup time is required to change
between colour and it's a sequence dependent
process based on the two colours. A multi objective
function was formulated to minimize the weighted
sum of sequence dependent setup times, average
inventory levels, and number of stock-outs.
In addition, Taşkın, and Ünal (2009) developed a
MIP model for the production and transportation
planning of a float glass manufacturing company
called Trakya Cam. The company produces various
product sizes in multi facilities. A model was built
with the objective of minimizing the total cost
including production, inventory, backorder, and
transportation cost.
In this paper, a mathematical model is developed
to integrate the production processes of fluorescent
lamp starting from mixing of raw material till the
storing of finished product. The model aimed at
minimizing the total operating cost including, raw
material, scheduled crushing, inventory at all levels,
and energy cost, while. In the developed model, the
optimum mix of raw materials is determined not
only based on input variation as developed by
Changchit and Terrell (1990), but also based on the
optimum cullet ratio. Also, the energy cost is
considered in the model to take into account the
relationship between using glass cullet and energy
saving as explained by Vishal, et. Al (2007) as well
as Štefanić and Pilipović (2011). In addition to the
mixing operation, the model takes into consideration
the balance between an in-series continuous-process
plant producing glass tubes followed by a discrete
plant assembling fluorescent lamps. Integration
between in sequence production stages is achieved,
so that the demand of the following stage is a
requirement from the previous stage. A major
distinction between the developed model and the
continuous models cited before is that the speed of
the continuous process is not constant and it changes
from one planning horizon to another depending on
demand. Therefore, the amount of raw materials
consumed and the output produced is dependent
upon that variable.
4 MATHEMATICAL MODELING
4.1 Symbol Definitions
In the following three sections, the model constant
parameter, sets, and decision variables are defined.
4.1.1 Constant Parameters
Symbol Definition
%E
m
Percentage of end-forming waste from the
weight of straight tube size m
%G
m
Percentage of cutting waste from the weight of
glass tube size m
A
t
Available hours per period t
CB
t
Raw material batch Cost at period t
CC
m
Cost of crushing one glass tube of size m
CI
E
m
Monthly cost to keep one unit of end-formed
tube of size m in inventory
CI
G
m
Cost of one glass tube in inventory of size m
CI
L
m
Cost to keep one lamp in inventory of size m
CN Cost per m
3
of natural gas used in furnace
CP
E
m
:
Cost to produce one unit of end-formed tube of
size m
CP
L
m
Cost to produce one unit of lamp of size m
CR
i
Cost per Kg of raw material i
D Outer diameter of glass tube
D
mt
Demand of fluorescent lamp of size m in period t
F(MG%)
Relation between cullet ratio percentage, and
natural gas consumption
F
jk
Chemical influence factor of oxide j on property
k
H Thickness of glass tubes
O
ij
Weight percentage of oxide j inside raw material
i
P
ij
Weight percentage of oxide j inside raw material
i
SI
B
Storage capacity of glass cullet
SI
E
Storage capacity of end-formed tubes
SI
G
Storage capacity of glass tubes
SI
L
Storage capacity of fluorescent lamps
SP
E
mt
Production capacity of end-formed tube of size
m in period t
SP
L
mt
Production capacity of fluorescent lamps of size
m in period t
SS
E
m
Safety stock of end-formed tubes of size m
SS
G
m
Safety stock of glass tubes of size m
SS
L
m
Safety stock of fluorescent lamps of size m
U
B
Lower limit for percentage of broken glass
U
j
Lower limit for percentage of oxide j
U
k
Lower limit of property k
U
P
Lower Limit of glass pull rate
V
B
Upper limit for percentage of broken glass (glass
cullet)
V
j
Upper limit for the percentage of oxide j
V
k
Upper limit of property k
V
P
Upper limit of glass pull rate
W Raw material batch Weight
X Standard aggregate tube length
X
m
Standard length of glass tube m
Y
m
Size factor of tube size m
ρ Density of glass
Optimization of Integrated Batch Mixing and Continuous Flow in Glass Tube Fluorescent Lamp
121

4.1.2 Sets
Symbol Definition
I
Set of raw materials used to form the glass
batch
J
Set of oxides forming the composition of
the output glass
K
Set of required properties of the output
glass, such as density and thermal
expansion
M Set of glass tubes sizes produced
T Set of planning periods
4.1.3 Decision Variables
Symbol Definition
B
t
Amount of broken glass (cullet) produced
in period t
C
mt
Amount crushed of glass tubes of size
m during period t
E
mt
Amount of end formed tubes m
produced in period t
G
mt
Number of glass tubes of size m produced
in period t
I
B
t
Inventory of broken glass at the end of
period t
I
E
mt
Inventory of end formed tubes of size
m at the end of period t
I
G
mt
Inventory of glass tubes of size m at
the end of period t
I
L
mt
Inventory of fluorescent lamp m at the
end of period t
L
mt
Amount of fluorescent lamps of size m
produced in period t
P
Glass pull rate of glass from the
furnace
Q
E
mt
Gross Requirements of end-formed tubes
of size m during period t
Q
G
mt
Gross Requirements of glass tubes of size
m during period t
R
it
Amount raw material i used in the
glass batch in period t
R
B
t
Amount broken glass used in the glass
batch in period t
4.2 Integrated Mathematical Model
4.2.1 Objective Function
The objective function is aimed at minimizing the
total cost which includes the cost of production,
inventory, scheduled crushed glass, raw material,
and natural gas.
Min.
∑∑
∈∈
.
+
.
+
∑∑
∈∈
.
+
.
+
.
+
∑∑
.
+(
)
⁄
∗
∈∈
∑∑
.
∗
∈∈
+∗
(
%
)
∗
(1)
4.2.2 Constraints
1. Production Capacity Constraints
A. Mass production processes (fluorescent lamp
assembly and end-formed tube production)
,∀∈&∈
(2)
,∀∈&∈
(3)
B. Continuous flow processes (glass tube
production)
(
/)∗
∈
−(
.)/(.∗∗
∗(−))=0,∀∈
(4)
Where the amount of glass tube produced in period t
is equal to amount of molten glass produced in t
(A
t
*P) over the mass of one lamp.
The glass pull rate has an operating range as follows
(5)
C. Glass Cullet Production
−..
∗∗
(
−
)
.
(
1−%
)
.
∈
+%
.
+%
.
=0,∀∈
(6)
The amount of cullet produced in t is equal to the
mass of one lamp multiplied by the cut loss amount
2. Inventory Safety Stock
,∀∈&∈
(7)
,∀∈&∈
(8)
,∀∈&∈
(9)
3. Storage Capacity
.
∈
,∀∈
(10)
.
∈
,∀∈
(11)
∑
.
∈
,∀∈
(12)
,∀∈
(13)
4. Linkage of In-Sequence Processes
−
= 0,∀∈&∈
(14)
−
=0,∀∈&∈
(15)
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
122

5. Production & Demand Balance
−
.
(
)
+
−
=0,
∀∈&∈
(16)
−
.
(
)
+
−
=0,
∀∈&∈
(17)
−
.
+
+
−
=0,
∀∈&∈
(18)
−
−
+/..
=0,∀∈
(19)
6. Oxide percentages upper limit & Lower Limits
∑
.
∑∑
.
,∀∈&
∈
(20)
The numerator is the amount in Kg of oxide j in all
raw materials and the broken glass divided by the
yielded glass batch weight.
The equations can be written in following linear
forms:
.
−
.
.
0,∀
∈&
∈
(21)
∑
.
−
.
∑∑
(
.
)
0,∀∈
&
∈
(22)
7. Broken glass percentage upper & lower limits
−
.
.
0,∀∈
(23)
−
.
.
0,∀∈
(24)
8. Properties upper & lower control limits
For each oxide, the weight percentage of that oxide
from the yielded batch weight is multiplied by a
chemical influence factor (F)
(
.
.
)−
∈
.
.
0,∀∈&∈
(25)
(
.
.
)−
∈
.
.
0,∀∈&∈
(26)
9. Batch Weight
,∀∈
∈
(27)
10. Non-negativity Constraint
All variables are higher than or equal to zero.
5 COMPUTATIONAL WORK
5.1 Computational Plan
In order to validate the model, it is tested against
base case data given by Al-Arabi Lamp and Glass
Factory. The model is used to generate the same
output variables, such as production and inventory
amounts. Input data includes actual demand forecast
for six months, cost figures for production,
inventory, and crushing, raw material chemical
composition, etc. Therefore, the plan goes as below:
• Linear approximation techniques are used
for the non-linear terms in the objective
function and constraints to transform the
integrated model into linear.
• The base case input parameters are fed to
the model and the results are compared vs.
the actual output variables to prove model
validity.
• Then, the integrated model is solved and
the optimum solution is compared with Al-
Arabi actuals.
• The last step is to test the sensitivity of the
integrated model to variability in the raw
material, energy, and crushing cost values.
Different scenarios are tested and the
model response is observed and analyzed.
All computational runs are solved using IBM-
ILOG CPLEX V.12.6.2 on an i7 HP ProBook4540s,
and the following assumptions are made:
• Raw material chemical compositions are
fixed over the planning horizon
• Glass pull rate are fixed over the planning
horizon, so once decided by the model, the
values are the same from one period to the
other.
5.2 Linear Approximations
5.2.1 Separable Programming Techniques
In order to solve the model as linear, the batch cost
term in the objective function (1), and the glass
cullet inventory balance constraints (19) needs to be
linearized. Moreover, a relationship between the
glass cullet percentage, and energy cost should be
figured out. First, the linearization of constraint (19)
and the batch cost term are done using separable
programming techniques, where the right hand side
of the equation can be expressed as the sum squared
of the two variables instead of multiplying both
variables. Faragallah (2016)
Optimization of Integrated Batch Mixing and Continuous Flow in Glass Tube Fluorescent Lamp
123
.
=(+
)/2 ,
.
=(−
)/2
(28)
.
−
.
=.
(29)
It is shown that for the given operating range of
glass pull rate (P) and the broken glass (
), Z
1
2
&
Z
2
2
can be expressed as linear functions as shown in
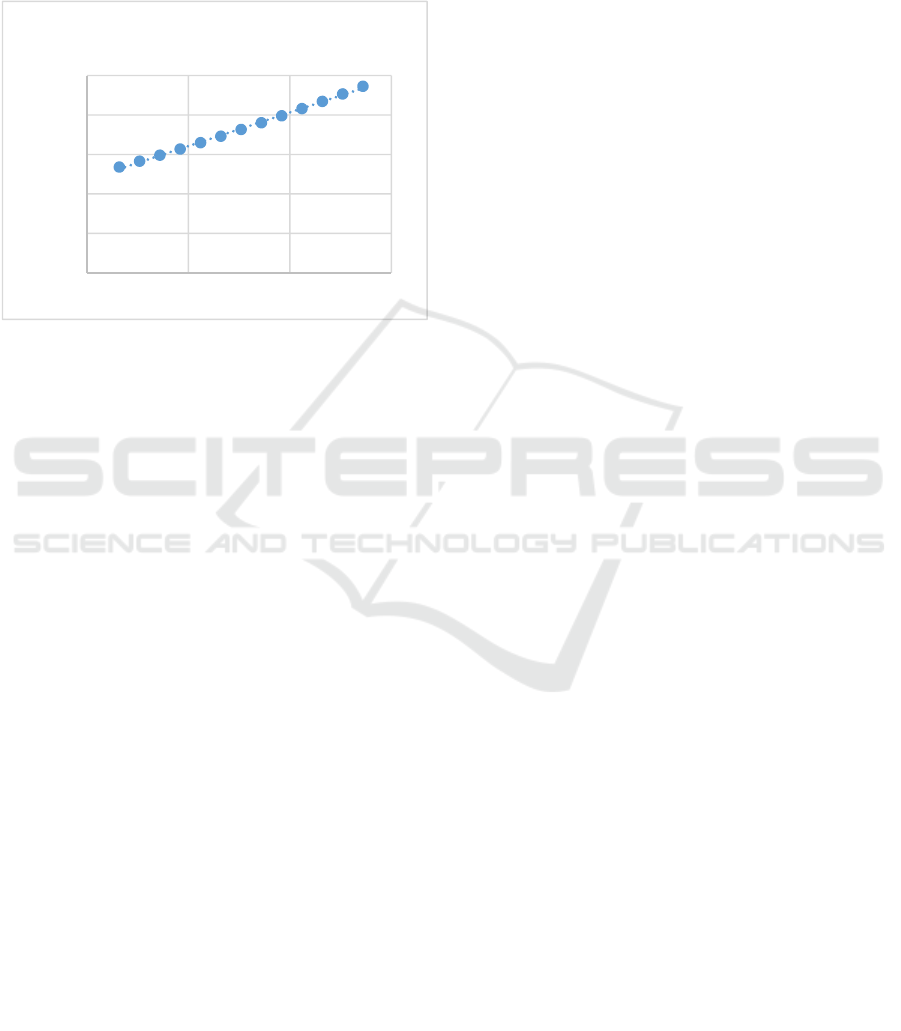
figure 1.
Figure 1: Linear Approximation for the Multiplication of P
&
.
Therefore, (19) can be expressed as
−
+
=
/∗(144.P
+708.
−101952)
(30)
The same methodology is used for the batch cost
term in the objective function, so the term can be
transformed into:
1.44.
∑
(
∈
245.216.−508.698.
+
73252.5)
(31)
5.2.2 Natural Gas Cost Formulation
According to Vishal, et. Al (2007) as well as
Štefanić and Pilipović (2011), the energy
consumption of melting glass is reduced by 2.5 – 3%
for every 10% of glass cullet addition to the batch.
The average natural gas consumption at 30% glass
cullet ratio is 742 m
3
/hr. (Abdelrahman 2015)
Therefore, a relationship can be derived between the
natural gas consumption and the cullet percentage as
shown below
F(MG%) = -86*MG% + 312.18 (32)
Therefore, the last term representing the natural
gas consumption cost in (Eq. 34) can be expressed
as:
720.
.
(
−86.
(
%
)
+312.18
)
(33)
Where
(
%
)
=(
)/(
∑∑
.
)
(34)
The term in (32) is a non-linear term, however,
from 2015 batch data from Al-Arabi factory, the
denominator for the operational range of cullet
percentage has an average value of 442.49 and a
standard deviation of 2.03. The model is tested with
the average value, and plus and minus 3 standard
deviations from the average, and the difference
between the three cases was neglected, so the
average value of 442.49 is used. Faragallah (2016)
5.3 Validation & Results
The developed model is used to generate the base
case data provided by Al-Arabi. Table 1 and table 2
show the demand data for 2014 and cost figures used
as an input. Table 3 shows the chemical composition
and oxide percentages of raw materials used. All the
input data was obtained from Al-Araby Glass
Factory. (Abdelrahman 2015)
Besides these data, the glass factory actual plan
was to set GPR at 750, cullet ratio of 30%, and to
run production for 19 hours a day, and 5 hours per
day of crushing. The plant total cost of production,
inventory, crushing, raw material, and energy was
LE 29,648,991.
These are the operating parameters fed to the
model and it proves efficiency by generate the same
production and inventory amounts of glass, end-
formed tubes, and lamps
Based on the input data, the number of decisions
variables are 188 and the number of constraints are
404 with 96 equalities constraints. The model is
solved in almost 240 seconds using CPLEX.
Then the model was solved to provide the
optimum solution, which is to run the glass factory
at 646 Kg/hr and a cullet ratio of 30%. Table 1, 2 &
3 provides the detailed optimum solution. The total
cost of the whole planning horizon, including
discrete process production cost, inventory cost,
crushing, raw material, and energy cost is equal to
22,488,970 + 739,000 + 1,194,102 + 1,408,674 +
1,634,000 = LE 27,464,746
With a total savings of LE 2,184,245 over that of Al-
Arabi lamp and glass factories actuals.
Z
1
2
= 852.Z
1
- 180076
R² = 0.998
0
50000
100000
150000
200000
250000
350 400 450 500
Z
1
2
vs. Z
1
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
124

Table 1: Optimum Result of End-Formed Tubes (EF) &
Lamps for 40 Watts.
Month
40 Watts lamp, 1000s units
Demand
Units Produced
Inventory
Level
EF Lamp EF Lamp
July 1,388.8 1,388.8 1,388.8 360 1,386
Aug 1,591.2 1,591.2 1,591.2 360 1,386
Sept 1,586 1,586 1,586 360 1,386
Oct 1,433.9 1,433.9 1,433.9 360 1,386
Nov 1,771.9 1,771.9 1,771.9 360 1,386
Dec 1,739.4 1,739.4 1,739.4 360 1,386
Table 2: Optimum Result of straight tubes for 40 Watts.
Month
40 Watts, 1000s units
Required Produced Inventory Crushed
July 1,388.8 1,764.3 1,386 375.47
Aug 1,591.2 1,721.5 1,386 130.3
Sept 1,586 1,721.5 1,386 135.5
Oct 1,433.9 1,878.7 1,386 444.77
Nov 1,771.9 1,814.5 1,386 425.91
Dec 1,739.4 1,752.9 1,386 135.32
Table 3: Optimum Glass Batch Mix.
Parameter Output
silica sand (Kg) 189.80
Soda Ash (Kg) 81.00
Dolomite (Kg) 45.20
Feldspar (Kg) 35.80
Borax (Kg) 4.90
Limestone (Kg) 7.82
Alumina (Kg) 0.00
Sulphate (Kg) 0.91
Carbon (Kg) 0.06
MG (Kg) 132.50
Density (gm/cm
3
) 2.488
Thermal Expansion (10
-7
*K
-1
) 100.60
Batch Cost, LE 271.61
5.4 Sensitivity Analysis
In this section, the impact of various cost figures on
the optimum solution is observed and analyzed. The
production cost is a major component of the total
cost structure, however, the production cost is driven
by the demand for lamps. Therefore, the focus is on
the effect of crushing, raw material, and energy cost
on the model results. A summary of the cost
structure for the optimum solution of the integrated
model is shown below:
Raw Material Cost = MLE 1.4086
Energy Cost = MLE 1.634
Crushing Cost = MLE 1.194
Inventory Cost = MLE 0.739
Production Cost = MLE 22.489
Total Cost = MLE 27.46
5.4.1 Impact of Raw Material & Natural
Gas Cost
Changes in Soda Ash, Silica Sand, and Borax cost
per ton are included in the sensitivity because they
represent more than 80% of the raw material cost
value. Based on historical data, changes in the cost
per ton for these materials are forecasted based on
the worst case scenario. Faragallah (2016) The same
was done for natural gas cost. However, the raw
material cost and the energy cost in the total cost
function increased without affecting the optimum
solution. Therefore, the model is insensitive to
changes in Silica Sand, Soda Ash, Borax, and
natural gas cost figures given that the remaining cost
figures of the objective function do not change.
5.4.2 Impact of Crushing Cost
The crushing cost at Al-Arabi factory is the
conversion cost to melt 1 Kg of glass cullet and
transform it to glass tubes again. (Elbendary 2015)
In order to reduce the crushing cost, the factory can
outsource percentage of the glass cullet. With close
chemical composition to that of the factory, the
outsourced cullet cost is 500 LE/ton. (Abdelrahman
2015)
Therefore, the effect of mixing the outsourced
cullet with the current batch mix is tested for
different percentages of outsourced cullet (5% -
20%).
Increasing the outsourced cullet percentage up to
5% causes the crushing cost and the glass pull rate to
decrease. Figure 2 summarizes the effect of
outsourced cullet over the crushing cost.
Figure 2: Total cost versus outsourced Cullet Percentage.
26
26,5
27
27,5
28
0% 5% 10% 15% 20% 25%
Cost (M LE)
Outsourced Cullet Percentage (%)
Effect of Outsourced Glass Cullet
Optimization of Integrated Batch Mixing and Continuous Flow in Glass Tube Fluorescent Lamp
125

From the above figures, increasing the
outsourced cullet percentage more than 15% doesn’t
have an impact on the optimum solution. Therefore,
the optimum solution of the integrated model is
achieved with 15% outsourced cullet ratio.
At this ratio, no crushing of straight tube is
needed. Therefore, the required cullet ratio in the
batch mix is achieved through the outsourced cullet
and the cut loss from operation. Accordingly, the
crushing cost is eliminated, the raw material and
energy cost is reduced because the optimum cullet
ratio in the batch mix changed from 30% to 35% due
to the introduction of outsourced cullet.
6 CONCLUDING REMARKS
Integration of batch, continuous, and discrete
manufacturing processes in florescent lamp
manufacturing was researched. In literature, glass
batch mixing, and continuous production planning
for glass furnaces were treated separately in the
literature found each by its own. Therefore, a
mathematical model was formulated to integrate the
optimum mixing of glass batch along with the
production planning of discrete glass tubes and
florescent lamps. The main factors affecting the
manufacturing process were considered. These
factors are the glass pull rate of molten glass from
the furnace which control the amount of glass tubes
produced, the percentage of glass cullet used in the
batch which affects the amount of crushed tubes to
meet the required cullet ratio, the optimum mix of
raw materials, and inventory levels of glass tubes
and lamps. The objective function was to reduce the
total manufacturing costs including crushing, raw
material, inventory, production cost, and energy cost
as a function in glass cullet percentage. The
objective function and some of the constraints
contained non-linear terms. Separable programming
methods were used to linearize the model. Then,
different Scenarios were tried to test the effect of
various parameters on the optimum solution. It was
found that changing in raw materials and energy cost
values changes the objective function value without
affecting the optimum solution. Moreover, trials
were made to reduce the crushing cost through using
glass cullet from outside sources. It was found that
with increasing the amount of outsourced cullet, the
glass pull rate along with the crushing cost
decreased dramatically till reaching zero. Also, the
glass cullet percentage increased causing the raw
material and energy costs to decrease. As a result,
the total cost decreases with the increase of
outsourced cullet ratio till reaching a constant value.
Therefore, using outsourced cullet ratio will help
reducing the amount of glass crushing, raw material
cost, and energy consumption.
The model proved to be a very helpful tool for
designing the optimum batch mix based on the raw
material chemical composition. In addition, the
model will facilitate the planning process of the two
factory as an integrated entity and will help
improving the total cost.
For future works, the model can be extended to
include diversification of customers of the glass
factory, which will reduce the unit cost. Deals from
other customers, such as other lamp producers,
laboratory glass ware companies, etc., should be
considered to increase the amount produced of glass
tubes. The following issues need to be taken into
account in selecting future customers:
• Quantities requested by the customer while
staying within the capacity of the glass
factory.
• Customization of each order, such as
different diameters and lengths which will
introduce set-up time to change from one
product to another. For example, changing
tube diameter may require to change the
GPR. This will cause production to stop for
some days based on the amount of change
and this may delay production to the main
customer which is the lamp factory, or to
other customers the factory decides to deal
with.
• Price discounts given to each customer
based on the quantity ordered and the level
of customization from the current situation.
REFERENCES
Abdelrahman, Khaed. Personal interview. 27 Sept. 2015
Almada-Lobo, Bernardo, José F. Oliveira, and Maria
Antónia Carravilla. "Production planning and
scheduling in the glass container industry: A VNS
approach." International Journal of Production
Economics 114.1 (2008): 363-375.
Changchit, Chaweng, and M. Palmer Terrell. "A
mathematical model for the calculation of ceramic
batch formulas." Applied Mathematical
Modelling 14.12 (1990): 641-648.
Díaz-Madroñero, Manuel, David Peidro, and Josefa Mula.
"A review of tactical optimization models for
integrated production and transport routing planning
decisions." Computers & Industrial Engineering 88
(2015): 518-535.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
126

Dutta, G., G. P. Sinha, and P. N. Roy. "Product-Mix
Optimizer for an Integrated Steel Plant." (2000).
Dutta, Goutam, et al. "A linear programming model for
distribution of electrical energy in a steel
plant." International Transactions in Operational
Research 1.1 (1994): 17-29.
Elbendary, Farid. Personal interview. 27 Sept. 2015
Fabian, Tibor. "A linear programming model of integrated
iron and steel production." Management Science 4.4
(1958): 415-449.
Faragallah, Mina W. "Optimization of Integrated Batch
Mixing & Continuous Flow in Glass Tube &
Fluorescent Lamp." MS Thesis. The American
University in Cairo (2016).
Hayta, Mehmet, and Ünsal Çakmakli. "Optimization of
wheat blending to produce bread making
flour." Journal of food process engineering 24.3
(2001): 179-192.
Khaimovich, M. M., and K. Yu Subbotin. "Automation of
batch formula calculation." Glass and Ceramics 62.3-
4 (2005): 109-112.
Khaimovich, M. M. "Account of cullet composition in
calculation of batch formulas." Glass and
Ceramics 62.11-12 (2005): 381-382.
Sardeshpande, Vishal, U. N. Gaitonde, and Rangan
Banerjee. "Model based energy benchmarking for
glass furnace." Energy Conversion and
Management48.10 (2007): 2718-2738.
Štefanić, Nedeljko, and Ana Pilipović. "Impact of glass
cullet on the consumption of energy and environment
in the production of glass packaging
material." Proceedings of the 9th WSEAS International
Conference on Environment, Ecosystems and
Development-EED'11.
Steuer, Ralph E. "Sausage blending using multiple
objective linear programming." Management
Science 30.11 (1984): 1376-1384.
Taşkın, Z. Caner, and A. Tamer Ünal. "Tactical level
planning in float glass manufacturing with co-
production, random yields and substitutable products.
"European Journal of Operational Research 199.1
(2009): 252-26.
Optimization of Integrated Batch Mixing and Continuous Flow in Glass Tube Fluorescent Lamp
127
