
Dynamic Agent-based Network Generation
Audren Bouadjio-Boulic, Frederic Amblard and Benoit Gaudou
IRIT - Smac team, Universit
´
e de Toulouse, 2 rue du doyen Gabriel Marty, 31042, Toulouse, France
Keywords:
Synthetic Network Generation, Agent-based Modeling, Network Dynamic.
Abstract:
Networks are a very convenient and tractable way to model and represent interactions among entities. For
example, they are often used in agent-based models to describe agents’ acquaintances. Yet, data on real-world
networks are missing or difficult to gather. Being able to generate synthetic but realistic social networks is
thus an important challenge in social simulation. In this article, we provide a very comprehensive and modular
agent-based process of network creation. We believe that the complexity of ABM (Agent-Based Models)
comes from the overall interactions of entities, but they could be kept very simple for better control over the
outcome. The idea is to use an agent-based simulation to generate networks: agent behaviors are rules for
the network construction. Because we want the process to be dynamic and resilient to nodes perturbation,
we provide a way for behaviors to spread among agents, following the meme basic principle - spreading by
imitation. Resulting generated networks are compared to a target network; the system automatically looks at
the best behavior distribution to generate this specific target network.
1 INTRODUCTION
The human society is composed of people in inter-
action. One of the most convenient way to represent
those interactions is to capture the corresponding re-
lations as a social network, i.e. mathematically by us-
ing a graph. The analysis of such networks allows to
compute some properties (density, centralities, ...) for
qualifying with precision the observed interactions.
Online networks are very well documented because
every interactions are consigned, but this is not the
case for those resulting of real-life interactions. Those
kind of networks are useful for simulating propaga-
tion of disease or opinion, for example. Data can be
missing or hidden, so it is often rather too difficult
or too long to gather enough information to describe
a complete network (Barrett et al., 2009). As a con-
sequence, tools are often used to generate synthetic
network with properties close to the real ones. Even
with successful data gathering, synthetic network can
be used for scalability matter to enlarge coherently a
real network while keeping the same overall proper-
ties.
They are two main approaches for this generation:
(1) by reproducing the process of creation or (2) by
reproducing network properties. For (1), the Agent-
Based Modeling (ABM) paradigm is frequently used.
The network generation process is based on simplified
but still realistic actor actions. For (2), in contrary, the
generation by-pass the real network formation pro-
cess. (2) can also be subdivided into two branches:
(2.a) stylized models – having few properties match-
ing the real network – or (2.b) precise models. Sty-
lized models are simple, like Small-World (Watts and
Strogatz, 1998) or Preferential-Attachment (Small
et al., 2008), focusing on matching few properties,
without a good precision; we can categorize them
as qualitative approaches. Besides, precise models
of (2.b) are more complex processes, using statisti-
cal models, such as Exponential Random Generator
Models (ERGM) (Robins, 2011) or stochastic model
as K-Graph Generator (Leskovec et al., 2010), for a
quantitative correspondence on far more properties.
With (2.a), results can be too far from the reality for
a realistic use of the network to execute even the sim-
plest process on it (Menezes and Roth, 2014). Using
(2.b), the network generation process can be too ab-
stract or too hard to configure.
Our goal in this article is to provide a dynamic net-
work generator, based on agent behaviors, coupling
agent actions and behaviors transmission. Our hy-
pothesis is to keep the model simple in order to re-
duce the probability of adding false assumptions and
to increase the control on its dynamic.
Our network creation process is led by an input
network used as target. Agents are characterized by
Bouadjio-Boulic A., Amblard F. and Gaudou B.
Dynamic Agent-based Network Generation.
DOI: 10.5220/0006202705990606
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 599-606
ISBN: 978-989-758-220-2
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
599

their behaviors that build and shape a network in
which they are the nodes. Their only two available
actions are the creation and destruction of links. Be-
sides, behaviors are spread through the network. We
are looking for a set of agents’ behaviors – among a
preset of existing ones – that will lead the simulation
to generate a network similar to the target one. Our
aim is to have an adaptive system, that is resilient, in
terms of properties, to addition and removal of nodes.
For these new nodes to be actors in the process of
network evolution, it is necessary for them to learn a
social behavior. A way to do that is to make behavior
spreadable among nodes. That is why we choose to
integrate a spreading mechanism.
The meme theory can be used as a propagation
mechanism. The main idea of memetic is that cultural
traits can be viewed as genes, sharing the reproduc-
tion, spread and mutation mechanisms. Memes are
also subject to selection by the environmental pres-
sure (Dawkins, 1976). It is convenient inter alia be-
cause memes ”leap” from man to man, depending on
the host compatibility, without their consent (Alvarez,
2004). Nevertheless, we only use memetic as a root
for our transmission process, because we do not take
into account the personalization phase of a behavior.
As a fitness function for guiding our system, we
compute a distance to the target network. This dis-
tance is based on the difference between properties of
the two networks (e.g. density, degree distribution)
and the result of processes run on both networks (e.g.
speed of information diffusion). Our postulate is: if
we can reproduce the properties of a network, the gen-
eration process becomes an acceptable way to explain
the whole network, even if it is in a stylized way (a bit
like the preferential attachment process being a plau-
sible explanation for the power law property (Small
et al., 2008)).
In the section 2, we present the related works in
networks generation, to introduce our contribution.
The details of our model is in the development sec-
tion. The section 4, Implementation and results, will
illustrate the model imitating a Scale-Free network.
The fith section will offer some discussions on postu-
lates taken by the model, along with the work to come.
The last part will be the occasion to draw a conclusion
on the system.
2 STATE OF THE ART
2.1 Social Network
A network is defined by a set of nodes and a set of
edges linking those nodes. The degree of a node is
defined by the number of edges it has. From a math-
ematical point of view, networks are thus graphs. So-
cial networks (SN) have some properties that differ-
entiate them from a random network; therefore those
properties can be used as a formal characterization of
a SN. They are often consequences of a specific pro-
cess of formation.
• For various reasons, people tend to become friend
with their friends’ acquaintances. From a graph
point of view, this is a triangle closure (or tran-
sitivity): if A is friend with B and C, B and C
meet each other and become friends as well. It
is possible to capture such tendency through the
clustering coefficient. For an undirected graph,
the clustering coefficient of a node n is:
C
n
=
2e
n
k
n
(k
n
− 1)
(1)
with k
n
the number of neighbours of n and e
n
the
number of connected nodes among them. The
higher the clustering is, the more interconnected
the nodes are.
• The Small World effect has been introduced by
Milgram (Milgram, 1967) as the ”six degrees of
separation” between person: anyone can reach
anyone within 6 hops of relatives on average. In
terms of network properties, it is a matter of av-
erage (shortest) path length between the nodes in
the network.
• SN among other kinds of networks have a scale
free property: few people are very famous, i.e.
well connected, while many other ones are poorly
served. The formal definition is that the degree
distribution of the nodes follows a power law, i.e.
a large number of nodes have few edges and a few
have many.
Those properties often come together while work-
ing in social networks.
2.2 Social Network Generation
For the generation of synthetic social networks, sev-
eral approaches have been proposed.
The Agent-Based Approach. The goal of using an
agent simulation for generating the network is to use
a realistic bottom up approach. Such models focus on
agent behaviors, based on some extend on real human
action. Morover, these methods facilitate the use of
real-world data as input and validation (Parunak et al.,
1998). It greatly simplify the test of what-if scenarii.
This kind of methods are most often ad hoc.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
600

Abstract Processes. It is possible to apply an ab-
stract process of network generation. The proposed
methods are often very simple but provide often only
good results on few properties at a time. These prop-
erties have been observed enough times on different
social networks to be considered as fundamental.
• Random network (RN) (Erdos and Renyi, 1959).
The only parameter is the probability for a node
to create an edge with another node. This process
assures a direct control on the density of the re-
sulting network.
• The Preferential Attachment (PA) algorithm
(Barabasi and Albert-L
´
aszl
´
o, 1999) provides a
network with the scale free property, i.e. a power
law distribution of degrees. The construction in-
volves an iterative process in which an incoming
node will be linked with a stronger probability to
an high degree network node.
• Small World (SW) (Watts and Strogatz, 1998)
generates networks with a correct clustering and
a small average path length, known as the small
world effect. The most cited model corresponds
to the construction from a regular lattice, rewiring
at random edges with a certain probability to an-
other random node.
Although these processes are very simple, they are
the most used, at least by the JASSS community (Am-
blard et al., 2015), mainly because their use is very
simple. They also allow modelers to test their sim-
ulation results based on a single but easy to control
network property.
Statistical or Stochastic Models. In those ap-
proaches, the existence of an edge between two given
nodes of the network is considered as a probability,
and the model will determine them. Those methods
have often a network as target, like it is the case for
the following items.
• p*/ERGM Exponential Random Generative Mod-
els (Robins, 2011) is a family of statistical mod-
els in which modelers has to choose a set of net-
work patterns (called terms or factors) that may
describe to a certain level of precision a given net-
work. A model fitting process allows to determine
the relative importance (factor value) of terms in
the observed network structure. Each factor value
expresses how likely the feature is to be found,
compared to a random network of the same size.
ERGM allows to generate networks with respect
to any valid combination of terms (e.g. degree
distribution, substructures, edges and nodes vari-
ables, etc.).
• For Kronecker Graphs (Leskovec et al., 2010),
the idea is to start from a 2x2 or 3x3 stochastic ad-
jacency matrix that will be enlarged by a recursive
method. Correct starting parameters will then be
searched by comparison with the target network.
This model is good at generating graphs with an
appropriate degree distribution and network diam-
eter. Also, properties on the adjacency matrix as-
sociated with the graph have good eigenvalues and
vectors.
• Menezes and Roth method (MR-method)
(Menezes and Roth, 2014) is searching for a good
formula defining p(i,j), the probability of having
a link between two nodes of a target network.
Generating a synthetic network with p(i,j) and
using a distance to a target network as the fitness,
the model uses a genetic algorithm in order to
make evolve p(i,i), trying to find the closest
synthetic network possible.
2.3 Contribution
Concerning the agent-based generation, while behav-
iors incorporated in agents are realistic, it is difficult
to get a network with good properties. Real phenom-
ena are more or less stylized and the results can be, in
the best case, correct in a qualitative way.
Concerning the abstract processes – SW, PA, RN
–, one can argue that resulting networks can be used
for qualitative results. In fact, far more network topol-
ogy properties influence the speed of propagation, as
Cointet and Roth (Cointet and Roth, 2007) pointed
out. They advise to use any real world network, even
from others field, to get better results. Classic stylized
networks give incoherent results mainly because these
networks do not take into account properties that do
matter for processes like propagation, e.g. the dia-
mond clustering that will slow down speed (a triangle
closure extended to four nodes). For the qualitative
approaches, network generation processes can be too
abstract or too hard to configure. Parameters cannot
be interpreted easily, and in the case of ERGM there
are some real difficulties using it without the required
knowledge.
Besides, our method is fundamentally different in
the approach while we hope being able to give close
quality of results, with a configuration-free method
and in a dynamic way.
3 MODEL DESCRIPTION
Our model need to be usable in several cases of appli-
cation, that is why available behaviors for the agents
Dynamic Agent-based Network Generation
601

Figure 1: Overall process: example of executing the behav-
ior ”Add a link to more connected agent”. [Action]: Add
link. [Attribute]: degree [Filter]: has a higher degree than
mine.
a. Selection of the acting agent and of the behavior to apply
b. Selection of candidate after a first pass of filtering c. Se-
lection of a single target d. Spreading of the behavior, end
of turn.
are generic. We don’t reproduce a specific process of
network creation. Instead, we want to find an abstract
and general model that can get us to the targeted net-
work. Many choices in the mechanisms of the model
have been made for having:
• a restrictive enough context for two distinct simu-
lations to give approximately the same result. We
will refer to this goal as (A - Restrain).
• a loose enough context to enable a large space of
networks that can be generated (B - Widen)
Going deeper in complexity has many drawbacks
such as increasing the number of parameters, while
we want to keep them at a reasonable number. More-
over, they have to be readable, understandable, and
easily searchable.
The evolution of the network is driven by two dy-
namics:
• Behaviors application by agents, that add and re-
move edges and thus shape the network
• Behaviors spreading among agents using the net-
work structure
3.1 Agent
The agents are the nodes of the network. They are
caracterized by their degree and by their behaviors,
for which they have two slots. One of these slots can
only contain a behavior embedding an add action, the
other slot receives a remove action. Agents have per-
fect informations about others attributes.
3.2 Behavior
3.2.1 Behavior Composition
A behavior is composed of three elements: (1) one
action, (2) filters and (3) attributes. An attribute can
be every kind of information characterizing an agent.
Then filter is applied in regard to those attributes, re-
straining the list of available agents on which the ac-
tion can be done. For example, the behavior: (1)[Ad-
dLink] on one agent having his (3)[degree] (2)[>] the
acting agent (3)[degree] (cf. Figure 2). If more than
one agent is available in the final set, the filter [Select
random target] is always applied in order to have the
action done on only one target. This helps keeping a
smooth dynamics in accordance to (A - Restrain).
Attributes. We choose to stay with one of the most
generic attribute available for an agent: his degree.
Agents have perfect information on other agents’ at-
tributes. New attributes can be easily intregrated.
Filter. The main logical comparators: >, <, =, 6=,
are available. The goal of filters is to narrow the star-
ting elements. Filters can be chained for a stronger
selectivity. A filter of unique selection, random, is
also available for returning randomly one element of a
list. For example, if agents have two attributes: degree
and the account balance. A behavior can be:
1. Action: add link
2. First filter: degree lower than mine
3. Second filter: balance greater than mine
4. Third filter: Select one agent randomly
It will return one agent from the list of agents having:
• Bigger balance than the acting node
• A degree inferior at the acting node
Some filters exist without attribute, for example the
random selection.
Actions. The action is applied on the set of agents
returned by the application of all filters. We are only
interested in the most basic kind of action, i.e. add an
undirected link and remove a link between the acting
agent and another. In order to keep the state of the
system readable, agent can only have one instance of
behavior per action. In other words, agents have a
maximum of two behaviors: one embedding an add
edge action, the other one being a remove link action,
respecting the (A - Restrain) principle.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
602

3.2.2 Available Behaviors
Implemented behaviors include following actions:
• Add an undirected edge
• Remove an existing edge
these actions are combined with these specific filters:
• Acting agent degree greater than (resp. lower
than) the target agent’s degree
• Agents having the highest degree (and the lowest)
• Agents reachable in a path of length n
• Random target
Figure 2: Detail of behavior execution.
3.2.3 Behavior Transmission
Originally we chose one of the most simple way
of transmission for the behaviors: direct imitation.
When an agent A applies on B an action, the agent
B will learn the whole behavior from A. Informa-
tion cascade highly depends on the initial fluctuations
(Easley and Kleinberg, 2010). But networks gener-
ated with the same initial parameters have to be sim-
ilar. To ensure the resilience to first transmissions, a
probability of transmission for each behavior is de-
fined rather than passing them at every application (A
- Restrain). In addition, agents can relearn behavior
replacing the previous he has in a specific action slot
(B - Widen). Thanks to that, behaviors learnt in the
beginning will just ”fuel” the network construction
dynamics.
However, this transmission rule has a drawback.
Some actions will not be able to be applied – and then
transmitted – in some network topology (e.g. the add
link to the node of highest degree will be applied only
once and will not propagate further). For these rea-
sons, we choose another way of transmission: upon
execution of a behavior, the receiver agent will have a
chance to get transmitted one of the acting agent be-
haviors (B - Widen), and not necessary the one that
has been applied. Following the previous example,
let consider an agent A having the highest degree of
the network and having two behaviors:
1. Add edge to highest degree
2. Remove edge randomly
When agent A will apply on agent B the behavior (2.),
the agent B will have the opportunity to learn one of
(1.) or (2.). Agents initialized with starting behaviors
will not replace them during the course of the simu-
lation. It will then avoid the disappearance of behav-
iors solemnly applied (and then transmitted) because
of their too high constraint of application, in accor-
dance with the (B - Widen) principle. Imitation often
provides a step of mutation or personalization of the
behavior (Dawkins, 1976) but we do not include it,
mainly for keeping control on process played during
the network formation (A - Restrain).
3.3 Scheduling
At each simulation step, an agent is chosen randomly.
First, this agent choose randomly one of its available
behaviors. Secondly, the agent tries to apply it by
looking at compatible agents, depending on filters and
attributes. Finally, The agent on which the behavior
has been executed can learn one of the acting agent
behavior, depending on the transmission probability.
A new step is started with the next agent.
4 SIMULATION AND RESULTS
4.1 Model Parameters and Initialisation
We work on 100 nodes, starting on a random network
of density 0.5. The random network is preferable to
an empty network because the latter make removing
behaviors depend on appliance of adding behavior.
The contrapositive is also true for complete network;
others starting networks have no justification for a
generic approach.
One behavior of each kind is distributed among
the population. Behaviors for the simulation and their
probability of transmission will then define the type
of network reachable by the simulation – if reaching
a stable final state. Besides, we initialize the other
nodes of the network with the following combinaison
of behavior: [Add an edge to a random node,remove
an edge from a random node], with a probability of
transmission of 0. This is made for ease initial behav-
ior transmissions. Two runs of simulations will then
differ on the probability of transmission for each of
these behavior.
A simulation is run on every combination of be-
havior distribution on the starting network, along with
Dynamic Agent-based Network Generation
603

combination of theirs probability of propagation. For
example, two behaviors with probability ranging from
0 to 0.2 with a step of 0.1 will provide 3
2
configura-
tion starting points.
4.2 Exploration
4.2.1 Computation of a Distance Between
Networks
The selection process of a good network highly de-
pends on which properties are taking into account in
the computation of the distance to the target network.
The weights between properties matters. Without any
information on the wanted network, we consider all
properties in a equivalent fashion. We then determine
a score of dissimilarity from 0 to 100 for each prop-
erties we find relevant, 0 being the equality. We then
normalize this distance at 100 for each properties.
(
(x − y)
maximum amplitude
) ∗ 100 (2)
with x and y being values of a properties, ranged
from 0 to maximum amplitude. We choose to take
into account the average degree distribution, the de-
gree distribution interquartile, the average clustering
of the nodes and the number of edges.
4.2.2 Automatic Space Research
The exploration is done in a exhaustive way, launch-
ing simulation for every combination of parameters,
waiting for the network to stabilize and comparing the
output to the target network. A score of distance is
computed, and the best network among the resulting
ones is selected.
4.3 Final State of the Dynamics of
Network Construction
We use the temporal variation of the network density
has a marker of stability: we consider that a network
is stable when its variation is below a given value.
Three state of behavior transmission dynamics can be
reached:
• Still Behaviors are not propagating anymore. Dis-
tribution of the different behavior in the popula-
tion has reached a final state;
• Cycling Spreading is still occurring. The distribu-
tion of behaviors is cycling among the population.
It is not still but can yet be detected;
• Chaotic Spreading occurs. The distribution dy-
namics does not follow any pattern.
Table 1: Final states reachable.
Behaviour spreading
Steady Cyclic Chaotic
Behavior
execution
Steady I.A - -
Cyclic II.A II.B -
Chaotic III.A III.B III.C
The same goes for behaviors execution. Table 1
is summarizing the possible joint states. Behavior
executed by agents do not necessary imply behavior
transmission, e.g. when the probability of transmis-
sion is at 0. There are some corner cases, for ex-
ample (II.A) where two agents cycle adding and re-
moving link between then, those two protagonists al-
ready sharing the same behaviors. Ideally, we would
like to have some networks generated after reaching
a (I.A) state, although it does not guaranty to behave
in a good way upon nodes addition (potentially not
propagating to them any behavior). Realistically, dy-
namics generating stable enough networks are more
in (II.A) and (II.B). Du to the dynamical process of
formation, the network won’t stop fluctuating most
of the time – both in term of behavior execution and
transmission. We decide to stop a run when the tem-
poral variation of the density reach a stability, or after
too many agents action.
4.4 Results
4.4.1 Target
The target network is a Scale-Free network, build with
the Preferential-Attachment model, with 100 nodes.
4.4.2 Run
The behaviors availables are :
• (I) Add edge to a node with a degree superior to
the acting agent (Add edge degree > mine)
• (II) Add edge to a node connected to a connected
node of the acting agent (Transitivity)
• (III) Add edge to the node with the highest degree
• (IV) Remove edge degree > mine
• (V) Remove edge degree < mine
Each behavior b have a probability of transmis-
sion P
t
(b) ranging from 0 to .9 with a .03 step. We
run the simulation for every combinaison of P
t
(b). In
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
604

order to have a idea of the reproductability of the net-
work creation process starting from the same config-
uration, we repeat three run of the same configuration
and compute Standard Deviation (SD) on each prop-
erties of the resulting networks.
4.4.3 Results and Score
The top results are in 2. The five behaviors b are
those describe in section 4.4.2. P
t
(b) is the proba-
bility of transmission of the behavior b upon execu-
tion. Each configuration is repeated 3 times, average
and Standard Deviation (SD) are computed on score
for each properties and on the result (we only display
SD on score). Density is the density of the final net-
work reach, avg DD the average degree distribution
over the three runs, DD interqtl, avg clust and avg
score being respectively the average degree distribu-
tion interquartile, the average clustering and the aver-
age score for the runs. This five properties are the one
used in the calcul of distance between the target and
the synthetic network. The lower score the better. The
first line of the array, Real Network, is the properties
of the target network. Others line are simulated one.
Figure 3: Network generated with the best set of behaviors.
Figure 4: Degree distribution of nodes in the best network.
3 is the network obtains. The final distribution of
behavior is:
• (I): 1% Add edge to a node with a degree superior
to the acting agent (Add edge degree > mine)
• (II): 1% Add edge to a node connected to a con-
nected node of the acting agent (Transitivity)
• (III): 95% Add edge to the node with the highest
degree
• (IV):1% Remove edge degree > mine
• (V): 98% Remove edge degree < mine
• (-): 1% Add edge to a random node (Initialization)
• (-): 1% Remove edge from a random node (Ini-
tialization)
even with a probability of transmission of a behavior
to 0, initial behavior are still available because starting
behavior on nodes cannot be replaced. 4 is the degree
distribution of the network with the best score.
Because no special weight has been associated to
the properties considerated for the score, networks
having some nodes without edges are not penalized
and have good results. The best network with a good
density is the second of the array, the previous one
having to many nodes without edges.
5 DISCUSSION AND FUTURE
IMPROVEMENTS
We are making some assumptions in the model, the
most important one being that we consider possible
to find rules that will lead to any kind of networks. In
other words, we try to find a dynamic process that will
generate a precise network, without being the original
process. Nothing guarantees that this process can be
used properly in a change of scale purpose, i.e. pre-
dicting the growth of the real network or even gener-
ating bigger network with the same properties. They
are initial configurations which do not converge to a
stable network, and the detection can be difficult, the
density undertaking strong variation.
The exhaustive research of the best initial configu-
ration, depending on the precision, can be pretty long
(3-4hours on a laptop) and a future amelioration will
be the use of a genetic algorithm to find the best set of
parameters.
Another very important improvement will be the
introduction of behaviors allowing adding or remov-
ing nodes in the network. This possibility open the
framework to imitate dynamical time evolution of net-
work, but will also be much more difficult to config-
ure, and will necessitate several ”pictures” of the tar-
geted network at different time to figure out the dy-
namic.
Dynamic Agent-based Network Generation
605
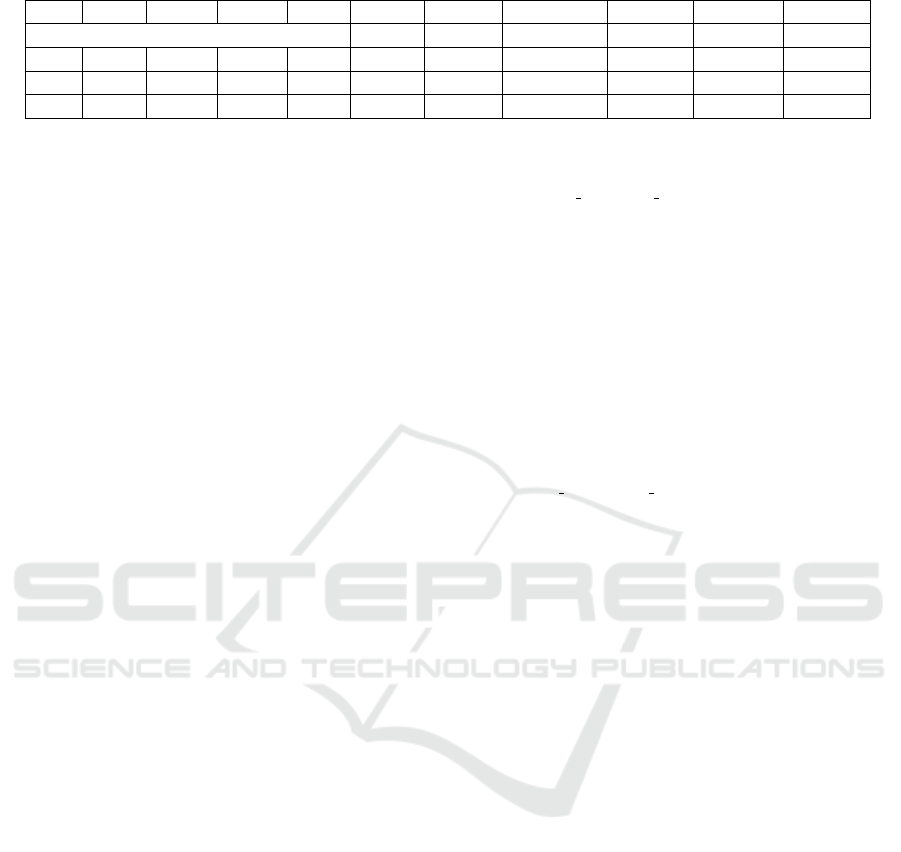
Table 2: Result of a simulation with five behaviors. See 4.4.3.
P
t
(I) P
t
(II) P
t
(III) P
t
(IV ) P
t
(V) density avg DD DD interqtl avg clust avg score SD score
Real network 0.02 1.98 1 0 0 0
0.03 0 0.6 0.06 0 0.001 0.12 0 0 6.71 0.06
0.06 0.06 0.06 0.06 0 0.01 1.14 1 0.046 6.9 0.89
0.09 0.6 0.06 0.09 0 0.028 2.86 5 0.09 16 3
6 CONCLUSION
Social network generation processes are often too
complicated to use or too abstract in the resulting net-
work properties. We offer a model of networks gen-
eration aiming a reproducing any kind of network,
guided by a topological distance to a target. Our
model is independant of the underlying process of
the target network formation, but it can be see as an
explainatory model. Mechanisms have been kept to
the simplest for readable and tractable purpose, and
the model do not need any configuration. We used a
Scale-Free network as a toy target, and results on gen-
erating this simple abstract model are promising. We
aim in future work at copying more complex struc-
tures.
REFERENCES
Alvarez, A. (2004). Memetics: An Evolutionary Theory of
Cultural Transmission. SORITES, (#15):24–28.
Amblard, F., Bouadjio-Boulic, A., Guti
´
errez, C. S., and
Gaudou, B. (2015). Which models are used in social
simulation to generate social networks?: a review of
17 years of publications in JASSS. In Proceedings of
the 2015 Winter Simulation Conference, pages 4021–
4032. IEEE Press.
Barabasi, A. and Albert-L
´
aszl
´
o, R. (1999). Emer-
gence of Scaling in Random Networks. Science,
286(5439):509–512.
Barrett, C. L., Beckman, R. J., Khan, M., Kumar, V. S. A.,
Marathe, M. V., Stretz, P. E., Dutta, T., and Lewis,
B. (2009). Generation and analysis of large synthetic
social contact networks. pages 1003–1014. IEEE.
Cointet, J.-P. and Roth, C. (2007). How Realistic Should
Knowledge Diffusion Models Be? Journal of Artifi-
cial Societies and Social Simulation, 10(3):5. bibtex:
cointet2007.
Dawkins, R. (1976). The selfish gene. Oxford University
Press, Oxford ; New York, new ed edition.
Easley, D. and Kleinberg, J. (2010). Networks, Crowds, and
Markets: Reasoning about a Highly Connected World.
Erdos, P. and Renyi, A. (1959). On random graphs I. Publ.
Math. Debrecen, 6:290–297.
Leskovec, J., Chakrabarti, D., Kleinberg, J., Faloutsos,
C., and Ghahramani, Z. (2010). Kronecker graphs:
An approach to modeling networks. The Journal of
Machine Learning Research, 11:985–1042. bibtex:
leskovec kronecker 2010.
Menezes, T. and Roth, C. (2014). Symbolic regression
of generative network models. Scientific Reports,
4:6284.
Milgram, S. (1967). The small World Problem. Psychology
Today, Vol. 2:60–67.
Parunak, H. V. D., Savit, R., and Riolo, R. L. (1998). Agent-
based modeling vs. equation-based modeling: A case
study and users’ guide. In International Workshop
on Multi-Agent Systems and Agent-Based Simulation,
pages 10–25. Springer.
Robins, G. (2011). Exponential random graph mod-
els for social networks. Encyclopaedia of Com-
plexity and System Science, Springer. bibtex:
robins exponential 2011.
Small, M., Xu, X., Zhou, J., Zhang, J., Sun, J., and Lu, J.-a.
(2008). Scale-free networks which are highly assorta-
tive but not small world. Physical Review E, 77(6).
Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics
of /‘small-world/’ networks : Article : Nature.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
606
