
Short Paper: Industrial Feasibility of Private Information Retrieval
Angela J
¨
aschke
1
, Bj
¨
orn Grohmann
2
, Frederik Armknecht
1
and Andreas Schaad
2
1
University of Mannheim, Germany
2
Huawei German Research Institute, Darmstadt, Germany
Keywords:
Private Information Retrieval, Industrial Use Case, Practicability, Overview, Implementation.
Abstract:
A popular security problem in database management is how to guarantee to a querying party that the database
owner will not learn anything about the data that is retrieved — a problem known as Private Information
Retrieval (PIR). While a variety of PIR schemes are known, they are rarely considered for practical use cases
yet. We investigate the feasibility of PIR in the telecommunications world to open up data of carriers to
external parties. To this end, we first provide a comparative survey of the current PIR state of the art (including
ORAM schemes as a generalized concept) as well as implementation and analysis of two PIR schemes for the
considered use case. While an overall conclusion is that PIR techniques are not too far away from practical
use in specific cases, we see ORAM as a more suitable candidate for further R&D investment.
1 BACKGROUND AND
MOTIVATION
The telecommunications world is undergoing a tran-
sition where carriers not only provide services such as
telephony or internet access, but also attempt to mon-
etize the huge amount of data associated with their
subscribers’ activity. Analyzing data like call statis-
tics or roaming behavior can be used to offer specif-
ically tailored services and packages. The combi-
nation of such data with other data from 3
rd
parties
can potentially result in even more value. As such,
one direction is to open up the existing databases to
subscribing external parties. In fact, it may well be
the case that two rivaling carriers allow each other
to query their subscriber databases, e.g. for detect-
ing fraudulent activities or faults in the network. An-
other real-world scenario is that of answering to the
demands of public authorities wanting to verify that
a user has been making a call at a certain time or to
assess whether a certain IMEI or IMSI is part of the
carriers subscriber base.
An open practical problem is how to guarantee
to the querying party that the database owner will
not learn anything about the data that is retrieved
— a problem known as Private Information Retrieval
(PIR) (Goldreich and Ostrovsky, 1996). Accordingly,
we assessed the feasibility of PIR schemes to support
such use cases, where the typical database consists of
400.000-800.000 entries of IMEIs and/or IMSIs. This
paper provides a comparative survey of PIR schemes
as part of Section 2. We then discuss two schemes
in detail, i.e. a Trapdoor Group scheme in Section
3.1 and an ORAM approach in Section 3.2. We pro-
vide detailed performance and runtime analysis data
in Section 4.
2 OVERVIEW AND
COMPARISON OF EXISTING
SCHEMES
The trivial solution for a user who wants to query a
database without the database server learning about
the query is to retrieve the entire database from the
server and ignore all except the queried entries. Of
course, this is very inefficient in terms of communica-
tion, but very efficient regarding computational effort
because there is (almost) none. Thus, the incurred ef-
fort provides a good starting point in that any new so-
lution should have less communication than this triv-
ial solution, often trading this for computational com-
plexity in some form.
We split existing works that realize some form
of private information retrieval into four main ap-
proaches. In a forthcoming paper, we present a de-
tailed overview of the different schemes, here we
only categorize the schemes into these high-level ap-
proaches. Some of the mentioned schemes have also
Jäschke, A., Grohmann, B., Armknecht, F. and Schaad, A.
Short Paper: Industrial Feasibility of Private Information Retrieval.
DOI: 10.5220/0006382003950400
In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 395-400
ISBN: 978-989-758-259-2
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
395

been presented in (Ostrovsky and Skeith(III), 2007)
and (Olumofin and Goldberg, 2011), and some obser-
vations about computational complexity can be found
in (Gasarch, 2004) and (Sion and Carbunar, 2007).
• Homomorphic Approaches: The user masks
(e.g., homomorphically encrypts) the queried in-
dex, and the server algebraically combines all in-
dices with the database entries to obtain a masked
version of only the queried entry. The user then
removes the mask to obtain the result. Publi-
cations following this general idea are (Kushile-
vitz and Ostrovsky, 1997), (Chang, 2004), (Mel-
chor et al., 2016) (Group Homomorphic), (Tros-
tle and Parrish, 2010) (Trapdoor Group), (Kiayias
et al., 2015; Lipmaa, 2009; Ishai and Paskin,
2007) (Branching Programs), (Melchor and Ga-
borit, 2007) (Lattice-based) and (Dor
¨
oz et al.,
2014) (FHE-based).
• ORAM Approaches: Comes from the field of
software protection, but can also be used to pro-
tect privacy in databases. ORAM requires a
slightly different setup: The database must be en-
crypted and thus there must be some key manage-
ment mechanism. In contrast to pure PIR, ORAM
offers the added option of writing, i.e., changing
or adding entries. Publications based on ORAM
are (Mayberry et al., 2014; Stefanov et al., 2013;
Ma et al., 2016) (ORAM-Tree), (Devadas et al.,
16 A) (Onion-ORAM), (Apon et al., 2014) (FHE-
ORAM) and (Lorch et al., 2013) (Parallel-Tree-
ORAM).
• Garbled Approaches: Since PIR consists of two
parties (the user and the server) trying to compute
a function (the correct database entry) without the
server learning the users input (the query index),
it is natural to look to Multiparty-Computation,
where two or more parties compute a function
together without learning any input except their
own, and the result of the computation. Publica-
tions involving this approach are (Lu and Ostro-
vsky, 2013; Gentry et al., 2014a; Gentry et al.,
2014b).
• Other Approaches: The ϕ-Hiding Approach
(Cachin et al., 1999), the Trapdoor Permutation
Approach (Kushilevitz and Ostrovsky, 2000), and
the Sender Anonymity Approach (Trostle and Par-
rish, 2010).
Table 1 compares the schemes from the above ap-
proaches, indicating a particularly good value with a
(light) green background and particularly unfavorable
aspects with a (darker) red background. The aspects
considered are Comm
U
(communication from user
to the server), Comm
S
(communication from server
to the user), Comp
U
(user computation effort) and
Comp
S
(server computation effort). The variables
used are:
• n is the number of database elements
• B is the block size
• λ is the security parameter
• M (resp. C) is the message (resp. ciphertext)
space of the encryption scheme
• m is a finite group order
The leftmost column denotes the approach as pre-
sented above: H for homomorphic, O for ORAM, G
for garbled and “-” if none apply.
3 CHOOSING AND OPTIMIZING
To test performance for the use cases described in
Section 1, we implemented two approaches — one
homomorphic and one ORAM-approach, as these dif-
fer greatly, yet can both solve our problem of PIR.
Concretely, we chose and modified a Trapdoor Group
Scheme based on (Trostle and Parrish, 2010) and the
Path-ORAM Scheme (Stefanov et al., 2013) for their
conceptual simplicity.
3.1 The (Optimized) Trapdoor Group
Scheme
The original scheme (Trostle and Parrish, 2010) only
allows retrieval of an entire row (i.e.,
√
n out of n)
of database entries, which we extend to allow single-
entry-retrieval and minimize communication. We
present this optimized scheme as a protocol:
Database Structure: n elements of Z
N
arranged as
a ln(n)-dimensional array with entries x
i
1
,...,i
ln(n)
,i
j
=
1,... ,n
1/ln(n)
for j = 1,...,ln(n).
Prerequisites: We assume that we work in the group
(Z
m
,+) and that m and N are coprime.
Queries: Suppose the user wants to query the element
x
i
∗
1
,...,i
∗
ln(n)
.
1. The user selects m as the group order above de-
pending on the required security level, but at least
m > N
dln(n)e
·n ·(N −1).
2. The user randomly selects secret b
j
∈ Z
∗
m
, j =
1,. .. ,ln(n) and ln(n) ·n
1/ln(n)
coefficients e
i, j
,i =
1,. .. ,n
1/ln(n)
, j = 1, .. ., ln(n) with three restric-
tions:
i. e
i, j
<
ln(n)
q
m
n·(N−1)
for all (i, j).
ii. For j = 1,...,ln(n): If i
∗
j
6= i,e
i, j
is a multiple
of N (i.e., e
i
= a
i
·N for some a
i
).
SECRYPT 2017 - 14th International Conference on Security and Cryptography
396
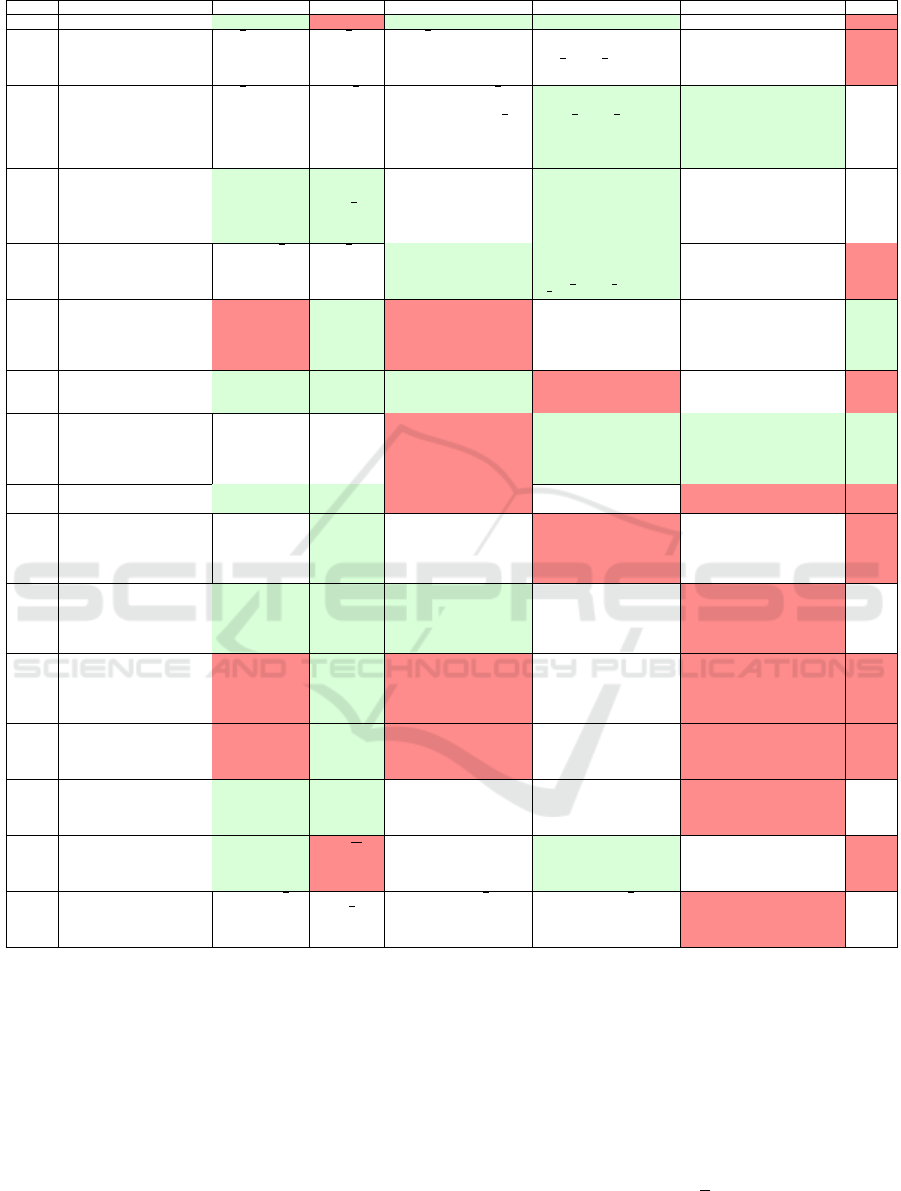
Table 1: A comparison of different PIR solutions.
Idea Scheme Comm
U
Comm
S
Comp
U
Comp
S
Comments Code
- Trivial 1 n ·B - - - x
H (Chang, 2004), (Melchor
et al., 2016), [Kushilevitz
and Ostrovsky, 1997]
(Group Homomorphic)
√
n ·log(|C|)
√
n ·
log(|C|)
√
n encryptions, 1
decryption
n scalar ciphertext
multiplications,
√
n ·log(
√
n) ciphertext
additions
C is the ciphertext space,
log(|C|) is the size of a
ciphertext.
x
H [Trostle and Parrish, 2010]
(Trapdoor Group)
√
n ·log
2
(m) O(
√
n ·
log
2
(m) +
n)
Generating m,
√
n
modular exponentiations/
multiplications +
√
n
discrete logs
n integer exponentiations/
multiplications
+
√
n ·log(
√
n) integer
multiplications/ additions
Group order m can be chosen
by user such that discrete log
is efficient (e.g., additive
group). Several queries can
be sent at once, so amortized
cost lower.
Not
pub
lic
H This paper (Optimized
Trapdoor Group)
ln(n)·n
1/ln(n)
·
log
2
(m)
O((log
2
(
m))
ln(n)
+
√
n)
Generating m,
ln(n) ·n
1/ln(n)
modular
exponentiations/
multiplications +ln(n)
discrete logs
O(n) integer
exponentiations/
multiplications +O(n)
integer multiplications/
additions
Group order m can be chosen
by user such that discrete log
is efficient (e.g., additive
group).
Not
pub
lic
H (Kiayias et al., 2015),
(Lipmaa, 2009), [Ishai and
Paskin, 2007] (Branching
Programs)
log(n) ·
√
n ·
log(|C|)
√
n ·
log(|C|)
log(n) encryptions and
decryptions
For k-ary branching
program (optimal k = 5):
n multiplications,
n
k
·
√
k ·log(
√
k) additions
C is the ciphertext space of
the Damg
˚
ard-Jurik
cryptosystem.
x
H [Melchor and Gaborit,
2007] (Lattice-based)
O(n ·N
2
·m) N ·m O(n ·N
x
) where x
depends on the matrix
multiplication algorithm
used, mostly a bit less
than 3.
2n ·N
2
multiplications
and 2N ·log(n·N)
additions.
Recommended as N = 50. X
C++
H (Dor
¨
oz et al., 2014)
(FHE-based)
log(C) log(C) One encryption, one
decryption
Depends on the concrete
FHE scheme used, likely
very expensive.
This is one extreme where
the server does all the work
and the user almost none.
x
O [Mayberry et al., 2014],
(Stefanov et al., 2013),
(Ma et al., 2016)
(ORAM-Tree)
O(log(n)
3
+
log(n)
2
·
log(|C|))
O(log(n)
3
+
log(n)
2
·
log(|C|))
log(n) recryptions for
each operation
- Supports writing as well.
Could be combined with
FHE to reduce user
communication and transfer
computation to the server.
X
Java
O (Devadas et al., 16 A)
(Onion-ORAM)
O(log(n)) O(B)
˜
O(B ·log
4
(n))
˜
ω(B ·log
4
(n)) The block size B needs to be
very large
˜
Ω(log
5
(n))
.
x
O (Apon et al., 2014)
(FHE-ORAM)
log(|C|) ·|op|,
op = ORAM
operation
written as
circuit
log(|C|) Convert operation into
circuit, encrypt values,
decrypt result.
Again depends on
concrete FHE scheme,
likely very expensive.
This seems worse than the
trivial FHE approach above,
but ORAM has a
write-operation which pure
PIR does not.
x
O (Lorch et al., 2013)
(Parallel-Tree-ORAM)
log(n) O(B) - log(n) recryptions for
each operation, but
parallelized.
Tree-ORAM outsourced to
server using secure
coprocessors (with which the
user communicates in
non-oblivious fashion).
Not
pub
lic
G Trivial Garbled Circuit >> n O(B) Transform function into
Boolean circuit, generate
4 keys for each gate,
compute 2 MACS for
each gate.
Evaluate the Boolean
circuit with the garbled
keys.
This is worse than the trivial
solution in every aspect
except server
communication.
x
G [Lu and Ostrovsky, 2013],
(Gentry et al., 2014a),
(Gentry et al., 2014b)
(Garbled RAM)
O(RAM-
execution time
of query)
O(B) Garble the query
(O(RAM-execution time
of query))
Evaluate garbled query
(O(RAM-execution time
of query))
The user also has to garble
and upload the database once
in the beginning.
x
- (Cachin et al., 1999)
(ϕ-Hiding)
log(n) + λ λ Effort of computing
ϕ-hiding m plus 2
modular exponentiations
Hamming-weight(n)
modular exponentiations
λ is logarithmic in n, with
recommended settings total
communication is
O(log
8
(n)).
Pseu
do
code
- [Kushilevitz and
Ostrovsky, 2000]
(Trapdoor Permutation)
O(B) n−
n
2B
(< O(n)
while
n > B
2
)
O(B) O(n ·B) User computation depends
on the trapdoor functions and
hardcore predicates used,
assumed O(n).
x
- [Trostle and Parrish, 2010]
(Sender Anonymity)
(λ + 1) ·
√
n (λ+ 1) ·
√
n
O(log(λ) ·
√
n) O(Q ·(λ + 1) ·
√
n), Q is
number of separate
queries sent (> 1!)
Very likely insecure, as
summing up all subqueries
yields sum of separate query
vectors.
Not
pub
lic
iii. For j = 1,. .. ,ln(n): If i
∗
j
= i,e
i, j
has the form
1 + a
l
·N for some a
l
.
3. The user sends the b
j
i
= b
j
· e
i, j
mod m to the
database. This constitutes the query.
Database Action: For j = 1,. .. ,ln(n): The database
computes x
i
1+ j
,...,i
ln(n)
:=
∑
n
1/ln(n)
k=1
b
j
k
·x
k,i
1+ j
,...,i
ln(n)
and
sends x := x
i
ln(n)+1
to the user. Operations in this step
are done over the integers, as the database does not
know the group order.
User Decoding: For j = 1, .. ., ln(n), the user sets
x = x ·(b
j
)
−1
mod m and transforms the result to N-
ary encoding. Then the least significant digit is the
requested database item x
i
∗
1
,...,i
∗
ln(n)
.
Security: In this new protocol, the size limit of the
e
i
’s has changed from the original version. This
requirement ensures getting the correct result with-
out wrapping around mod m in the decoding phase.
The security of the original scheme relies on the as-
sumption that given the
√
n PIR request elements
Short Paper: Industrial Feasibility of Private Information Retrieval
397

(b
1
,. .. ,b
√
n
), where b
i
= b · e
i
mod m and the e
i
’s
are chosen according to the constraints detailed above
(with the a
i
’s in 2.ii. and 2.iii. selected uniformly
at random), any computationally bounded adversary
can output the correct m only with negligible proba-
bility. Indicators for the hardness of this assumption
(called Hidden Modular Group Order Assumption),
i.e., how much information about the group order is
leaked by the queries, are presented in the original
paper (Trostle and Parrish, 2010), along with a reduc-
tion from the PIR protocol to this assumption. For
our improved scheme, it can easily be verified that
√
n > ln(n) ·n
1/ln(n)
for n ≥ 213. As databases are
generally much larger than 213 elements, we can base
security on the security of the original scheme, since
we will be sending less query elements and thus leak-
ing at most as much data as the original scheme.
3.2 The Path-ORAM Scheme
The second solution we implemented is the Path-
ORAM scheme from (Stefanov et al., 2013) with
non-recursive position map storage. We describe the
scheme with some parameters as we implemented
them instead of the generic version:
Database Structure: The database is held in a binary
tree of height L = dlog
2
(n)e with 2
L
leaves. Each
leaf (called a “bucket”) holds up to 5 database en-
tries (and is filled with dummy entries if it contains
less). There are far more buckets than database el-
ements. The bucket is encrypted by the user with
AES in CBC mode, where each database entry con-
sists of 1 or 2 AES-Blocks (128 bits each) depend-
ing on the chosen parameter setting (see Section 4).
Thus, each bucket contains 5 or 10 AES Blocks plus
the IV, so 6 or 11 blocks in total. Also, the user main-
tains a local stash S (which acts as a temporary stor-
age space) and a lookup table (called “position map”)
mapping database blocks to the leaves of the binary
tree. We assume that the database is already initial-
ized, as setup is rather tedious and must only be done
once before the first query is made, making it irrele-
vant for performance comparisons.
Queries: To retrieve an entry, the user looks up what
tree leaf the data block is mapped to in the position
map and reads the entire path from root to leaf into the
local stash S (which may contain some elements from
previous queries), as the entry will be in some bucket
on this path (or in the stash). The entry is mapped to a
new leaf randomly and the data is replaced in case of
a write operation. Then, all elements in the stash are
reencrypted and written to the server in a bottom-up
manner: Each entry in the stash is placed in a bucket
on the path to the (old) leaf as far away from the root
as possible, guaranteeing that the maximum amount
of blocks can be placed into the tree. The bucket is
filled up with dummy blocks and encrypted with AES
in CBC-mode with a random IV. Sometimes, some
elements from the stash can’t be placed into the tree,
these remain in the client stash and are placed into
a bucket in a future query. If too many of these el-
ements accumulate and the stash overflows, we say
that the ORAM has failed. We chose a stash size of
220 blocks.
Security: We implemented the scheme without
changing it, so the original security analysis holds.
4 PERFORMANCE
We now present the performance of our two chosen
schemes. Times were measured on an Intel Core i5-
4570 CPU with 3.20GHz and constitute average val-
ues, and the number of database entries was derived
from our use case (400.000 − 800.000 with some
smaller numbers for scale). The entries are random
numbers of lengths 256 (resp. 128) bits to simulate
the IMEIs and (or) IMSIs. The AES implementa-
tion in the ORAM scheme was wolfcrypt. Regard-
ing memory
1
for our use case, the Trapdoor Group
scheme requires a group order m of at least 3756 bits.
This implies a server memory of about 25.6MB for
the database, and about 1.317GB for storing interme-
diate results, so roughly 1.345GB in total. The mem-
ory requirement on the user side is only about 34kB.
In the ORAM-scheme, user memory is about 2.1MB,
whereas server memory strongly depends on the num-
ber of entries and got so large that we could not supply
data for 800.000 entries because our allotted memory
limit was exceeded.
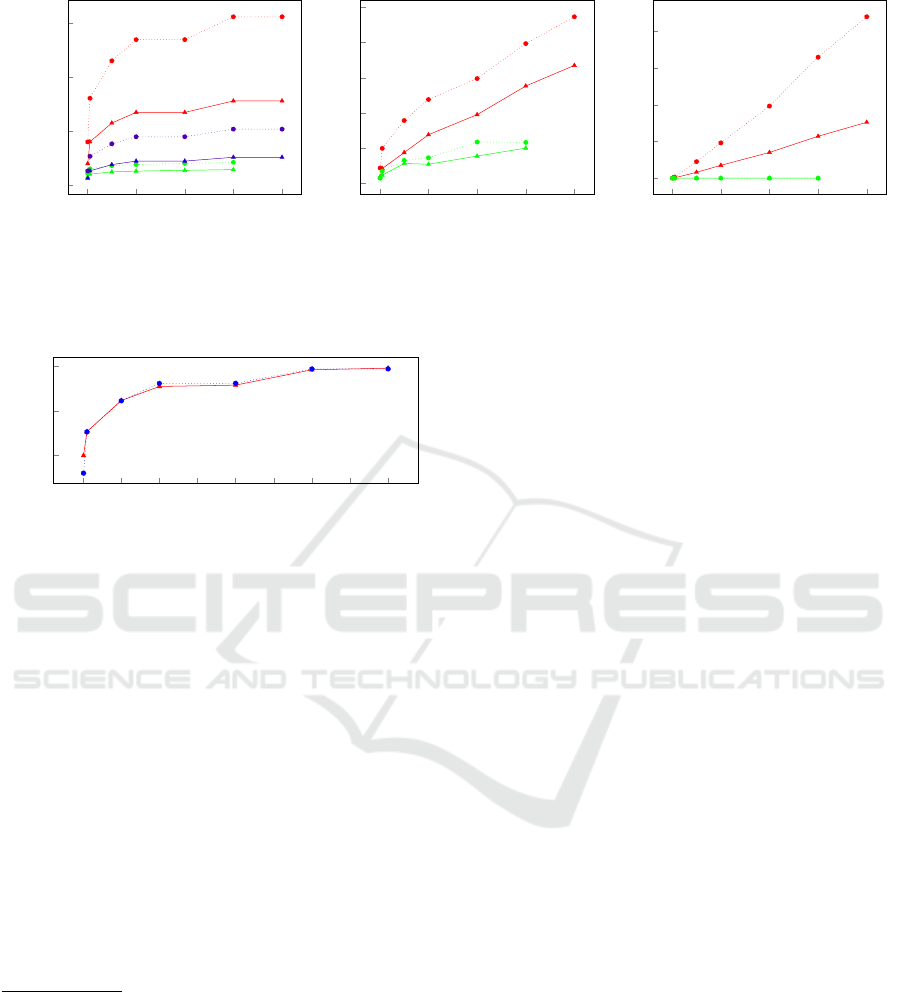
For the more traditional PIR metrics, we split the
performance into three main components: Commu-
nication (Figure 1a), user computational effort (1b)
and server computational effort (1c) and plot the ef-
fort for different numbers of database entries. In each
diagram, the dotted plots represent entries of length
256 bits, and the solid plots are entries of length
128 bits. The green plots always correspond to the
ORAM scheme, and the red plots to the Trapdoor-
Group scheme. In the communication figure, red is
the amount of data sent from the user to the server
in the Trapdoor-Group scheme, blue is the amount of
data sent from the server to the user in the Trapdoor-
Group scheme, and green is the amount of data sent
from user to server or vice versa (as these values
are equal) in the ORAM scheme. User computa-
tion encompasses decrypting, reading and encrypting
1
Theoretical results, not actually measured.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
398
0 200 400
600
800
0
100
200
300
Number of Records (x1000)
Communication (KBits)
(a) Communication.
0 200 400
600
800
0
1
2
3
4
5
Number of Records (x1000)
Time in milliseconds (ms)
(b) User Comp.
0 200 400
600
800
0
1
2
3
4
Number of Records (x1000)
Time in seconds (s)
(c) DB Comp.
Figure 1: Performance of the two approaches: Red (top 2 lines) is Trapdoor-Group (user to server in communication), green
(bottom 2 lines) is ORAM, blue (middle 2 lines) is server to user communication (Trapdoor-Group). Dotted is 256 bit, solid
is 128 bit database entries.
0 100 200 300 400
500 600
700 800
15
20
25
Number of Records (x1000)
Time in milliseconds (ms)
Figure 2: User setup without prime generation for 128 (red)
and 256 (blue) bit inputs.
in the ORAM scheme, and the decoding step in the
Trapdoor-Group scheme
2
.
5 CONCLUSION AND FUTURE
WORK
We see that ORAM performs better in all aspects,
even though the Trapdoor-Group protocol actually
performs worse in terms of user computation than
Figure 1b implies (see Footnote 2). Thus, for the use
case of this paper, ORAM is the better solution —
provided that the server has enough memory to store
the tree. If, however, memory is the constraining fac-
tor rather than speed (which seems unlikely in today’s
world), the Trapdoor Group protocol would be the
2
There is a user setup phase which incurs computational
effort but was not included in Figure 1b. The reason is
that m was computed as a prime by calling nextprime()
from the GMP-library in our code. This function’s run-
time varies enormously, dominating total time. This could
be easily be circumvented in reality once the parameters
of the database are set, e.g., by picking m randomly from
a large list of primes, or choosing m as not prime and im-
plementing constraints on the secret values instead. Either
way, this additional cost really needs to be added to the
time in Figure 1b. The time for user setup without this
prime generation can be seen in Figure 2.
better choice both for user and for the server.
For future work, an interesting aspect could be the
“levels” observed in Figure 1a for the Trapdoor Group
scheme (i.e., the values for 200,000 and 400, 000
entries seem similar, as do those for 600, 000 and
800,000), which we suppose comes from the dln(n)e
exponent in the constraint for the size of the group
order m (where n is the number of database entries).
REFERENCES
Apon, D., Katz, J., Shi, E., and Thiruvengadam, A. (2014).
Verifiable oblivious storage. In PKC.
Cachin, C., Micali, S., and Stadler, M. (1999). Compu-
tationally private information retrieval with polyloga-
rithmic communication. In EUROCRYPT.
Chang, Y. (2004). Single database private information re-
trieval with logarithmic communication. In ACISP.
Devadas, S., van Dijk, M., Fletcher, C. W., Ren, L., Shi, E.,
and Wichs, D. (2016-A). Onion ORAM: A constant
bandwidth blowup oblivious RAM. In TCC.
Dor
¨
oz, Y., Sunar, B., and Hammouri, G. (2014). Bandwidth
efficient PIR from NTRU. In FC Workshops BITCOIN
and WAHC.
Gasarch, W. I. (2004). A survey on private information re-
trieval (column: Computational complexity). Bulletin
of the EATCS.
Gentry, C., Halevi, S., Lu, S., Ostrovsky, R., Raykova, M.,
and Wichs, D. (2014a). Garbled RAM revisited. In
EUROCRYPT.
Gentry, C., Halevi, S., Raykova, M., and Wichs, D. (2014b).
Outsourcing private RAM computation. In FOCS.
Goldreich, O. and Ostrovsky, R. (1996). Software protec-
tion and simulation on oblivious rams. J. ACM.
Ishai, Y. and Paskin, A. (2007). Evaluating branching pro-
grams on encrypted data. In TCC.
Kiayias, A., Leonardos, N., Lipmaa, H., Pavlyk, K., and
Tang, Q. (2015). Optimal rate private information re-
trieval from homomorphic encryption. PoPETs.
Short Paper: Industrial Feasibility of Private Information Retrieval
399

Kushilevitz, E. and Ostrovsky, R. (1997). Replication is
NOT needed: SINGLE database, computationally-
private information retrieval. In FOCS.
Kushilevitz, E. and Ostrovsky, R. (2000). One-way trap-
door permutations are sufficient for non-trivial single-
server private information retrieval. In EUROCRYPT.
Lipmaa, H. (2009). First CPIR protocol with data-
dependent computation. In ICISC.
Lorch, J. R., Parno, B., Mickens, J. W., Raykova, M., and
Schiffman, J. (2013). Shroud: ensuring private access
to large-scale data in the data center. In FAST.
Lu, S. and Ostrovsky, R. (2013). How to garble RAM pro-
grams. In EUROCRYPT.
Ma, Q., Zhang, J., Peng, Y., Zhang, W., and Qiao, D.
(2016). SE-ORAM: A storage-efficient oblivious
RAM for privacy-preserving access to cloud storage.
In CSCloud.
Mayberry, T., Blass, E., and Chan, A. H. (2014). Efficient
private file retrieval by combining ORAM and PIR. In
NDSS.
Melchor, C. A., Barrier, J., Fousse, L., and Killijian, M.
(2016). XPIR : Private information retrieval for ev-
eryone. PoPETs.
Melchor, C. A. and Gaborit, P. (2007). A lattice-based
computationally-efficient private information retrieval
protocol. IACR Cryptology ePrint Archive, 446.
Olumofin, F. and Goldberg, I. (2011). Revisiting the com-
putational practicality of private information retrieval.
In FC.
Ostrovsky, R. and Skeith(III), W. E. (2007). A survey of sin-
gle database PIR: techniques and applications. PKC.
Sion, R. and Carbunar, B. (2007). On the practicality of
private information retrieval. In NDSS.
Stefanov, E., van Dijk, M., Shi, E., Fletcher, C. W., Ren,
L., Yu, X., and Devadas, S. (2013). Path ORAM: an
extremely simple oblivious RAM protocol. In CCS.
Trostle, J. T. and Parrish, A. (2010). Efficient computation-
ally private information retrieval from anonymity or
trapdoor groups. In ISC.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
400
