Graph Community Discovery Algorithms in Neo4j with a

Regularization-based Evaluation Metric

Andreas Kanavos, Georgios Drakopoulos and Athanasios Tsakalidis

Computer Engineering and Informatics Department, University of Patras, Achaia 26504, Greece

Keywords:

CNM Algorithm, Community Discovery, Graph Databases, Graph Mining, Graph Signal Processing, Louvain

Algorithm, Newman-Girvan Algorithm, Neo4j, Regularization, Walktrap Algorithm.

Abstract:

Community discovery is central to social network analysis as it provides a natural way for decomposing a

social graph to smaller ones based on the interactions among individuals. Communities do not need to be

disjoint and often exhibit recursive structure. The latter has been established as a distinctive characteristic of

large social graphs, indicating a modularity in the way humans build societies. This paper presents the im-

plementation of four established community discovery algorithms in the form of Neo4j higher order analytics

with the Twitter4j Java API and their application to two real Twitter graphs with diverse structural properties.

In order to evaluate the results obtained from each algorithm a regularization-like metric, balancing the global

and local graph self-similarity akin to the way it is done in signal processing, is proposed.

1 INTRODUCTION

Twitter is currently the most popular microblogging

platform and the stage for ongoing political, ﬁnan-

cial, and cultural conversations with a vast amount

of tweets being posted on a daily basis. Decom-

posing a Twitter social graph to communities yields

a deeper insight to these seemingly chaotic interac-

tions. However, community discovery is by no means

a trivial task. Besides the large volume of accounts,

tweets, retweets, and hashtags that need to be exam-

ined, necessarily implying parallel or distributed pro-

cessing, the question of what constitutes a commu-

nity, although posed in easily understood terms, re-

mains to be deﬁnitively answered. This does not im-

ply that no formal community deﬁnition exists. Quite

the contrary, a plethora of such deﬁnitions has been

in fact proposed, for instance in (Carrington et al.,

2005), (Fortunato, 2010), (Newman, 2010), which

successfully capture crucial aspects of human social

organization. However, they differ in key aspects and,

therefore, lead to different community detection algo-

rithms.

Similarly, there are a number of ways to assess

the clustering quality, namely community coherence.

However, most of the existing coherence metrics

are either prohibitively expensive, such as the maxi-

mum distance between vertices, or are prone to out-

liers, such as the diameter-based metrics (Drakopou-

los et al., 2015b) (Drakopoulos et al., 2016). To this

end, a coherence metric balancing global and local

self-similarity properties with a rationale similar to

the signal processing regularization criterion

K =

x − As

+ µ

, µ

> 0 (1)

which given a data vector x, possibly with noise and

outliers, computes a smoother version s thereof by

combining global and local patterns coded in matri-

ces A and B respectively. µ

(Drakopoulos and Mega-

looikonomou, 2016) controls their contribution to s.

Graph databases such as Neo4j

, GraphDB

, and

BrightstarDB

provide production grade front- or

back-end graph storage. In addition, they also offer

graph analytics such as link prediction and minimum

spanning trees (Panzarino, 2014) (Robinson et al.,

2013). Higher order analytics, such as community

discovery, constitute a signiﬁcant addition as they of-

fer deeper insight in the graph structure.

The primary contribution of this paper is twofold.

Four community discovery algorithms, namely the

Newman-Girvan, the Walktrap, the Louvain, and the

CNM were implemented in Java over Neo4j. More-

over, the results of these algorithms applied to two

Twitter graphs created with Twitter4j

are evalu-

www.neo4j.com

www.ontotext.com

www.brightstardb.com

http://twitter4j.org/en/index.html

Kanavos, A., Drakopoulos, G. and Tsakalidis, A.

Graph Community Discovery Algor ithms in Neo4j with a Regularization-based Evaluation Metric.

DOI: 10.5220/0006382104030410

In Proceedings of the 13th International Conference on Web Information Systems and Technologies (WEBIST 2017), pages 403-410

ISBN: 978-989-758-246-2

403

ated with a regularization-like criterion which is efﬁ-

ciently computed and relies on the fundamental self-

similarity property of scale-free graphs.

The rest of this paper is structured as follows.

Section 2 provides an overview of community detec-

tion algorithms. The main characteristics of graph

databases are described in section 3. The inherent

high order nature of graph communities and four im-

plemented algorithms are outlined in section 4. Fi-

nally, section 5 describes the datasets used in this pa-

per and the results obtained from executing the com-

munity detection algorithms in Neo4j, whereas sec-

tion 6 concludes by recapitulating the main ﬁndings

and exploring future research directions.

Table 1: Paper notation.

Symbol Meaning

= Deﬁnition or equality by deﬁnition

deg(v

) Degree of vertex v

Complete graph with n vertices

,. .., v

) Path with vertices v

,. .., v

{

}

Set containing elements s

Cardinality of set S or

{

}

Sequence of items s

2 RELATED WORK

Community detection is related mostly to graph clus-

tering (Scott, 2000), Web retrieval (Newman, 2010),

and user inﬂuence (Carrington et al., 2005). Con-

cerning graph clustering, it can be performed either

structurally or spectrally. In the former case parti-

tioning is based on the properties of the graph adja-

cency matrix (Kernighan and Lin, 1970) (Shi and Ma-

lik, 2000), whereas in the latter connectivity patterns

such as edge density or modularity (Newman, 2004b)

(Newman, 2004a) play a primary role with notable

examples being (Blondel et al., 2008), (Girvan and

Newman, 2002). Vertex ranking, computed for in-

stance with PageRank (Brin and Page, 1998) includ-

ing its variants (Langville and Meyer, 2006) or HITS

(Kleinberg, 1998), can be used to build communities

with vertices which share common topics. Authority

estimation can also be used to construct graph com-

munities. In (Agichtein et al., 2008) several graph

features as well as hub and authority scores are used

to model the relative importance of a given user. Al-

ternatively, in the expertise ranking model (Jurczyk

and Agichtein, 2007), authorities are derived by per-

forming link analysis to the graph induced from in-

teractions between users. Moreover, in (Weng et al.,

2010) authors employ Latent Dirichlet Allocation and

a PageRank variant to cluster the graph according to

topics and subsequently the authorities for each topic

are identiﬁed. This was extended in (Pal and Counts,

2011) with additional features, advanced clustering

and real-time capabilities. In addition, a previous

work regarding inﬂuential communities identiﬁcation

is presented in (Kafeza et al., 2014). Finally, an over-

all and extensive overview of the community discov-

ery ﬁeld is (Fortunato, 2010).

Signal regularization is a common technique aim-

ing at deriving a smoother or cleaner version of

a data vector without altering the regions of inter-

est. It has numerous applications in signal process-

ing (Drakopoulos and Megalooikonomou, 2016), ma-

chine learning (Girosi et al., 1995), system identi-

ﬁcation (Johansen, 1997), and inverse problem the-

ory (Vogel, 2002), while it also has connections to

Sobolev space theory (Adams and Fournier, 2003)

and to reproducible kernel Hilbert space theory (At-

touch and Az

e, 1993).

The interest in the graph processing ﬁeld has been

invigorated with the advent of open source graph

databases such as Neo4j, GraphDB and BrightStar.

Graph processing is usually implemented with the

use of massive distributed graph computing systems

like Google Pregel and graph based machine learning

frameworks like GraphLab. In these systems, graphs

play a twofold role as the data ﬂow model and as the

learning model.

3 ARCHITECTURE AND

SOFTWARE

Graph databases such as Neo4j constitute one of the

four major database technologies collectively known

as NoSQL. RDBMSs assume that data can be repre-

sented in a structured and tabular manner. However,

the modern Web and the IoT generate unstructured or

semistructured, higher order, linked data which can-

not be easily described by a schema. The primary

properties of Neo4j include (Robinson et al., 2013)

(Panzarino, 2014) (Drakopoulos et al., 2015a)

Property 1. Neo4j is schemaless.

Property 2. Neo4j conforms to BASE requirements.

Property 3. The property graph model is the primary

conceptual data model of Neo4j.

Property 4. Neo4j supports SPARQL, a W3C RDF

query language, and Gremlin, a path query language

(Drakopoulos et al., 2015a). However, queries to

a Neo4j system are mostly submitted in Cypher, an

ASCII art, pattern based, declarative language. The

basic Cypher query has the form

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies

404

[ s t a r t ]

match

[ with [ as ]]

where

r e t u r n <e x p r e s s i o n >

[ order by <f u n c t i o n > [ d es c ] ]

Cypher queries can be submitted directly in Neo4j

console or, most frequently, through an application

over a Neo4j API. For Java the Neo4j API is included

in the Neo4j NetBeans extension library.

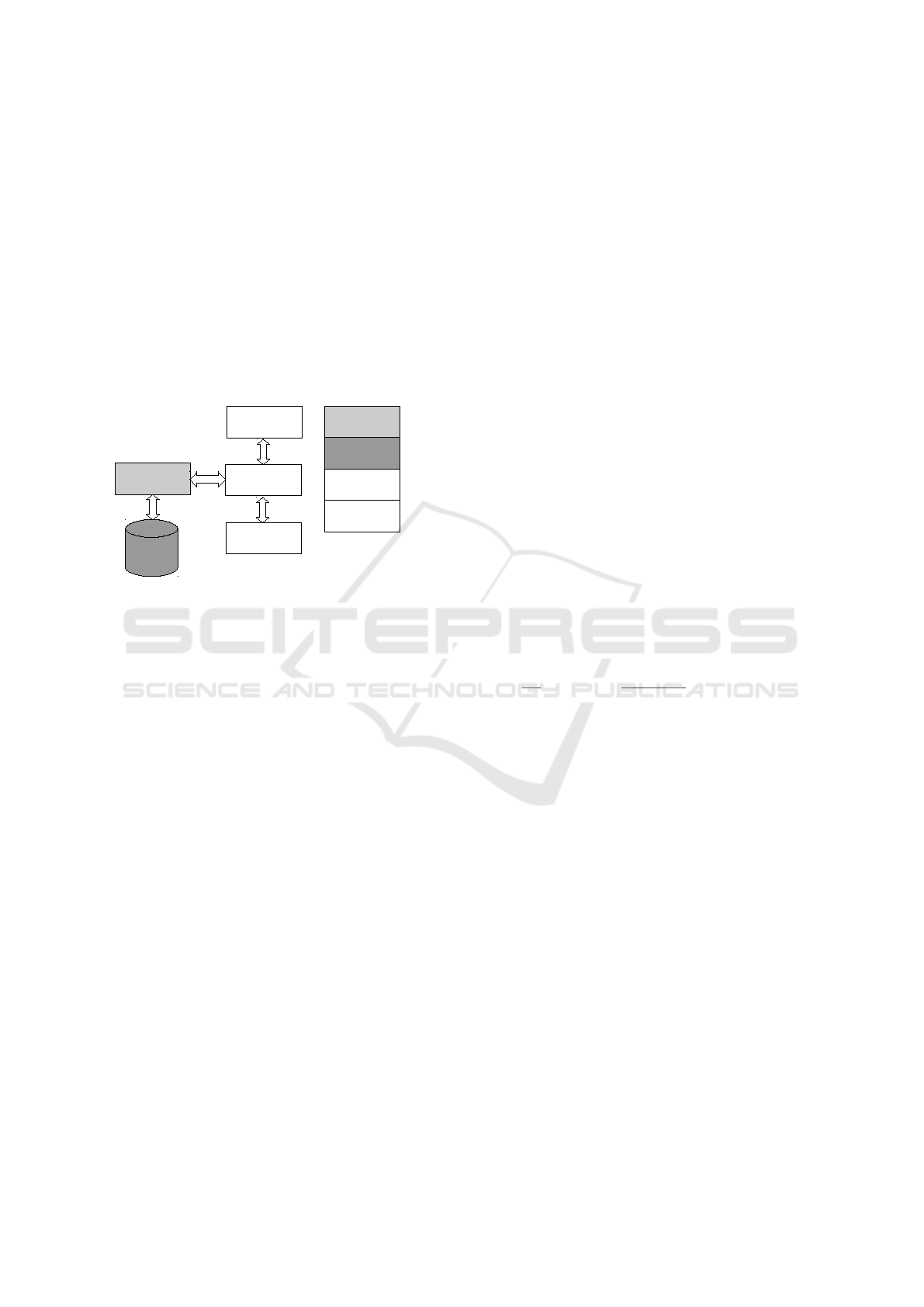
Figure 1 illustrates its components, including the

social crawler, Neo4j, and the graph analytics, as well

as the data ﬂow between them.

Neo4j

Twitter

crawler

Java

driver

Client

NetBeans

library

White box

(user)

White box

(developer)

Gray box

Black box

Figure 1: System architecture.

The social crawler has been implemented in Java

using the Twitter4j API for collecting Twitter data

and NetBeans for interfacing with Neo4j. Concerning

system conﬁguration, the Twitter crawler is currently

inaccessible from the client, excluding thus any loops

with user feedback in subsequent Twitter crawlings.

The Neo4j version is 2.2.5, the latest available ver-

sion at the beginning of development.

4 COMMUNITY DISCOVERY

This section outlines four popular community detec-

tion algorithms. It should be noted that these commu-

nity detection algorithms rely on the inherently higher

order information found as the graph structure. The

latter is expressed in terms of the number of vertices

or edges that need to be visited or traversed respec-

tively in order to compute a graph function. Typi-

cal examples include the diameter or the number of

shortest paths connecting two given vertices. This can

be at least partly attributed to the linked graph nature

which balances local and global information. There-

fore, graph processing systems should be of similar

nature, if useful information is to be extracted.

A manifestation of the higher order nature of the

graph community detection problem is that the small-

est community is a triangle. In terms of vertices, it can

be considered as a third order quantity. If a triangle

is closed, then it is a third order quantity in terms of

edges as well. This stems from the fact that single re-

lationships between individuals, namely edges in so-

cial graphs, do not qualify as communities. Thus, in

a group there has to be at least one common acquain-

tance connecting the individuals in this group. This is

reﬂected by the fact that successful community detec-

tion algorithms rely on higher order metrics directly

or indirectly. For instance, graph clustering or spec-

tral graph partitioning algorithms exploit higher or-

der constructs such as the primary eigenvector or the

resolvent of the graph adjacency matrix (Benzi and

Boito, 2010).

4.1 Louvain Algorithm

Louvain or multilevel algorithm (Blondel et al., 2008)

is a hierarchical clustering algorithm operating on

weighted graphs. Initially each vertex is a single com-

munity. Then, communities are progressively merged

with neighboring ones based on the local edge density

change. The objective is to create communities where

edge density is high, while intercommunity density

remains low.

Louvain algorithm expresses the intuitive notion

of edge density with modularity, a scalar m ranging

from −1 to +1 is deﬁned as

(

∑

(i, j)



i, j

−

deg(v

)deg(v

)



∈ c

∧ v

∈ c

0, v

∈ c

(2)

In (2) c

and c

denote the communities v

and v

belong to and w

i, j

is the weight of (i, j). Although

the Louvain algorithm can be applied to unweighted

graphs, the result is always a weighted graph where

weights are proportional to local edge density. An

unweighted graph is treated as a weighted graph with

initial weights equal to one.

Modularity is maximized through a sequence of

two alternating steps. In the ﬁrst step, each v

merged with each of its neighbors into a single com-

munity C and the modularity change ∆m is computed

as the difference between the new modularity minus

the old one. Finally, v

is assigned to the c

yielding

the bigger ∆m. In the second step, a new graph is con-

structed where all vertices belonging to the same com-

munity are merged into a single vertex. All edges con-

necting two communities form a single edge whose

weight is the sum of the individual weights.

Graph Community Discovery Algorithms in Neo4j with a Regularization-based Evaluation Metric

405

Algorithm 1: Louvain (multilevel) algorithm.

Require: Graph G (V, E)

Ensure: G is partitioned into communities

1: if G is unweighted then

2: for all (v

) ∈ E do

3: w

i, j

← 1

4: end for

5: end if

6: k ← 0 and V

← V and E

← E

7: for all v

∈ V

8: v

becomes a separate community

9: end for

10: Compute m as in (2)

11: repeat

12: for all v

∈ V

13: for all v

6= v

(i, j) ∈ E

14: Assign temporarily v

to c

15: Compute ∆m.

16: end for

17: end for

18: Assign v

to c

with the biggest ∆m

19: Merge vertices of c

to a single vertex

20: Merge edges within c

to a single loop

21: Merge edges between c

and c

to a single edge

22: k ← 1 and update V

, E

23: until no ∆m can occur.

24: return

4.2 Newman-Girvan Algorithm

Newman-Girvan or edge betweeness algorithm (Gir-

van and Newman, 2002) relies on betweeness central-

ity, an edge centrality metric which counts the fraction

of the number of the shortest paths connecting two

vertices v

and v

a given edge e

is part of, denoted

by ζ

i, j

, to the total number of shortest paths connect-

ing v

and v

, denoted by ζ

i, j

. Then the betweeness

centrality for e

, denoted by B

, is computed by aver-

aging over each vertex pair







(

)

∑

(

)

∈V ×V

i, j

, v

6= v

1, v

= v

(3)

In (Girvan and Newman, 2002) a process for

computing B

for each e

, in a manner resembling

breadth-ﬁrst search, is described. The rationale is that

vertices belonging to different communities should

rely on edges connecting communities for informa-

tion exchange. However, note that the converse does

not need to be true. Moreover, depending on graph

topology, some of the community connecting edges

may not be high ranked in terms of betweeness cen-

trality, as other edges may be more preferable. There-

fore, the edge e

∗

with the highest betweeness central-

ity should be removed and subsequently the process

should be again applied to the new graph. Eventually,

all edges connecting communities will be identiﬁed.

Intuitively, the edge sequence

∗

should contain the

graph bridges as well, which are a subset of the com-

munity connecting edges. In case the graph becomes

disconnected, then the process is repeated for each of

the connected components.

Algorithm 2: Newman-Girvan algorithm.

Require: Graph G (V, E); Termination criterion τ

Ensure: G is partitioned into communities

1: while E 6= ∅ and τ

not satisﬁed do

2: Compute B

as in (3)

3: e

∗

← argmax

{

}

4: E ← E \

{

∗

}

5: end while

6: return

4.3 Walktrap Algorithm

Walktrap algorithm is based on the principle of ran-

dom walker. Starting from any random vertex the ran-

dom walker will eventually spend more time steps in

densely interconnected graph segments, as it is more

probable for a randomly picked edge to lead to an-

other vertex inside the segment than to a vertex out-

side it. Since such densely connected segments in-

tuitively correspond to communities, random walks

based metrics for community detection has been pro-

posed in (Pons and Latapy, 2005). The probability

that the walker moves from v

to v

i, j

A[i, j]

deg(v

)

(4)

where A denotes the adjacency matrix

A[i, j]

(

1, i = j ∨ (i, j) ∈ E

0, i 6= j ∧ (i, j) 6∈ E

∈

{

0,1

}

(5)

As the probability that the random walker reaches

from v

through a path of length `, is denoted by

i, j

, then if v

and v

belong to the same community,

then p

i, j

should be large for at least large values of `.

Note that the converse is not always true, depending

on graph topology

i, j

∑

∏

(

)

∈π

i, j

(6)

where

π =



,. .., v

`+1



= ` (7)

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies

406

Equations lay the groundwork for deﬁning the dis-

tance d

i, j

between v

and v

i, j

∑

k=1



i,k

− p

j,k



deg(v

)

(8)

The transition probability p

C,k

from any vertex be-

longing to a community C to v

in ` steps, is deﬁned

C,k

∑

i∈C

i,k

(9)

Generalizing (8), the distance r

between the

communities C

and C

is deﬁned as

∑

k=1



− p



deg(v

)

(10)

Algorithm 3: Walktrap algorithm.

Require: Graph G (V, E); Termination criterion τ

Ensure: G is partitioned into communities

1: for all v

∈ V do

2: Assign v

to a separate community

3: end for

4: repeat

5: for all distinct community pairs C

and C

6: Compute r

as in (10).

7: end for

8: Merge communities which minimize r

9: until one community remains.

10: return

4.4 CNM Algorithm

The CNM algorithm is also a hierarchical vertex par-

titioning algorithm. As such, initially each vertex

constitutes a separate community. Then, neighbor-

ing communities are progressively merged to larger

ones until no more merging is feasible according to

the structurality criterion a. For a single vertex v

, a

is deﬁned as

deg(v

)

(11)

For two neighboring vertices, ∆a

i, j

is deﬁned as

∆a

i, j

−

deg(v

)deg(v

)

(12)

and it is zero for non-neighboring vertices. ∆a

i, j

corresponds to the structural changes incurred from

adding (i, j) to a community. In order to keep track of

∆a

i, j

, they are stored in a sparse matrix. Also the com-

munities are stored in a binary tree where the leaves

are the individual vertices. Each time two commu-

nities are merged, the resulting community is their

parent at the tree. Moreover, the two corresponding

columns of the ∆a

i, j

sparse matrix are merged and

their elements are updated according to the following

rules (assuming communities i and j are to be fused):

• If community k is linked with communities i and

j, then

∆a

j,k

= ∆a

i,k

+ ∆a

j,k

(13)

• If community k is linked with community i but not

with j, then

∆a

j,k

= ∆a

i,k

− 2a

(14)

• Finally, if community k is linked with community

j but not with i, then

∆a

j,k

= ∆a

j,k

− 2a

(15)

Algorithm 4: CNM algorithm.

Require: Graph G (V, E); Termination criterion τ

Ensure: G is partitioned into communities

1: Assign each vertex to a separate community

2: for all discrete pairs (v

) ∈ V ×V do

3: Compute pairwise ∆a

i, j

as in (12)

4: end for

5: repeat

6: for all remaining communities do

7: Compute pairwise ∆a

i, j

as in (12)

8: end for

9: Find max ∆a

i, j

and fuse communities

10: Update binary tree and a

and matrix ∆a

i, j

11: until one community is left.

12: return

5 Results

5.1 Data Synopsis

Deﬁnition 1. The (log)completeness σ

(σ

) of a

graph is deﬁned as the ratio of the (log)number of

edges to the (log)number of edges of K





(

− 1)

≈

log





≈

log

2log

(16)

Graph Community Discovery Algorithms in Neo4j with a Regularization-based Evaluation Metric

407

Deﬁnition 2. The (log)density ρ

(ρ

) of a graph is

deﬁned as the ratio of the (log)number of edges to the

(log)number of vertices.

log

≈ 2σ

(17)

Notice that the base of the logarithm affects nei-

ther σ

nor ρ

since

log

x =

log

, x 6= 0 (18)

It follows from (16) and (17) that

(19)

implying a balance between density, which connects

the number of vertices and edges of the same graph,

and completeness, which relates the number of edges

of a graph to those of K

In order to demonstrate the differences between

the algorithms of section 4, two social graphs with

anonymized Twitter users were constructed. Twit-

ter4j retrieved users as well as information regarding

who follows whom using a topic sampling approach.

A keyword search query collected the users whose

tweets or retweets contained #Grexit, a trendy and po-

litically highly controversial topic, whereas a second

query used the hashtag #SocialNetwork, a generic and

by no means inciendiary topic. Subsequently, users

following each other or having a common follower

were connected with an edge as in (Kanavos et al.,

2014). Tables 2 and 3 review graphs #SocialNetwork

and #SocialNetwork respectively. Both seem to have

similar properties on a macroscopic scale, however

the seemingly subtle differences correspond to sig-

niﬁcant structural differences at the community level

stemming from the nature of the two topics.

Table 2: #Grexit graph sunopsis.

Feature Value Feature Value

Directed True Weighted False

3696

8225

2.2313 ρ

1.0973

0.0012 σ

0.5486

5.2 Analysis

Table 2 outlines the size of each community, ex-

pressed as a percentage of the total number of ver-

tices, as generated by the four aforementioned algo-

rithms. Louvain and CNM algorithms yield fewer

Table 3: #SocialNetwork graph sunopsis.

Feature Value Feature Value

Directed True Weighted False

4246

12054

2.8387 ρ

1.1249

0.0013 σ

0.5624

communities than Newman-Girvan and Walktrap.

Another observation is that communities tend to be

clustered in size.

Table 4: Community sizes (%) of #Grexit graph.

id Edge Walktrap Louvain CNM

1 9.30 10.50 6.50 9.70

2 6.10 12.60 13.60 10.20

3 5.10 7.00 11.20 22.10

4 13.10 7.20 6.40 18.50

5 2.70 11.20 7.90 14.30

6 13.20 10.20 12.50 11.40

7 5.20 8.40 13.60 5.50

8 15.10 6.30 12.20 8.30

9 12.10 5.50 6.30 -

10 11.10 11.40 5.20 -

11 1.10 2.10 4.60 -

12 3.40 3.40 - -

13 2.50 4.20 - -

Table 5: Community sizes (%) of #SocialNetwork graph.

id Edge Walktrap Louvain CNM

1 9.10 12.50 6.90 9.70

2 6.60 14.60 18.40 12.00

3 5.10 7.10 13.20 25.10

4 15.10 7.10 6.70 18.50

5 2.80 13.30 7.90 17.30

6 15.20 11.20 13.50 11.90

7 5.40 9.40 18.20 5.50

8 15.10 6.50 15.20 -

9 13.10 5.60 - -

10 12.50 12.70 - -

A metric for evaluating the clustering quality

is inspired by the regularization cost function from

(Drakopoulos and Megalooikonomou, 2016)

J(λ

) = J

+ λ

, λ

∈ R

(20)

where λ

is a strictly positive factor expressing the

relative importance of J

compared to J

The ﬁrst term measures the combined and

weighted relative deviation of k-th community in

terms of logdensity and logcompleteness in macro-

scopic or global scale, namely from the entire graph

∑

k=1



− ρ



− σ



(21)

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies

408

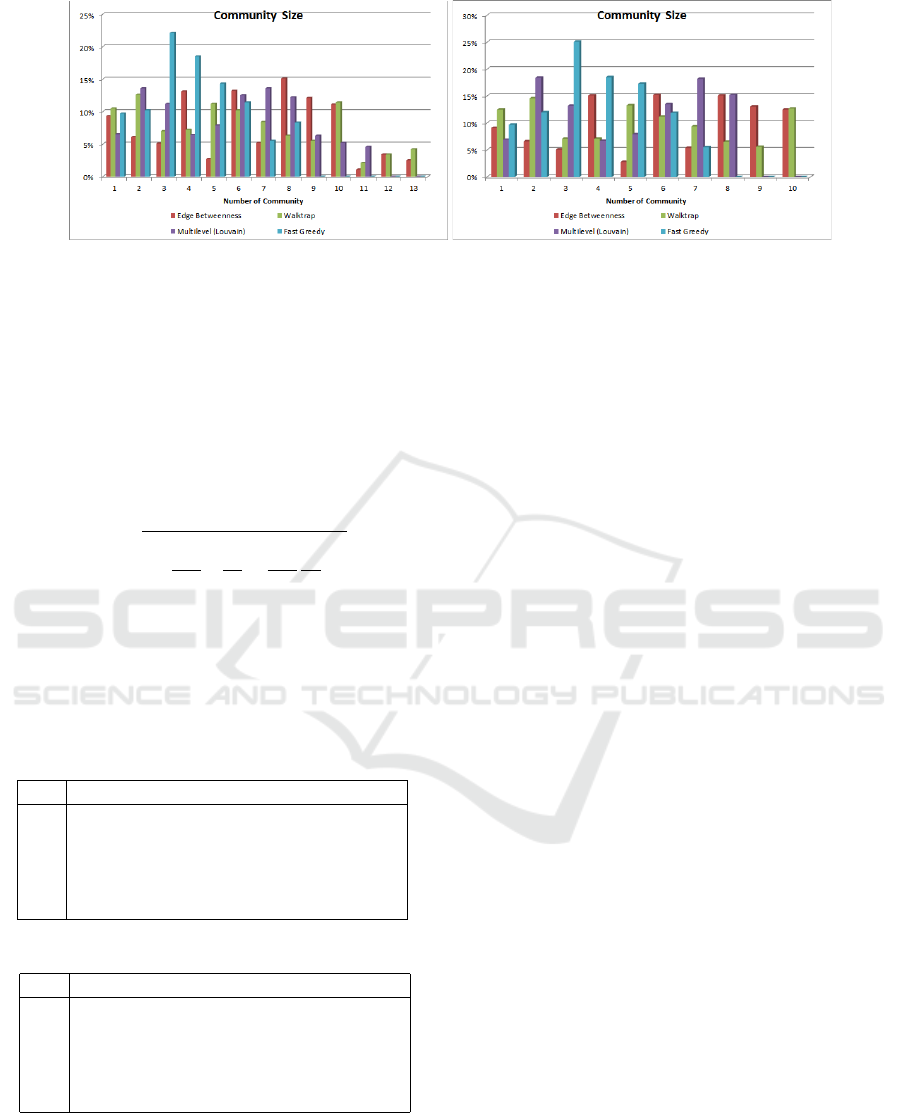
(a) #Grexit (b) #SocialNetwork

Figure 2: Graph community sizes.

where ρ

and σ

are the logdensity and the logcom-

pleteness of the k-th community whereas C

is the set

of communities. The weight of each community is the

ratio of its vertices to the total number of vertices.

The second term quantiﬁes the combined and

weighted deviation from the expected scale-free be-

havior, again expressed in terms of logdensity and

logcompleteness as in (19), in microscopic or local

scale, namely at the community level

∑

k=1



−



(22)

Once communities are derived, computing logdensity

and logcompleteness is straightforward. This is an

advantage over community metrics such as diameter.

Moreover, J(λ

) is less prone to outliers and captures

the scale-free behavior of the graph.

Table 6: J score for #Grexit graph.

Edge Walktrap Louvain CNM

0.1 14.94 15.55 13.67 21.44

0.3 11.61 12.69 12.33 18.12

0.5 09.11 11.07 10.59 18.37

0.7 08.42 11.01 11.12 19.95

0.9 09.73 12.45 13.49 21.17

Table 7: J score for #SocialNetwork graph.

Edge Walktrap Louvain CNM

0.1 18.42 20.42 20.61 25.34

0.3 17.75 20.11 19.70 24.99

0.5 18.04 19.23 17.44 23.18

0.7 19.78 18.92 18.63 22.34

0.9 20.53 19.53 21.00 21.53

As a general remark, there is no single optimum

value for λ

. Nonetheless, Newman-Girvan is consis-

tently better with Walktrap and Louvain closely fol-

lowing and sharing the second position. CNM has the

worst performance, which can be attributed to the fact

that it creates fewer communities, which are bound

to be heterogeneous. As Newman-Girvan is typically

an exhaustive algorithm, it seems that Louvain and

Walktrap algorithms are balanced options.

6 CONCLUSIONS AND FUTURE

WORK

This paper outlines the implementation of Newman-

Girvan, Walktrap, Louvain, and CNM community de-

tection algorithms over Neo4j. Also, a criterion for

assessing the compactness of the communities com-

bining global and local scale-free graph behavior is

proposed and tested on the results of applying these

algorithms to two real Twitter graphs created from a

neutral as well as a politically charged topic.

As future work, the scalability properties of com-

munity discovery should be considered in parallel or

distributed environments. In addition, the proposed

criterion should be tested on larger graphs. Finally,

regarding λ

, a scheme for computing its optimum

value in ﬁner granularity should be developed.

REFERENCES

Adams, R. A. and Fournier, J. J. (2003). Sobolev spaces,

volume 140. Academic press.

Agichtein, E., Castillo, C., Donato, D., Gionis, A., and

Mishne, D. (2008). Finding high-quality content in

social media. In Web Search and Data Mining confer-

ence (WSDM), pages 183–194. ACM.

Attouch, H. and Az

e, D. (1993). Approximation and reg-

ularization of arbitrary functions in Hilbert spaces by

the Lasry-Lions method. In Annales de l’IHP Analyse

non lin

eaire, volume 10, pages 289–312.

Benzi, M. and Boito, P. (2010). Quadrature rule-based

bounds for functions of adjacency matrices. Linear

Algebra and its Applications, 433(3):637–652.

Graph Community Discovery Algorithms in Neo4j with a Regularization-based Evaluation Metric

409

Blondel, V. D., Guillaume, J.-L., Lambiotte, R., and Lefeb-

vre, E. (2008). Fast unfolding of community hierar-

chies in large networks. Journal of Statistical Me-

chanics: Theory and Experiment, P1000.

Brin, S. and Page, L. (1998). The PageRank citation rank-

ing: Bringing order to the web. Stanford Digital Li-

brary.

Carrington, P. J., Scott, J., and Wasserman, S. (2005). Mod-

els and Methods in Social Network Analysis. Cam-

bridge University Press.

Drakopoulos, G., Baroutiadi, A., and Megalooikonomou,

V. (2015a). Higher order graph centrality measures

for Neo4j. In Conference of Information, Intelligence,

Systems, and Applications (IISA).

Drakopoulos, G., Kanavos, A., Makris, C., and Mega-

looikonomou, V. (2015b). On converting community

detection algorithms for fuzzy graphs in Neo4j. In In-

ternational Workshop on Combinations of Intelligent

Methods and Applications, CIMA 2015.

Drakopoulos, G., Kanavos, A., Makris, C., and Mega-

looikonomou, V. (2016). Comparing algorithmic prin-

ciples for fuzzy graph communities over Neo4j. In Ad-

vances in Combining Intelligent Methods, pages 47–

73.

Drakopoulos, G. and Megalooikonomou, V. (2016). Reg-

ularizing large biosignals with ﬁnite differences. In

International Conference of Information, Intelligence,

Systems, and Applications (IISA).

Fortunato, S. (2010). Community detection in graphs.

Physics Reports, 486:75–174.

Girosi, F., Jones, M., and Poggio, T. (1995). Regulariza-

tion theory and neural networks architectures. Neural

computation, 7(2):219–269.

Girvan, M. and Newman, M. (2002). Community structure

in social and biological networks. Proceedings of the

National Academy of Sciences, 99(2):7821–7826.

Johansen, T. A. (1997). On Tikhonov regularization, bias

and variance in nonlinear system identiﬁcation. Auto-

matica, 33(3):441–446.

Jurczyk, P. and Agichtein, E. (2007). Discovering author-

ities in question answer communities by using link

analysis. In Conference of Information and Knowl-

edge Management (CIKM), pages 919–922.

Kafeza, E., Kanavos, A., Makris, C., and Vikatos, P. (2014).

T-PICE: Twitter personality based inﬂuential com-

munities extraction system. In IEEE International

Congress on Big Data, pages 212–219.

Kanavos, A., Perikos, I., Vikatos, P., Hatzilygeroudis, I.,

Makris, C., and Tsakalidis, A. (2014). Conversation

emotional modeling in social networks. In Interna-

tional Conference on Tools with Artiﬁcial Intelligence

(ICTAI), pages 478–484.

Kernighan, B. and Lin, S. (1970). An efﬁcient heuristic pro-

cedure for partitioning graphs. The Bell System Tech-

nical Journal, 49(1):291–307.

Kleinberg, J. M. (1998). Authoritative sources in a hyper-

linked environment. In Symposium of Discrete Algo-

rithms (SODA), pages 668–677.

Langville, A. and Meyer, C. (2006). Google’s PageRank

and Beyond: The Science of Search Engine Rankings.

Princeton University Press.

Newman, M. E. (2004a). Detecting community struc-

ture in networks. The European Physical Journal B-

Condensed Matter and Complex Systems, 38(2):321–

330.

Newman, M. E. (2004b). Fast algorithm for detecting com-

munity structure in networks. Physical Review E,

69(6).

Newman, M. E. (2010). Networks: An Introduction. Oxford

University Press.

Pal, A. and Counts, S. (2011). Identifying topical author-

ities in microblogs. In Web Search and Data Mining

(WSDM), pages 45–54.

Panzarino, O. (2014). Learning Cypher. PACKT publish-

ing.

Pons, P. and Latapy, M. (2005). Computing communities in

large networks using random walks.

Robinson, I., Webber, J., and Eifrem, E. (2013). Graph

Databases. O’Reilly.

Scott, J. (2000). Social Network Analysis: A Handbook.

SAGEPublications Ltd.

Shi, J. and Malik, J. (2000). Normalized cuts and image

segmentation. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 22(8):888–905.

Vogel, C. R. (2002). Computational methods for inverse

problems. SIAM.

Weng, J., Lim, E.-P., Lim, J., and Jiang, Q. H. (2010). Twit-

terrank: Finding topic-sensitive inﬂuential twitterers.

In Web Search and Data Mining (WSDM), pages 261–

270.

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies

410