
An Algebraic Collision Avoidance Approach for Unmanned Aerial
Vehicle
Adriana Dapena
1
, Mar
´
ıa Jos
´
e Souto-Salorio
2
, Ana Dorotea Tarr
´
ıo-Tobar
3
and Paula M. Castro
1
1
Department of Computer Engineering, Universidade da Coru
˜
na, Coru
˜
na, Spain
2
Department of Computer Science, Universidade da Coru
˜
na, Coru
˜
na, Spain
3
Department of Mathematics, Universidade da Coru
˜
na, Coru
˜
na, Spain
Keywords:
Collision Avoidance, Control and Supervision Systems, Characteristic Polynomial, Engineering Applications,
Hyperboloid Structure, Modelling and Simulation, Unmanned Aerial Vehicle.
Abstract:
In this paper we address the problem of avoidancing collisions between an Unmanned Aerial Vehicle (UAV)
and a rigid surface. The UAV is modelled as an unique sphere envolving the UAV or as multiple spheres only
envolving the motors. The UAV flies inside a rigid hyperboloid structure typically used in architecture. The
collision is detected by means of the study of the characteristic polynomial associated to quadric surfaces.
Computer simulation results included in this paper will show both the accuracy and the low computational
cost exhibited by the proposed method.
1 INTRODUCTION
Collision detection between two or more rigid bodies
is based on determining whether any of the solids
makes contact at one or more points (Brozos-V
´
azquez
et al., 2016), (Choi et al., 2006). This problem has
a great interest in many fields such as robotics (Choi
et al., 2006), (Steinbach et al., 2006), computer graph-
ics (Jia et al., 2006), animation and computer simu-
lated environments (C. O’Sullivan, 1999), etc.
From a mathematical point of view, the contact
between rigid bodies can be determined by saying that
the surfaces are in contact when their intersection is
not an empty set of points. Then, given two surfaces,
the question is to know whether they intersect or not.
Most work in the literature devoted to the study
of collision detection only considers convex bodies
(Choi et al., 2006), (Jia et al., 2006). Moreover,
most of the proposed algorithms are indeed valid
only under that condition of convexity. Recently, in
(Brozos-V
´
azquez et al., 2016), the authors have pre-
sented a study in which one of the bodies was not
convex (in fact, that was a hyperboloid). Since hyper-
boloid structures are doubly ruled surfaces, this type
of architectural structures is very strong against buck-
ling and cheaper than other singly ruled surfaces, like
cylinders or cones. For this reason, the hyperboloid
structure is used in architecture to design cooling tow-
ers, water towers, cathedrals, air traffic control towers,
and so on.
Because of its potential for commercial, military,
law-enforcement, research, and other purposes, Un-
manned Aerial Vehicles (UAVs) have received con-
siderable attention in recent years. The fast develop-
ment of this field has required the design of robust
collision avoidance systems which are based, in gene-
ral, on the combination of information acquired from
several sensors, which implies processing latency and
complexity (Giancarmine et al., 2008). If the surface
shape changes in height (like occurs with the hyper-
boloid structure) those sensors must be used for the
registration of this information in all directions. Col-
lision avoidance methods based on computing the dis-
tance from the UAV to the surface are adequate in
most situations where that surface shape is similar for
all height positions.
The method presented in this paper is oriented to
predict collisions when an UAV is flying inside a hy-
perboloid structure. We propose to model the UAV
using multiples spheres adapted to its shape. Using
the results presented in (Brozos-V
´
azquez et al., 2016),
we propose several algorithms for collision avoidance
by means of the study of the roots of a character-
istic polynomial associated to quadric surfaces. In
those algorithms, the conditions for collision detec-
tion are evaluated before any UAV movement so that
only valid movements are allowed thus avoiding such
262
Dapena, A., Souto-Salorio, M., Tarrío-Tobar, A. and Castro, P.
An Algebraic Collision Avoidance Approach for Unmanned Aerial Vehicle.
DOI: 10.5220/0006410002620269
In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2017) - Volume 2, pages 262-269
ISBN: Not Available
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

collisions. We will show that this collision detection
can be performed using a reduced number of opera-
tions.
This paper is organized as follows. Section 2
briefly introduces some ideas about the collision
avoidance systems in the literature similar to our pro-
posal. Section 3 contains the mathematical formula-
tion of the proposed method for collision avoidance,
which will be applied in Section 4 when an UAV is
flying inside a hyperboloid structure for tasks of mo-
nitoring, maintenance or control. Section 5 includes
the simulation results and, finally, Section 6 contains
the main conclusions about this work.
2 COLLISION AVOIDANCE
SYSTEMS
Collision Avoidance Systems (CASs) for UAV con-
sist of two main functions: firstly, sensing and de-
tection, and secondly, collision avoidance/maneuver
approach. The first one refers to the way of ac-
quiring useful information about its surrounding en-
vironment, as for example, the UAV position or its
speed/heading, environment conditions... This task
can be done using active and/or passive sensors and
communication equipments. The second function,
i.e. the collision avoidance/maneuver approach, in-
cludes mechanisms for trajectory calculation and dis-
tance estimation (Albaker and Rahim, 2009), (Pham
et al., 2015). In particular, the geometric approaches
perform this second function using geometry, usually
by means of the simulation of the UAV trajectories
and the calculation of the shortest distance to the sur-
rounding obstacles in a 2-D space (Park et al., 2018),
(Strobel and Schwarzbach, 2014). For this purpose,
such geometric approaches make use of information
such as location, speed or heading of the UAV with
respect to obstacles, which is frequently obtained by
Automatic Dependent Surveillance-Broadcast (ADS-
B). Geometric approaches are specially useful when
the UAV is inside simple surfaces as cylinders or
spheres, in which the surface shape remains un-
changed with height. However, for hyperboloid sur-
faces, on which we focus in this work, this property
can not be assumed.
In this paper, we will consider only the colli-
sion between the UAV and a rigid surface (the hy-
perboloid) which represents the structure walls. For
collision avoidance, an UAV could employ contour or
schematic maps specially useful for indoor environ-
ments (Krokowicz et al., 2010). For regular structures
(like squares or cylinders), this map is quite simple
since it remains unchanged for all height. However,
the hyperboloid surfaces are more complex because
they change with height. For this reason, we focus
on collision avoidance in the real scenario of an UAV
flying inside a hyperboloid structure (like a cooling
tower in a power station). The information used by
the proposed method is minimal, since only requires
the knowledge of the UAV position, speed and turn
angle. We hope that the ideas presented in this work
can be extended to different surfaces for other real ap-
plications.
3 MATHEMATICAL
FORMULATION
We consider a circular hyperboloid of one sheet
centred at the origin and described by the following
equation
H :
x
2
a
2
+
y
2
a
2
−
z
2
c
2
= 1,for a,c > 0. (1)
Using the standard notation for projective spaces, we
can find the matrix H associated to the surface H . Let
x = (x, y, z, 1)
T
be a generic vector in homogeneous
coordinates not placed at infinity. Then, x
T
Hx = 0
defines the surface H , where H is given by
H =
a
−2
0 0 0
0 a
−2
0 0
0 0 −c
−2
0
0 0 0 −1
. (2)
Moreover, we also consider a spherical surface of
radius r > 0 whose centre is at (x
0
,y
0
,z
0
), defined by
the following equation
S :(x −x
0
)
2
+ (y −y
0
)
2
+ (z −z
0
)
2
= r
2
. (3)
As above, we can express this equation in matrix
form using homogeneous coordinates in this way
S =
1 0 0 −x
0
0 1 0 −y
0
0 0 1 −z
0
−x
0
−y
0
−z
0
−r
2
+ x
2
0
+ y
2
0
+ z
2
0
.
(4)
The characteristic polynomial of both surfaces H
An Algebraic Collision Avoidance Approach for Unmanned Aerial Vehicle
263

and S is a polynomial of degree 4 given by
f (λ) = det(λH + S) =
(a
2
+ λ)g(λ)
a
4
c
2
,
(5)
where
g(λ) = −(a
2
+ λ)[(c
2
−λ)(r
2
+ λ) + z
2
0
λ]
+λ(c
2
−λ)(x
2
0
+ y
2
0
)
= λ
3
+ a
2
λ
2
+ a
1
λ + a
0
,
(6)
where a
0
, a
1
, and a
2
are the real coefficients of g(λ).
Therefore, we can directly conclude that one root of
f (λ) = 0 is λ
1
= −a
2
and that the other roots are also
roots of the cubic equation g(λ) = 0.
3.1 Calculation of g(λ) Roots
In this section we will show how to obtain the dis-
criminant ∆ from the cubic polynomial g(λ), which
will be used for detecting collision between the UAV
and the hyperboloid surface i.e., for determining if the
UAV movement is valid or not, instead of directly cal-
culating the roots of g(λ).
Cardano’s formulas can be applied to g(λ) for de-
tecting contacts between H and S employing simple
calculations, as described in the following.
Thus, based on the roots of g(λ), we can deter-
mine the position of the sphere with respect to the hy-
perboloid (Brozos-V
´
azquez et al., 2016). Considering
r < a, Table 1 shows all the cases defining the relative
position between S and H .
In general, for a monotonic polynomial
λ
3
+ a
2
λ
2
+ a
1
λ + a
0
, the following real para-
meters can be defined
Q =
3a
1
−a
2
2
9
,
R =
9a
2
a
1
−27a
0
−2a
3
2
54
,
∆ = Q
3
+ R
2
.
(7)
From Table 1, you can see that this parameter ∆
could be used as discriminant to cluster that relative
position between S and H into two groups (contact,
for ∆ ≥ 0, and non-contact, for ∆ < 0), although
it does not provide enough information about the
non-contact case since S can be interior or exterior
to H i.e., about if the scenario corresponds to the
first row of Table 1 or to the second one. For only
this purpose, we will be forced to compute the roots
of g(λ) so that their sign will allow us to distinguish
both scenarios. Since all the roots are real-valued
when ∆ < 0, the following expressions will be used
for their computation
φ =
1
3
acos
R
p
−Q
3
!
,
λ
2
= 2
p
−Qcos (φ) −
a
2
3
,
λ
3
= 2
p
−Qcos
φ +
2π
3
−
a
2
3
,
λ
4
= 2
p
−Qcos
φ +
4π
3
−
a
2
3
,
(8)
where R and Q are the parameters defined in Equation
(7).
4 COLLISION AVOIDANCE
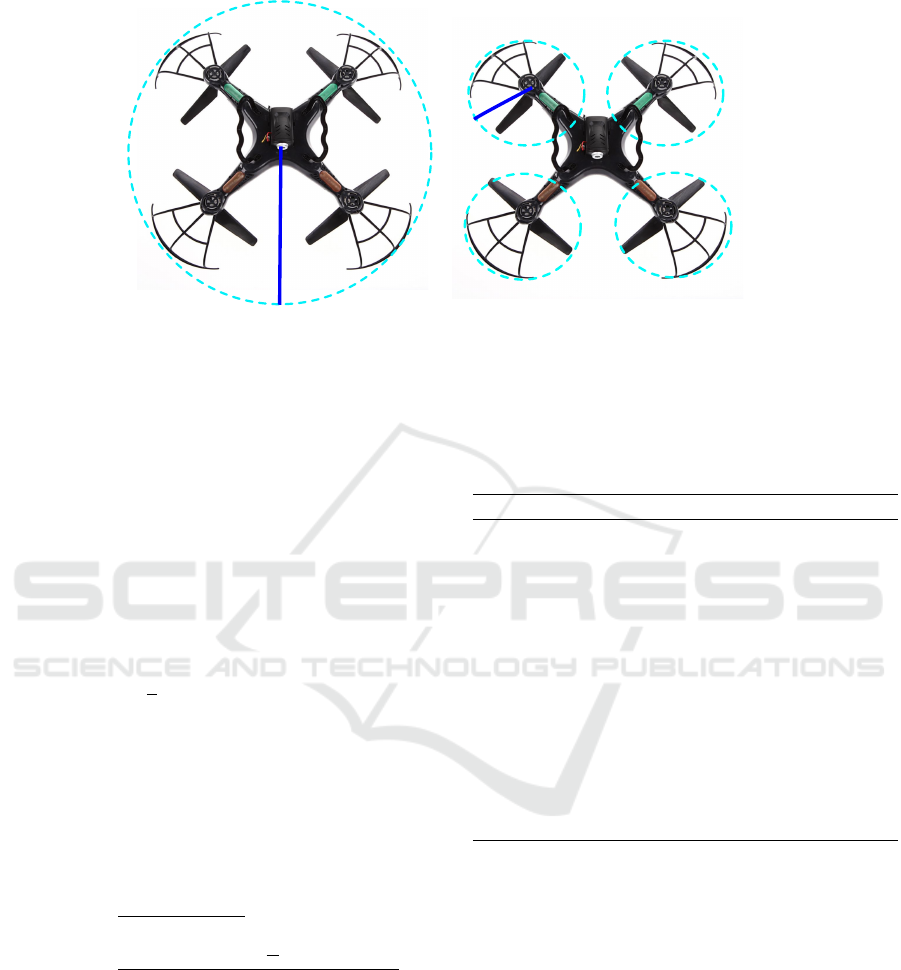
In this paper we consider UAVs with four motors, like
those shown in Figure 1, although this development
could be applied for any number of motors. As first
approach, the UAV is modelled as one sphere with its
centre in the UAV centre (see Figure 1(a)). As second
approach, the UAV is modelled as multiple spheres,
four in our case, centred at each of its motors (see
Figure 1(b)).
4.1 UAV Model of One Sphere
Firstly, we will model the UAV according to the
representation of Figure 1(a). In this figure you
can see that the UAV is represented by means of
one sphere S with radius r centred at (x
0
,y
0
,z
0
).
Considering the definition of the characteristic
polynomial given in Equation (5) and the matrices of
Equations (2) and (4), we can obtain the coefficients
of g(λ) of Equation (6). Thus, the coefficients of this
characteristic polynomial are given by
a
0
= −a
2
c
2
r
2
,
a
1
= −(a
2
c
2
−a
2
r
2
+ c
2
r
2
−c
2
x
2
0
−c
2
y
2
0
+ a
2
z
2
0
),
a
2
= a
2
−c
2
+ r
2
−z
2
0
−x
2
0
−y
2
0
.
(9)
Since we are interested in determining when the UAV
moves to a valid position (i.e. if the UAV moves in
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
264
Table 1: General relative position between S and H.
Description Roots of g(λ) ∆ UAV Movement
S interior to H All the roots are real and
different: two negative,
one positive
∆ < 0 Valid
S exterior to H All the roots are positive
real and different
∆ < 0 Non-valid
Centre of S interior to H . S tangent to H . All the roots are real,
and two equal: two
equal negative, one po-
sitive
∆ = 0 Non-valid
Centre of S exterior to H . S tangent to H . All the roots are positive
real, and two equal
∆ = 0 Non-valid
Intersection of S and H . One root is positive real
and two are complex
conjugate
∆ > 0 Non-valid
the interior of H ), and taking into account the clas-
sification of Table 1, we could detect collisions from
the study of the roots. Notice that the computational
complexity associated to the calculation of these roots
can be reduced considering that ∆ ≥ 0 corresponds to
non-valid movements. Moreover, if ∆ < 0 S could be
interior or exterior to H . However, with the root sign
we can determine if S is interior to H or not.
The following algorithm, termed Algorithm 1, de-
tails the procedure.
Algorithm 1: One sphere.
Compute ∆.
If ∆ < 0
Compute the root λ
2
.
If λ
2
< 0, then valid movement (interior),
otherwise
Compute the root λ
3
.
If λ
3
< 0, then valid movement (interior),
otherwise non-valid movement.
otherwise non-valid movement.
4.2 UAV Model of Four Spheres
We consider in this subsection the spheres S
1
,S
2
,S
3
,
and S
4
, all of them with radius r
1
, to model the
four motors of our UAV, as shown in Figure 1(b).
Considering that the UAV is centred at (x
0
,y
0
,z
0
), the
centre of each motor sphere, denoted by (x
c
,y
c
,z
c
),
can be mathematically expressed as follows
x
c
= x
0
+
l
√
2
2
(cos(g) −sin(g)) = x
0
+
l
√
2
2
T
1
,
y
c
= y
0
+
l
√
2
2
(cos(g) + sin(g)) = y
0
+
l
√
2
2
T
2
,
z
c
= z
0
,
(10)
where T
1
and T
2
are obviously given by
T
1
= cos(g) −sin(g),
T
2
= cos(g) + sin(g).
(11)
Notice that for the initial position given in Figure 1,
the spheres S
1
, S
2
, S
3
, and S
4
respectively have an-
gles of −π/2, 0, π/2, and 3π/2. In general, the an-
gle of S
2
, S
3
, and S
4
can be computed from the angle
of S
1
, denoted by g
1
, by using g
1
+ (i −1)π/2, with
i = 2, 3,4, respectively.
Considering Equation (10), we have that
x
2
c
+ y
2
c
=
x
0
+
l
√
2
2
T
1
!
2
+
y
0
+
l
√
2
2
T
2
!
2
= x
2
0
+
l
2
2
T
2
1
+ l
√
2x
0
T
1
+ y
2
0
+
l
2
2
T
2
2
+ l
√
2y
0
T
2
= x
2
0
+ y
2
0
+ l
2
+ l
√
2(T
1
x
0
+ T
2
y
0
),
(12)
An Algebraic Collision Avoidance Approach for Unmanned Aerial Vehicle
265
r
r
1
s
s
3
s
1
s
2
s
4
(a) (b)
Figure 1: UAV models: (a) one sphere; (b) four spheres.
where we have used T
2
1
+ T
2
2
= 2. Substituting
Equation (12) into Equation (9), we obtain
a
1
(g) = A
1
+ c
2
C(g),
a
2
(g) = A
2
−C(g),
(13)
where
A
1
= −(a
2
c
2
−a
2
r
2
1
+ c
2
r
2
1
−c
2
x
2
0
−c
2
y
2
0
+a
2
z
2
0
) + l
2
c
2
,
A
2
= a
2
−c
2
+ r
2
1
−z
2
0
−x
2
0
−y
2
0
−l
2
,
C(g) = l
√
2(T
1
x
0
+ T
2
y
0
),
(14)
with T
1
and T
2
as defined in Equation (11). From
these expressions and considering the definition of
a
0
of Equation (9), we can compute ∆(g) for each
sphere by using the following expressions
Q(g) =
3a
1
(g) −a
2
(g)
2
9
,
R(g) =
9a
2
(g)a
1
(g) −27(
r
1
r
)
2
a
0
−2a
2
(g)
3
54
,
∆(g) = Q(g)
3
+ R(g)
2
.
(15)
For this UAV model, the collision detection can be
performed applying the Algorithm 1 for each sphere.
However, with the goal of reducing the computational
complexity, we propose a two-step algorithm. For
the first step, we will analyse the position of the to-
tal sphere S . When ∆ < 0, we use the same procedure
as done in Algorithm 1 to determine if the movement
is valid or non-valid. Otherwise, when ∆ ≥ 0, we re-
fine the decision by computing the discriminant ∆(g)
for the four spheres.
The resulting algorithm is summarized as detailed
below, and we will referred to as Algorithm 2.
Algorithm 2: Four spheres.
For the sphere S of radius r, compute ∆.
If ∆ < 0
Compute the root λ
2
.
If λ
2
< 0, then valid movement (interior),
otherwise
Compute the root λ
3
.
If λ
3
< 0, then valid movement (interior),
otherwise non-valid movement.
otherwise
Compute ∆(g
1
+ (i −1)π/2) for i = 2,3, 4, with g
1
being the S
1
angle,
If all ∆(g
1
+ (i −1)π/2) < 0, then valid movement
(interior),
otherwise non-valid movement.
5 EXPERIMENTAL RESULTS
We consider a computer simulated environment
where the hyperboloid models the cooling tower of
a power station. This tower has a height of 35.6 m
and a base diameter of 36.5m. The UAV has a radius
of 25 cm. Different motor radius have been consid-
ered in our simulations. Figure 2(a) shows the UAV
model. The UAV flies inside the cooling tower fol-
lowing a random trajectory determined as follows:
• Straight UAV movement with probability 0.25.
• Down or up UAV movement with probability
0.25.
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
266
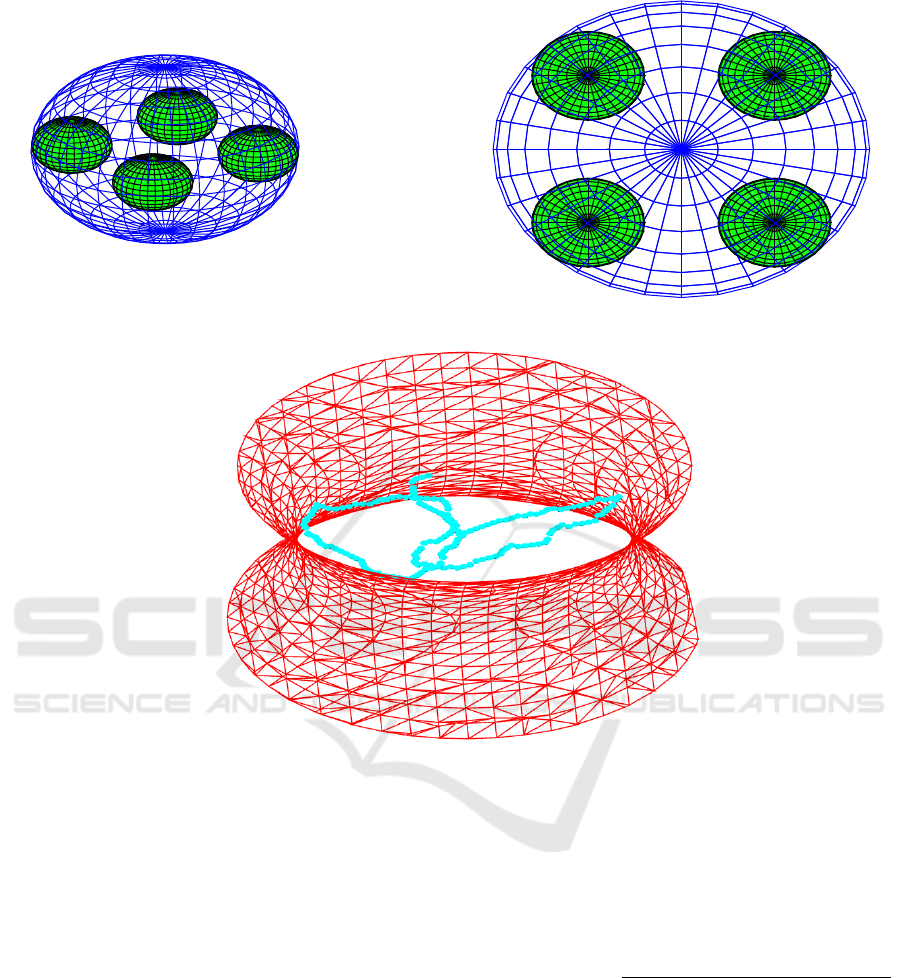
(a) UAV model: 3-D and 2-D views.
(b) Example of an UAV trajectory.
Figure 2: Computer simulations.
• UAV random turn with angle in [−π/4,π/4] with
probability 0.5.
• UAV turn of angle −π/2 or π/2 if a non-valid
movement is detected with Algorithm 1.
We consider that the UAV follows a trajectory of
D = 500 meters with a speed of v m/s. Before any
movement, the UAV evaluates the Algorithm 1 or the
Algorithm 2 to determine if the movement is valid.
This prediction is done considering the position of
the UAV in t seconds, i.e. its response time. For a
non-valid movement, the UAV turns and tries a new
movement. Figure 2(b) plots only one realization of
our simulations.
We are interested in comparing the performances
of both proposed algorithms for different motor
radius. We have considered 5, 7.5, and 10 cm of
radius. Table 2 shows the results obtained for this
comparison between the Algorithm 1 (model of one
sphere) and the Algorithm 2 (model of four spheres)
considering different speeds and response times. The
following expression has been evaluated
ε(%) = 100 ×
non-valid movements with Alg. 2
non-valid movements with Alg. 1
.
(16)
For all response times, we can see that there exists
a considerable difference between both algorithms for
a radius of r = 5cm. This difference reduces when the
radius increases since the volume of the small spheres
is similar to the volume of the big one. For instance,
the accuracy achieved with the Algorithm 1 is higher
than a 90% for all speeds with a radius of r = 10 cm.
An Algebraic Collision Avoidance Approach for Unmanned Aerial Vehicle
267

Table 2: Comparison of the proposed algorithms in terms of ε(%) for three different UAV response times.
(a) t = 10 ms
Speed (m/s) 5 6 7 8 9
Precision (cm) 5 6 7 8 9
Radius 5 51.49 52.22 58.30 66.22 70.86
(cm) 7.5 79.20 82.92 88.09 91.05 92.15
10 91.01 93.82 94.91 94.07 96.61
(b) t = 50 ms
Speed (m/s) 5 6 7 8 9
Precision (cm) 25 30 35 40 45
Radius 5 68.18 68.29 69.42 70.49 81.81
(cm) 7.5 86.56 89.83 90.40 93.41 93.22
10 92.82 93.54 94.40 98.10 99.12
(c) t = 100 ms
Speed (m/s) 5 6 7 8 9
Precision (cm) 50 60 70 80 90
Radius 5 68.42 71.42 75.90 80.00 83.33
(cm) 7.5 89.00 91.81 99.20 99.50 95.71
10 94.61 95.33 96.00 98.50 99.70
6 CONCLUSIONS
We have modelled the UAV as a spherical surface cen-
tred at the UAV centre or as four spherical surfaces re-
spectively centred at each one of the four motor cen-
tres. We have shown that the roots of a character-
istic polynomial can be used to decide if there is or
not contact between the UAV and a rigid surface. We
have considered a hyperboloid surface due its archi-
tectural properties and to its presence in real scenarios
that could require control or maintenance, although
the ideas here presented could be used for other sur-
face types. Both proposed algorithms have a very low
computational complexity since they are computing
the roots of that characteristic polynomial only a very
reduced number of times.
The results obtained from computer simulations
show that the algorithm for collision detection based
on a model of sphere per UAV motor is more adequate
when a high or medium distance precision or equiv-
alently, low response times, is needed. However, the
method based on only one sphere could be used for
requirements of low precision or, equivalently, high
response times.
ACKNOWLEDGEMENTS
This work has been funded by the Xunta de
Galicia (ED431C 2016-045, ED341D R2016/012),
the Agencia Estatal de Investigaci
´
on of Spain
(TEC2016-75067-C4-1-R) and ERDF funds of the
EU (AEI/FEDER, UE).
REFERENCES
Albaker, B. and Rahim, N. (2009). A survey of collision
avoidance approaches for unmanned aerial vehicles.
In IEEE International Conference for Technical Post-
graduates (TECHPOS), pages 1–7.
Brozos-V
´
azquez, M., Pereira-S
´
aez, M., Souto-Salorio, M.,
and Tarr
´
ıo-Tobar, A. D. (2016). Contact detection be-
tween a sphere and a hyperboloid by means of the
roots of a characteristic polynomial. arXiv preprint
arXiv:1602.06744.
C. O’Sullivan, J. D. (1999). Real-time collision detection
and response using sphere-trees. In 15th Spring Con-
ference on Computer Graphics, pages 83–92.
Choi, Y.-K., Wang, W., and Liu, Y. (2006). Continuous
collision detection for two moving elliptic disks. IEEE
Transactions on Robotics, 22:213–224.
Giancarmine, F., Accardo, D., Moccia, A., Carbone,
C., Ciniglio, U., Corraro, F., and Salvatore, L.
(2008). Multi-sensor-based fully autonomous non-
cooperative collision avoidance system for unmanned
ICINCO 2017 - 14th International Conference on Informatics in Control, Automation and Robotics
268

air vehicles. Journal of aerospace computing, infor-
mation, and communication, 5(10):338–360.
Jia, X., Choi, Y.-K., Mourrain, B., and Wang, W. (2006).
An algebraic approach to continuous collision detec-
tion for ellipsoids. Computer Aided Geometric De-
sign, 28:164–176.
Krokowicz, T., Gasca, M., Voos, H., and Ucinski, D.
(2010). Indoor navigation for quadrotor uavs using
schematic environment maps. In Robotics in Alpe-
Adria-Danube Region (RAAD), 2010 IEEE 19th In-
ternational Workshop on, pages 457–462. IEEE.
Park, J.-W., Oh, H.-D., and Tahk, M.-J. (2018). UAV colli-
sion avoidance based on geometric approach. In IEEE
SICE Annual Conference, pages 2122 – 2126.
Pham, H., Smolka, S. A., Stoller, S. D., Phan, D., and
Yang, J. (2015). A survey on unmanned aerial ve-
hicle collision avoidance systems. arXiv preprint
arXiv:1508.07723.
Steinbach, K., Kuffner, J., Asfour, T., and Dillmann, R.
(2006). Efficient collision and self-collision detec-
tion for humanoids based on sphere trees hierarchies.
In 6th IEEE-RAS International Conference on Hu-
manoid Robots.
Strobel, A. and Schwarzbach, M. (2014). Cooperative sense
and avoid: Implementation in simulation and real
world for small unmanned aerial vehicles. In IEEE
International Conference on Unmanned Aircraft Sys-
tems (ICUAS), pages 1253–1258.
An Algebraic Collision Avoidance Approach for Unmanned Aerial Vehicle
269
