
Study on the Fidelity of Biodevice T7 DNA Polymerase
Ming Li
1
, Zhong-Can Ou-Yang
2
and Yao-Gen Shu
1,2
1
School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
2
CAS Key Laboratory of Theoretical Physics, Institute of Theoretical Physics,
Chinese Academy of Sciences, Beijing 100190, China
Keywords:
Biodevice, DNA Polymerase, Fidelity, 1st-order Terminal Effects.
Abstract:
We proposed a comprehensive kinetic model of steady-state copolymerization and obtain analytical solution
of the high replication fidelity of the biodevice DNA polymerase. Our analytical calculations definitively
show that the neighbor effects are the key factor of the overall fidelity. These analytical results were further
demonstrated by T7 DNAp whose fidelity (10
6
) is well described by the 1st-order neighbor effect.
1 INTRODUCTION
DNA polymerase (DNAp) is an amazing biodevice,
its template-directed DNA replication is the most im-
portant reaction in cells, and high replication fidelity
is crucial to maintain the genetic stability of cells. The
replication process is catalyzed by DNAp which has
two domains. One is a polymerase (P site) which can
add correct units (nucleotides forming Waston-Crick
base pair with the template) to the reactive end of the
growing DNA chain with a much higher efficiency
than incorrect ones. The other domain is an exonu-
clease (E site) which can excise the ending unit of the
growing chain once it’s peeled off the template and
transferred from P to E. It is believed that both do-
mains contribute to the overall fidelity of the copoly-
merization process significantly. But how they coop-
erate is not yet quantitatively understood.
The kinetic proofreading mechanism correctly
points out that the replication fidelity of the biodevice
is not determined thermodynamically by the free
energy difference, but kinetically by the incorpo-
ration rate difference, between the match and the
mismatch. Though the detailed matching is very
complex, DNA replication can be approximately
regarded as a binary copolymerization process of
matched nucleotides (denoted as A for convenience)
and mismatched nucleotides (denoted as B). Based
on the kinetics of steady-state copolymerization with
higher-order terminal effect(Shu et al., 2015) which
is a hot topic in macromolecule due to the alternate
depolymerization step of two monomers such as A
and B, we have expanded above theory into template-
Figure 1: The minimal scheme of the first-order proofread-
ing model(Song et al., 2017). X
s
,X
e
represents the state of
DNAp when the primer terminus is in the synthesis (s) site
or the exonuclease (e) one respectively. When the primer
terminus is in the exonuclease site, one does not need to
distinguish between ∼A
e
(∼B
e
). However, it is still conve-
nient to use ∼A
e
(∼B
e
) to denote the immediate state when
the terminus switches back to the polymerase site. By set-
ting all the excision rates equal to r
e
, we obtain the models
for real DNAp. Under the steady-state conditions, the dNTP
addition rate can be expressed as f
s
X
2
X
1
= k
X
2
X
1
[X
1
], where
k
X
2
X
1
is a pseudo-first-order rate constant, [X
1
] is the con-
centration of the incoming dNTP (to calculate the intrinsic
fidelity, one often sets [A]=[B]). The rates of sliding of the
primer terminus X
2
X
1
into the exonuclease and polymerase
active site are designated k
se
X
2
X
1
and k
es
X
2
X
1
respectively.
copolymerization, such as DNA replication, including
higher order neighbor effect and proofreading(Song
et al., 2017). The quantitative understanding of
high fidelity DNA polymerase was highlighted by
https://jphysplus.iop.org/2017/01/26/a-quantitative-
understanding-of-high-fidelity-dna-polymerase/,
however, the mathematical derivation in this 15
pages
′
article is too sophisticated to be understood
by chemist and biologist, as well as there are too
many assumptions as emphasized in Section 3.2
(bio-relevant conditions).
In this paper, we focus on the simplest situation,
the 1st-order neighbor effect, and derive a general
Li, M., Ou-Yang, Z-C. and Shu, Y-G.
Study on the Fidelity of Biodevice T7 DNA Polymerase.
DOI: 10.5220/0006636101350139
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 3: BIOINFORMATICS, pages 135-139
ISBN: 978-989-758-280-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
135
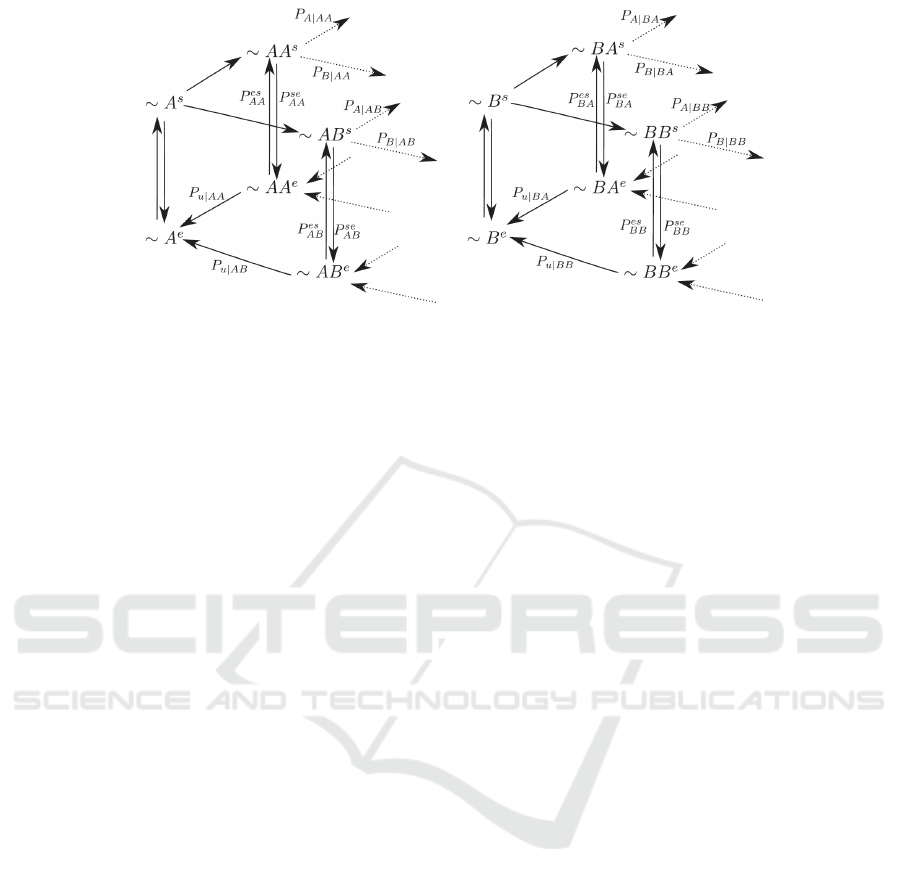
Figure 2: Branching model for the first-order polymerization and excision(Song et al., 2017).
formula of the high replication fidelity of the biode-
vice such as T7 DNAp. For readability of the paper,
we first simply introduce the first-order proofreading
model(Song et al., 2017) in Section 2, then derive the
general formula of the DNAp fidelity in first-order
proofreading model in section 3, and estimate the fi-
delity of T7 DNAp in section 4. Finally, we will dis-
cuss the results in section 5 and hope the general for-
mula is instructive for experimental fidelity verifica-
tion of other DNAp.
2 FIRST-ORDER
PROOFREADING MODEL
The match between the incoming nucleotide dNTP
and the template (i.e. the canonical Watson-Crick
base pairings such as A-T and G-C) in the replica-
tion process plays a central role for any organism to
maintain its genome stability, whereas mismatch (8
non-canonical Watson-Crick base pairings such as A-
A, A-C, A-G, T-T, T-C, T-G, C-C and G-G ) may in-
troduce genetic mutation, and thus the error rate of
replication must be kept very low. In living cells,
the replication fidelity is controlled mainly by DNAp
which catalyzes the template-directed DNA synthe-
sis. For simplification, matched or mismatched dNTP
is represented by A or B respectively throughout this
paper. The superscript s or e means that the primer
terminus is in the polymerase (i.e. synthesis) site or
the exonuclease site, respectively.
In this section, we will discuss the general first-
order proofreading model Fig.1 to demonstrate the
basic ideas of our approach. Following the same logic
of steady-state copolymerization kinetics in a two-
component (A, B) system(Shu et al., 2015), we use
P
s
X
n
···X
1
and P
e
X
n
···X
1
to denote the occurrence probabil-
ity of the terminal sequence X
n
··· X
1
in the synthe-
sis (polymerase) and excision (exonuclease) site re-
spectively, X
i
= A, B. N
X
n
···X
1
is defined as the total
number of sequence X
n
··· X
1
appearing in the primer
chain.
The overall incorporation rate of se-
quence X
n
··· X
2
X
1
(n ≥ 2) is defined as
˙
N
X
n
···X
2
X
1
≡ J
X
n
···X
2
X
1
= J
s
X
n
···X
2
X
1
+ J
e
X
n
···X
2
X
1
, where
J
s
X
n
···X
2
X
1
= f
s
X
2
X
1
P
s
X
n
···X
2
, J
e
X
n
···X
2
X
1
= −r
e
X
2
X
1
P
e
X
n
···X
2
X
1
.
The kinetic equations of P
m
X
n
···X
2
X
1
(n ≥ 1,m = s, e)
can be written as,
˙
P
s
X
n
···X
2
X
1
= J
s
X
n
···X
2
X
1
−
˜
J
s
X
n
···X
2
X
1
∗
− J
se
X
n
···X
2
X
1
˙
P
e
X
n
···X
2
X
1
= J
e
X
n
···X
2
X
1
−
˜
J
e
X
n
···X
2
X
1
∗
+ J
se
X
n
···X
2
X
1
(1)
where
˜
J
s
X
n
···X
1
∗
= J
s
X
n
···X
1
A
+ J
s
X
n
···X
1
B
,
˜
J
e
X
n
···X
1
∗
=
J
e
X
n
···X
1
A
+ J
e
X
n
···X
1
B
, J
se
X
n
···X
2
X
1
= k
se
X
2
X
1
P
s
X
n
···X
2
X
1
−
k
es
X
2
X
1
P
e
X
n
···X
2
X
1
. And P
s
X
i
···X
1
= P
s
AX
i
···X
1
+ P
s
BX
i
···X
1
,
J
s
X
i
···X
1
= J
s
AX
i
···X
1
+ J
s
BX
i
···X
1
(i ≥ 1) and so on.
The steady state is defined as
˙
P
m
X
n
···X
2
X
1
= 0 for any
n ≥ 1. To analytically solve these coupled equations,
we extend the logic of steady-state copolymerization
kinetics and propose the following factorization con-
jecture(Shu et al., 2015):
P
m
X
n
···X
2
X
1
=
n
∏
i=3
P
s
X
i
X
i−1
"
n
∏
i=3
P
s
X
i−1
#
−1
P
m
X
2
X
1
(2)
where n ≥ 3, m = s,e. By this factorization conjec-
ture, the original unclosed equations can be reduced
to the following closed equations of the eight basic
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
136

variables P
m
X
2
X
1
(m = s,e)(Shu et al., 2015):
J
e
BA
− J
e
AB
= J
se
B
, J
s
BA
− J
s
AB
= J
se
A
J
s
AA
− J
se
AA
J
s
BA
− J
se
BA
=
P
s
AA
P
s
BA
J
s
AB
− J
se
AB
J
s
BB
− J
se
BB
=
P
s
AB
P
s
BB
J
e
AA
+ J
se
AA
J
e
BA
+ J
se
BA
=
P
s
AA
P
s
BA
J
e
AB
+ J
se
AB
J
e
BB
+ J
se
BB
=
P
s
AB
P
s
BB
J
se
A
+ J
se
B
= 0,
∑
X,Y=A,B
(P
s
XY
+ P
e
XY
) = 1.
(3)
3 THE FIDELITY OF DNA
REPLICATION WITHIN
FIRST-ORDER
PROOFREADING
Here, we only discuss the kinetic-based fidelity, since
it can be rigorously defined and calculated within the
framework of our basic theory. We define the fidelity
as ϕ = N
A
/N
B
. N
A
is the total number of incorpo-
rated matches in the primer, N
B
is the total number
of mismatches. Once the steady-state kinetic equa-
tions such as equations (3) are solved numerically
or analytically, the total flux J
A
(= J
s
A
+ J
e
A
),J
B
(=
J
s
B
+ J
e
B
) can be calculated. Since
˙
N
A
= J
A
,
˙
N
B
= J
B
and d(N
A
/N
B
)dt = 0 (in steady state), we can calcu-
late the replication fidelity exactly by ϕ = N
A
/N
B
=
J
A
/J
B
. However, it is often impossible to solve the ki-
netic equations analytically. To circumvent this prob-
lem, we introduce below an alternative method, the
infinite-state Markov chain method, to calculate ϕ.
The first-order proofreadingscheme can be rewrit-
ten as a branching model shown in Fig.2. The steady-
state growth of primer can be completely character-
ized by four groups of transition probabilities:
P
X|X
2
X
1
≡
δ
X
1
X
(δ
X
1
A
+ δ
X
1
B
)(1+ β
X
2
X
1
)
,
P
se
X
2
X
1
≡
β
X
2
X
1
1+ β
X
2
X
1
,
P
es
X
2
X
1
≡
α
X
2
X
1
1+ α
X
2
X
1
,
P
u|X
2
X
1
≡ 1− P
es
X
2
X
1
=
1
1+ α
X
2
X
1
.
where β
X
2
X
1
= k
se
X
2
X
1
/[ f
s
AA
(δ
X
1
A
+δ
X
1
B
)] with δ
X
2
X
1
=
f
s
X
2
X
1
/ f
s
AA
, while α
X
2
X
1
= k
es
X
2
X
1
/r
e
X
2
X
1
. Since any in-
corporated nucleotide (either A or B) has a chance to
be excised, only those not being excised account for
the final composition of the primer. Thus the fidelity
for the first-order terminal model can be defined as,
ϕ ≡
Q
AA
+ Q
BA
Q
AB
+ Q
BB
(4)
whereQ
X
2
X
1
is the probability that X
1
is added to
the terminal X
2
and never being excised, satisfying
Q
AA
+ Q
AB
+ Q
BA
+ Q
BB
= 1. Q
X
2
X
1
can be explic-
itly expressed as Q
X
2
X
1
≡
ˆ
P
X
2
X
1
P
nuX
2
X
1
, where
ˆ
P
X
2
X
1
is the probability that adding X
1
to the terminal X
2
,
P
nuX
2
X
1
is the probability of the terminal X
2
X
1
never
being excised. The absolute values of
ˆ
P
X
2
X
1
are not
known a prior, but the following equalities obviously
hold:
ˆ
P
AA
ˆ
P
AB
=
P
A|AA
P
B|AA
=
P
A|BA
P
B|BA
=
f
s
AA
f
s
AB
,
ˆ
P
BA
ˆ
P
BB
=
P
A|AB
P
B|AB
=
P
A|BB
P
B|BB
=
f
s
BA
f
s
BB
,
(5)
Considering the fact that the number of AB should
equal to the number of BA in the copolymer chain, we
have the following intrinsic constraint:
Q
AB
(=
ˆ
P
AB
P
nuAB
) = Q
BA
(=
ˆ
P
BA
P
nuBA
). (6)
To calculate P
nuX
2
X
1
, we define P
euX
2
X
1
≡ 1 −
P
nuX
2
X
1
as the probability of the terminal X
2
X
1
ever
being excised. P
euX
2
X
1
satisfy the following iterative
equations(Song et al., 2017):
P
euX
2
X
1
=
ˆ
P
u|X
2
X
1
P
se
X
2
X
1
P
es
X
2
X
1
1
G
X
2
X
1
−
1
T
X
2
X
1
. (7)
where
G
X
2
X
1
≡ 1− P
es
X
2
X
1
(
ˆ
P
A|X
2
X
1
P
euX
1
A
+
ˆ
P
B|X
2
X
1
P
euX
1
B
)
= 1−
α
X
2
X
1
(δ
X
1
A
P
euX
1
A
+ δ
X
1
B
P
euX
1
B
)
(1+ α
X
2
X
1
)(1+ β
X
2
X
1
)(δ
X
1
A
+ δ
X
1
B
)
T
X
2
X
1
≡
1
1− P
se
X
2
X
1
P
es
X
2
X
1
=
ρ
X
2
X
1
+ α
X
2
X
1
β
X
2
X
1
ρ
X
2
X
1
,
where ρ
X
2
X
1
= 1 + α
X
2
X
1
+ β
X
2
X
1
. and
ˆ
P
u|X
2
X
1
=
P
u|X
2
X
1
P
se
X
2
X
1
T
X
2
X
1
,
ˆ
P
X|X
2
X
1
= P
X|X
2
X
1
T
X
2
X
1
. Because of
G
X
2
X
1
= 1−∆ (see DISCUSSION section in detailed),
P
euX
2
X
1
=
T
X
2
X
1
α
X
2
X
1
1
G
X
2
X
1
−
1
T
X
2
X
1
≈
T
X
2
X
1
− 1
α
X
2
X
1
+
T
X
2
X
1
(δ
X
1
A
P
euX
1
A
+ δ
X
1
B
P
euX
1
B
)
(ρ
X
2
X
1
+ α
X
2
X
1
β
X
2
X
1
)(δ
X
1
A
+ δ
X
1
B
)
=
β
X
2
X
1
ρ
X
2
X
1
1+
δ
X
1
A
P
euX
1
A
+ δ
X
1
B
P
euX
1
B
β
X
2
X
1
(δ
X
1
A
+ δ
X
1
B
)
. (8)
Study on the Fidelity of Biodevice T7 DNA Polymerase
137
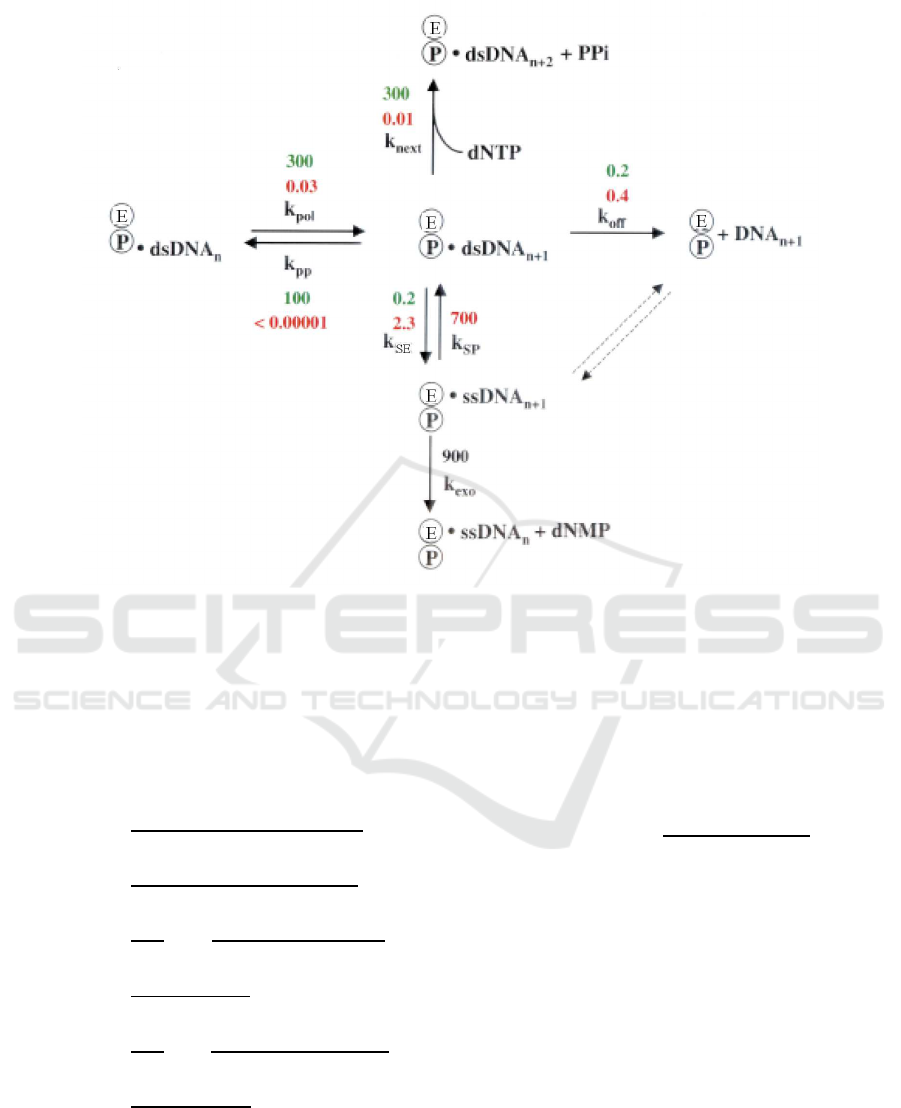
Figure 3: Kinetic scheme for proofreading by T7 DNAp(Kunkel and Bebenek, 2000). The rates (all per second) are shown in
green for correct base pairs and in red for incorrect base pairs. The rates of sliding into the exonuclease and polymerase active
site are designated k
SE
and k
SP
, respectively, where E and P correspond to the exonuclease and polymerase active sites. The
k
exo
value is the rate of excision of ssDNA. Comparing with the the minimal scheme of the first-order proofreading model as
shown in Fig.3, the corresponding kinetic key parameters are: f
s
AA
≈ 300 s
−1
, f
s
AB
≈ 0.03 s
−1
, f
s
BA
≈ 0.01 s
−1
, f
s
BB
≈ 0.0
s
−1
, k
se
AB
≈ 2.3 s
−1
, k
se
AA
≈ 0.2 s
−1
, k
es
AX
1
≈ 700 s
−1
, and r
e
X
2
X
1
≈ 900 s
−1
, X
i
=A,B. So that β
AA
∼ 7× 10
−4
≪ 1, while
β
AB
∼ 230 ≫ 1.
Then
P
euAA
=
β
AA
(δ
AA
+ δ
AB
) + δ
AB
P
euAB
(α
AA
+ β
AA
)δ
AA
+ ρ
AA
δ
AB
(9)
P
euBB
=
β
BB
(δ
BA
+ δ
BB
) + δ
BA
P
euBA
(α
BB
+ β
BB
)δ
BB
+ ρ
BB
δ
BA
(10)
P
euAB
=
β
AB
ρ
AB
1+
δ
BA
P
euBA
+ δ
BB
P
euBB
β
AB
(δ
BA
+ δ
BB
)
=
λ
A
+ ε
BA
P
euBA
ρ
AB
(11)
P
euBA
=
β
BA
ρ
BA
1+
δ
AA
P
euAA
+ δ
AB
P
euAB
β
BA
(δ
AA
+ δ
AB
)
=
λ
B
+ ε
AB
P
euAB
ρ
BA
(12)
where λ
X
≡ β
X
¯
X
+ g
¯
X
¯
X
β
¯
X
¯
X
, g
BB
≡ δ
BB
/[(α
BB
+
β
BB
)δ
BB
+ ρ
BB
δ
BA
], ε
BA
≡ δ
BA
(1 + g
BB
)/(δ
BA
+
δ
BB
), g
AA
≡ δ
AA
/[(α
AA
+ β
AA
)δ
AA
+ ρ
AA
δ
AB
] and
ε
AB
≡ δ
AB
(1+ g
AA
)/(δ
AA
+δ
AB
). The key variables,
P
euX
2
X
1
, can be calculated by combining equations
(9)-(12), for example,
P
euAB
=
λ
A
ρ
BA
+ λ
B
ε
BA
ρ
BA
ρ
AB
− ε
AB
ε
BA
(13)
4 THE FIDELITY OF T7 DNAP
In Fig.3, we list experimental values of some kinetic
parameters for T7 DNAp. The dNTP concentration
appearing in the pseudo-first-order rates of dNTP in-
corporation (i.e. the polymerization rates, see the
caption) is often set as 100 µM which is the typical
value under physiological conditions. In such cases,
there exists huge difference in the order of magni-
tudes of the parameters. For example, addition of
matched nucleotide at the polymerase site is very fast,
and always much faster than mismatch addition, that
is,δ
AB
≪ δ
AA
= 1; once mismatch happens, the ad-
dition rate of nucleotide is also very lower, and the
primer terminus AB will very rapidly slide to the ex-
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
138

onuclease, which means δ
BA
≪ 1 and β
AB
≫ 1; espe-
cially, continuous mismatch additions are impossible,
i.e., δ
BB
∼ 0 and β
BB
→ ∞. These intrinsic charac-
teristics of high fidelity DNAp enable us to suggest
reasonable approximations to simplify the above cal-
culation and obtain explicit mathematical expressions
of ϕ in terms of some key parameters. for example,
P
euAB
≈ 1−
1+ α
AB
β
AB
P
euAA
=
β
AA
+ δ
AB
P
euAB
α
AA
∼ 10
−4
P
euBB
=
β
BB
+ P
euBA
ρ
BB
∼ 1
then
P
nuAB
≈
1+ α
AB
β
AB
P
nuAA
≈ 1
P
nuBB
≈ 0
A very simple expression of the replication fidelity
can be derived:
ϕ ≈ 1+
Q
AA
Q
AB
= 1 +
1
δ
AB
P
nuAA
P
nuAB
(14)
≈ 1+
f
s
AA
f
s
AB
r
e
r
e
+ k
es
AB
k
se
AB
f
s
BA
≈ 10
6
,
which can be divided into two parts: the first one
is contributed by the P site: ϕ
s
≡ f
s
AA
/ f
s
AB
≈ 10
4
,
while the second one is contributed by E site: ϕ
e
≡
k
se
AB
r
e
/[(k
es
AB
+r
e
) f
s
BA
] ≈ 10
2
, thus, the overall fidelity
ϕ = ϕ
s
ϕ
e
≈ 10
6
, which is consistent with the experi-
mental result in vitro.
5 DISCUSSION
We proposed a comprehensive kinetic model and ob-
tain analytical solution of the high replication fidelity
of biodevice DNA polymerase. The basic assumption
is that there can be nearest (1st) neighbor interactions
in the copolymerization process. Our analytical cal-
culations definitively show that the neighbor effects
(reflected in the kinetic rate parameters) are the key
factor of the overall fidelity. Considering the nearest
neighbor effect, if the P site can add a correct unit
to the correct terminus with a much faster rate than
adding an incorrect one, the ratio of these two rates
can be very large, meaning that the P site contributes
significantly to the overall fidelity. When an incorrect
unit is incorporated, the E site may discard it if the
unstable terminus is transferred from P to E quickly
enough before the incorrect unit is buried by the next
incorporation of correct unit. In this way, the E site
can also make a significant contribution to fidelity.
These analytical results were further demonstrated by
T7 DNAp whose fidelity (10
6
) is well described by
the 1st-order neighbor effect.
It must be pointed that the high fidelity DNAp
maybe has intrinsic mechanism: the addition of
matched nucleotide at the polymerase site is very
fast, and always much faster than mismatch addition
(δ
AB
≪ δ
AA
= 1); once mismatch happens, the ad-
dition rate of nucleotide is also very lower, and the
primer terminus AB will very rapidly slide to the ex-
onuclease (δ
BA
≪ 1 and β
AB
≫ 1); especially, contin-
uous mismatch additions rarely occours (δ
BB
∼ 0 and
β
BB
→ ∞).
The parameters of k
BA
are not needed because of
the intrinsic constraint (6). The number of needed ki-
netic parameters shown in Fig.3 also can be cut back
if the normalization
∑
Q
X
2
X
1
= 1 is engaged.
ACKNOWLEDGEMENTS
The authors thank the financial support by the
National Natural Science Foundation of China
(No.11574329, 11774358, 11322543, 11105218,
11675180, 11421063, 11647601, 11675017), The
Fundamental Research Funds for the Central Uni-
versities (No.2017EYT24), The Joint NSFC-ISF
Research Program(No.51561145002), CAS Inter-
disciplinary Term(No.2060299) and QYZDY-SSW-
SYS008.
REFERENCES
Kunkel, T. A. and Bebenek, K. (2000). DNA replication
fidelity. Annu. Rev. Biochem., 69:497–529.
Shu, Y. G., Song, Y. S., Ou-Yang, Z. C., and Li, M. (2015).
A general theory of kinetics and thermodynamics of
steady-state copolymerization. J.Phys.: Condens.
Matter, 27:235105.
Song, Y. S., Shu, Y. G., Zhou, X., Ou-Yang, Z. C., and
Li, M. (2017). Proofreading of DNA polymerase: a
new kinetic model with higher-order terminal effects.
J.Phys.: Condens. Matter, 29:025101.
Study on the Fidelity of Biodevice T7 DNA Polymerase
139
