
Towards a Stable Quantized Convolutional Neural Networks:
An Embedded Perspective
Motaz Al-Hami
1,3
, Marcin Pietron
2,3
, Raul Casas
3
, Samer Hijazi
3
and Piyush Kaul
3
1
Department of Computer Information Systems, Hashemite University, Zarqa 13133, Jordan
2
Department of Computer Computer Science and Electrical Engineering, AGH University, Cracow, Poland
3
Cadence Design Systems, San Jose, California, U.S.A.
Keywords:
Deep Learning, Quantization, Convolutional Neural Networks.
Abstract:
Nowadays, convolutional neural network (CNN) plays a major role in the embedded computing environment.
Ability to enhance the CNN implementation and performance for embedded devices is an urgent demand.
Compressing the network layers parameters and outputs into a suitable precision formats would reduce the
required storage and computation cycles in embedded devices. Such enhancement can drastically reduce the
consumed power and the required resources, and ultimately reduces cost. In this article, we propose several
quantization techniques for quantizing several CNN networks. With a minor degradation of the floating-point
performance, the presented quantization methods are able to produce a stable performance fixed-point net-
works. A precise fixed point calculation for coefficients, input/output signals and accumulators are considered
in the quantization process.
1 INTRODUCTION
CNN paradigm architecture has shown a state-of-art
performance in the field of image recognition bench-
marks (Ciresan et al., 2011). Studying other differ-
ent aspects of this network would enhance the net-
work use and implementation in embedded devices.
The underlying architecture of the CNN might vary
from one network to another, and recent architectures
have shown large number of layers. Some architec-
tures might include hundreds of layers, millions of co-
efficients and even require billions of operations (He
et al., 2015).
CNN has different types of layers. Convolutional
layers are the ones that consume the majority of com-
putation. In these layers multiply-accumulate opera-
tions (MACs) are performed extensively, leading to
a large number of consumed MACs cycles. While
typical applications that use parallel GPUs perform
floating-point data format, the embedded systems and
specially the real-time ones require a fixed-point for-
mat (Dipert et al., 2017).
A key property of CNN is its resistance to noise,
while keeping performance stable. Hence, treating
any degradation resulted from quantization process
as a new source of noise, makes CNN a preferable
choice to do this job. In this article, we focus on
quantizing the CNN for both coefficients and (in-
put/ output) data with a reduced precision format
(8-bits). The quantization process can be applied
to both inference and training processes. Training
deep neural networks is done by applying many small
changes to the network coefficients. These small ad-
justments utilize higher precision format which ac-
cumulate slowly over time and converge to optimal
values. There are research efforts to use quantized
representations for the training process, but in gen-
eral more bits are needed for training than for infer-
ence (Lin et al., 2016), (Hubara et al., 2016b), (Cour-
bariaux et al., 2014b), (Hubara et al., 2016a), (Gupta
et al., 2015), (Esser et al., 2015). Our work focuses
on quantization for inference as most real-time em-
bedded systems at the moment will only be deployed
with this mode of operations (Dipert et al., 2017).
This article introduces a novel hybrid quantization
(HQ) approach. (HQ) quantizes a network layer data
points (i.e. both coefficients and data) at different lev-
els. Hence, the network performance stability might
be guaranteed using a specific HQ level.
In short, the Motivation is: Enhancing the CNN
capability to be implemented for embedded devices
by reducing the required storage for the network, and
the performed computations on these low powered de-
vices. Such enhancement should keep the CNN per-
Al-Hami, M., Pietron, M., Casas, R., Hijazi, S. and Kaul, P.
Towards a Stable Quantized Convolutional Neural Networks: An Embedded Perspective.
DOI: 10.5220/0006651305730580
In Proceedings of the 10th International Conference on Agents and Artificial Intelligence (ICAART 2018) - Volume 2, pages 573-580
ISBN: 978-989-758-275-2
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
573

formance stable for the inference task. Our Contribu-
tion is: (1) We generate a stable CNN network with a
reduced precision format (8-bits) for both coefficients
and (input/ output) data. (2) We apply a hybrid quan-
tization HQ approach. (3) We use a k-means quanti-
zation approach which reduces the network computa-
tion complexity.
A K-means approach for CNN compression has
been used in (Han et al., 2016b). A key difference be-
tween this compression method and our work is a di-
mensionality of the clusters. In (Han et al., 2016b) the
clustered points are single coefficients which makes it
difficult to achieve efficiency in an embedded proces-
sor, especially with vector processors that can handle
hundreds of coefficients and data samples in parallel
with a single instruction.
The paper is organized as follows. The related
works is described in section 2. The floating-point
and fixed-point representation and the mapping be-
tween them is discussed in Section 3. Additionally
it explains the CNN architecture and how complex-
ity of a CNN is measured. Section 4 reviews the
hybrid quantization approach. K-means quantization
approach is described in Section 6, and Finally con-
clusion remarks appear in Section 7.
2 RELATED WORKS
Many works have shown CNN quantization (An-
war et al., 2015), (Gysel et al., 2014), (Lin et al.,
2016). A common strategy is to quantize all coef-
ficients in a single layer with specified number of
bits to represent the integer and fractional parts (An-
war et al., 2015), (Gysel et al., 2014) based on the
range of values of the coefficients set. In (Van-
houcke et al., 2011) an 8-bits CNN implementation is
compared to an implementation with 32-bits floating-
point for speech recognition to speed-up throughput.
In (Hwang and Sung, 2014) a fixed-point network
with ternary weights and 3-bits activations was pre-
sented. Several methods attempt to binarize weights
and the activations in neural networks (Hubara et al.,
2016a), (Courbariaux et al., 2015), (Soudry et al.,
2014), (Rastegari et al., 2016). All of them resulted
in significant drop in accuracy relative to floating-
point performance. The most efficient among them
is the XNOR-Net (Rastegari et al., 2016) architec-
ture which achieves comparable results to floating-
point format using only binary weights. Complex-
ity reduction of CNN can be achieved by several
other techniques (e.g. SVD reduction, reducing filter
sizes) (Han et al., 2016a), (Han et al., 2016b), (Hin-
ton and Salakhutdinov, 2006). SqueezeNet (Iandola
et al., 2016) is an example of compressed version
of AlexNet (Krizhevsky et al., 2012), reducing 60M
parameters to only 0.5M parameters while fully pre-
serving its accuracy. There are also other new ap-
proaches for image object recognition like Hierarchi-
cal Temporal Memory based on neocortex architec-
ture (Wielgosz and Pietron, 2017), (Wielgosz et al.,
2016), (Pietron et al., 2016a), (Pietron et al., 2016b)
which is suitable for embedded systems. A K-means
approach for CNN compression has been used in
(Han et al., 2016b). Recently, many tools have been
developed for CNN. Many of them take into account
the quantization of the networks. Ristretto tool quan-
tizes CNNs using two phases. In the first phase con-
ventional quantization is used. In the second phase,
there is a fine tuning process where the network is re-
trained using the reduced precision formats of the first
phase (Gysel et al., 2014), (Gysel, 2016). The Tensor-
Flow (Google, 2017) learning framework now pro-
vides facilities for quantization where floating-point
numbers in a certain range are quantized/ dequantized
(to/ from) 8-bits precision format.
3 NETWORK QUANTIZATION
Quantization is the process of constraining values
from a continuous domain into discrete levels of val-
ues. As long as more bits are used in the quantization,
as long as the number of levels may increase. In our
case, the domain is floating-point representation (
˘
f ).
A floating-point number can be represented as:
˘
f = m · b
e
(1)
m ∈ Z is the mantissa, b = 2 is the base, and e ∈ Z is
the exponent value. In case of single precision float-
ing point format according to the IEEE-754 standard,
the mantissa is assigned 23-bits, the exponent is as-
signed 8-bits, and 1-bit is assigned for the sign indi-
cator. Therefore, the set of values that can be defined
by this format is described by:
˘
f
single
: {±2
−126
,... ,±(2 −2
−23
) × 2
127
}. (2)
Similarly, a reduced precision IEEE-754 mini-float
format assigns 10-bits of mantissa, 5-bits of exponent
and the sign bit.
Currently, GPUs with parallel processing being
applied to machine learning operate mainly using the
single precision format. In contrast, embedded DSPs
and the latest GPUs operate with 8-bit and 16-bit
fixed-point (
¯
f ) processing that restricts numbers to the
range:
¯
f : 2
−F
· {−2
T −1
,. .. ,2
T −1
− 1} (3)
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
574
where T = {8,16} is the total used bits and represents
conventional bit-width. F is a shift down (or up) that
determines fractional length, or number of fractional
bits. I is the integer length, I = T −F − 1 for signed
numerical representation. When the fractional length
varies over individual coefficients or data samples, or
over small groups of numbers this format is also re-
ferred to as dynamic fixed-point (Courbariaux et al.,
2014b), (Gysel, 2016).
Assuming S is a dataset of points, it is possi-
ble to define a general mapping from a floating-point
data point x ∈ S to fixed-point q as follows (assuming
signed representation)
q
fxp
= Q (x
flp
) = µ + σ · round(σ
−1
· (x − µ)). (4)
To utilize the full range of the input, one can set:
µ =
1
2
(max
x∈S
x + min
x∈S
x),σ = 2
1−T
· max
x∈S
|x − µ| (5)
Alternatively, µ can be interpreted and measured as
the mean of a distribution of x and σ as the range
of the distribution to be represented before saturation.
Drawbacks of this approach are the need to calculate
and maintain the quantities µ, σ and to apply the nor-
malization procedure in (4).
A second simpler approach uses the magnitude of
values and assign int bits I to cover the maximum
absolute value such that:
I = d(log
2
(max
x∈S
|x|))e (6)
The rest of available bits are assigned to the fraction
bits F and the sign bit.
Yet another approach can define I and F based on
data points distribution histogram. Assuming a given
percentage (i.e a large portion of the histogram data
points like 99.9 %) to be covered in the quantization
assigned I and F . In this case, there will be a small
percentage of the data points considered as outliers.
To determine the effects of saturation (i.e. outliers),
one can experiment the performance with different
saturation levels.
3.1 Complexity Reduction Analysis
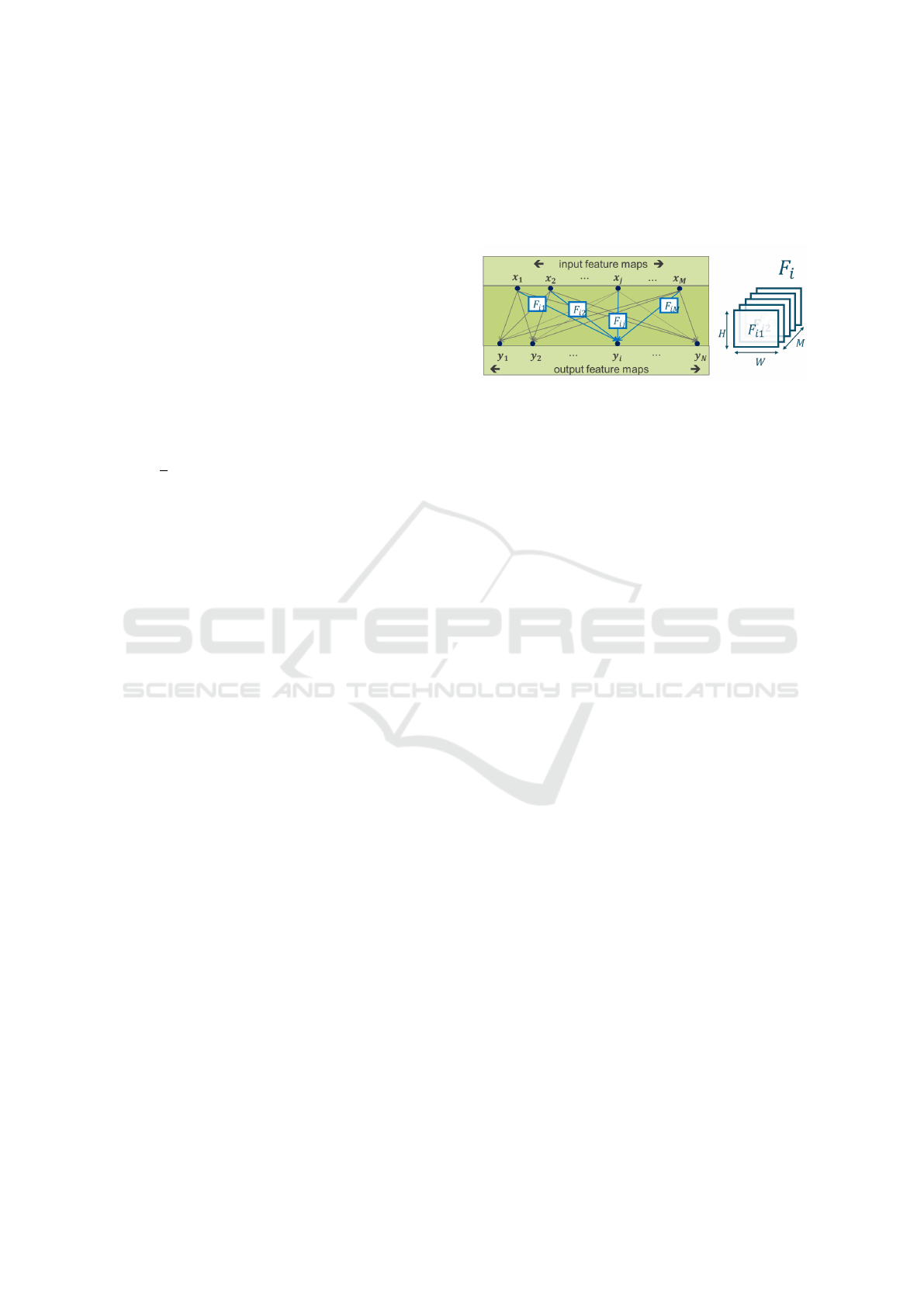
Typically, the layers of a CNN network have neurons
that generate outputs feature maps y
i
, i = 1...N as fol-
lows
y
i
= b
i
+
M
∑
j=1
(F
i j
◦ x
j
) (7)
where F
i j
is a single two-dimensional (2D) convo-
lutional kernel with dimensions H × W . The op-
erator ◦ represents the convolution operation and
b
i
is the bias vector. Fig. 1 illustrates one three-
dimensional (3D) kernel
¯
F
i
= (F
i1
,..., F
iM
) with di-
mensions H ×W × M. Altogether, the N three-
dimensional kernels form one four-dimensional (4D)
set of filter coefficients.
Figure 1: Convolutional layer structure, and the order of a
layer kernels in the convolving process.
The number of multiply-accumulate (MAC) oper-
ations and cycles spent during the execution of Fig. 1
in a practical implementation is often used as the
metric for complexity of a CNN (Courbariaux et al.,
2014a). Assuming each output feature map y
i
has P
output pixels (i.e. image data) the total number of
MAC calculations for a convolutional filtering opera-
tion is MACs = (P · H ·W · M · N).
Complexity may be interpreted in terms of the
size of the hardware blocks required to implement
the MAC operations or also in terms of the total
or average number of cycles required by a proces-
sor to perform these operations. In order to com-
pare the reduction in complexity across quantization,
we adopt the MAC complexity of 8-bits operations
with notation < coeff,data >=< 8b,8b > as a refer-
ence unit. Other quantization formats can be com-
pared relative to the complexity of < 8b, 8b > oper-
ations. For instance, if 4-bits representation is used
for both coefficients and data < 4b, 4b > the relative
complexity is approximately 1/4 that of < 8b,8b >.
Similarly, floating-point operations < flp,flp > will
have approximately 9× to 10× of the complexity of
< 8b, 8b > since there are 3× the number of bits to
represent the mantissas plus the remaining work re-
quired to handle exponents. Table 1 calculates the
complexity for the 4
th
convolutional layer of AlexNet
for various quantization formats.
3.2 Convolutional Neural Network
Quantization Systems
This section reviews the TensorFlow and Ristretto
quantization systems and compares them to the quan-
tization system proposed in this work. The Tensor-
Flow system has an open source quantization mod-
ule (TensorFlow, 2017). The quantization process
uses min, max values (TensorFlow, 2017) to quantize
Towards a Stable Quantized Convolutional Neural Networks: An Embedded Perspective
575

Table 1: The parameters of 4
th
AlexNet convolutional layer
and its computational complexity in various quantization
formats.
Format
< coeff,data >
Relative Complexity
[M MACs]
< 8b,8b > 224 = HPWMN
< 4b,8b >
112 =
1
2
< 8b,8b >
< 4b,4b >
56 =
1
4
< 8b,8b >
< flp,flp > ≥ 2016 = 9 < 8b,8b >
N = 256,P = 27
2
,M = 48, H = W = 5
both data and coefficients. The floating-point num-
bers uses buckets indices as a mapping to quantized
values. There is also Dequantization process where
the centers of the buckets are mapped back to floating-
point value as an approximate estimation for the orig-
inal values. The range of convolutional layers outputs
are estimated analytically.
Ristretto is a system developed by the Laboratory
for Embedded and Programmable Systems (LEPs) for
University of California, Davis (Gysel et al., 2014).
Ristretto is mainly based on dynamic fixed-point and
mini-float representation. However, a powers-of-two
mode is also available. Ristretto uses fine tuning
to recover from any loss in accuracy after its initial
trimming phase of quantization. In this quantization
schema the quantization is based on ranges (max) of
data and coefficients measured empirically. Also, no
support for accumulator quantization below 32-bits.
The main advantages of the Ristretto system are
its wide range of reduced representation formats and
fine tuning approach. The drawback is lack of ac-
cumulator quantization. Our solution offers a wide
spectrum of layer quantization modes like 4D, 3D
and 2D quantization (Hybrid Quantization discussed
in the next section) and clustered kernels, or K-means
approach that allows advanced quantization based on
statistics and automatic tuning. The key feature in
TensorFlow is a new reduced format represented by
integer values. The drawback is that min and max
values must be known at each stage of CNN evalua-
tion.
4 HYBRID QUANTIZATION
This section explores Hybrid Quantization (HQ) of a
CNN network. In HQ coefficients are represented in a
hybrid fashion by assigning different fixed-point for-
matting to different partitions of convolutional layers
and feature maps. For instance, different precisions
(i.e. numbers of bits) and different formats (i.e. I ,
F ) can be assigned to each 2D filter or 3D kernel
of a convolutional layer. Fully connected layers are
only treated as 4D kernels. Similarly, different preci-
sions and formats can be assigned to different parti-
tions of the input and/or output feature maps. Defin-
ing precisions and formats in a hybrid fashion adds
overhead for representation both in terms of storage
space and facilities to decode it. Nevertheless, it can
bring about a significant improvement in CNN accu-
racy when compared to a homogeneous quantization
(i.e. 4D). Varying formats for intermediate accumu-
lated values can be specified in the same hybrid fash-
ion. There are three different formatting schemes are
summarized as follows:
(a) 4D-HQ (b) 3D-HQ (c) 2D-HQ
Figure 2: Different quantization schemes.
Figure 3: 4D quantization problem when outliers appears
in the data (Y axis - magnitudes of coeffs, X axis - id of
coeffs).
• Layer-based or 4D-HQ: Entire layer kernels are
quantized using the same precision format. In
Fig. 2(a) all coefficients in the 4D convolutional
kernels F
i j
are quantized by the same F ,I preci-
sion format.
• Kernel-based or 3D-HQ:
Coefficients in each 3D kernel in a layer are quan-
tized independently. In Fig. 2(b) each 3D kernel
with filters
¯
F
i
= (F
i1
,..., F
iM
) is quantized inde-
pendently with precision format F [i], I [i] for each
i.
• Filter-based or 2D-HQ:
Each 2D filter (each channel in a kernel) in each
kernel in a layer is quantized independently. In
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
576
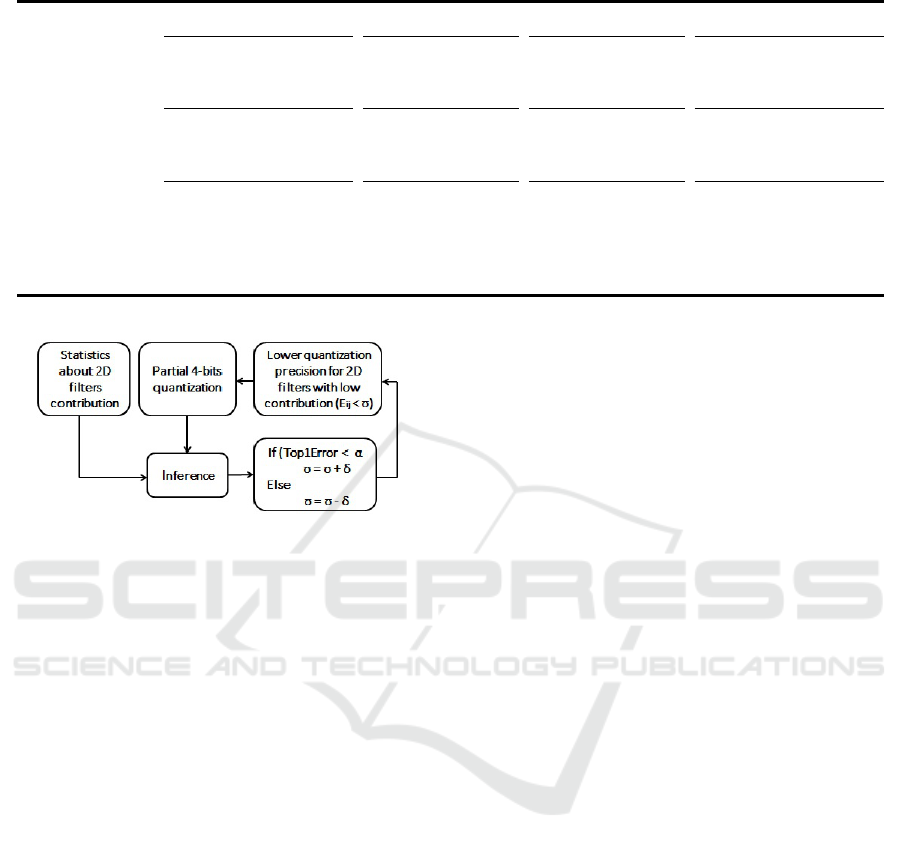
Table 2: Comparison of quantization performance for 8-bits AlexNet.
Format < coeff,data > Quantization Top-1 Error[%] Complexity [M MACs]
Ristretto < flp,flp >
< 8b,8b > no Fine Tuning
with Fine Tuning
43.1
44.0
43.9
6516
724
724
TensorFlow < flp,flp >
< 8b,flp >
< 8b,8b >
4D
4D
42.2
46.2
51.0
6512
2172
724
Ours < flp, flp >
< 8b,flp >
< 8b,8b >
< 8b,8b >
< 8b,8b >
3D
2D
3D
4D
42.2
42.3
42.7
42.5
61.5
6516
2172
724
724
724
Figure 4: Automatic tuning. α is the reference Top-1 Er-
ror. f is the energy threshold. δ is the energy adjustment
amount.
Fig. 2(c) each filter F
i j
is quantized independently
with formatting F [i, j], I [i, j] for each pair i, j.
For large data precision, homogeneous quantization
(i.e. 4D) is sufficient enough to quantize the data
points. The problem appears with low precision for-
mat, the assigned quantized levels are not sufficient
enough to represent all data points in all layer ker-
nels with satisfied accuracy. In 3D quantization, the
maximum absolute value in each kernels controls the
kernel quantization format. Hence, it reduces the gap
between the data points and the maximum absolute
value. When using 2D quantization, the quantization
produces more efficient quantization, where we re-
strict the maximum absolute value to each 2D filter
independently. This effect is described on Fig. 3. The
data point in the red circle (which might seem as an
outlier) affects the layer quantization format using the
homogeneous quantization (4D). However, using 3D
or 2D quantization this effect can be drastically re-
duced. Therefore kernel quantization (3D) were per-
formed in case of
<8b,8b > AlexNet quantization to
achieve 1% loss in accuracy in relative to floating-
point representation.
Next, we evaluate the performance of various HQ
modes and compare against Ristretto and TensorFlow
quantization of AlexNet of the the ImageNet valida-
tion set (ILSVRC2012 dataset), as shown in Table 2.
Our baseline floating-point AlexNet network (i.e. pre-
trained network in MatConvNet framework) (Vedaldi
and Lenc, 2015). This baseline is also ported to a
fixed-point C-model. In the C-model, coefficients and
input data in each layer are quantized to 8-bits while
intermediate accumulator values at the output of a
convolutional filter are quantized to 32-bits. Those
values are quantized back to 8-bits before being sent
to the next layer. Both 3D-HQ and Ristretto experi-
ence < 1.0% drop in accuracy relative to the floating-
point performance. The quantization in TensorFlow
experiences a much higher drop in accuracy (Ten-
sorFlow rounding mode), more than 4% despite the
use of floating-point to represent data. Our attempts
to quantize both data and coefficients in TensorFlow
failed to produce reliable results.
Several networks have been tested against our pro-
posed quantization strategy. The goal is to quantize
the networks while keeping the performance within
the range less than 1% performance degradation rela-
tive to the floating-point performance (Table 5). We
applied <8b,8b > quantization precision to all net-
works. Hybrid quantization 4D and 3D are used in
the quantization.
5 ADVANCED AUTOMATIC
QUANTIZATION
Investigating the performance of mixing 8-bits and 4-
bits precision format on different network layers has
a lot of insights, specially for embedded devices. Uti-
lizing some statistics gathered during the evaluation
of the CNN, we can decide which parts of the net-
work should use (8-bits/ 4-bits) precision format. In
this quantization scheme, the energy contribution E
i j
of each 2D filter F
i j
is accumulated over a set of probe
Towards a Stable Quantized Convolutional Neural Networks: An Embedded Perspective
577

Table 3: Hybrid quantization of the 4
th
layer in AlexNet (40% of coefficients are in 4-bits format), all biases are in 8-bits.
Experiment Layers: 1, 18 4 7, 9, 11, Top-1 Savings
14, 16 Error [%] [%]
Conservative Baseline < 8b, 8b > < 8b, 8b > < 8b,8b > 42.7 0
Moderate < 8b, 8b > < 4b, 8b > (40%) < 4b, 8b > 43.1 30
Aggressive < 8b, 8b > < 4b, 8b > (100%) < 4b, 8b > 64.1 44
Table 4: K-means quantization of Convolutional Layer 4 of AlexNet (all other layers are kept in < flp,flp >).
Quantization Base Residuals Top-1 Complexity Layer Network
Method Format Format Error [%] [M Macs] Savings Savings
2D-HQ Baseline < 8b, 8b > 42.7 224
2D-HQ < 4b, 8b > 65.9 112 50% 15%
K-means < 8b, 8b > < 8b,8b > 42.2 227 -2% -0.6%
K-means < 8b, 8b > < 4b,8b > 42.7 117 48% 15%
images as follows:
E
i j
=
∑
probe
images
∑
pixels
p
|y
i j
(p)|
2
(8)
where y
i j
= F
i j
∗ x
j
are partial feature maps. Essen-
tially, the quantization scheme assigns baseline preci-
sion (i.e. 8-bits) to 2D filters with high energy con-
tribution and lower precision (i.e. 4-bits) to 2D filters
with low energy contribution based on some energy
threshold f. An automatic threshold tuning and quan-
tization procedure was developed to minimize com-
plexity through quantization while maintaining a ref-
erence level of Top-1 Error α. The procedure is illus-
trated in Fig. 4.
Table 3 shows the results of this quantization
scheme. The Conservative experiment utilizes 8b 2D-
HQ quantization throughout all layers. In the Mod-
erate experiment, the layers (1, 18) are quantized
to <8b,8b >. The most computationally expensive
Layer 4 is quantized with 40% of its 2D filters in
<4b,8b > format and all other layers use <4b, 8b >
quantization. The Moderate experiment suffers < 1%
loss in accuracy relative to floating-point but results
in 30% savings in complexity relative to the Conser-
vative experiment. The Aggressive experiment com-
pletely quantizes Layer 4 to <4b,8b > resulting in a
drastic loss in accuracy.
6 K-MEANS QUANTIZATION
K-means approach splits a layer coefficients kernels
into two parts, basis filters G
`(i)
(i.e. approximations)
and residual filters
˜
F
i
(i.e. differences) leading to
F
i
= G
`(i)
+
˜
F
i
. The K-means clustering algorithm splits
a layer kernels into k centroids kernels serves as ap-
proximate kernels for their related cluster groups. The
residual kernels are the difference between the orig-
inal kernels and their corresponding approximation
centroids.
The base and residual filters are assigned differ-
ent quantization formats in order to reduce complex-
ity while maintaining accuracy. In this work we apply
K-means clustering to derive a set of K < N basis 3D
kernels. These kernels are formatted with <8b,8b >
precision. The residual kernels are assigned lower
precision, i.e. <4b, 8b > or <4b,4b >. The final y
i
can be described as:
y
i
= b
i
+
M
∑
j=1
G
`(i), j
◦ x
j
| {z }
<8b,8b>
+
˜
F
i j
◦ x
j
| {z }
<4b,8b>,<4b,4b>
(9)
where G
`(i), j
are the basis filters assigned to each 3D
kernel via some mapping `(·) : [1..N] 7→ [1..K]. The resid-
ual filters are given by
˜
F
i j
= F
i j
− G
`(i), j
. Assuming the
base kernels use <8b,8b > precision and the residuals
use <4b,8b >, the effective complexity savings of this
approach is a factor of (0.5N −K)/N. The implementa-
tion is as follows: the input is convolved with K basis
kernels and generate K temporary feature maps. Next,
the output of the residual filters are added to their
corresponding base filter temporary feature maps to
yield the final output of the convolutional layer. A
disadvantage of this approach is that the temporary
feature maps have to be stored. Table 4 shows the
performance of the K-means approach for convolu-
tional Layer 4 in AlexNet, the layer with the largest
complexity (all other layers are kept in floating-point
format). While 2D-HQ formatting to <4b,8b > re-
sults in 50% reduction in complexity of the layer, the
loss in accuracy is drastic. K-means quantization to
<8b,8b > format with K = 4 is attempted as a base-
line (i.e. K is chosen to be 4 based on empirical exper-
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
578

Table 5: Comparison of different CNN models using the proposed quantization approach (FLP - floating point, FXP - fixed
point).
Top-5 Error [%] Top-1 Error [%] FXP Configuration
FLP FXP FLP FXP Coeff Data
Caffe-AlexNet 20.33 20.51 43.35 43.64 8b, 4D 8b, 4D
20.33 20.43 43.35 43.52 8b, 3D 8b, 4D
MatConvNet-AlexNet 19.93 34.28 42.36 58.83 8b, 4D 8b, 4D
19.93 20.13 42.36 42.53 8b, 3D 8b, 4D
GoogleNet 13.54 13.60 34.89 34.90 8b, 4D 8b, 4D
13.54 13.58 34.89 35.09 8b, 3D 8b, 4D
Vgg-VeryDeep-19 10.64 10.72 29.48 29.93 8b, 4D 8b, 4D
10.64 10.61 29.48 29.62 8b, 3D 8b, 4D
Cactus-it6 8.05 9.34 25.26 27.48 8b, 3D 8b, 4D
ResNet-50 8.29 8.80 25.11 26.25 8b, 4D 8b, 4D
8.29 8.63 25.11 25.78 8b, 3D 8b, 4D
ResNet-101 7.61 8.36 23.96 25.69 8b, 4D 8b, 4D
8.61 7.91 23.96 24.59 8b, 3D 8b, 4D
ResNet-152 7.23 8.11 23.51 24.96 8b, 4D 8b, 4D
7.23 8.07 23.51 25.05 8b, 3D 8b, 4D
Table 6: Hybrid clustered quantization of AlexNet.
Base < 8b, 8b >
Residuals Layer 1: < 8b, 8b >
all others : < 4b, 8b >
Top-1 Error 44.1%
k - clusters k = 2 for layers 1, 4,
11, 14, 16
k = 3 for layer 7
k = 6 for layer 9
k = 4 for layer 18
Complexity [M MACs] 422
Network Savings 41.6%
iments), yielding a slight increase of 2% in complex-
ity and no significant change in performance. Next,
K-means quantization to <4b,8b > format leads to
48% complexity reduction in the layer and no degra-
dation in accuracy relative to <8b,8b >. In Table 6 we
apply K-means quantization to <4b,8b > to all layers
of the network except Layer 1, which is the layer most
sensitive to perturbations. The net savings for the net-
work is > 40% with a degradation in accuracy < 2%.
In this experiment we chose different k values for dif-
ferent layers (i.e. based on empirical experiments).
7 CONCLUSIONS AND FURTHER
WORK
In this work we presented a novel quantization meth-
ods for deep convolutional neural networks. The sys-
tem reduces memory requirements, area for process-
ing elements and overall power consumption for hard-
ware accelerators. Our research shows that the most
popular CNN architectures can be quantized to 8-
bits for both coefficients and data outputs with minor
degradation in accuracy compared to floating-point.
Hybrid quantization and clustered quantization al-
low the use of advanced quantization (e.g. <4b,8b >)
without significant decrease in performance. Our sys-
tem is both fast and automated. It was implemented
in MatConvnet and ported to a C-model. We consider
adding new features in the future such as: exploit-
ing other statistics of the network in quantization pro-
cess, further optimizing the K-means approach, net-
work weights binarization (Rastegari et al., 2016) and
(Zhang and Liu, 2016), applying fine-tuning and use
re-training in quantization process. These additional
features will help to reduce the bit-width even further,
and to reduce the computational complexity.
Towards a Stable Quantized Convolutional Neural Networks: An Embedded Perspective
579

REFERENCES
Anwar, S., Hwang, K., and Sung, W. (2015). Fixed point
optimization of deep convolutional neural networks
for object recognition. Speech and Signal Processing
IEEE International Conference.
Ciresan, D., Meier, U., M., G. L., and Schmidhuber, J.
(2011). Flexible, high performance convolutional neu-
ral networks for image classification. Proceedings of
the Twenty-Second International Joint Conference on
Artificial Intelligence, 2:1237–1242.
Courbariaux, M., Bengio, Y., and David, J. (2015). Bina-
ryconnect: Training deep neural networks with binary
weights during propagations. Advances in Neural In-
formation Processing Systems.
Courbariaux, M., Bengio, Y., and Jean-Pierre, D. (2014a).
Training deep neural networks with low precision
multiplications. ArXiv e-prints, abs/1412.7024.
Courbariaux, M., David, J.-P., and Bengio, Y. (2014b).
Training deep neural networks with low precision
multiplications. arXiv preprint arXiv:1412.7024.
Dipert, B., Bier, J., Rowen, C., Dashwood, J., Laroche,
D., Ors, A., and Thompson, M. (2016 (accessed
February 20, 2017)). Deep learning for object
recognition: Dsp and specialized processor optimiza-
tions. http://www.embedded-vision.com/platinum-
members/embedded-vision-alliance/embedded-
vision-training/documents/pages/cnn-dsps.
Esser, S., Appuswamy, R., Merolla, P., Arthur, J., and
Modha, D. (2015). Backpropagation for energy-
efficient neuromorphic computing. in: Advances in
neural information processing systems. Advances in
Neural Information Processing Systems.
Google (2016 (accessed February 22, 2017)). Tensorflow.
https://www.tensorflow.org.
Gupta, S., Agrawal, A., Gopalakrishnan, K., and
Narayanan, P. (2015). Deep learning with limited nu-
merical precision. Proceedings of the 32nd Interna-
tional Conference on Machine Learning.
Gysel, P. (2016). Ristretto: Hardware-oriented approxima-
tion of convolutional neural networks. arXiv preprint
arXiv:1605.06402.
Gysel, P., Motamedi, M., and Ghiasi, S. (2014). Hardware-
oriented approximation of convolutional neural net-
works. ArXiv e-prints, arXiv:1604.03168.
Han, S., Liu, X., Mao, H., Pu, J., Pedram, A., Horowitz,
M. A., and Dally, W. J. (2016a). Eie: Efficient in-
ference engine on compressed deep neural network.
arXiv preprint arXiv:1602.01528.
Han, S., Mao, H., and Dally, W. J. (2016b). Deep compres-
sion: Compressing deep neural networks with prun-
ing, trained quantization and huffman coding. arXiv
preprint arXiv:1602.01528.
He, K., Zhang, X., Ren, S., and Sun, J. (2015). Deep resid-
ual learning for image recognition. arXiv:1512.03385.
Hinton, G. E. and Salakhutdinov, R. R. (2006). Reducing
the dimensionality of data with neural networks. Sci-
ence, 313(5786):504–507.
Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., and
Y., B. (2016a). Binarized neural networks: Train-
ing neural networks with weights and activations con-
strained to +1 or -1. arxiv 2016.
Hubara, I., Courbariaux, M., Soudry, D., El-Yaniv, R., and
Y., B. (2016b). Quantized neural networks: Training
neural networks with low precision weights and acti-
vations. arxiv 2016.
Hwang, K. and Sung, W. (2014). Fixed-point feedforward
deep neural network design using weights +1, 0, and
-1. Signal Processing Systems, 2014 IEEE Workshop
on, IEEE (2014).
Iandola, F. N., Moskewicz, M. W., Ashraf, K., Han, S.,
Dally, W. J., and Keutzer, K. (2016). Squeezenet:
Alexnet-level accuracy with 50x fewer parameters and
0.5mb model size. arXiv preprint arXiv:1602.07360.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in neural information process-
ing systems, pages 1097–1105.
Lin, D., Talathi, S., and Annapureddy, V. (2016). Fixed
point quantization of deep convolutional networks.
ICLR 2016.
Pietron, M., Wielgosz, M., and Wiatr, K. (2016a). Formal
analysis of htm spatial pooler performance under pre-
defined operation condition. International Joint Con-
ference on Rough Sets.
Pietron, M., Wielgosz, M., and Wiatr, K. (2016b). Parallel
implementation of spatial pooler in hierarchical tem-
poral memory. International Conference on Agents
and Artificial Intelligence.
Rastegari, M., Ordonez, V., Redmon, J., and Farhadi, A.
(2016). Xnor-net: Imagenet classification using bi-
nary convolutional neural networks. ArXiv e-prints,
arXiv:1603.05279.
Soudry, D., Hubara, I., and Meir, R. (2014). Expecta-
tion backpropagation: parameter-free training of mul-
tilayer neural networks with continuous or discrete
weights. Signal Processing Systems (SiPS), IEEE
Workshop.
TensorFlow (2017 (accessed July 12,
2017)). Tensorflow quantization.
http://www.tensorflow.org/performance/quantization.
Vanhoucke, V., Senior, A., and Mao, M. (2011). Improv-
ing the speed of neural networks on cpus. Proc. Deep
Learning and Unsupervised Feature Learning NIPS
Workshop.
Vedaldi, A. and Lenc, K. (2015). Matconvnet – convolu-
tional neural networks for matlab. In Proceeding of
the ACM Int. Conf. on Multimedia.
Wielgosz, M. and Pietron, M. (2017). Using spatial pooler
of hierarchical temporal memory to classify noisy
videos with predefined complexity. Journal of Neu-
rocomputing.
Wielgosz, M., Pietron, M., and Wiatr, K. (2016). Opencl-
accelerated object classification in video streams us-
ing spatial pooler of hierarchical temporal memory.
Journal IJACSA.
Zhang, L. and Liu, B. (2016). Ternary weight networks.
arXiv:1605.04711.
ICAART 2018 - 10th International Conference on Agents and Artificial Intelligence
580
