
Wavelet Cepstral Coefficients for Electrical Appliances Identification
using Hidden Markov Models
Abdenour Hacine-Gharbi
1
and Philippe Ravier
2
1
LMSE laboratory, University of Bordj Bou Arréridj, Elanasser, 34030 Bordj Bou Arréridj, Algeria
2
PRISME laboratory, University of Orleans, 12 rue de Blois, 45067 Orleans, France
Keywords: Non-Intrusive Load Monitoring (NILM), Electrical Appliances Identification, Feature Extraction (FE),
Harmonic Analysis, Short-Time Fourier Series (STFS), Wavelet Analysis, Discrete Wavelets, Wavelet
Cepstral Coefficient (WCC), Hidden Markov Models (HMM), Features Relevance, Wrappers Feature
Selection (WFS).
Abstract: In previews work, a construction of electrical appliances identification system has been proposed using
Hidden Markov Models combined with STFS (Short-Time Fourier Series) features extraction. This paper
proposes many extensions: (i) a larger spectral band up to the maximum frequency value for the analysis of
the data is investigated, but requiring a higher dimensionality of the STFS feature vector; (ii) a more
compact representation than the SFTS vector is investigated with the wavelet based approaches; (iii) the
relevance of the wavelet based features are investigated using feature selection procedure. The results show
that increasing the number of harmonics in STFS from 50 to 249 does not necessarily improve the CR
because of the peaking phenomenon observed with high dimensionality. The wavelet cepstral coefficients
(WCC) descriptor with 8 cycle time analysis windows presents a higher performance comparing to the
STFS, discrete wavelet energy (DWE) and log wavelet energy (LWE) descriptors. Recommendations are
also given for selecting wavelet family, the mother wavelet order within the family and the decomposition
depth. It turns out that the Daubechies wavelet of order 4 and decomposition depth 6 (or Coiflet wavelet
with order 2 and depth 7) is recommended in order to achieve the better CR values.
1 INTRODUCTION
1.1 Motivation
For electricity providers, accessing to detailed
energy consumption at the appliance level helps in
regulating the electric power delivery / demand
balance. Indeed, demand responses can be
modulated by targeting specific user and appliance
groups. For the customers, the energy disaggregation
information helps improving their energy
consumption efficiency.
This objective can be achieved in the frame of
smart grids with the use of sensors, communications,
computation abilities and control systems. In order
to infer what appliances are operating in a home,
home’s power consumption must be disaggregated
into individual appliances. An energy meter allows
the access to the energy consumption information of
the appliance or group of appliances. A
disaggregated consumption thus necessitates the
deployment of many meters at home. This solution
is fastidious, not flexible and costly. Conversely, the
non-intrusive appliance load monitoring (NIALM or
NILM) solution necessitates the installation of a
single device only at the house’s power. NIALM
techniques aim at disaggregating total electricity
consumption to individual contributions of each
load. Their design requires many stages: data
acquisition, event detection, feature extraction, event
classification and finally energy computation (Basu,
2014). The event classification quality highly
depends on the relevance of the features extracted
from the acquired data. We have investigated in a
previous paper (Nait-Meziane, et al., 2016) the
contribution of the transient part of the turn on
currents to the appliance identification rate. A
pattern recognition system was created considering
short time Fourier series coefficients (STFS) at the
input of a hidden Markov model (HMM) classifier.
The study demonstrated an interest in considering
the transient part in addition to the steady state part
Hacine-Gharbi, A. and Ravier, P.
Wavelet Cepstral Coefficients for Electrical Appliances Identification using Hidden Markov Models.
DOI: 10.5220/0006662305410549
In Proceedings of the 7th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2018), pages 541-549
ISBN: 978-989-758-276-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
541

of the current signals for an improved identification
rate.
The purpose now is to extent this study to (i) a
larger analysis spectral band up to the maximum
frequency value which requires a higher
dimensionality of the STFS feature vector; (ii) a
more compact representation than the STFS vector
using other potentially interesting features such as
wavelet based approaches; (iii) the investigation of
the features relevance using feature selection
procedure.
1.2 Related Work
In (Nait-Meziane, et al., 2016), the use of HMM
models were introduced to solve the electrical
appliance identification problem based on high-
frequency sampled signals. The HMM classifier
were designed using extracted features from the
current signals.
The current signals remain periodic at the rate of
the main power frequency with possible high
distortions. These current signals can be analyzed
with the coefficients of Discrete Fourier Series
(DFS) decomposition. For a samples periodic
signal, the DFS coefficients are
expressed as
with
. In the steady state part of the
active current signals, the magnitude of these
coefficients should be constant whatever the location
of the considered time period.
For transient electrical current signals, however,
the periodicity property is lost and strictly speaking
this formula is no more correct. Nevertheless, the
DFS coefficients still catch the greatest part of the
signal energy. Moreover, the design of a HMM
system requires the definition of many states which
input features must be time-varying. For most of the
appliances, the DFS coefficients magnitude varies
along the time because of transient turn-on part,
appliance regime changes or power fluctuations.
This is the reason why the current signals were
segmented into overlapping successive windows
with DFS coefficients computed on each window.
The resulting STFS coefficients are obtained as
DFS coefficients computed around each time
location as:
with
and being the total
number of samples of the current signal. For the
tested PLAID dataset, the number was 500
samples at 30 kHz frequency for the 60 Hz cycle-
time and the overlapping was 50% of the window
size, i.e. where is the segment number.
Different choices for the identification system
were investigated: the use of transient vs. steady-
state signals, the use of even vs. odd-order
harmonics features, and the optimal feature vector
size. The conclusion of this study was that the
combined use of the transient part of the electrical
current signals with only a few odd-order harmonics
allows constructing an appliance identification
system that is accurate, fast, and less complex in
terms of memory occupancy and computations.
Another choice for the characterization of the
transient electrical current signals has been proposed
in (Nait Meziane, et al., 2017). Novel features
extracted from a proposed mathematical model for
modelling the turn-on transient current are
introduced and used in order to classify electrical
appliances. The model of the current is an amplitude
modulated sum-of-sinusoids with additive white
Gaussian noise (Naït Meziane, et al., 2015). The
sinusoids frequencies are known and are odd order-
harmonics of the fundamental frequency (the
frequency of the main power). The amplitude
modulation, or envelope, describes the current
amplitude variation of the turn-on transient part as a
time polynomial expression of an exponential
function until reaching the steady-state part with a
unity envelope.
The results showed that the amplitude-related
features of this model are the most suited for
appliance identification (giving a classification rate
of 98.57% evaluated on COOLL database) whereas
the envelope related features are the most adapted
for appliance clustering.
Moreover, these features were analysed for the
sake of selecting a set of features that is relevant for
appliance classification. A feature selection
procedure using a wrapper approach for
identification was carried out corroborating the
previous results.
2 WCC FEATURE EXTRACTION
We introduce in this section a new feature for NILM
based on wavelet theory and cepstral calculus.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
542

2.1 Wavelet Processing for NILM
Feature Extraction
The features extracted from the electrical signals are
expected to characterise the electrical appliances.
More precisely for NILM, the features should be
relevant for appliances identification, i.e. they
should be able to explain the electrical appliances
classes during their consumption periods. The role
of features is to provide a compact representation of
the data. They should be as relevant as possible and
their number should be minimal. Classical features
used in electrical engineering are the current and
voltage root mean square values and the
instantaneous power with the active and reactive
parts. However, these averaged values partly hide
the rich information contained in the frequency
domain. Indeed, the measured voltage and current
remain periodic at the period of the AC power main.
The current signal in particular may have a lot of
distortions which can be analyzed with the
coefficients of DFS since the signal remains periodic
as operated in (Nait-Meziane, et al., 2016).
However, the period must be exactly known
otherwise the computation may lack some
information.
The nonstationarity of the data can otherwise be
caught with the Short Time Fourier Transform
(STFT). The differences with STFS rely on segment
length and segment windowing choice possibilities.
Actually, the STFT is a specific case of the Cohen’s
class time-frequency representations. Each case is
defined by a specific kernel function giving rise
many time-frequency methods like Wigner-Ville,
Choï-Williams... Nevertheless all these approaches
are not as appropriate as the time scale methods for
the characterization of transient signals. Indeed, the
multi-resolution and time-frequency localization
properties of the time-scale methods are particularly
suited for the simultaneous analysis of short time
fast events and long time slow events. This is the
case for electrical signals where the slow events are
related to the steady state periodic behaviour of the
AC power and the fast events are the electrical
changes like impulses, transient phases between
steady state phases or electrical discharges.
We thus propose to use wavelet-based signal
decomposition instead of STFS or STFT for the
feature extraction procedure. The scale effect of the
wavelet transform is obtained by applying a scale
factor to the time course of a mother analysing
wavelet. The mother wavelet should also present
oscillations in order to extract a spectral content
around its rescaled central frequency. The time-
varying spectral analysis is obtained just by applying
a temporal shift factor to the mother wavelet before
scaling. The wavelet transform was thus first
expressed in the continuous domain as continuous
wavelet transform (CWT). The discrete wavelet
transform (DWT) was second elaborated in the
mathematical frame of multi resolution analysis
providing two digital filters and. The first
one is a low pass filter and the second one is a high
pass filter.
The discrete wavelet coefficients
and
can be produced, at each level, by the recursion
formula:
Note that the mother wavelet does not directly
appear in these recursive expressions but its
continuous waveform can be retrieved from the
sequence. Similarly, another continuous waveform
(the so-called scaling function) can be retrieved from
the sequence.
The algorithm is initialized at level 0 by
setting
defined on samples. At each
iteration, the filters split the full data bandwidth in
low and high frequency bands (the result can
therefore be down sampled by a factor 2 which is the
dyadic scale factor in the discrete version, see the
term in the formula). Low frequency components are
thus represented by the approximation coefficients
while high frequency components are
represented by the detail coefficients
. The
DWT wavelet coefficients at the decomposition
depth can be put in a vector as the concatenation
of the detail coefficients computed at all the scales
plus the remaining approximation coefficients
computed at scale
.
Because of the factor 2 down-sampling, the number
of coefficients
at iteration is
. This
means that the number of samples is
preserved in the DWT domain with coefficients.
The maximal decomposition depth can be
but practically depends of the filters length.
A reduced dimensionality of the features can be
obtained by computing any energy measure or
information measure from the wavelet coefficients at
each scale (Gray and Morsi, 2015).
2.2 Review of Wavelets in NILM
Wavelet processing was introduced in NILM at the
Wavelet Cepstral Coefficients for Electrical Appliances Identification using Hidden Markov Models
543

beginning of the 2000s. The first works used the
wavelet scale decomposition ability for electrical
signal analysis. Indeed, the harmonic Fourier series
expression can be decomposed in different scale
components which permits to highlight some
changes in harmonic components because of the
filter bank effect of the wavelet decomposition
(Cristaldi, Monti, and Ponci, 2003). This wavelet
property also allows a precise detection of the
beginning and the end of the turn-on transient parts
of the electrical currents (Su, Lian, and Chang,
2011).
The work proposed in (Figueiredo, de Almeida,
and Ribeiro, 2011) uses the reversibility property of
the DWT for a denoising stage before NILM
processing by selecting certain coefficients to retain,
and discarding the others considered as noise.
The authors in (Duarte, Delmar, Goossen,
Barner, and Gomez-Luna, 2012) are the only ones
using the CWT in NILM for the characterization of
switching voltage transients. The complex Morlet
mother wavelet was applied at chosen
decomposition scales. The scale values were
experimentally found such that the 3dB bandwidths,
obtained for each selected scale, cover the whole
signal bandwidth without overlapping.
In (Gray and Morsi, 2015), the energy of the
detail coefficients was used and their computation at
each scale was used as the feature vector
components for classification. The classification
accuracy was also evaluated and compared using
features obtained by various orders of Daubechies
(Db) wavelets. They showed that higher order Db
wavelets (and Db5 in particular) exhibit higher
classification accuracy.
In (Tabatabaei, Dick, and Xu, 2017), the authors
also calculate the energy of the wavelet coefficients
at each scale using Haar wavelets and use them as
the feature vector instead of the wavelet coefficients.
Finally, an adapted wavelet specifically designed for
NILM application was proposed by (Gilis,
Alshareef, and Morsi, 2016) (Gillis and Morsi,
2017). The authors also applied the DWT on a
derivative pre-processing of the data: for each
samples period, the difference signal between
and was considered.
However, the improvement achieved by the
newly designed filter is found to be small compared
to Db wavelets.
2.3 Wavelet Cepstral Coefficients
(WCC)
In the previous section, the authors took advantage
of the wavelet transform for the electrical signals
analysis in the NILM problem. Many of the authors
reduced the dimensionality in the DWT domain by
computing a discrete wavelet energy (DWE)
features set composed of the wavelet coefficients
energies evaluated on each scale as:
At this step, other measures on the wavelet
coefficients have been proposed in the literature
covering various application domains such that
Teager-Kaiser energy, the log of the energy, the
hierarchical energy (Didiot, Illina, Fohr, & Mella,
2010), or information measures like entropy. (El-
Zonkoly and Desouki, 2011).
In the speech processing domain, the logarithm is
often used in order to highlight the harmonic content
and to separate transfer functions. For a speech-
music discrimination application, the authors in
(Didiot, Illina, Fohr, and Mella, 2010) introduced the
log wavelet energy (LWE) computed on normalized
energies:
In this speech domain, the classical features are
the Mel Frequency Cepstral Coefficients (MFCC)
and the authors compared the LWE-based
discrimination approach with the MFCC-based one.
The MFCC is a Fourier transform (FT) approach
where the log of the energy is computed in different
frequency bands (with a Mel filter applied). The
inverse Discrete Cosinus Transform (DCT) is
applied for the decorrelation of the coefficients. By
replacing in this procedure the FT by the DWT, the
Wavelet Cepstral Coefficients (WCC) can be
obtained. This new typology of features has already
been proposed in the speech (Lei and Kun, 2016). In
a bat classification problem, the authors of
(Gladrene, Juliet, and Jayapriya, 2015) go beyond by
also proposing the Dual-Tree Complex WCC.
Indeed, the DWT is based on real valued oscillating
wavelets whereas the FT basically uses complex-
valued oscillating sinusoids. So the Dual-Tree
Complex Wavelet Transform has been proposed for
enhancing the DWT because it answers to some
shortcomings of the DWT as the oscillations, the
shift variance, aliasing and lack of directionality.
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
544
In the NILM domain, (Kong, Kim, Ko, and Joo,
2015) partly investigated this idea using the
quefrency position and amplitude of the dominant
peaks in the smoothed cepstrum of the voltage signal
as appliance features to distinguish ON/OFF
appliances. But their work did not exploit the DWT.
We thus propose to use the WCC features for the
NILM problem. The following experiments aim to
identify the most suitable wavelet family as well as
the optimal decomposition level. The second step
will investigate the feature selection problem using
DWE, LWE or WCC features.
3 EXPERIMENTS AND RESULTS
We present in this section a number of experiments
we carried out to evaluate the performance of the
WCC based feature extraction method for the task of
appliance identification. In these experiments, the
WCC coefficients are used as features to identify 11
electrical appliances of Plaid dataset using HMM
classifier based identification system (Nait-Meziane,
et al., 2016). Three experiments are conducted in
order (i) to compare the performance of the WCC
features to other features commonly used in the
literature; (ii) to search for the optimal combination
of mother wavelet and decomposition level; (iii) to
analyze the WCC features relevance after feature
selection procedure.
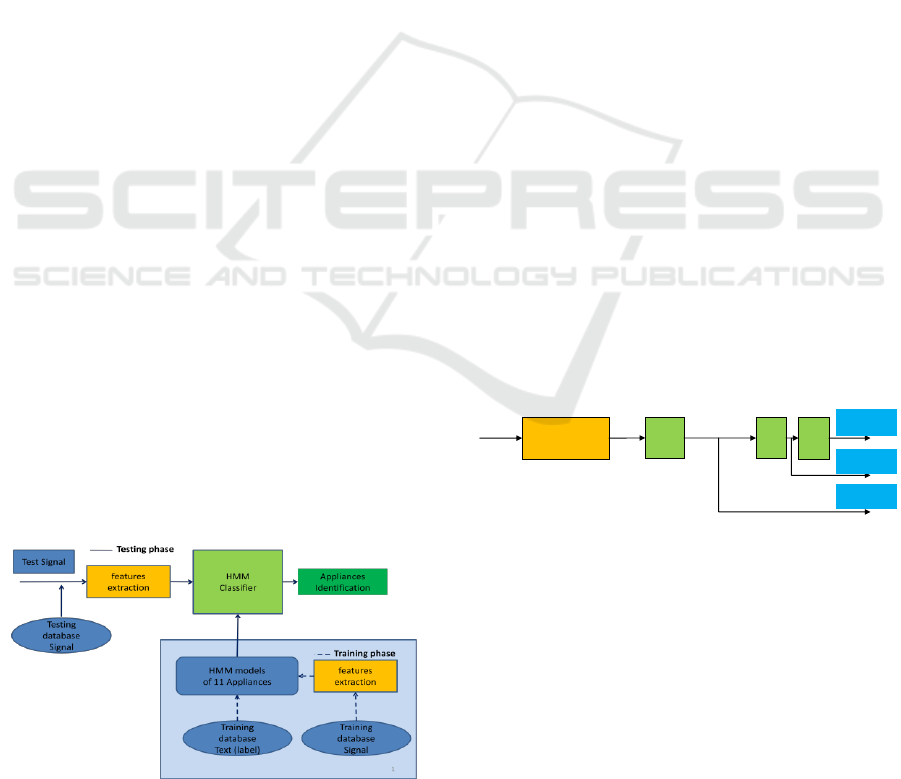
3.1 HMM based Identification System
The standard appliances identification system
presented in (Nait-Meziane, et al., 2016) has been
used in this work. The HMM based classifier system
is composed of two principal phases, the training
phase (learning) and the classification phase
(testing) as presented in fig 1. Therefore, the
database is divided into a training database and a
testing database.
Figure 1: HMM-models-based electrical appliances
identification.
Both phases need firstly a feature extraction
step which consists in converting the temporal
current waveforms signal into a sequence of
features vectors (STFS coefficients). The total
active current signals (transient and steady state
phases) were considered because this repartition
gives better CR results than those obtained with the
steady state phase only as demonstrated in (Nait-
Meziane, et al., 2016). This sequence is considered
as input sequence of observations to the HMM
classifier. In (Nait-Meziane, et al., 2016), STFS
feature vectors are computed on 50% overlapping
window, each of 16.7 ms duration (one 60 Hz
cycle-time).
The training phase consists to model each
appliance signature by HMM model of 3 states, each
one being associated to GMM model of 3 Gaussians.
In this phase, the system learns occurrences of the
training database: the sequences of feature vectors of
the training corpus are used for estimating the
parameters of each HMM model using the
embedded Baum-Welch reestimation algorithm
performed by HEREST HTK command (Young,
Kershaw, Odell, and Ollason, 1999).
In the classification phase, the classifier uses the
trained HMM models for assigning each input
feature vectors sequence to one of 11 appliances
using the Viterbi algorithm (HVITE command). The
testing dataset is used to evaluate the performance of
the identification system. The performance
evaluation is based on Classification Rate (CR)
defined in (Nait-Meziane, et al., 2016).
In this paper, the STFS feature extraction process
has been replaced by DWE / LWE / WCC features.
This process is represented in fig.2.
Figure 2: process of DWE / LWE / WCC feature
extraction with Hamming windowing.
The PLAID dataset has been used for the
experiments. PLAID is a public dataset of current
and voltage measurements taken from 55 houses.
This dataset contains electric signatures of 11
appliance types with a total of 1074 signals
(current and voltage) sampled at a 30 kHz rate
(Gao, Giri, Kara, and Bergès, 2014).
In this work, the dataset is divided into a training
set and a testing set; each one is composed of 537
current signals with the consideration that all the
1
, ,
,
Frames
Electrical
Signal
Windowing and
frame formation
DWT
Log
DCT
Sequence of
LWE vectors
Sequence of
DWE vectors
Sequence of
WCC vectors
Wavelet Cepstral Coefficients for Electrical Appliances Identification using Hidden Markov Models
545

houses (55 in total) have examples in the training and
in the testing sets.
3.2 Comparative Study between STFS
and DWE / LWE / WCC
This experiment allows evaluating the advantage of
WCC compared to STFS coefficients and DWE
(Discrete Wavelet decomposition based calculus
Energy) descriptors for the task of electrical
appliances identification. Another case of WCC
descriptor consists to calculate only the log of
energy at each decomposition level without DCT
transform (Didiot, Illina, Fohr, and Mella, 2010) in
order to keep the interpretation of coefficients as
frequency band energies. We called the last
descriptor as LWE (Log wavelet decomposition
based energy).
Furthermore, this experiment allows extending
the last work presented in (Nait-Meziane, et al.,
2016) by using a larger spectral band of signal and
considering descriptors up to the maximal frequency
(Fs/2 = 15 kHz). Hence the STFS set is composed on
249 coefficients without taking the DC component
(0 Hz).
In (Gray and Morsi, 2015), the authors used the
DWT for the classification problem in NILM and
concluded that the order 5 Daubechies wavelet Db5
gave the best performance in this family. For this
reason, we firstly take the Db5 wavelet with
maximum wavelet decomposition level of =5 (the
maximum depth obtained regarding the wavelet
filter of Db5 and the number of samples =500,
using wmaxlev Matlab command). Thus, the DWE,
LWE and WCC descriptors have a dimension of 6
(energies in 5 levels, plus energy of approximation).
3.2.1 HMM Number of States (NS)
In this experiment, we search for the optimal states
number of models in different cases of descriptor.
The component number of GMM model is fixed to
three (Nait-Meziane, et al., 2016). Table 1 gives the
CR values with optimal number of states (NS
opt
)
when varying NS from 1 to 8. From these results we
can give the following points:
- enlarging the bandwidth from 50 to 249
harmonic features for the SFTS descriptor produces
lower CR results probably because of the peaking
phenomenon observed with high dimensionality
(Jain, Duin, and Mao, 2000);
- the SFTS gives the best CR with a reduced 50-
dimension feature vector with 4 HMM states;
- in the case of large bandwidth, the STFS and
WCC descriptors give the best CR of 93.48% with
respectively NS equal to 7 and 6. However the
WCC descriptor is a very compact representation
with a 6-dimension features vector compared to the
STFS descriptor with a large 249-dimension
features vector;
- taking only the wavelet energy as feature
without the log gives the poorest performances as
already noticed by (Gray and Morsi, 2015).
Hence, this result demonstrates the superiority of
the WCC descriptor to the other full band
descriptors regarding both CR and dimensionality.
Table 1: Performance Comparison of the CR (%) for
STFS, DWE, LWE and WCC features using DB5 at level
5 for the HMM Optimal Number of States (NS
OPT
).
STFS
(50
features)
STFS
(249
features)
DWE
LWE
WCC
NS
opt
4
7
8
5
6
CR
94.41
93.48
77.65
93.30
93.48
3.2.2 Duration Window
This experiment allows investigating performance
improvement taking into account the advantages of
wavelet analysis in the case of non stationary signal
segments compared to the STFS analysis. For this
reason, we propose to increase the window analysis
until 12 cycle time (200 ms). This experiment
considers the identification system with Db5 wavelet
and with a decomposition level equal to 5. Table 2
shows the accuracy for different values of window
duration. The result shows that increasing the
window duration until 8 cycles improves the CR
achieving the 97.01% maximal value. Hence, for the
next sections, we will consider window durations
equal to 8 cycle time.
3.2.3 Choice of the Mother Wavelet and
Decomposition Level
Many papers use the Haar wavelets which are rough
and cannot smoothly follow a continuous signal,
although this characteristic is beneficial when
studying signals with sharp transitions. By
considering successive convolution operations of the
Haar scaling function (a rectangular function) with
itself, many smoother wavelets can be obtained.
These are the famous Daubechies wavelets where
the number of convolutions defines the order of the
Daubechies wavelet. So the purpose of this section is
to evaluate the impact of the smoothness as well as
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
546

the impact of the wavelet family on the CR. Other
mother wavelet families which members are defined
by an order also exist and can be used.
This experiment will permit to select the optimal
wavelet mother within its family and the optimal
decomposition level. In this work, we consider the
following wavelet families:
- the Daubechies family with orders 1 to 8: Db1
or Haar, Db2, ... , Db8;
- the Coiflets family with orders 1 to 5: Coif1,
Coif2,..., Coif5;
- the Symlets family with orders 1 to 8: Sym1,
Sym2, ..., Sym8.
For the first experiment, we consider the HMM
identification system with 6 states and a window
duration of 8 cycle time, with 50% overlapping
between successive windows.
Table 3 shows that the higher CR value of
97.01% is achieved with the Daubechies wavelet of
order 5 with a decomposition level equal to 5. Table
4 presents the CR taking the same conditions as the
last experiment but increasing the overlapping to 2/3
of the window duration (66.66%). The results show
globally the improvement with last value of
overlapping. The Daubechies wavelet of order 4
with a decomposition level equal to 6 gives the best
performance with CR equal to 97.20%. This result
demonstrates that the Daubechies wavelets family
gives the best performance results in the case of high
orders and high decomposition levels (in particular
order 4, 5 and levels 6 and 7).
This latter experiment was also carried out using
the Coiflets and the Symlets wavelet families
previously cited. The Coiflets with order 2 with level
7 gives the best value of CR equal to 97.20%. Also,
the Symlets wavelet with order 4 and level 6 gives
the highest CR of 97.01% (table omitted).
We can conclude from these experiments that
WCC descriptor based on Daubechies or Symlets
wavelet families gives the highest performance
results in the case of high order (4) and high level
(6) values. In the case of Coiflets family, the best
result is given taking order 2 and level 7.
Hence, whatever the wavelet family or order, the
best performance results are obtained with high
decomposition levels.
3.2.4 Feature Selection using a Wrapper
Approach
In this experiment, we study the relevance of
different descriptors by selecting the most relevant
features explaining the appliances classes or types.
In this work, we applied the wrapper-based
sequential forward search (SFS) algorithm (Kohavi
and John, 1997). This algorithm adds sequentially at
each selection step the feature that gives the highest
CR. This algorithm has been used in (Hacine-
Gharbi, Petit, Ravier, and Nemo, 2015) (Nait
Meziane, et al., 2017).
We consider the LWE and WCC descriptors
taking into account the Daubechies wavelet of order
4 with level 6. Hence, 7 features are considered for
each descriptor. Table 5 displays the CR as a
function of the total number of selected features at
iteration. Also this figure gives the selected feature
number (Sel#) at iteration j. Several remarks can be
drawn from Table 5:
- the first selected feature in the case of LWE is
feature # 7 which corresponds to the
approximation spectral band;
- globally, the first four LWE features strongly
explain the classes. Most of these features
correspond to high decomposition levels (in
particular levels 6 and 5 and approximation
feature 7). Hence we can conclude that the most
information quantity about appliances is
localised in the low spectral bands and the higher
spectral band corresponding to level 2.
4 CONCLUSIONS
In this paper, a novel wavelet based feature
extraction approach has been presented for electrical
appliance identification. The first goal was to
investigate a larger spectral band analysis in STFS
feature extraction step applied on a previous
identification system based on HMM classifier and
evaluated on PLAID database. This system requires
a higher dimensionality of the STFS feature vector.
The second goal is to search a more compact
representation than the SFTS vector using wavelet
based approaches such as DWE and LWE proposed
in NILM domains. In this work, we have presented a
novel features extraction approach for NILM
domain that extracts features from the DCT of log
energies computed at each detail scale and at the
approximation level of the DWT. Through several
experiments and a comparison study, we can draw
the following conclusions:
- enlarging the bandwidth produces 249 features
without improving the CR obtained with 50
features probably because of the peaking
phenomenon observed with high dimensionality;
- the WCC descriptor with 8 cycle time analysis
windows presents higher performance results
Wavelet Cepstral Coefficients for Electrical Appliances Identification using Hidden Markov Models
547
compared to the STFS, DWE and LWE
descriptors;
- the Daubechies wavelet of order 4 and
decomposition depth 6 (or Coiflet wavelet with
order 2 and depth 7) is recommended in order to
achieve the better CR values.
ACKNOWLEDGMENT
This study was supported by the Région Centre-Val
de Loire (France) as part of the project MDE–MAC3
(Contract n° 2012 00073640).
Table 2: CR (%) obtained with respect to the duration of analysis window (expressed in number of cycles, one cycle is
16.67 MS long).
# cycles
WCC
93.48
94.41
94.97
95.71
95.34
96.46
95.15
97.01
96.46
96.46
96.27
96.46
Table 3: CR (%) obtained with respect to Order n of Daubechies mother wavelets and Decomposition level p. ovelapping
between segments equals 50%
p
DbN
1
2
3
4
5
6
7
8
9
10
11
Db1
78.73
80.41
85.26
85.82
87.87
86.57
86.38
69.78
70.15
69.22
64.74
Db2
73.88
85.26
91.42
91.60
93.47
94.96
92.72
80.78
78.92
78.54
Db3
73.13
88.43
90.11
94.59
96.08
96.08
94.03
84.51
82.09
Db4
72.57
89.74
89.37
93.66
95.52
95.90
95.15
87.31
86.57
Db5
71.46
89.74
89.93
93.84
97.01
95.90
94.40
86.57
Db6
70.34
89.74
89.93
93.10
94.59
95.52
96.27
87.50
Db7
68.84
89.18
90.30
92.16
95.15
94.96
94.96
85.82
Db8
68.47
89.37
90.30
91.79
95.71
95.15
94.78
89.55
Table 4: CR (%) obtained with respect to Order n of Daubechies mother wavelets and Decomposition level p. ovelapping
between segments equals 66%
p
DbN
1
2
3
4
5
6
7
8
9
10
11
Db1
82.09
81.16
86.75
87.50
90.67
88.62
89.18
80.78
78.36
78.73
77.43
Db2
75.19
87.50
92.72
91.79
95.34
96.46
96.46
87.500
88.06
88.06
Db3
73.69
89.18
93.10
94.59
95.15
95.52
95.34
91.04
88.81
Db4
72.77
90.11
90.49
91.79
96.46
97.20
96.27
93.28
90.86
Db5
71.64
90.11
92.16
93.10
94.96
96.64
96.83
94.96
Db6
72.20
89.37
90.30
93.28
96.27
94.96
96.46
93.28
Db7
71.08
89.18
89.93
94.03
95.15
96.46
96.64
93.47
Db8
69.59
88.81
90.49
91.79
95.15
96.27
96.83
95.34
Table 5: CR as a function of the number of selected features for descriptors: LWE and WCC; is the iteration number;
Sel#is the selected feature number, the lowest value represents the highest frequency band while the highest value
represents the lowest frequency band; CR is considered taking all the features selected at iteration.
LWE
Sel#
7
2
6
5
1
4
3
CR
55.60
85.63
92.72
94.4
94.78
95.34
94.96
WCC
Sel#
3
2
6
4
1
7
5
CR
58.77
82.65
91.98
94.78
96.64
96.46
97.20
ICPRAM 2018 - 7th International Conference on Pattern Recognition Applications and Methods
548

REFERENCES
Basu, K. (2014). Classifcation techniques for non-
intrusive load monitoring and prediction of residential
loads. Université de Grenoble: PhD Thesis.
Cristaldi, L., Monti, A., & Ponci, F. (2003). Three-phase
Load Signature: a wavelet-based approach to power
analysis. 6th International Workshop on Power
Definitions and Measurements under Non-Sinusoidal
Conditions. Milano.
Didiot, E., Illina, I., Fohr, D., & Mella, O. (2010). A
Wavelet-Based Parameterization for Speech/Music
Discrimination. Computer Speech & Language, 341-
357.
Duarte, C., Delmar, P., Goossen, K. W., Barner, K., &
Gomez-Luna, E. (2012). Non-Intrusive Load
Monitoring Based on Switching Voltage Transients
and Wavelet Transforms. Future of Instrumentation
International Workshop (FIIW). Gatlinburg, USA.
El-Zonkoly, A., & Desouki, H. (2011). Wavelet entropy
based algorithm for fault detection and classification
in FACTS compensated transmission line. Electrical
Power and Energy Systems, 1368-1374.
Figueiredo, M. B., de Almeida, A., & Ribeiro, B. (2011).
Wavelet Decomposition and Singular Spectrum
Analysis for Electrical Signal Denoising. IEEE
International Conference on Systems, Man, and
Cybernetics (SMC), (pp. 3329-3334). Anchorage,
USA.
Gao, J., Giri, S., Kara, E. C., & Bergès, M. (2014).
PLAID: A Public Dataset of High-resoultion Electrical
Appliance Measurements for Load Identification
Research: Demo Abstract. 1st Conference on
Embedded Systems for Energy-Efficient Buildings (pp.
198-199). Memphis, USA: ACM.
Gilis, J. M., Alshareef, S. M., & Morsi, W. (2016).
Nonintrusive Load Monitoring Using Wavelet Design
and Machine Learning. IEEE Transactions On Smart
Grid, 320-328.
Gillis, J. M., & Morsi, W. G. (2017). Non-Intrusive Load
Monitoring Using Semi-Supervised Machine Learning
and Wavelet Design. IEEE Transactions on Smart
Grid, 8.
Gladrene, S. B., Juliet, V., & Jayapriya, K. A. (2015).
Dual Tree Complex Wavelet Cepstral Coefficient–
based Bat Classification in Kalakad Mundanthurai
Tiger Reserve. International Journal of Computer
Science and Information Technologies, 3663-3671.
Gray, M., & Morsi, W. (2015). Application of Wavelet-
Based Classification in Non-Intrusive Load
Monitoring. IEEE 28th Canadian Conference on
Electrical and Computer Engineering, (pp. 41-45).
Halifax, Canada.
Hacine-Gharbi, A., Petit, M., Ravier, P., & Nemo, F.
(2015). Prosody Based Automatic Classification of the
Uses of French ‘oui’ as Convinced or Unconvinced
Uses. 4th International Conference on Pattern
Recognition Applications and Methods (ICPRAM).
Lisboa, Portugal.
Jain, A., Duin, R., & Mao, J. (2000, Jan). Statistical
pattern recognition: a review. (IEEE, Ed.) Trans.
Pattern Analysis and Machine Intelligence, 22,(1), 4-
37.
Kohavi, R., & John, G. H. (1997). Wrappers for feature
subset selection. Artificial intelligence, 273-324.
Kong, S., Kim, Y., Ko, R., & Joo, S. (2015). Home
appliance load disaggregation using cepstrum-
smoothing-based method. IEEE Trans. Consumer
Electron., 24-30.
Lei, L., & Kun, S. (2016). Speaker Recognition Using
Wavelet Cepstral Coefficient, I-Vector, and Cosine
Distance Scoring and Its Application for Forensics.
Journal of Electrical and Computer Engineering, 11.
Nait Meziane, M., Hacine-Gharbi, A., Ravier, P.,
Lamarque, G., Le Bunetel, J.-C., & Raingeaud, Y.
(2017). Electrical Appliances Identification and
Clustering using Novel Turn-on Transient Features.
6th International Conference on Pattern Recognition
Applications and Methods (ICPRAM), (pp. 647-652).
Porto, Portugal.
Naït Meziane, M., Ravier, P., Lamarque, G., Abed-
Meraim, K., Le Bunetel, J.-C., & Raingeaud, Y.
(2015). Modeling and estimation of transient current
signals. Signal Processing Conference (EUSIPCO),,
(pp. 2005-2009). Nice, France.
Nait-Meziane, M., Hacine-Gharbi, A., Ravier, P.,
Lamarque, G., Le Bunetel, J.-C., & Raingeaud, Y.
(2016). Electrical Appliances Identification using
HMM to Model Transient and Steady-state Current
Signals. 4th International Conference on Pattern
Recognition Applications and Methods (ICPRAM).
Rome, Italy.
Su, Y.-C., Lian, K.-L., & Chang, H.-H. (2011). Feature
Selection of Non-intrusive Load Monitoring System
using STFT and Wavelet Transform. 8th IEEE
International Conference on e-Business Engineering,
(pp. 293-298).
Tabatabaei, S. M., Dick, S., & Xu, W. (2017). Toward
Non-Intrusive Load Monitoring via Multi-Label
Classification. IEEE Transactions on Smart Grid, 26-
40.
Young, S., Kershaw, D., Odell, J., & Ollason, D. (1999).
The HTK Book. Cambridge: Entropic Ltd.
Wavelet Cepstral Coefficients for Electrical Appliances Identification using Hidden Markov Models
549
